2. Navigation collage, Jimei University, Xiamen 361021, China
熟练而正确地使用雷达是航海人员的必备技能,国际海事组织(international maritime organization,IMO)制定的STCW公约[1]规定,必须经过雷达使用方面的特殊训练才能取得适任证书。和真雷达相比,雷达模拟器能够根据训练需要模拟不同港口、不同天气和海况条件下的雷达回波图像,能够实时加入其他运动物标,因此在雷达使用培训中主要使用雷达模拟器而不是真雷达进行训练。电子工程类专业人员设计的雷达模拟器[2-4]主要服务于雷达设计制造过程中的测试、评估等,并不适用于训练目的,用于训练目的的雷达模拟器要求雷达回波图像具有高真实感。
国内能够提供航海模拟器的主要是几家航海院校,主要采用由电子海图或其他数据源抽取地物的岸线形状数据并与扫描线求交的方式生成雷达图像[5-6],这种二维数据模型由于不包含详细的物标高程信息(仅表示岸线的线段有高程信息,而陆地内部的高程信息全部忽略),很难提供精确的算法进行物标间或物标不同部位间遮挡关系的判断,陆地内部的回波仅以根据岸线平均高度、反射特性等属性生成的一定长度的射线来表示或完全填充。这显然与真实雷达回波有较大差距。改进的方案是用等高线[7-8]或高度图实现[9],等高线法需要进行求交计算,计算效率不高,且容易出现长条状的回波,高度图法实现精确的遮挡判断须逐点计算斜率,难以满足实时性要求。
三维图形在表示物体的空间关系方面具有明显优势,作者所在的团队开始了由三维模型视景图形生成雷达图像的研究。雷达电磁波与光线相似,射线跟踪算法可用于生成雷达回波,但射线跟踪算法随场景复杂度的增加计算量显著增大,此种方法面临的主要问题是如何进行快速求交计算[10]。文献[11]提出了通过三维绘制技术生成雷达图像的基本方法,但在计算雷达探测距离、坐标转换等方面仍需要完善,尤其是透视投影foreshortening现象对雷达回波质量会产生较为严重的影响,需要重点加以研究解决。另外,雷达电磁波的传播特性、反射特性与光线存在一些较为明显的差别,并不能用从颜色转换而来的灰度值代替雷达回波强度。针对雷达探测距离计算、坐标变换中的死点和盲点现象以及透视投影foreshortening现象对雷达回波图像生成的影响做深入研究。
1 计算雷达探测距离建立航海场景的三维模型并渲染至帧缓存,则生成的视景图形中每个像素都包含有对象的深度信息,若能将深度信息转化为雷达探测距离,像素就可看作是场景中物标的距离采样,若按雷达波束特性来设置视见体的各项参数,那么生成的视景图形内所有像素就可看作是雷达波束范围内物标的距离采样集合,把集合中的每个像素按雷达探测距离映射到扫描线的相应位置就能形成一条雷达径向扫描线,按圆周方位动态设置视见体的朝向,生成一系列按圆周方位排列的扫描线并映射到屏幕上就可以实现雷达的圆周扫描。
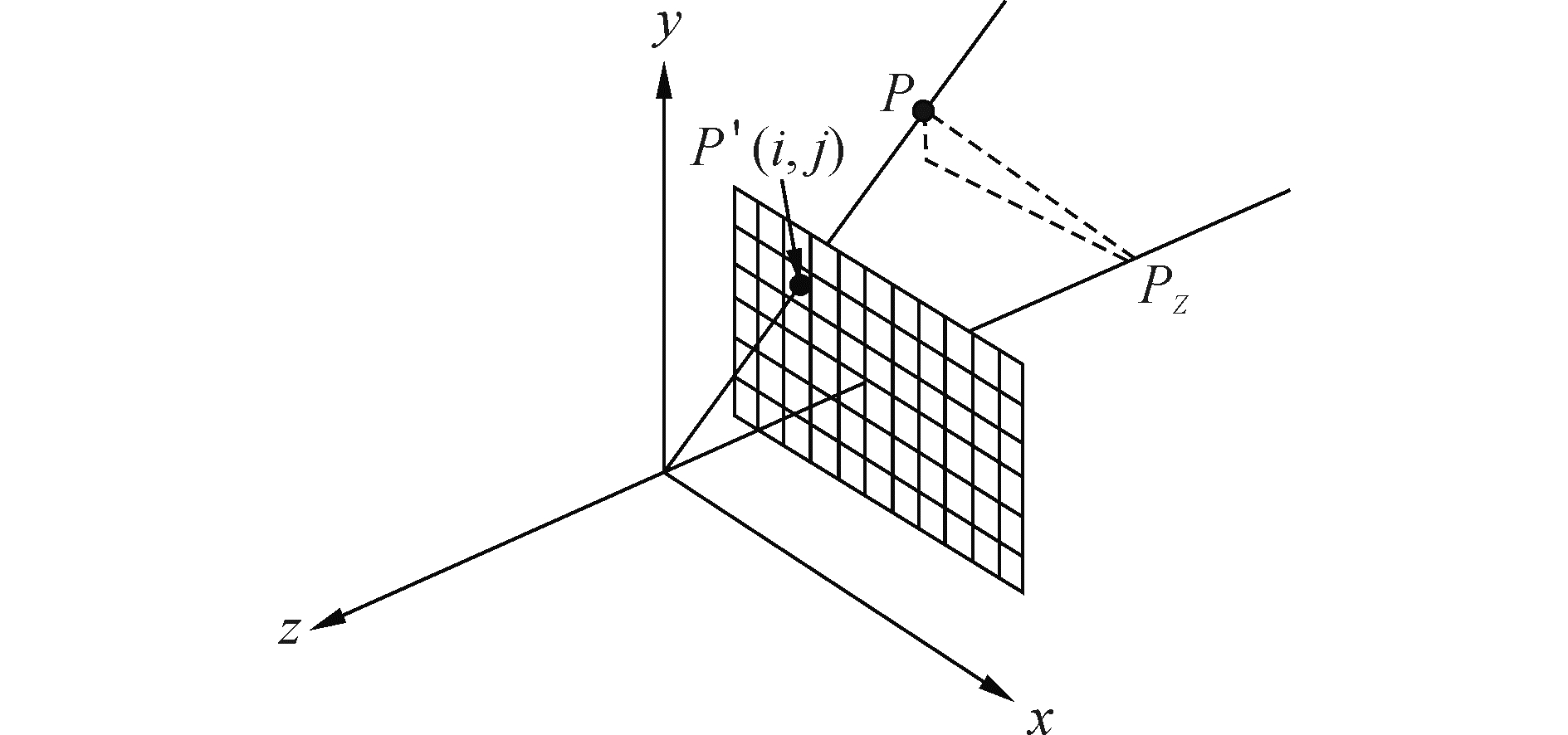
如图 1所示,若在视坐标系中有一点P,坐标为(xe,ye,ze),则点P到视点O的距离即雷达探测距离d应为
| $ d = \sqrt {x_{\text{e}}^2 + y_{\text{e}}^2 + z_{\text{e}}^2} $ | (1) |
|
| 图1 视坐标系下的雷达探测距离 Figure 1 Radar range in the camera space |
在顶点着色器中,可以得到顶点的世界坐标Vworld和模型视变换矩阵Mv、投影矩阵P,先将顶点由世界坐标系变换到视坐标系:
| $ {V_{eye}} = \boldsymbol{M}{V_{{\text{world}}}} $ | (2) |
然后利用式(1) 计算雷达探测距离d并作为输出变量传递给片元着色器。值得注意的是,此处得到的d是三维模型中某个顶点的雷达探测距离,之后OpenGL还要进行图元装配和光栅化,而片元着色器得到的是经光栅化阶段插值的雷达探测距离d。变量d的声明形式不同,光栅化阶段的插值方式也不同,为保证片元处理器得到正确的雷达探测距离,变量d声明时应使用noperspective关键字进行限定[12]。最后进行投影变换并把投影变换后的顶点坐标(xp, yp,zp,w)赋值给顶点着色器内置变量gl_Position以保证场景按照透视投影方式进行处理。
在片元着色器中,获取雷达探测距离d后,通过深度缓存传递给雷达模拟主程序。雷达探测距离d是一个比较大的值,而深度缓存位于[0.0,1.0]范围内,考虑到后续环节会把雷达探测距离映射到雷达量程范围内,可以设置一个Uniform变量,将当前的雷达量程R传入片元着色器,令:
| $ d' = d/R $ | (3) |
将d′写入缓存,雷达模拟主程序读取缓存即可获取采样点(像素)的雷达探测距离。
2 生成径向扫描线IMO 2004年12月6日通过经修订的雷达设备性能标准[13](下文简称雷达性能标准)要求雷达的距离精度“在30 m或所用量程1%的较大者之内”,根据这一规定,单条扫描线只要由100个(含)以上的点组成即可满足标准。设雷达的方位采样精度为δB,那么完成圆周扫描需要生成的扫描线数量S为
| $ S = 360/{\delta _{\text{B}}} $ | (4) |
可建立一个二维数组用以容纳生成的扫描线,由于本文使用纹理映射方式进行坐标变换,因此建立一个S×T的纹理,纹理图像的一列作为一条扫描线,为便于区分,本文将纹理图像中保存的扫描线称为纹理空间扫描线。第一条纹理空间扫描线的真方位为000°,第i(i∈[0,S-1])条纹理扫描线对应的真方位为
| $ {B_i} = {\delta _{\text{B}}}i $ | (5) |
纹理图像的高度T根据雷达距离精度确定,由于当前雷达显示器尺寸与制定标准时相比明显增大,根据仿真试验,T≥200才能获得质量较好的雷达回波图像。
理想的生成扫描线方法是将视见体的垂直视场角设置为天线的垂直波束宽度,水平视场角为天线的水平波束宽度,视口宽度设置为一个像素,生成的只有一列像素的视景图形包含了波束范围内物标的距离信息,读取每个像素的距离信息并映射到扫描线的对应位置,就可形成一条与雷达波束特征吻合的径向扫描线。但天线旋转周期约2~4 s,在一个周期内生成完整的覆盖360°范围的雷达回波图像至少需要1 000条左右的扫描线,这就要求生成单条扫描线的绘制和计算工作在1~2 ms内完成,显然是不现实的。故此需要将水平视场角扩大,一次生成多条扫描线。
选取一个合适的水平视场角θh(如10°),从真北起第m次绘制的视方向指定为真方位:
| $ {B_{{\text{center}}}} = m{\theta _{\text{h}}}- \frac{{{\delta _{\text{B}}}}}{2} + \frac{{{\theta _{\text{h}}}}}{2}{\text{, }}m \in \left[{0, \frac{{360}}{{{\theta _{\text{h}}}}}-1} \right] $ | (6) |
将视口宽度X设为(视口高度Y的取值见后文):
| $ X = S\frac{{{\theta _{\text{h}}}}}{{360}} = \frac{{{\theta _{\text{h}}}}}{{{\delta _{\text{B}}}}} $ | (7) |
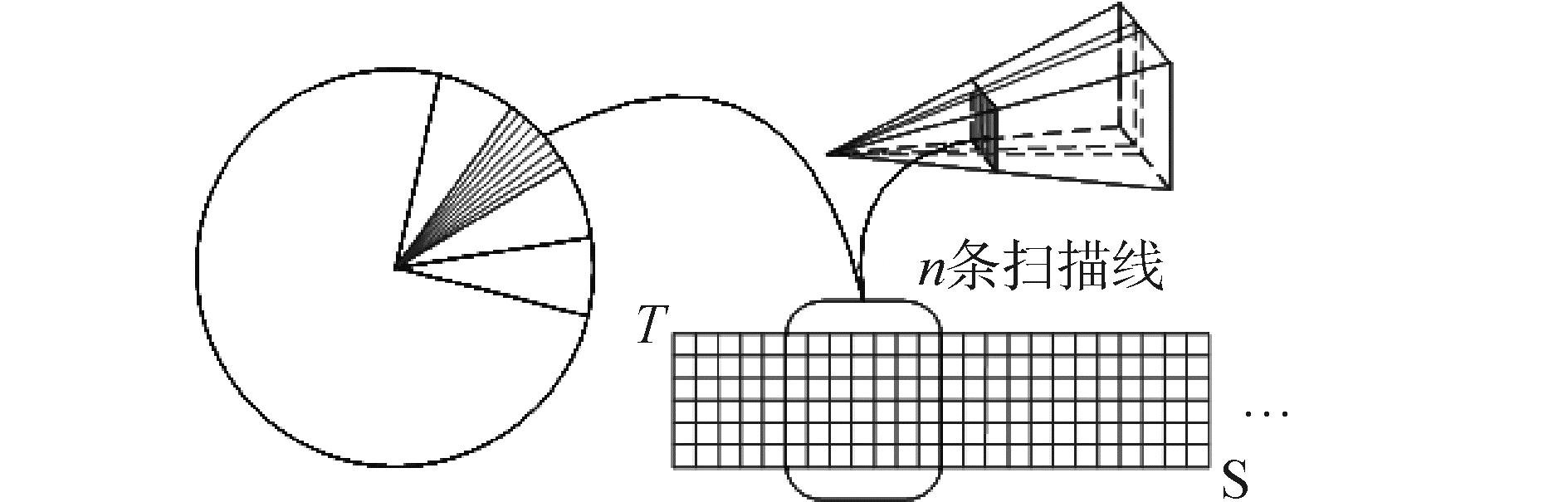
那么每一列像素对应于视见体中视场角(近似)为δB的一小片纵向视见体如图 2所示,可用以生成一条单独的扫描线,一次绘制共可生成X条扫描线,每条扫描线方位间隔(近似)为δB。
|
| 图2 生成多条扫描线 Figure 2 Generating a number of scanning lines per rendering |
对于第m次绘制生成的第n条扫描线,其在纹理图像中的位置i为
| $ i = mX + n, \;\;n \in \left[{0, X-1} \right] $ | (8) |
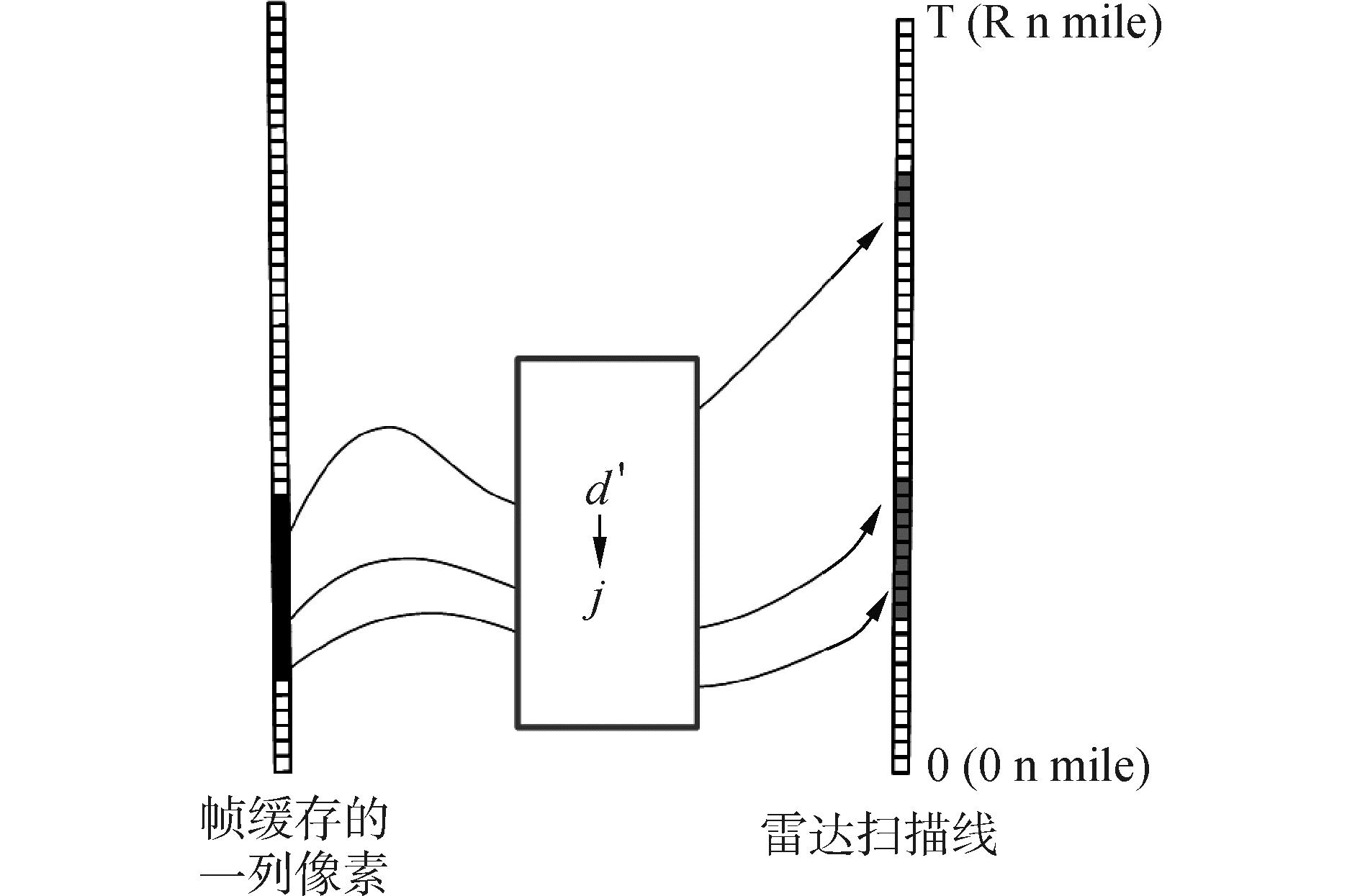
如图 3所示,单条扫描线生成的过程如下:
|
| 图3 单条扫描线生成 Figure 3 The generation of single scanning line |
1) 将该条扫描线上所有的点颜色置为雷达背景色;
2) 对于帧缓存一列像素的每一点,读取深度缓存,得到该像素对应的深度值d′;
3) 若d′≥1.0,说明像素区域内没有物标,直接丢弃,若d′<1.0,令:
| $ j = d'T $ | (9) |
将j取整并把扫描线第j个点设置为回波颜色。
因此,纹理图像保存了圆周扫描所需的全部纹理扫描线,且随着视点和视见体朝向的变化不断更新。
3 极坐标到平面直角坐标的转换扫描线生成以后,还要将扫描线上各点按其方位和距离绘制到屏幕上形成雷达回波图像。扫描线可看作极坐标系下的点集,可按照极坐标与平面直角坐标的关系进行转换:
| $ \left\{ {\begin{array}{*{20}{c}} {x = r\sin \theta } \\ {y = r\cos \theta } \end{array}} \right. $ | (10) |
式中:r为回波点与原点的屏幕距离,θ为扫描线的方位(从真北起算,顺时针度量)。
真雷达的坐标转换一般通过硬件实现[14],效率较高。但雷达模拟程序没有专门的硬件,一般通过软件实现,由于需要转换的坐标数量很大,可使用查找表法[15-16]提高计算速度,即事先将需要转换的极坐标点进行预计算并将平面直角坐标结果存储在一个数组中,生成扫描线后直接在数组中查找相应的平面直角坐标,可快速完成坐标转换。
扫描转换过程当中比较容易出现的问题是死点和盲点现象。盲点是指在原点附近多个极坐标变换到同一个直角坐标中,该坐标数据不停变化,导致该点不断闪烁;死点是回波图像边缘部分直角坐标不能通过极坐标变换而访问,回波图像边缘出现蝶形分布的黑点(图 4)。常用的消除死点方法有死点偏移访问法、增加方位分辨率法和死点循环覆盖法[17]。

|
| 图4 雷达图像中的死点 Figure 4 Dead points in radar echo image |
本文采用纹理映射方法进行坐标转换,一方面坐标转换可获得显卡硬件加速,另一方面可以很好地解决死点问题。
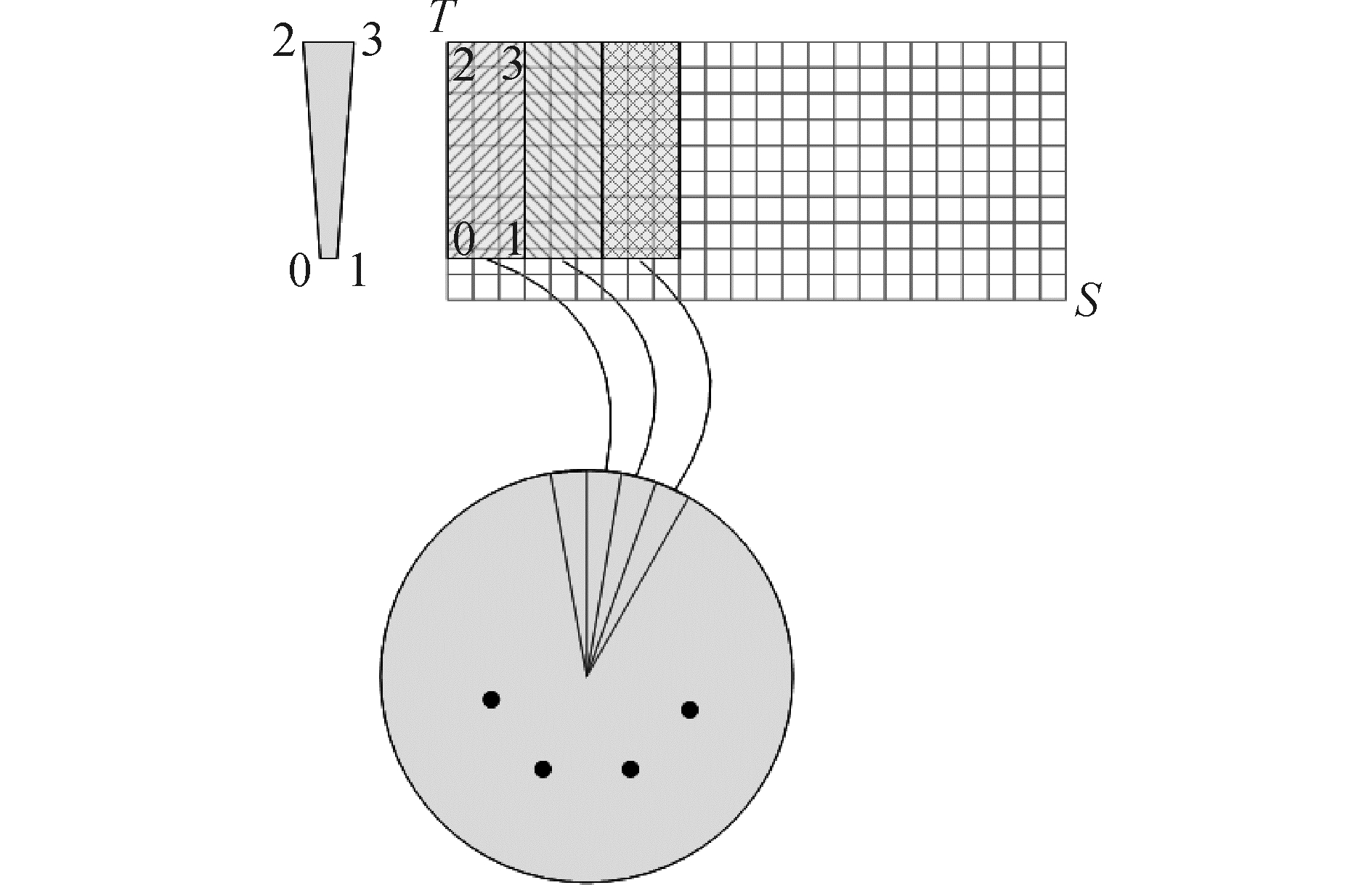
生成扫描线时已经将扫描线保存在S×T的纹理图像中,只要将扫描线从纹理空间映射到屏幕空间即可实现回波从极坐标到平面直角坐标的转换进而生成动态更新的完整雷达图像。如图 5所示,把雷达回波圆形显示区域分为若干小扇形区域,扇形的数量根据显示器的尺寸确定。因雷达最小作用距离内不会产生雷达回波,故可用等腰梯形来代替小扇形。对于每个扇形,假设对应的圆心角φ°,雷达显示区域半径为Recho,最小作用距离为Rmin,对于第i个梯形,令其四个顶点的坐标分别为
| $ \left\{ {\begin{array}{*{20}{c}} {\left( {{R_{{\text{min}}}}{\text{cos}}\left( {\varphi i} \right), {R_{{\text{min}}}}{\text{sin}}\left( {\varphi i} \right)} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;} \\ {({R_{{\text{min}}}}{\text{cos}}\left( {\varphi \left( {i + 1} \right)} \right), {R_{{\text{min}}}}{\text{sin}}\left( {\varphi \left( {i + 1} \right)} \right)} \\ {({R_{{\text{echo}}}}{\text{cos}}\left( {\varphi \left( {i + 1} \right)} \right), {R_{{\text{echo}}}}{\text{sin}}\left( {\varphi \left( {i + 1} \right)} \right)} \\ {({R_{{\text{echo}}}}{\text{cos}}\left( {\varphi i} \right), {R_{{\text{echo}}}}{\text{sin}}\left( {\varphi i} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \end{array}} \right. $ | (11) |
|
| 图5 纹理映射坐标变换换示意图 Figure 5 Coordinate transformation by texture map |
相应地,第i个梯形的四个顶点对应的纹理坐标分别为
| $ \left\{ {\begin{array}{*{20}{c}} {\left( {\left( {\varphi /360} \right)i, {R_{{\text{min}}}}/{R_{{\text{echo}}}}} \right)\;\;\;\;\;\;\;\;} \\ {\left( {\left( {\varphi /360} \right)\left( {i + 1} \right), {R_{{\text{min}}}}/{R_{{\text{echo}}}}} \right)} \\ {\left( {\left( {\varphi /360} \right)\left( {i + 1} \right), {R_{{\text{echo}}}}} \right)\;\;\;\;\;\;\;} \\ {\left( {\left( {\varphi /360} \right)i, {R_{{\text{echo}}}}} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;} \end{array}} \right. $ | (12) |
即顶点0指定对应的纹理扫描线区域的左下角点,顶点1对应右下角点,顶点2对应右上角点,顶点3对应左上角点。显然,这里的很多计算是可以离线预计算的,不会对仿真主程序的运行速度造成影响。根据纹理映射特性,所有扫描线都按正确的方位转换到了雷达图像的相应位置,形成了完整的雷达图像。
纹理映射方式扫描转换的优点是显而易见的。根据纹理映射的特性,映射到屏幕边缘的纹理图像会被拉伸,这样即使扫描线数量不足也不会发生死点现象,而靠近扫描中心的网格会被压缩,扫描中心附近的像素是多条扫描线合并的结果,而不是被重复绘制多次,不会发生盲点现象。纹理映射扫描转换的特性与雷达的扫描方式契合度非常高,不仅适用于雷达图像仿真程序,对软件化雷达的坐标转换也有参考价值。另外,这种方式的坐标变换将扫描线存储在纹理空间,在映射到屏幕上时可以有多种不同的组合方式,前文介绍的为最简单的一种,下面介绍一种能逼真地仿真雷达水平波束宽度的映射方式。
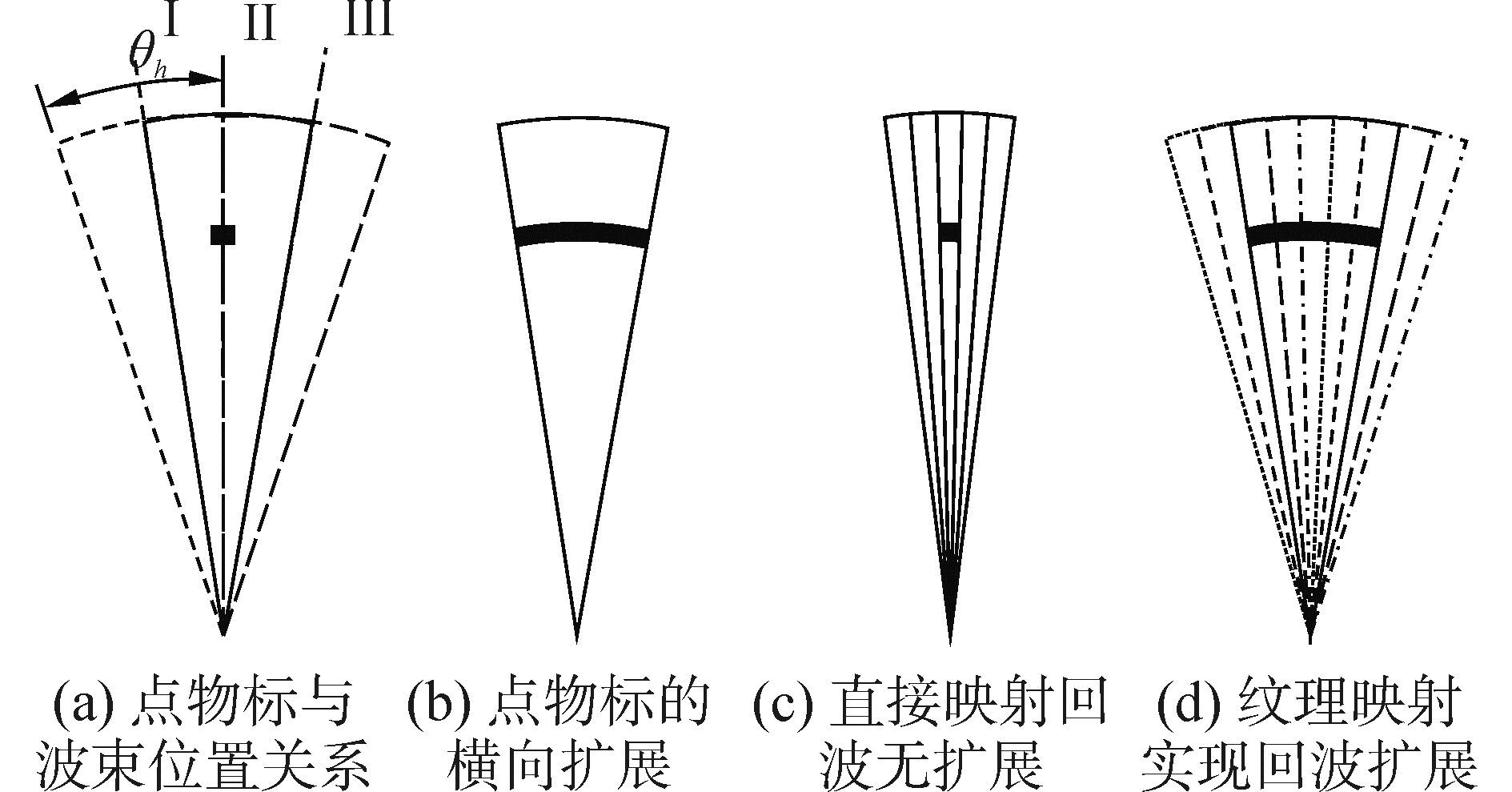
如图 6(a)所示,对于点物标(忽略物标大小),由于水平波束有一定的宽度,当雷达波束中心位于位置Ⅰ时物标已位于波束内,雷达屏幕上出现回波,波束继续旋转至位置Ⅱ直至位置Ⅲ,雷达一直能够探测到此物标,物标在雷达屏幕上的回波不再是一个点而是向两侧各扩展约θh/2,形成类似图 6(b)所示的图像。本文纹理空间扫描线的方位采样率较真雷达方位精度高,若直接将纹理扫描线映射到屏幕上,如图 6(c)回波不会向两侧扩展,模拟图像与真雷达相比显得“过于单薄”。以往的航海雷达图像仿真方法都是直接进行坐标变换,为了避免出现过多的死点,扫描线的精度也比较高,情形与图 6(c)类似。为达到图 6(b)的扩展效果,令梯形对应的圆心角φ与θh相等,每次只映射一条扫描线,这样每条扫描线都在横向(与扫描线垂直的方向)被拉伸至水平波束宽度,将三角形在圆心处的角设为水平波束宽度θh,图 6(c)的图像变为图 6(d)的情形,扩展幅度与真雷达一致。但图 6(d)中由于每条扫描线都被扩展,扫描线间相互重叠,需要把纹理空间扫描线上无回波的点设置为透明并开启融合功能,使被遮挡的扫描线不被其他扫描线遮蔽而能显示在屏幕上,这样就实现了图 6(b)所示的回波方位扩展效果。由于雷达水平波束宽度不大,上述方法用三角形代替扇形带来的距离误差也不会太大(若实际雷达的水平波束宽度较宽可为每条扫描线生成多个三角形)。总体来看,使用纹理映射方式进行坐标变换,可在不必进行大量计算的前提下仿真由于雷达水平波束具有一定宽度形成的回波扩展效果。
|
| 图6 利用纹理映射仿真水平波束宽度 Figure 6 Texture mapping method for simulating the horizontal beam width |
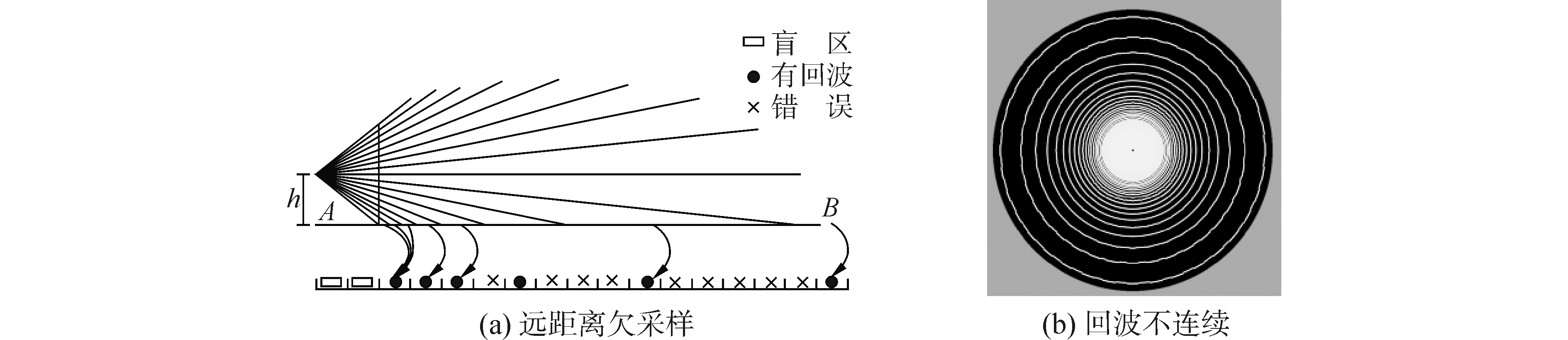
透视投影foreshortening现象决定了同样大小的物体在视景图形中位于近处时覆盖的像素较多,而位于远处时覆盖的像素较少,也就是说,对于一个像素,在帧缓存中读取的雷达探测距离越大表明像素对应的实地面积(应该)越大;反之,读取的雷达探测距离越小表明像素对应的实地面积越小,一个像素代表的实地面积呈现远大近小的现象。像素是雷达探测距离的采样点,这意味着对距离的采样是不均匀的,远大近小。与透视投影不同,雷达对场景内物标的距离采样是均匀的,并不会出现远大近小的现象,因此,作为距离采样点的像素与扫描线上的点并非一一对应的关系。如图 7(a)所示,AB是水平面,雷达天线高度为h,近处一个像素代表的实地距离较小,多个像素的深度值映射到雷达扫描线上的同一点,造成过采样,而在远处,一个像素代表的实地距离已相当长,而在生成扫描线时,仅将其视为一个独立的距离采样点而映射为雷达扫描线上的一个点,扫描线上大量的点未被覆盖,造成欠采样,其结果是本应具有连续回波的扫描线中断了,且距离越远断点之间的距离越长。水平面形成的雷达回波图像如图 7(b)所示,本应布满屏幕的回波,在圆心附近的小区域内还算正常,外围却变成了一个个同心圆环。
|
| 图7 水平面形成的雷达扫描线和回波 Figure 7 The scanning line and the echo image generated from a horizontal plane |
出现上述现象的前提是物标足够大,其在近平面上的投影可以覆盖整个像素区域。若物标较小,其投影不足以覆盖整个像素区域,且有几个小物标同时处于像素对应实地区域内,那么经深度测试就只有最近的物标被保留下来,其他物标则被丢弃,若被丢弃的物标事实上并没有被遮挡就将造成物标丢失。
综上所述,透视投影对生成雷达回波图像的不利影响主要体现在远处雷达数据采样率不足上,其造成的结果,一是远处大形物标回波不连续,二是远处邻近小物标易丢失。
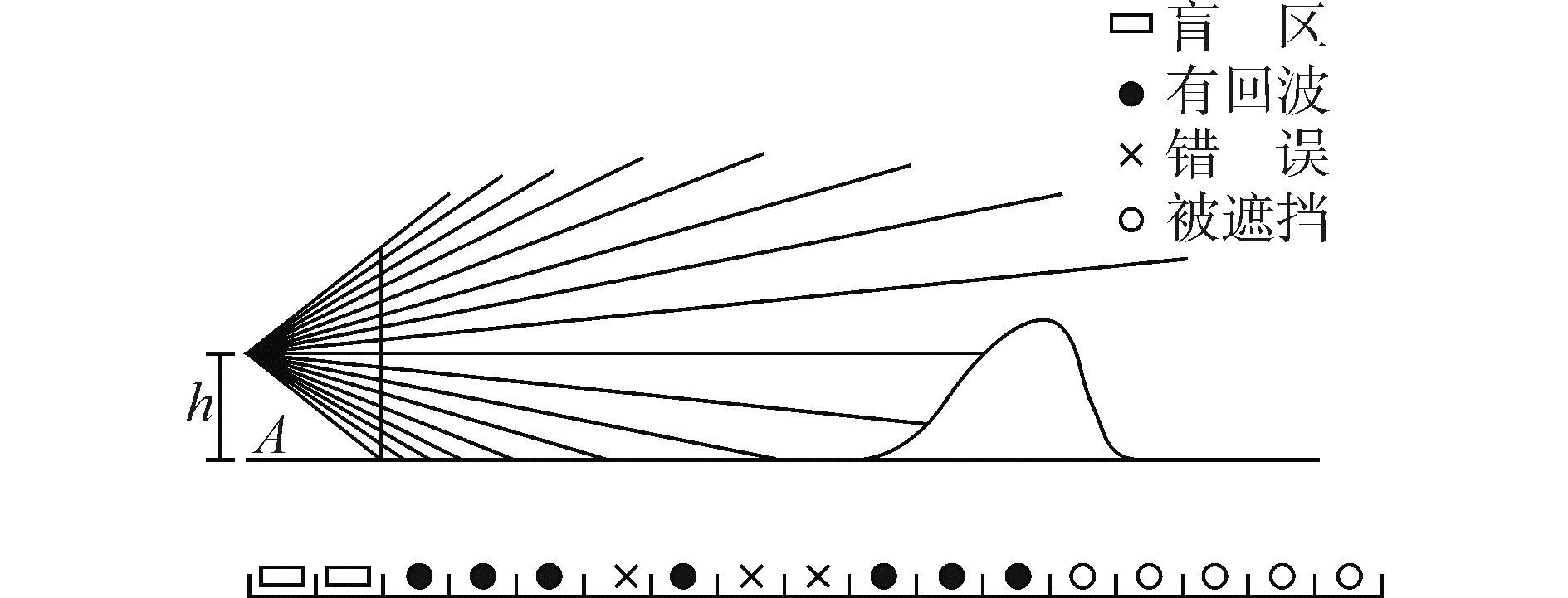
4.2 雷达探测距离采样率雷达物标不是简单的平面,雷达探测距离采样率也不仅仅受到距离的影响。如图 8所示,远处有一隆起的小岛,虽然距离也较远,但其占据的像素却较多,距离采样率较高,小岛的回波不会出现中断现象。研究表明,雷达探测距离采样率除了受物标距离的影响,还受物标高度、倾角、以及视见体参数设置等诸多因素的影响,深入研究发现,物标倾角对距离采样率的影响非常大,以下将对此作深入分析。
|
| 图8 有坡度的岛屿形成的雷达扫描线 Figure 8 The scanning line generated from the slope of island |
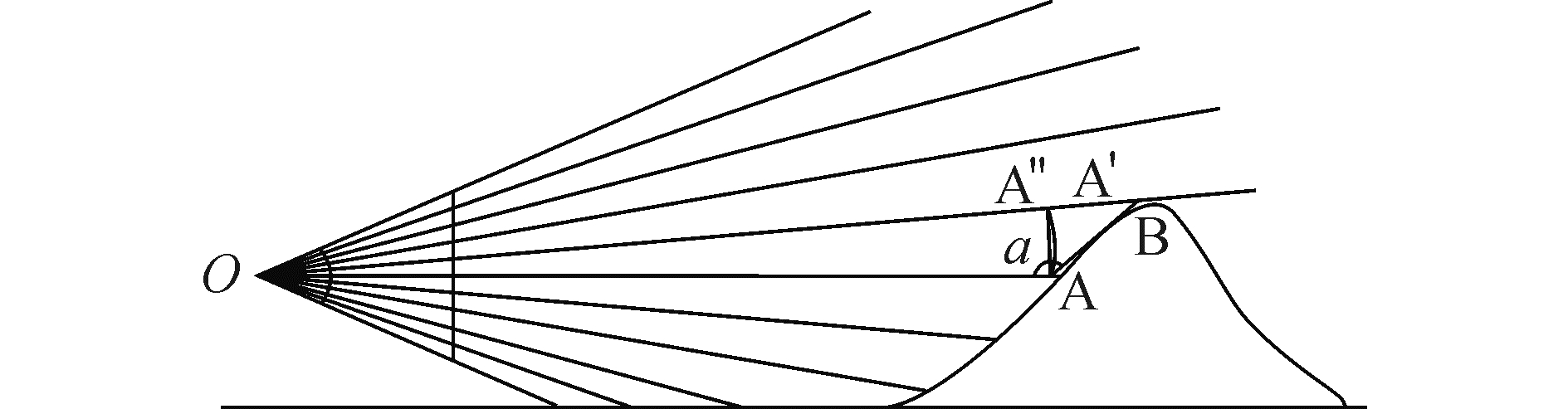
如图 9所示,O点为视点,AB为光栅化后任意一个经深度测试被保留下来的片元。AB可能是陆地、岛屿、礁石等地形的表面,也可能是航标、船舶、低空飞行器等人工或运动物标,片元在视见体中的位置由物标与雷达天线的相对位置决定。OA和OB分别为某一像素的边界与视点O的连线,也可将其视为雷达电磁波射线,简称射线。假设该片元足够大而占据了整个像素区域,那么雷达在探测AB片元时得到径向长度应为A点和B点到天线的距离差:
| $ {l_{{\text{ray}}}} = OB-OA $ | (13) |
|
| 图9 雷达探测距离采样率 Figure 9 The sampling rate of radar range data |
以原点O为圆心过A作圆弧交OB于A′,则:
| $ {l_{{\text{ray}}}} = A'B $ | (14) |
设垂直视场角为θv,近裁剪面的距离为Znear,生成的视景图形为X×Y个像素(生成视景图形的横向分辨率为X纵向分辨率为Y),单个像素在视点O处对应的角∠AOB近似为(忽略每个像素对应的垂直视场角变化):
| $ \angle AOB = {\theta _{\text{v}}}/Y $ | (15) |
鉴于该角非常小(如θv为20°,Y为800像素),过A作OB的垂线交OB于A″,以A″B代替A′B,设A点到视点O的距离为d,AB与射线OA的夹角为α,则:
| $ {l_{{\text{ray}}}} = A'B \approx A''B = AA''/{\rm{tan}}\left( {\angle ABA''} \right) $ | (16) |
| $ \because \angle ABA'' = {\text{π}}-\alpha-{\theta _{\text{v}}}/Y \approx {\text{π}}-\alpha $ | (17) |
| $ AA'' \approx AA' \approx d\left( {{\theta _{\text{v}}}/Y} \right) $ | (18) |
| $ \therefore {l_{{\text{ray}}}} \approx d\left( {{\theta _{\text{v}}}/Y} \right)\cot \left( {{\text{π}}-\alpha } \right) =-d\left( {{\theta _{\text{v}}}/Y} \right)\cot \alpha $ | (19) |
接下来片元的径向长度被映射到纹理扫描线上,设雷达回波图像的量程为R,扫描线纹理高度为T,那么扫描线上单个点代表的实地长度为
| $ {u_{{\text{scanline}}}} = R/T $ | (20) |
将其称为纹理扫描线单位长度,令:
| $ \begin{gathered} k = {l_{{\text{ray}}}}/{u_{{\text{scanline}}}} =-\frac{{d\left( {{\theta _{\text{v}}}/Y} \right)\cot \alpha }}{{R/T}} \hfill \\ =-\left( {d/R} \right)\left( {T/Y} \right){\theta _{\text{v}}}\cot \alpha \hfill \\ \end{gathered} $ | (21) |
那么:
1)k=1,片元径向长度等于纹理扫描线单位长度,一个像素刚好映射到纹理扫描线上的一个点,不会产生扫描线中断现象;
2)k < 1,片元径向长度小于纹理扫描线单位长度,多个像素将映射到纹理扫描线的同一点,即过采样,不会产生回波中断现象,但扫描线上的点被多次写入;
3)k>1,片元径向长度大于纹理扫描线单位长度,一个像素对应纹理扫描线上的多个点,即欠采样,若该像素只映射为扫描线上的一个点,将产生回波中断现象。
k值较好地反映了片元径向长度和纹理扫描线单位长度的关系,可用于判断雷达探测距离采样是否满足生成纹理扫描线的需要,因此,将k定义为雷达探测距离采样率。
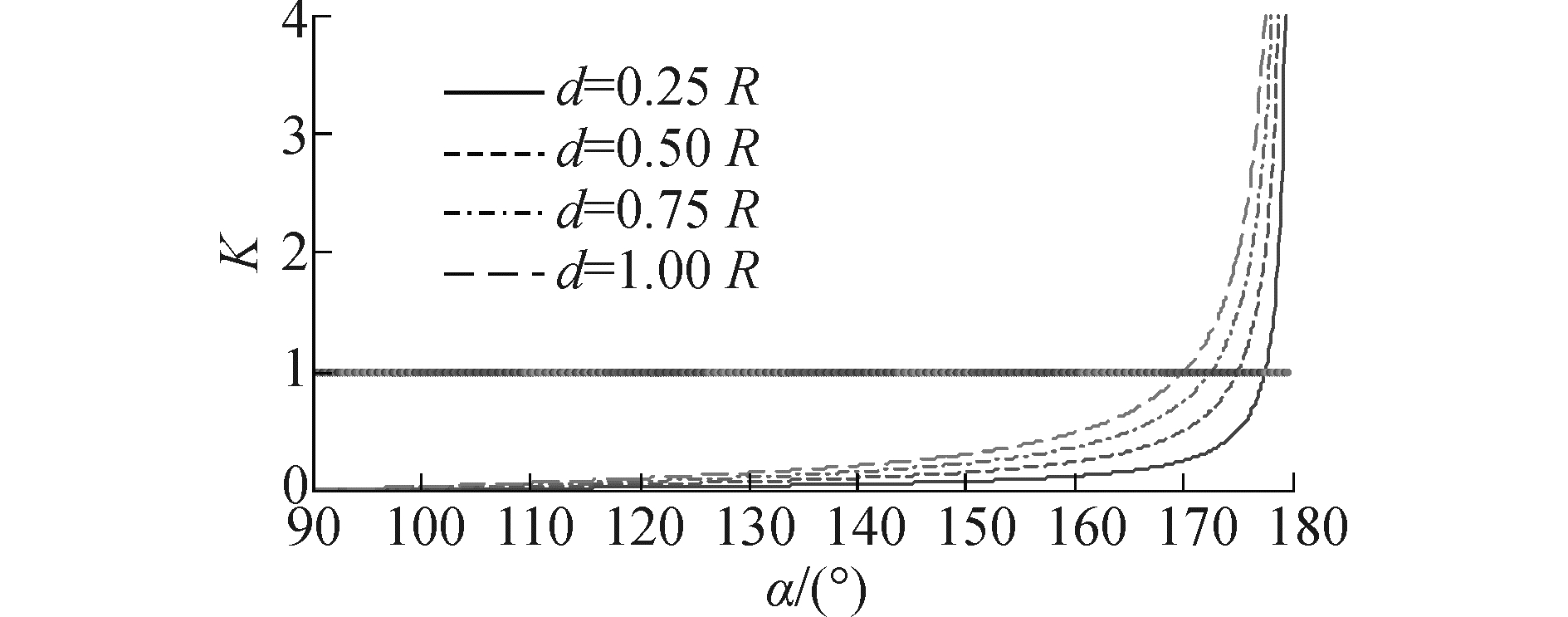
在特定的雷达模拟程序中,垂直视场角θv应根据实际雷达参数进行设置,可视为常量,扫描线纹理高度T和三维视景图形的高度Y受到计算效率和硬件设备性能的影响,设置值也是相对固定的,因此,雷达探测距离采样率k主要受物标与视点的距离d和物标与射线的交角α的影响。图 10是雷达探测距离采样率曲线图,从图中可看出:
|
| 图10 雷达探测距离采样率曲线图 Figure 10 The curves of sampling rate of radar range data 图中Y:800 T:400 θv:20° |
1) 生成的雷达回波图像越接近屏幕中心雷达探测距离采样率越好,越接近屏幕边缘(接近量程R处)雷达探测距离采样率越差;
2) 物标与射线的交角α较小时,雷达采样率的变化不大,大体上随着距离的增加而增加,但若α较大,尤其是大于170°时,雷达探测距离采样率迅速恶化,交角越接近180°恶化越严重,交角α对雷达探测距离采样率的影响要远大于距离对雷达探测距离采样率的影响。
4.3 远距离处雷达探测距离采样率过低问题的缓解措施Foreshortening现象一定程度上影响了雷达图像质量,现根据前文的分析结果以及雷达物标的实际情况作进一步分析并提出一些缓解措施。
1) 直接提高雷达探测距离采样率。
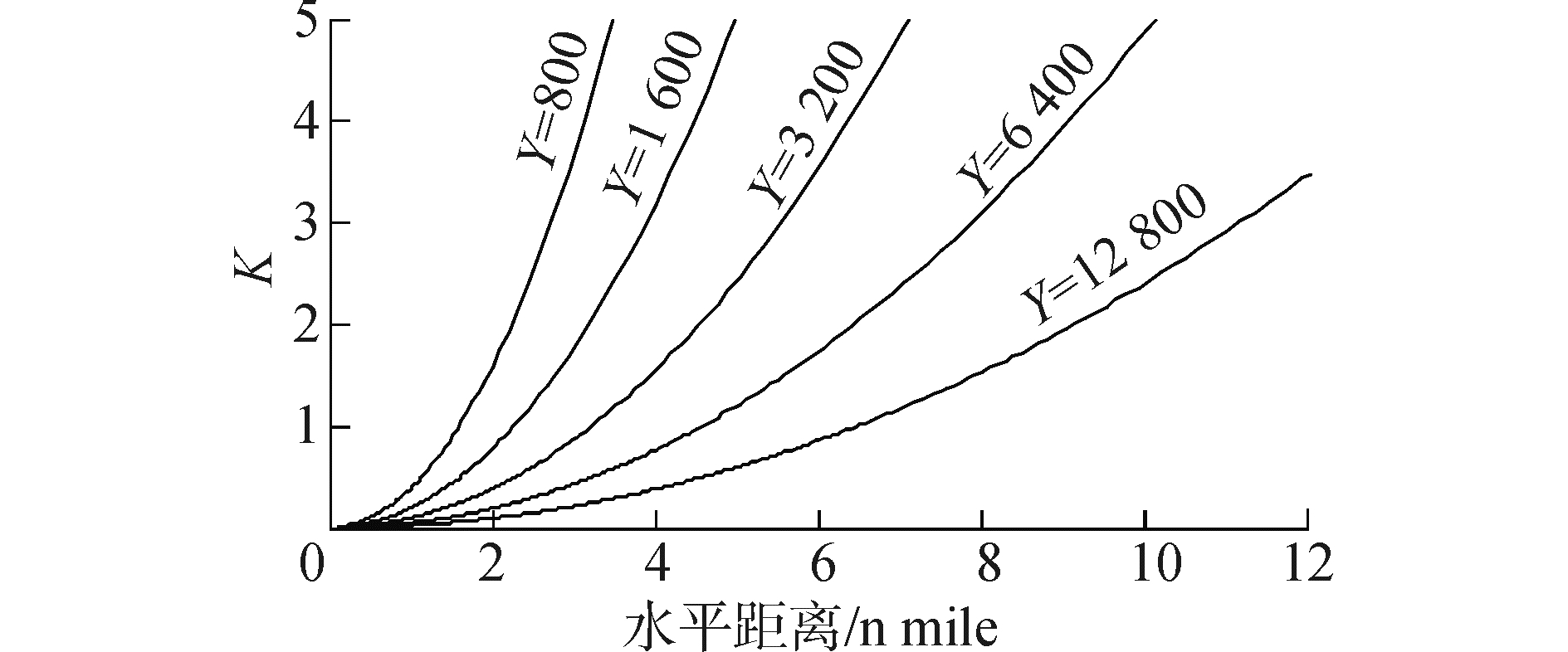
式(21) 中量程R、物标与天线的距离d和天线垂直波束宽度θv均相对固定,T应根据雷达距离精度进行设置。在离屏渲染模式下,视景图形纵向分辨率Y是可以改变的,Y与k成反比例关系,Y越大雷达探测距离采样率越好。增加视景图形的纵向分辨率Y是改善距离采样率的最直接方法。对于水平面,当T取200、θv取20°时雷达探测距离采样率k的曲线如图 11所示,可见,随着Y值的增加雷达探测距离采样率k越来越小。
|
| 图11 不同Y值下水平距离与雷达探测距离采样率的关系 Figure 11 The relationship of the horizontal distance and the sampling rate of radar range in different Y |
直接提高雷达探测距离采样率对回波中断现象和小物标易丢失现象都有明显改善,但上述方法也存在不足,一是受图形硬件性能的制约,Y值的设置受到限制,二是随着Y值的增加计算量也会增大。因此,该方法可明显提高图像质量但在目前硬件条件下尚不能完全解决问题。
2) 合理建模。
根据前文的分析,物标与射线的交角对雷达探测距离采样率影响显著,因此,对物标合理建模也可在很大程度上避免雷达探测距离采样率过低带来的问题。
航海人员对不同的雷达物标关注程度是不同的,对那些航海人员不是很关心的物标可在建模阶段进行修改以改善仿真效果,下面就航海人员感兴趣的几类物标分别进行分析:
① 自然地貌。起伏的陆地、沙滩、陡峭海岸、岛屿、礁石等都具有一定的高程,表面与射线的交角容易满足要求,产生的雷达回波具有较好的真实感。事实上,航海人员感兴趣的大多数物标都能生成较好的回波,只有大面积近于水平的表面容易受到影响,但在真实航海环境中,这样的物标是不多见的。平静的水面不产生回波(海杂波的仿真是一个较大的主题,本文不做讨论),只有大面积的平坦陆地受影响较大,其回波图像与前文所述水平面的回波类似。对于航海人员来说,更关心的是岸线的回波而非陆地内侧的地貌或建筑,因此,可将大片平坦陆地的岸线附近表面适当增加倾斜角度而将内陆的大片平面去掉,这样可以取得较好的仿真效果,同时也不影响雷达模拟器的实际使用。
② 水工建筑物。码头、防波堤等水工建筑物顶面一般是水平的,回波较差,但其侧面与电磁波入射方向的交角在90°左右,总体来看,生成的图像效果也可接受。但当船舶位于细长型物体的端部方向且距离较远时,产生的雷达回波图像由于视景图形本身出现走样而出现断断续续或时隐时现的现象。出现这一现象时,则应更多地从改善视景图形生成中反走样的功能入手。
③ 助航标志与船舶。一般的商船较大,上层建筑高大,生成雷达回波较好。小渔船和一般的浮标尺度较小,高度有限,虽然在较远距离就可被发现,但生成的雷达图像较真雷达小,同时因其尺度小,在远距离也容易出现回波丢失现象。解决这一问题,可以借鉴LOD技术的思想,但不是在远距离时使用简化模型,而是将对象依离视点的距离而适当缩放,使其距离较远时在水平或垂直方向上占据更多的像素而避免丢失,而近距离时又不会显得过大。
3) 提高方位采样率。
对于物标丢失问题,也可通过提高方位采样率的方法解决。如图 12所示,在一个像素区域内有两个小物标,若两个物标并不在同一方位上,在方位精度较低的情况下远处的物标被丢弃,但若将方位采样率提高,则两个物标虽然在距离上不能被分开,却可以映射到不同的扫描线上,从而在方位上被分离,仍然可以形成两个不同的物标。本文采用纹理映射方式进行坐标转换,雷达方位采样率和雷达方位精度是分离的,因此可通过提高方位采样率的方法缓解小物标丢失现象。

|
| 图12 提高方位采样率 Figure 12 Improving the sampling rate of bearing |
雷达性能标准对无杂波条件下远距离目标和海岸线的探测能力要求见表 1,因X波段探测要求高于S波段,本文根据该表所列物标特征进行建模,经仿真试验表明,生成的雷达仿真图像能够满足性能标准所列要求。
| 目标描述 | 目标特征海平面以上高度/m | 探测距离/n mile | |
| X波段 | S波段 | ||
| 海岸线 | 60 | 20 | 20 |
| 海岸线 | 6 | 8 | 8 |
| 海岸线 | 3 | 6 | 6 |
| SOLAS船舶(5 000 t以上) | 10 | 11 | 11 |
| SOLAS船舶(500 t以上) | 5.0 | 8 | 8 |
| 典型的导航浮标 | 3.5 | 4.6 | 3.0 |
| 无雷达反射器,船长为10 m的小船 | 2.0 | 3.4 | 3.0 |
图 13(a)是大连港卫星图片,图 13(b)是烟台到大连客轮上拍摄的真实雷达图像,图 13(d)是本文利用视景图形绘制方法生成的大连港仿真雷达图像,通过对比可看出,物标间遮挡关系明确,回波向陆地延伸长度合理,与图 13(c)现有雷达雷达模拟器中的图像相比回波图像质量有了明显改善,真实感更好。

|
| 图13 现有模拟雷达图像与本文仿真试验结果(大连港) Figure 13 The simulating image and the present radar image in the radar simulator (Dalian harbor) |
本文从雷达工作原理与透视投影的相似性出发,将帧缓存中的像素视为雷达数据采样点,通过读取帧缓存生成扫描线并进而生成雷达图像,仿真结果表明:
1) 基于透视投影视景图形绘制生成雷达图像的方法实际上是基于雷达工作原理的仿真,较现有以二维数据为基础通过扫描线求交方式生成航海雷达图像的方法有了极大的进步,为从原理上仿真雷达图像开辟了全新的思路。
2) 透视投影foreshortening现象导致远距离处雷达探测距离采样率过低,远处低矮平坦物标雷达图像断裂,可通过提高采样率、合理建模等方法缓解,但不能完全消除;
3) 采用纹理映射的方式进行坐标变换,不但可以借助硬件加速实现坐标变换,有效消除死点和盲点现象,还实现了雷达扫描线采样数据与屏幕扫描线数据的分离,从而为提高方位精度解决物标丢失问题提供了保障,为对雷达波束的仿真等多种特性的实现提供了更多更灵活的方式。
本文仅解决了生成雷达图像基本方法中存在的一些问题,还有很多问题有待于进一步研究,如雷达电磁波的传播损耗和不同物标后向散射特性对雷达回波强度的影响,雷达数据建模与三维视景建模的差异,地球曲率对雷达可视范围的影响等,在新方法下如何实现雷达增益、调谐、假回波、二次反射回波、雨雪与海浪杂波等雷达培训教学所需特殊效果等也是亟待解决的问题。这里提及的一些问题,现已列入相关研究中。
| [1] | IMO S. Including 2010 manila amendments: stcw convention and stcw code[M]. IMO publishing, 2011. |
| [2] | SHAHID U, QADIR S, HAIDER Z, et al. Design and implementation of multi mode radar target simulator using direct digital synthesizer[C]//Proceedings of International Bhurban Conference on Applied Sciences and Technology. Islamabad, Pakistan, 2009: 155-158. |
| [3] | QUAN Yinghui, GAO Xiaoxiao, LI Yachao, et al. The design and implementation of a multi-waveform radar echo simulator[J]. Review of scientific instruments, 2015, 86(10): 104702. DOI:10.1063/1.4932311 |
| [4] |
宋兵兵, 潘明海, 梁志恒, 等. 高精度干涉测高雷达回波快速实现方法[J].
哈尔滨工程大学学报, 2015, 36(11): 1494–1498.
SONG Bingbing, PAN Minghai, LIANG Zhiheng, et al. Fast implementation method of high-precision interferometric radar echo simulation[J]. Journal of Harbin Engineering University, 2015, 36(11): 1494–1498. |
| [5] |
金一丞, 尹勇.
航海模拟器[M]. 北京: 科学出版社, 2013: 331-352.
JIN Yicheng, YIN Yong. Marine simulator[M]. Beijing: Science press, 2013: 331-352. |
| [6] |
王胜正, 黄玉贵. 基于电子海图的真实感航海雷达图像仿真方法[J].
计算机应用, 2014, 34(10): 3024–3028.
WANG Shengzheng, HUANG Yugui. Method of marine radar image simulation based on electronic chart display information system[J]. Journal of computer applications, 2014, 34(10): 3024–3028. DOI:10.11772/j.issn.1001-9081.2014.10.3024 |
| [7] |
丛琳, 任鸿翔, 刘彤, 等. 航海雷达模拟器中真实感雷达图像的仿真[J].
中国航海, 2011, 34(4): 5–8.
CONG Lin, REN Hongxiang, LIU Tong, et al. Realistic radar image simulation in maritime radar simulator[J]. Navigation of China, 2011, 34(4): 5–8. |
| [8] |
陈杰, 杨神化, 曹士连. 基于OPENGL的雷达/ARPA模拟器[J].
计算机系统应用, 2012, 21(6): 126–131.
CHEN Jie, YANG Shenhua, CAO Shilian. Radar/ARPA simulator based-on opengl[J]. Computer systems & applications, 2012, 21(6): 126–131. |
| [9] | RANAWEERA W, JABBAR S, WICKRAMARACHCHI R, et al. A lightweight approach to simulate a 2D radar coverage for virtual maritime environments.[C]//8th International Conference on Computer Science & Education. Colombo, Sri Lanka, 2013: 402-406. |
| [10] |
史可鉴, 王斌, 朱恬倩, 等. GPU上的kD-tree雷达模拟加速[J].
计算机辅助设计与图形学学报, 2010, 22(3): 440–448.
SHI Kejian, WANG Bin, ZHU Tianqian, et al. Radar simulation with kd-tree on the GPU[J]. Journal of computer-aided design & computer graphics, 2010, 22(3): 440–448. |
| [11] |
王进成, 金一丞, 曹士连. 使用三维场景绘制技术模拟雷达图像[J].
大连海事大学学报, 2014, 40(4): 79–84.
WANG Jincheng, JIN Yicheng, CAO Shilian. Radar images simulation by using 3D scene rendering technology[J]. Journal of Dalian Maritime University, 2014, 40(4): 79–84. |
| [12] | MARK S, KURT A. The opengl graphics system: a specification (version 4.3(compatibility Profile)-February 14, 2013)[EB/OL].[2015-12] https://www.open-gl.org/registry/#apispecs. |
| [13] | IMO. IMO resolution MSC.192(79): revised recomme-ndation on performance standards for radar equipment[S]. 2004. |
| [14] | YOO J, BAE J, KIM J, et al. PC-based implement of the maritime radar display unit[C].//Signals, systems and computers, 1996.1996 Conference Record of the Thirtieth Asilomar Conference on. IEEE Xplore, 1996: 474-480. |
| [15] |
梁景新, 薛余网. PPI雷达信号微机显示中的快速极坐标-直角坐标映射[J].
上海交通大学学报, 1999, 33(1): 57–60.
LIANG Jingxin, XUE Yuwang. Quick polar coordinates to orthogonal coordinates mapping method in PPI radar signal displaying[J]. Journal of Shanghai Jiaotong University, 1999, 33(1): 57–60. |
| [16] |
徐展翼, 欧阳宁, 韩传久. 高速PPI光栅扫描显示系统坐标转换设计与实现[J].
桂林电子工业学院学报, 2003, 23(1): 57–60.
XU Zhanyi, OUYANG Ning, HAN Chuanjiu. Design and realization of polar coordinates-orthogonal Coordinates conversion in high-speed radar PPI signal displaying system[J]. Journal of Guilin University of Electronic Technology, 2003, 23(1): 57–60. |
| [17] |
范多亮. 雷达显示终端中的"死点"分析[J].
信息化研究, 2010, 36(3): 13–15.
FAN Duoliang. The analyze of "deadpoint" in radar display terminal[J]. Informatization research, 2010, 36(3): 13–15. |



