船舶制造过程包括分段组立、预舾装,分段涂装和分段搭载等工序。涂装作业处于船体生产过程的中间位置,有着承前启后的作用。前面工序由于场地、原材料供应等因素影响,延时严重;后续工序由于船坞搭载计划变更,交货期提前。这使得分段涂装作业的加工时间要求非常严格。因此,提高分段涂装作业的效率对缩短船舶制造周期有着重要的作用。分段涂装作业包括冲砂和喷涂工序。分段冲砂指的是冲砂队对砂房中的分段表面进行二次除锈。冲砂结束的分段应及时涂上底漆,防止表面氧化。分段喷涂是喷涂队对分段涂漆作业。根据船舶建造质量和工艺规划要求,分段喷涂一般要分几次进行,喷涂次数与规定的涂层厚度有关,并且各度喷涂之间要有一定的干燥时间。分段涂装调度过程不仅要考虑冲砂和喷涂阶段的时间约束,还需考虑冲砂车间和喷涂车间的空间约束及喷涂队的派遣。因此,船舶分段涂装作业可归结为带有时间和空间约束的重入调度问题。
现阶段国内外对分段涂装调度的研究较少。Cho等[1]针对分段涂装调度,设计了包含操作策略算法、分段调度算法、安排算法和分派算法的空间调度系统。在此基础上,Kwon等[2]提出了分段涂装调度的混合整数规划模型,并采用结合优先级调度规则和diagonal-fill空间调度方法的两阶段启发式算法求解。但是上述文献侧重于分段的空间调度,未考虑分段的重入喷涂和时间约束。张志英等[3-4]研究了带有时间和空间约束的分段涂装重入调度问题。但假设所有分段只重入一次,且重入之间的干燥时间均相同。这很难满足实际的分段涂装调度要求。
Su[5]证明了带有等待时间约束的两阶段单机调度过程是一个NP-Hard问题。显然,带有时间和空间约束的分段涂装重入过程是一个更为复杂的NP-Hard问题。求解此类问题的常用方法为启发式与元启发式算法。前者可在合理时间内求出较为满意的解,但易陷入局部最优解;后者通过乱数搜寻策略,提高了解的优化能力,但由于计算效率低而不能满足复杂调度问题的需求。而超启发式算法[6]结合了这两者的优势,只需将底层算法修改便可在不同领域应用,因此近几年在图形着色[7]、课程表安排[8-9]等问题中得到了深入地研究。但在分段涂装调度领域中的应用还很少见。
基于上述分析,本文针对分段涂装作业重入调度问题,提出了以最小化最大完工时间为目标函数,带有时间和空间约束的批-离散机重入调度模型。在此基础上,构造基于重排策略的启发式算法进行求解,得到优化后的分段涂装调度方案。
1 问题描述分段涂装作业重入调度过程如图 1所示:有m个冲砂车间,v个喷涂车间及r个喷涂队。

|
| 图1 分段涂装作业重入调度过程 Figure 1 Block-painting reentrant process |
分段到达冲砂车间后,工人对砂房里的分段同时进行冲砂,每一个冲砂车间可等效为一台并行批处理机。砂房中能放入的分段越多,冲砂效率越高。冲砂结束后的分段移至喷涂车间,由选定的喷涂队在一定时间内进行一度喷涂。分段至少要经过2次喷涂才能结束加工,各度喷涂之间存在干燥时间下限约束。为了便于追溯和控制分段涂层的质量,一个分段的各度喷涂作业均由同一支喷涂队完成。分段喷涂作业要求在涂装房内完成,但由于船厂往往无法提供足够的涂装房。据IMO协会规范,除一度喷涂外,剩余喷涂作业可移至堆场完成。
因此,可将上述调度问题描述为:FHm,(PMk)k=1mbatch1,recrc2,Mj2Cmax[10]。其中,FHm表示该问题属于多阶段混合流水车间调度问题,(PMk)k=1m表明每阶段都为并行机,batch1表示第一阶段为批处理机,recrc2表示第二阶段为重入过程,Mj2表示分段重入所选的喷涂队是其一度喷涂的喷涂队,Cmax指目标函数为最小化完工时间。
2 模型建立 2.1 模型假设为研究方便,对分段涂装作业重入调度问题,进行以下假设:1) 分段的投影形状为矩形。2) 所有分段在初始时刻均可加工。3) 各阶段之间有足够的缓存区;忽略分段进出各车间所需的搬运时间和其他生产准备时间。4) 劳动力充足,不考虑罢工、缺勤等约束劳动力的情况。5) 假定冲砂时间只与分段的投影面积有关,并事先确定。6) 假定每个分段的各度喷涂时间相同,并事先确定。根据历史数据,将检查和报验时间计入喷涂时间内。7) 同一分段在不同的温度下干燥时间不同。为便于估算分段的干燥时间,假定所有分段在温度25 ℃的环境下干燥。
2.2 符号列表任意一个分段i均可用六元组(xi,yi,x′i,y′i,wi,li)表示;其中(xi,yi)为分段i的左下角坐标,(x′i,y′i)为分段i的右上角坐标,(wi,li)分别表示分段i的宽度和长度。为了便于建立分段涂装作业重入调度模型,引入如下符号与变量:
1) 索引:i为分段索引,i∈I{1,2,…,h}; j为分段工序索引,j∈J{1,2,…,n};Oij为分段i的第j道工序索引;β为批索引,β∈B{1,2,…,b};α为批中分段索引,α∈A{1,2,…,Gβ};f为冲砂车间索引,f∈F{1,2,…,m};k为喷涂队索引,k∈K{1,2,…,r};l为喷涂车间索引,l∈L{1,2,…,v};t为时间索引。
2) 参数:wti为分段i冲砂结束到一度喷涂之间的等待时间上限,h,i∈I;dtij为分段i第j道工序结束后的干燥时间下限,h,i∈I,j≥2;ptij为第i分段第j道工序的加工时间,h,i∈I,j∈J; si为分段i的投影面积,m2,i∈I; H为冲砂车间宽度,m;W为冲砂车间长度,m;sbf为第f个冲砂车间的面积,m2,f∈F;spl为第l个喷涂车间的面积,m2,l∈L;E为无穷大数。
3) 变量:stij为分段i的第j道工序加工开始时间,i∈I,j∈J{1,2,…,n};ftij为分段i的第j道工序加工完成时间,i∈I,j∈J{1,2,…,n};STβ为第β批分段冲砂开始时间,β∈B;PTβ为第β批分段冲砂时间,β∈B;FTβ为第β批分段冲砂结束时间,β∈B;若Xiβ=1,则Oi1被分派至批β内,反之为0;若φijlt=1,则t时Oij被分派至喷涂车间l,反之为0;若σijkt=1,则t时Oij被喷涂队k喷涂,反之为0;若λβft=1,则t时批β被分派至冲砂车间f,反之为0;若Ziji′j′=1,则Oij优先于Oi′j′加工,反之为0;若Zijij′=1,则Oij优先于Oij′加工,反之为0。
2.3 数学模型模型的目标函数和约束条件如下:
| $min~{{C}_{max}}=min\left( \underset{i=1}{\overset{h}{\mathop{max}}}\,~f{{t}_{in}} \right)$ | (1) |
| $s.t.~0\le {{x}_{i}} <x_{i}^{'}\le W\wedge 0\le {{y}_{i}}<y_{i}^{'}\le H,i\in I$ | (2) |
| $\begin{align} & \left( x_{i}^{'}-{{x}_{i}}={{w}_{i}}\wedge y_{i}^{'}-{{y}_{i}}={{h}_{i}} \right)\vee \\ & \left( x_{i}^{'}-{{x}_{i}}={{h}_{i}}\wedge y_{i}^{'}-{{y}_{i}}={{w}_{i}} \right) i\in I \\ & {{x}_{i}}\ge x\prime _{i}^{'}\vee x_{i}^{'}\ge x{{\prime }_{i}}\vee {{y}_{i}}\ge y\prime _{i}^{\prime }\vee y_{i}^{'}\ge y{{\prime }_{i}} \\ \end{align}$ | (3) |
| $i,i\prime \in I;i\ne i\prime $ | (4) |
| $\sum\limits_{\beta =1}^{b}{{{X}_{i\beta }}}=1,i\in I$ | (5) |
| $\sum\limits_{\beta =1}^{b}{\lambda _{\beta f}^{t}}\le 1,f\in F$ | (6) |
| $\sum\limits_{i=1}^{h}{{{s}_{i}}{{X}_{i\beta }}}\le s{{b}_{f}},\beta \in B,f\in F$ | (7) |
| $\sum\limits_{i=1}^{h}{{{X}_{i\beta }}}\le r,\beta \in B$ | (8) |
| $P{{T}_{\beta }}\ge p{{t}_{ij}}{{X}_{i\beta }},\beta \in B,i\in I,j=1$ | (9) |
| $F{{T}_{\beta }}=S{{T}_{\beta }}+P{{T}_{\beta }},\beta \in B$ | (10) |
| $\begin{align} & s{{t}_{ij}}=S{{T}_{\beta }}{{X}_{i\beta }}+E1-{{X}_{i\beta }}, \\ & S{{T}_{\beta }}\ge 0,\beta \in B,i\in I,j=1 \\ \end{align}$ | (11) |
| $f{{t}_{ij}}=F{{T}_{\beta }}{{X}_{i\beta }}+E1-{{X}_{i\beta }},\beta \in B,i\in I,j=1$ | (12) |
| $\sum\limits_{i=1}^{h}{\varphi _{ijl}^{t}}{{s}_{i}}\le s{{p}_{l}},l\in L,j>1$ | (13) |
| $\sum\limits_{k=1}^{r}{\sigma _{ijk}^{t}}\le 1,i\in I,j>1$ | (14) |
| $p{{t}_{ij}}=p{{t}_{i(j+1)}},i\in I,j>1$ | (15) |
| $\begin{align} & \exists !k\in K:\sum\limits_{j=2}^{n}{\sigma _{ijk}^{t}}=n-1 \\ & t\in [s{{t}_{ij}},s{{t}_{ij}}+p{{t}_{ij}}],i\in I,j\in J,k\in K,n\ge 3 \\ \end{align}$ | (16) |
| $\exists !l\in L:\varphi _{ijl}^{t}=1,t\in [s{{t}_{ij}},s{{t}_{ij}}+p{{t}_{ij}}],i\in I,j=2$ | (17) |
| $0\le s{{t}_{i(j+1)}}-f{{t}_{ij}}\le w{{t}_{i}},i\in I,j=1$ | (18) |
| $s{{t}_{i(j+1)}}-s{{t}_{ij}}-p{{t}_{ij}}\ge d{{t}_{ij}},i\in I,j>1$ | (19) |
| $\begin{align} & E(2-{{\sigma }_{ijk}}-{{\sigma }_{i\prime j\prime k}})+E(1-{{Z}_{iji\prime j\prime }})+ \\ & s{{t}_{i\prime j\prime }}-s{{t}_{ij}}-p{{t}_{ij}}\ge k{{t}_{ij}},~ \\ & i\in I,j>1,j\prime >1,k\in K \\ \end{align}$ | (20) |
| $\begin{align} & E(2-{{\sigma }_{ijk}}-{{\sigma }_{ij\prime k}})+E(1-{{Z}_{ijij\prime }})+ \\ & s{{t}_{ij\prime }}-s{{t}_{ij}}-p{{t}_{ij}}\ge k{{t}_{ij}}, \\ & i\in I,j>1,j\prime >1,k\in K,j\le j\prime \\ \end{align}$ | (21) |
约束(2)规定每个分段的面积都小于冲砂车间的面积。约束(3)定义分段在放置过程中可正交旋转。约束(4)表示各分段在摆放过程中互不重叠。约束(5)确保每个分段只能被分派到一个批中。约束(6)规定一个冲砂车间在同一时间至多加工一批分段。约束(7)确保每批分段的投影面积之和不超过冲砂车间的面积。约束(8)限定一个批次中的分段数不超过喷涂队的数量,以保证冲砂后的分段,都能分派到不同的喷涂队。约束(9)定义了分段实际冲砂时间为批中各分段单独冲砂所需时间的最大值。约束(10)确保每批分段在冲砂过程中,一旦开始就不能中断,直到完成冲砂作业。约束(11)和(12)分别定义了分段的冲砂开始时间和结束时间要求。约束(13)规定各喷涂车间内的分段投影面积之和不能超过喷涂车间的面积。约束(14)确保一个喷涂队在同一时间至多喷涂一个分段。约束(15)规定分段各度喷涂的加工时间相同。约束(16)保证喷涂阶段,分段至少重入1次,且喷涂过程不能被中断,由同一个喷涂队完成作业。约束(17)表明分段一度喷涂必须在喷涂车间内完成。约束(18)限定了分段冲砂后的等待时间不能超过相应的等待时间上限约束。约束(19)规定了分段重入之间的等待时间必须超过相应的干燥时间下限。约束(20)和(21)表明了分段在喷涂阶段的加工顺序要求。
3 基于重排策略的启发式算法分段涂装作业重入调度包含分段空间组批和重入调度过程。分段空间组批过程存在3类约束:1)面积约束,批中分段面积之和不超过冲砂车间的面积;2)空间约束,矩形分段在冲砂车间内不能重叠摆放,简化为平面约束;3)数量约束,批中分段数不能超过喷涂队总数。因此,分段空间组批过程可简化为二维装箱问题。在装箱过程中,需确定分段进入车间的顺序和在车间中的摆放位置。为了减少冲砂车间的批空间浪费,采用约束凝聚聚类算法[11](constrained agglomerative clustering of batches,CACB)获得不考虑空间约束的分批集合Rβ。再结合基于多类型个体改进方法(multiple-type individual enhancement scheme,MIE)[12]的模拟退火算法对Rβ进行随机排序得到R′β,将R′β作为分段进入各车间的顺序;利用最大接触策略确定分段在车间的摆放位置,并得到最终批集合R″β。
分段重入调度有其特殊性与复杂性,体现在:1)重入次数不确定,分段喷涂需重入1~5次;2)重入时间不确定,分段重入之间受干燥时间下限约束。3)分段重入不需再选择喷涂队,由为其一度喷涂的喷涂队完成。分段重入过程的研究包括了喷涂队的派遣和喷涂队对分段的加工顺序的确定。论文先利用最大剩余加工时间策略(maximum remaining process time strategy,MRTS)确定喷涂队上分段的加工顺序,并提出了基于MRTS和遗传算法的超启发式算法进行分段的重入调度,得到最大完工时间maxhi=1 ftin。然后通过基于MIE的SA算法实现分段的组批重排,进行新一轮的计算,直到获得较优的调度方案为止。基于重排策略的启发式算法(batch ranking heuristic algorithm,BRHA)的算法框架如图 2所示。

|
| 图2 基于重排策略的启发式算法框图(BRHA) Figure 2 Heuristic algorithm frame based on ranking strategy |
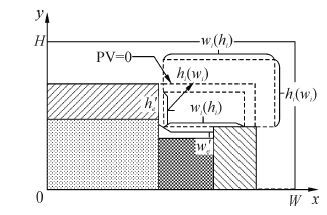
以冲砂车间左下角为坐标原点(0,0),建立笛卡尔坐标系。其中,x、y分别为车间的长度和宽度方向。令第一个进入冲砂车间的分段左下角坐标(xi,yi)=(0,0),后入分段置于其右方或上方。为便于确定分段的摆放位置,将已放置分段的右侧轮廓线相连接的虚线称为包络线[13] (图 3),后入分段置于包络线上。定义在包络线上从垂直到水平的所有交点为可行位置P集合,如图 3中的位置1、2和3。由此得到后入分段的可行位置集合如式(22),(x,y)为后入分段左下角的坐标。
| $\begin{align} & S\left( p \right)=\left\{ \left( x,y \right) \right.\forall i\in I, \\ & (x\ge x_{i}^{\prime }\vee y\ge y_{i}^{\prime })\wedge x_{i}^{\prime }\le W,y_{i}^{\prime }\le \left. H \right\} \\ \end{align}$ | (22) |
考虑到包络线越平滑,后入的分段越能充分地利用车间空间;因此,选择分段与包络线接触最大的可行位置作为分段最终放入车间的位置。由于分段可正交旋转,所以评判分段与包络线接触的量化函数PV(position value)如下所示:
| $PV=\left\{ \begin{matrix} \begin{align} & \text{min}\left\{ \left( \left| {{w}_{i}}-w_{e}^{'} \right|+\left| {{h}_{i}}-h_{e}^{'} \right| \right) \right., \\ & \left. \left( \left| {{w}_{i}}-h_{e}^{'} \right|+\left| {{h}_{i}}-w_{e}^{'} \right| \right) \right\} \\ \end{align} \\ +\infty \\ \end{matrix} \right.$ | (23) |
式中:h′e和w′e分别为可行位置P对应的包络线长与宽(如图 3)。PV值越小,表明分段与包络线接触越大。当分段长、宽都小于包络线的长和宽时,分段长和宽的值越大,PV值越小。当分段长和宽与包络线的长和宽都相等时,PV值达到最小值0。当分段长、宽都大于包络线的长和宽时,分段长和宽的值越小,PV值也越小,如图 4所示。因此,最大接触策略为:利用式(23)计算分段所有可行位置的PV值,在min PV对应的可行位置放入分段,得到分段的空间分批方案。

|
| 图3 可行位置S(p) Figure 3 Feasible position S(p) |
|
| 图4 基于最大接触策略的PV函数示意图 Figure 4 PV function based on the maximum contact strategy |
超启发式算法的思想最早可追溯到1963年[14],按规则生成机制分为选择超启发式和生成超启发式算法。其中,选择启发式算法是将启发式搜索规则进行选择组合,对于求解复杂调度问题,比一般启发式算法更具有优势。分段涂装调度需将分段派给车间和喷涂队,运用一种调度规则无法获得合适的搜索空间,因此选用超启发式算法通过不同调度规则的选择组合,能得到更为合理的分段涂装计划。选择超启发式算法分为高层算法和底层规则。高层算法是采用元启发式算法来选择底层规则的搜索策略;底层规则为具体的调度方法。从均衡喷涂队负荷的角度,研究确定了以下启发式规则作为分段派遣到各个喷涂队的方法。其中,RJk为t时喷涂队k上待加工分段Oij的集合, p为分段当前待处理工序。
1) 最大剩余加工时间规则(MRT):剩余所需加工时间越大的分段,优先安排加工,MRT的确定如式(24)。剩余加工时间相同的分段,选择剩余重入次数最多的分段优先加工。
| $MRT=\underset{k\in K}{\mathop{max}}\,\sum\limits_{i\in R{{J}_{k}}}{\left( \left( n-p+1 \right)p{{t}_{i}}+\sum\limits_{j=p}^{n-1}{k{{t}_{ij}}} \right)}$ | (24) |
2) 最大重入次数规则(MRN):分段剩余重入次数越多,越先加工,MRN的确定如式(25)。为了减少喷涂队由于分段干燥造成的空闲状态,当分段剩余重入次数相同时,选择剩余加工时间大的分段,优先喷涂。
| $MRN=\underset{k\in K}{\mathop{max}}\,\sum\limits_{i\in R{{J}_{k}}}{{{\left( n-p \right)}_{i}}}$ | (25) |
3) 最大平均加工时间规则(MPT):分段的平均重入喷涂时间越大,越先加工,MPT的确定如下:
| $MPT=\frac{MRT}{MRN}$ | (26) |
4) 先到先加工规则(FIFS):先到达喷涂队的分段,优先加工。
论文采用遗传算法作为高层算法。令h为具体的启发式规则;c为调用底层规则的次数,c=c1,c2,…csize,

|
| 图5 底层规则组合方案 Figure 5 Bottom rule set |
根据时间属性的不同,喷涂队加工待喷涂的分段分为待一度喷涂的分段和重入喷涂的分段。前者由于存在等待时间上限约束,所以一旦喷涂队空闲,该分段将优先加工。后者则存在干燥时间下限约束。为进一步确定重入喷涂分段在喷涂队上的加工优先级,引入MRTS策略:令Oi2加工优先级为2;剩余加工时间最大的分段Oij优先级为1,其余分段加工优先级为0。若存在分段Oij既属于一度喷涂,又拥有最大剩余加工时间,则其加工优先级为2+1=3,依次类推;从而确定t时分段在喷涂队k上的加工顺序。综上所述,采用目标函数作为适应度函数,得到基于MRTS策略和GA的超启发式算法流程为:
1) 初始化迭代次数gener=0,种群规模M,迭代最大次数Gmax,交叉概率pc,变异概率pm,分段调度规则组合方案Sgener。
2) 对S进行交叉、变异,得到方案S′gener。
3) 按S′gener方案将分段分派到喷涂队。
4) 执行MRTS策略,按优先级的高低加工分段,再用FIFO规则将分段分派给喷涂车间。计算各染色体的适应度函数,保存该代最佳染色体。
5) 计算概率
6) gener=gener+1;若gener <Gmax,转2)。
3.3 BRHA算法框架基于上述分析,得到求解分段涂装重入调度问题的BRHA算法流程如下:
1) 输入起始温度Ts,结束温度Tf,冷却率β。
2) 初始化:执行CACB算法、最大接触策略、超启发式算法得到分段空间分批结果Rβ,makespan和分段涂装调度方案SS。
3)按MIE策略对Rβ随机排序得R′β后,执行最大接触策略获得分段空间分批结果R″β。
4) 执行超启发式算法,得到R″β的makespan、SS′,计算Δ=makespanRβ-makespanR″β。
5) 若Δ <0,则Rβ=R″β,SS=SS′,转步骤7)。
6) 若Δ≥0,R=Rnd()。若R <min1-e-ΔT,则Rβ=R″β,SS=SS′。
7) T=β×T。若T>Tf,转步骤3)。
4 实例验证与数值分析 4.1 实例验证为了验证模型和BRHA算法的有效性,以上海某大型造船厂的涂装车间为例,利用Matlab2013a软件,在处理器为1.2 GHz,内存为4 GB的计算机上进行求解。该造船厂有3个冲砂车间,4个喷涂车间和4个喷涂队。分段在车间内摆放时要留有一定的通道空间,因此取车间面积的60%作为有效面积。分段个数30,冲砂后的等待时间为1~4 h,干燥时间为12~24 h,部分分段的涂装数据如表 1所示,冲砂车间和喷涂车间的数据如表 2所示。算法输入参数:初始温度Ts为运行10次BRHA所得平均最小完工时间的1.5倍,冷却速率Ts=0.97,最终温度Tf=0.1;种群规模为30,迭代次数为30,染色体交叉概率pc=0.9,变异概率pm=0.09。
| 分段编号 | 长/m | 宽/m | 面积/m2 | 冲砂时间/h | 喷涂时间/h |
| 1 | 13.5 | 19.3 | 260.6 | 7.4 | 5.0 |
| 2 | 16.9 | 11.1 | 187.6 | 5.6 | 4.5 |
| 3 | 6.8 | 15.2 | 103.4 | 4.8 | 5.0 |
| 4 | 10.9 | 4.0 | 43.6 | 3.6 | 3.0 |
| 5 | 12.5 | 9.5 | 118.8 | 3.8 | 3.0 |
| 6 | 5.8 | 4.3 | 24.9 | 3.7 | 4.0 |
| 7 | 15.3 | 6.9 | 105.6 | 6.0 | 6.0 |
| 8 | 15.4 | 22.7 | 349.6 | 7.4 | 7.0 |
| 9 | 15.5 | 24.2 | 375.1 | 9.3 | 5.5 |
| 10 | 13.0 | 21.0 | 273.0 | 5.8 | 6.0 |
| 车间编号 | 长/m | 宽/m | 面积/m2 |
| 1号冲砂车间 | 45 | 30 | 1 350 |
| 2号冲砂车间 | 45 | 30 | 1 350 |
| 3号冲砂车间 | 50 | 27 | 1 350 |
| 1号喷涂车间 | 50 | 36 | 1 800 |
| 2号喷涂车间 | 27 | 24 | 648 |
| 3号喷涂车间 | 27 | 24 | 648 |
| 4号喷涂车间 | 48 | 40 | 1 920 |
运行程序,分段的空间分批结果如图 6所示,据此计算冲砂车间的平面利用率(表 3)。分段第12批分批结束后,只有20号分段未分派至任何批中,所以第13批中只包含一个分段,车间的平面利用率比其他批低。从表 3可得到车间的平均平面利用率为70.21%(不计第13批)。因此,BRHA算法得到的分段空间分批方案,能更好地利用冲砂车间的面积。

|
| 图6 分段空间分批布置图 Figure 6 Blocks spatial batching |
| 批号 | 批面积和/m2 | 利用率/% |
| 1 | 533.6 | 65.9 |
| 2 | 536.9 | 66.3 |
| 3 | 712.7 | 88 |
| 4 | 547 | 67.5 |
| 5 | 727.1 | 89.8 |
| 6 | 700.7 | 86.5 |
| 7 | 589.6 | 72.8 |
| 8 | 401.7 | 49.6 |
| 9 | 477.6 | 59 |
| 10 | 582.1 | 71.9 |
| 11 | 564.5 | 69.7 |
| 12 | 451.1 | 55.7 |
| 13 | 212.9 | 26.3 |
| — | — | — |
分段分派到喷涂队时采用的调度规则如表 4所示。当喷涂车间空间不足时,完成一度喷涂的分段必须搬到堆场。表 5给出了分段离开喷涂车间的时间范围。当分段最晚离开喷涂车间的时间为零时,表明该分段整个喷涂过程都在喷涂车间进行。分段的最终涂装调度计划如图 7所示。从图 7可得到分段涂装作业最大完工时间为214.79 h。
| 分段编号 | 派遣规则 |
| 1 | MRT |
| 2 | MRT |
| 3 | MRT |
| 4 | MRT |
| 5 | MRN |
| 6 | MRN |
| 7 | MPT |
| 8 | MRT |
| 9 | MRT |
| 10 | MRN |
| 11 | MRN |
| 12 | MRN |
| 13 | MRN |
| 14 | MPT |
| 15 | FIFS |
| 16 | FIFS |
| 17 | FIFS |
| 18 | MRT |
| 19 | MRT |
| 20 | MRT |
| 21 | MRN |
| 22 | MRN |
| 23 | MPT |
| 24 | MPT |
| 25 | MPT |
| 26 | MPT |
| 27 | FIFS |
| 28 | FIFS |
| 29 | FIFS |
| 30 | MRT |
| 车间编号 | 分段编号 | 喷涂开始时间/h | 最早离开时间/h | 最晚离开时间/h |
| 1 | 26 | 5.8 | 12.8 | 21.8 |
| 1 | 17 | 12.8 | 18.8 | 20.8 |
| 1 | 14 | 12.8 | 18.8 | 20.8 |
| 1 | 11 | 21.8 | 28.8 | 28.8 |
| 1 | 8 | 20.8 | 27.8 | 29.8 |
| 1 | 23 | 24.8 | 28.8 | 36.8 |
| 1 | 10 | 28.8 | 34.8 | 36.8 |
| 1 | 20 | 27.8 | 32.8 | 39.8 |
| 1 | 16 | 29.8 | 36.8 | 39.8 |
| 1 | 15 | 36.8 | 44.8 | 0 |
| 1 | 5 | 40.8 | 43.8 | 0 |
| 1 | 12 | 39.8 | 45.3 | 0 |
| 1 | 21 | 44.8 | 48.8 | 0 |
| 2 | 2 | 5.6 | 10.1 | 20.8 |
| 2 | 1 | 20.8 | 25.8 | 30.8 |
| 2 | 30 | 30.8 | 35.8 | 42.3 |
| 2 | 3 | 42.3 | 47.3 | 0 |
| 2 | 22 | 55.8 | 60.8 | 0 |
| 2 | 4 | 54.8 | 57.8 | 0 |
| 2 | 6 | 57.8 | 61.8 | 0 |
| 3 | 24 | 5.8 | 12.8 | 0 |
| 3 | 7 | 6 | 12 | 0 |
| 4 | 18 | 12 | 18 | 43.8 |
| 4 | 13 | 18.8 | 24.8 | 46.3 |
| 4 | 19 | 15.8 | 21.8 | 53.3 |
| 4 | 29 | 43.8 | 48.8 | 53.3 |
| 4 | 25 | 46.3 | 53.3 | 64.8 |
| 4 | 9 | 53.3 | 58.8 | 71.8 |
| 4 | 27 | 64.8 | 70.3 | 0 |
| 4 | 28 | 71.8 | 78.8 | 0 |

|
| 图7 分段涂装重入调度甘特图 Figure 7 Gantt chart of block-painting reentrant scheduling |
分段涂装重入调度过程需同时考虑车间和喷涂队的分派,兼具时间和空间约束,比一般的调度问题复杂,难以找到合适的下界。因此,本文从超启发式和整体算法两个方面验证算法的最优性。为了验证超启发式算法的优越性,选用HMRT、HMRN、HMPT、HFIFS这4个算法进行对比。这4个算法与BRHA算法的不同之处在于,前者分别选用调度规则中的一种完成分段到喷涂队的派遣。引入相对偏差θ来表示算法所得目标值与相对最优值的距离比值,θ越小,解的性能越好。θ由式(27)计算得到,refCmin表示对应算法所得的目标函数值。
| $\theta = \frac{{\left( {re{f_{{C_{min}}}} - min({C_{min}})} \right)}}{{min({C_{min}})}} \times 100\% $ | (27) |
在表 6中,f2/l3/k4表示有2个冲砂车间,3个喷涂车间和4支喷涂队,其他依次类推。从表 6中可看出,BRHA算法解的平均相对偏差为0.1%,而对比算法的平均相对偏差在3%~17%。因此,在不同的问题模型和分段数量下,BRHA算法性能要明显优于HMRT、HMRN、HMPT和HFIFS算法。这充分说明了引入规则选择的超启发式算法可以很好地改善调度规则集合,进一步提升BRHA算法的性能。
| 问题模型 | 分段个数 | min(Cmin) | BRHA | HMRT | HMRN | HMPT | HFIFS | |||||||||
| Cmin | θ/% | Cmin | θ/% | Cmin | θ/% | Cmin | θ/% | Cmin | θ/% | |||||||
| f2/l3/k4 | 30 | 214.6 | 214.6 | 0.0 | 222.6 | 3.7 | 228.3 | 6.4 | 224.3 | 4.5 | 220.7 | 2.8 | ||||
| f2/l3/k4 | 50 | 324.9 | 324.9 | 0.0 | 359.3 | 10.6 | 347.7 | 7.0 | 353.3 | 8.7 | 339.6 | 4.5 | ||||
| f2/l3/k4 | 70 | 466.6 | 466.6 | 0.0 | 511.8 | 9.7 | 516.7 | 10.7 | 516.3 | 10.7 | 475.3 | 1.9 | ||||
| f2/l3/k4 | 100 | 660.7 | 660.7 | 0.0 | 754.9 | 14.3 | 749.8 | 13.5 | 722.2 | 9.3 | 663.1 | 0.4 | ||||
| f3/l3/k4 | 70 | 465.3 | 465.3 | 0.0 | 513.4 | 10.3 | 519.6 | 11.7 | 541.3 | 16.3 | 478.2 | 2.8 | ||||
| f3/l4/k4 | 70 | 340.6 | 342.7 | 0.6 | 525.3 | 54.2 | 340.6 | 0.0 | 522.2 | 53.3 | 380.9 | 11.8 | ||||
| f3/l4/k5 | 70 | 377.3 | 377.3 | 0.0 | 435.3 | 15.4 | 421.6 | 11.7 | 451.0 | 19.6 | 380.9 | 1.0 | ||||
| f4/l5/k5 | 70 | 364.2 | 364.2 | 0.0 | 428.8 | 17.7 | 453.2 | 24.4 | 447.8 | 22.9 | 367.3 | 0.8 | ||||
| 平均值 | 401.8 | 402.0 | 0.1 | 468.9 | 17.0 | 447.2 | 10.7 | 472.3 | 18.2 | 413.2 | 3.2 | |||||
此外,为了验证BRHA整体算法的最优性,增加了与文献[4]HPSO算法的对比分析。在HPSO算法中,采用最大接触和MRTS策略分别进行分段空间组批和喷涂队上分段加工顺序的确定。选取100个分段,喷涂车间和冲砂车间数据与实验验证部分一致。运行程序,算法的收敛曲线如图 8所示。

|
| 图8 BRHA与HPSO算法收敛曲线 Figure 8 BRHA and HPSO algorithm convergence curves |
BRHA算法在130代左右趋于稳定,得到分段涂装结束时间为658 h;而HPSO算法在165代左右收敛,目标函数值为668 h。这表明了BRHA算法比HPSO算法提前收敛,并且得到的解更优。因此,在求解带有空间和时间约束的分段涂装作业重入调度问题中,BRHA算法比HPSO算法更具有优势。
5 结论本文研究了船舶分段涂装作业的重入调度问题,得出以下结论:
1) 综合考虑分段干燥时间,重入时间及冲砂车间的平面约束,确定以最小化最大完工时间作为评价调度方案的评价指标;
2) 提出了基于重排策略的启发式算法来优化分段调度方案;
3) 通过不同分段数量、车间规模以及与其他算法的对比实验分析,证明该算法可以提高分段涂装作业效率,同时可为船厂制定车间级分段涂装调度方案提供有效的依据。但是本文未考虑露天堆场的空间约束。如果涂装作业的分段太多,在有限的场地和作业时间里,可能无法安排指定的工作计划,需进一步研究。
| [1] | CHO K K, CHUNG K H, PARK C, et al. A spatial scheduling system for block painting process in shipbuilding[J]. CIRP annals-manufacturing technology, 2001, 50(1): 339–342. |
| [2] | KWON B, LEE G M. Spatial scheduling for large assembly blocks in shipbuilding[J]. Computers & industrial engineering, 2015, 89: 203–212. |
| [3] |
张志英, 林晨, 杨连生, 等. 面向分段涂装作业的混合流水车间调度[J].
上海交通大学学报, 2014, 48(3): 382–387.
ZHANG Zhiying, LIN Chen, YANG Liansheng, et al. Block-painting-operation-oriented hybrid flow shop scheduling[J]. Journal of Shanghai JiaoTong University, 2014, 48(3): 382–387. |
| [4] |
林晨, 张志英. 考虑运输时间窗的批-离散混合流水车间调度[J].
计算机集成制造系统, 2014, 21(9): 2427–2434.
LIN Chen, ZHANG Zhiying. Batch-discrete hybrid flow shop scheduling with transportation in time windows[J]. Computer integrated manufacturing systems, 2014, 21(9): 2427–2434. |
| [5] | SU L H. A hybrid two-stage flowshop with limited waiting time constraints[J]. Computers & industrial engineering, 2003, 44(3): 409–424. |
| [6] | BURKE E K, GENDREAU M, HYDE M, et al. Hyper-heuristics:a survey of the state of the art[J]. Journal of the operational research society, 2013, 64(12): 1695–1724. |
| [7] | ELHAG A, ÖZCAN E. A grouping hyper-heuristic framework:application on graph colouring[J]. Expert systems with applications, 2015, 42(13): 5491–5507. |
| [8] | KALENDER M, KHEIRI A, ÖZCAN E, et al. A greedy gradient-simulated annealing selection hyper-heuristic[J]. Soft computing, 2013, 17(12): 2279–2292. |
| [9] | AHMED L N, ÖZCAN E, KHEIRI A. Solving high school timetabling problems worldwide using selection hyper-heuristics[J]. Expert systems with applications, 2015, 42(13): 5463–5471. |
| [10] | RUIZ R, VÁZQUEZ-RODRÍGUEZ J A. The hybrid flow shop scheduling problem[J]. European journal of operational research, 2010, 205(1): 1–18. |
| [11] | CHEN Huaping, DU Bing, HUANG G Q. Scheduling a batch processing machine with non-identical job sizes:a clustering perspective[J]. International journal of production research, 2011, 49(19): 5755–5778. |
| [12] | LIN T L, HORNG S J, KAO T W, et al. An efficient job-shop scheduling algorithm based on particle swarm optimization[J]. Expert systems with applications, 2010, 37(3): 2629–2636. |
| [13] | WEI Lijun, ZHANG Defu, CHEN Qingshan. A least wasted first heuristic algorithm for the rectangular packing problem[J]. Computers & operations research, 2009, 36(5): 1608–1614. |
| [14] | FISHER H, THOMPSON G L. Probabilistic learning combinations of local job-shop scheduling rules[C]//MUTH J F, THOMPSON G L. Industrial Scheduling. Englewood Cliffs, New Jersey:Prentice Hall, 1963:225-251. |



