2. Technical Development Department, Nanjing Guangbo Engineering Technology Co. Ltd., Nanjing 210007, China
随着世界航运业的快速发展,船舶的安全性,特别是船舶的倾覆问题[1-4]越来越受到各界的关注。目前船舶在波浪作用下的抗倾覆性研究主要集中于甲板上浪时的倾覆问题[5]及参数横摇问题[6-7]两个方面。Troesch等将甲板上浪近似为一阶静水力,用概率统计的方法计算了随机波浪中船舶的非线性横摇运动,以及甲板上浪导致的倾覆问题[8]。Liu等采用概率密度函数研究了随机海浪中甲板上浪船舶的运动特性,用概率密度函数的形状判定了船舶横摇运动的稳定性[9]。文献[10]改进了复原力之辐射力和绕射力部分与横摇角线性假定[11-12],根据横摇角动态计算复原力之辐射力和绕射力部分,提出了一种随机波中船舶参数横摇的数值预报方法,并通过试验和数值模拟研究了随机波中参数横摇的实际非各态历经的特点。[13]
另外,刘威等运用船舶碰撞的能量及动量守恒等基本理论,分析了船舶的质量比、速度比及船舶稳性变化等因素对小型船舶受撞即时倾覆的影响[14]。李叶兴等通过物理模型试验对大型油轮的水流力进行了研究[15]。万俊等进而给出了弯道中环流对船舶产生的倾覆力矩的计算表达式[16]。综上所述,目前的研究中大多单独考虑波浪和水流对船舶倾覆的影响,而较少综合考虑波浪、水流及拦阻索的共同作用。本文将从考虑三者共同作用的角度对船舶横向撞击拦阻系统后的抗倾覆问题进行研究。
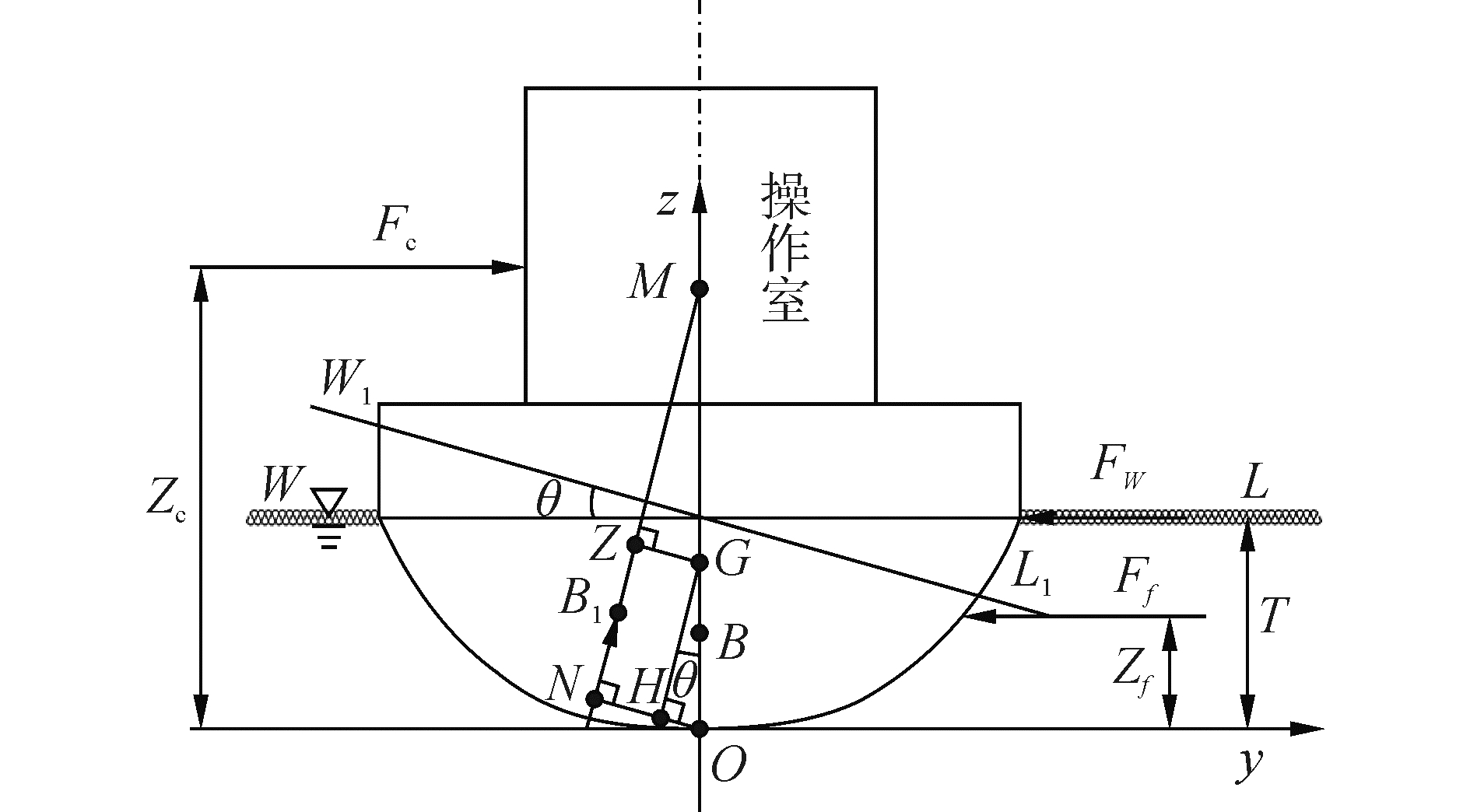
1 船舶在拦阻系统作用下横倾的稳性分析船舶横向撞击拦阻系统后,由于外力矩作用发生横倾,而船体通过自身复原力矩的作用抵抗这种倾斜,此时其受力如图 1。图中取过重心G的垂线与船底基线的交点O为坐标原点,船舶横向为y轴方向,竖直向上为z轴正方向,M点为船舶的稳心。
|
| 图1 拦阻系统作用下船舶的受力示意图 Figure 1 The force schematic diagram of ship under the action of retardation system |
1) 不考虑风荷载的作用。
2) 假定船舶的外力矩为波浪力产生的力矩与水流力和拦阻索作用力产生的横倾力矩的线性叠加,即横倾角由波浪产生的横摇角与横倾力矩产生的倾角相加得到。
3) 假定无波浪作用时,船舶在横倾力矩单独作用下只做旋转运动,此时水流力和拦阻索作用力大小相等,方向相反。
4) 由于船舶水下部分呈流线型,暂不考虑船舶横倾过程中吃水深度的变化,且对船舶横倾进行动稳性分析时,将分布的水流力等效为恒定的集中力,并不考虑横倾力矩随倾角的变化。
5) 假定波浪引起的横摇角与波幅成正比。
1.1 横倾力矩的计算根据外力矩由波浪产生的力矩与横倾力矩线性叠加的假定,得船舶的总外力距:
| $ {M_{\text{e}}} = {M_{\text{t}}} + {M_{\text{w}}} $ | (1) |
式中: Mw为波浪作用产生的力矩,Mt为水流力与拦阻索共同作用产生的力矩(横倾力矩)。根据图 1中的几何关系和相关假定可得横倾力矩:
| $ {M_{\text{t}}} = {F_{\text{e}}}{Z_{\text{c}}}-{F_{\text{f}}}{Z_{\text{f}}} = {F_{\text{f}}}\left( {{Z_{\text{c}}}-{Z_{\text{f}}}} \right) $ | (2) |
式中: Ff为水流力;Zf为水流力作用点距基线的高度,取Zf=T/2,T为船舶吃水;Fc为拦阻索对船舶的作用力;Zc 为拦阻索作用点距基线的高度。根据港口工程荷载规范[17],作用于船舶的水流力:
| $ {F_{\text{f}}} = \rho {C_{\text{c}}}{U^2}A/2 $ | (3) |
式中: ρ为海水密度,取ρ=1 025 kg/m3;Cc为水流阻力系数,依据港口工程荷载规范[17],取Cc=2.32;U为水流相对于船舶的速度;A为船舶水下部分垂直于水流方向的投影面积,由于不计吃水深度的变化,可取A=LPPT,其中LPP 为船舶垂线间长。
1.2 波浪作用对船舶横倾的影响船舶在波浪作用下会产生纵荡、横荡、垂荡、横摇、纵摇和艏摇等运动。其中,横摇对船舶横撞拦阻系统后抗倾覆性的影响不得不考虑。然而,真实海况中的波浪为不规则波,且横摇运动会影响波浪的作用,形成流固耦合问题,很难进行较为精确的理论求解。本文采用数值模拟的方法,通过建立三维水动力模型求解出船舶在不同频率与方向波浪下的横摇角θw。
1.2.1 静稳性分析如图 1所示,当船舶正浮于水线 WL时,浮心为B,在外力矩作用下倾斜θ角度后,水线斜至W1L1,浮心从B点移至B1点,过G点向倾斜后浮力作用线作垂线交于Z点,由图中的几何关系可知:
| $ \overline {GZ} = \overline {ON}-\overline {OH} $ | (4) |
式中:
| $ {l_\theta } = {y_{{\text{b1}}}}\cos \theta + {z_{{\text{b1}}}}\sin \theta $ | (5) |
| $ {\operatorname{l} _{\text{g}}} = {z_{\text{g}}}\sin \theta $ | (6) |
式中: yb1为倾斜后浮心B1的纵坐标,zb1为倾斜后浮心B1的垂向坐标,zg为重心G到基线的距离。因此,联立式(4)~(6) 得到船舶的静复原力矩:
| $ {M_{\text{r}}} = Dg{l_{\text{s}}}{\text{ = }}Dg\left( {{y_{{\text{b1}}}}\cos \theta + {z_{{\text{b1}}}}\sin \theta-{z_{\text{g}}}\sin \theta } \right) $ | (7) |
式中: D为船舶的排水量,g 为重力加速度。
稳性交叉(横截)曲线是一族以排水体积(量)为横坐标,以形状稳性力臂 lθ为纵坐标的等倾角曲线。如果给定排水量D和重心高度zg,则可以通过稳性交叉(横截)曲线求得一条横坐标为倾角θ,纵坐标为形状稳性力臂lθ的曲线(形状稳性力臂曲线),进而在该曲线上减掉各对应倾角下的重量稳性力臂lg,即可得到静稳性曲线(静稳性力臂ls随倾角θ 的变化曲线)[18]。
1.2.2 动稳性分析上述的静稳性问题是假定船舶受到外力矩的静力作用,船舶倾斜缓慢而忽略不计其角速度和角加速度。考虑到船舶横撞拦阻系统时存在外力矩的动力作用,因此需要进行相应的动稳性分析。在动稳性分析中,外力矩与复原力矩相等时,因惯性的缘故,船舶不会停止而要继续倾斜,只有当外力矩所做的功与复原力矩的功完全抵消时,船才会停止倾斜。该平衡角称为动平衡角 θd 。根据外力矩与复原力矩做功平衡有[18]:
| $ {M_{\text{d}}}{\theta _{\text{d}}} = {T_{\text{d}}} = {T_{\text{r}}} = \int_0^{{\theta _{\text{d}}}} {{M_{\text{r}}}} {\text{d}}\theta $ | (8) |
| $ {M_{\text{d}}} = \int_0^{{\theta _{\text{d}}}} {{M_{\text{r}}}} {\text{d}}\theta /{\theta _{\text{d}}} $ | (9) |
式中: Md为动倾力矩,Td为动倾力矩所做的功,Tr 为静复原力矩所做的功。
在已知静稳性曲线时,可根据式(8)、(9) 确定动倾力矩 Md与动倾角θd 的关系。为了安全起见,本文综合考虑船舶的静稳性与动稳性,以船舶动稳性分析求出的动倾力矩的大小为计算依据。
2 算例与结果分析船舶长LOA=45.37 m;垂线间长LPP=41.90 m;型宽B=9.20 m;型深H=3.40 m;驾驶室至艉升高甲板高度HO=4.80 m;艉升高甲板至基线高度HD=4.13 m;拦阻索作用点距基线高度4.13≤Zc≤8.93。船舶空载到港和满载出港时的相关参数如表 1所示。
| 载重条件 | 排水量/t | 重心高度/m | 吃水/m | 不同倾角下的形状稳性力臂/m | |||||||
| 10° | 20° | 30° | 40° | 50° | 60° | 70° | 80° | ||||
| 空载到港 | 239.90 | 2.607 | 0.88 | 1.382 | 2.313 | 2.835 | 3.190 | 3.226 | 3.125 | 2.826 | 2.447 |
| 满载出港 | 781.52 | 2.758 | 2.50 | 0.751 | 1.416 | 1.883 | 2.173 | 2.338 | 2.393 | 2.301 | 2.058 |
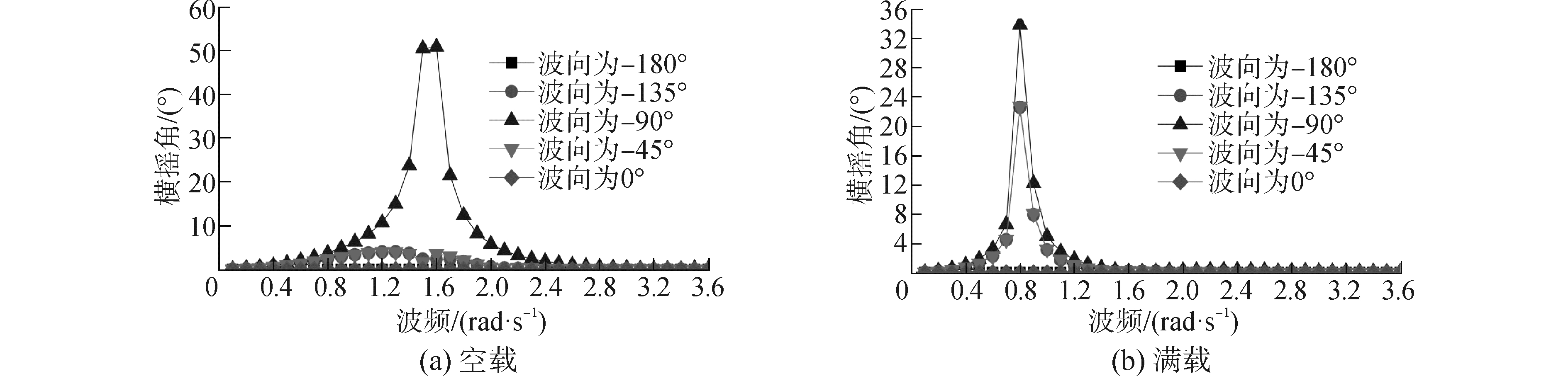
根据船舶的相关参数建立船舶模型,利用ANSYS-AQWA软件,计算得到其在不同频率与方向波浪(波幅a为1 m)作用下的横摇角如图 2所示。观察图 2可以发现,垂直于船长方向的波浪所引起的横摇角最大。对于周期5 s≤Tw≤6 s的波浪,其波频1.05≤ω≤1.26 rad/s,在此类波浪作用下,船舶空载时的横摇角θw≤15°;满载时的横摇角θw≤5°。
|
| 图2 船舶在不同方向和频率波浪作用下的横摇角 Figure 2 The ship roll angles under the action of waves with different directions and frequencies |
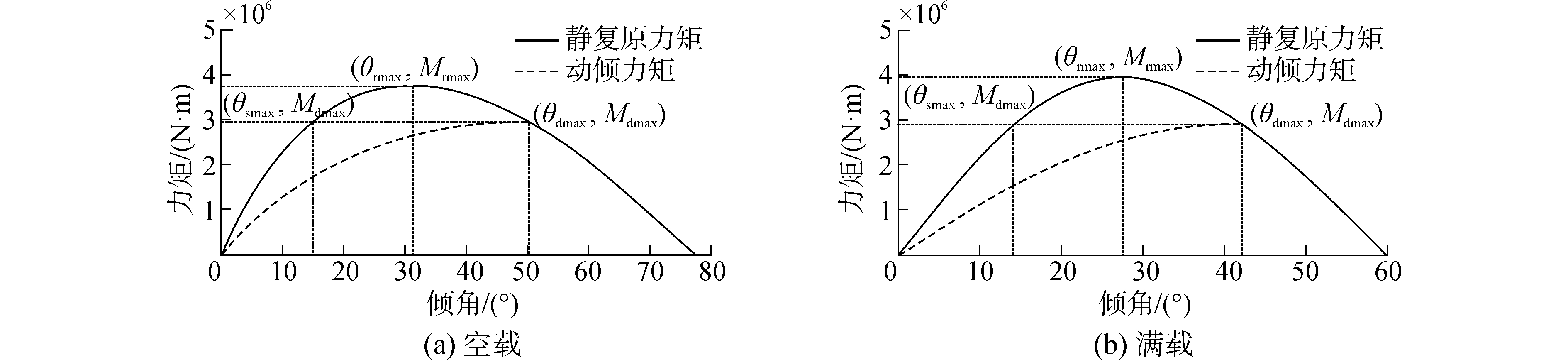
根据式(5)~(7)、式(9) 及表 1中的数据,可以得到船舶的静稳性和动稳性力矩曲线如图 3所示。从图中可以看出:静复原力矩mr随着倾角θ的增大先增大后减小; 动倾力矩Md随着动倾角θd的增加而非线性地增加。它们的最大值如表 2所示(θsmax为考虑动稳性时的最大静倾角)。
|
| 图3 力矩与倾角的关系 Figure 3 The relationship between moments and dip angles |
| 载重条件 | 静稳性 | 动稳性 | |||
| Mrmax/(N·m) | θrmax/(°) | Mdmax/(N·m) | θdmax/(°) | θsmax/(°) | |
| 空载到港 | 3.74×106 | 31.6 | 2.95×106 | 50.5 | 15.4 |
| 满载出港 | 3.95×106 | 27.7 | 2.91×106 | 42.3 | 14.3 |
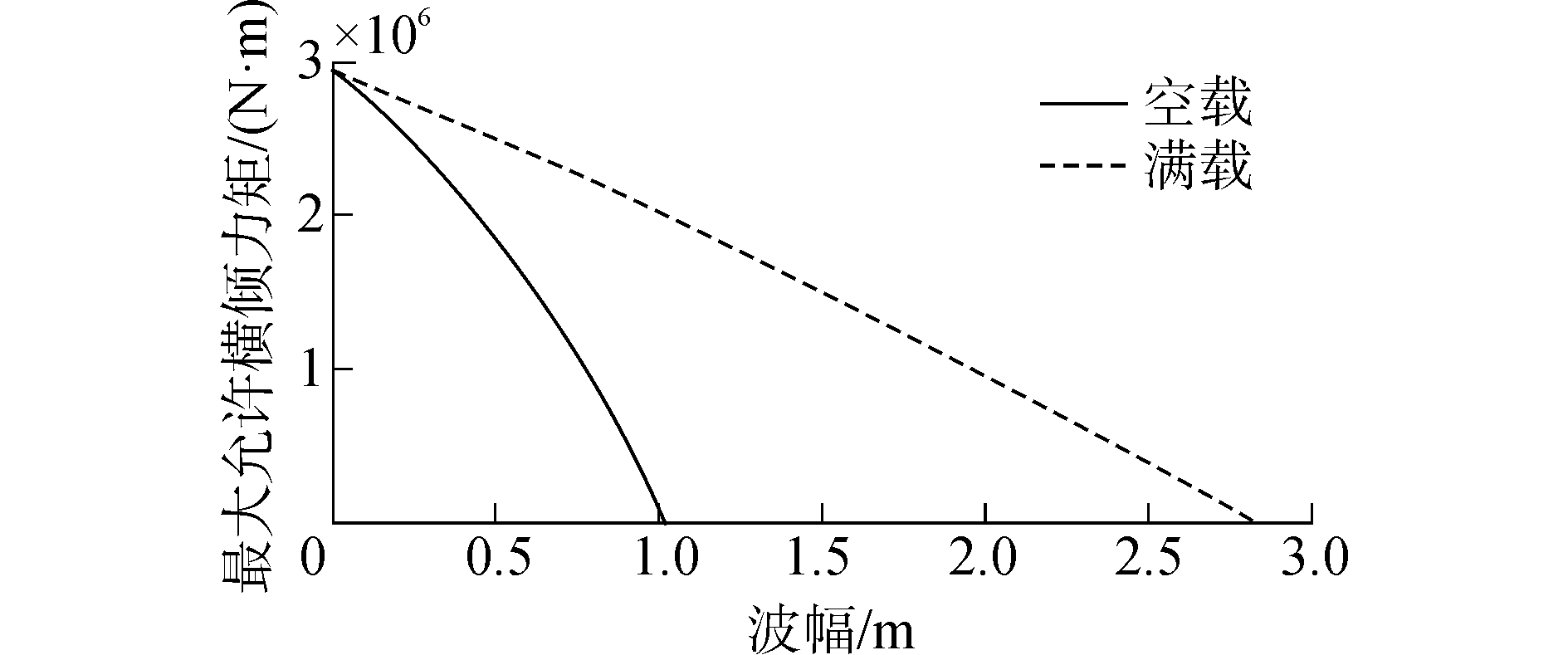
本文考虑最安全的情况进行计算,即以图 3中静稳性力矩曲线的 0~θsmax段为计算依据。假定波幅与横摇角成正比,将该段曲线x方向减去波幅对应的横摇角θw,y方向减去相应的波浪力矩Mw,并将相应的横摇角转化为波幅a,即可得到最大允许横倾力矩Mtmax与波幅a的关系曲线如图 4所示。
|
| 图4 最大允许横倾力矩与波幅的关系 Figure 4 The relationship between maximum heeling moment and its corresponding wave height |
由图 4可知,最大允许横倾力矩 Mtmax随波幅a的增加而减小;在不考虑波浪作用时, 船舶空载与满载的最大允许横倾力矩十分接近;但是,波浪对空载船舶的影响更大,要使满载船舶在波浪单独作用下不发生倾覆,则波幅a≤2.82 m;而要使空载船舶在波浪单独作用下不发生倾覆,则波幅a≤1.02 m。
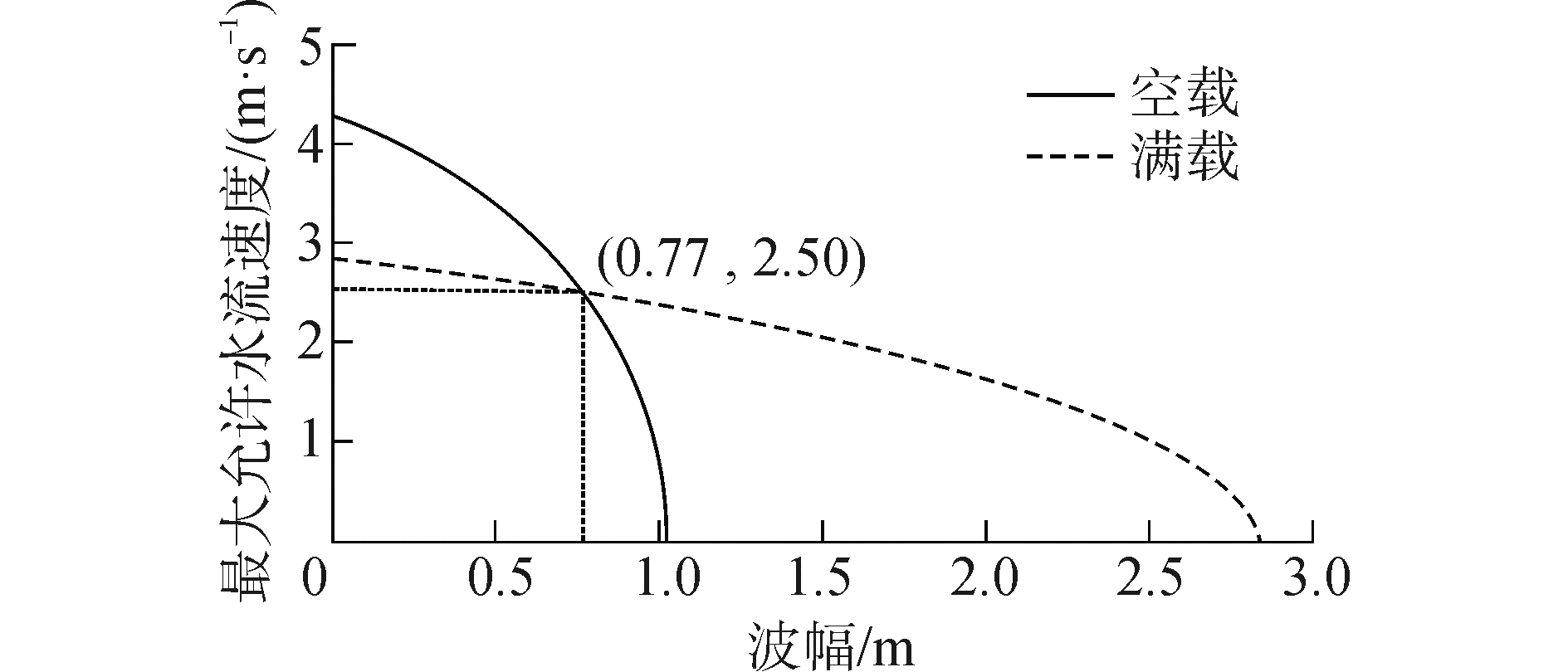
2.2 最大允许水流速度与波幅的关系根据图 4及式(2)、(3) 得到拦阻索作用高度Zc=4.13 m时,最大允许水流速度Umax随波幅a的变化曲线,如图 5所示。观察图 5可以发现,最大允许水流速度Umax随波幅a的增大而非线性地减小,且减小的速度越来越快;相对于满载船舶,波浪对空载船舶倾覆的影响更大;波幅a=0.5 m时,若要使空载船舶不发生倾覆,则应满足水流速度U<3.39 m/s;要使满载船舶不发生倾覆,则应满足水流速度U<2.64 m/s;当波幅a=0.77 m时,船舶空载与满载时不发生倾覆的最大允许速度相同,即Umax=2.5 m/s。
|
| 图5 最大允许水流速度随波幅的变化曲线 Figure 5 The relationship between permissible maximum velocity of water and wave height |
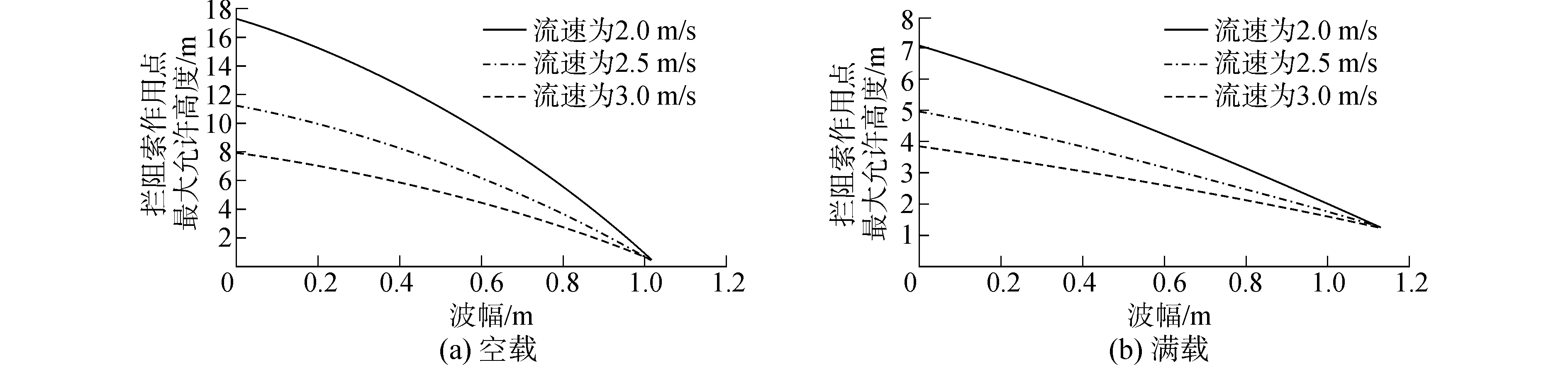
分别做出U=2.0 m/s、U=2.5 m/s、U=3.0 m/s条件下,拦阻索作用点最大允许高度 Zcmax 随波幅a的变化曲线如图 6所示。波幅a=0.5 m时,拦阻索作用点最大允许高度Zcmax的相关数据如表 3所示。由图 6及表 3可以发现,在波幅a=0.5 m条件下,U=2.0 m/s时船舶空载不会有发生倾覆的危险;但对于更高的流速,如U=2.5 m/s时要保证作用高度 Zc≤7.24 m, U=3.0 m/s时要保证作用高度Zc≤5.16 m,船舶才不会倾覆。对于满载船舶,U=2.0 m/s、U=2.5 m/s时要分别保证作用高度Zc≤6.27 m和Zc≤4.46 m,船舶才不会倾覆,U=3.0 m/s时,船舶会发生倾覆。此外,图 6(a)、(b)均体现了拦阻索作用点最大允许高度Zcmax随波幅的增大而非线性减小的规律。
|
| 图6 不同流速下,拦阻索作用点最大允许高度与波幅的关系曲线 Figure 6 The relationship between the permissible maximum action height and the wave amplitude under various velocities |
| 载重条件 | 拦阻索作用点的最大允许高度/m | ||
| U=2.0 m/s | U=2.5 m/s | U=3.0 m/s | |
| 空载到港 | 11.07 | 7.24 | 5.16 |
| 满载出港 | 6.27 | 4.46 | 3.48 |
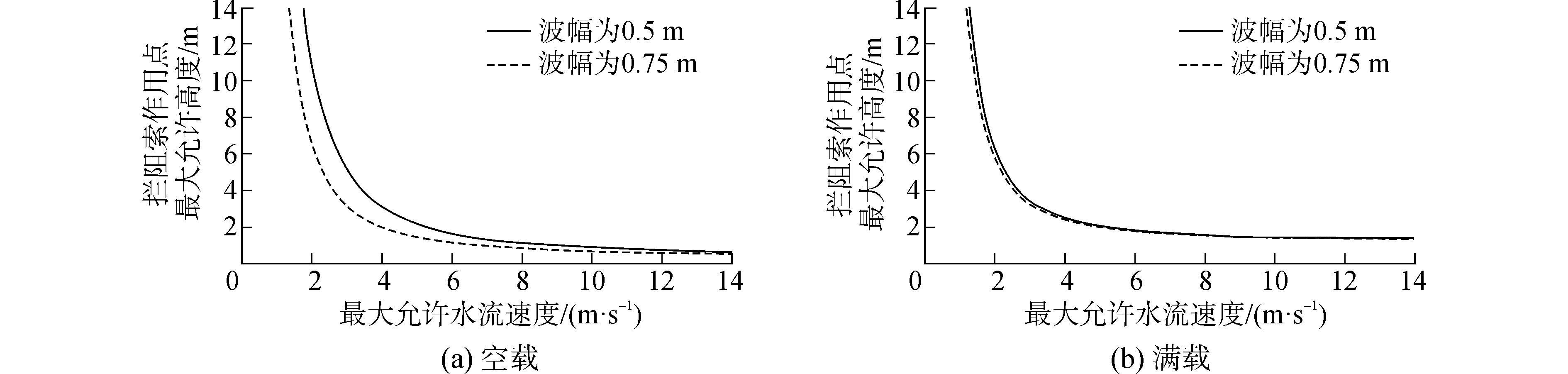
船舶在空载和满载条件下不同波幅波浪作用时,拦阻索作用点最大允许高度Zcmax与最大允许流速Umax的关系曲线如图 7所示。观察图 7可以发现:拦阻索作用点最大允许高度Zcmax与流速Umax成反比。同时,图 7是判定船舶在波浪作用下是否倾覆的重要依据,即可以确定任意流速(或作用高度)下的极限作用高度(或流速)。当船舶的状态参数点落在曲线以下部分船舶不发生倾覆,落在曲线以上则发生倾覆,曲线上的点为临界状态(同理,可判断其他波幅条件下的拦阻索作用点最大允许高度Zcmax与流速Umax)。
|
| 图7 拦阻系统最大允许作用高度与最大允许流速的关系 Figure 7 The relationship between the permissible maximum action height and the permissible maximum velocity of water |
本文为判断船舶在撞击拦阻系统后的抗倾覆性提供了一种近似方法,该方法假定船舶的横倾由波浪作用和水流力作用的线性叠加产生,并通过数值模拟求出船舶在波浪作用下的横摇角,进而确定波浪波幅、最大允许水流速度及拦阻索最大允许作用高度间的关系。
1) 垂直于船长方向的波浪对船舶的横摇影响最大。
2) 相对于满载船舶,波浪对空载船舶倾覆的影响更大。
3) 推导了静稳性力矩 Mr和动倾力矩Md与倾角θ的关系,并在此基础上得到了拦阻索最大允许作用高度Zcmax和最大允许水流速度Umax 随波幅的增大而减小的规律。
4) 给出了波幅为a=0.5 m和a=0.75 m时,船舶在空载和满载条件下,拦阻索作用最大允许高度Zcmax与最大允许流速Umax的关系曲线,为判定船舶在波浪和水流作用下的稳性提供了重要依据。
然而,本文的研究也存在一些不足,如仅考虑了恒定外力矩下的船舶抗倾覆问题,并假设了波浪与水流力对船舶为线性作用。因此,若要得到更精确的结果,则在分析中还应考虑风荷载、吃水深度变化以及拦阻索作用力的偏心等问题,并且船舶与波浪及水流的流固耦合问题也将大大增加问题求解的复杂性。
| [1] | CAGLAYAN I, STORCH R L. Stability of fishing vessels with water on deck―a review[J]. Journal of ship research, 1982, 26(2): 106–116. |
| [2] | TAYLAN M. Static and dynamic aspects of a capsize phenomenon[J]. Ocean engineering, 2003, 30(3): 331–350. DOI:10.1016/S0029-8018(02)00027-6 |
| [3] | WANG Hongming, SUN Peiting, SHI Changfeng, et al. Capsize probability research on sailing ship's roll[J]. Journal of ship mechanics, 2011, 15(12): 1353–1361. |
| [4] |
姜治芳, 黄卫刚, 邱辽原, 等. 内倾船型的非线性横摇仿真分析[J].
中国舰船研究, 2014, 9(1): 40–45,51.
JIANG Zhifang, HUANG Weigang, QIU Liaoyuan, et al. Simulation analysis of non-linear roll of a tumblehome hull ship[J]. Chinese journal of ship research, 2014, 9(1): 40–45,51. |
| [5] |
刘利琴, 唐友刚, 张若瑜. 甲板上浪船舶随机横摇响应的数值模拟[J].
天津大学学报, 2011, 44(7): 571–576.
LIU Liqin, TANG Yougang, ZHANG Ruoyu. Numerical simulation of random rolling response of ship with water on deck[J]. Journal of Tianjin University, 2011, 44(7): 571–576. |
| [6] |
常永全, 范菊, 朱仁传, 等. 迎浪船舶的参数横摇分析[J].
水动力学研究与进展A辑, 2008, 23(2): 204–211.
CHANG Yongquan, FAN Ju, ZHU Renchuan, et al. Analysis of ship parametric rolling in head sea[J]. Journal of hydrodynamics A, 2008, 23(2): 204–211. |
| [7] |
李红霞, 唐友刚, 刘利琴, 等. 船舶随浪中参数激励非线性随机横摇运动计算[J].
哈尔滨工程大学学报, 2007, 28(3): 247–252.
LI Hongxia, TANG Yougang, LIU Liqin, et al. Simulation of the parametrically excited nonlinear rolling of ship in random following seas[J]. Journal of Harbin Engineering University, 2007, 28(3): 247–252. |
| [8] | MCCUE L, TROESCH A. Probabilistic determination of critical wave height for a multi-degree of freedom capsize model[J]. Ocean engineering, 2005, 32(13): 1608–1622. DOI:10.1016/j.oceaneng.2004.10.024 |
| [9] | LIU Liqin, TANG Yougang. Stability of ships with water on deck in random beam waves[J]. Journal of vibration and control, 2007, 13(3): 269–280. DOI:10.1177/1077546307073676 |
| [10] |
鲁江, 顾民, 马坤, 等. 随机波中船舶参数横摇研究[J].
船舶力学, 2012, 16(8): 893–900.
LU Jiang, GU Min, MA Kun, et al. A study on parametric rolling in irregular waves[J]. Journal of ship mechanics, 2012, 16(8): 893–900. |
| [11] |
鲁江, 马坤, 黄武刚. 规则波中船舶复原力和参数横摇研究[J].
海洋工程, 2011, 29(1): 61–67.
LU Jiang, MA Kun, HUANG Wugang. Research on roll restoring variation and parametric rolling in waves[J]. Ocean engineering, 2011, 29(1): 61–67. |
| [12] | LU Jiang, UMEDA N, MA K. Theoretical study on the effect of parametric rolling on added resistance in regular head seas[J]. Journal of marine science and technology, 2011, 16(3): 283–293. DOI:10.1007/s00773-011-0127-0 |
| [13] | BULIAN G, FRANCESCUTTO A, UMEDA N, et al. Qualitative and quantitative characteristics of parametric ship rolling in random waves in the light of physical model experiments[J]. Ocean engineering, 2008, 35(17): 1661–1675. |
| [14] |
刘威, 朱发新, 温小飞, 等. 船舶稳性及受撞即时倾覆影响因素分析研究[J].
机电设备, 2013, 30(4): 20–23.
LIU Wei, ZHU Faxin, WEN Xiaofei, et al. Study on stability and influencing factors of instant capsizing of ship collision[J]. Electromechanical equipment, 2013, 30(4): 20–23. |
| [15] |
李叶兴, 陈国平, 严士常, 等. 大型油轮水流力试验研究[J].
水运工程, 2012(9): 12–17.
LI Yexing, CHEN Guoping, YAN Shichang, et al. On ship current force under different current angles[J]. Port & water engineering, 2012(9): 12–17. |
| [16] |
万俊, 刘星, 牙琪敏, 等. 弯道中环流对船舶产生的倾覆力矩计算分析[J].
水运工程, 2007(1): 30–32.
WAN Jun, LIU Xing, YA Qimin, et al. Study and calculations of capsizing moment of circumfluence on ships in curving channels[J]. Port & water engineering, 2007(1): 30–32. |
| [17] |
JTS 144-1-2010, 港口工程荷载规范[S]. 北京: 人民交通出版社, 2010.
JTS 144-1-2010, Load code for harbor engineering[S]. Beijing: China communications press, 2010. |
| [18] |
刘红.
船舶原理[M]. 上海: 上海交通大学出版社, 2009: 123-128.
LIU Hong. Principles of naval architecture[M]. Shanghai: Shang Hai Jiao Tong University Press, 2009: 123-128. |



