ROV(remote operated vehicle)是人类在海洋探索和开发中的重要工具,运动控制技术是ROV的关键技术之一,是各国研究机构的研究热点,而ROV推进系统模型是设计运动控制策略的基础。液压伺服系统具有系统体积小、重量轻、控制精度高、响应速度快的优点,广泛用于ROV的推进系统。按照所使用的调速方法不同,ROV液压推进系统又可以分为节流调速系统和容积调速系统两大类[1]。节流调速系统通过改变控制阀的节流口大小,调节液压马达的转速,如加拿大ASE公司的HYSUB作业型ROV。容积调速系统则是通过改变液压马达的排量进行调速,容积调速系统虽然相对复杂且成本较高,但效率较高,发热量小,控制精确,且变量马达的排量普遍较大,易获得大流量高转速,广泛应用于大功率ROV,如英国Perry Slingsby公司生产的TRITON系列作业型ROV等。基于其以上优良性质,上海交通大学水下工程研究所研制的“海龙二号”ROV液压推进系统采用了基于变量马达的容积调速系统。以往对于ROV推进系统的研究多侧重于推力控制分配算法,而对液压推进器伺服控制系统控制模型研究较少[1-3]。文献[4]根据推进器的推力-油压-流量曲线图来计算定量液压推进器的控制输入,文献[5]对ROV定量液压推进器控制系统输入输出关系进行了线性化,并且利用阶跃响应系统辨识法得到了系统的二阶模型,但阶跃响应法辨识误差较大。以上均未涉及变量液压推进器伺服控制系统建模,而液压推进器伺服控制系统中诸如液压缸等构件的内部参数难以测量,因此有必要参数化其数学模型,对其进行辨识,以便得到一个可以更客观的反映推进器性能的控制模型,为控制策略的研究提供一个可靠的基础。为此,作者设计了辨识试验,采用改进的遗传算法对ROV变量液压推进器伺服控制系统进行了辨识。
遗传算法源于自然进化与遗传机制,将‘优胜劣汰,适者生存’的生物进化原理引入待辨识参数形成的编码串联群体中,在解空间中进行大规模、全局、并行搜索,使种群朝全局最优的方向收敛。遗传算法有着极强的鲁棒性,与梯度类优化算法相比,遗传算法可以明显地改善辨识结果,但本身存在着易早熟,局部搜索能力较低的不足[6-7]。捕食搜索算法是一种用于解决组合优化问题的空间搜索策略,它是在模拟动物捕食行为的基础上提出的,是一种平衡全局搜索能力和局部开发能力的方法[8]。应用捕食搜索算法寻优时,先在整个搜索空间进行全局搜索,直到找到一个较优解,然后在较优解附近区域进行集中搜索,直到搜索很多次也没有找到更优解,从而放弃局部搜索转为全局搜索。
受此启发,本文提出了一种深度捕食策略,较好地解决了搜索效率问题,特别是变异方式的改进,有效提高了算法的局部搜索能力。同时,遗传算法初始种群的个体分布状况直接影响算法的全局收敛能力,在标准遗传算法中交叉机制能够搜索包含当前种群极小模式中的所有个体, 但却不能搜索到不在当前种群极小模式中的个体[9]。
当然, 初始种群中若最优解的信息较少也可以通过群体的进化来得到, 从而达到最优解, 但由于算子本身的随机性, 仅靠算子是不能确保算法搜索到最优解区域的,本文基于均匀实验设计,提出了一种新的种群初始化方法,较好的解决了遗传算法的全局收敛性性问题。
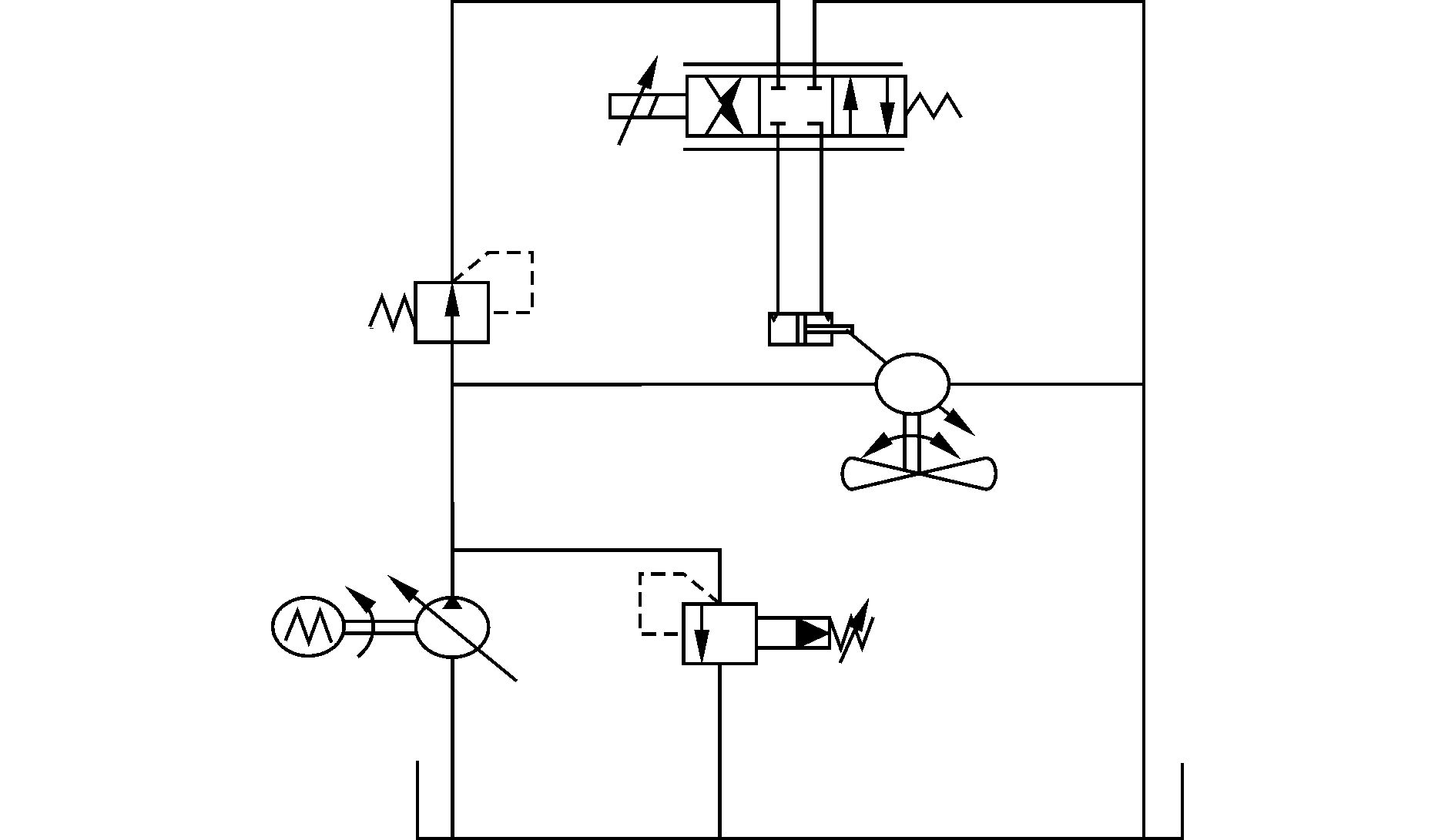
1 ROV液压推进器伺服控制系统建模“海龙二号”ROV变量液压推进器伺服控制系统的主要部件包括:Star200液压伺服阀、液压缸、变量马达、连接管路、螺旋桨。马达的排量由伺服阀控液压缸装置控制,伺服阀的阀开口大小与给定信号成比例,控制液压缸活塞运动,活塞位移对应变量马达斜盘倾角,进而控制马达的排量,从而控制马达转矩与桨的推力。液压原理如图 1所示。
|
| 图1 ROV推进器液压原理图 Figure 1 Hydraulic schematic diagram of ROV thruster |
考虑到伺服阀的带宽在100Hz左右,远高于液压缸与变量马达带宽,因此伺服阀的动态特性可以忽略,近似为比例环节。
1) 伺服阀数学模型的建立。
| ${{X}_{v}}(s)/I(s)={{K}_{bv}}$ | (1) |
式中:Kbv为伺服阀增益系数,m/A;Xv为伺服阀芯位移量,m;I为输入电流,A。
2) 液压缸数学模型[10]。
| $Z(s)=\frac{\frac{{{K}_{q}}}{A}{{X}_{v}}(s)-\frac{{{K}_{ce}}}{{{A}^{2}}}(1+\frac{{{V}_{t}}}{4{{\beta }_{e}}{{K}_{ce}}}s)s{{F}_{L}}(s)}{(\frac{s}{{{w}_{r}}}+1)(\frac{{{s}^{2}}}{w_{0}^{2}}+2\frac{{{\zeta }_{0}}}{{{w}_{0}}}{{s}^{2}}+1)}$ | (2) |
式中:Z为液压缸活塞位移量,m;Kq为伺服阀在稳定工作点附近的流量增益,m3/s;Kce为总流量压力系数,m5/N·s;A为液压缸活塞有效面积,m2;Vt为两腔的总容积,m3;βe为有效体积弹性模量,N/m3;FL为作用在活塞上的任意负载力,N;w0为综合固有频率,Hz;wr为惯性环节的转折频率,Hz;ζ0为综合阻尼比。
3) 斜盘环节数学模型的建立。
| $\gamma (s)=Z(s)/L=K(\varphi )Z(s)$ | (3) |
式中:L为变量活塞油缸施力点与斜盘铰接点的距离,m;γ为变量马达斜盘倾角,rad;K(φ)为变量马达斜盘倾角系数。
4) 变量马达环节数学模型的建立[10]。
| $\frac{M(s)}{\gamma (s)}=\frac{{{D}_{m0}}({{w}_{m0}}{{D}_{m0}}+{{C}_{t}}{{p}_{10}}+\frac{{{V}_{0}}{{p}_{10}}}{{{\beta }_{e}}}s)}{{{C}_{t}}+\frac{{{V}_{0}}}{{{\beta }_{e}}}s}$ | (4) |
式中:M为马达输出,N·s;Dm0为变量马达的最大排量,m3;wm0为调节变量马达时的初始转速,rad/s;Ct为变量马达的总泄露系数,m5/N·s;p10为调节变量马达时高压侧的初始压力,Pa;V0为马达工作腔及连接管道的总容积,m3。
5) 扭矩-桨推力环节数学模型。
| $T(s)={{K}_{TM}}(s)\centerdot M(s)$ | (5) |
式中:KTM为扭矩至推力的转换子。
6) 系统的传递函数。
| $\frac{T(s)}{I(s)}=\frac{{{K}_{z}}(1+\frac{{{V}_{0}}{{p}_{10}}}{{{\beta }_{e}}({{w}_{m0}}{{D}_{m0}}+{{C}_{t}}{{p}_{10}})}s)}{(\frac{s}{{{w}_{r}}}+1)(\frac{1}{{{w}_{0}}^{2}}{{s}^{2}}+\frac{2{{\zeta }_{0}}}{{{w}_{0}}}s+1)(1+\frac{{{V}_{0}}}{{{\beta }_{e}}{{C}_{t}}}s)}$ | (6) |
式中:Kz=KbvKqKφDm0KTM(wm0Dm0+Ctp10)/A。
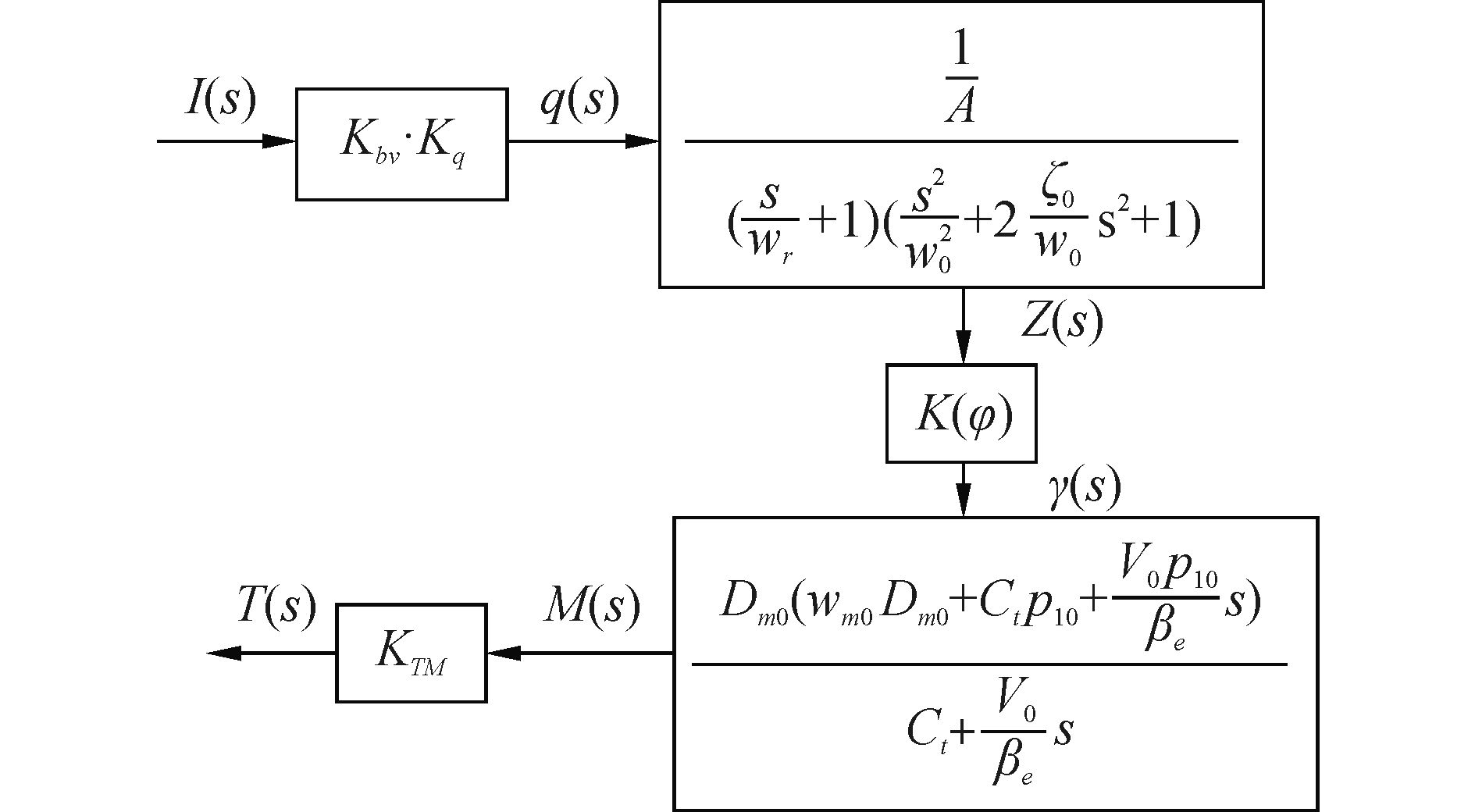
由理论推导知,ROV变量液压推进器伺服控制系统的控制模型为四阶时变线性模型,如式(6) ,系统传递函数方框图如图 2。
|
| 图2 系统传递函数方框图 Figure 2 Block diagram of transfer function |
但考虑到工程实际,辨识到三阶模型已经足够,因为弹性模量βe量级在108左右,零点与第四个极点负实部的绝对值很大,且彼此接近,对应的响应分量衰减迅速,对系统性能影响甚微,可以忽略[11]。故系统的传递函数可简化为
| $\frac{T(s)}{I(s)}=\frac{K}{(\frac{s}{{{w}_{r}}}+1)(\frac{1}{{{w}_{0}}^{2}}{{s}^{2}}+\frac{2{{\zeta }_{0}}}{{{w}_{0}}}s+1)}$ | (7) |
系统辨识的方法很多,遗传算法是一种基于进化论的非梯度并行优化算法,能在复杂空间进行鲁棒搜索,所以本文采用遗传算法完成ROV变量液压推进器伺服控制系统的辨识工作,并针对遗传算法易早熟,难以找到精确最小值等问题,进行了改进。由式(7) 可知:
| $\begin{align} & G(s)=\frac{T(s)}{I(s)}=\frac{K}{(\frac{s}{{{w}_{r}}}+1)(\frac{1}{{{w}_{0}}^{2}}{{s}^{2}}+\frac{2{{\zeta }_{0}}}{{{w}_{0}}}s+1)}= \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{{{a}_{1}}}{{{s}_{3}}+{{a}_{2}}{{s}^{2}}+{{a}_{3}}s+{{a}_{4}}} \\ \end{align}$ | (8) |
辨识参数集为
| $J=\gamma \centerdot \sum\limits_{i=1}^{N}{\frac{1}{2}}{{({{y}_{i}}-{{{\hat{y}}}_{i}})}^{2}}$ | (9) |
式中:N为测试数据的数量,yi为模型第i个测试样本的输出,γ为常数因子。在推力的实际测量过程中存在一定的干扰误差,目标函数值不可能达到理想状态
| $F(\hat{X})=\frac{1}{J(\hat{X})}$ | (10) |
无论是从遗传算法的基础理论还是从算子的运算方式上讲, 交叉操作对初始种群的依赖性较强, 而遗传算法的搜索速度主要依赖于交叉计算, 所以, 初始种群的优劣也会对算法的快速性产生较大的影响。确定初始种群的核心就是希望初始种群拥有合理的多样性并在尽可能少的代数内将寻优搜索引导到最优解区域[12]。均匀设计是解决这一问题科学而有效的方法。均匀设计可以用最少的信息来获取空间最多信息。均匀设计表产生的方法很多,从算法简便性出发,现采用拉丁方法产生均匀设计表Un(ns)[13]。具体构造方法如下:
1) 给定水平数n, 用1, 2, …, n作为拉丁方元素。给定[1, 2, …, n]的一个置换,例如[2, 1, 3, …, n],将该向量每个元素左移一格,第一个元素移到向量的最后位置,得到[1, 3, …, n, 2] ,重复此操作n-1次,得到的n个向量组成一个拉丁方。
2) 任一拉丁方就是一个Un(nn)。该拉丁方共n!个。
3) 引入均匀性度量函数中心化L2-偏差:
| $\begin{align} & \text{C}{{\text{D}}_{\text{2}}}(P)=[{{\left( \frac{13}{12} \right)}^{n}}-\frac{{{2}^{1-n}}}{n}\sum\limits_{k=1}^{n}{\prod\limits_{i=1}^{n}{(}}2+\left| {{x}_{ki}}-\frac{1}{2} \right|- \\ & \ \ \ \ \ {{\left| {{x}_{ki}}-\frac{1}{2} \right|}^{2}}+\frac{1}{{{n}^{2}}}\sum\limits_{k,l=1}^{n}{\prod\limits_{i=1}^{n}{(}}1+\frac{1}{2}\left| {{x}_{ki}}-\frac{1}{2} \right|+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \left| {{x}_{li}}-\frac{1}{2} \right|-\frac{1}{2}\left| {{x}_{ki}}-{{x}_{li}} \right|){{]}^{\frac{1}{2}}} \\ \end{align}$ | (11) |
以此函数作为检验标准从n!个拉丁方中挑一个均匀性最好的Un*(nn)。
4) 从Un*(nn)中挑选s列,使之均匀性最好,构成Un(ns)。
5)
遗传算法的收敛主要是取决于交叉算子和变异算子。交叉算子提供了全局搜索能力,而变异算子则提供了局部搜索能力[14]。进化初期,应确保种群在大范围内搜索,进行全局搜索以避免过早收敛,进化后期,种群成熟度较高,个体更加逼近最优解,种群应该在局部范围内搜索,重点搜索,尽可能提高精度。捕食搜索策略是一种平衡全局搜索能力和局部开发能力的方法。将其应用到遗传算法中,以适应度的变化来实现全局搜索和局部优化的切换。以最大化适应度为目标,历代最好适应度为BestF(kg-1) ,当代最好适应度为BestF(kg) 。两者的比值
为提高局部搜索能力,将变异方式进行改进,从当前种群中随机选择三个个体Xp1、Xp2、Xp3,并且i≠p1≠p2≠p3。
| ${{X}_{i,j}}(t+1)={{X}_{B,j}}+F\centerdot ({{X}_{{{p}_{2}},j}}(t)-{{X}_{{{p}_{3}},j}}(t))$ |
式中:F为变异因子,p1、p2、p3为随机整数,表示个体在种群中序号,XB(t) 为当前种群中最好的个体。变异时利用差异化向量进行变异操作,并且借鉴了当前种群最好个体的信息,可加快收敛速度。
| $\left\{ \begin{align} & {{P}_{c1}}={{P}_{c1\max }}-({{P}_{c1\max }}-{{P}_{c1\min }})\centerdot kg/G \\ & {{P}_{m1}}={{P}_{m1\max }}+({{P}_{m1\max }}-{{P}_{m1\min }})\centerdot kg/G \\ \end{align} \right.$ | (12) |
式中:kg为当前进化代数,G为总进化代数,Pc1max、Pc1min分别为最大、最小交叉概率,Pm1max、Pm1min分别为最大、最小变异概率。
2.3 改进遗传算法的实现步骤1 )设置算法运行参数,种群大小n,编码长度L,最大进化代数G,局部搜索代数nn,遗传算子操作概率Pc1max、Pc1min、Pm1max、Pm1min、Pc2、Pm2 ,参数搜索范围向量Xmin、Xmax,初始化种群。
2 )计算种群中个体的适应度。
3) 选择:根据个体适应度大小按适度比例法选择个体,采用精英保留策略保留最优个体。
4) 计算当代最佳适应度与历代最佳适应度之比g,决定交叉和变异概率以及变异方式。若g>k, 进行局部搜索,否则转6) 。
5) 进行局部搜索。
6) 判断局部搜索代数m是否大于nn,若是则进行全局搜索,否则转4) 。
7) 进行全局搜索。
8) 进化终止条件判断,如满足条件,则停止计算输出最佳结果,否则转2) 。
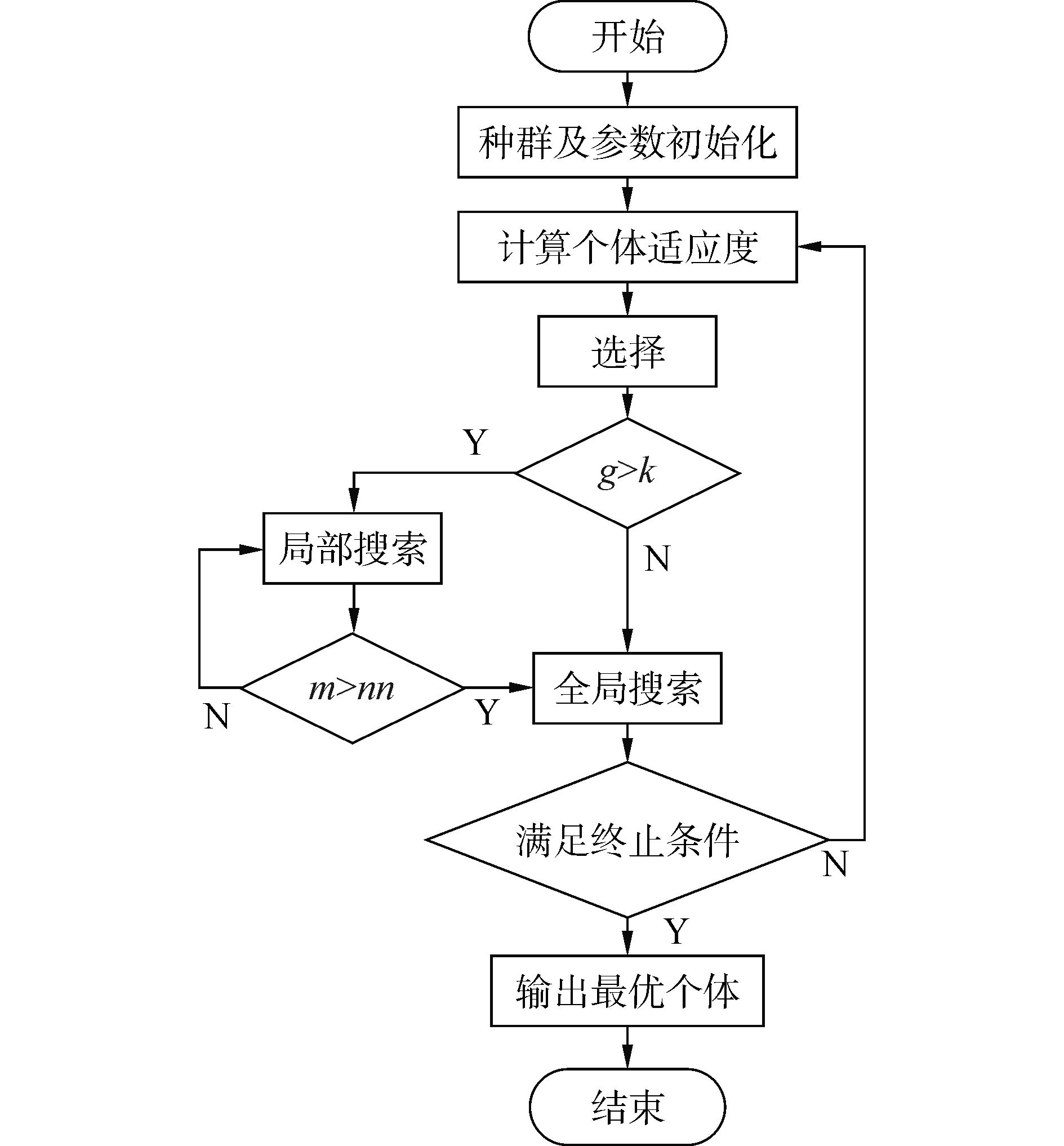
改进遗传算法流程如图 3所示。
|
| 图3 改进遗传算法流程图 Figure 3 Flow chart of improved genetic algorithm |
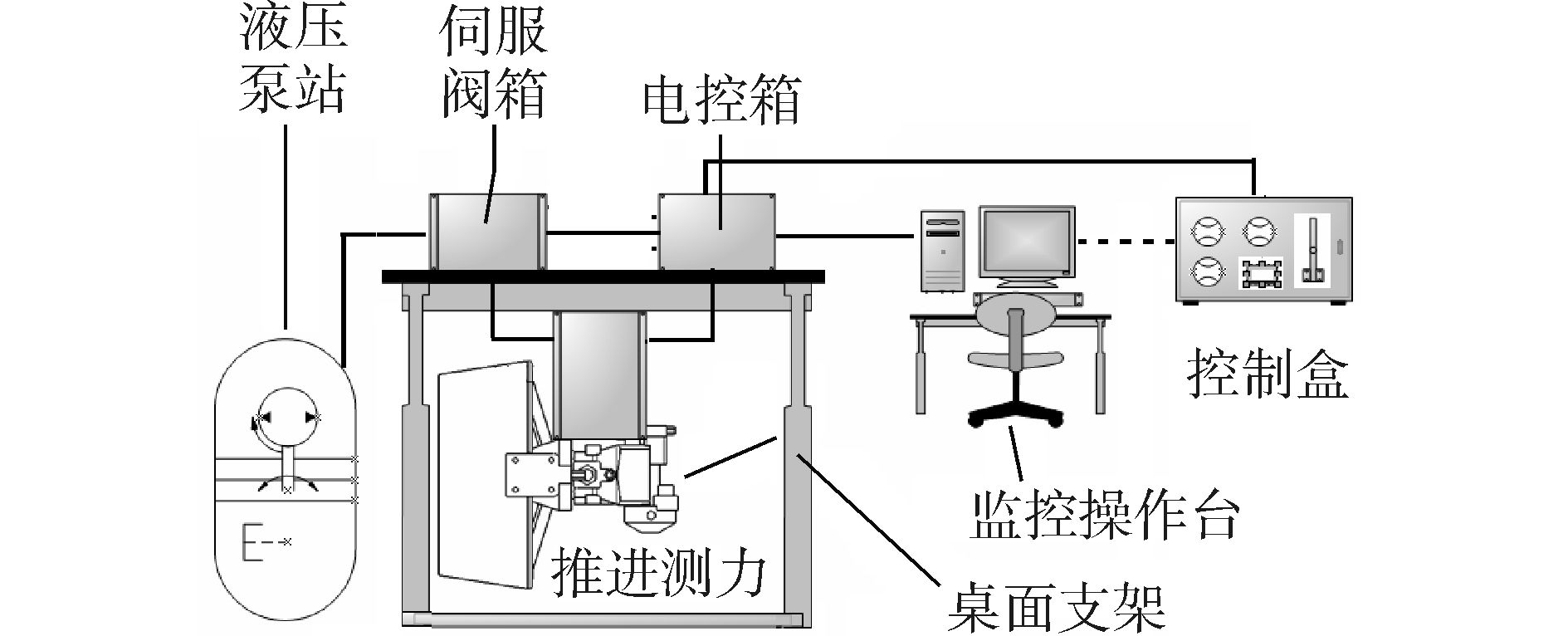
本文试验是在上海交通大学水下工程研究所液压伺服试验平台上进行的,该平台是集机械、电控、液压与仪表为一体的综合性能试验台, 主要由液压泵站、伺服阀箱、电控箱、推进测力单元、手操面板、桌面支架和监控操作台组成,如图 4所示。
|
| 图4 液压伺服平台组成图 Figure 4 Composition diagram of hydraulic platform |
利用该平台能够实现对单推进器的液压伺服控制和油压、推力等关键参数的测量与记录。试验采样频率为100Hz,其输入电压范围为-10~10V,S型拉力传感器EVT-10A的量程为-4900~4900N,精度2.0±10%mV/V。首先对拉压力传感器进行标定,验证其准确性,然后安装推进器、油压传感器和流量传感器等,将台架放入水底后,再进行水池测试。选择正弦信号作为输入信号,记录推力数据。试验布置如图 5所示。

|
| 图5 试验布置图 Figure 5 Picture of test |
设定种群规模为n=30,Pc1max=0.8,Pm1max=0.18,Pm1min=0.1,Pc2=0.2,Pm2=0.4,k=1。总迭代次数为100时,可以达到较好的辨识效果。
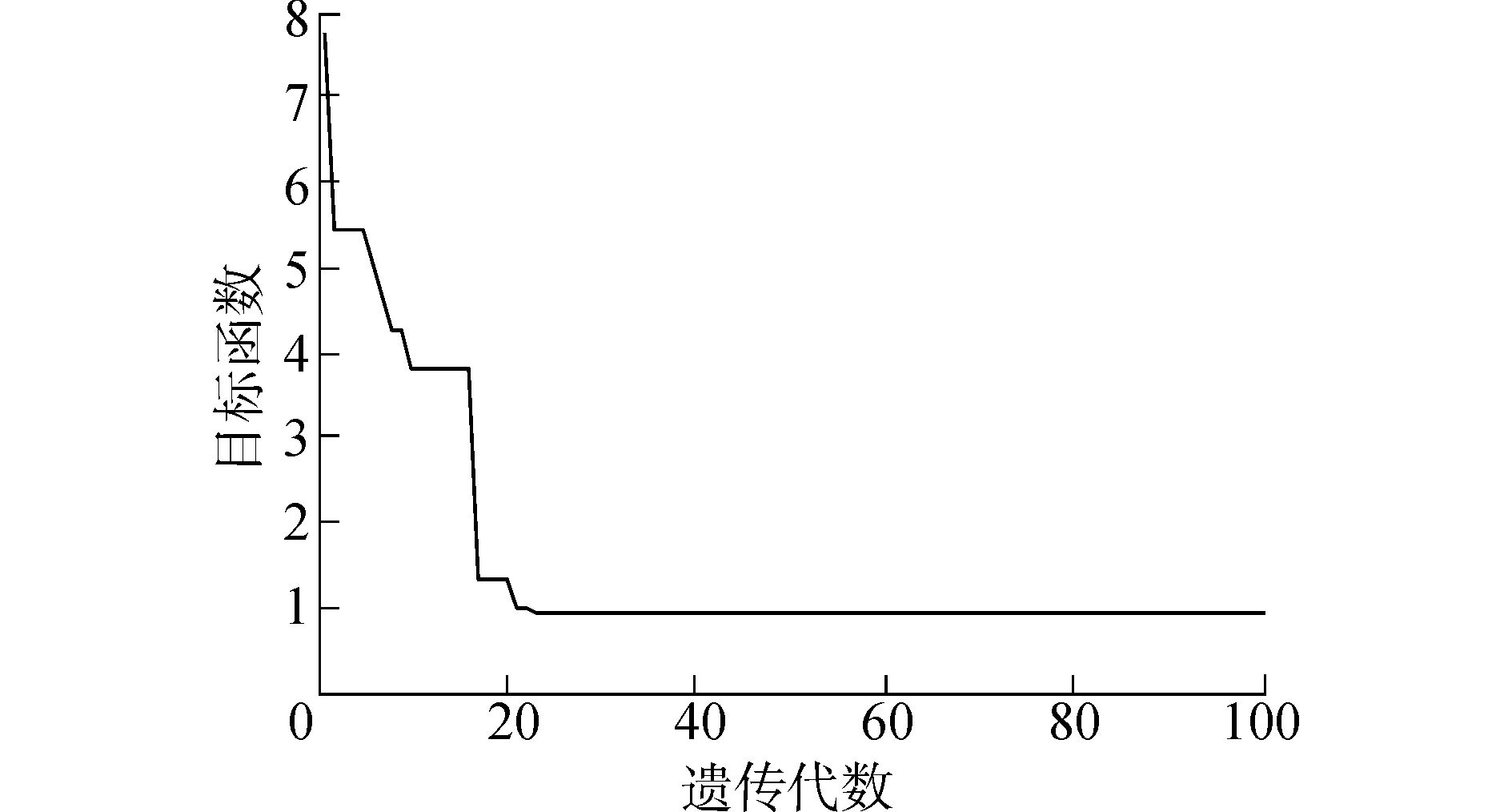
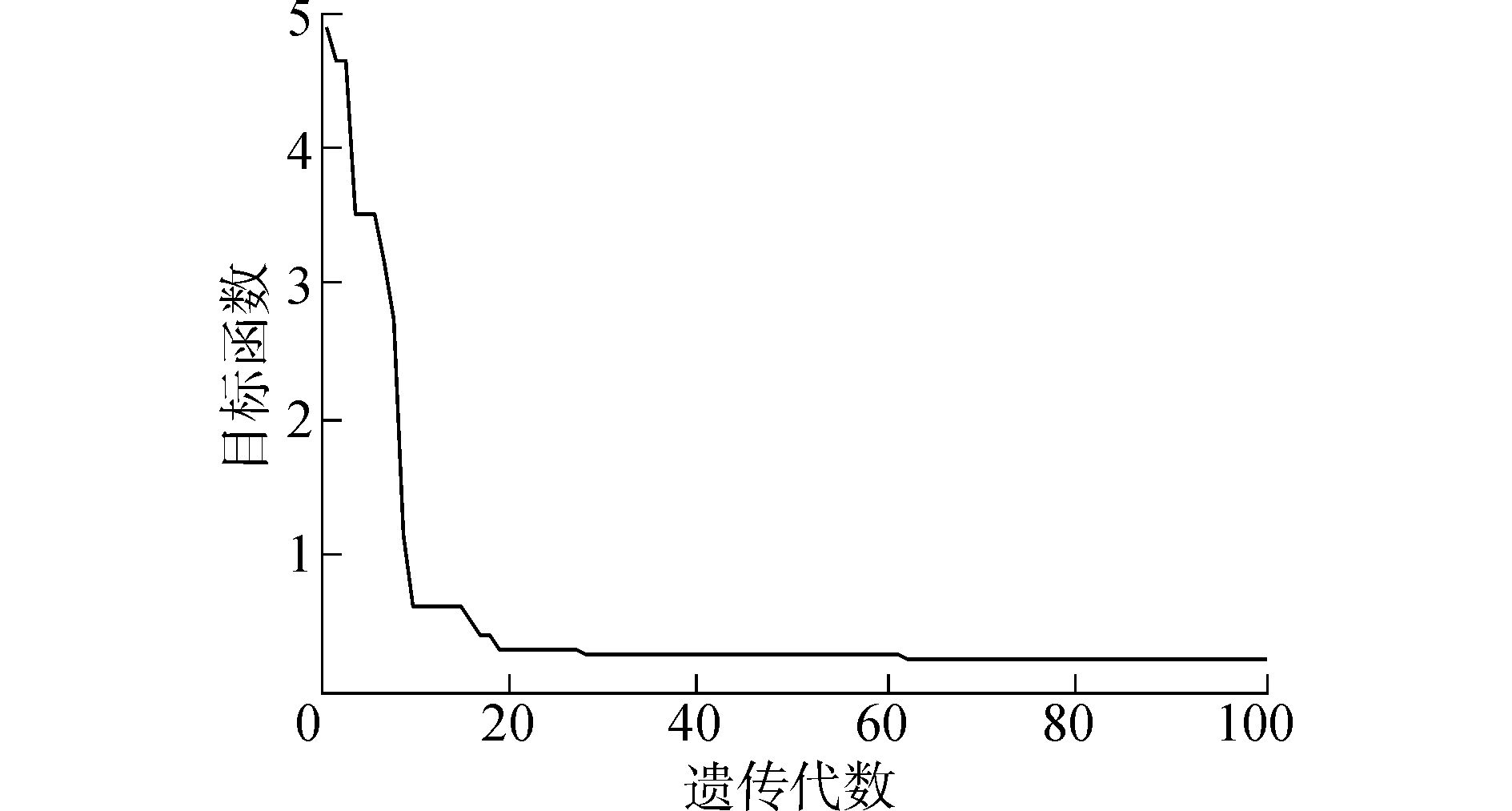
以试验输入和去除高频扰动后的试验输出作为样本数据,分别采用未改进遗传算法和改进遗传算法对参数进行10次重复辨识,结果如表 1所示。图 6、图 7为典型算例目标函数变化图,采用未改进遗传算法辨识参数时,大约在25代左右目标函数值基本收敛到0.73,继续运算时目标函数值停滞不前,程序陷入“局部最小值”,很难再进一步得到更准确的结果。而采用改进遗传算法能够跳出“局部最优”且收敛速度明显增快,目标函数值达到0.13,经过相同次数的迭代运算目标函数值更小,因此,改进遗传算法的计算结果与实际结果的符合程度更高,辩识出的参数更准确。根据改进遗传算法辨识得到的最优个体建立ROV变量液压推进器的控制模型:
| $\frac{T(s)}{I(s)}=\frac{80.431}{(s+7.09)({{s}^{2}}+6.056s+265.5)}$ |
| 遗传算法 | 平均进化代数 | 平均目标函数值 | 最小目标函数值 |
| 未改进 | 38.7 | 0.80 | 0.73 |
| 改进 | 35.8 | 0.17 | 0.13 |
|
| 图6 未改进遗传算法目标函数 Figure 6 Convergence process of unimproved GA |
|
| 图7 改进遗传算法目标函数 Figure 7 Convergence process of improved GA |
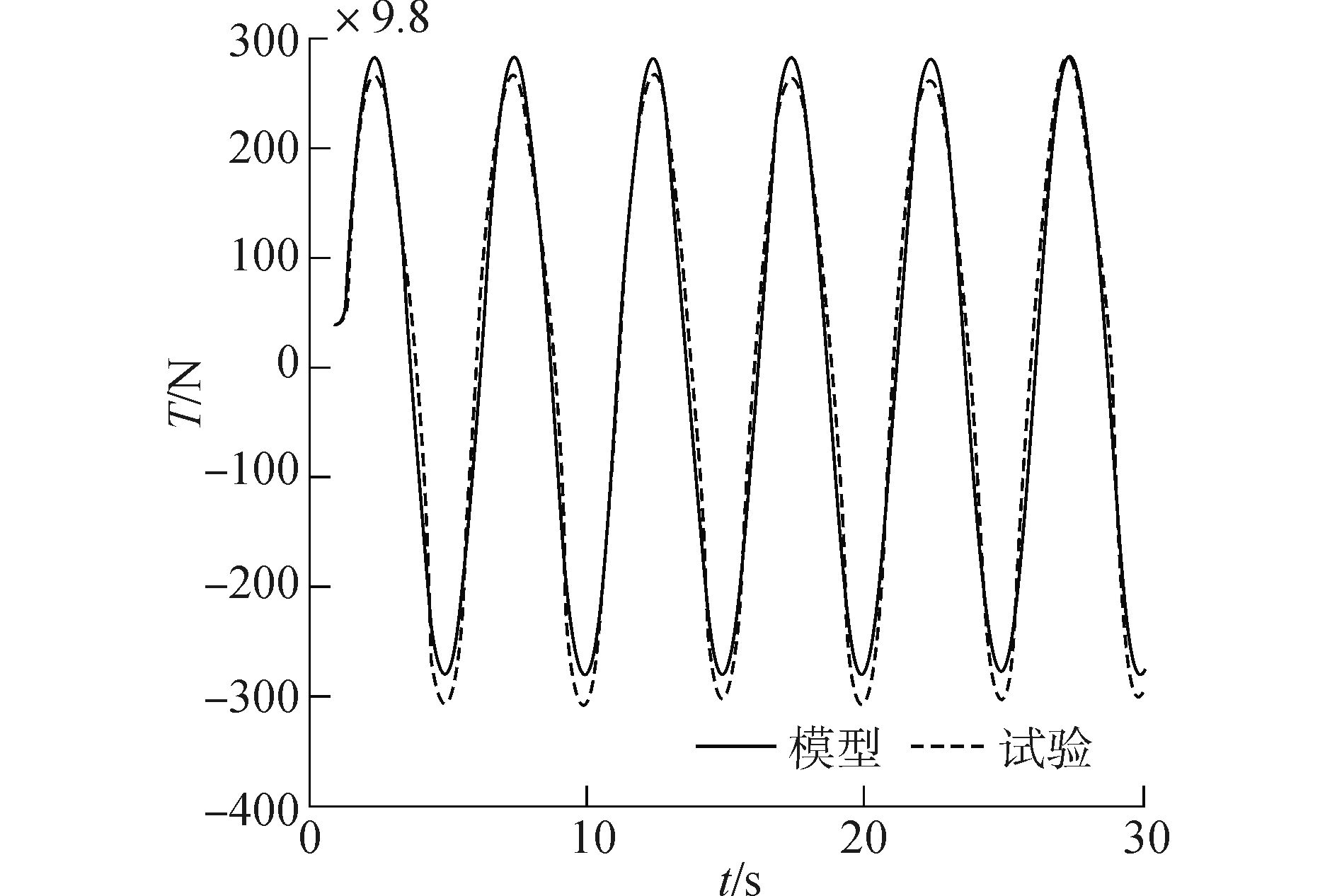
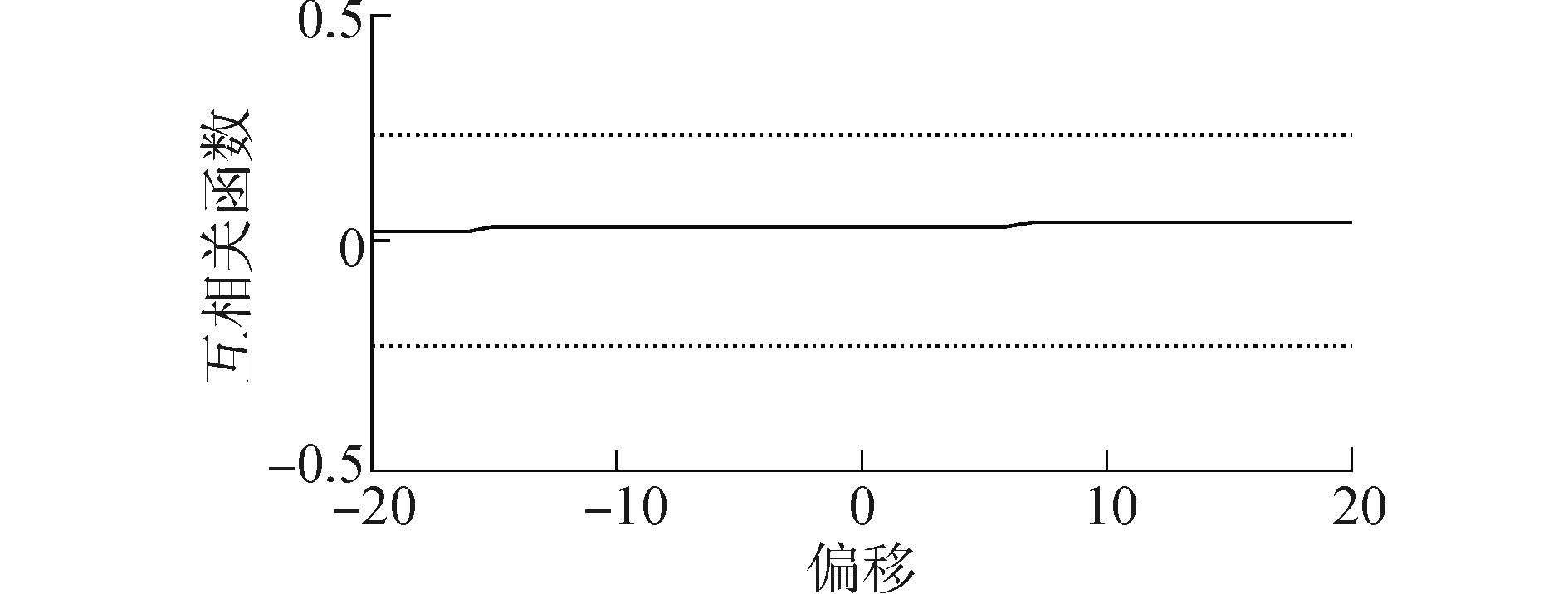
给予所得模型与试验相同的输入信号,模型输出与试验输出比较如图 8,拟合率达到92.3%,仿真结果与实验结果的吻合程度很好。模型残差分析如图 9,由图可知,模型输出残差与输入的互相关函数曲线位于99%置信区间内,可以认为输入与残差是独立的,即没有未被模型识别的输入输出关联。
|
| 图8 试验与模型输出推力比较图 Figure 8 Trust curve of experiment data and model simulation results |
|
| 图9 输入与模型输出残差的互相关函数图 Figure 9 Cross correlation function between input and residuals |
为进一步检验模型的正确性,使用未用于辨识的8组试验数据进行验证,如图 10~12。
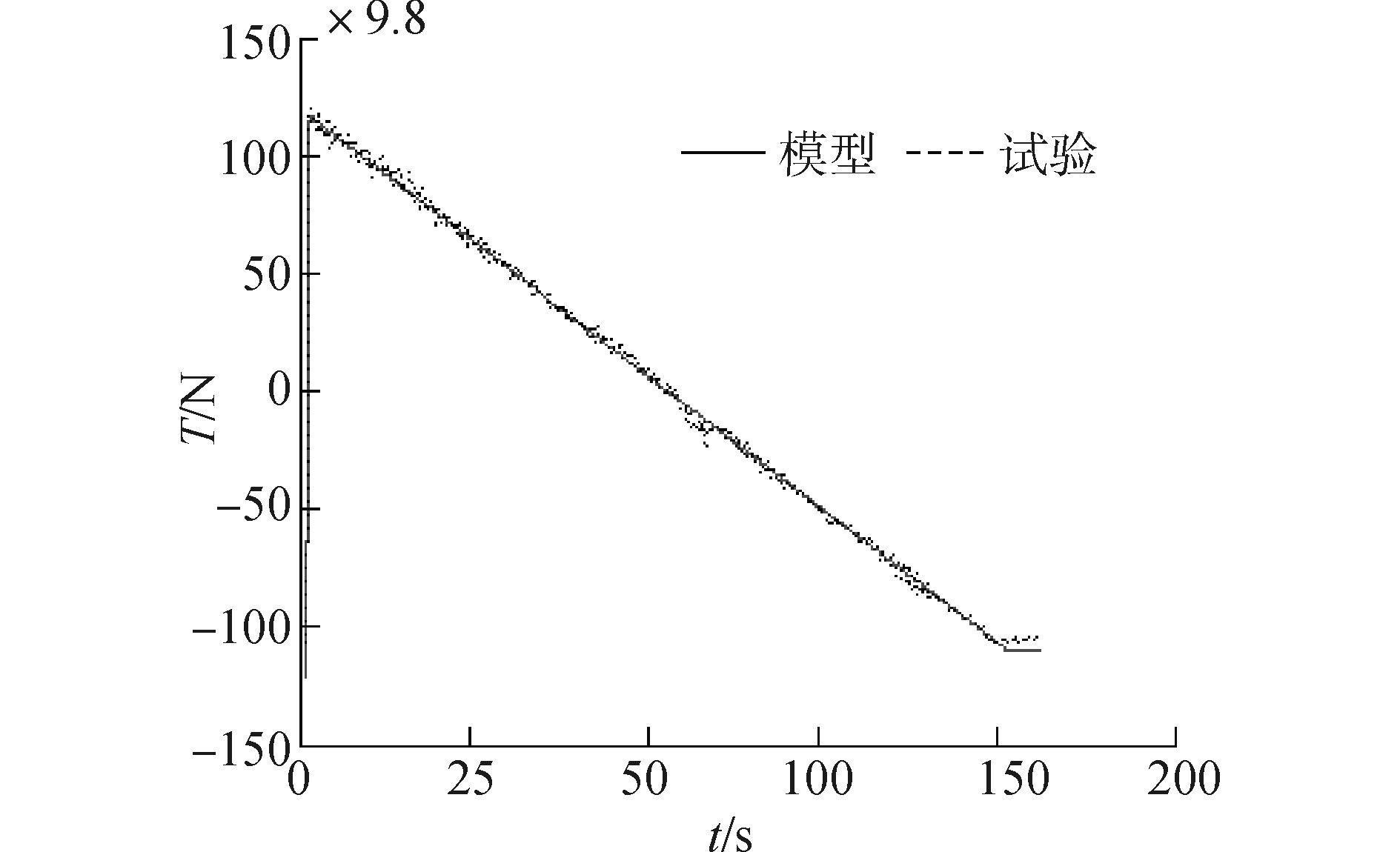
|
| 图10 线性输入下的推力时间曲线(正) Figure 10 Trust curve of linear input(positive) |
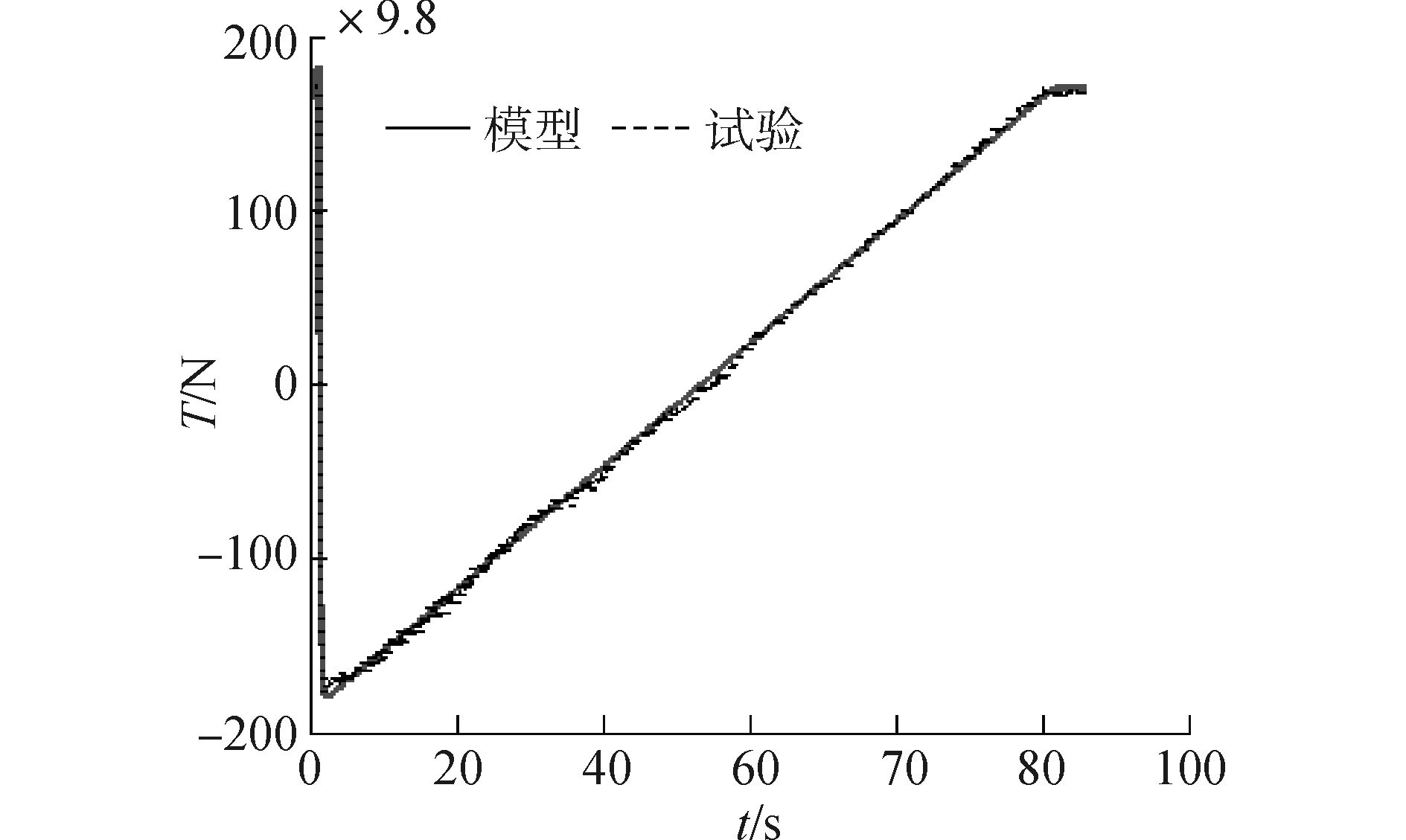
|
| 图11 线性输入下的推力时间曲线(反) Figure 11 Trust curve of linear input(negative) |
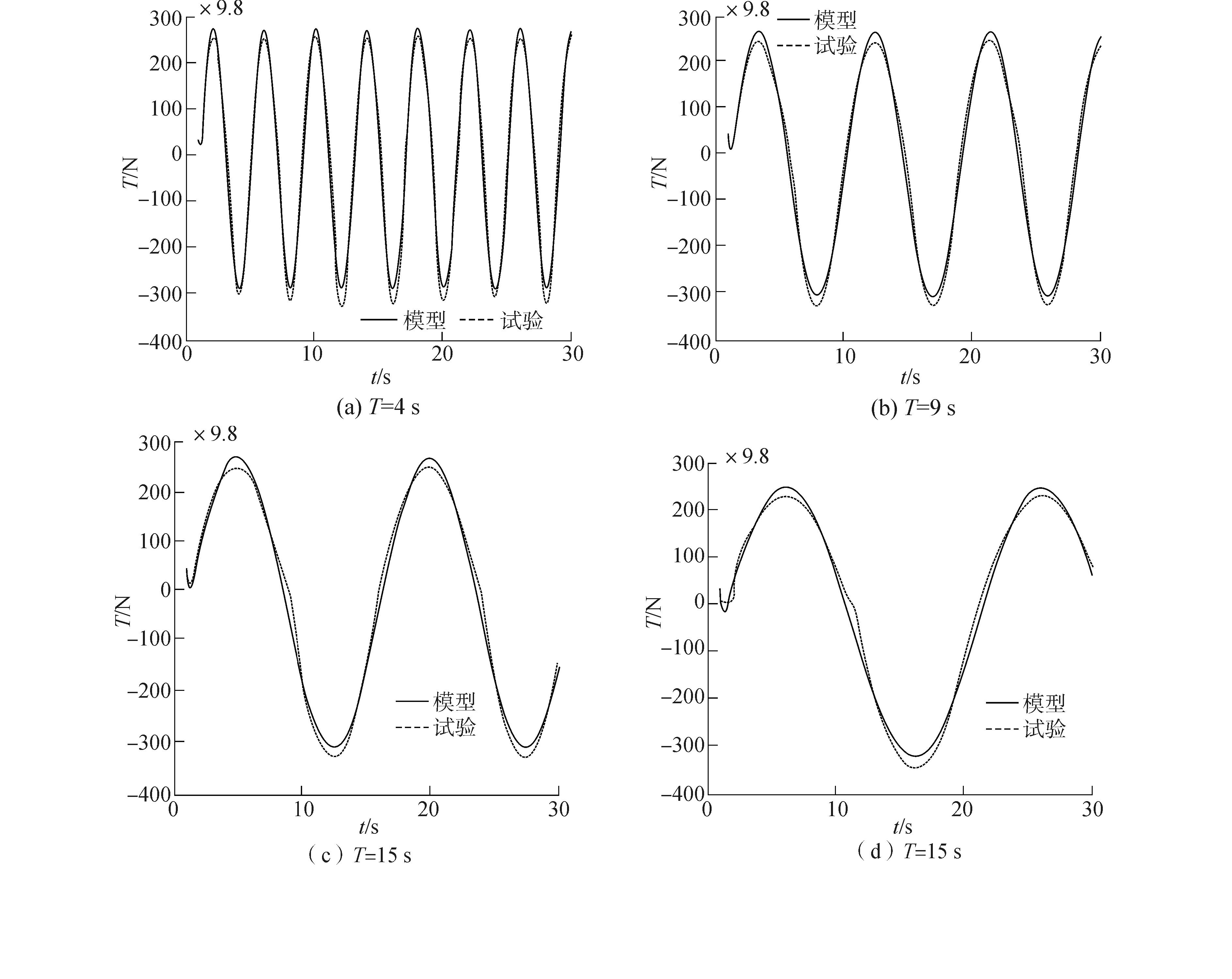
|
| 图12 不同周期下的推力时间曲线 Figure 12 Trust curve of different period |
图 10、图 11为线性输入时,模型与试验输出对比图,拟合率分别为91.4%、90.8%。图 12为正弦信号输入时,模型与试验输出对比图,其中,图 12(a)正弦信号周期为4s,拟合率为91.4%, 图 12(b)为9s,拟合率为90.4%, 图 12(c)为15s, 拟合率为90.2%,图 12(d)为20s,拟合率为89.1%。由此可知模型具有优良的预报性能。
综上所述,可以认为采用改进遗传算法辨识出的模型较高程度地符合实际系统,可以用于后续计算与研究,同时也说明了本文辨识方法的有效性和可行性。
4 结论1) 本文对“海龙二号”ROV变量液压推进器伺服控制系统进行了建模和分析,在难以得到液压缸及变量马达内部尺寸等参数的情况下,通过系统辨识试验得到了较为精确的系统模型,并使用多组试验数据对模型进行了验证。
2) ROV变量液压推进器伺服控制系统的控制模型与实际系统吻合良好,为后续推进系统改进、设计及控制策略分析提供了可靠的基础。
3) 本文所提出的改进变异方式的遗传算法有效抑制了遗传算法的早熟现象,具有较快的收敛速度,同时克服了其局部寻优能力差的缺点,并且通过多次运算验证,改进的算法稳定性较好,此改进遗传算法可用于其他工程模型的辨识与研究。
| [1] |
朱康武. 作业型ROV多变量位姿鲁棒控制方法研究[D]. 杭州:浙江大学, 2012.
ZHU Kangwu. Research on multivariable robust position and attitude control of work-class ROV[D]. Hangzhou:Zhejiang University, 2012. http://d.wanfangdata.com.cn/Thesis/Y2154950 |
| [2] | JIANG Shuqiang, JIN Hongzhang, WEI Fengmei. Bi-criteria optimal fault-tolerable control for SY-II remote operated vehicle[J]. Journal of Shanghai jiaotong university (science), 2013, 18(5): 542–548. DOI:10.1007/s12204-013-1438-6 |
| [3] |
魏延辉, 陈巍, 杜振振, 等. 深海ROV伺服控制方法研究及其仿真[J].
控制与决策, 2015, 30(10): 1785–1790.
WEI Yanhui, CHEN Wei, DU Zhenzhen, et al. Servo control method of ROV and simulation[J]. Control and decision, 2015, 30(10): 1785–1790. |
| [4] |
刘西佳. 基于AMESim作业型ROV液压推进系统的设计与仿真[D]. 青岛:中国海洋大学, 2014.
LIU Xijia. Design and simulation of work-class ROV hydraulic propulsion system based on AMESim[D]. Qingdao:Ocean University of China, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10423-1014329289.htm |
| [5] |
马新军. 作业型ROV液压系统研制与艏向控制技术研究[D]. 杭州:浙江大学, 2013.
MA Xinjun. Development of the hydraulic system and research on the heading control technique of work-class ROV[D]. Hangzhou:Zhejiang University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10335-1013303539.htm |
| [6] | AKRAMIZADEH A, FARJAMI A A, KHALOOZADEH H. Nonlinear Hammerstein model identification using genetic algorithm[C]//Proceedings of IEEE International Conference on Artificial Intelligence Systems. Divnomorskoe, Russia:IEEE, 2002:351-356. https://www.computer.org/web/csdl/index/-/csdl/proceedings/icais/2002/1733/00/01048039.pdf |
| [7] |
于莹莹, 陈燕, 李桃迎. 改进的遗传算法求解旅行商问题[J].
控制与决策, 2014, 29(8): 1483–1488.
YU Yingying, CHEN Yan, LI Taoying. Improved genetic algorithm for solving TSP[J]. Control and decision, 2014, 29(8): 1483–1488. |
| [8] | LINHARES A. Preying on optima:a predatory search strategy for combinatorial problems[C]//Proceedings of 1998 IEEE International Conference on Systems, Man, and Cybernetics. San Diego, CA:IEEE, 1998, 3:2974-2978. http://ieeexplore.ieee.org/xpl/tocresult.jsp?isnumber=15661&isYear=1998 |
| [9] |
徐宗本, 高勇. 遗传算法过早收敛现象的特征分析及其预防[J].
中国科学E(辑), 1996, 26(4): 364–375.
XU Zongben, GAO Yong. Character analysis and prophylactic of genetic algorithm's premature convergence[J]. Science in China (series E), 1996, 26(4): 364–375. |
| [10] |
万丽荣, 赵胜刚, 沈潇, 等. 基于MATLAB/SIMU-LINK的变量泵变量马达调速系统动态仿真[J].
煤矿机械, 2007, 28(2): 26–28.
WAN Lirong, ZHAO Shenggang, SHEN Xiao, et al. Dynamic simulation of variable displacement pump and variable displacement motor volume speed-modulating system based on MATLAB/SIMULINK[J]. Coal mine machinery, 2007, 28(2): 26–28. |
| [11] |
李良, 谢建, 黄建招. 动态面滑模控制在大型液压起竖系统中的应用研究[J].
兵工学报, 2014, 35(2): 235–240.
LI Liang, XIE Jian, HUANG Jianzhao. Dynamic surface sliding mode control for large hydraulic erecting system[J]. Acta armamentarii, 2014, 35(2): 235–240. |
| [12] |
何大阔, 王福利, 贾明兴. 遗传算法初始种群与操作参数的均匀设计[J].
东北大学学报:自然科学版, 2005, 26(9): 828–831.
HE Dakuo, WANG Fuli, JIA Mingxing. Uniform design of initial population and operational parameters of genetic algorithm[J]. Journal of northeastern university:natural science, 2005, 26(9): 828–831. |
| [13] |
孙先仿, 范跃祖, 宁文如. U*均匀设计的均匀性研究[J].
应用概率统计, 2001, 17(4): 341–345.
SUN Xianfang, FAN Yuezu, NING Wenru. On the uniformity of U-uniform designs[J]. Chinese journal of applied probability and statistics, 2001, 17(4): 341–345. |
| [14] |
袁伟杰, 刘贵杰, 朱绍锋. 基于遗传算法的自治水下机器人水动力参数辨识方法[J].
机械工程学报, 2010, 46(11): 96–100.
YUAN Weijie, LIU Guijie, ZHU Shaofeng. Identification method of hydrodynamic parameters of autonomous underwater vehicle based on genetic algorithm[J]. Journal of mechanical engineering, 2010, 46(11): 96–100. DOI:10.3901/JME.2010.11.096 |



