2. College of Computer and Control Engineering, Qiqihar University, Qiqihar 161006, China
在工程实际中,复合材料的一个缺陷就是其不同组分的热膨胀系数不同,这种不匹配所产生的残余应力会造成材料开裂[1],使用功能梯度材料(FGM)可以降低这种不匹配。但是这种非均匀材料在温度变化下也会产生巨大的热应力[2],因此有必要对温度变化后的FGM裂纹问题进行分析。该研究主要关注FGM作为耐温材料有并含共线裂纹的热应力断裂问题。
许多学者对热应力下的FGM断裂问题进行了研究。有限元方法在数值研究方面使用较多,如Henriques等[3]研究了不同温度变化下的FGM的热应力问题。Moghaddam等[4]研究了稳态温度梯度下含有3D曲线形非平面裂纹的FGM性能。Parandvar等[5]研究了随机压力和热载荷共同作用下的FGM问题,并假设材料属性变化用幂函数来描述。Heotokoglou等[6]开发了有限元代码分析了热力问题。J-积分及其他数值方法也广泛应用于该类问题的数值分析中,如文献[7-12],其中Petrova等[10]用指数函数来描述材料属性。在断裂问题的理论求解方面,Guo等[13-16]提出了一个解析模型分析了跨界面裂纹问题,正交各向异性功能梯度条的I-型裂纹问题以及动态裂纹问题,Ding等[17]研究了热力荷载下正交各向异性梯度涂层-基底热弹性问题,在该研究中单裂纹平行于材料自由表面。Guo等[18]研究了FGM热冲击断裂行为。Huang等[19]研究了材料属性任意变化的FGM热荷载断裂问题。
值得注意的是,无论裂纹问题的数值求解还是理论求解,已有的研究中多假设材料属性用某种特殊的函数来描述,如幂函数[5]、指数函数[10, 13-18]或线性函数[19]。而实际上预定义材料属性不符合实际应用中FGM属性随空间位置而任意分布这一特性。在近30年中,适用于研究任意属性的FGM断裂问题的解析模型很少出现。Guo等[20, 22]和Bai等[21]提出的PE模型是解决任意属性FGM断裂问题最具代表性的一种模型,是基于非均匀材料非均匀分层的思想,该模型还可用来解决随机属性[22]和混合型裂纹问题[23]。然而,基于非均匀分层思想的解析模型应用于热应力下任意属性多裂纹问题的求解还鲜有研究。
本文将基于前人工作,使用非均匀分层方法研究含有共线裂纹的任意热机械属性功能梯度条I-型热应力断裂问题,给出材料属性、材料自由表面温度分布变化、裂纹几何参数及裂纹间交互作用对裂尖热应力强度因子(TSIF)的影响。
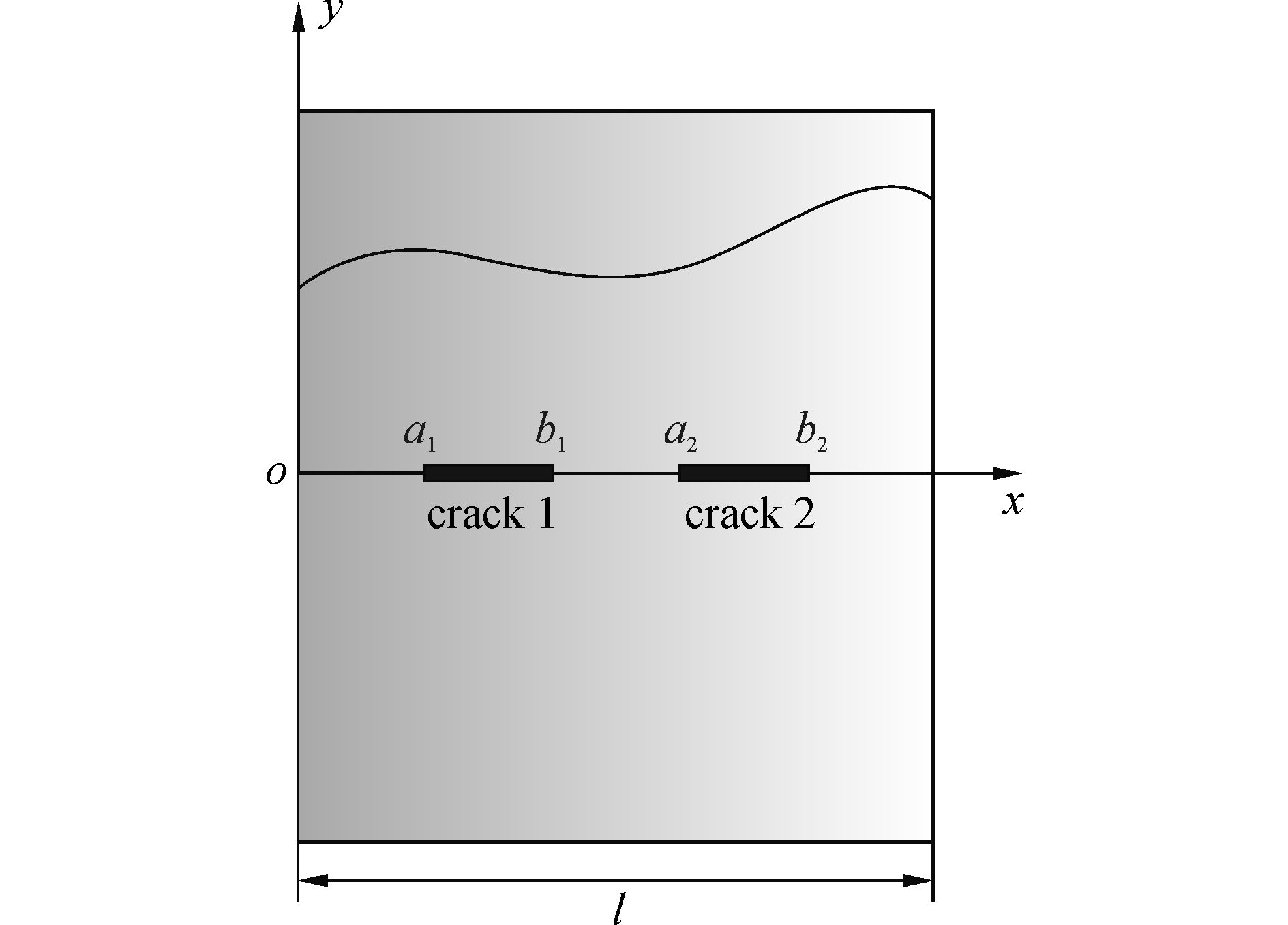
1 求解裂纹问题含有裂纹的功能梯度条平面弹性问题如图 1所示。两个共线裂纹垂直于含有任意热机械属性功能梯度条的自由表面,该材料的热机械属性仅随x轴变化。如图 1,功能梯度条的厚度为l,y=0为对称面,因对称性对应的裂纹问题只需考虑y <0部分即可。
|
| 图1 含有共线裂纹的任意属性功能梯度条结构 Figure 1 The geometry of the collinear cracks embedded in the FGMs with thermomechanical properties |
由于FGM属性随空间位置而变化,故此类问题很难求得解析解。而使用非均匀分层方法可以很好的处理该问题。假设功能梯度条的实际剪切模量可表示为
| $G(x)=\zeta (x)$ | (1) |
式中ζ(x)是一个已知的任意实函数。为了接近材料的真实属性,将功能梯度条沿x方向分成M个非均匀层,每一层的属性随指数形式变化,即可表示为
| ${{G}_{n}}(x)={{G}_{n0}}{{\text{e}}^{{{\delta }_{n}}x}},n=1,2,\cdots ,M$ | (2) |
式中:下标n表示第n层,ln-1和ln分别表示第n层上下表面x轴坐标。因此第n层位于x=ln-1和x=ln之间,并且有l0=0以及lM=l。这样实际的材料属性就可以由一系列的指数函数来模拟。
由于每层上下表面的属性就是材料的实际属性,因此有
| $\left\{ \begin{align} & {{G}_{n}}({{l}_{n-1}})=\zeta ({{l}_{n-1}})={{G}_{n0}}{{\rm{e}}^{{{\delta }_{n}}{{l}_{n-1}}}} \\ & {{G}_{n}}({{l}_{n}})=\zeta ({{l}_{n}})={{G}_{n0}}{{\rm{e}}^{{{\delta }_{n}}{{l}_{n}}}} \\ \end{align} \right.\\n=1,2,\cdots ,M$ | (3) |
由式(3)可解得δn和Gn0:
| $\left\{ \begin{align} & {{\delta }_{n}}=\frac{1}{{{l}_{n}}-{{l}_{n-1}}}\ln \left[ \frac{\zeta ({{l}_{n}})}{\zeta ({{l}_{n-1}})} \right] \\ & {{G}_{n0}}=\zeta ({{l}_{n}}){{\rm{e}}^{-{{\delta }_{n}}{{l}_{n}}}} \\ \end{align} \right.\\n=1,2,\cdots ,M$ | (4) |
针对该双裂纹问题,用σnxx、σnyy和σnxy表示总应力,unx和uny表示总位移;σnxx(k)、σnyy(k)和σnxy(k)表示每个裂纹对应的应力分量,unx(k)和uny(k)表示每个裂纹对应的位移分量,这里k (k = 1,2)表示两个裂纹。于是应力与位移的总量与分量的关系可表示为
| $\begin{align} & \left[ {{\sigma }_{nxx}}\ \ \ {{\sigma }_{nxy}}\ \ \ \ {{\sigma }_{nyy}} \right]=\sum\limits_{k=1}^{2}{\left[ \sigma _{nxx}^{(k)}\ \ \ \sigma _{nxy}^{(k)}\ \ \ \ \sigma _{nyy}^{(k)} \right],} \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ n=1,2,\cdots ,M \\ \end{align}$ | (5) |
| $\left[ {{u}_{nx}}\ \ {{u}_{ny}} \right]=\sum\limits_{k=1}^{2}{\left[ u_{nx}^{(k)}\ \ \ u_{ny}^{(k)} \right]}\ \ ,n=1,2,\cdots ,M$ | (6) |
针对应力分量,裂纹问题的本构方程和平衡方程可表示为
| $\begin{align} & \left[ \begin{matrix} \sigma _{nxx}^{(k)}\ \\ \sigma _{nyy}^{(k)} \\ \ \sigma _{nxy}^{(k)} \\ \end{matrix} \right]=\frac{{{G}_{n}}(x)}{{{\kappa }_{n}}(x)-1}\left[ \begin{matrix} 1+{{\kappa }_{n}}(x) & 3-{{\kappa }_{n}}(x) & 0 \\ 3-{{\kappa }_{n}}(x) & 1+{{\kappa }_{n}}(x) & 0 \\ 0 & 0 & {{\kappa }_{n}}(x)-1 \\ \end{matrix} \right]\centerdot \\ & \left[ \begin{matrix} \frac{\partial u_{nx}^{(k)}}{\partial x} \\ \frac{\partial u_{ny}^{(k)}}{\partial y} \\ \frac{\partial u_{nx}^{(k)}}{\partial y}+\frac{\partial u_{ny}^{(k)}}{\partial x} \\ \end{matrix} \right],k=1,2;n=1,2,\cdots M;i=1,2 \\ \end{align}$ | (7) |
| $u_{nij,j}^{(k)}=0,k=1,2;i,j=x,y;n=1,2,\cdots M$ | (8) |
已有的研究[1, 20]表明在此类问题中,泊松比可取常数。因此,平面应变时有κn(x)=3-4υ;平面应力时有κn(x)=(3-υ)/(1+υ)。
该问题的边界条件和连续性条件为
| ${{\sigma }_{1xi}}(0,y)=0,-\infty <y<\infty ;i=x,y$ | (9) |
| ${{\sigma }_{Mxi}}(h,y)=0,-\infty <y<\infty ;i=x,y$ | (10) |
| $\sigma _{nxy}^{(k)}(x,0)=0,n=1,2,\cdots M;k=1,2$ | (11) |
| $\left\{ \begin{align} & {{u}_{ny}}(x,0)=0 \\ & 0<x<{{a}_{1}}或b1<x<{{a}_{2}}或{{b}_{2}}<x<l \\ \end{align} \right.$ | (12) |
| $\sigma _{nyy}^{(k)}(x,o)=-\sigma _{yy}^{T}(x),{{a}_{k}}<x<{{b}_{k}};k=1,2$ | (13) |
| ${{u}_{ni}}({{l}_{n}},y)={{u}_{(n+1)i}}({{l}_{n}},y),i=x,y;n=1,2,\cdots M-1$ | (14) |
| ${{u}_{nxi}}({{l}_{n}},y)={{\sigma }_{(n+1)xi}}({{l}_{n}},y),i=x,y;n=1,2,\cdots M-1$ | (15) |
将式(7)带入式(8)并应用傅里叶变换,可得到位移分量表达式为
| $\left\{ \begin{align} & u_{nx}^{(k)}(x,y)=\frac{1}{2\text{ }\!\!\pi\!\!\text{ }}\int_{-\infty }^{\infty }{\sum\limits_{j=1}^{2}{{{f}_{n1j}}}}(s)A_{n1j}^{(k)}{{\text{e}}^{{{\lambda }_{n1j}}y-isx}}\text{d}s+ \\ & \ \ \ \ \ \frac{2}{\text{ }\!\!\pi\!\!\text{ }}\int_{0}^{\infty }{\sum\limits_{j=1}^{2}{{{f}_{n2j}}}}(\alpha )A_{n2j}^{(k)}{{\text{e}}^{{{\lambda }_{n2j}}(\alpha )x}}\cos (\alpha y)\text{d}\alpha \\ & u_{ny}^{(k)}(x,y)=\frac{1}{2\text{ }\!\!\pi\!\!\text{ }}\int_{-\infty }^{\infty }{\sum\limits_{j=1}^{2}{{{f}_{n1j}}}}(s)A_{n1j}^{(k)}{{\text{e}}^{{{\lambda }_{n1j}}y-isx}}\text{d}s+ \\ & \ \ \ \ \ \frac{2}{\text{ }\!\!\pi\!\!\text{ }}\int_{0}^{\infty }{\sum\limits_{j=1}^{2}{A_{n2j}^{(k)}}}{{\text{e}}^{{{\lambda }_{n2j}}(\alpha )x}}\sin (\alpha y)\text{d}\alpha \\ \end{align} \right.$ | (16) |
将方程(16)代入方程(7)可得到应力分量:
| $\left\{ \begin{align} & \sigma _{nxx}^{(k)}(x,y)= \\ & \ \ \ {{\text{e}}^{{{\delta }_{n}}x}}[(\frac{1}{2\text{ }\pi \text{ }}\int_{-\infty }^{\infty }{\sum\limits_{j=1}^{2}{{{b}_{n1j}}}}(s)A_{n1j}^{(k)}{{\text{e}}^{{{\lambda }_{n1j}}y-isx}}\text{d}s)+ \\ & \ \ \frac{2}{\text{ }\pi \text{ }}\int_{0}^{\infty }{\sum\limits_{j=1}^{4}{{{b}_{n2j}}}}(\alpha )A_{n2j}^{(k)}{{\text{e}}^{{{\lambda }_{n2j}}x}}\cos (\alpha y)\text{d}\alpha ] \\ & \sigma _{nyy}^{(k)}(x,y)= \\ & \ \ {{\text{e}}^{{{\delta }_{n}}x}}[\frac{1}{2\text{ }\pi \text{ }}\int_{-\infty }^{\infty }{\sum\limits_{j=1}^{2}{{{c}_{n1j}}}}(s)A_{n1j}^{(k)}{{\text{e}}^{{{\lambda }_{n1j}}y-isx}}\text{d}s)+ \\ & \ \ \ \frac{2}{\text{ }\pi \text{ }}\int_{0}^{\infty }{\sum\limits_{j=1}^{4}{{{c}_{n2j}}}}(\alpha )A_{n2j}^{(k)}{{\text{e}}^{{{\lambda }_{n2j}}x}}\cos (\alpha y)\text{d}\alpha ] \\ & \sigma _{nxy}^{(k)}(x,y)= \\ & \ \ {{\text{e}}^{{{\delta }_{n}}x}}[\frac{1}{2\text{ }\pi \text{ }}\int_{-\infty }^{\infty }{\sum\limits_{j=1}^{2}{{{d}_{n1j}}}}(s)A_{n1j}^{(k)}{{\text{e}}^{{{\lambda }_{n1j}}y-isx}}\text{d}s)+ \\ & \ \ \ \frac{2}{\text{ }\pi \text{ }}\int_{0}^{\infty }{\sum\limits_{j=1}^{4}{{{d}_{n2j}}}}(\alpha )A_{n2j}^{(k)}{{\text{e}}^{{{\lambda }_{n2j}}x}}\sin (\alpha y)\text{d}\alpha ] \\ \end{align} \right.$ | (17) |
将方程(16)和(17)分别代入方程(6)和(5)可得到总位移和总应力表达式为
| $\left\{ \begin{align} & {{u}_{nx}}(x,y)= \\ & \ \ \ \sum\limits_{k=1}^{2}{[\frac{1}{2\text{ }\!\!\pi\!\!\text{ }}\int_{-\infty }^{\infty }{\sum\limits_{j=1}^{2}{{{f}_{n1j}}}}(s)A_{n1j}^{(k)}{{\text{e}}^{{{\lambda }_{n1j}}y-isx}}\text{d}s]+} \\ & \ \ \ \frac{2}{\text{ }\!\!\pi\!\!\text{ }}\int_{0}^{\infty }{\sum\limits_{j=1}^{4}{{{f}_{n2j}}}}(\alpha )A_{n2j}^{t}{{\text{e}}^{{{\lambda }_{n2j}}(\alpha )x}}\cos (\alpha y)\text{d}\alpha \\ & {{u}_{ny}}(x,y)=\sum\limits_{k=1}^{2}{[\frac{1}{2\text{ }\!\!\pi\!\!\text{ }}\int_{-\infty }^{\infty }{\sum\limits_{j=1}^{2}{{{f}_{n1j}}}}(s)A_{n1j}^{(k)}{{\text{e}}^{{{\lambda }_{n1j}}y-isx}}\text{d}s]+} \\ & \ \ \ \frac{2}{\text{ }\!\!\pi\!\!\text{ }}\int_{0}^{\infty }{\sum\limits_{j=1}^{4}{{{f}_{n2j}}}}(\alpha )A_{n2j}^{t}{{\text{e}}^{{{\lambda }_{n2j}}(\alpha )x}}\sin (\alpha y)\text{d}\alpha \\ \end{align} \right.$ | (18) |
| $\left\{ \begin{align} & {{\sigma }_{nxx}}(x,y)= \\ & \ \ \ \ \sum\limits_{k=1}^{2}{\text{ }\!\![\!\!\text{ }{{\text{e}}^{{{\delta }_{n}}x}}}(\frac{1}{2\text{ }\!\!\pi\!\!\text{ }}\int_{-\infty }^{\infty }{\sum\limits_{j=1}^{2}{{{b}_{n1j}}}}(s)A_{n1j}^{(k)}{{\text{e}}^{{{\lambda }_{n1j}}y-isx}}\text{d}s)]+ \\ & \ \ \ {{\text{e}}^{{{\delta }_{n}}x}}[\ \frac{2}{\text{ }\!\!\pi\!\!\text{ }}\int_{0}^{\infty }{\sum\limits_{j=1}^{4}{{{b}_{n2j}}}}(\alpha )A_{n2j}^{t}{{\text{e}}^{{{\lambda }_{n2j}}x}}\cos (\alpha y)\text{d}\alpha ] \\ & {{\sigma }_{nyy}}(x,y)= \\ & \ \ \ \ \sum\limits_{k=1}^{2}{\text{ }\!\![\!\!\text{ }{{\text{e}}^{{{\delta }_{n}}x}}}(\frac{1}{2\text{ }\!\!\pi\!\!\text{ }}\int_{-\infty }^{\infty }{\sum\limits_{j=1}^{2}{{{c}_{n1j}}}}(s)A_{n1j}^{(k)}{{\text{e}}^{{{\lambda }_{n1j}}y-isx}}\text{d}s)]+ \\ & \ \ \ {{\text{e}}^{{{\delta }_{n}}x}}[\ \frac{2}{\text{ }\!\!\pi\!\!\text{ }}\int_{0}^{\infty }{\sum\limits_{j=1}^{4}{{{b}_{n2j}}}}(\alpha )A_{n2j}^{t}{{\text{e}}^{{{\lambda }_{n2j}}x}}\cos (\alpha y)\text{d}\alpha ] \\ & {{\sigma }_{nxy}}(x,y)= \\ & \ \ \ \ \sum\limits_{k=1}^{2}{\text{ }\!\![\!\!\text{ }{{\text{e}}^{{{\delta }_{n}}x}}}(\frac{1}{2\text{ }\!\!\pi\!\!\text{ }}\int_{-\infty }^{\infty }{\sum\limits_{j=1}^{2}{{{d}_{n1j}}}}(s)A_{n1j}^{(k)}{{\text{e}}^{{{\lambda }_{n1j}}y-isx}}\text{d}s)]+ \\ & \ \ \ {{\text{e}}^{{{\delta }_{n}}x}}[\ \frac{2}{\text{ }\!\!\pi\!\!\text{ }}\int_{0}^{\infty }{\sum\limits_{j=1}^{4}{{{d}_{n2j}}}}(\alpha )A_{n2j}^{t}{{\text{e}}^{{{\lambda }_{n2j}}x}}sin(\alpha y)\text{d}\alpha ] \\ \end{align} \right.$ | (19) |
在式(16)~(19)中,s和α是傅里叶变量,fnij、bnij、 cnij、 dnij和λnij(i = 1,2)可求,An1j(k)和An2jt为待求。
下面通过定义新的辅助函数来表达An1j(k):
| $\left\{ \begin{align} & {{\psi }^{(1)}}(x)=\partial u_{ny}^{(1)}(x,0)/\partial x,{{a}_{1}}<x<{{b}_{1}} \\ & {{\psi }^{(2)}}(x)=\partial u_{ny}^{(2)}(x,0)/\partial x,{{a}_{2}}<x<{{b}_{2}} \\ \end{align} \right.$ | (20) |
由式(11)、(17)、(18)和(20)可得
| $\left\{ \begin{align} & A_{n1j}^{(1)}={{d}_{n12}}i/[({{d}_{n12}}-{{d}_{n11}})s]\int_{{{a}_{1}}}^{{{b}_{1}}}{{{\psi }^{(1)}}}(t){{\rm{e}}^{\rm{i}st}}\rm{d}t \\ & A_{n1j}^{(2)}={{d}_{n11}}i/[({{d}_{n12}}-{{d}_{n11}})s]\int_{{{a}_{2}}}^{{{b}_{2}}}{{{\psi }^{(2)}}}(t){{\rm{e}}^{\rm{i}st}}\rm{d}t \\ \end{align} \right.\\n=1,2,\cdots M;j=1,2$ | (21) |
由边界条件和连续性条件以及辅助函数,经过冗长的推导,最终使得An2jt也可用辅助函数ψ(r)表示,最终使用文献[24-25]方法可以求得两个裂纹的奇异积分方程组。应用文献[26-27]中使用的Lobatto-Chebyshev数值方法来求解奇异积分方程组。该未知的 ψ(r)可表示为
| $\psi (r)=f(r)/\sqrt{1-{{r}^{2}}}$ | (22) |
经过繁琐的推导[27-28],最终可求得两个裂纹的热应力强度因子表达式如下:
| $\left\{ \begin{align} & \frac{4\sqrt{2}{{G}_{ni10}}}{(1+\kappa )\sqrt{{{b}_{i}}-{{a}_{i}}}}{{\rm{e}}^{\delta ni{{1}^{a}}i}}{{f}_{i}}({{a}_{i}}) \\ & {{k}_{\rm{I}}}({{b}_{i}})=\underset{x\to {{b}_{i}}}{\mathop{\lim }}\,\sqrt{2(x-{{b}_{i}})}\sigma _{yy}^{T}= \\ & -\frac{4\sqrt{2}{{G}_{ni10}}}{(1+\kappa )\sqrt{{{b}_{i}}-{{a}_{i}}}}{{\rm{e}}^{\delta ni{{2}^{b}}i}}{{f}_{i}}({{b}_{i}}) \\ \end{align} \right.\\ i=1,2$ | (23) |
式中σyyT的求解在下面给出。
2 求解热应力假设该热应力问题是准静态的,热弹性耦合影响可忽略不计,该裂纹问题可以通过叠加求解,即不含裂纹的FGM热应力问题以及等温下裂纹表面含有与热应力等效的方向相反的荷载问题[2]。通过叠加,该问题就可以转化为求解裂纹表面载荷为-σyyT的裂纹问题。
为了求解热应力定义如下参数:导热系数、热膨胀系数、剪切模量、杨氏模量和泊松比分别为λ(x)、α(x)、G(x)、E(x)、υ。稳态热传导方程可表示为
| $\partial [\lambda (x)\partial T/\partial x]\partial x=0$ | (24) |
求解温度场:
| $T(x)={{T}_{1}}+({{T}_{2}}-{{T}_{1}})\left[ \int_{0}^{x}{1}/\lambda (x)\text{d}x \right]/\left[ \int_{0}^{l}{1}/\lambda (x)\text{d}x \right]$ | (25) |
式中:T1 和 T2分别表示功能梯度条上下表面的温度,则无裂纹下的热应力(平面应变条件下)求解为
| $\begin{align} & \sigma _{yy}^{T}(x)=E(x)\{Ax+B-\alpha (x)(1+\upsilon )\centerdot \\ & \ \ \ \ [(T(x)-{{T}_{0}})]\}/(1+{{\upsilon }^{2}}) \\ \end{align}$ | (26) |
式中:T0是功能梯度条的初始温度。A 和B可以由如下边界条件求得
| $\left\{ \begin{align} & \int_{0}^{l}{\sigma _{yy}^{T}(x)}\text{d}x=0 \\ & \int_{0}^{l}{x\sigma _{yy}^{T}(x)}\text{d}x=0 \\ \end{align} \right.$ | (27) |
将所求σyyT代入式(23)即可求得TSIF。
3 算例与结果分析设计了一些算例,探讨热应力下带有任意属性的功能梯度条的TSIF的特性。设实际材料热机械属性可以用任意实函数来描述,在该部分,为了考察不同材料属性对TSIF的影响,我们分别用指数函数、幂函数和线性函数来表示材料热机械属性的变化。用指数函数表示热机械属性时,有
| $\left\{ \begin{align} & G(x)={{G}_{0}}{{\text{e}}^{\delta (x/l)}} \\ & \lambda (x)={{\lambda }_{0}}{{\text{e}}^{\eta (x/l)}} \\ & \alpha (x)={{\alpha }_{0}}{{\text{e}}^{\omega (x/l)}} \\ \end{align} \right.$ | (28) |
当用幂函数表示材料热机械属性时,有
| $\left\{ \begin{align} & G(x)={{G}_{0}}\text{+(}{{G}_{M}}\text{-}{{G}_{0}}){{(x/l)}^{P}} \\ & \lambda (x)={{\lambda }_{0}}\text{+(}{{\lambda }_{M}}\text{-}{{\lambda }_{0}}){{(x/l)}^{P}} \\ & \alpha (x)={{\alpha }_{0}}\text{+(}{{\alpha }_{M}}\text{-}{{\alpha }_{0}}){{(x/l)}^{P}} \\ \end{align} \right.$ | (29) |
式中:p的取值为1、2、1/2。当p值取为1时,表示材料热机械属性用线性函数来描述。
对热应力强度因子进行无量纲化:无量纲热应力强度因子定义为kI(ai)/k0和kI(bi)/k0 (i =1,2)。其中,
| ${{E}_{M}}/{{E}_{0}}=10,\ \ \ \ \ \ {{\lambda }_{M}}/\ {{\lambda }_{0}}=10,\ \ \ \ \ {{\alpha }_{M}}/{{\alpha }_{0}}=2$ |
下面考虑升温变化稳定后,功能梯度条的上下表面温度一致(T1=T2)的稳态温度场情况,考察一个裂纹长度和相对初始温度变化对另一个裂纹TSIF的影响。
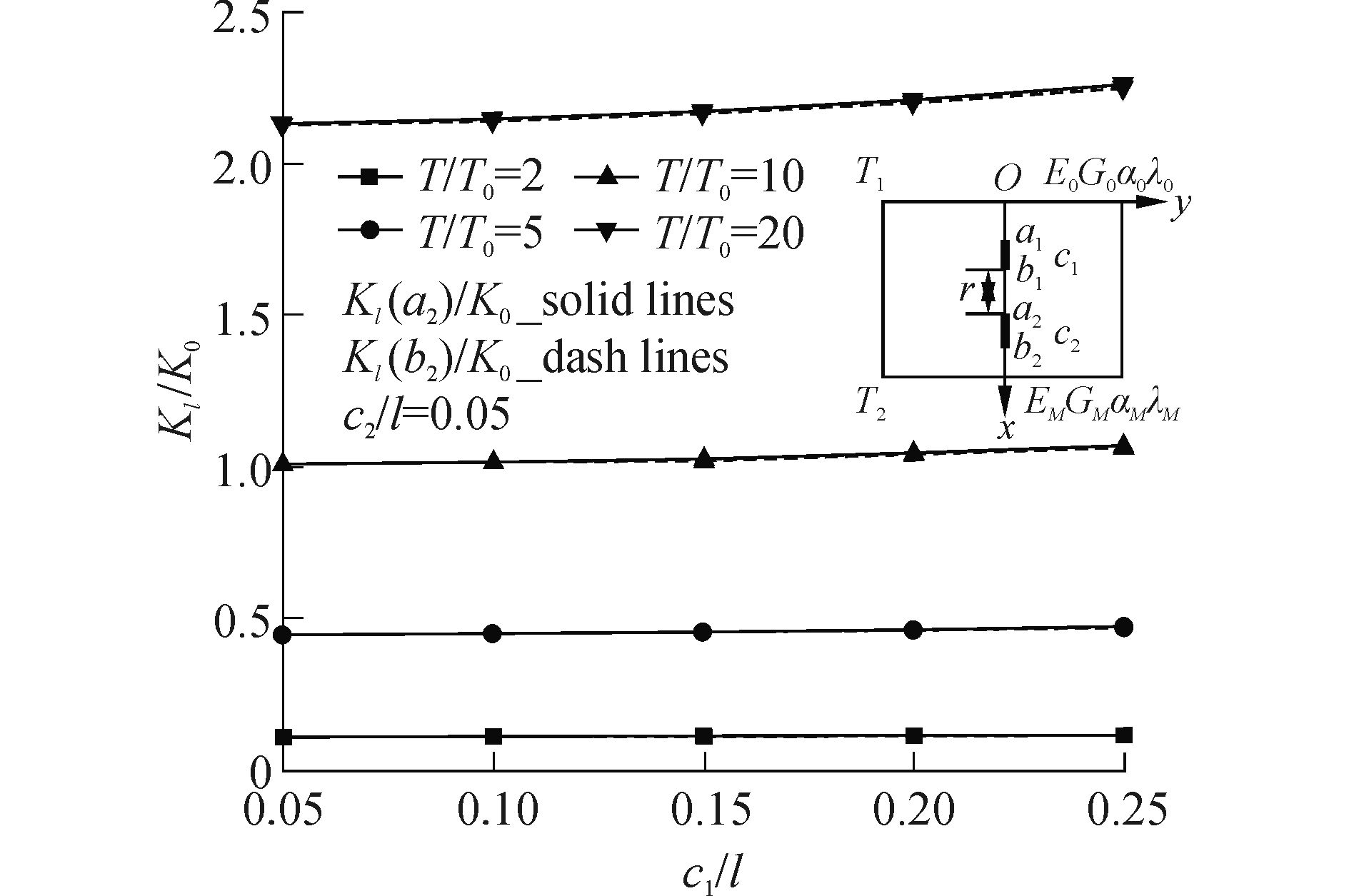
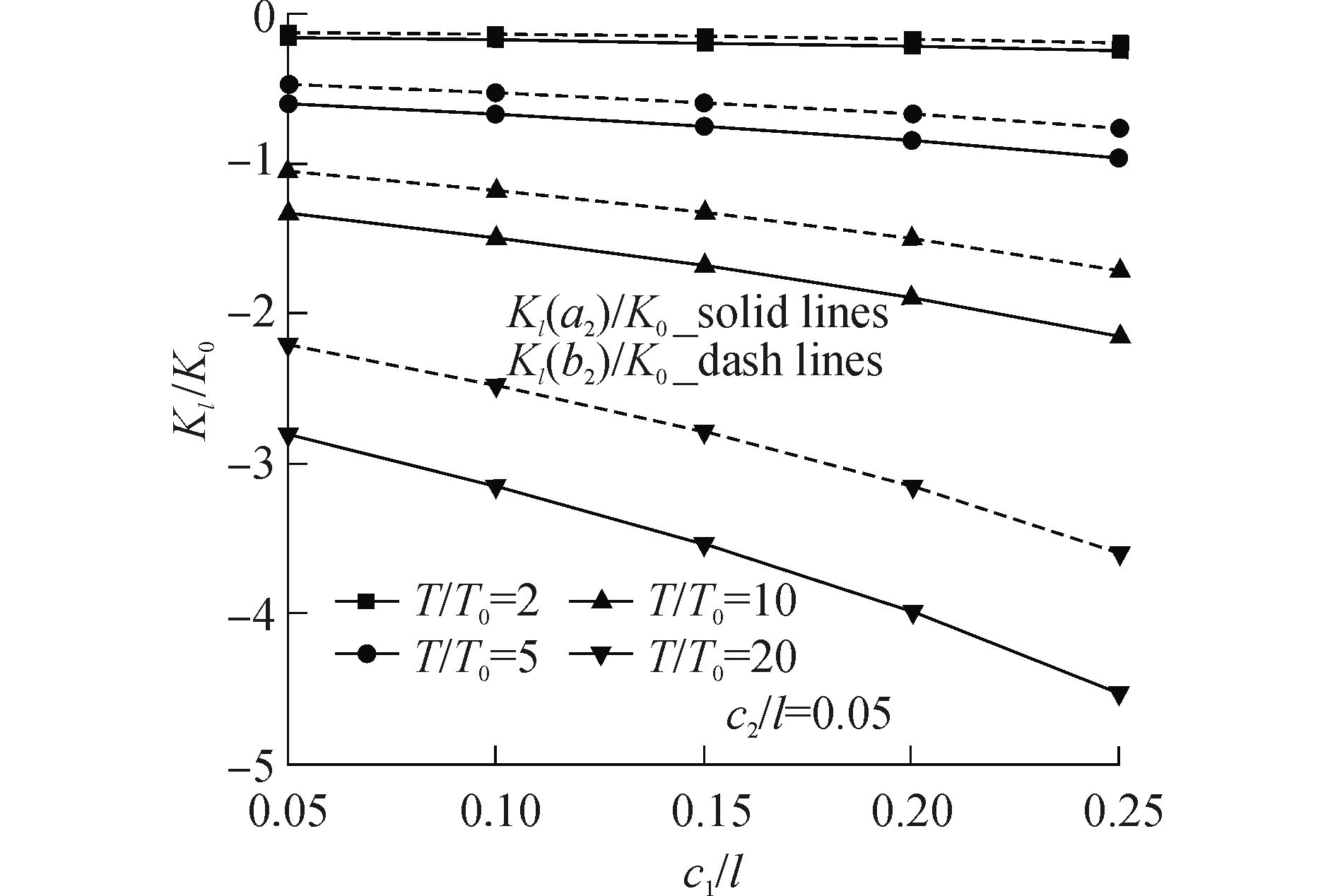
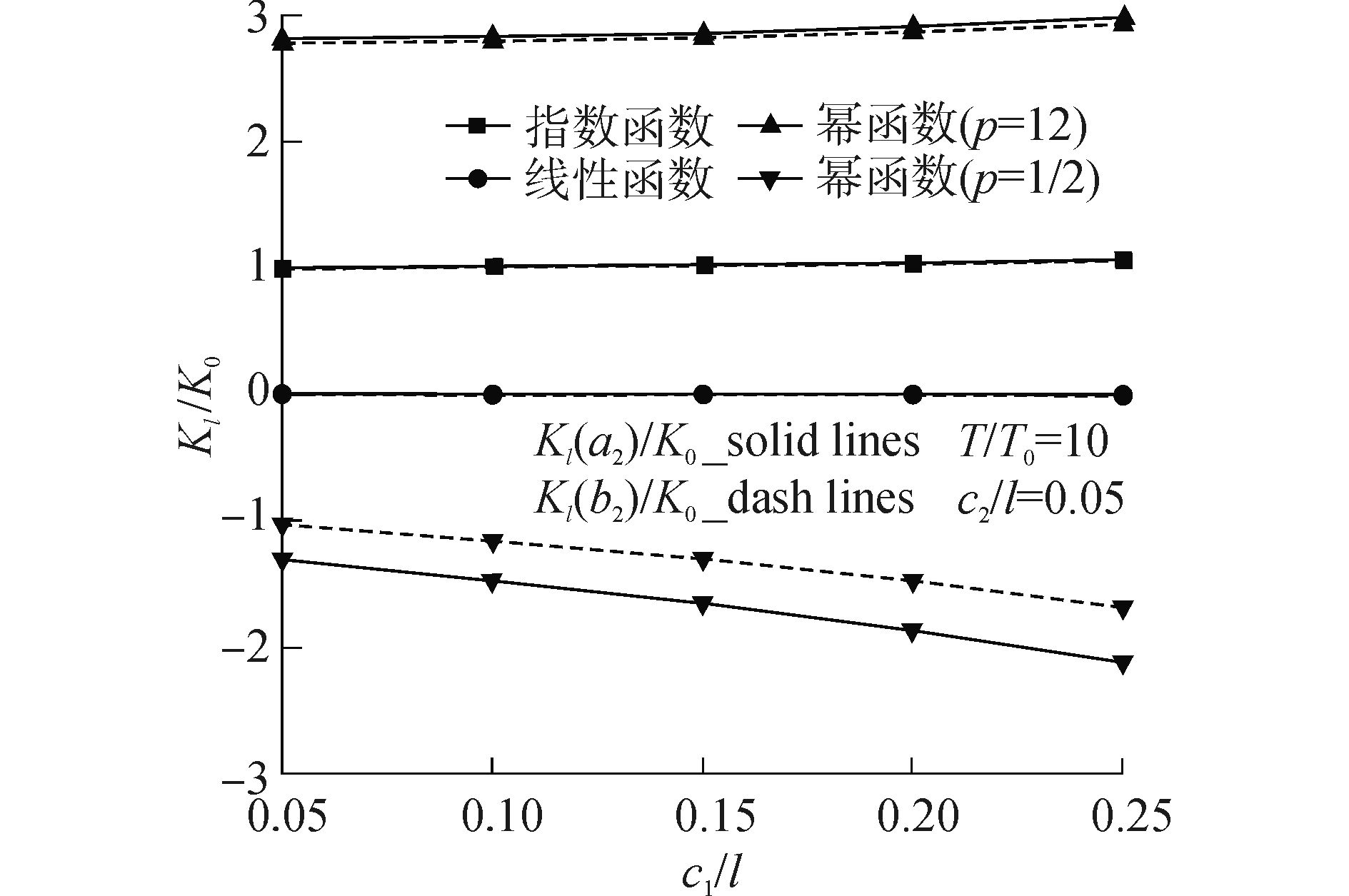
图 2和图 3 分别以材料热机械属性为指数函数和幂函数(p =1/2)表示时,升温达到稳态(T=T1=T2),裂纹2无量纲化TSIF的变化情况。图 4给出了不同材料热机械属性在稳态温度场下对裂纹TSIF影响的对比。
|
| 图2 热机械属性按指数函数变化时裂纹2的无量纲化热应力强度因子随裂纹1长度及温度比变化关系 Figure 2 Normalized TSIFs of crack 2 versus normalized crack length of crack 1 under uniform temperature changes when all the thermomechanical properties are expressed by exponential functions |
|
| 图3 热机械属性按幂函数(g=1/2)变化时裂纹2的无量纲化应力强度因子随裂纹1长度及温度比变化关系 Figure 3 Normalized TSIFs of crack 2 versus normalized crack lengths of crack 1 under uniform temperature changes when all the thermomechanical properties are expressed by power-law functions (g=1/2) |
|
| 图4 升温稳态温度场下材料属性按不同函数形式变化时裂纹2无量纲化热应力强度因子变化情况 Figure 4 TSIFs of crack 2 in a heated FGM strip with different types of distribution patterns of material properties |
1) c2/l较小时,当T/T0一定时,裂纹2的无量纲化TSIF受c1/l变化影响不大;当c1/l一定时,T/T0越大,无量纲TSIF越大。
2)当FGM热机械属性由幂函数(p = 1/2)表示时,发现裂纹2的无量纲TSIF为负值。这表明在该条件下,裂纹2的裂尖出现了闭合。值得注意的是,负的应力强度因子是无意义的,若不考虑负号,仅就其值的变化仍然符合1)所述。
3)当FGM热机械属性由线性函数表示时,在图 4所示的条件下,裂纹2的无量纲化TSIF值几乎为0。这表明在同等条件下,和其他函数描述材料属性相比,用线性函数表示材料热机械属性对升温稳态温度场不敏感。
4)从图 4可以看到,在一定稳态温度场下,用不同的函数形式描述描述材料属性梯度变化,c1/l一定,用不同函数表示材料热机械属性时,获取的裂纹2的无量纲化TSIF值明显不同。
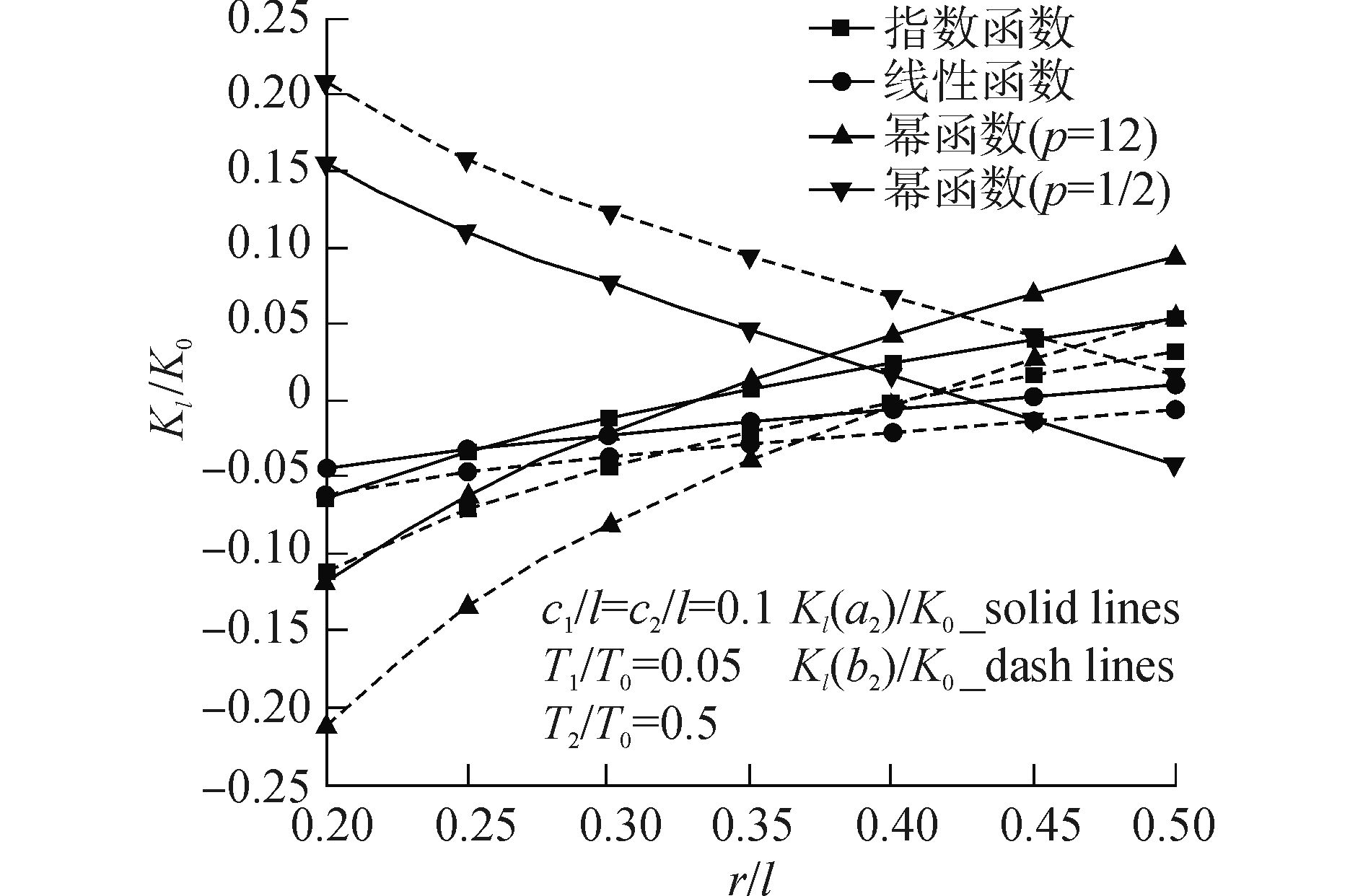
3.2 共线裂纹内裂尖距变化下的热应力强度因子下面考察两个共线裂纹相对尺寸固定,沿x轴相对位置发生对称变化时,在不同的材料热力学属性及温度场下,内裂尖相对距离变化对两个裂纹的TSIF的影响。用r表示两个共线裂纹内裂尖的距离,即r=a2-b1。图 5~6给出了T1/T0=0.05和T2/T0=0.5条件下,两个裂纹的无量纲化TSIFs在不同热机械属性下随r/l的变化情况。
|
| 图5 降温及不同材料属性条件下裂纹1的无量纲化TSIF随r/l变化关系 Figure 5 Normalized TSIFs of crack 1 versus r/l with different properties under nonuniform and cooling surface temperat |
|
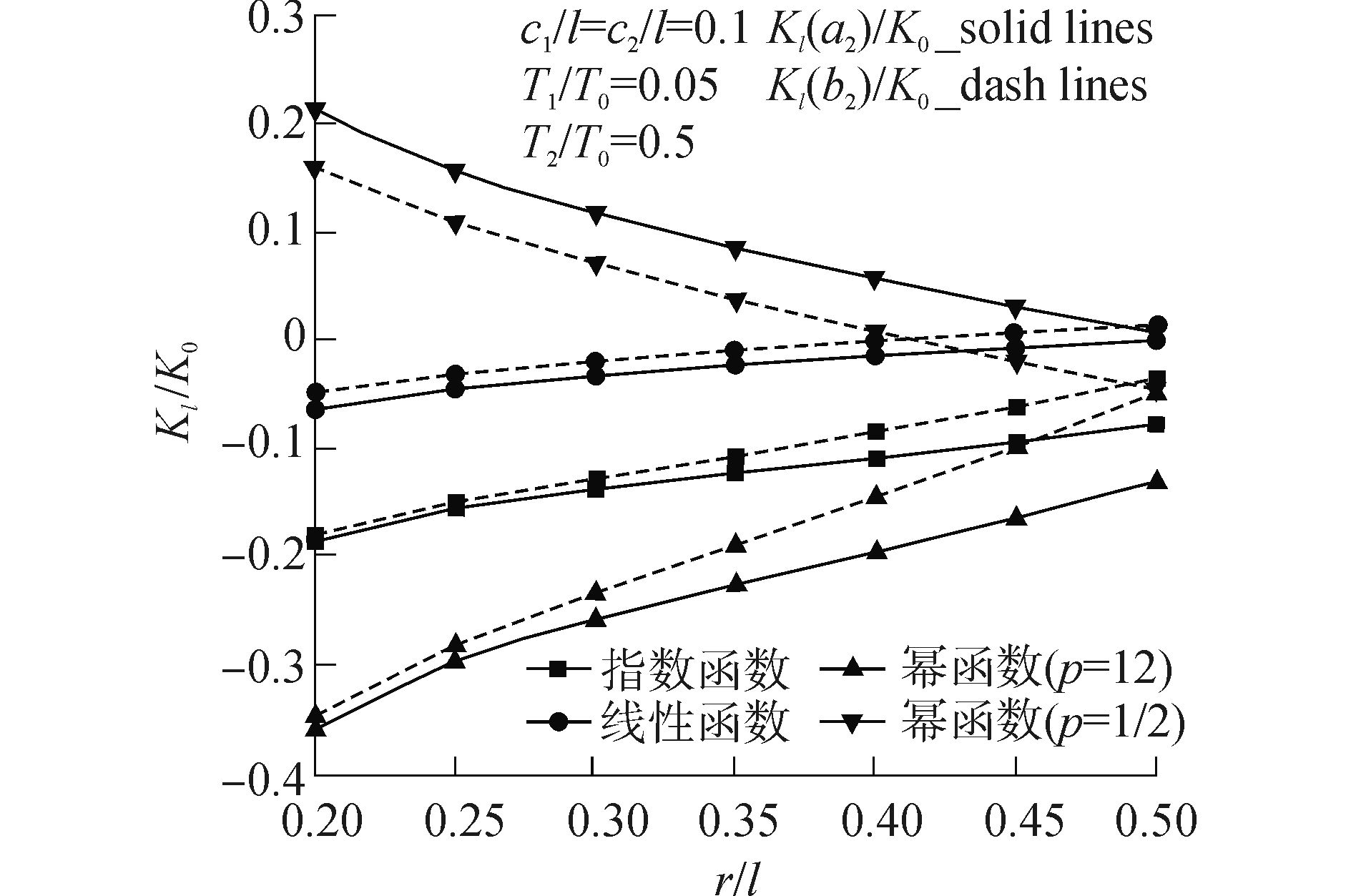
| 图6 降温及不同材料属性下裂纹2的无量纲化TSIF随r/l变化关系 Figure 6 Normalized TSIFs of crack 2 versus r/l with different properties under nonuniform and cooling surface temperature |
从图 5可以发现:当热机械属性用指数函数表示时,随着r/l的减小,裂纹1逐渐进入受压区域,此时,无量纲化TSIF为负值。当材料的热机械属性用线性函数和幂函数(p = 2)表示时,无量纲化kI的曲线与指数函数表示下的曲线有近乎相同的变化趋势,只是同等条件下的无量纲化kI数值大小不同。而当材料属性用幂函数(p = 1/2)表示时,无量纲化kI的曲线变化趋势较其他明显不同。以上现象表明在分析稳态温度场下FGM裂纹问题时,特别是分析实际工程问题时,对材料热机械属性的描述应更加慎重。
从图 6可以发现:裂纹2的无量纲化TSIF曲线的走向与裂纹1的曲线走向类似,不同的是若不考虑TSIFs的负号,裂纹2有kI(a2)/k0>kI(b2)/k0。而且,当r/l较小时,不同材料属性下求得的无量纲化TSIF差别比较明显。
4 结论本文研究了含有共线裂纹的任意属性功能梯度条I-型热应力断裂问题。在稳态温度荷载下对功能梯度条进行分层处理,研究了温度变化、材料属性和裂纹几何尺寸变化对TSIF的影响。结果表明:
1) 使用同一理论模型用不同函数形式(指数函数、线性函数和幂函数)描述FGM的热机械属性,求得的TSIF的值差异显著;
2) 热机械属性的分布形式可以用来控制裂纹的闭合状态;
3) 不同材料属性下求得的裂纹TSIF是有差异的,分析该类问题时,如已有文献将材料属性描述成单一函数形式将不能全面反映材料的热应力断裂性质;
4) FGM不同的热机械属性可能对TSIF有显著影响,因此对极端温度条件下使用的FGM,应对其材料属性的设计给予更多的关注。
| [1] | SHBEEB N I, BINIENDA W K, KREIDER K L. Analysis of the driving forces for multiple cracks in an infinite nonhomogeneous plate, Part I:theoretical analysis[J]. Journal of applied mechanics, 1999, 66(2): 492–500. DOI:10.1115/1.2791074 |
| [2] | ERDOGAN F, WU B H. Crack problems in FGM layers under thermal stresses[J]. Journal of thermal stresses, 1996, 19(3): 237–265. DOI:10.1080/01495739608946172 |
| [3] | HENRIQUES B, MIRANDA G, GASIK M, et al. Finite element analysis of the residual thermal stresses on functionally gradated dental restorations[J]. Journal of the mechanical behavior of biomedical materials, 2015, 50: 123–130. DOI:10.1016/j.jmbbm.2015.06.003 |
| [4] | MOGHADDAM A S, ALFANO M. Determination of stress intensity factors of 3D curved non-planar cracks in FGMs subjected to thermal loading[J]. Engineering fracture mechanics, 2015, 146: 172–184. DOI:10.1016/j.engfracmech.2015.07.040 |
| [5] | PARANDVAR H, FARID M. Nonlinear reduced order modeling of functionally graded plates subjected to random load in thermal environment[J]. Composite structures, 2015, 126: 174–183. DOI:10.1016/j.compstruct.2015.02.006 |
| [6] | NIKOLARAKIS A M, THEOTOKOGLOU E E. Numerical analysis of transient stress field of a functionally graded nickel-zirconia profile under thermal loading[J]. Journal of thermal stresses, 2015, 38(10): 1085–1103. DOI:10.1080/01495739.2015.1073497 |
| [7] | DAG S, YILDIRIM B, TOPAL S. Computational methods for inclined cracks in orthotropic functionally graded materials under thermal stresses[J]. Journal of thermal stresses, 2013, 36(10): 1001–1026. DOI:10.1080/01495739.2013.788408 |
| [8] | GUO Fengnan, GUO Licheng, HUANG Kai, et al. Thermal fracture analysis of nonhomogeneous plate with interfaces under uniform heat flow[J]. Journal of thermal stresses, 2014, 37(7): 771–793. DOI:10.1080/01495739.2014.885345 |
| [9] | HOSSEINI S S, BAYESTEH H, MOHAMMADI S. Thermo-mechanical XFEM crack propagation analysis of functionally graded materials[J]. Materials science and engineering:A, 2013, 561: 285–302. DOI:10.1016/j.msea.2012.10.043 |
| [10] | PETROVA V, SCHMAUDER S. Modelling of thermal fracture of functionally graded/homogeneous bimaterial structures under thermo-mechanical loading[J]. Key engineering materials, 2014, 592: . |
| [11] | GUO Fengnan, GUO Licheng, YU Hongjun, et al. Thermal fracture analysis of nonhomogeneous piezoelectric materials using an interaction energy integral method[J]. International journal of solids and structures, 2014, 51(3/4): 910–921. |
| [12] | ZHANG Yanyan, GUO Licheng, NODA N. Investigation methods for thermal shock crack problems of functionally graded materials-Part Ⅱ:combined analytical-numerical method[J]. Journal of thermal stresses, 2014, 37(3): 325–339. DOI:10.1080/01495739.2013.839854 |
| [13] | GUO Licheng, WANG Zhihai, ZHANG Li. A fracture mechanics problem of a functionally graded layered structure with an arbitrarily oriented crack crossing the interface[J]. Mechanics of materials, 2012, 46: 69–82. DOI:10.1016/j.mechmat.2011.10.007 |
| [14] | GUO Licheng, WU Linzhi, ZENG Tao, et al. Mode I crack problem for a functionally graded orthotropic strip[J]. European journal of mechanics-a/solids, 2004, 23(2): 219–234. DOI:10.1016/j.euromechsol.2003.12.006 |
| [15] | GUO Licheng, WU Linzhi, ZENG Tao, et al. The dynamic fracture behavior of a functionally graded coating-substrate system[J]. Composite Structures, 2004, 64(3/4): 433–441. |
| [16] | GUO Licheng, NODA N. Dynamic investigation of a functionally graded layered structure with a crack crossing the interface[J]. International journal of solids and structures, 2008, 45(1): 336–357. DOI:10.1016/j.ijsolstr.2007.08.015 |
| [17] | DING Shenghu, ZHOU Yueting, LI Xing. Thermal stress analysis of an embedded crack in a graded orthotropic coating-substrate structure[J]. Journal of thermal stresses, 2015, 38(9): 1005–1021. DOI:10.1080/01495739.2015.1040313 |
| [18] | GUO Licheng, NODA N. Investigation methods for thermal shock crack problems of functionally graded materials-Part I:analytical method[J]. Journal of thermal stresses, 2014, 37(3): 292–324. DOI:10.1080/01495739.2013.839853 |
| [19] | HUANG Ganyun, WANG Yuesheng, YU Shouwen. A new model of functionally graded coatings with a crack under thermal loading[J]. Journal of thermal stresses, 2004, 27(6): 491–512. DOI:10.1080/01495730490451440 |
| [20] | GUO Licheng, NODA N. Modeling method for a crack problem of functionally graded materials with arbitrary properties-piecewise-exponential model[J]. International journal of solids and structures, 2007, 44(21): 6768–6790. DOI:10.1016/j.ijsolstr.2007.03.012 |
| [21] | BAI Xiaoming, GUO Licheng, WANG Zhihai, et al. A dynamic piecewise-exponential model for transient crack problems of functionally graded materials with arbitrary mechanical properties[J]. Theoretical and applied fracture mechanics, 2013, 66: 41–51. DOI:10.1016/j.tafmec.2013.09.001 |
| [22] | GUO Licheng, WANG Zhihai, NODA N. A fracture mechanics model for a crack problem of functionally graded materials with stochastic mechanical properties[J]. Proceedings of the royal society A:mathematical, physical and engineering sciences, 2012, 468(2146): 2939–2961. DOI:10.1098/rspa.2012.0156 |
| [23] | WANG Zhihai, GUO Licheng, ZHANG Li. A general modelling method for functionally graded materials with an arbitrarily oriented crack[J]. Philosophical magazine, 2014, 94(8): 764–791. DOI:10.1080/14786435.2013.863437 |
| [24] | ERDOGAN F, WU B H. The surface crack problem for a plate with functionally graded properties[J]. Journal of applied mechanics, 1997, 64(3): 449–456. DOI:10.1115/1.2788914 |
| [25] | LONG X, DELALE F. The general problem for an arbitrarily oriented crack in a FGM layer[J]. International journal of fracture, 2004, 129(3): 221–238. DOI:10.1023/B:FRAC.0000047798.43634.e3 |
| [26] | ERDOGAN F, GUPTA G D. On the numerical solution of singular integral equations[J]. Quarterly of applied mathematics, 1972, 29(4): 525–534. DOI:10.1090/qam/1972-29-04 |
| [27] | GUO Licheng, NODA N. Fracture mechanics analysis of functionally graded layered structures with a crack crossing the interface[J]. Mechanics of materials, 2008, 40(3): 81–99. DOI:10.1016/j.mechmat.2007.06.005 |
| [28] | PAN Haizhu, SONG Tianshu, WANG Zhihai. An analytical model for collinear cracks in functionally graded materials with general mechanical properties[J]. Composite structures, 2015, 132: 359–371. DOI:10.1016/j.compstruct.2015.05.055 |



