2. 天津海事局 船员考试中心, 天津 300451;
3. 中海石油环保服务有限公司, 天津 300451;
4. 国家安全水运中心, 湖北 武汉 430062
2. Seafarers Examination Center, Tianjin Maritime Safety Administration, Tianjin 300451, China;
3. China Offshore Environment Services, Tianjin 300451, China;
4. National Engineering Research Center for Water Transport Safety, Wuhan 430062, China
所谓“粒子法”是把海上溢油油膜离散化为大量油粒子,每个油粒子代表一定油量。每个油粒子在表层海流作用下漂移,而油膜扩展可以通过油粒子随机运动来体现。油膜厚度分布通过一定海面面积内油粒子的个数、体积、质量来计算。该预测方法在油膜迎风压缩和主风向拉伸方面非常具有合理性。
国外学者20世纪60年代开始对溢油扩展进行研究。Fay[1]对于溢油扩展过程提出的三阶段理论最为经典,该研究将溢油扩展过程分为三个阶段,分别是惯性力、粘性力和表面张力扩展阶段并通过实验得出三个阶段扩展公式。但该理论假定油膜始终为圆形并以恒定流或实验室的静水条件为前提,与实际情况相差较大,因此该理论与实际测量存在较大差异。后来很多学者对这一方法进行了改进,Lehretal[2]通过海上现状的观测,对Fay理论及其扩展公式进行进一步修正,将风的因素加入到计算油膜扩展的公式中。20世纪80年代中期之后,越来越多的学者将“油粒子”思想应用到溢油模型中。Johansen和Elliot等提出,“油粒子”思想区别于对流扩散方法模拟溢油过程,它将溢油分成大量小油粒子,基于拉格朗日粒子跟踪法[3-4],预测每个油粒子在海水中的漂移轨迹,从而直观模拟出油膜在风和波浪等作用下漂移的实际情况。各国研究者基于“油粒子”思想对溢油模型进行了深入的研究。本文通过海上试验获得的模拟溢油漂浮物GPS数据,验证“粒子跟踪法”的预测精度,为渤海海域溢油应急提供了技术支持。
1 溢油漂移模型的建立本文选取国际流行的“粒子跟踪法”设计的三维模型对渤海溢油轨迹进行模拟预测。
1.1 油膜扩展输移预测剪流和湍流引起的扩散过程属于随机运动,可用随机走动法实现模拟。由于每个粒子的随机运动而导致整个粒子云团在水体中的扩散过程[5-6]。对于水体表面随机扩散过程可描述为
| ${r_\alpha } = R{\left( {6k\alpha t} \right)^{1/2}}$ |
式中:rα为α=(x,y) 方向上的湍动扩散距离,R为[-1, 1]间均匀分布随机数,k为α方向上的湍流扩散系数,t为时间步长。
溢油的漂移是平流过程、扩散过程和风共同作用的结果。
第i个粒子在t时段内的位移可表示为
| ${x_i} = {u_i}t + r_x^\prime {\rm{, }}\quad {y_i} = {v_i}t + r_y^\prime $ |
式中:ui=uf+αwx,yi=vf+αwy,rx′、ry′表示在x、y方向上的随机移动距离,uf、vf可由环境动力学模型求出。α为经验系数取0.03,wx、wy为风速在x、y方向上的分量。
由于每个粒子代表一定的油量,根据标识粒子所在的位置和所代表的油量可计算溢油的扩展面积,再根据粒子所走过的海域,可计算扫海面积。
1.2 油膜轨迹预测在环境动力模型提供的环境动力参数的基础上,采用欧拉—拉格朗日追踪方法,进行油膜中心轨迹的预测[7-8]。油膜中心漂移速度,取决于海面风速与表层流速,是空间和时间的函数,其值用油膜中心点所在网格点上的速度内插而得。空间每个网格点上的速度在某时刻为
| ${V_L} = {V_r} + \alpha {V_{{\rm{wind}}}}$ |
式中:Vr为网格点上表层流速;Vwind网格点上的预报风速;α为风因子,取0.03。
油膜中心点所在位置公式为
| $S = {S_0} + \int\limits_t^{t + t} {{V_l}\left( {x\left( t \right),y\left( t \right),t} \right){\rm{d}}t} $ |
式中:S0为初始时刻,S为油膜中心点所在位置。
由于空间和时间不同,流况不同,有时风速、风向也不同,所以在不同地点、不同时刻发生溢油后所追踪到的油膜中心运移轨迹就不同。
2 溢油漂移模型验证方案为验证“粒子跟踪法”在渤海海域的适用性,本文采用橙子替代油粒子的实验方法,对溢油漂移预测轨迹与溢油模拟物漂移轨迹的一致性进行验证。
试验时间:2015年8月4日-2015年8月7日;漂流时间:2015年8月7日;试验时间:6 h (12:00-18:00);试验地点:东经118°40′00″,北纬38°46′00″。
本次海上实验设施设备如表 1所示。
| 仪器/设备 | 数量/个 | 规格 | 用途 |
| 实验船只 | 1 | 带有GPS定位装置 | 布放漂浮物,并进行跟踪 |
| 漂浮物 | 1 000 | 水果,密度略小于海水密度,颜色鲜艳 | 示踪,海面漂浮模拟溢油 |
| 风速风 向仪 | 1 | 精度0.1 m/s以上风速风向仪 | 监测风向和风速 |
| 望远镜 | 1 | 8-24X50(选用大口径低倍数望远镜) | 进行海面漂浮物搜寻 |
| 拍照、 摄像设备 | 1 | 拍照达千万像素级,路线达到720P | 拍摄 |
为了能够对溢油模型的可靠性进行有效的验证,选择合适的漂流物是至关重要的一个环节,基于以下因素,选取橙子作为实验漂流物:
1) 橙子的形状接近于正圆,因此在个方向上的受力是一致的,与模型中“粒子”的特点相符;
2) 经过测量并计算,橙子的密度约为0.93 g/cm3,与渤海海域所产原油的密度较为接近;
3) 橙子的颜色为橘黄色,在试验过程中,便于试验人员的观测;
4) 橙子是可以食用的,试验结束后不用进行回收,不会对海洋环境造成污染。
2.2 实验步骤1) 在陆上 (有良好互联网信号的宾馆内) 以及船只上,架设好现场纪录数据用电脑;
2) 在船只上,沿下风处投下漂流物,时间最好是可对海面进行正常观测的范围 (即凌晨6:00至下午14:00之间投放)。
3) 在接收电脑上连续采集船只的GPS信息。
4) 实验开始前1 h开始,每20 min记录一次风速风向数据。
5) 实验时间暂定6~10 h (根据海面观测情况确定观测时间)。试验结束后,因水果不会对海洋造成二次污染所以无需回收。
注意事项:船舶在追踪模拟漂浮物时,要保持船位位于漂浮物下风约50 m处,确保船舶的轨迹与模拟漂浮物的轨迹一致。
3 渤海海域潮流场及气象条件 3.1 潮汐海流 3.1.1 计算区域设置本文所建立的海域数学模型计算域范围为A (大连老虎牙) 和B (威海小石岛) 两点以及岸线围成的北黄海及渤海海域,计算域坐标范围为北纬37°04′14.22″~40°58′08.25″,东经117°29′33.27″~122°4′9.92″。模拟采用三角网格,用动边界的方法对干、湿网格进行处理。整个模拟区域内由8 121个三角单元组成[9]。
3.1.2 水深和岸界水深:选取中国人民解放军海军航海保证部制作的1:100万海图 (10011号),15万 (11370号、11570号、11710号、11770、11840号、11910号、11932号) 海图以及工程附近海域水深地形测量资料。岸界:采用以上海图中岸界、908山东省海岸线勘测资料以及工程附近海岸线勘测资料。
3.1.3 大海域模型水边界输入开边界:全球模型调和求得开边界的M2、S2、K1、O1、M4和MS4六个分潮调和常数值,并输入计算模型。
| $\zeta = \sum\limits_{i = 1}^n {\{ {f_i}{H_i}{\rm{cos}}[{\sigma _i}t + ({V_{oi}} + {V_i}) - {G_i}]\} } $ |
式中:fi、σi是第i个分潮 (这里共取六个分潮:M2、S2、O1、K1、M4和MS4) 的交点因子和角速度;Hi和Gi是调和常数,分别为分潮的振幅和迟角;Voi+Vi是分潮的幅角。
闭边界:以大海域和工程周边岸线作为闭边界。
3.1.4 计算时间步长和底床糙率模型计算时间步长根据CFL条件进行动态调整,确保模型计算稳定进行,最小时间步长1 s。底床糙率通过曼宁系数进行控制[10],曼宁系数n取32~55 m3/s。
3.1.5 水平涡动粘滞系数采用考虑亚尺度网格效应的Smagorinsky公式计算水平涡粘系数,表达式如下
| $A = c_s^2{l^2}\sqrt {2{S_{ij}}} $ |
式中:cs为常数,l为特征混合长度,由Sij=
根据上述模型结合渤海海域的实际情况,通过计算仿真得知,渤海大部分海域潮流为往复流。涨潮时,潮流进入渤海海峡后分流,部分向北流入辽东湾,部分流向渤海湾,部分向南流入莱州湾;落潮时,潮流场结构与涨潮时基本相同,流向相反。涨潮时流速大于落潮时流速。
为验证潮流场计算结果的准确性,选取了5个观测点进行实际观测,经过实际观测可发现计算流速与实测值之间存在10%的误差,经过计算可得模拟流速在3~4 h小于实测流速10 cm/s,在6 h内将会出现1.08 km的误差。
3.2 实验气象条件实验所在海域气象条件如下:实验时间选择在2015年8月7日中午12:00至下午18:00,当天天气晴、能见度大于5 n mile,气温30℃,偏南风3~4级,气压101.5 kPa,流向偏南,流速小于1.2 kn。
4 溢油漂移模型验证实验 4.1 目标跟踪试验测试人员投放漂浮物 (橙子),沿船只下风处投下漂流物,投放时间为12:00,可对海面进行正常观测。同时,观察漂流物吃水及汇集漂浮状态。

|
| 图1 投放漂流物 Figure 1 Drifting material |
按照溢油的类型,观察漂流物在海上的漂浮情况,通过船舶自带GPS定位系统连续跟踪定位漂浮物位置信息数据,并对地理数据进行漂移路线绘图。
8月7日12:00分投放漂流物,投放漂浮物后,设备信号接收情况正常,通过船舶GPS定位系统进行连续跟踪监测。漂流物从 (118°40′00″,38°46′00″) 地理位置投入海水后,在漂移过程中受试验海域的风力和洋流影响,漂移方向出现了四次变化比较大的拐点。
第1次 (2015年8月7日13:20分) 由西北方向变为向西南方向,第2次 (2015年8月7日15:07) 由偏西方向变为偏南方向,第3次2015年8月7日16:38) 由南偏西方向变为南向,第4次 (2015年8月7日17:18) 由南偏西方向变为南向。在试验过程中,监测船于8月7日12:00分从开始跟踪漂浮物,对漂浮物进行中远距离跟踪监测。监测船连续跟踪6 h后,于18:00分左右开始返航。8月7日19:00左右,监测船再次出发,根据定位坐标信息在指定海域发现投放漂流物,因水果不会对海洋造成二次污染所以无需回收,试验结束。

|
| 图2 监测船跟踪漂流物 Figure 2 Monitoring ship tracking drift |

|
| 图3 监测船根据定位信息发现漂流物 Figure 3 The monitoring ship finds the drift according to the location information |
试验过程中预先准备投放的橙子数量约为1 000余个,橙子的颜色与海水的色差较大,便于观察与跟踪,同时,如果入海时间过长容易造成目标物漂移分散,不便于试验的观察和跟踪,所以此次试验时间设定为6 h。
基于以上情况,根据试验监测要求,本次订购的卫星遥感影像图可对漂流物进行位置信息跟踪。
图 4为针对本次海上验证试验方案,订购 (118°40′00″,38°46′00″) 位置的卫星遥感影像数据,卫星过境时间为8月7日16:45。

|
| 图4 试验订购卫星遥感影像数据 Figure 4 Test for satellite remote sensing image data |
试验结束后,试验技术人员以30 min为一段时间,将本次参加试验的漂流物位置及距离进行分析。其漂移坐标及累计漂移距离如表 2所示。
| 试验时间 | 漂流物经纬度坐标 (东经/北纬) | 累计漂移距离/m |
| 12:00 | 118.399 78°/38.461 041° | 0 |
| 12:30 | 118.382 22°/38.458 972° | 335 |
| 13:00 | 118.369 94°/38.454 222° | 676 |
| 13:30 | 118.358 83°/38.452 917° | 1 447 |
| 14:00 | 118.358 19°/38.449 833° | 1 968 |
| 14:30 | 118.354 28°/38.448 667° | 2 456 |
| 15:00 | 118.322 69°/38.448 333° | 3 359 |
| 15:30 | 118.316 22°/38.447 111° | 4 017 |
| 16:00 | 118.29 989°/38.445 778° | 4 805 |
| 16:30 | 118.287 99°/38.443 833° | 5 156 |
| 17:00 | 118.282 22°/38.440 667° | 5 359 |
| 17:30 | 118.279 94°/38.439 333° | 5 617 |
| 18:00 | 118.276 83°/38.438 111° | 5 805 |
试验结束后,试验技术人员将漂流物的定位漂移数据与漂移预测数据进行对比,从漂移路线,漂移趋势等方面进行研究。
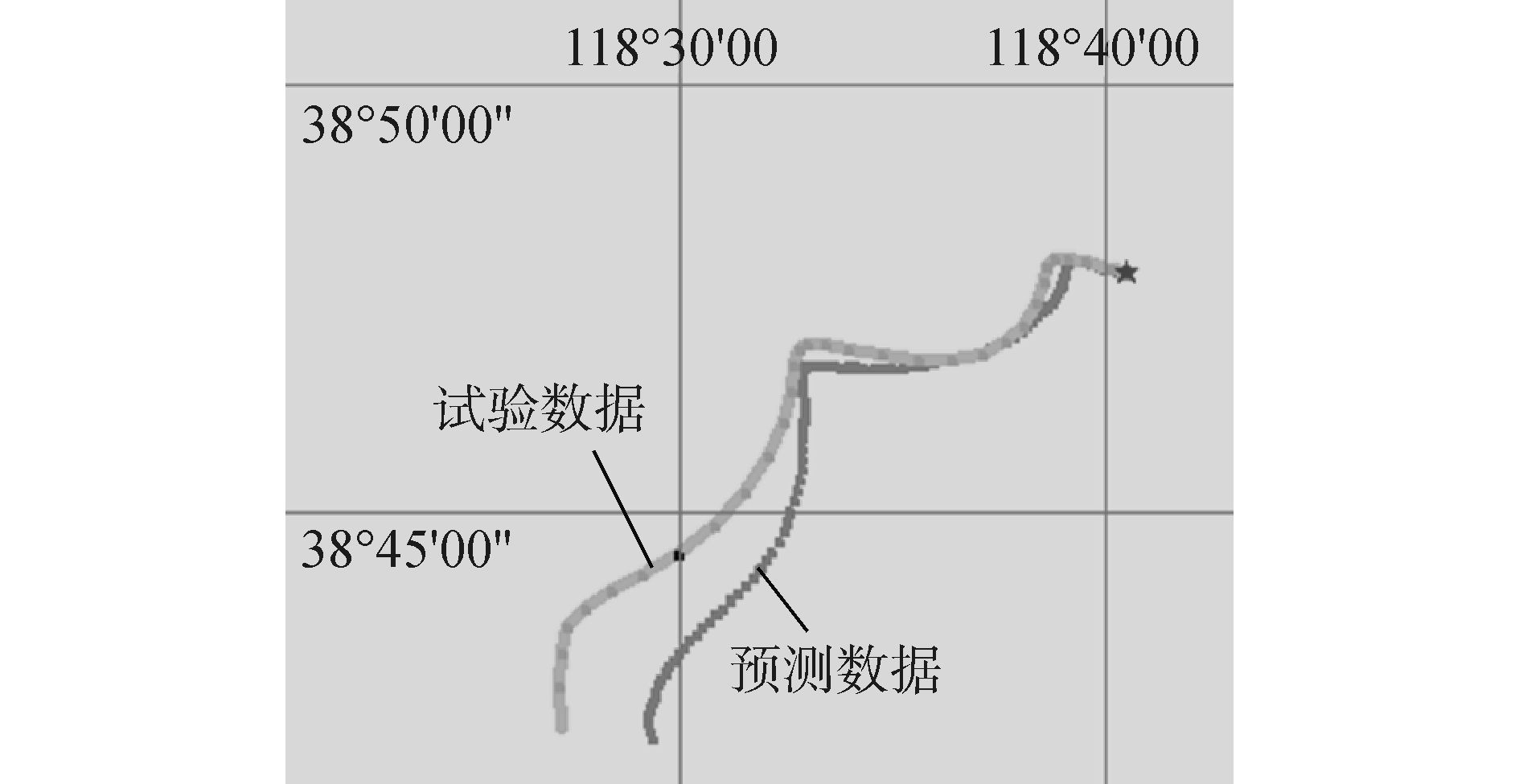
由图 5给出了GPS跟踪试验得到的实测漂移轨迹和漂移预测计算得到的漂移轨迹,分别为图中的右下和左上轨迹。图中可以明显看出试验过程中漂移方向的几次转变。其中,从起始位置至第二次转变位置附近,实测漂移路线和预测系统模拟的路线吻合度很高,之后,二者虽出现偏差,但是整体来说,实测的漂移轨迹与溢油漂移预测的轨迹趋势保持一致,累计漂移距离、漂移速度一致,且6 h内最大距离差为1.2 km,经计算误差小于10%。
|
| 图5 试验数据与预测数据对比验证 Figure 5 Comparison of test data and prediction data |
本次研究试验后期实测的轨迹和预测模拟的轨迹出现偏差,风速较大时漂移速度小于实际油膜漂移速度,漂浮物不能以实际油膜漂移速度漂移,导致漂移路径和模型预测路径出现一些偏差。随后,由于试验误差累积效应,偏移距离随试验时间逐渐增大,但从试验漂移轨迹趋势、漂移距离、漂移速度等各方面均与预测结果具有较高的拟合度。
6 结论本文以橙子作为漂流物替代溢油油膜,对粒子跟踪法溢油模型在渤海中的适应性进行实际试验,对试验数据和模型计算数据进行对比,可得到结论:
1) 漂流物与溢油模型预测轨迹之间存在10%的误差,与潮流场误差一致,可知潮流场误差是造成模拟误差的主要原因。
2) 经过验证实测数据和模型计算数据之间存在的误差小于10%,在可接受范围之内,表明粒子跟踪法溢油漂移预测模型能有效适用于渤海海域。
3) 研究表明应用橙子作为漂流物替溢油进行海上试验验证溢油模型的方法是科学可行的。
4) 经验证适用于渤海海域的粒子跟踪法溢油模型能够对渤海海域的溢油应急预警提供决策支持,进一步提升了渤海海域的溢油应急预警水平。
| [1] | FAY J A. Oil on the sea[M]. New York: Plenum Press, 1969: 53-63. |
| [2] | LEHR W J, CEKIRGE H M, FRAGA R J, et al. Empirical studies of the spreading of oil spills[J]. Oil and petrochemical pollution, 1984, 2(1): 7–11. DOI:10.1016/S0143-7127(84)90637-9 |
| [3] |
汪守东. 基于Lagrange追踪的海上溢油预报模型研究[D]. 大连: 大连理工大学, 2008: 25-63.
WANG Shoudong. Research on offshore oil spill prediction model based on Lagrange tracking [D]. Dalian: Dalian University of Technology, 2008: 25-63. |
| [4] |
徐艳东. 海上溢油风化过程及其预测模型研究[D]. 青岛: 中国海洋大学, 2006.
XU Yandong. Study on weathering process and prediction model of oil spill at sea [D]. Qingdao: Ocean University of China, 2006. |
| [5] | CHEN Fanghui, YAPA P D. Modeling gas separation from a bent deepwater oil and gas jet/-plume[J]. Journal of marine systems, 2004, 45: 189–203. DOI:10.1016/j.jmarsys.2003.11.005 |
| [6] | ASCE Task Comnitte on Modeling of Oil Spills. State-of-the-art review of modeling transport and fate of oil spills[J]. Journal of Hydraulic Engineering, 1996, 122(11): 104–118. |
| [7] |
龙绍桥. 海上溢油行为与归宿数值模拟及其对环境的影响研究[D]. 青岛: 中国海洋大学, 2006: 32-47.
LONG Shaoqiao. Study on the behavior and fate of oil spill at sea and its impact on environment [D]. Qingda: Ocean University of China, 2006: 32-47. |
| [8] |
李大鸣, 陈海舟, 付庆军. 海上溢油数学模型的研究与应用[J].
哈尔滨:哈尔滨工程大学学报, 2008, 29(12): 1291–1297.
LI Daming, CHEN Haizhou, FU Qingjun. Oil spill model research and application[J]. Harbin: Journal of Harbin Engineering University, 2008, 29(12): 1291–1297. |
| [9] |
李孟国, 曹祖德. 海岸河口潮流数值模拟的研究与进展[J].
海洋学报, 1999, 21(1): 111–125.
LI Mengguo, CAO Zude. Research and development of numerical simulation of tidal current in the estuary[J]. Journal of oceanography, 1999, 21(1): 111–125. |
| [10] |
李庆红, 赵军方, 张永刚. 大连附近海域潮汐潮流的三维数值模拟[J].
海洋测绘, 2003, 23(2): 48–52.
LI Qinghong, ZHAO Junfang, ZHANG Yonggang. Three dimensional numerical simulation of tidal current in the vicinity of Dalian sea[J]. Marine surveying and mapping, 2003, 23(2): 48–52. |
| [11] | ALIREZA B, PARVIZ G, MOHAMMAD A F. Sound scattering from rough bubbly ocean surface based on modified sea surface acoustic simulator and consideration of various incident angles and sub-surface bubbles′ radii[J]. Journal of marine science and application, 2016, 15(3): 275–287. DOI:10.1007/s11804-016-1374-6 |
| [12] | AMIRI A, PANAHI R, RADFAR S. Parametric study of two-body floating-point wave absorber[J]. Journal of marine science and application, 2016, 15(1): 41–49. DOI:10.1007/s11804-016-1342-1 |



