耐压球壳是载人潜器的关键部件,在载人潜器的设计中占有重要地位。然而,耐压球壳的设计存在众多不确定性,如模型的假设和简化分析等,这些均可能导致设计误差的产生。相比而言,有开孔加强结构耐压球壳的不确定性更多,这些不确定性因素的任何微小变化都可能对设计结果产生很大的影响,进一步对载人潜器的安全性,乃至总体性能造成严重的影响。因此,在有开孔加强结构耐压球壳的设计过程中,必须考虑不确定性因素的影响。
对于耐压结构设计所存在的众多不确定性,已经引起了众多学者的关注。张伟等[1] 建立了潜艇耐压圆柱壳壳板失效的失效函数,总结了设计参数对于潜艇耐压圆柱壳结构失效的影响程度,为潜艇的设计、制造和使用提供了参考。白旭[2]分析了球柱组合壳结构的不确定因素,建立了基于失效模式的可靠性模型,采用多岛遗传算法进行了模型的求解,优化结果明显。操安喜等[3]基于非概率可靠性分析理论,研究了影响球壳结构可靠性的不确定参数的描述方法,对于结构的可靠性指标的获取方法进行了研究,采用区间运算方法获得了定量的结构非概率可靠性指标,并进行了实例验证。
稳健性由Taguchi[4]提出,其在产品设计阶段通过优化设计方案,尽量减少质量波动,从而获得低成本、高性能、高可靠性的产品[5]。李锋等[6]考虑了设计变量和其他随机变量的变异性对结构疲劳寿命的影响,将结构疲劳寿命稳健性优化问题构造成包含结构疲劳寿命均值和标准差的双目标优化问题。程妍雪等[7]在考虑了不确定性对结构性能的影响的基础上,将6σ设计引入到耐压壳优化设计。周定智等[8]提出了一种基于多目标优化和C稳健性设计的车顶结构轻量化设计方法,并将该方法应用到汽车的轻量化设计中。
本文以有开孔加强结构耐压球壳为研究对象,对于开孔加强的样本点进行了有限元分析,为降低分析难度,进行了设计变量的灵敏度分析,完成了设计变量的筛选,得到了有开孔加强结构耐压球壳的近似模型,建立了有开孔加强结构耐压球壳多响应多目标稳健性优化模型,进行了模型的稳健性优化求解,得到了更加稳健的设计方案。
1 有限元分析模型的建立 1.1 开孔加强结构形式载人潜器耐压球壳开孔众多,如人员出入舱口、观察窗、电缆贯穿、管子贯穿等。其中,出入舱口和观察窗开孔较大,是耐压球壳设计中的重要内容。
将观察窗座固定,只针对出入舱口加强展开研究。耐压球壳出入舱口的加强形式及相关参数见图 1,耐压球壳所采用的高强度钢材料参数见表 1。
| 弹性模量 E/MPa | 泊松比ν | 屈服强度 σs/MPa | 抗拉强度 σb/MPa |
| 2×105 | 0.3 | 785 | 820 |
采用ABAQUS软件进行耐压球壳极限强度Pcr的求解。初始缺陷采用初挠度代替,取为0.07mm,初始增量步为0.01,最小增量步10-5,最大增量步0.1,总增量步数100。
材料的真实应力应变曲线由工程应力应变曲线转换得到。高强度钢的工程应力应变曲线拟合表达式为[9]
| $\sigma =\left\{ \begin{align} & \begin{matrix} E\varepsilon & (0\le \sigma <588~MPa) \\ \end{matrix} \\ & \begin{matrix} {{A}_{0}}+{{A}_{1}}\varepsilon +{{A}_{2}}{{\varepsilon }^{2}}+{{A}_{3}}{{\varepsilon }^{3}} & (588~MPa\le \sigma <785~MPa) \\ \end{matrix} \\ & \begin{matrix} {{B}_{0}}+{{B}_{1}}\varepsilon +{{B}_{2}}{{\varepsilon }^{2}} & (785~MPa\le \sigma <820~MPa) \\ \end{matrix} \\ \end{align} \right.$ | (1) |
式中:σ为工程应力,ε为工程应变,E为弹性模量,Ai和Bj为拟合参数,其中,A0=-885.7,A1=8.830 55×105,A2=-1.605 909 7×108,A3=9.989 296 6×109,B0=724.74,B1=1.107 12×104,B2=-1.407 835×105[9]。
计算时要求消除结构刚体位移,取3个点约束球壳6个方向自由度,其中网格模型在Z轴的节点1,T1=T2=0;在X轴上的节点2和3,T2=T3=0。通常通过安全系数K对于耐压球壳的强度储备进行表达,hg为工作深度,hjx为极限深度,hj为计算深度。K、hg、hjx、hj之间存在以下关系:
| ${{h}_{g}}=\left( 0.85\text{ }\!\!\tilde{\ }\!\!\text{ }0.9 \right){{h}_{jx}}$ | (2) |
| ${{h}_{j}}=K{{h}_{jx}}$ | (3) |
式中:K取1.5[10],hg=0.90hjx。球壳壳板应力应满足:
| $\sigma ={{P}_{j}}R/2t\le 0.85{{\sigma }_{s}}$ | (4) |
规范[10]对承受外压的耐压球壳开孔区域的应力计算要求为:围壁板与球壳体连接处板边缘的中面周向应力不得超过材料屈服强度σs的1.15倍。目标载人潜器的工作深度为1 500 m,则耐压球壳载荷可通过式(5)求得
| ${{P}_{j}}=0.009\text{ }8{{h}_{j}}=24.5~MPa$ | (5) |
则耐压球壳需要施加24.5 MPa的水压,经过换算在开孔加强处施加等效载荷136.278 MPa。
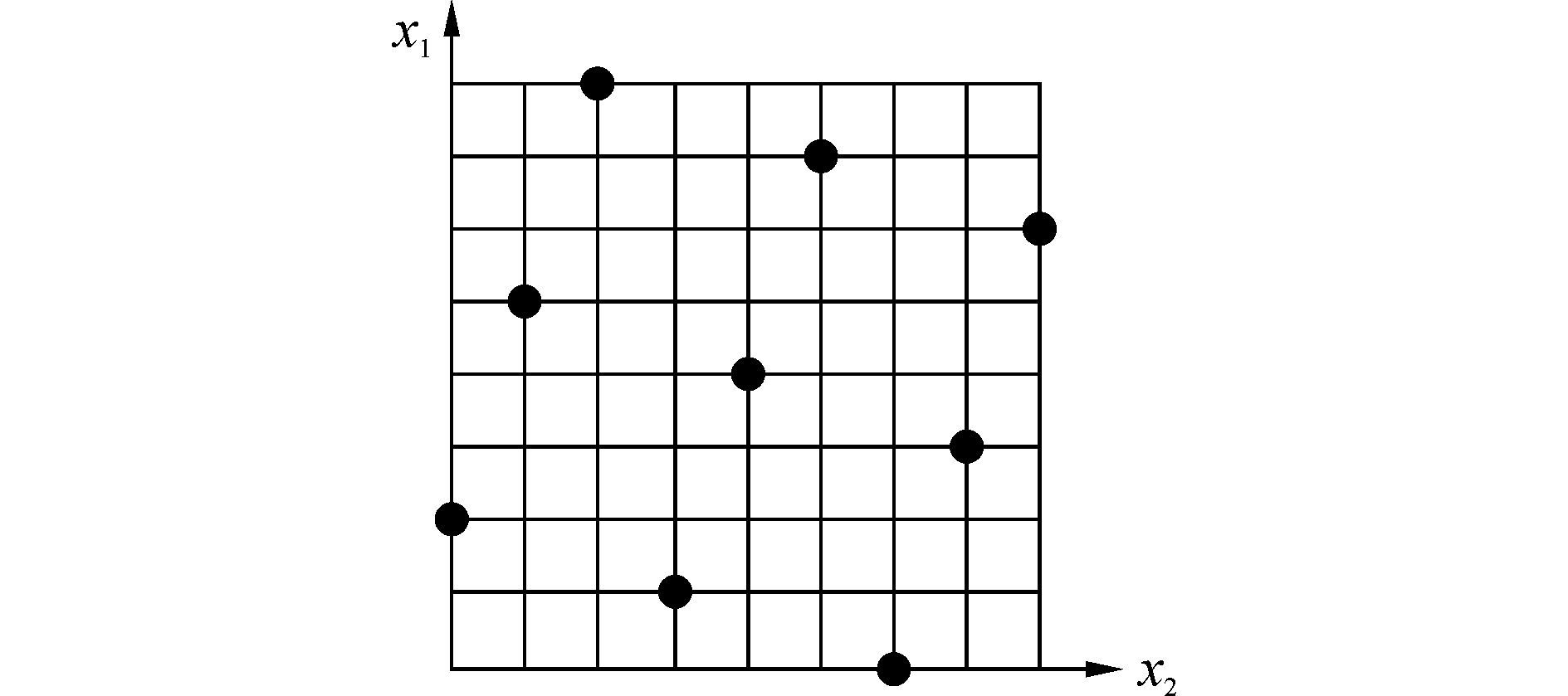
2 设计变量的选取与灵敏度分析 2.1 样本点的选取拉丁超立方设计具有空间填充能力有效、可拟合非线性响应、可人为控制试验次数等优点,但存在不可重复性、试验点分布不均可能导致设计空间区域的丢失等缺点。最优拉丁超立方(Opt-LHD)使随机拉丁超立方设计的均匀性得到了改进,使因素和响应的拟合更加精确真实,Opt-LHD使所有的试验点尽量均匀的分布在设计空间,具有非常好的空间填充性和均衡性。图 2给出了2因子、9水平的Opt-LHD样本点的分布情况。

|
| 图1 开孔加强结构形式 Figure 1 Opening reinforcement structure |
|
| 图2 最优拉丁超立方样本点的分布 Figure 2 Distribution of Opt-LHD sample points |
图 1中,R为固定值,因此,将其余5个设计变量采用Opt-LHD选取32个样本进行计算,得到设计变量对于响应值极限载荷Pcr的设计灵敏度排列图见图 3。通过图 3可以看出,五个设计变量对于Pcr的灵敏度按照x1、x4、x3、x2、x5的顺序降低,虽然x5的大小影响着人员出入口的等效载荷的大小,但这种载荷的变化范围不是很大,综合考虑选取x1、x2、x3、x4四个设计变量作为研究目标的设计变量。

|
| 图3 设计变量灵敏度排列图 Figure 3 Pareto diagram of design variables sensitivity |
响应面模型(response surface method,RSM)的实质是将响应值与变量之间的未知映射关系通过简单的函数关系进行表达。其本质是进行多项式求解,具有透明性高、简单、高效的特点。RSM按照阶数可分为一阶、二阶、三阶和四阶。其中,二阶RSM的表达形式为[11]
| $\hat{y}(x)={{a}_{0}}+\sum\limits_{i=1}^{n}{{}}{{b}_{i}}{{x}_{i}}+\sum\limits_{i=1}^{n}{{}}{{c}_{ii}}x_{i}^{2}+\sum\limits_{1\le i\ne j\le n}^{{}}{{}}{{d}_{ij}}{{x}_{i}}{{x}_{j}}$ | (6) |
式中:
RSM的拟合精度采用复相关系数R2进行预测,R2的取值范围为[0,1],R2的取值与1的接近程度反映了近似模型拟合精度,其取值越接近1则拟合精度越高。R2表达式为
| ${{R}^{2}}=1-\frac{\sum\limits_{i=1}^{n}{{}}{{({{y}_{i}}\text{-}{{{\hat{y}}}_{i}})}^{2}}}{\sum\limits_{i=1}^{n}{{}}{{({{y}_{i}}-{{{\bar{y}}}_{i}})}^{2}}}$ | (7) |
式中:yi为第i个样本对应的状态变量的响应值、
针对x1、x2、x3、x4四个设计变量,采用Opt-LHD选取16个样本点,进行耐压球壳重量M、极限载荷Pcr、球壳体壳板应力为σ1、围壁板与球壳体连接处板边缘的中面周向应力为σ2四个响应值的计算和二阶响应面拟合。得到模型系数及R2见表 2。
| 系数 | 重量/kg | 极限 载荷/MPa | 壳板 应力/MPa | 壳板 应力/MPa |
| 常数项 | -2 124.58 | -88.778 7 | 12 340.48 | -16 768.1 |
| x1 | 85.001 77 | 5.844 628 | -673.399 | 962.866 3 |
| x2 | 14.384 17 | 1.259 951 | -24.734 6 | 29.001 04 |
| x3 | 21.073 33 | 2.106 532 | -30.826 6 | 41.598 66 |
| x4 | 112.409 8 | -8.556 22 | -108.486 | 141.257 4 |
| x1x1 | 2.637 787 | -0.336 94 | 13.070 96 | -18.336 4 |
| x2x2 | 0.100 449 | -0.003 98 | 0.170 055 | -0.206 38 |
| x3x3 | -0.031 64 | -0.019 85 | 0.204 57 | -0.261 19 |
| x4x4 | -0.040 79 | -0.003 23 | 1.337 403 | -2.746 18 |
| x1 x2 | -1.542 72 | 0.009 82 | -0.714 05 | 0.592 458 |
| x1 x3 | -0.837 42 | 0.039 914 | 0.711 368 | -0.852 49 |
| x1 x4 | 0.071 509 | 0.345 78 | 0.992 274 | -1.371 22 |
| x2 x3 | 0.027 598 | -0.011 16 | 0.041 469 | -0.107 02 |
| x2x4 | -0.005 94 | -0.006 08 | 0.583 404 | -0.258 24 |
| x3x4 | -0.052 27 | 0.028 352 | -0.591 98 | 0.797 744 |
| R2 | 0.999 7 | 0.961 3 | 0.951 2 | 0.968 5 |
表 2中,R2均在0.95以上,说明近似模型的拟合精度较高,满足工程的需要。将表 2的系数代入式(6)便可得到相应的近似模型。
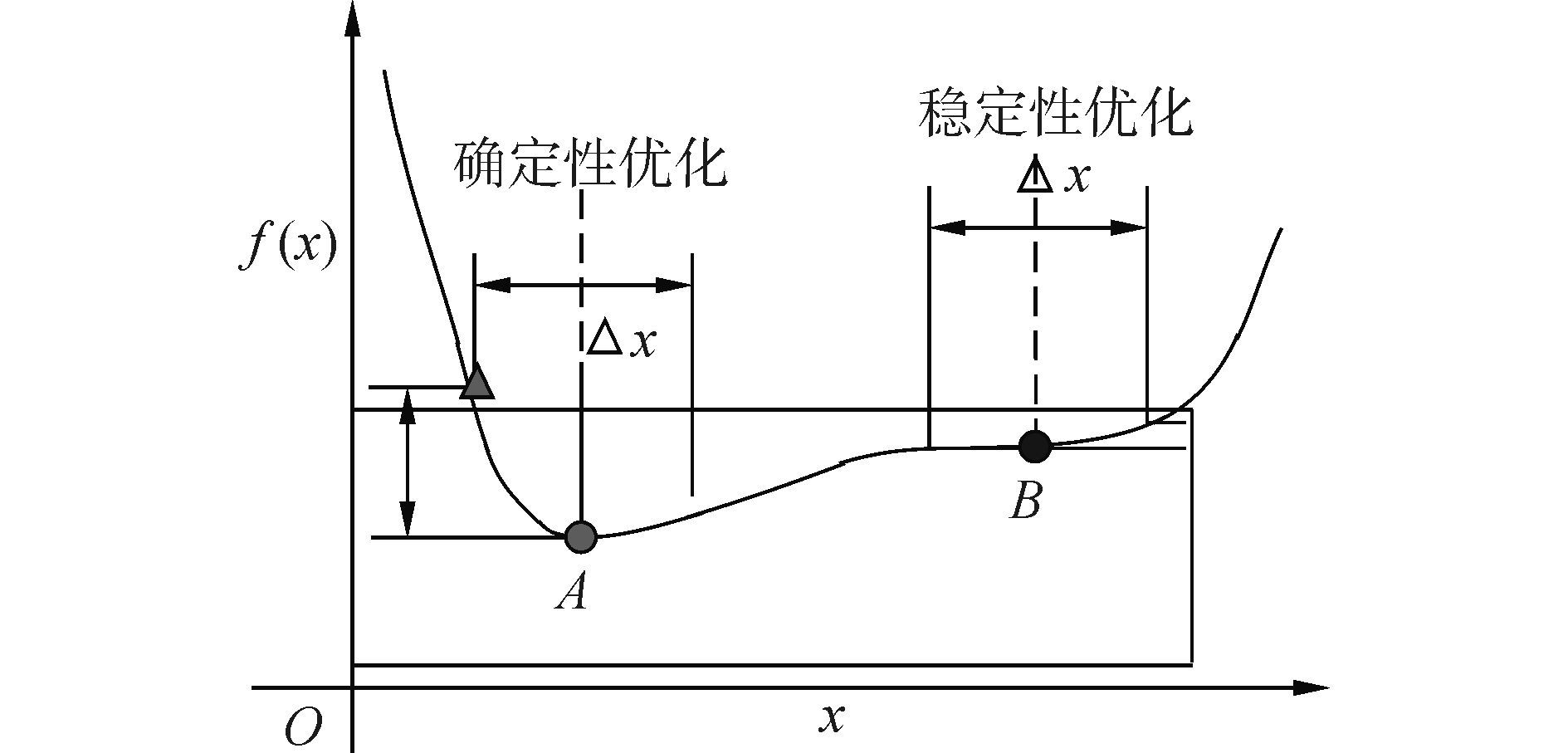
4 稳健性和蒙特卡洛抽样 4.1 稳健性优化稳健性优化也称为鲁棒性设计,其通过对于产品设计、制造、材料等偏差和环境变化等带来的风险进行分析,力求提高产品质量。比如说产品性能与某个因素有关,因素状态变化时,产品的性能也随之变化,如果某因素状态的变化对产品的性能影响不大,即产品性能的变化相对于该因素状态的变化很小的,就可以说产品性能对该因素的变化是不敏感的,又称是稳健的,或者说产品性能对该因素的变化是具有稳健性的。图 4给出了确定性优化与稳健性优化的比较。
|
| 图4 确定性优化与稳健性优化比较 Figure 4 Deterministic optimization compared with robust optimization |
图 4中,目标函数f(x) 的确定性优化最小值在A点处,但若设计变量x在最小点A处产生±Δx的波动,就会造成目标函数f(x)性能损失过大,甚至会超出可行域范围内。对此则有必要对产品实行稳健性优化。相对于稳健性设计优化点B而言,虽然B点相对于A点f(x)的性能有所损失,但B点明显比A点的稳健性更高,也就更具有工程实践意义。
4.2 稳健性优化设计的评价准则6σ的稳健性设计是一种常用的稳健性设计优化的方法,σ指的是标准差,它是用来度量分散程度的一个指标。基于6σ的稳健性设计的概念源于商业,设计目的是为了让设计变量在均值μ的±6σ范围内波动的时候,仍能够使得性能参数在可接受的范围之内,这种离差水平,称为σ水平n。
4.3 蒙特卡洛抽样蒙特卡洛方法以概率统计理论为基础,当所求问题的解是某个事件的概率,或者是某个随机变量的期望值时,通过某种“实验”的方法,得出该事件发生的频率,或者该随机变量若干个具体观察值的算术平均值,通过它得到问题的解[12]。蒙特卡洛抽样分为简单随机抽样和描述性抽样,简单随机抽样是最基本的一种抽样技术,它通过产生均匀分布的随机数序列然后将随机数序列转化为项对应的随机变量值。蒙特卡洛方法是基于重复实验创建双响应面模型,分别对质量特性的均值和方差建立响应面模型,通过蒙特卡洛方法求得样本的均值和方差的直接表达式为
| $\left\{ \begin{align} & {{\mu }_{Y}}=\frac{1}{N}\sum\limits_{i=1}^{N}{{}}g\left( {{x}_{i}} \right) \\ & \sigma _{Y}^{2}=\frac{1}{N-1}{{\left[ \sum\limits_{i=1}^{N}{{}}g({{x}_{i}})-{{\mu }_{Y}} \right]}^{2}} \\ \end{align} \right.$ | (8) |
一般而言,多目标优化问题可以表述为
| $\left\{ \begin{align} & min\{{{f}_{1}}\left( x \right),{{f}_{2}}\left( x \right),\ldots ,{{f}_{k}}\left( x \right)\} \\ & s.t.~{{g}_{j}}\left( x \right)\le 0j=1,2,\ldots ,J \\ & {{x}_{L}}\le x\le {{x}_{U}} \\ \end{align} \right.$ | (9) |
式中:f1(x),f2(x),…,fk(x),是k个目标函数;gj(x)是第j个约束条件;J为约束个数;xL、xU 分别是设计变量x的上下约束边界。在这个数学模型之中并没有考虑由于设计参数的不确定性波动而导致的目标函数的摄动。则问题的多目标稳健性优化模型可以表示为
| $\left\{ \begin{align} & min\{{{f}_{1}}({{Y}_{\mu 1(X)}},{{Y}_{\sigma 1(X)}}),{{f}_{2}}({{Y}_{\mu 2(X)}},{{Y}_{\sigma 2(X)}}),\ldots , \\ & {{f}_{k}}\left( {{Y}_{\mu K(X)}},{{Y}_{\sigma K(X)}} \right)\} \\ & s.t.~{{g}_{\mu j}}\left( x \right)+\eta {{g}_{\sigma j}}\left( x \right)\le 0 \\ & {{x}_{L}}+\eta {{x}_{\sigma }}\le {{x}_{\mu }}\le {{x}_{U}}-\eta {{x}_{\sigma }} \\ \end{align} \right.$ | (10) |
式中:Yμ1(X),Yμ2(X),…,Yμk(X)、Yσ1(X),Yσ2(X)…,Yσk(X)分别表示第K个目标函数的均值和方差,gμj(x)、gσj(x)为第j个约束的均值和方差,向量xμ、xσ为x的均值和方差。
在考虑物理不确定性时,将制造误差引入作为设计变量的随机变量,且这些设计变量均服从正态分布[11],给方差变异系数赋0.01的典型的制造误差。表 3为随机设计变量概率表。
| 设计变量 | 设计空间/均值 | 变异系数 |
| x1 | [20,27] | 0.01 |
| x2 | [65,85] | 0.01 |
| x3 | [65,85] | 0.01 |
| x4 | [22,25] | 0.03 |
以质量和极限载荷作为目标函数,中面应力和壳板应力作为约束,则有开孔加强结构耐压球壳的确定性优化模型为
| $\left\{ \begin{align} & min\{M;{{P}_{cr}}\} \\ & s.t.~\{{{\sigma }_{1}}\le 0.85{{\sigma }_{s}};{{\sigma }_{2}}\le 1.15{{\sigma }_{s}} \\ & DV:{{x}_{1}};{{x}_{2}},{{x}_{3}},{{x}_{4}}, \\ \end{align} \right.$ | (11) |
则多响应多目标稳健性优化模型为
| $\left\{ \begin{align} & min\{\bar{\omega }{{M}_{\mu }}+\left( 1-\bar{\omega } \right){{M}_{{{\sigma }^{2}}}};\bar{\omega }{{P}_{\mu }}+\left( 1-\bar{\omega } \right){{P}_{{{\sigma }^{2}}}}\} \\ & s.t.~\{{{\mu }_{\sigma 1}}+n{{\sigma }_{\sigma 1}}\le 0.85{{\sigma }_{s}};{{\mu }_{\sigma 2}}+n{{\sigma }_{\sigma 2}}\le 1.15{{\sigma }_{s}}; \\ & 24.5\le {{\mu }_{\sigma 2}}-n{{\sigma }_{\sigma 2}}\} \\ & DV:{{x}_{1}};{{x}_{2}},{{x}_{3}},{{x}_{4}}, \\ \end{align} \right.$ | (12) |
式中:n=3或6,ω=0.9。
采用蒙特卡洛描述性抽样得到100组设计变量,将其代入响应面模型,计算出目标函数响应的均值和方差。
第二代非支配排序遗传算法(NSGA-II)基于基本遗传算法,根据个体间的支配关系在选择算子执行前进行分层,之后再进行选择操作。使较好个体有更大的机会遗传到下一代,进而得到更为满意的多目标优化结果。
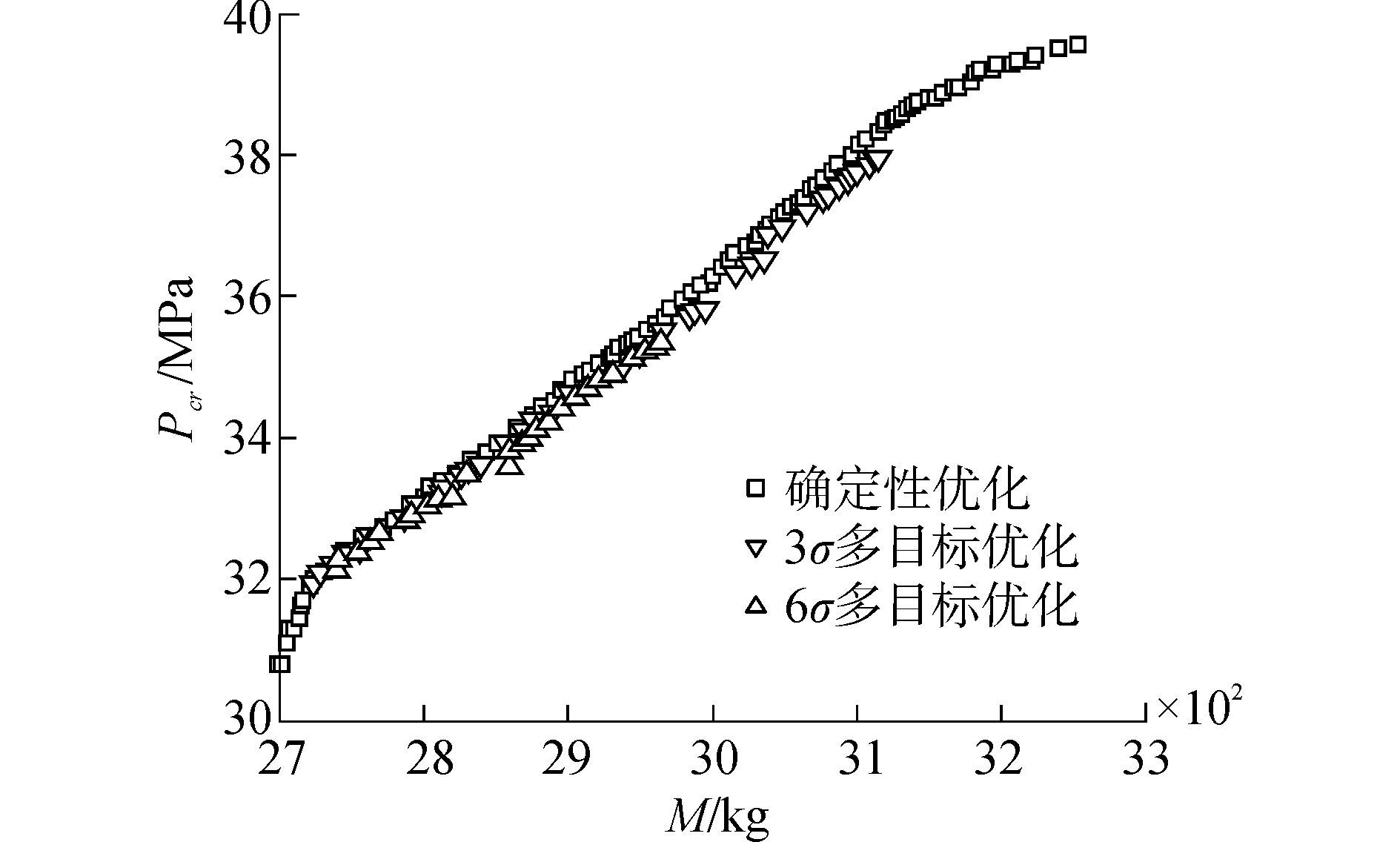
采用NSGA-II进行确定性优化、多响应多目标稳健性优化的求解,NSGA-II的具体原理见文献[13]。NSGA-II设置为:种群大小60,最大遗传进化代数100,交叉概率0.75,变异分布指数100,求解得到的Pareto 前沿见图 5。
|
| 图5 稳健性优化Pareto前沿 Figure 5 Robust optimization Pareto solution set |
图 5中,包含3σ和6σ水平的稳健性前沿,可以看出,两者虽然在最优性上较确定性优化稍差,但稳健性更高,采用最小距离法(TMDSM)[14]确定图 5中三个解集的设计方案。其中,确定性优化方案称为初始方案、3σ优化确定的方案称为方案1,6σ优化确定的方案称为方案2,将三个方案的参数列于表 4。
| 参数 | 初始方案 | 方案1 | 方案2 |
| x1/(°) | 25 | 24.808 | 24.442 |
| x2/(°) | 77 | 76.722 | 78.341 |
| x3/(°) | 75 | 72.136 | 70.561 |
| x4/mm | 23 | 22.444 | 23.179 |
| σ1/MPa | 610.2 | 604.226 | 585.46 |
| σ2/MPa | -637.6 | -634.172 | -617.6 |
| Pcr/MPa | 33.4 | 33.412 | 33.997 |
| M/kg | 2 964.99 | 2 823.173 | 2 883.986 |
表 4中,相比初始方案,方案1和方案2在重量方面优化结果明显,分别减重141.817和81.004 kg,其余目标函数差距不大。
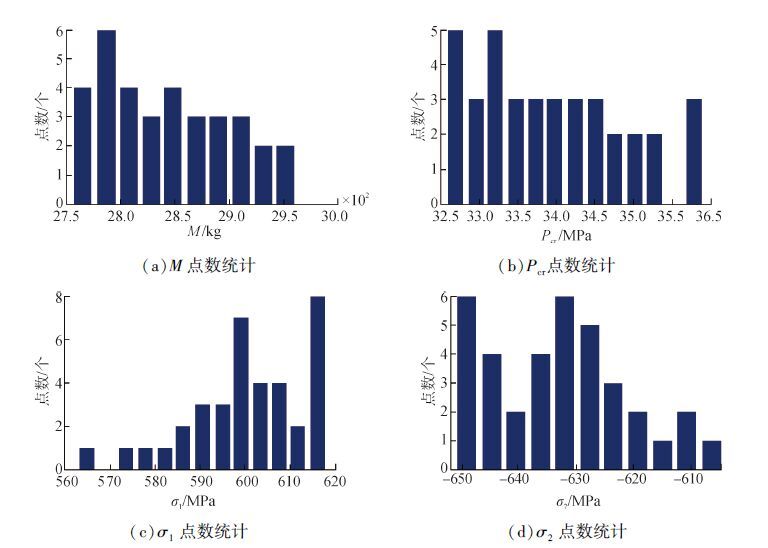
对于方案1的设计变量,采用描述性蒙特卡洛进行100次抽样,进行方案1的稳健性评估,统计出不同均值处的次数,通过统计分析计算出方案1在既定设计变量值处的均值和方差,见图 6。
|
| 图6 蒙特卡洛模拟下响应值频次图 Figure 6 Frequency response value of Monte Carlo simulation |
通过蒙特卡洛模拟统计得出总应力和中面周向应力的质量水平,对于中面周向应力,由于约束上界限值较高,在此不列出中面周向应力的σ水平图,总应力的质量水平见图 7,均值为605.865 MPa,标准差为15.721 MPa。
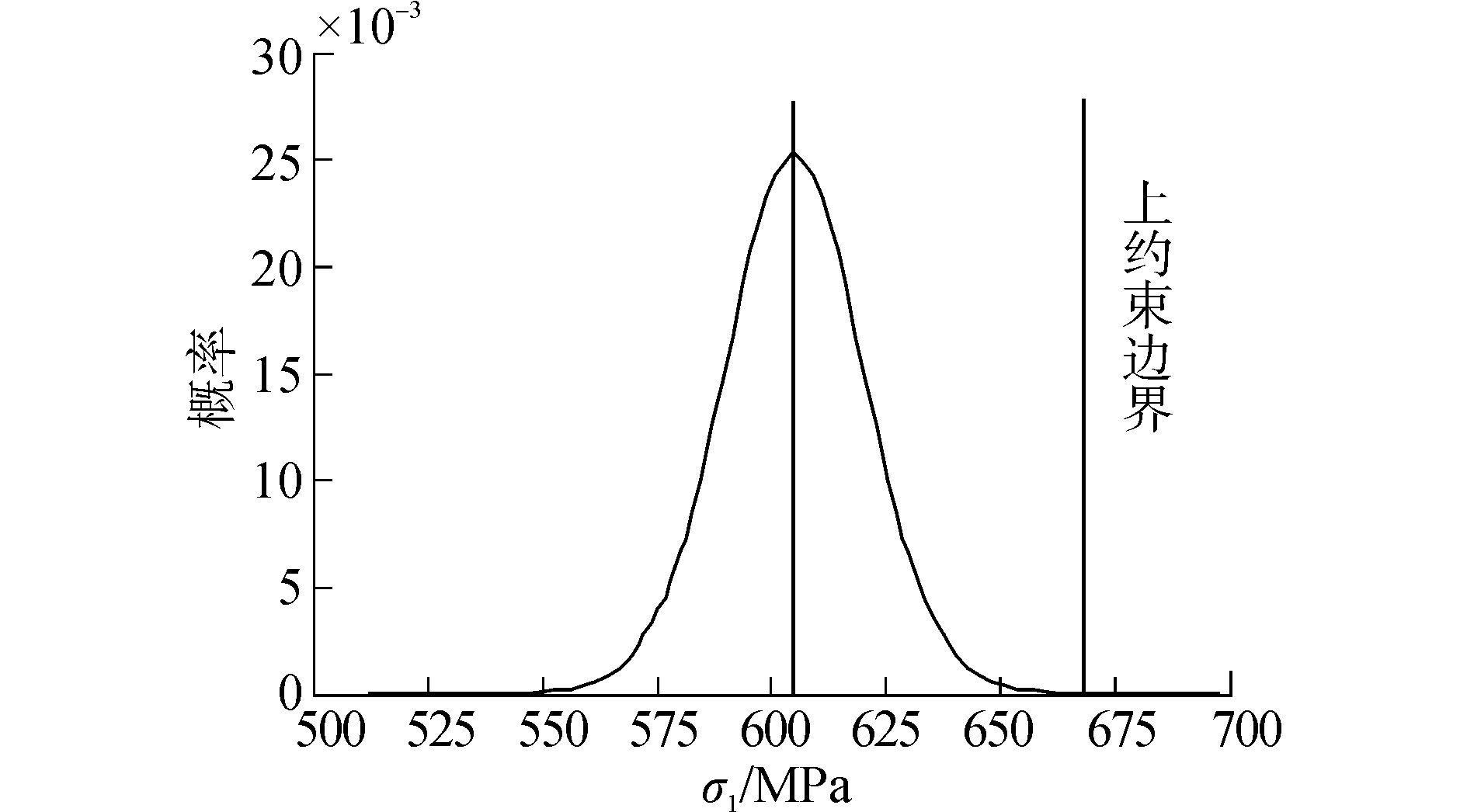
|
| 图7 3σ稳健性优化总应力概率分布图 Figure 7 Total stress probability distribution of 3σrobust optimization |
使用同样的方法对方案2进行质量评估,进一步将初始方案、方案1和方案2的总应力的概率图绘于同一图中,见图 8。
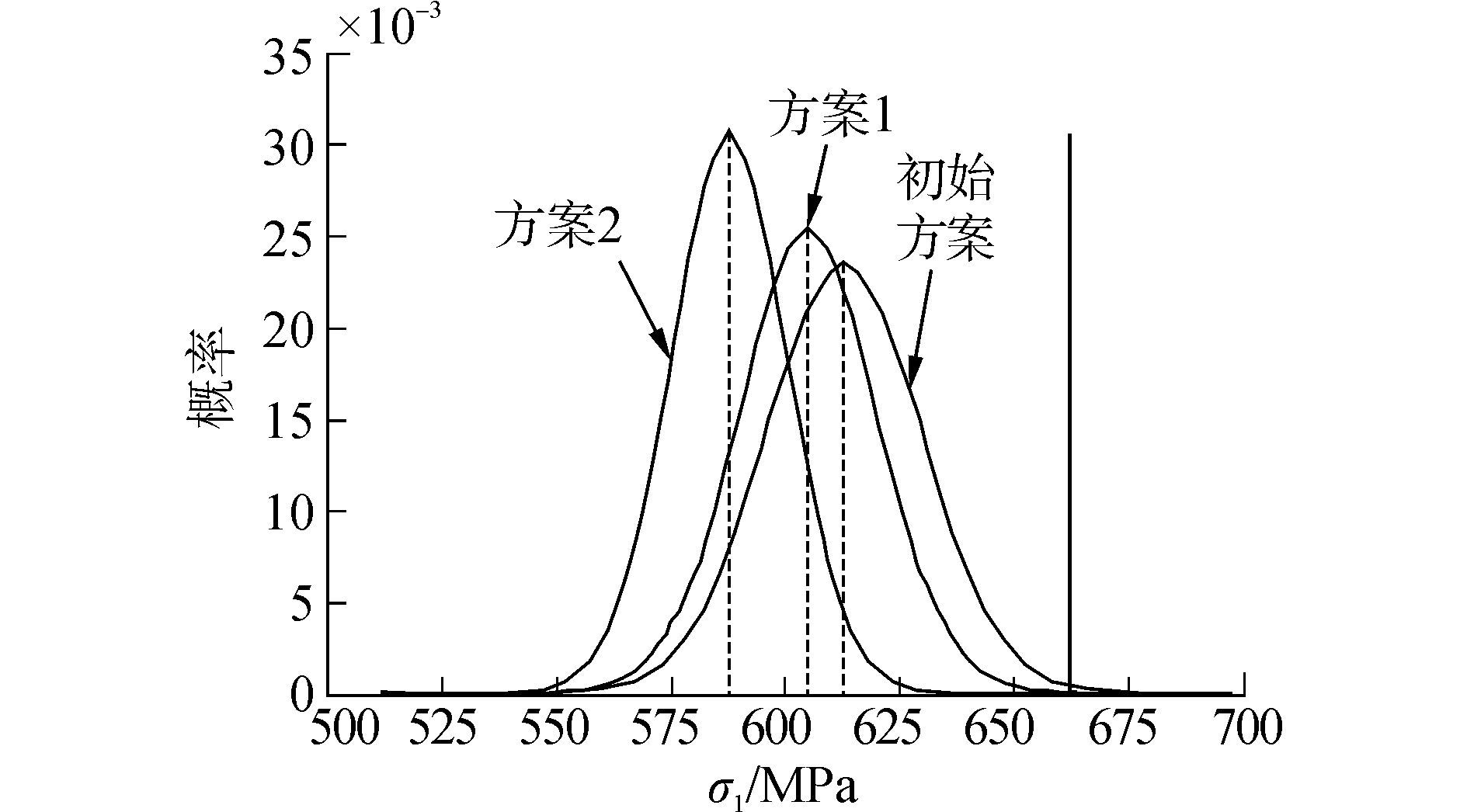
|
| 图8 稳健性优化总应力概率分布对比 Figure 8 Total stress probability distribution of robust optimize |
图 8中,曲线1代表初始设计方案,曲线2为方案1,曲线3为方案2。从图 8可以看出,随着σ水平的提高,总应力的均值越偏离约束边界,且应力的概率分布图变得越来越修长,即应力以较大的概率分布在均值附近。说明方案1、方案2与初始方案相比在极限载荷这个目标上没有较大的变化。
6 结论通过对有开孔加强结构耐压球壳的稳健性优化的研究,得到结论如下:
1) 基于灵敏度分析方案完成设计变量维数的降低,有利于模型的简化,可显著降低设计与计算分析难度;采用响应面模型替代真实模型进行优化问题的求解,在满足模型精度要求的同时,能大幅度降低计算花费,可提高耐压球壳的设计效率;
2) 相比确定性多目标优化,基于稳健性优化的多响应多目标优化的Pareto 解的分布范围有所缩小,说明基于稳健性的设计方案的解更加稳定、可靠;
3) 相比初始设计方案,优化方案在减重方面优化结果明显,但6σ减重的幅度要小于3σ,但应力值的波动较小,说明随着稳健性水平的提高,要求增加耐压球壳的厚度,才能在约束条件方面有更高的稳健性水平,从而导致耐压球壳的质量增加。
| [1] |
张伟, 毛秀兰, 崔维成. 影响潜艇结构壳板失稳的各因素灵敏性分析[J].
船舶力学, 2001, 5(4): 47–53.
ZHANG Wei, MAO Xiulan, CUI Weicheng. Sensitivity analysis of shell buckling of marine structure cylinder shell[J]. Journal of ship mechanics, 2001, 5(4): 47–53. |
| [2] |
白旭. 基于风险的球柱组合壳结构性能分析[D]. 哈尔滨:哈尔滨工程大学, 2013:91-106.
BAI Xu. Risk-based analysis of structural performance for sphere-cylinder combined shell[D]. Harbin:Harbin Engineering University, 2013:91-106. http://cdmd.cnki.com.cn/Article/CDMD-10217-1014134081.htm |
| [3] |
操安喜, 崔维成. 基于区间的耐压球壳非概率可靠性分析[J].
中国造船, 2014, 55(1): 38–45.
CAO Anxi, CUI Weicheng. Non-probabilistic reliability analysis of spherical pressure hulls based on interval number theory[J]. Shipbuilding of China, 2014, 55(1): 38–45. |
| [4] | TSUI K L. An overview of Taguchi method and newly developed statistical methods for robust design[J]. ⅡE transactions, 1992, 24(5): 44–57. |
| [5] |
景立新. 基于操纵稳定性的汽车悬架稳健性设计研究[D]. 长春:吉林大学, 2011:5-7.
JING Lixin. Studies on the Robust of vehicle suspension based on handing and stability[D]. Changchun:Jilin University, 2011:5-7. http://cdmd.cnki.com.cn/Article/CDMD-10183-1012257560.htm |
| [6] |
李锋, 孟广伟, 周振平, 等. 结构疲劳寿命稳健性优化设计[J].
机械工程学报, 2010, 46(2): 155–158.
LI Feng, MENG Guangwei, ZHOU Zhenping, et al. Robust design of structural fatigue life[J]. Journal of mechanical engineering, 2010, 46(2): 155–158. DOI:10.3901/JME.2010.02.155 |
| [7] |
周定智, 王霄, 刘会霞, 等. 基于稳健性和多目标优化的车顶结构轻量化设计研究[J].
机电工程, 2015, 32(9): 1170–1175.
ZHOU Dingzhi, WANG Xiao, LIU Huixia, et al. Roof structure lightweight design based on robustness and multi-objective optimization[J]. Journal of mechanical & electrical engineering, 2015, 32(9): 1170–1175. |
| [8] |
程妍雪, 庞永杰, 杨卓懿, 等. 基于径向基神经网络模型的耐压壳6σ设计[J].
上海交通大学学报, 2014, 48(4): 493–497.
CHENG Yanxue, PANG Yongjie, YANG Zhuoyi, et al. 6σ design for pressurized cylindrical shells based on RBF[J]. Journal of Shanghai Jiaotong University, 2014, 48(4): 493–497. |
| [9] |
曲文新. 载人潜水器耐压壳结构设计与分析[D]. 哈尔滨:哈尔滨工程大学, 2013:12, 36.
QU Wenxin. Structure design and analysis of pressure hull in manned submersible[D]. Harbin:Harbin Engineering University, 2013:12, 36. http://cdmd.cnki.com.cn/Article/CDMD-10217-1014132662.htm |
| [10] |
中国船级社. 潜水系统与潜水器入级与建造规范[S]. 北京:中国船级社, 2014:42, 83.
China Classification Society. Rules for the construction and classification of diving systems and submersibles[S]. Beijing:China Classification Society, 2014:42, 83. |
| [11] |
杨卓懿, 庞永杰. 响应面模型在耐压壳优化设计中的应用研究[J].
哈尔滨工程大学学报, 2010, 31(6): 689–692.
YANG Zhuoyi, PANG Yongjie. Application of the response surface model to optimize of a pressure shell[J]. Journal of Harbin Engineering University, 2010, 31(6): 689–692. |
| [12] |
柳高洁. 自行火炮结构动力学分析及优化设计研究[D]. 南京:南京理工大学, 2009:47.
LIU Gaojie. Research on structure dynamics analysis optimization design of self propelled gun[D]. Nanjing:Nanjing University of Science and Technology, 2009:47. http://cdmd.cnki.com.cn/Article/CDMD-10288-2009196676.htm |
| [13] |
刘峰, 韩端锋. 载人潜器载人舱出入舱口加强结构优化[J].
武汉理工大学学报, 2014, 36(10): 63–68.
LIU Feng, HAN Duanfeng. Optimization of manned submersible manned cabin hatch reinforcement[J]. Journal of Wuhan University of Technology, 2014, 36(10): 63–68. |
| [14] | SUN Guangyong, LI Guangyao, ZHOU Shiwei, et al. Crashworthiness design of vehicle by using multiobjective robust optimization[J]. Structural and multidisciplinary optimization, 2011, 44(1): 99–110. DOI:10.1007/s00158-010-0601-z |



