近年来,欠驱动水面船舶的航迹跟踪控制问题,因其挑战性及其在航海领域内广泛的实际应用,受到了学者们极大的关注[1]。欠驱动水面船舶运动控制的主要难点是横向未装备驱动装置,缺少可用的控制输入[2-3]。由于欠驱动水面船舶所具有的驱动器个数少于其自由度,所以具有加速度不可积分的二阶非完整约束条件,不满足著名的Brockett必要条件,不能转化为无漂链式系统[4-6],因此其控制设计非常具有挑战性。尽管如此,已经有许多学者在航迹跟踪控制问题上通过使用多种控制方法取得了有意义的研究成果,这些方法包括自适应控制[7-8]、线性代数方法[9]、模型预测控制[10-11]、Backstepping方法[12-13]、神经网络控制[14-15]、动态面控制方法[16]、滑模控制方法[18-22]等。其中,滑模控制方法因其简单易行、响应速度快、对外界干扰和参数摄动具有鲁棒性的特点在控制领域得到了广泛的应用。Ashrafiuon等最早将滑模控制方法应用在欠驱动船舶航迹跟踪问题中,算法考虑了船舶参数不确定性,利用纵荡跟踪误差设计一阶滑模,横向跟踪误差设计二阶滑模,成功跟踪了直线轨迹和曲线轨迹,并在无人船模型试验中进行了验证[18]。于瑞亭等研究了在外界环境干扰和模型参数辨识不确定情况下的欠驱动水面船舶航迹跟踪控制问题,设计了一种二阶滑模控制器[19]。杨震等结合神经网络和滑模控制方法设计了一种神经滑模鲁棒控制器[20]。Li等将自抗扰控制技术与滑模控制技术结合,设计了船舶航向跟踪控制器和航迹跟踪控制器[22]。以上方法存在一个共性问题是都没有考虑有限时间稳定性。
论文对外界环境干扰影响下的欠驱动水面船舶航迹跟踪控制有限时间稳定性问题进行了研究,采用终端滑模控制方法[23],实现了预期有限时间内的航迹跟踪控制,并在控制器设计中引入了辅助滑模面[24],避免了终端滑模控制器中可能会出现的控制器奇异问题。最后通过仿真验证了所提出方法的有效性。
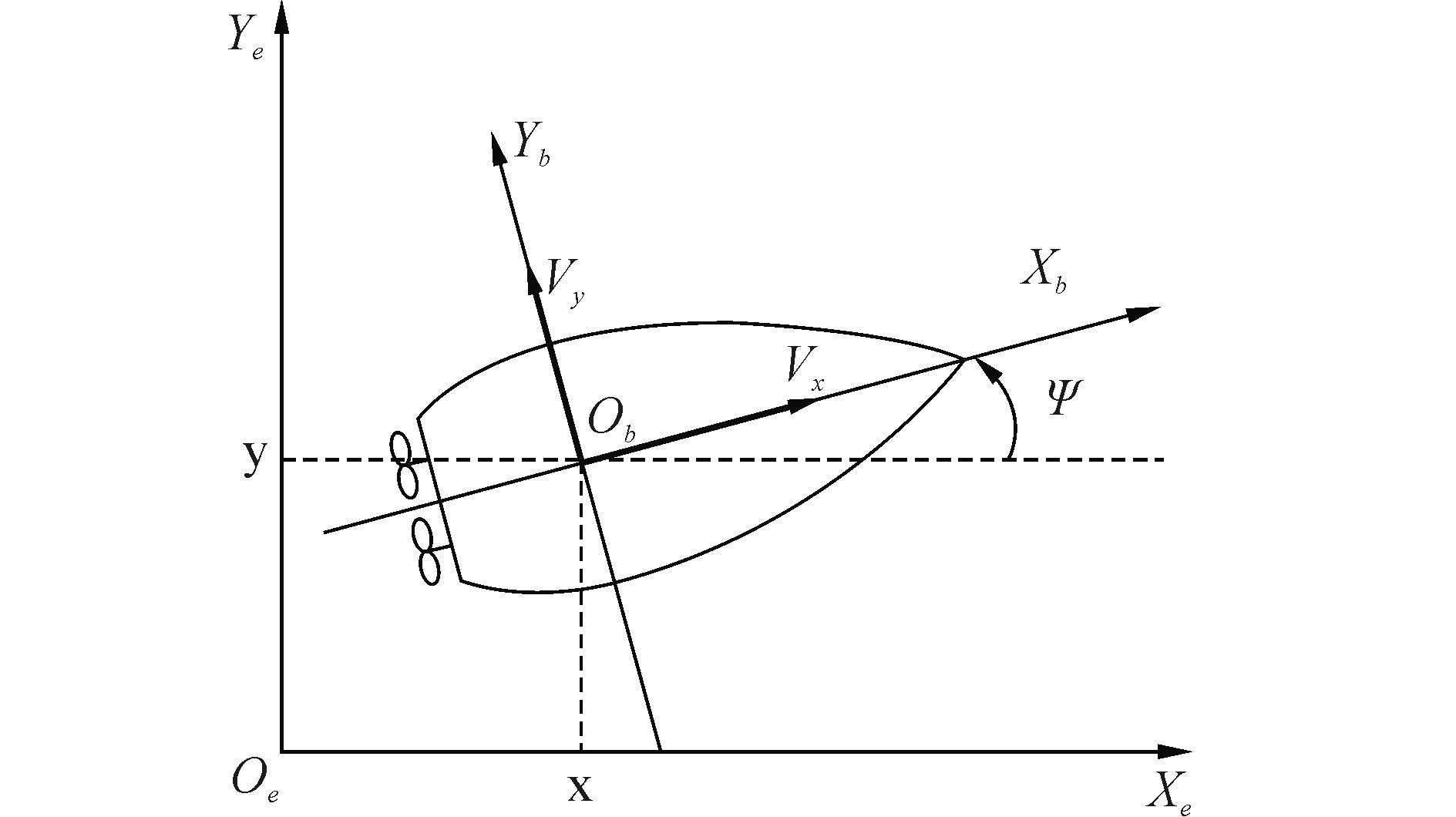
1 欠驱动水面船舶数学模型 1.1 欠驱动水面船舶数学模型本文中的船舶航迹跟踪问题是针对水面船舶,只需考虑船舶前进、横漂和艏摇三个自由度的运动问题[25]。图 1为船舶平面运动变量描述图。
|
| 图1 船舶平面运动变量描述图 Figure 1 Planar model of a surface vessel |
欠驱动水面船舶的动力学方程和运动学方程表示为[2]
| ${\mathit{\boldsymbol{\dot \eta }}} = \mathit{\boldsymbol{R}}\left( \psi \right)v$ | (1) |
| $\mathit{\boldsymbol{M\dot v}} + \mathit{\boldsymbol{C}}\left( \mathit{\boldsymbol{v}} \right)\mathit{\boldsymbol{v}} + D\left( \mathit{\boldsymbol{v}} \right)\mathit{\boldsymbol{v}} = \mathit{\boldsymbol{\tau }} + \mathit{\boldsymbol{\omega }}$ | (2) |
式中:η
| $\mathit{\boldsymbol{R}}\left( \psi \right) \buildrel \Delta \over = \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}\;\psi } & { - {\rm{sin}}\;\psi } & 0\\ {{\rm{sin}}\;\psi } & {{\rm{cos}}\;\psi } & 0\\ 0 & 0 & 1 \end{array}} \right]$ | (3) |
其中,RT(ψ)=R-1(ψ)。
M∈R3×3, 是惯性参数矩阵:
| $\mathit{\boldsymbol{M}} = {\mathit{\boldsymbol{M}}^{\rm{T}}} = \left[ {\begin{array}{*{20}{c}} {{m_{11}}} & 0 & 0\\ 0 & {{m_{22}}} & {{m_{23}}}\\ 0 & {{m_{32}}} & {{m_{33}}} \end{array}} \right]$ | (4) |
通过选择合适的物体固定坐标系原点[8],m23能够满足m23=0。
C(v)∈R3×3, 是科里奥利和向心力矩阵:
| $\mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} 0 & 0 & {{c_{13}}}\\ 0 & 0 & {{c_{23}}}\\ { - {c_{13}}} & { - {c_{23}}} & 0 \end{array}} \right]$ | (5) |
式中:
D(v)∈R3×3,是水动力阻尼参数矩阵:
| $\mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} {{d_{11}}} & 0 & 0\\ 0 & {{d_{22}}} & {{d_{23}}}\\ 0 & {{d_{32}}} & {{d_{33}}} \end{array}} \right]$ | (6) |
假设惯性参数矩阵和水动力阻尼参数矩阵都是常值对角矩阵,则式(2) 的简化模型如下
| $\left\{ {\begin{array}{*{20}{l}} {{m_{11}}{{\dot v}_x} - {m_{22}}{v_y}{w_z} + {d_{11}}{v_x} = {F_X} + {\omega _1}}\\ {{m_{22}}{{\dot v}_y} + {m_{11}}{v_x}{w_z} + {d_{22}}{v_y} = 0 + {\omega _2}}\\ {{m_{33}}{{\dot w}_z} + {m_{22}}{v_y}{v_x} - {m_{11}}{v_x}{v_y} + {d_{33}}{w_z} = {T_z} + {\omega _3}} \end{array}} \right.$ | (7) |
注1:考虑船舶没有侧推器,即Fy=0。两个螺旋桨产生前进方向上的推进力和首摇运动转向力矩,即τ=[Fx 0 Tz]T,与欠驱动水面船舶一致。
1.2 有限时间稳定性现在介绍将用到的有限时间稳定性引理。首先考虑如下非线性动态系统:
| $\mathit{\boldsymbol{\dot x}}\left( t \right) = f\left( {\mathit{\boldsymbol{x}}\left( t \right)} \right),\mathit{\boldsymbol{x}}\left( 0 \right) = {\mathit{\boldsymbol{x}}_0},t \ge 0,$ | (8) |
式中:x(t)∈ξ⊆Rn,是系统的状态矢量;ξ是开集;0∈ξ,f(x(t))在ξ上是连续的,f(0)=0。
针对系统(8),有如下引理:
引理1[26] 考虑非线性动态系统(8),设ξ′∈ξ为与式(8) 相关的不变集。假设存在一个连续微分方程
V(x(t)):ξ→R,实数c>0,α∈(0,1),如此,V(x)=0,x∈ξ;V(x)>0,x∈ξ/ξ′且V′(x)f(x)≤-c(V(x))a,x∈ξ。则不变集ξ′是具有有限时间稳定性的。并且调节时间函数满足:
| $T({\mathit{\boldsymbol{x}}_0}) \le \frac{1}{{c\left( {1 - \alpha } \right)}}{(V({\mathit{\boldsymbol{x}}_0}))^{1 - a}}$ | (9) |
式中,x0在ξ′的开邻域内。
注2:有限时间稳定性保证了系统每一个状态都能在预期有限时间内到达系统的原点,引理1给出了不变集的有限时间稳定性。
2 跟踪控制器设计及稳定性分析船舶运动的运动学方程为
| $\left\{ {\begin{array}{*{20}{l}} {\dot x = {v_x}{\rm{cos}}\;\psi - {v_y}{\rm{sin}}\;\psi }\\ {\dot y = {v_x}{\rm{sin}}\;\psi + {v_y}{\rm{cos}}\;\psi }\\ {\dot \psi = {w_z}} \end{array}} \right.$ | (10) |
由(7) 得
| $\left\{ {\begin{array}{*{20}{l}} {{{\dot v}_x} = \frac{{{m_{22}}}}{{{m_{11}}}}{v_y}{w_z} - \frac{{{d_{11}}}}{{{m_{11}}}}{v_x} + \frac{1}{{{m_{11}}}}{F_x} + \frac{1}{{{m_{11}}}}{\omega _1}}\\ {{{\dot v}_y} = - \frac{{{m_{11}}}}{{{m_{22}}}}{v_x}{w_z} - \frac{{{d_{22}}}}{{{m_{22}}}}{v_y} + \frac{1}{{{m_{22}}}}{\omega _2}}\\ {{{\dot w}_z} = \frac{{{m_{11}} - {m_{22}}}}{{{m_{33}}}}{v_x}{v_y} - \frac{{{d_{33}}}}{{{m_{33}}}}{w_z} + \frac{1}{{{m_{33}}}}{T_z} + \frac{1}{{{m_{33}}}}{\omega _3}} \end{array}} \right.$ | (11) |
式中:η=[x y ψ]T表示船舶在惯性坐标系中的位置,v=[vx vy wz]T表示船舶在物体固定坐标系中的速度,mij和dij是正常数。
对(10) 求导得
| $\left\{ {\begin{array}{*{20}{l}} {\ddot x\left( t \right) = {u_1}\left( t \right) + {{\tilde \omega }_1}\left( t \right)}\\ {\ddot y\left( t \right) = {u_2}\left( t \right) + {{\tilde \omega }_2}\left( t \right)}\\ {\ddot \psi \left( t \right) = {u_3}\left( t \right) + {{\tilde \omega }_3}\left( t \right)} \end{array}} \right.$ | (12) |
其中
| $\begin{array}{l} {u_1}\left( t \right) = \left( {\frac{{{m_{22}}}}{{{m_{11}}}}{v_y}{w_z} - \frac{{{d_{11}}}}{{{m_{11}}}}{v_x} - {v_x}{w_z} + \frac{1}{{{m_{11}}}}{F_x}} \right){\rm{cos}}\;\psi + \\ \quad \quad \quad \left( {\frac{{{m_{11}}}}{{{m_{22}}}}{v_x}{w_z} - {v_x}{w_z} + \frac{{{d_{22}}}}{{{m_{22}}}}{v_y}} \right){\rm{sin}}\;\psi \\ {u_2}\left( t \right) = \left( {\frac{{{m_{22}}}}{{{m_{11}}}}{v_y}{w_z} - \frac{{{d_{11}}}}{{{m_{11}}}}{v_x} - {v_y}{w_z} + \frac{1}{{{m_{11}}}}{F_x}} \right){\rm{sin}}\;\psi + \\ \quad \quad \quad \left( { - \frac{{{m_{11}}}}{{{m_{22}}}}{v_x}{w_z} + {v_x}{w_z} - \frac{{{d_{22}}}}{{{m_{22}}}}{v_y}} \right){\rm{cos}}\;\psi \\ {u_3}\left( t \right) = \frac{{{m_{11}} - {m_{22}}}}{{{m_{33}}}}{v_x}{v_y} - \frac{{{d_{33}}}}{{{m_{33}}}}{w_z} + \frac{1}{{{m_{33}}}}{T_z}\\ {{\tilde \omega }_1}\left( t \right) \buildrel \Delta \over = \frac{1}{{{m_{11}}}}{\omega _1}{\rm{cos}}\;\psi - \frac{1}{{{m_{22}}}}{\omega _2}{\rm{sin}}\;\psi \\ {{\tilde \omega }_2}\left( t \right) \buildrel \Delta \over = \frac{1}{{{m_{11}}}}{\omega _1}{\rm{sin}}\;\psi + \frac{1}{{{m_{22}}}}{\omega _2}{\rm{cos}}\;\psi \\ {{\tilde \omega }_3}\left( t \right) \buildrel \Delta \over = \frac{1}{{{m_{33}}}}{\omega _3} \end{array}$ |
假设1 外界干扰项
控制目标是使以上系统的状态在有限时间内达到且保持期望的稳态值。设跟踪目标的期望轨迹方程为ηL(t),t≥0。
引入误差变量为
| $\mathit{\boldsymbol{e}}\left( t \right) \buildrel \Delta \over = \left[ {\begin{array}{*{20}{l}} {{e_x}\left( t \right)}\\ {{e_y}\left( t \right)}\\ {{e_\psi }\left( t \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {x\left( t \right) - {x_L}\left( t \right)}\\ {y\left( t \right) - {y_L}\left( t \right)}\\ {\psi - {\psi _L}} \end{array}} \right],t \ge 0$ | (13) |
| $\left\{ {\begin{array}{*{20}{l}} {{{\ddot e}_x}\left( t \right) = - {{\ddot x}_L}\left( t \right) + {u_1}\left( t \right) + {{\tilde \omega }_1}\left( t \right),}\\ {{e_x}\left( 0 \right) = {e_{ox}},}\\ {{{\dot e}_x}\left( 0 \right) = {{\dot e}_{ox}}} \end{array}} \right.$ | (14) |
| $\left\{ {\begin{array}{*{20}{l}} {{{\ddot e}_y}\left( t \right) = - {{\ddot y}_L}\left( t \right) + {u_2}\left( t \right) + {{\tilde \omega }_2}\left( t \right),}\\ {{e_y}\left( 0 \right) = {e_{oy}},}\\ {{{\dot e}_y}\left( 0 \right) = {{\dot e}_{oy}}} \end{array}} \right.$ | (15) |
| $\left\{ {\begin{array}{*{20}{l}} {{{\ddot e}_\psi }\left( t \right) = - {{\ddot \psi }_L} + {u_3}\left( t \right) + {{\tilde \omega }_3}\left( t \right),}\\ {{e_\phi }\left( 0 \right) = {e_{o\phi }},}\\ {{{\dot e}_\phi }\left( 0 \right) = {{\dot e}_{o\phi }}} \end{array}} \right.$ | (16) |
定义非线性滑模面S为
| $\mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right) = \mathit{\boldsymbol{\dot e}} + \mathit{\boldsymbol{CR}}\left( \mathit{\boldsymbol{e}} \right){\left| \mathit{\boldsymbol{e}} \right|^{\frac{1}{2}}},\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right) \in {{\bf{R}}^3} \times {{\bf{R}}^3},$ | (17) |
其中C=diag(c1, c2, c3),ci>0,i=1,2,3;R(e)
根据滑模控制理论,令
| $\mathit{\boldsymbol{\tilde u}} = {{\mathit{\boldsymbol{\ddot \eta }}}_L} - \frac{1}{2}\mathit{\boldsymbol{C}}d\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right) - \mathit{\boldsymbol{K}}{\rm{sign}}\left( {\mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)} \right),\left( {\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)} \right) \in \mathit{\boldsymbol{M}},$ | (18) |
其中,
| ${\rm{sign}}\left( {S\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)} \right) = \left[ {\begin{array}{*{20}{c}} {{\rm{sign}}({S_1}(\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}))}\\ {{\rm{sign}}({S_2}(\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}))}\\ {{\rm{sign}}({S_3}(\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}))} \end{array}} \right]$ | (19) |
注3:通过设
| $d\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right) \buildrel \Delta \over = \left[ {\begin{array}{*{20}{c}} {{{\dot e}_1}} & {{{\left| {{e_1}} \right|}^{ - \frac{1}{2}}}}\\ {{{\dot e}_2}} & {{{\left| {{e_2}} \right|}^{ - \frac{1}{2}}}}\\ {{{\dot e}_3}} & {{{\left| {{e_3}} \right|}^{ - \frac{1}{2}}}} \end{array}} \right]$ | (20) |
式中:M⊂R3×R3,d(·,·)是有界的。
定义M为
| $\mathit{\boldsymbol{M}} \buildrel \Delta \over = \{ \left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right) \in {{\bf{R}}^3} \times {{\bf{R}}^3}:{\left\| {\mathit{\boldsymbol{d}}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)} \right\|_\infty } \le \lambda \} $ | (21) |
其中,
| $\lambda \buildrel \Delta \over = {\left\| \mathit{\boldsymbol{C}} \right\|_\infty } + \delta ,\delta > 0$ | (22) |
引理2[23]:考虑误差动态式(14)~(16),如果滑模控制器的增益ki,i=1,2,3,满足
| ${k_i} = {\alpha _i} + \sigma $ | (23) |
且
| ${\alpha _i} > \frac{{{\lambda ^2} - {c_i}\lambda }}{2} > 0,$ | (24) |
则由式(21) 定义的设定集M是不变的。
对于初始条件(
| ${\mathit{\boldsymbol{S}}_{{\rm{aux}}}}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right) = \mathit{\boldsymbol{\dot e,}}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right) \in {{\bf{R}}^3} \times {{\bf{R}}^3},$ | (25) |
定义辅助滑模面Saux为
| ${\mathit{\boldsymbol{S}}_{{\rm{aux}}}} \buildrel \Delta \over = \{ \left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right) \in {{\bf{R}}^3} \times {{\bf{R}}^3}:{\mathit{\boldsymbol{S}}_{{\rm{aux}}}}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right) = 0\} $ | (26) |
令
| ${{\mathit{\boldsymbol{\tilde u}}}_{{\rm{aux}}}} = {{\mathit{\boldsymbol{\ddot \eta }}}_L} - {\mathit{\boldsymbol{K}}_{{\rm{aux}}}}{\rm{sign}}\left( {{\mathit{\boldsymbol{S}}_{{\rm{aux}}}}} \right.\left. {\left( {e,\dot e} \right)} \right),\left( {e,\dot e} \right) \notin \mathit{\boldsymbol{M}}$ | (27) |
其中
| $\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\tilde u}}}_{aux}} = {{[{u_1}_{\;{\rm{aux}}}{u_2}_{\;{\rm{aux}}}{u_3}_{\;{\rm{aux}}}]}^{\rm{T}}},}\\ {{\mathit{\boldsymbol{K}}_{{\rm{aux}}}} \buildrel \Delta \over = {\rm{diag}}[{k_{1{\rm{aux}}}}{k_{2{\rm{aux}}}}{k_{3{\rm{aux}}}}],} \end{array}$ |
且
| ${k_{{\rm{aux}}}} = {\alpha _{{\rm{aux}}}} + \sigma ,{\alpha _{{\rm{aux}}}} > 0$ | (28) |
定理1 由终端滑模控制律(18) 和(27) 及水面船舶运动系统(10) 和(11) 组成的闭环系统能够在有限时间内跟踪期望轨迹,并且使得系统的状态在有限时间内达到且保持期望的稳态值。
证明:首先考虑初始条件
| $V({\mathit{\boldsymbol{S}}_{{\rm{aux}}}}\left. {\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)} \right) = \frac{1}{2}{\mathit{\boldsymbol{S}}_{{\rm{aux}}}}^{\rm{T}}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right){\mathit{\boldsymbol{S}}_{{\rm{aux}}}}(\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}})$ | (29) |
对V求导得
| $\begin{array}{l} \dot v({\mathit{\boldsymbol{S}}_{{\rm{aux}}}}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)) = {\mathit{\boldsymbol{S}}_{{\rm{aux}}}}^{\rm{T}}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right){{\mathit{\boldsymbol{\dot S}}}_{{\rm{aux}}}}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right) = \\ {\mathit{\boldsymbol{S}}_{{\rm{aux}}}}^{\rm T}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)[ - {\mathit{\boldsymbol{K}}_{{\rm{aux}}}}{\rm{sign}}({\mathit{\boldsymbol{S}}_{{\rm{aux}}}}\left. {\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)} \right) + \mathit{\boldsymbol{\tilde \omega }}\left( t \right)] = \\ - \sum\limits_{i = 1}^3 {{\alpha _{{\rm{iaux}}}}} \left| {{\mathit{\boldsymbol{S}}_{{\rm{aux}}}}} \right.\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)\left| { - \sigma } \right|{\mathit{\boldsymbol{S}}_{{\rm{aux}}}}\left. {\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)} \right| + \\ \mathit{\boldsymbol{\tilde \omega }}\left( t \right){\mathit{\boldsymbol{S}}_{{\rm{aux}}}}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right) \le {\rm{ }} - \sum\limits_{i = 1}^3 {{\alpha _{{\rm{iaux}}}}} \left| {{\mathit{\boldsymbol{S}}_{{\rm{aux}}}}} \right.\left. {\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)} \right| \le \\ - \mathop {{\rm{min}}}\limits_{i = 1,2,3} \{ {\alpha _{{\rm{iaux}}}}\} {\mathit{\boldsymbol{e}}^{\rm{T}}}{\mathit{\boldsymbol{S}}_{{\rm{aux}}}}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right) \le \\ - \sqrt 2 \mathop {{\rm{min}}}\limits_{i = 1,2,3} \{ {\alpha _{{\rm{iaux}}}}\} {(V({\mathit{\boldsymbol{S}}_{{\rm{aux}}}}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)))^{\frac{1}{2}}} \end{array}$ | (30) |
根据文献[25],滑模面具有有限时间稳定性,分散滑模控制器式(18) 切换到式(27)。
考虑另外一种条件,
| $V\left( {\mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)} \right) = \frac{1}{2}{\mathit{\boldsymbol{S}}^{\rm{T}}}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)\mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)$ | (31) |
对V求导,得
| $\begin{array}{l} \dot v\left( {\mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)} \right) = {\mathit{\boldsymbol{S}}^{\rm{T}}}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)\dot S\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right) = \\ {\mathit{\boldsymbol{S}}^{\rm T}}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)[ - K{\rm{sign}}\left( {S\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)} \right) + \mathit{\boldsymbol{\tilde \omega }}\left( t \right)] = \\ - \sum\limits_{i = 1}^3 {{\alpha _i}} \left| {{S_i}} \right.\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)\left| { - \sigma } \right|{S_i}\left. {\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)} \right| + \mathit{\boldsymbol{\tilde \omega }}\left( t \right){\mathit{\boldsymbol{S}}^{\rm{T}}}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right) \le \\ - \sum\limits_{i = 1}^3 {{\alpha _i}} \left| {{S_i}} \right.\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)\left| \le \right. - \mathop {{\rm{min}}}\limits_{i = 1,2,3} \left\{ {{\alpha _i}} \right\}{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right) \le \\ - \sqrt 2 \mathop {{\rm{min}}}\limits_{i = 1,2,3} \left\{ {{\alpha _i}} \right\}{\rm{ }}{\left( {V\left( {\mathit{\boldsymbol{S}}\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right)} \right)} \right)^{\frac{1}{2}}},\left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right) \in \mathit{\boldsymbol{M}} \end{array}$ | (32) |
同样根据文献[25],误差状态能在有限时间内到达滑模面。
此外,根据式(17),闭环误差动态定义为
| $\begin{array}{l} \dot v\left( \mathit{\boldsymbol{e}} \right) = \sum\limits_{i = 1}^3 {{\rm{sign}}} \left( {{e_i}} \right){{\dot e}_i} = \\ - \sum\limits_{i = 1}^3 {{c_i}} {\left| {{e_i}} \right|^{\frac{1}{2}}} = - {\mathit{\boldsymbol{e}}^{\rm{T}}}c{\left| \mathit{\boldsymbol{e}} \right|^{\frac{1}{2}}} \le \\ - \left\| {{c^{ - 1}}} \right\|_\infty ^{ - 1}{\left( {v\left( \mathit{\boldsymbol{e}} \right)} \right)^{12}},\mathit{\boldsymbol{e}} \in \mathit{\boldsymbol{S}} \end{array}$ | (33) |
因此,根据引理1误差状态能够在有限时间内收敛到原点,既而保证了船舶能够在有限时间内跟踪期望轨迹。
3 仿真验证现在对上述所设计的控制器进行计算机仿真研究,以演示其性能及效果。数值仿真采用文献[2]中的水池试验用的船模参数进行仿真实验,具体参数如下:
m11=200 kg,m22=250 kg,m33=80 kg,
d11=70 kg/s,d22=100 kg/s,d33=50 kg/s
外界环境时变干扰采用文献[17]中的模型,如下:
| $\begin{array}{l} {{\tilde \omega }_1}\left( t \right) = 0.255\;4\;{\rm{cos}}\;(0.5t)\;{\rm{sin}}\;\left( {0.2t} \right) + \\ \quad \quad \quad 0.196\;{\rm{sin}}\;(0.3t)\;{\rm{cos}}\;(0.4t)\\ {{\tilde \omega }_2}\left( t \right) = 0.01\;{\rm{sin}}\;(0.2t)\\ {{\tilde \omega }_3}\left( t \right) = 0.05\;{\rm{sin}}\;(0.9t)\;{\rm{cos}}\;(0.2t) \end{array}$ |
期望的运动轨迹为圆形轨迹:
XL=3sin(t),YL=3cos(t)。
船舶的初始值为:η1=[0 0 -1/2]T。
滑模面参数为C1=diag[3, 3, 3]。
控制增益参数为K=Kaux=diag[2, 2, 2]。
为了更好地说明所设计的控制器效果,与传统的线性滑模控制方法做仿真实验进行比较,该线性滑模面设计如下:
| $S = \left( {\mathit{\boldsymbol{e}},\mathit{\boldsymbol{\dot e}}} \right) = \mathit{\boldsymbol{\dot e}} + \mathit{\boldsymbol{C}}R\left( \mathit{\boldsymbol{e}} \right)$ |
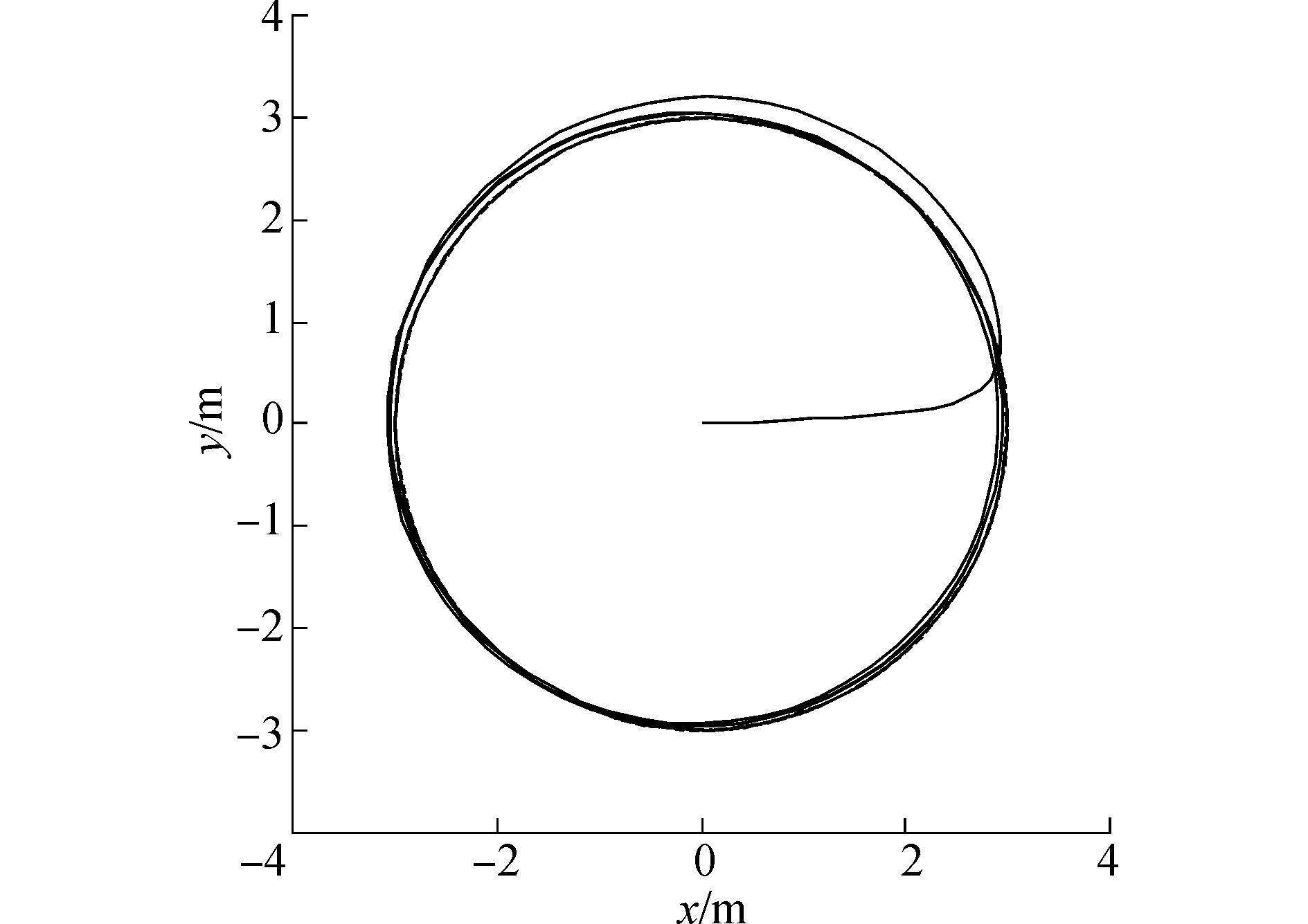
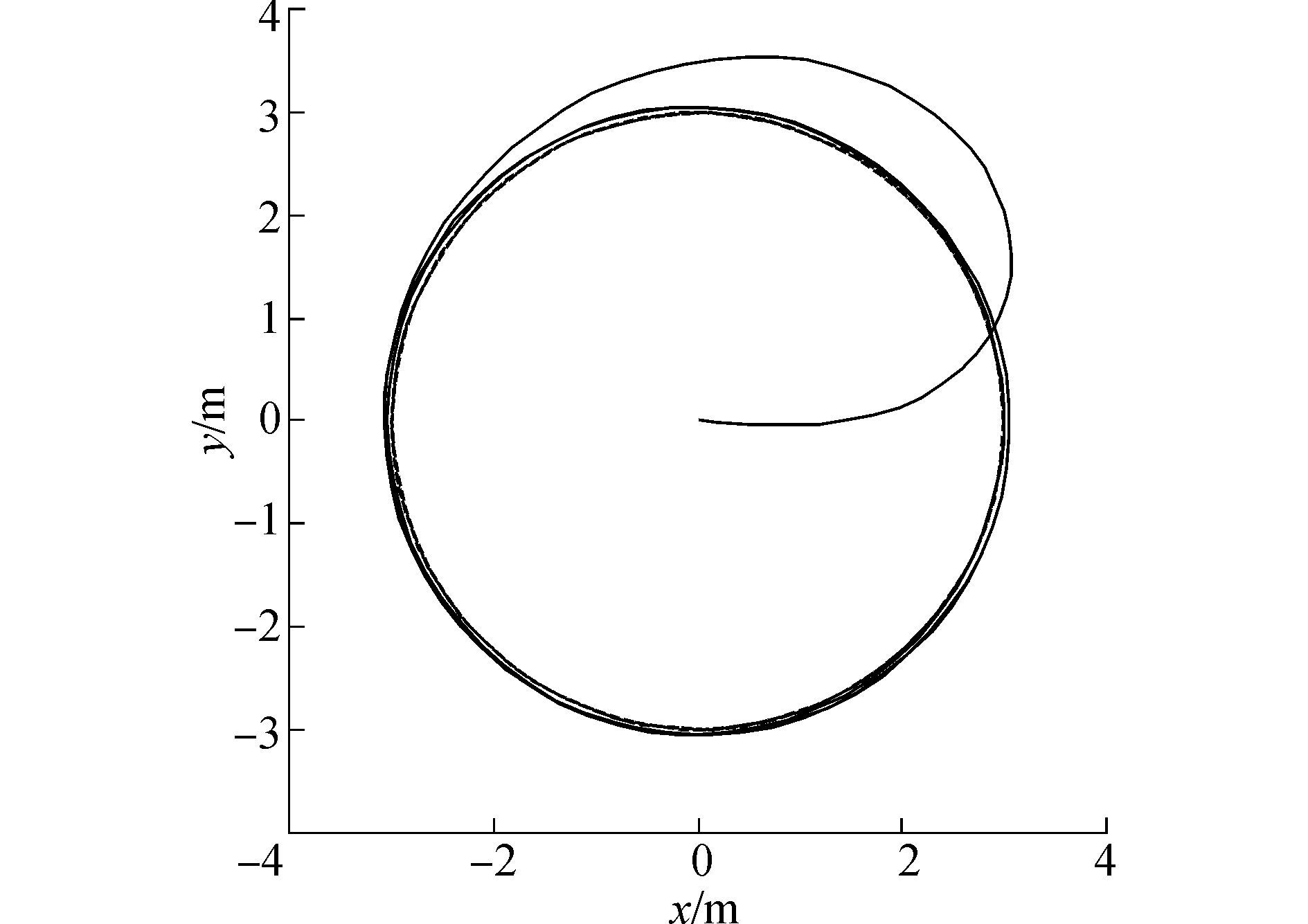
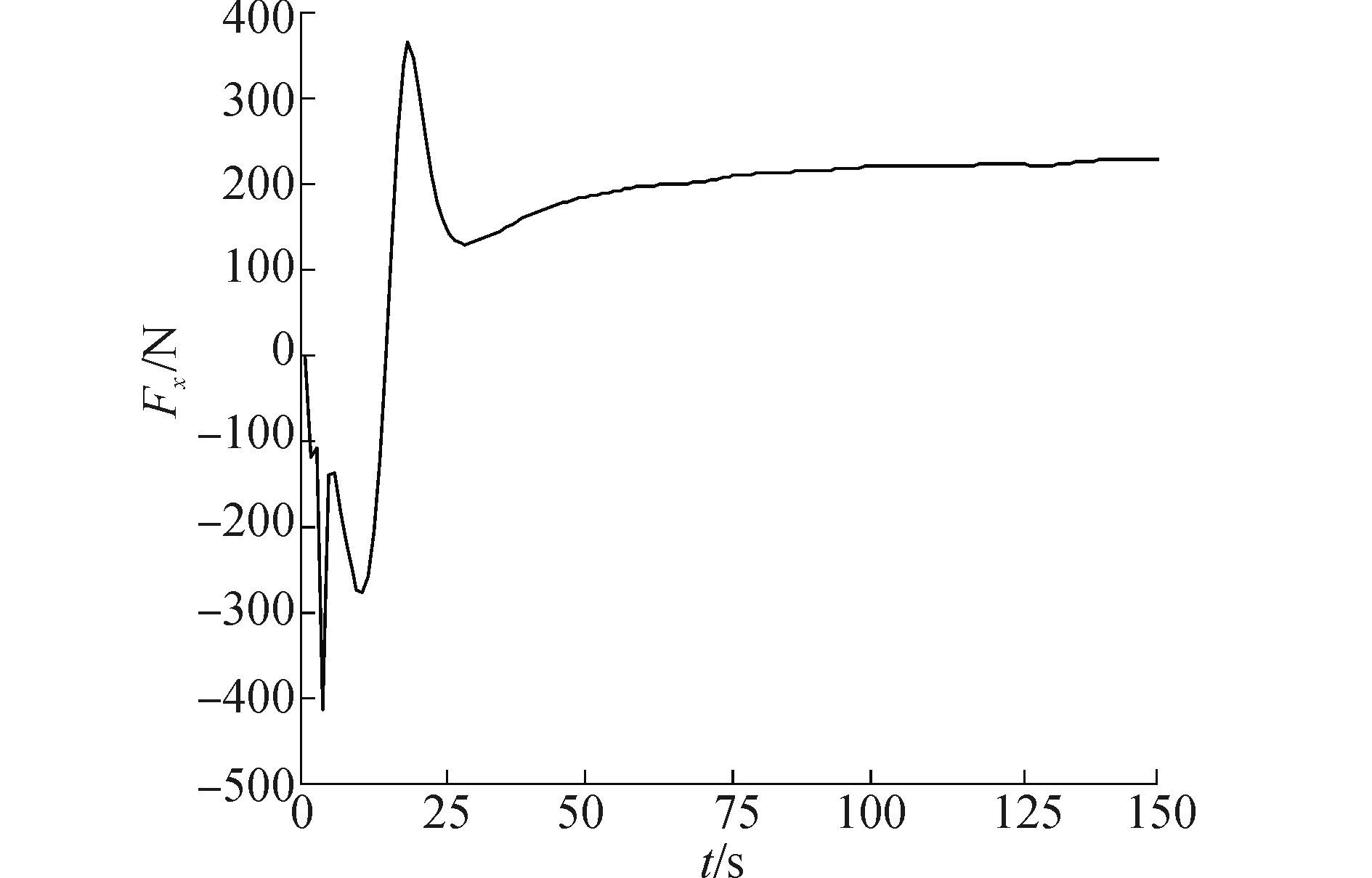
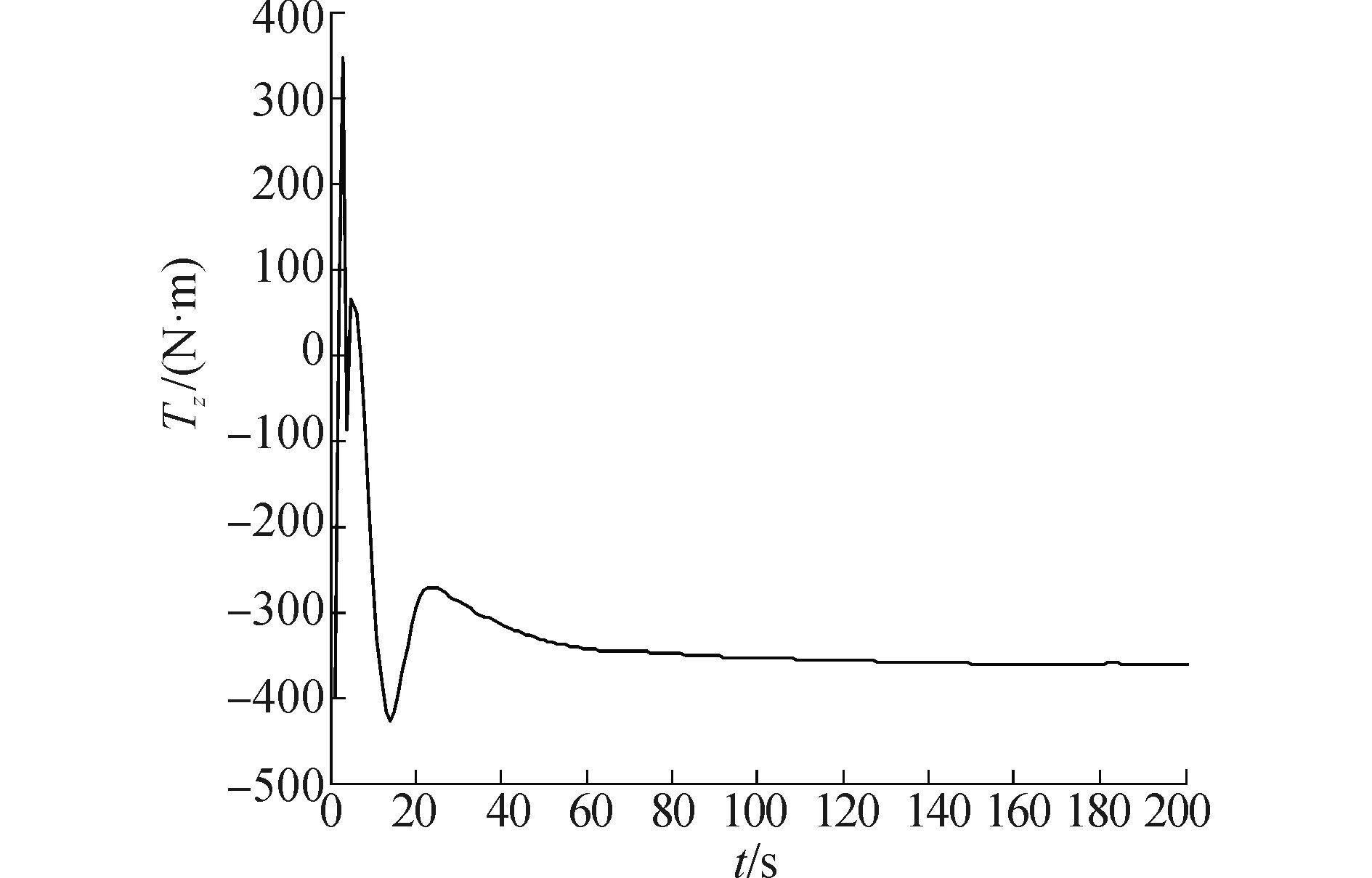
仿真结果见图 2~5。图 2表示设计的控制方法下欠驱动船舶的跟踪轨迹。图 3表示线性滑模控制下欠驱动船舶的跟踪轨迹。图 4表示控制力曲线。图 5表示控制力矩曲线。从仿真结果可以看出。设计的算法能在更短的时间跟踪上期望轨迹。线性滑模控制器和所设计的终端滑模航迹跟踪控制器都可以使船舶在一定时间后稳定的跟踪期望轨迹,但是终端滑模控制器收敛速度更快,调整时间更短。此外,从图 4和图 5可以看出,控制器的控制输入是有界的,且未出现奇异值问题。
|
| 图2 欠驱动水面船舶的跟踪轨迹(TSMC) Figure 2 Tracking trajectory of USV(TSMC) |
|
| 图3 欠驱动水面船舶跟踪轨迹(SMC) Figure 3 Tracking trajectory of USV(SMC) |
|
| 图4 控制力曲线 Figure 4 Response of control forces |
|
| 图5 控制力矩曲线 Figure 5 Response of control torques |
通过对欠驱动水面船舶的有限时间航迹跟踪控制器设计,并进行数值仿真实验可以得到以下结论:
1) 控制器设计中采用了终端滑模控制方法,与传统的船舶航迹跟踪控制方法相比,具有有限时间收敛及快速收敛的特性。
2) 通过设计辅助线性滑模面,避免了控制器采用终端滑模方法可能会出现奇异值得问题。
3) 给出的航迹跟踪控制算法闭环稳定性条件易于达到,并且设计方法的可操作性较强,因此在实际应用中具有一定的参考价值。
此外,设计过程中未考虑模型未知、通信时延等复杂情况,这些问题是下一阶段的研究重点。
| [1] |
郭晨, 汪洋, 孙福春, 等. 欠驱动水面船舶运动控制研究综述[J].
控制与决策, 2009, 24(3): 321–329.
GUO Chen, WANG Yang, SUN Fuchun, et al. Survey for motion control of underactuated surface vessels[J]. Control and decision, 2009, 24(3): 321–329. |
| [2] | FOSSEN T I. Guidance and control of ocean vehicles[M]. Upper saddle river, New York: Wiley Interscience, 1994. |
| [3] | DO K D, PAN J. Control of ships and underwater vehicles[M]. Springer, 2009. |
| [4] | SORDALEN O J, EGELAND O. Exponential stabilization of nonholonomic chained systems[J]. IEEE transactions on automatic control, 1995, 40(1): 35–49. DOI:10.1109/9.362901 |
| [5] | REYHANOGLU M. Exponential stabilization of an underactuated autonomous surface vessel[J]. Automatica, 1997, 33(12): 2248–2254. |
| [6] | PETTERSEN K Y. Exponential stabilization of an underactuated vehicles[D]. Trondheim: Norwegian university of science and technology, 1996. https://www.researchgate.net/publication/224228565_Exponential_Stabilization_of_an_Underactuated_Surface_Vessel |
| [7] | DO K D, JIANG Z P, PAN J. Robust adaptive path following of underactuated ships[J]. Automatica, 2004, 40(6): 929–944. DOI:10.1016/j.automatica.2004.01.021 |
| [8] | DO K D. Global robust adaptive path-tracking control of underactuated ships under stochastic disturbances[J]. Ocean engineering, 2016, 111: 267–278. DOI:10.1016/j.oceaneng.2015.10.038 |
| [9] | SERRANO M E, SCAGLIA G J E, GODOY S A, et al. Trajectory tracking of underactuated surface vessels: A linear algebra approach[J]. IEEE Transactions on control systems technology, 2014, 22(3): 1103–1111. DOI:10.1109/TCST.2013.2271505 |
| [10] | YAN Z, WANG J. Model predictive control for tracking of underactuated vessels based on recurrent neural networks[J]. IEEE Journal of oceanic engineering, 2012, 37(4): 717–726. DOI:10.1109/JOE.2012.2201797 |
| [11] |
柳晨光, 初秀民, 王乐, 等. 欠驱动水面船舶的轨迹跟踪模型预测控制器[J].
上海交通大学报, 2015, 49(12): 1842–1854.
LIU Chenguang, CHU Xiumin, WANG Le, et al. Trajectory tracking controller for underactuated surface vessels based on model predictive control[J]. Journal of Shanghai Jiaotong University, 2015, 49(12): 1842–1854. |
| [12] | DONG Zaopeng, WAN Lei, LI Yueming, et al. Trajectory tracking control of underactuated USV based on modified backstepping approach[J]. International journal of naval architecture and ocean engineering, 2015, 7(5): 817–832. DOI:10.1515/ijnaoe-2015-0058 |
| [13] |
曾薄文, 朱齐丹, 于瑞亭. 欠驱动水面船舶的曲线航迹跟踪控制[J].
哈尔滨工程大学学报, 2011, 32(10): 1317–1322.
ZENG Bowen, ZHU Qidan, YU Ruiting. Curve tracking of an underactuated surface vessel[J]. Journal of Harbin Engineering University, 2011, 32(10): 1317–1322. DOI:10.3969/j.issn.1006-7043.2011.10.010 |
| [14] |
王耀禄, 郭晨. 欠驱动船舶RBF神经网络路径自适应跟踪控制[J].
大连海事大学学报, 2015, 41(1): 1–5.
WANG Yaolu, GUO Chen. Path flowing control for underactuated surface vessels based on RBF neural network[J]. Journal of Dalian Maritime University, 2015, 41(1): 1–5. |
| [15] | ZHENG Zewei, SUN Liang. Path following control for marine surface vessel with uncertainties and input saturation[J]. Neurocomputing, 2015, 177: 158–167. |
| [16] | WANG H, WANG D, PENG Z H, et al. Adaptive dynamic surface control for cooperative path following of underactuated marine surface vehicles via fast learning[J]. IET Control theory and applications, 2013, 7(15): 1888–1898. DOI:10.1049/iet-cta.2013.0021 |
| [17] | PENG Zhouhua, WANG Dan, LAN Weiyao, et al. Robust leader-follower formation tracking control of multiple underactuated surface vessels[J]. China ocean engineering, 2012, 26(3): 521–534. DOI:10.1007/s13344-012-0039-8 |
| [18] | ASHRAFIUON H, MUSKE K R, MCNINCH L C, et al. Sliding-mode tracking control of surface vessels[J]. IEEE Transactiona on industrial electronics, 2008, 55(11): 4004–4012. DOI:10.1109/TIE.2008.2005933 |
| [19] | YU Ruiting, ZHU Qidan, XIA Guihua, et al. Sliding mode tracking control of an underactuated surface vessel[J]. Control theory and applications, IET, 2012, 6(3): 461–466. DOI:10.1049/iet-cta.2011.0176 |
| [20] |
朱齐丹, 于瑞亭, 夏桂华, 等. 风浪流干扰及参数不确定欠驱动船舶航迹跟踪的滑模鲁棒控制[J].
控制理论与应用, 2012, 29(7): 959–964.
ZHU Qidan, YU Ruiting, XIA Guihua, et al. Sliding-mode robust tracking control for underactuated surface vessels with parameter uncertainties and external disturbances[J]. Control theory and applications, 2012, 29(7): 959–964. |
| [21] |
杨震, 刘繁明, 王岩. 欠驱动船舶路径跟踪的神经滑模控制[J].
中国造船, 2015, 56(2): 45–55.
YANG Zhen, LIU Fanming, WANG Yan. Path following of underactuated surface vessels based on neural sliding mode[J]. Shipbuildig of China, 2015, 56(2): 45–55. |
| [22] | LI R H, LI T S, BU R X, et al. Active disturbance rejection with sliding mode control based course and path following for underactuated ships[J]. Mathematical problems in engineering, 2013, 2013: 1–9. |
| [23] | MASOOD G, SERGEY G N, GARRETT C. Finite-time tracking using sliding mode[J]. Journal of the franklin institute, 2014, 351(5): 2966–2990. DOI:10.1016/j.jfranklin.2014.02.001 |
| [24] | YU Xinghuo, MAN Zhihong. Model reference adaptive control systems with terminal sliding modes[J]. International journal of Control, 1996, 64(6): 1165–1176. DOI:10.1080/00207179608921680 |
| [25] | 贾欣乐, 杨盐生. 船舶运动数学模型:机理建模与辨识建模[M]. 大连: 大连海事大学出版社, 1999. |
| [26] | NERSESOV S G, NATARAJ C, AVIS J M. Design of finite-time stabilizing controllers for nonlinear dynamical systems[C]//IEEE Conference on Decision and Control, 2007, 1740-1745. |



