良好的动态特性是轮胎设计的关键因素,轮胎结构模态频率和振型的研究可以预测轮胎与路面激励、悬架系统等发生相互作用的可能性,从而可通过结构的优化改进避开共振频率。车辆性能的分析及悬挂系统的设计开发也依赖于对轮胎振动特性的研究。因此,研究轮胎的振动特性对轮胎的优化设计具有重要意义。管迪华等利用锤击和激振器激振等方法对轮胎各种频带下的振动特性进行了试验研究,在此基础上建立了轮胎振动模型,并对轮胎模态参数变化的规律进行了分析[1-4];P. Kindt等基于弹性环模型对不同频带下的面内模态、动特性模态、扭转模态等进行了研究,并对滚动状态下的轮胎动态力学特性进行了评估分析[5-6];赵国群等[7]采用数值计算和模态试验相结合的方法,对充气压力和负荷变化对层合结构的轮胎振动模态参数的影响进行了研究;Byoung Sam Kim等[8]对不同规格轮胎的固有频率及模态振型随充气压力、负荷、轮胎结构材料分布变化的规律进行了研究;危银涛等[9]基于有限元分析和模态试验分析了充气压力、带束层参数及帘线和橡胶模量对轮胎振动固有频率的影响,并揭示了轮胎振动特性与使用条件及材料特性之间的相互关系。朱茂桃等[10]利用内积相关度理论对车身有限元计算模态和试验模态进行了振型相关性分析,辨别出振型所对应的模态频率,验证了有限元计算模型的正确性。
为解决传统充气轮胎刺破受损、高速爆胎等问题,安全轮胎技术已成为轮胎工业研究的热点。目前,国内外学者研发的非充气安全轮胎存在自重和刚度较大、加工工艺复杂等关键问题,且仍处于概念阶段。为解决以上问题,本课题组提出了一种新型非充气弹性车轮,该车轮在实现充气轮胎基本功用的同时,能够避免刺扎、爆胎和爆损等问题,所以该弹性车轮更满足于特种车辆(军事车辆、越野车、抢险救灾车等) 的安全使用要求。
在前期研究的基础上[11-12],本文基于有限元计算和模态试验相结合的分析方法对所设计的新型非充气弹性车轮的振动特性进行研究,根据试验模态参数和结构设计变量的灵敏度分析对车轮有限元模型进行修正,并结合内积相关度理论对其修正后的有限元计算模态和试验模态进行相关性研究。
1 机械弹性车轮结构新型机械弹性车轮是通过机械连接弹性复合结构代替传统轮胎充气弹性结构,其车轮主要由輮轮(橡胶胎圈、弹性环、卡环)、轮毂、销轴、铰链组等部件构成,如图 1所示[12]。

|
| 图1 机械弹性车轮结构 Figure 1 Structure of the MEW |
机械弹性车轮工作过程中,车轴传给轮毂的垂直载荷与扭矩使铰链组由平衡状态变为预紧状态,进而拉动輮轮产生拉力,该力沿车轮外圆的切向分力克服车轮与地面的静摩擦力,使得车轮滚动。由于轮毂以铰链组悬挂于輮轮内,来自路面的激励大部分将为輮轮所承受,并瞬时随其弹性变形和相应铰链组的瞬时弯曲所缓解,故该车轮具有不同于普通充气轮胎的缓冲减振性能。
2 机械弹性车轮有限元模态分析有限元模态分析可看成求解具有有限个自由度的线弹性系统运动方程。在分析过程中,若有限元模型不考虑能量的耗散,可忽略结构阻尼对其模态频率及振型的影响,其矩阵表达式为
| $ (\boldsymbol{K}-{{\omega }^{2}}\boldsymbol{M})\boldsymbol{\varphi} =0 $ | (1) |
亦可写为
| $ \left( \boldsymbol{K}-\lambda \text{ }\boldsymbol{M} \right)\boldsymbol{\varphi} =0 $ | (2) |
式中:K为结构刚度矩阵,M为质量矩阵,λ=ω2为特征值,ω为结构的固有频率,φ为对应的特征向量。
求解可得n个特征值λi及对应的特征向量φi,即为模态频率和振型。
机械弹性车轮橡胶体结构和弹性钢丝环的迟滞变形特性决定该车轮阻尼特性,其阻尼效果比充气轮胎更加显著,因此,在模态分析时要考虑复模态问题,其有阻尼振动系统的自由振动方程为
| $ \boldsymbol{M\ddot{x}}+\boldsymbol{C\dot{x}}+\boldsymbol{Kx}=0 $ | (3) |
式中:M、C、K分别为系统的质量矩阵、阻尼矩阵和刚度矩阵;ẍ、ẋ、x分别为加速度向量、速度向量和位移向量。
复模态分析的目的是计算有阻尼系统的模态,并用于确定所研究对象的结构稳定性。其分析实质是将线性振动微分方程组中的物理坐标变换为模态坐标,使得方程组解耦,则方程(3) 可改写为:
| $ ({{p}^{2}}\boldsymbol{M}+p\boldsymbol{C}\text{ }+\boldsymbol{K})\boldsymbol{\varphi} =0 $ | (4) |
式中:p为特征值,φ为对应的特征向量。
在实模态分析基础上,通过实模态投影生成的子空间上形成复特征值问题,并使用Hessenberg缩减方法提取复模态参数。将矩阵投影到由n个实模态特征向量组成的空间上,可得:
| $ \left\{ \begin{align} & {{\boldsymbol{M}}^{*}}={{[{{\varphi }_{1}}\ldots {{\varphi }_{n}}]}^{\text{T}}}~\boldsymbol{M}[{{\varphi }_{1}}\ldots {{\varphi }_{n}}] \\ & {{\boldsymbol{C}}^{*}}={{[{{\varphi }_{1}}\ldots {{\varphi }_{n}}]}^{\text{T}}}~\boldsymbol{C}[{{\varphi }_{1}}\ldots {{\varphi }_{n}}] \\ & {{\boldsymbol{K}}^{*}}={{[{{\varphi }_{1}}\ldots {{\varphi }_{n}}]}^{\text{T}}}~\boldsymbol{K}[{{\varphi }_{1}}\ldots {{\varphi }_{n}}] \\ \end{align} \right. $ | (5) |
式(4) 亦可写为:
| $ ({{p}^{2}}{{\boldsymbol{M}}^{*}}+p{{\boldsymbol{C}}^{*}}+{{\boldsymbol{K}}^{*}}){{\boldsymbol{\varphi} }^{*}}=0 $ | (6) |
方程的复特征值和复特征向量可分别表示为:p=α+βi,φ=[φ1 … φn]Tφ*。阻尼系数可通过式ξ=
机械弹性车轮的輮轮主要由橡胶体、帘布、弹性钢丝环等多种材料构成,如图 2所示。輮轮结构组份材料的不同决定车轮不同的特性,为了尽可能准确地模拟车轮性能,需要对輮轮结构的复合材料进行力学性能研究。

|
| 图2 层合结构模型 Figure 2 Laminated structure model |
輮轮中的帘布复合材料属于三维正交各向异性复合材料,具有近似体积不可压缩性和非线性的本构关系。初始模型中,帘线的方向向量和基体的法向向量相同,为了较好的表征橡胶材料力学特性,通常采用Mooney-Rivlin超弹性本构模型进行描述,其应变能函数W是变形张量不变量(I1, I2, I3) 的函数,即W=W(I1, I2, I3),橡胶又为不可压缩性材料,即I3=1,则应变能函数模型为
| $ W=\sum\limits_{i=0,j=0}^{n}{{{C}_{ij}}}{{(\text{ }{{\boldsymbol{I}}_{1}}-3)}^{i}}{{(\text{ }{{\boldsymbol{I}}_{2}}-3)}^{j}} $ | (7) |
式中:I1、I 2为左Cauchy-Green变形张量中的第1和2基本不变量,Cij为材料参数,则有:
| $ {{\boldsymbol{I}}_{1}}=\text{tr}E={{E}_{ii}}=\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2} $ | (8) |
| $ \begin{align} & {{\boldsymbol{I}}_{2}}=\frac{1}{2}\left[ {{(\text{tr}E)}^{2}}-\text{tr}{{E}^{2}} \right]={{E}_{ii}}= \\ & \ \ \ {{({{\lambda }_{1}}{{\lambda }_{2}})}_{2}}+{{({{\lambda }_{2}}{{\lambda }_{3}})}_{2}}+{{({{\lambda }_{3}}{{\lambda }_{1}})}_{2}} \\ \end{align} $ | (9) |
I1、I2、I3为二阶张量不变量,下角标1、2和3表示3个相互垂直的方向,且材料只有单方向拉伸,则有:λ1λ2λ3=1,对于輮轮的橡胶材料,∂W/∂I 2远远小于∂W/∂I 1,且近似为零,故有Yeoh模型为
| $ W={{C}_{10}}({{\boldsymbol{I}}_{1}}-3)+{{C}_{20}}{{({{\boldsymbol{I}}_{1}}-3)}^{2}}+{{C}_{30}}{{(\text{ }{{\boldsymbol{I}}_{1}}-3)}^{3}}~ $ | (10) |
式中:Yeoh模型能够充分的描述橡胶-帘布复合材料的性能,并且仅可由单轴拉伸试验确定其材料的系数。采用Instron公司的万能拉伸测试仪对輮轮橡胶体材料进行单向拉伸试验,试样取件为胎面层、胎内层等橡胶-帘线复合材料,测试结果如图 3所示。σ-ε曲线的形状取决于橡胶-帘线材料的分布含量,通过测试结果的分析,可得Yeoh模型的材料参数,如表 1所示。机械弹性车轮不同组件的材料性能参数如表 2所示。

|
| 图3 橡胶-帘布复合材料应力-应变曲线 Figure 3 The stress-strain curve of rubber-curtain composite |
| 组件 | C10/MPa | C01/MPa | C20/MPa | C30/MPa | 密度ρ/(t·m-3) |
| 胎面层 | 0.563 67 | 0.004 36 | - | - | 1.279 |
| 胎内层 | 0.467 15 | 0.003 27 | - | - | 1.256 |
| 帘布层 | 0.706 44 | - | 4.923 17 | 4.136 75 | 1.217 |
| 组份材料 | 杨氏模量E/MPa | 泊松比μ | 密度ρ/(t·m-3) |
| 弹性环 | 0.196 | 0.30 | 7.81 |
| 铰链组 | 0.205 | 0.29 | 7.85 |
| 轮毂 | 0.205 | 0.30 | 7.80 |
将机械弹性车轮模型进行适当的简化,不考虑车轮花纹对分析的影响。輮轮中的胎面、基部胶和帘布层均属于复合材料,弹性钢丝环层为加强筋层,为方便模型建立,基于Gough-Tangorra微观力学理论,采用Hyper Mesh的复合材料前处理模块Hyper Laminate进行铺层离散。获得輮轮模型,轮毂、铰链组等部件均属于各向同性材料,采用六面体单元进行离散。利用interfaces面板功能建立輮轮层合体之间的接触关系,选择Auto可通过周围单元的刚度确定Gap单元的刚度,准确地模拟接触条件,防止接触节点的穿透。采用Spring单元模拟铰链之间的转动副及回位弹簧,与轮毂、輮轮关联构成完整的车轮有限元模型。不施加任何载荷,约束轴向方向自由度,并设置计算卡片信息,最终建立的车轮结构有限元模型如图 4所示,共有314 693个节点,267 535个实体单元。

|
| 图4 车轮结构有限元模型 Figure 4 FE model of the MEW |
运用RADIOSS模块中的Lanczos算法和Hessenberg缩减法对有限元模型进行数值模态计算,与试验振型结果进行对照,选出与试验模态振型相近的计算模态振型及所对应的频率,得出前六阶带阻尼结构的模态频率和振型,如表 3所示。
| 阶次 | 1 | 2 | 3 | 4 | 5 | 6 |
| 模态频率/Hz | 29.431 | 76.780 | 84.156 | 135.372 | 146.673 | 196.077 |
| 错动 | 椭圆 | 三瓣 | 四瓣 | 五瓣 | 六瓣 | |
| 模态振型 |  |
 |
 |
 |
 |
 |
机械弹性车轮进行模态试验的基本原理是将其离散化,其弹性和阻尼特性用线性模型来描述,系统的振动微分方程为
| $ \boldsymbol{M\ddot{x}}\left( t \right)+\boldsymbol{C\dot{x}}\left( t \right)+\boldsymbol{Kx}\left( t \right)=\boldsymbol{F}\left( t \right) $ | (11) |
式中:M、C和K分别为系统的质量矩阵、阻尼矩阵和刚度矩阵;ẍ(t)、ẋ(t) 和x(t) 分别为系统节点的加速度矩阵、速度矩阵和位移矩阵;F(t) 为系统节点的激励力矩阵,其中t为时间。
在振动模态试验中,对式(11) 两边进行傅里叶变换可得
| $ {{(\text{j}\omega )}^{2}}\boldsymbol{MX}\text{ }\left( \omega \right)+\text{j}\omega CX\left( \omega \right)+KX\left( \omega \right)=F\left( \omega \right) $ | (12) |
式中:F(ω)、X (ω) 分别为激振力F(t) 和位移响应向量x(t) 的傅里叶变换。
令
| $ \boldsymbol{H}\left( \omega \right)=-{{\omega }^{2}}\boldsymbol{M}+\text{j}\omega \boldsymbol{C}+\boldsymbol{K} $ | (13) |
式(12) 可简化为
| $ \boldsymbol{X}\left( \omega \right)=\boldsymbol{H}\left( \omega \right)\times \boldsymbol{F}\left( \omega \right) $ | (14) |
式中H(ω) 为传递函数矩阵。
当在第j点激振时,在i点测响应,可得传递函数矩阵中第j行i列元素为
| $ {{H}_{ij}}\left( \omega \right)=\sum\limits_{r=1}^{n}{\frac{{{\varphi }_{ir}}{{\varphi }_{jr}}}{{{K}_{r}}-{{\omega }^{2}}{{M}_{r}}+j\omega {{C}_{r}}}} $ | (15) |
式中:φir、φjr为i、j点振型元素。
式(15) 表达了传递函数与模态参数之间的关系,该式分母与响应点、激振点无关,仅与频率和阻尼有关,因此,无论在哪一点进行测量,获得的传递函数的分母值相同。对结构上一点激振,多点测量响应,即可得到传递函数矩阵的某一列,进而计算出模态参数。
3.2 模态测试系统机械弹性车轮自由悬置,采用移动力锤法进行径向激振试验,并利用模态试验分析软件LMS Test. Lab进行识别分析,试验设备如表 4所示。
| 设备名称 | 型号 |
| 多通道数据采集系统 | SCM205 |
| 模态试验分析系统 | LMS Test. Lab 13A |
| 模态力锤 | 086C03 |
| 加速度传感器 | 333B30 |
| 计算机工作站 | Dell |
采用单点激振多点拾振的方法对机械弹性车轮进行模态分析,利用棕绳将车轮自由悬置,由于自由悬置的自振频率(小于1 Hz) 远低于车轮一阶固有频率(约为30 Hz),因此可忽略支撑对模态参数提取的影响。设置频带为512 Hz和频率分辨率为0.83 Hz,进行自由模态试验,如图 5所示。

|
| 图5 机械弹性车轮模态试验 Figure 5 Modal experiment of the MEW |
考虑机械弹性车轮结构的特点,针对车轮面内振动模态,在胎面径向中心圆处均匀布置12个测点,形成的车轮模态试验测点布置如图 6所示。
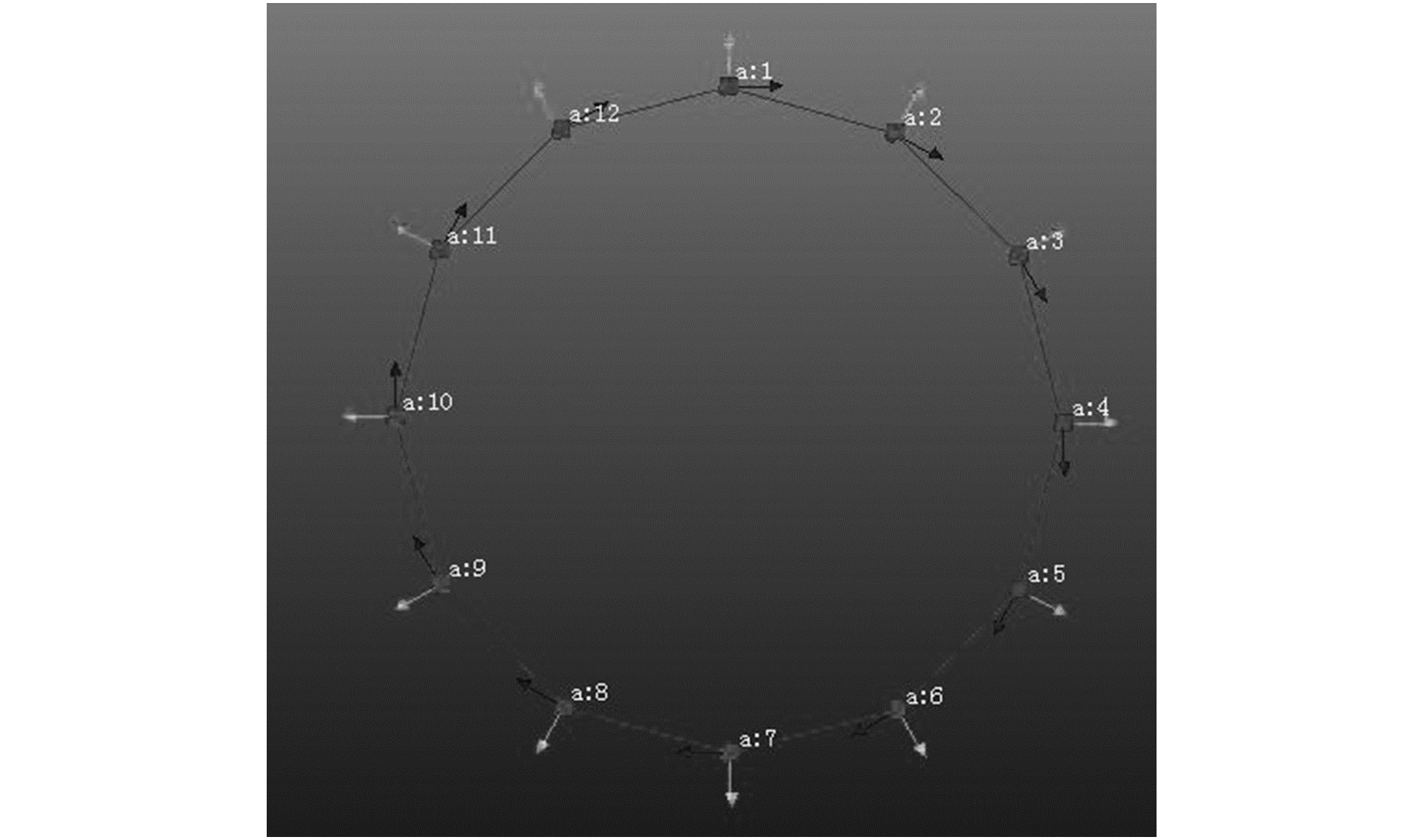
|
| 图6 车轮测点布置图 Figure 6 Test points distribution |
测试前多次试测,以避免激振点处于节点上,可减少模态的丢失。采用PolyMAX识别技术,在模态重叠、大阻尼系统及噪声干扰等情况下都可得出清晰的稳态图,不仅能够很好地识别出低频范围的模态参数,而且还可以较好地识别高频范围的模态参数,同时还可以识别出高度密集的模态和重根模态。利用PolyMAX模态分析方法得到车轮测试结果的稳态图,如图 7所示。
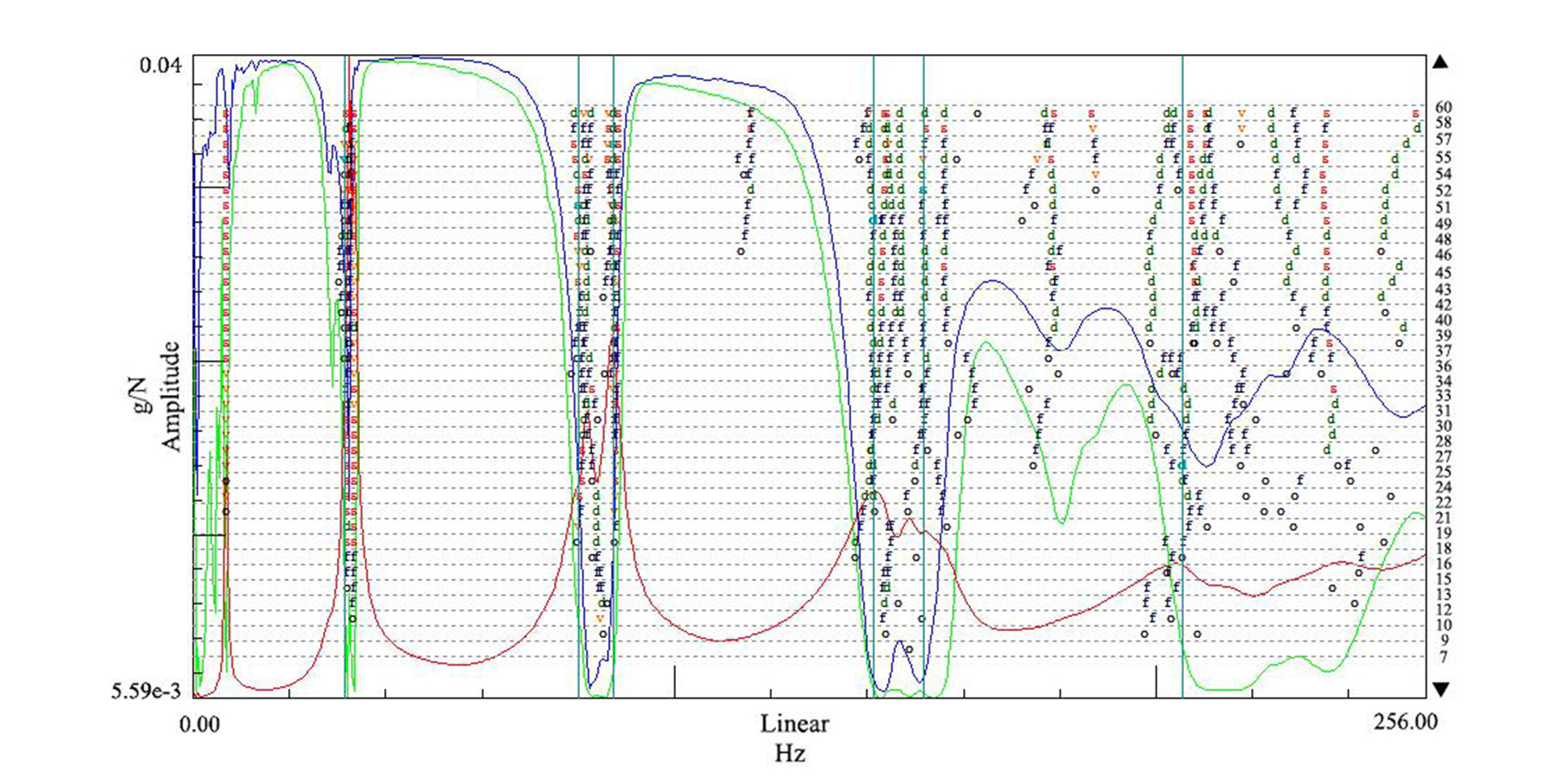
|
| 图7 PolyMAX识别的稳态图 Figure 7 Stabilization chart of PolyMAX recognition 注:o表示未找到极点;f表示频率稳定(在给定精度内);v表示频率和模态参与因子稳定;d表示频率和阻尼稳定;s表示3种参数全部稳定(在给定精度内) |
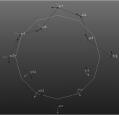
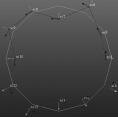
根据频响函数矩阵的多行与多列数据参数识别及模态试验PolyMAX识别方法,得出的机械弹性车轮径向激振模态试验结果,如表 5所示。
| 阶次 | 1 | 2 | 3 | 4 | 5 | 6 |
| 模态频率/Hz | 33.398 | 81.826 | 87.659 | 141.674 | 156.513 | 205.875 |
| 错动 | 椭圆 | 三瓣 | 四瓣 | 五瓣 | 六瓣 | |
| 模态振型 |  |
 |
 |
 |
 |
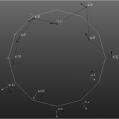 |
由上述试验结果分析可得,在所加激振力范围内,力的大小对车轮的固有频率影响较小,说明轮胎在此加力范围内是线性的。从振型图可以看出,对于低阶模态,车轮表现为实模态,振型形状相对规整,但到第四阶模态开始显现复模态的特性,形状不再规整,振型图由幅值所得,各点之间的相位差不再为0°或180°。
4 机械弹性车轮有限元模型修正在车轮有限元建模过程中,对輮轮层合结构、铰链组的连接等进行的简化,导致了有限元模型质量矩阵存在一定的误差。对于车轮简化模型,为提高有限元模型的精度,可通过改进材料属性有效地补偿几何模型的误差。鉴于有限元和试验模态频率之间的误差,结合结构设计变量的灵敏度分析,对其车轮结构有限元模型进行修正。
考虑多自由度系统的无阻尼振动特征方程为
| $ (\boldsymbol{K}-\boldsymbol{{{\lambda }_{i}}M}){{\boldsymbol{\varphi} }_{i}}=0 $ | (16) |
式中:λi、φi分别为系统特征方程的第i阶特征值和特征向量。
由Rayleigh法可得第i阶固有频率与振型的关系为
| $ \omega _{i}^{2}=\frac{\boldsymbol{\varphi} _{i}^{\text{T}}\boldsymbol{K\varphi} {{~}_{i}}}{\boldsymbol{\varphi} _{i}^{\text{T}}\boldsymbol{M}{{\boldsymbol{\varphi} }_{i}}} $ | (17) |
假设系统的振型已进行了模态质量归一化,则有:
| $ \boldsymbol{\varphi }_{i}^{\text{T}}\boldsymbol{M}{{\boldsymbol{\varphi} }_{i}}=I $ | (18) |
将式(17) 和(19) 分别对结构参数Sj求微分可得:
| $ (\frac{\partial \boldsymbol{K}}{\partial {{S}_{j}}}-\frac{\partial {{\lambda }_{i}}}{\partial {{S}_{j}}}\boldsymbol{M}-{{\lambda }_{i}}\frac{\partial \boldsymbol{M}}{\partial {{S}_{j}}})\text{ }{{\boldsymbol{\varphi} }_{i}}+(\text{ }\boldsymbol{K}-{{\lambda }_{i}}\boldsymbol{M})\frac{\partial {{\boldsymbol{\varphi} }_{i}}}{\partial {{S}_{j}}}=0 $ | (19) |
| $ {{\left( \frac{\partial {{\boldsymbol{\varphi} }_{i}}}{\partial {{S}_{j}}} \right)}^{\text{T}}}\boldsymbol{M}{{\boldsymbol{\varphi} }_{i}}+\boldsymbol{\varphi} _{i}^{\text{T}}\boldsymbol{M}\frac{\partial {{\boldsymbol{\varphi} }_{i}}}{\partial {{S}_{j}}}+\varphi _{i}^{\text{T}}\frac{\partial \boldsymbol{M}}{\partial {{S}_{j}}}{{\boldsymbol{\varphi} }_{i}}=0 $ | (20) |
根据正交性条件整理式(19) 和(20) 可得第i阶特征值对参数Sj的导数,即第i阶模态频率对第Sj个设计参数的灵敏度为
| $ \frac{\partial {{\lambda }_{i}}}{\partial {{S}_{j}}}=\boldsymbol{\varphi} _{i}^{\text{T}}(\frac{\partial \boldsymbol{K}}{\partial {{S}_{j}}}-{{\lambda }_{i}}\frac{\partial \boldsymbol{M}}{\partial {{S}_{j}}}){{\boldsymbol{\varphi} }_{i}} $ | (21) |
由式(21) 可以看出,结构参数Sj的改变直接影响质量矩阵M和刚度矩阵K,进而改变固有模态频率ωi。在輮轮建模过程中,忽略了弹性钢丝环内的孔隙率对计算结果的影响,而车轮结构其余部件的几何和材料参数都是根据设计和试验测试进行设定的,故假定其余结构部件的建模误差不计,取对质量矩阵和刚度矩阵影响较大的弹性钢丝环的等效弹性模量和等效密度作为修正参数。
结合试验模态参数和OptiStruct优化分析方法对车轮结构的有限元模型进行修正[13-14]。对弹性钢丝环的待修正参数进行一定范围的随机摄动,可直接或间接地调整有限元模型的质量矩阵M和刚度矩阵K,使有限元计算的模态频率和振型尽可能接近试验模态分析的结果。以车轮结构前6阶模态频率作为修正目标,取车轮自重为主要性能约束条件,设目标函数为:
| $ {{f}_{\text{obj}}}={{\sum\limits_{i=1}^{n}{\left( \frac{{{\omega }_{i}}}{\omega _{i}^{\text{exp}}}-1 \right)}}^{2}},i=1,2,\ldots ,n $ | (22) |
式中:ωi为第i阶计算模态频率;ωiexp为第i阶试验模态频率。
依据迭代收敛准则,对初始有限元模型进行逐步修正,经过迭代后计算与实测频率收敛到允许误差范围内,迭代后的结构参数的修正值见表 6所示。
| 参数值 | 弹性钢丝环 | |
| 弹性模量/MPa | 等效密度/(kg·m-3) | |
| 初始值 | 1.960×105 | 7.810×103 |
| 修正值 | 2.016×105 | 7.712×103 |
| 变化率/% | -2.86 | 1.25 |
分析表明,通过调整弹性钢丝环的等效弹性模量和等效密度,可显著改善车轮的模态和振型,修正后的模态频率如表 7第Ⅳ列所示。
| 模态阶次 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
| 试验值/Hz | 初始值/Hz | 字母变量|(Ⅱ-Ⅰ)/Ⅰ|/% | 修正值/Hz | 字母变量|(Ⅱ-Ⅰ)/Ⅰ|/% | |
| 1 | 33.398 | 29.431 | 11.88 | 32.425 | 2.91 |
| 2 | 81.826 | 76.780 | 6.17 | 80.134 | 2.07 |
| 3 | 87.659 | 84.156 | 3.99 | 85.947 | 1.95 |
| 4 | 141.674 | 135.372 | 4.49 | 139.492 | 1.54 |
| 5 | 156.513 | 146.673 | 6.28 | 154.026 | 1.59 |
| 6 | 205.875 | 196.077 | 4.76 | 202.638 | 1.57 |
由表 7数据可知,经过模型修正,各阶计算模态频率与试验模态频率的误差得到明显缩小,车轮结构的模态频率最大误差由修正前的11.88%降到修正后的2.91%,说明经过修正后的有限元分析模型的精度得到大幅度提高。
5 有限元模态与试验模态的相关性分析为了进一步验证有限元模型,为机械弹性车轮振动特性的研究提供支撑,需进行有限元计算模态和试验模态两则分析结果的相关性研究,求出两者相关度,若相关度越高,说明两种模型的吻合程度就越好。
5.1 内积相关度设R n是n维实线性空间,定义内积〈·, ·〉为:对任意的X=[x1 x2 … xn]T,Y=[ y1 y2 … yn]T∈ Rn,定义〈X, Y〉=
设X∈Rn为试验模态经实模态提取后的试验振型,Y∈R n为有限元模态的计算振型,X与Y在空间(R n, 〈·, ·〉) 中的内积相关度定义为PC (X, Y)=
有限元计算和试验模态所得的车轮前六阶振型,并不能够直观的表达两者之间的一致性,需将获得的模态振型抽象为Hilbert空间中的点,并设各点对应一个向量,利用向量之间的夹角来描述有限元计算模态与试验模态的相关性。试验模态分析所得到的结果为复模态,模态振型的每一个分量包含两部分,分别为反应振动幅度的幅值和相位,为此需要进行实模态的提取,在整体结构振动偏移量最大时,取各个节点的偏移值作为试验模态振型的各个分量。
设某阶试验模态振型为
| $ \boldsymbol{A}={{\left[ ({{r}_{1}},{{T}_{1}})\text{ }({{r}_{2}},{{T}_{2}})\text{ }\ldots \text{ }({{r}_{n}},{{T}_{n}}) \right]}^{\text{T}}} $ | (23) |
式中:rk和Tk分别为振型第k个分量的幅值和相位,k=1, 2, …, n。
取Tmax为E(T)=
| $ \begin{align} & \boldsymbol{X}=[{{r}_{1}}\text{sin}\left( {{T}_{\text{max}}}+{{T}_{1}} \right)\ \ \ \ \ {{r}_{2}}\text{sin}\left( {{T}_{\text{max}}}+{{T}_{2}} \right) \\ & \ \ \ \ \ \ \ \ \ \ \ \ldots \text{ }{{r}_{n}}\text{sin}({{T}_{\text{max}}}+{{T}_{n}}){{]}^{\text{T}}} \\ \end{align} $ | (24) |
式中:X为提取的某阶模态振型矩阵,risin (Tmax+Ti) 为提取后的某阶模态振型的第i个分量,i=1, 2, …, n。
取试验的某阶振型,将其提取为实模态振型X,取修正后的有限元计算模态中某阶与试验自由度一致的振型Yk,计算内积相关度PC (X, Yk)(k=1, 2, …),确定其可信度。
利用Mtalab软件编写相关的程序,对其修正后的有限元模态和试验模态进行内积相关度计算,计算结果如表 8和9所示。
| 内积相关度值 | 计算模态 | 试验模态 | |||
| 阶次 | 频率/Hz | 阶次 | 频率/Hz | ||
| 0.965 2 | 1 | 32.425 | 1 | 33.398 | |
| 0.951 9 | 2 | 80.134 | 2 | 81.826 | |
| 0.956 7 | 3 | 85.947 | 3 | 87.659 | |
| 0.951 5 | 4 | 139.492 | 4 | 141.674 | |
| 0.952 3 | 5 | 154.026 | 5 | 156.513 | |
| 0.947 4 | 6 | 202.638 | 6 | 205.875 | |
| 计算模态 | 试验模态 | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 0.965 2 | 0.312 4 | 0.221 6 | 0.295 7 | 0.299 3 | 0.318 3 |
| 2 | 0.313 9 | 0.951 9 | 0.227 8 | 0.306 6 | 0.187 9 | 0.264 5 |
| 3 | 0.231 7 | 0.185 3 | 0.956 7 | 0.351 4 | 0.346 5 | 0.308 6 |
| 4 | 0.289 9 | 0.162 5 | 0.143 6 | 0.951 5 | 0.159 8 | 0.174 2 |
| 5 | 0.302 6 | 0.221 4 | 0.213 9 | 0.216 8 | 0.952 3 | 0.281 7 |
| 6 | 0.206 8 | 0.173 6 | 0.271 5 | 0.218 3 | 0.381 2 | 0.947 4 |
通过上述计算结果表明,修正后的有限元计算模态与试验模态的振型及所对应的模态频率吻合性较好,说明基于内积相关度分析具有较高的可靠性,同时也验证了有限元建模及修正分析方法的有效性。
6 结论1) 针对新型机械弹性车轮的振动特性,利用有限元计算和模态试验相结合的分析方法对其进行研究,并识别出与试验模态振型相对应的有限元模态振型及所对应的模态频率。
2) 基于结构设计变量的灵敏度分析和试验模态参数对车轮结构的有限元模型进行了修正,修正后的有限元分析模型的精度得到大幅度提高,为机械弹性车轮的进一步研究,如响应分析、谱分析以及结构动态优化设计等奠定了基础。
3) 修正后的有限元模态参数和试验模态参数具有较高的相关度,表明了车轮结构有限元建模及修正分析方法的正确性,同时也说明了基于内积相关度的分析方法能够为车轮优化设计提供指导。
| [1] |
管迪华, 刘德文. 轮胎结构动特性的试验模态分析[J].
振动与冲击, 1996, 15(1): 60–67.
GUAN Dihua, LIU Dewen. Experimental modal analysis of tires structural dynamic characteristics[J]. Journal of vibration and shock, 1996, 15(1): 60–67. |
| [2] |
管迪华, 董培蕾, 范成建. 轮胎自由与约束悬置的模态试验与综合分析[J].
汽车工程, 2003, 25(4): 353–355.
GUAN Dihua, DONG Peilei, FAN Chengjian. Modal experiment and analysis of free and fixed suspended tires[J]. Automotive engineering, 2003, 25(4): 353–355. |
| [3] |
管迪华, 彭会, 范成建. 轮胎模态试验分析的研究[J].
汽车工程, 2005, 27(6): 691–695.
GUAN Dihua, PENG Hui, FAN Chengjian. A research on tire modal testing analysis[J]. Automotive engineering, 2005, 27(6): 691–695. |
| [4] | YAM L H, GUAN D H, ZHANG A Q. Three-dimensional mode shapes of a tire using experimental modal analysis[J]. Experimental mechanics, 2000, 40(4): 369–375. DOI:10.1007/BF02326482 |
| [5] | KINDT P, SAS P, DESMET W. Development and validation of a three-dimensional ring-based structural tyre Model[J]. Journal of sound and vibration, 2009, 326(3/4/5): 852–869. |
| [6] | KINDT P, SAS P, DESMET W. Measurement and analysis of rolling tire vibrations[J]. Optics and lasers in engineering, 2009, 47(3/4): 443–453. |
| [7] | GUAN Yanjin, CHENG Gang, ZHAO Guoqun, et al. Investigation of the vibration characteristics of radial tires using experimental and numerical techniques[J]. Journal of reinforced plastics and composites, 2011, 30(24): 2035–2050. DOI:10.1177/0731684411431764 |
| [8] | KIM B S, CHI C H, LEE T K. A study on radial directional natural frequency and damping ratio in a vehicle tire[J]. Applied acoustics, 2007, 68(5): 538–556. DOI:10.1016/j.apacoust.2006.07.009 |
| [9] |
冯希金, 郑小刚, 危银涛, 等. 轮胎振动特性的有限元分析及关键影响因素研究[J].
轮胎工业, 2013, 33(1): 12–20.
FENG Xijin, ZHENG Xiaogang, WEI Yintao, et al. Finite element analysis on tire vibration and study on its key influencing factors[J]. Tire industry, 2013, 33(1): 12–20. |
| [10] |
朱茂桃, 何志刚, 徐凌, 等. 车身模态分析与振型相关性研究[J].
农业机械学报, 2004, 35(3): 13–15.
ZHU Maotao, HE Zhigang, XU Ling, et al. Mode analysis of car-body and its correlative research shape[J]. Transactions of the Chinese society of agricultural machinery, 2004, 35(3): 13–15. |
| [11] |
赵又群, 李小龙, 张明杰, 等. 机械弹性车轮随机振动理论与数值分析[J].
哈尔滨工业大学学报, 2015, 47(7): 47–51.
ZHAO Youqun, LI Xiaolong, ZHANG Mingjie, et al. Theoretical and numerical analysis on the random vibration of mechanical elastic wheel[J]. Journal of Harbin institute of technology, 2015, 47(7): 47–51. |
| [12] |
汪伟, 赵又群, 姜成, 等. 基于新型机械弹性车轮的整车平顺性分析[J].
中国机械工程, 2013, 24(22): 3114–3117.
WANG Wei, ZHAO Youqun, JIANG Cheng, et al. Ride comfort of vehicle on new mechanical elastic wheel[J]. China mechanical engineering, 2013, 24(22): 3114–3117. |
| [13] |
王北京, 王红岩. 车辆典型部件结构的有限元模型修正方法[J].
装甲兵工程学院学报, 2011, 25(6): 40–44.
WANG Beijing, WANG Hongyan. Updating method of finite element model for structures of typical components of vehicle[J]. Journal of academy of armored force engineering, 2011, 25(6): 40–44. |
| [14] |
高云凯, 蓝晓理, 陈鑫. 轿车车身模态修改灵敏度计算分析[J].
汽车工程, 2001, 23(5): 352–355.
GAO Yunkai, LAN Xiaoli, CHEN Xin. The sensitivity analysis of car body modal modification[J]. Automotive engineering, 2001, 23(5): 352–355. |
| [15] |
曹奇英, 张准, 李健康, 等. 基于内积的模态相关分析[J].
应用力学学报, 1998, 15(4): 135–138.
CAO Qiying, ZHANG Zhun, LI Jiankang, et al. Mode correlative analysis based on the interior cumulation relativity[J]. Chinese journal of applied mechanics, 1998, 15(4): 135–138. |
| [16] | CHANG Y B, YANG T Y. Dynamic analysis of a radial tire by finite elements and modal expansion[J]. Journal of sound and vibration, 1984, 96(1): 1–11. DOI:10.1016/0022-460X(84)90588-1 |
| [17] | KOZHEVNIKOV I F. The vibrations of a free and loaded tyre[J]. Journal of applied mathematics and mechanics, 2006, 70(2): 223–228. DOI:10.1016/j.jappmathmech.2006.06.010 |
| [18] | JIA L, XU Y, ZHANG J. Free vibration analysis of radial pneumatic tires using bezier functions[J]. Journal of sound and vibration, 2005, 285(4/5): 887–903. |
| [19] | SUGIYAMA H, SUDA Y. Non-linear elastic ring tyre model using the absolute nodal coordinate formulation[J]. Proceedings of the institution of mechanical engineers, part K:journal of multi-body dynamics, 2009, 223(3): 211–219. DOI:10.1243/14644193JMBD184 |



