2. Institute of Nuclear and New Energy Technology, Tsinghua University, Beijing 100084, China
超临界二氧化碳 (S-CO2) 布雷顿循环在中等压力 (8~20 MPa) 和中等温度 (450~650 ℃) 条件下具有较高的热效率,高于同等条件下的蒸汽朗肯循环和氦气布雷顿循环[1-3]。而且,其系统紧凑,设备体积小,易于模块化建设,具备良好的潜在经济性。国际上已提出将S-CO2作为堆芯冷却剂和能量转换工质,用于第四代核能系统中的钠冷快堆和铅冷快堆[4-11]。
目前S-CO2布雷顿循环受到了广泛研究,美国Sandia国家实验室建成了小规模S-CO2布雷顿闭合循环试验装置,并利用计算机模型对该试验装置进行了数值模拟分析;法国初步完成了可应用于钠冷快堆的S-CO2热电转换系统的设计和Na/S-CO2热交换器设计;日本进行了可应用于钠冷快堆的S-CO2能量转换系统初步设计,完成了S-CO2循环的热工水力试验;韩国进行了S-CO2与其设计的钠冷快堆KALIMER-600以及第四代钠冷快堆的耦合设计。
我国目前对S-CO2布雷顿循环的研究并不多。段承杰等基于麻省理工学院提出的再压缩循环模式对S-CO2的热力循环进行了初步分析,并与氦气动力循环进行了比较[12-14]。黄彦平等介绍了当前国际上S-CO2应用于核反应堆系统的相关研究进展,分析了传热关系式,并开展了自然循环实验研究[15]。张国杰设计了试验系统,用于研究S-CO2的压缩特性[16]。张墩煌等对S-CO2作为第四代核反应堆系统内能量转换系统进行了建模及技术成熟度分析,同时对S-CO2布雷顿再压缩循环建模分析及参数优化[17-19]。西安交通大学也对S-CO2部分预冷循环进行建模及参数优化,对循环经济性进行了初步分析。本文通过计算机工具,建立S-CO2闭式再压缩布雷顿循环热力分析模型,研究系统压力、温度、以及换热器压降对系统热效率的影响。
1 S-CO2闭式再压缩布雷顿循环S-CO2闭式再压缩布雷顿循环系统示意图如图 1所示。系统由热源 (反应堆)、透平、高温回热器、低温回热器、冷却器、主压缩机、再压缩机、管道和阀门等部件组成。系统所对应的温熵图如图 2所示。

|
| 图1 S-CO2闭式再压缩布雷顿循环系统 Figure 1 S-CO2 closed recompression Brayton cycle |
|
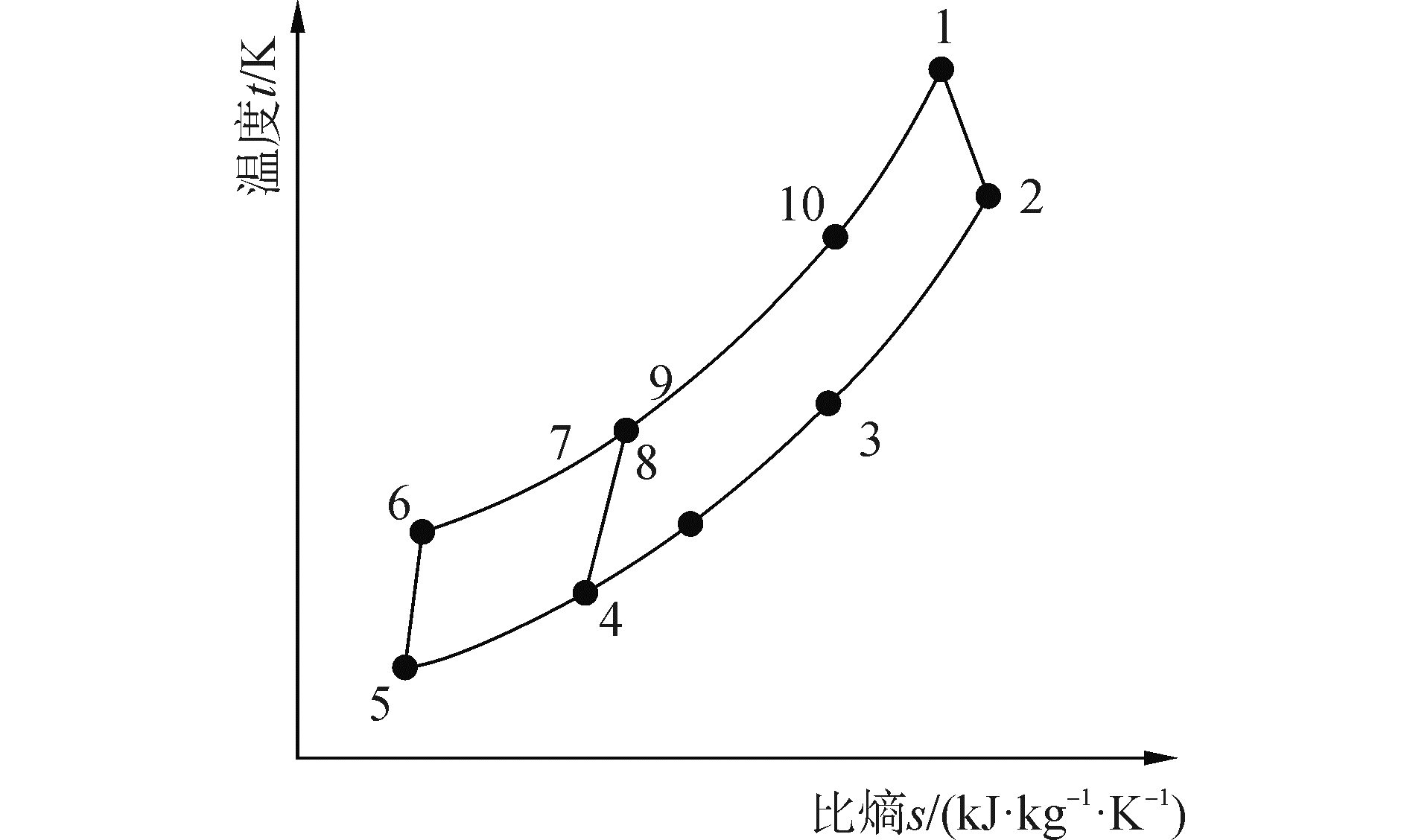
| 图2 S-CO2闭式再压缩布雷顿循环温熵图 Figure 2 T-s sketch of S-CO2 recompression Brayton cycle |
CO2工质首先进入透平做功 (过程1至2),做功后的CO2进入高温回热器进行定压放热 (过程2至3),加热低温侧工质,然后进入低温回热器 (过程3至4) 定压放热。通过低温回热器后,一部分工质分流直接进入再压缩压缩机绝热压缩 (过程4至8),另一部分工质进入预冷器定压放热后 (过程4至5),进入主压缩机绝热压缩 (过程5至6),然后通过低温回热器定压吸热 (过程6至7),从低温回热器流出的工质与再压缩机出口的两部分工质混合进入高温回热器定压吸热 (过程9至10),再通过主换热器或堆芯吸收热量 (过程10至1),完成整个循环过程。
2 热力循环计算模型使用Python 2.7作为工具,建立S-CO2布雷顿循环热力计算稳态分析模型。S-CO2数据库选用美国国家标准与技术研究所 (NIST) 发布的REFPROP数据库[18]。
2.1 透平及压缩机模型压缩机与透平模型假设在等熵效率为ηisen的情况下运行。叶轮机械所做功 (wi) 为
| $ {w_i} = {h_{{\rm{in}}}}-{h_{{\rm{out}}, i}} $ | (1) |
式中:hin为工质入口比焓,hout,i为工质出口比焓。压缩机的实际比功 (wcomp) 由等熵效率得出:
| $ {w_{{\rm{comp}}}} = \frac{{{w_i}}}{{{\eta _{{\rm{i}}sen}}}} $ | (2) |
透平的实际比功 (wturbine) 为
| $ {w_{{\rm{turbine}}}} = {w_i}{\eta _{isen}} $ | (3) |
根据能量平衡,可得出叶轮机械出口工质实际比焓 (hout):
| $ {h_{{\rm{out}}}} = {h_{{\rm{in}}}}-w $ | (4) |
通过出口比焓和出口压力确定叶轮机械出口工质热力学状态。
2.2 换热器模型换热器是S-CO2布雷顿循环中最重要的部件之一。高温回热器、低温回热器和冷却器的性能直接影响系统的热效率。目前对于布雷顿循环的初步分析中,多采用换热效率作为衡量换热器换热能力的参数。不过,换热效率相同的条件下,换热器的尺寸可能有很大的差别,而换热器的尺寸和形式对压降会产生显著的影响。
为了更直观地表示单位尺寸换热器的换热能力,建模时采用热阻的倒数 (UA,U为换热系数,A为换热面积) 表征换热器的性能。同一种换热器在相同工况下,换热系数差别不大。UA越大则表示换热面积越大,则换热器体积更大。UA越小表示换热面积越小,则换热器体积更小。换热器的布置形式均采用逆流式。
换热器模型沿流动方向划分为n个的节点,以便更准确的描述CO2物性变化的影响。
对于各个节点,两侧工质的平均比热容 (
| $ \dot C = \dot m\frac{{{h_{{\rm{in}}}}-{h_{{\rm{out}}}}}}{{{T_{{\rm{in}}}}-{T_{{\rm{out}}}}}} $ | (5) |
各个节点的换热效率ε可确定为
| $ \varepsilon = \frac{{{{\dot Q}_{_i}}}}{{{{\dot C}_{\min }}\left( {{T_{{\rm{hot, in}}}}-{T_{{\rm{cold, in}}}}} \right)}} $ | (6) |
式中:
逆流换热器中子换热器的传热单元数NTU为
| $ {\rm{NTU = }}\left\{ {\begin{array}{*{20}{c}} {\frac{{\log \left( {\frac{{1-\varepsilon {C_{\rm{R}}}}}{{1-\varepsilon }}} \right)}}{{1-{C_{\rm{R}}}}}\;\;\;\;\;\;\;{C_{\rm{R}}} \ne 1\;\;}\\ {\frac{\varepsilon }{{1 - \varepsilon }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{C_{\rm{R}}} = 1} \end{array}} \right. $ | (7) |
式中:CR为高温侧与低温侧两侧工质热容率,即较小者与较大者的比值:
| $ {C_{\rm{R}}} = \frac{{{C_{\min }}}}{{{C_{\max }}}} $ | (8) |
各个节点的热导可由NTU和两侧工质中最小热容率决定:
| $ U{A_i} = {\rm{NTU}}{{\dot C}_{\min }} $ | (9) |
总换热器热导UA为各个节点UA值的总和:
| $ UA = \sum\limits_{i = 1}^{N{\rm{hxrs}}} {U{A_i}} $ | (10) |
确定了透平和压缩机的效率,以及换热器的换热能力后,只需确定系统流量、运行的压力、压比、透平入口温度、排热温度以及再压缩份额后,S-CO2闭式再压缩布雷顿循环系统就完全确定下来了。
为了研究压力对系统稳态性能的影响,分别将压缩机出口压力、压比、换热器压降作为变量,改变系统的温度、换热器换热能力等参数,研究不同工况下各参数对系统最大热效率的影响。
需要说明的是,各个换热器、压缩机及透平之间的管路假设为绝热。在进行压降分析时,作为一项初步研究,在不涉及换热器具体形式的情况下,压降以绝对压力的百分比形式表示。
3 系统稳态特性分析 3.1 压缩机出口压力对热效率的影响系统的压力和温度对热效率有着明显的影响。循环中最高压力为压缩机出口压力。一般来说,增加压力可以提高循环效率。当热源温度为700 ℃,排热温度分别为32 ℃和55 ℃的情况下,设置不同的换热器单位化UA,并计算最佳压比,得到系统在当前状态下的最大热效率,效率随压缩机出口压力变化如图 3所示。
|
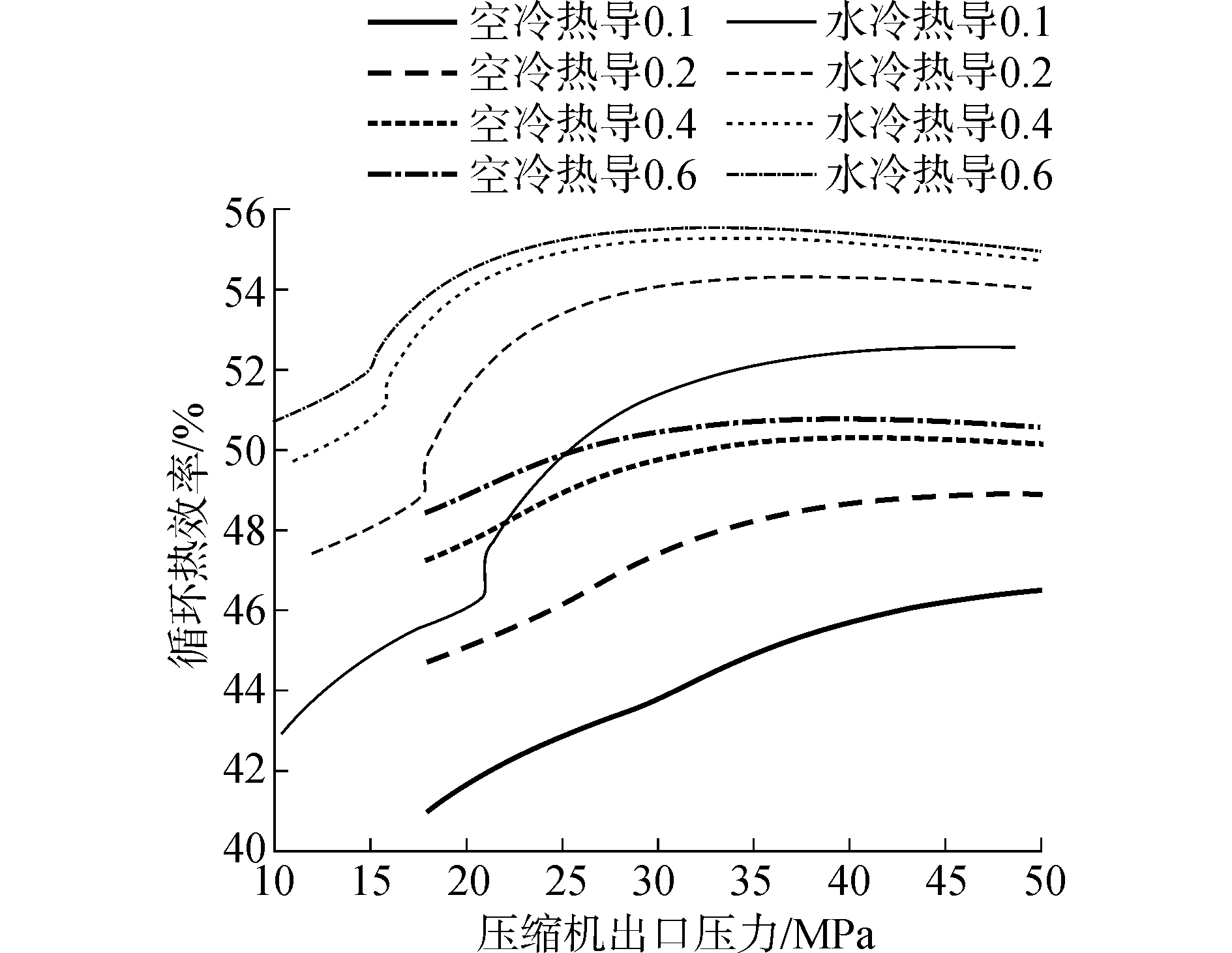
| 图3 系统压力对热效率的影响 Figure 3 The effect of system pressure on thermal efficiency |
如图 3所示,在压力较低的范围内,随着压缩机出口压力的增加,两种排热温度情况下系统的最高循环热效率都相应增加。但是,对于压缩机入口温度为32 ℃工况下,当UA大于0.3(kW/K)/kW时,压缩机出口压力大于28 MPa后,随着压缩机入口压力的增加,循环热效率几乎没有变化。这表明当换热器的换热能力达到一定阈值后,提高系统压力并调整压比并不会带来循环最高热效率的增加。对于压缩机入口温度为55 ℃工况下,系统表现出相同趋势,但换热器的阈值UA提高到了0.4(kW/K)/kW,压力高于30 MPa后提高压力不会带来循环效率的增加。
从图 3中也可以看出,在压力相同的情况下,增大换热器的UA能够有效地增加系统的热效率。此外,排热温度的高低对系统热效率影响十分显著。在系统压力以及换热器UA一定的情况下,32 ℃排热温度下的系统热效率比55 ℃排热温度下的系统热效率提高了约4%。
3.2 压比对热效率的影响压比是布雷顿循环系统最重要的参数之一。设定循环最低温度32 ℃,最高温度 (透平入口温度) 为700 ℃,不同压缩机出口压力下,循环最优热效率随压缩机压比的变化如图 4所示。
|
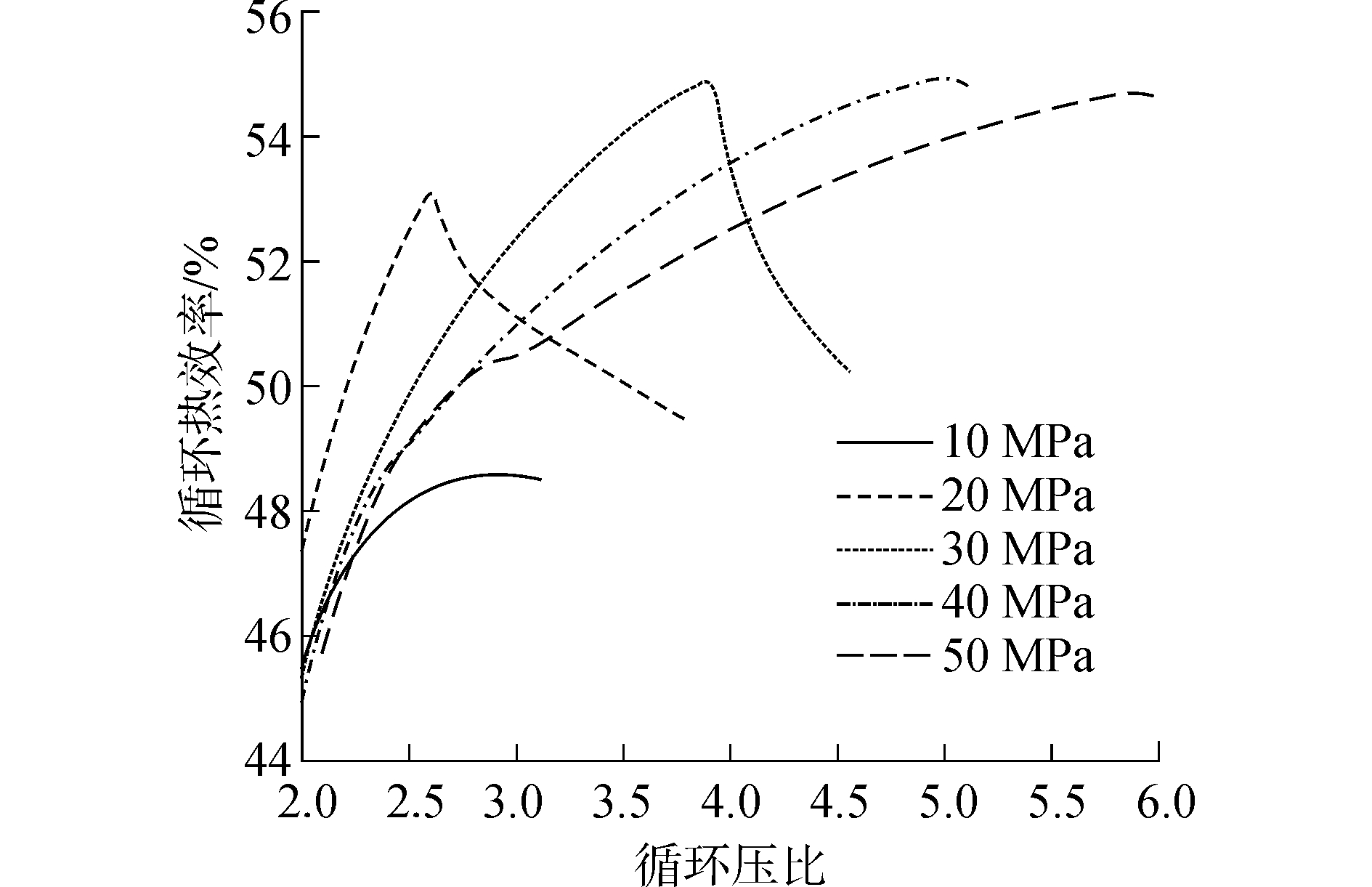
| 图4 压比对系统热效率的影响 Figure 4 The effect of pressure ratio on thermal efficiency |
随着压比的增加,循环热效率先增大,后减小。由此可见,对不同的压缩机出口压力,都存在相应的最佳循环压比。
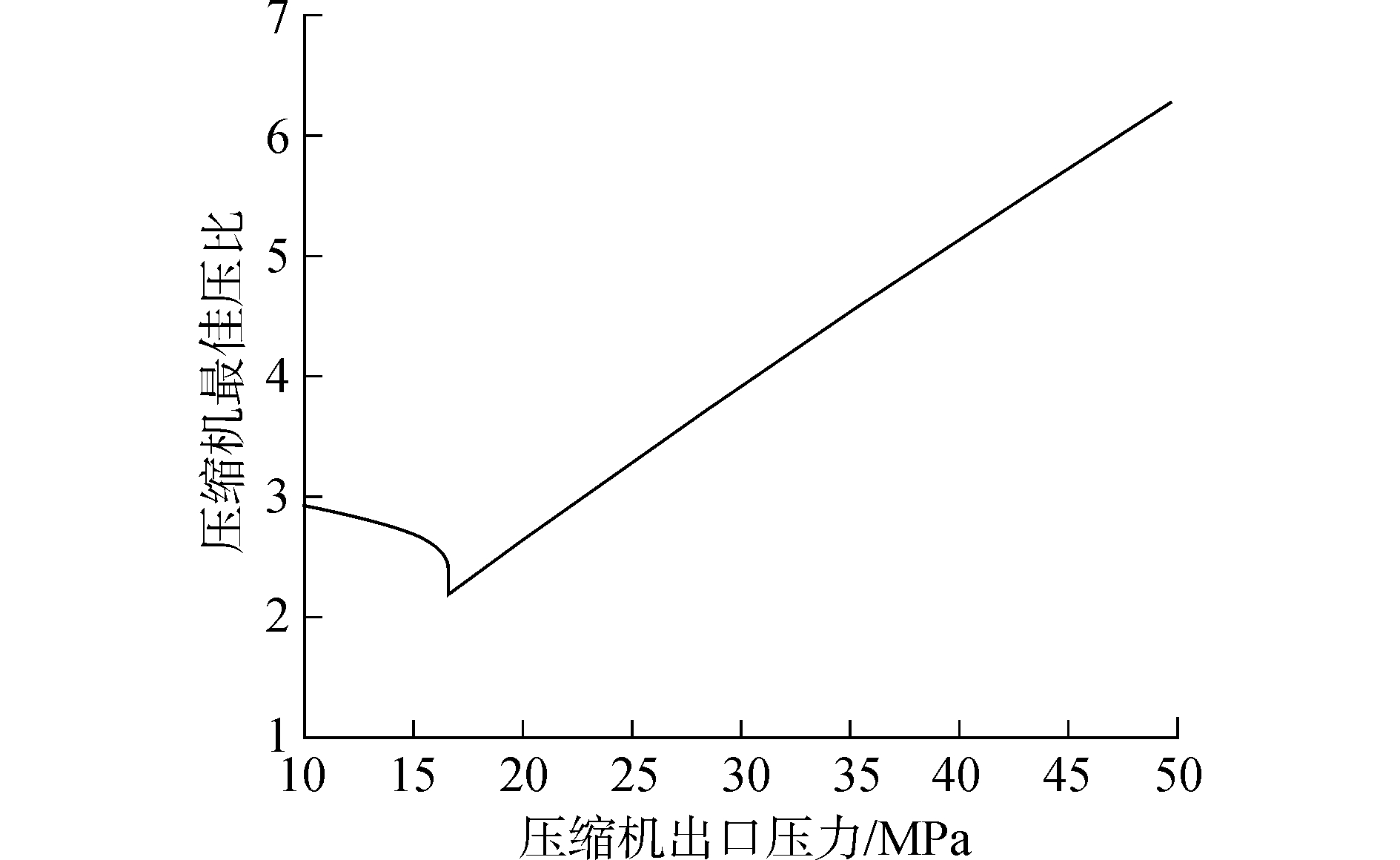
随着压缩机出口压力的增大,相应最佳压比如图 5所示。对不同的压缩机出口温度,效率随压比变化趋势较为类似。随着压比的增加,循环热效率先增大,后减小。由此可见,对不同的压缩机出口压力,都存在相应的最佳循环压比。随着压缩机出口压力的增大,相应最佳压比如图 5所示。在压缩机出口压力小于16.5 MPa时,随着出口压力的增加,最佳压比是逐渐减小的;当压缩机出口压力大于16.5 MPa后,最佳压比随着压缩机出口压力的增大而线性增加。这是因为循环中压缩机最佳入口压力与压缩机入口温度准临界压力Psc曲线相吻合,在16.5 MPa内,最优压缩机入口压力随着出口压力的增加而增加,大于16.5 MPa后基本为常数,因此最佳压比呈现先减小后增大的趋势。这是由于压缩机出口压力大于16.5 MPa时,压缩机入口压力最优值为当前温度下的准临界压力,而压缩机出口压力较小时,更大的压比可带来更多的收益。
|
| 图5 最佳循环压比随压缩机出口压力变化 Figure 5 Optimal pressure ratio under different system pressure |
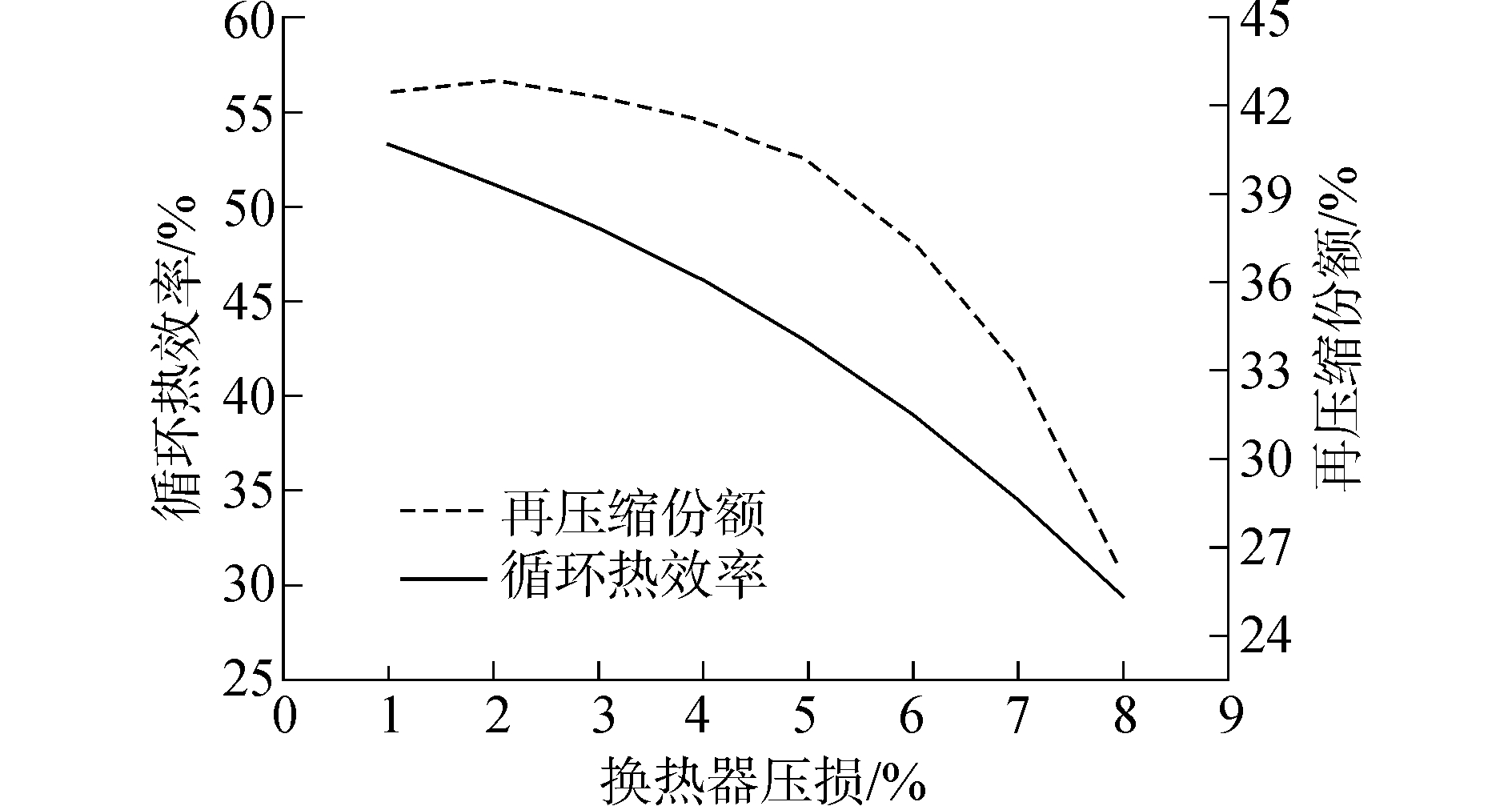
S-CO2布雷顿循环为了达到所需要的换热器UA,换热器需要较大的换热面积。目前在美国开展的实验研究中,采用印刷电路板式换热器。提高换热面积,通常会导致流道截面变小,工质在换热器中的压降增大,因此有必要研究换热器压降对循环效率的影响。取循环最低温度为32 ℃,循环最高温度700 ℃,换热器单位化UA为0.3(kW/K)/kW,循环最高压力为20 MPa,研究换热器压降对循环热效率的影响。S-CO2布雷顿循环中共有3个换热器,假设管道内没有压降,循环整体压降即为换热器压降之和。各个换热器压降由1%增加至8%,循环热效率及再压降份额随换热器压降变化如图 6所示。
|
| 图6 循环热效率及再压缩份额随换热器压降变化 Figure 6 Influence of pressure loss to thermal efficiency and recompression ratio |
如图 6所示,当换热器压降增大时,循环热效率急剧下降,当换热器压降为1%时,循环热效率高达53.3%,当换热器压降为8%时,循环热效率仅为29.4%。同时再压缩份额也变化剧烈。这是由于换热器压降变化,导致主压缩机及再压缩压缩机入口参数发生变化,进而影响主压缩机及再压缩压缩机出口工质热工状态。高温回热器与低温回热器重要保证回热平衡,因此再压缩份额发生较大变化;同时换热器压降也会导致透平运行工况的变化,降低透平输出功,在回热度及透平机械运行工况的两种因素的影响下,随着换热器压降的增加,循环热效率急剧下降。
4 结论S-CO2再压缩闭式布雷顿循环设计工况运行性能取决于多种因素,本文通过对循环系统及其主要组件进行建模,分析了压缩机出口压力、压缩机压比及换热器压降对循环热效率的影响,主要结论如下。
1) 当系统中换热器的换热能力达到一定的阈值后,提高压缩机出口压力不能持续提高循环效率。从系统热效率角度,循环中最优压缩机出口压力通常在28~35 MPa范围内,压缩机出口压力高于最优值后,提高压力并不会提高循环热效率。
2) 对不同压缩机出口压力,均存在最佳压比值。随着压缩机出口压力的增大,最佳压比值先减小,后增大。
3) 换热器压损的增大会大幅降低循环热效率,同时影响系统再压缩份额,随着换热器压损的增加,系统再压缩份额急剧减小。
| [1] | US DOE. A technology roadmap for generation IV nuclear energy systems, GIF-002-00[R].[S.l.]:US DOE Nuclear Energy Research Advisory Committee and the Generation IV International Forum, 2002. |
| [2] | DOSTAL V, DRISCOLL M J, HEJZLAR P. A supercritical carbon dioxide cycle for next generation nuclear reactors[R]. MIT-ANP-TR-100, 2004. |
| [3] | ISHIYAMA S, MUTO Y, KATO Y, et al. Study of steam, helium and supercritical CO 2 turbine power generations in prototype fusion power reactor[J]. Progress in nuclear energy, 2008, 50(2): 325–32. |
| [4] | DYREBY J, KLEIN S, NELLIS G, et al. Design considerations for supercritical carbon dioxide Brayton cycles with recompression[J]. Journal of engineering for gas turbines and power, 2014, 136(10): 101701. DOI:10.1115/1.4027936 |
| [5] | DOSTAL V, HEJZLAR P, DRISCOLL M J. The supercritical carbon dioxide power cycle:comparison to other advanced power cycles[J]. Nuclear technology, 2006, 154(3): 283–301. |
| [6] | FEHER E G. The supercritical thermodynamic power cycle[J]. Energy conversion, 1968, 8(2): 85–90. DOI:10.1016/0013-7480(68)90105-8 |
| [7] | ABRAM T, ION S. Generation-IV nuclear power:a review of the state of the science[J]. Energy policy, 2008, 36(12): 4323–30. DOI:10.1016/j.enpol.2008.09.059 |
| [8] | KATO Y, NITAWAKI T, MUTO Y. Medium temperature carbon dioxide gas turbine reactor[J]. Nuclear engineering and design, 2004, 230(1): 195–207. |
| [9] | MURTY K, CHARIT I. Structural materials for Gen-IV nuclear reactors:challenges and opportunities[J]. Journal of nuclear materials, 2008, 383(1): 189–95. |
| [10] | KEMM K. Development of the South African Pebble Bed modular reactor system[J]. The Uranium Institute, 2000, 24: . |
| [11] | PARMA E J, WRIGHT S A, VERNON M E, et al. Supercritical CO2 direct cycle gas fast reactor (SC-GFR) concept[C]//Proceedings of the Proceedings of the Supercritical CO2 Power Cycle Symposium. Boulder, USA, 2011. |
| [12] |
段承杰, 杨小勇, 王捷. 超临界二氧化碳布雷顿循环的参数优化[J].
原子能科学技术, 2011(12): 1489–1494.
DUAN Chengjie, YANG Xiaoyong, WANG Jie. Parameters optimization of supercritical carbon dioxide[J]. Atomic energy science and technology, 2011(12): 1489–1494. |
| [13] |
段承杰, 王捷, 杨小勇. 反应堆超临界CO2 Brayton循环特性[J].
原子能科学技术, 2010(11): 1341–1348.
DUAN Chengjie, YANG Xiaoyong, WANG Jie. Features of of supercritical carbon dioxide Brayton cycle coupled with reactor[J]. Atomic energy science and technology, 2010(11): 1341–1348. |
| [14] |
段承杰, 王捷, 杨小勇, 等. CO2与He动力循环比较[J].
核动力工程, 2010(6): 64–69.
DUAN Chengjie, WANG Jie, YANG Xiaoyong, et al. Comparison of of CO2power cycle to He cycle[J]. Nuclear power engineering, 2010(6): 64–69. |
| [15] |
黄彦平, 王俊峰. 超临界二氧化碳在核反应堆系统中的应用[J].
核动力工程, 2012(3): 21–27.
HUANG Yanping, WANG Junfeng. Applications of Supercritical carbon sioxide in nuclear reactor system[J]. Nuclear power engineering, 2012(3): 21–27. |
| [16] |
张国杰. 超临界二氧化碳闭式循环压缩特性试验系统设计[D]. 哈尔滨: 哈尔滨工程大学, 2013
ZHANG Guojie. The design of Supercritical carbon dioxide closed cycle compression system[D]. Harbin:Harbin Engineering University, 2013. |
| [17] |
梁墩煌, 张尧立, 郭奇勋, 等. 核反应堆系统中以超临界二氧化碳为工质的热力循环过程的建模与分析[J].
厦门大学学报:自然科学版, 2015, 54(5): 608–13.
LIANG Dunhuang, ZHANG Yaoli, Guo Qixun, et al. Modeling and analysis of nuclear reactor system using S-CO2 Brayton cycle[J]. Journal of Xiamen University:Natural Science, 2015, 54(5): 608–13. |
| [18] |
梁墩煌, 房超, 郭奇勋, 等. 压力对超临界二氧化碳闭式布雷顿循环系统热效率的影响[C]//第十四届全国反应堆热工流体学术会议暨中核核反应堆热工水力技术重点实验室2015年度学术年会, 北京, 中国, 2015.
LIANG Dunhuang, FANG Chao, GUO Qixun, et al. The effect of pressure on system thermal efficiency of supercritical carbon dioxide Brayton cycle[C]//RGLT2015, Beijing, 2015. |
| [19] |
张尧立, 梁墩煌, 房超, 等. 超临界二氧化碳布雷顿循环热工特性研究[C]//第十四届全国反应堆热工流体学术会议暨中核核反应堆热工水力技术重点实验室2015年度学术年会, 北京, 中国, 2015.
ZHANG Yaoli, LIANG Dunhuang, FANG Chao, et al. Thermal performance of S-CO2 Brayton cycle.[C]//RGLT2015. Beijing, China, 2015. |
| [20] | NIST Reference Fluid Thermodynamic and Transport Properties-REFPROP, Version 8.0.[EB/OL]. Lemmon E W, Huber M L, McLinden M O. NIST Standard Reference Database 23.2010.Http://webbook.nist.gov. |



