2. Kunming Shipbuilding Equipment Co., Ltd., Kunming 650217, China
在潜艇初步设计阶段,其操纵性水动力系数的准确获取对操纵性的预报起关键性的作用。由于艇后螺旋桨的抽吸作用改变了艇体尾部流场分布和边界层厚度,从而导致潜艇水动力性能产生变化。姚震球等[1]基于滑移网格对带桨与不带桨艇体阻力与艇尾流场进行了数值模拟,PAN Yucun等[2]对无桨SUBOFF潜艇操纵性水动力系数进行了数值模拟,Yingsan Wei等[3]对带桨潜艇尾部流体噪声进行了模拟与分析,A.G.L.Holloway等[4]对不同外型潜艇主艇体完成了回转试验的数值模拟,ZHANG Nan等[5]对近水面潜艇直航桨艇干扰完成了数值模拟,A.Saeidinezhad等[6]对无桨潜艇完成了拘束模型攻角试验,分析了周围流场的变化机理,CAO Liushuai等[7]运用不同湍流模型对SUBOFF无桨潜艇回转运动完成了数值模拟,S.Zaghi等[8]基于重叠网格对无桨潜艇操纵面完成了数值模拟,获取了舵角水动力系数,WU Xiaocui等[9]对SUBOFF无桨潜艇直航、回转等工况完成了数值模拟,结果与实验值符合较好。可见诸多研究者均针对潜艇不带桨情况获取操纵性水动力系数,从而进行潜艇操纵性能的预报,但是潜艇实际航行则是在带桨情况下完成的,故无桨理想化的模型水动力系数的获取将导致操纵性预报有所失真,从而影响潜艇的操纵性能。
故此,以某全附体潜艇缩比模型为研究对象,在循环水槽中利用VPMM完成带桨和不带桨潜艇模型斜航、纯升沉、纯俯仰、纯横荡、纯摇艏及舵角试验,获取该潜艇模型的操纵性线性水动力系数,并对比分析了变化的趋势及原因。
1 试验模型、设备及目的 1.1 模型及循环水槽以某全附体潜艇为研究对象,该潜艇模型包括主艇体、围壳、围壳舵、十字型尾舵翼,主尺度及主要参数见表 1。在舵翼前加装辅助翼以保证水流光顺的通过舵翼表面,有效提高舵效。围壳舵、十字型尾舵翼断面采用NACA0012翼型,模型外壳采用玻璃钢材料制作;按照缩比模型试验标准,完成桨模的绘制,并采用不锈钢加工制作,基本参数见表 2。
| 艇体物理属性 | 水动力模型 |
| 艇长L/m | 3.08 |
| 型宽B/m | 0.3 |
| 艇高D/m | 0.37 |
| 最大横截面积SM/m2 | 0.1 |
| 主艇体横截面积S/m2 | 0.073 |
| 排水质量/kg | 234.37 |
| 重心/m | 0.02, 0, 0 |
| 转动惯量Ix, Iy, Iz/(kg·m2) | 3.6,129.4,134.5 |
试验在哈尔滨工程大学水下机器人技术重点实验室循环水槽中完成,图 1为试验中安装完毕的带桨全附体潜艇模型。循环水槽稳流工作段尺寸:长7 m,宽1.7 m,水深1.5 m,即水槽横截面积SA=1.7×1.5 m2;最大流速2 m/s,常用工作流速为0.3~1.8 m/s;流场不均匀度小于2%;流速不稳定性小于2%;水平流向偏差小于±0.5°;湍流度0.7%~2.0%;自由液面驻波高度小于7 mm;从阻塞效应来看,要求模型横截面积与水槽工作段湿截面积SA之比小于3%,就本文而言,如果以主艇体横截面积算,S/SA=2.86%,满足试验要求。

|
| 图1 带桨潜艇模型安装示意图 Figure 1 Installation diagram of submarine model with propeller |
模型加工以后,为完成操舵试验,需在模型艏部和艉部加装水密舵机及驱动螺旋桨旋转的水密电机,然后进行模型配置和浮态调整。按照《操纵性水动力系数试验指导书》,为满足模型在水中处于正浮状态,同时减小非定常试验过程中内流对测力的影响,在模型空腔内配备一定量与水密度相当的物质,并计算得到水动力模型的质量、转动惯量、重心位置,具体数值见表 1;以浮心为坐标原点,测力天平安装要求测力中心点和浮心的纵向位置误差应该不大于1 mm,以减小试验测力误差。
流速选定:当水动力模型Re超过临界雷诺数Recr,模型的尺度效应可以忽略。物体绕流运动中,边界层内流动状态转捩及流动分离不仅取决于来流Re数,而且依赖于来流湍流度、壁面粗糙度以及外部主流压力梯度,因此试验段来流湍流度ε对边界层、阻力和升力都有很大影响,应尽可能降低ε值,然而水槽的固有属性使得水流湍流度ε一般为1.2%~2.0%[10],其中湍流度ε对平板Recr影响的试验结果表明:当ε=1.2%~2.0%时,Recr≈(3.5~5.0)×105。根据《操纵性水动力系数试验指导书》意见,试验缩比模型长度为3.08 m, 理论上在上述工作流速段试验中Re数均超过Recr,但尽可能使Re较大,减小尺度效应,同时避免流速过高,水流不稳定,自由表面兴波较大,水中气泡含量过高等对试验的影响,选取试验流速为1.2 m/s。对应Re约为3.6×106,满足试验要求。
1.3 试验目的为研究螺旋桨及其运行对潜艇操纵性水动力系数的影响,对无桨与带桨全附体潜艇模型进行拘束模型试验,比较两种模型下获取的水动力系数的变化情况,为后期潜艇潜器操纵性预报仿真和CFD数值模拟奠定一定的基础和提供参考依据。
2 基本理论与拘束模型试验 2.1 潜艇操纵运动线性方程潜艇在水下的运动可分为水平面运动和垂直面运动,在螺旋桨推动作用下,通过对潜艇的操纵面控制,以达到潜艇水下空间运动。采用根据国际拖曳水池会议(ITTC) 和造船与轮机工程学会(SNAME) 术语公报的体系推荐的潜艇坐标系如图 2所示,惯性坐标系为E-ξηζ,运动坐标系为o-xyz。

|
| 图2 坐标系示意图 Figure 2 The diagram of coordinate |
不考虑横滚和纵荡,在线性假定下,可得潜艇在水平面和垂直面的四自由度操纵运动方程[11]:
水平面运动:
| $ \left\{ \begin{array}{l} \left({{I_z}-{N_{\dot r}}} \right)\dot r+\left({m{x_G}-{N_{\dot v}}} \right)\dot v+\left({mU-{N_r}r} \right)r - {N_v}v={N_{{\delta _r}}}{\delta _r}\\ \left({m - {Y_{\dot v}}} \right)\dot v+\left({mU - {Y_r}} \right)r+\left({m{x_G} - {Y_{\dot r}}} \right)\dot r - {Y_v}v={Y_{{\delta _r}}}{\delta _r} \end{array} \right. $ | (1) |
垂直面运动:
| $ \left\{ \begin{array}{l} \left({m-{Z_{\dot w}}\dot w} \right)\dot w-\left({m{x_G}+{Z_{\dot q}}} \right)\dot q-\left({mU+{Z_q}} \right)q - {Z_w}w={Z_{\delta s}}{\delta _s}+{Z_{{\delta _{fp}}}}{\delta _{fp}}\\ \left({{I_y} - {M_{\dot q}}} \right)\dot q+\left({mU{x_G} - {M_q}} \right)q - \left({m{x_G}+{M_{\dot w}}} \right)\dot w - {M_w}w={M_{{\delta _s}}}{\delta _s}+{M_{{\delta _{fp}}}}{\delta _{fp}} \end{array} \right. $ | (2) |
式中:m为潜艇模型的质量,xG为重心的x坐标,U为潜艇的航行速度,Iy、Iz为绕y、z轴的质量惯性矩,Nṙ、Yṙ、Z
由上述操纵运动分析,试验内容即可分为垂直面和水平面试验,垂直面试验包括冲角、纯升沉、纯俯仰、升降舵、围壳舵试验,为避免测力天平支杆的影响,模型以围壳指向水槽槽底的方式安装;水平面试验包括漂角、纯横荡、纯摇艏、方向舵试验[12]。
2.2 拘束模型定常试验 2.2.1 斜航试验斜航试验为冲角、漂角试验。通过调节平面运动机构垂直面内的角度和改变模型的安转方式,以达到冲角α和漂角β的试验测试,α、β∈[-10°,10°],Δα、Δβ=1°, 其六分力由水密天平测得,考虑到垂向力Z和力矩M随垂向速度w的变化曲线的非线性效应,故采用非线性拟合,取线性部分无因次化得到线性速度系数Z′w、M′w、Y′v、N′v,其中无因次化参数选取L=3.08 m,水密度ρ=1×103 kg/m3,流速v=1.2 m/s。带桨模型试验时螺旋桨进速系数J=0.01。结果汇总于表 3中。以攻角为例,试验结果如图 3。
| 水动力系数 | 带桨×10-2 | 无桨×10-2 | 带桨相对无桨 增量百分比/% |
| N′v | -1.603 | -1.676 | 4.37 |
| Y′v | -6.190 | -6.132 | -0.94 |
| Y′r | 1.191 | 1.128 | 5.56 |
| N′r | -0.719 | -0.701 | -2.61 |
| Z′w | -2.770 | -2.360 | -17.33 |
| M′w | 0.496 | 0.779 | -36.33 |
| Z′q | -0.940 | -0.908 | -3.49 |
| M′q | -0.553 | -0.521 | -6.09 |
| Z′ẇ | -1.282 | -1.414 | 9.32 |
| M′ẇ | -0.054 | -0.052 | -3.35 |
| Z′ | -0.009 | -0.009 | -1.61 |
| M′ | -0.088 | -0.085 | -2.44 |
| Y′ | -1.646 | -1.660 | 4.17 |
| N′ | -0.063 | -0.057 | -11.68 |
| Y′ṙ | -0.149 | -0.159 | 6.30 |
| N′ṙ | -0.168 | -0.163 | -2.88 |
| Z′δs | -0.650 | -0.523 | -24.25 |
| M′δs | -0.305 | -0.234 | -30.51 |
| Y′δr | -0.758 | -0.653 | -16.10 |
| N′δr | 0.363 | 0.312 | 16.45 |
| Z′δfp | -0.582 | -0.611 | 4.72 |
| M′δfp | 0.132 | 0.120 | 9.86 |

|
| 图3 垂向力Z、俯仰力矩M随垂向速度w的变化 Figure 3 Vertical force Z, pitch moment M changes with vertical speed w |
舵角试验是在冲角α和漂角β为零的情况下,通过水密舵机系列改变方向舵、升降舵、围壳舵舵角,δfp∈[-25°, 25°],δr、δs∈[-30°, 30°], Δδfp、Δδr、Δδs=5°。测得作用在艇体上相应的水动力,并在失速角范围内经线性拟合,无因次化得到舵角系数Y′δr、N′δr、Z′δs、M′δs、Z′δfp、M′δfp,结果汇总于表 3。以升降舵为例, 测试结果如图 4所示。

|
| 图4 垂向力Z、俯仰力矩M随升降舵舵角δs变化 Figure 4 Vertical force Z、pitching moment M changes with elevator δs |
简谐运动试验分为:纯升沉、纯俯仰、纯横荡、纯摇艏试验。即驱动模型在来流中做纯升沉或纯俯仰运动,或将模型滚转90°安装做纯横荡或纯摇艏运动。纯俯仰和纯摇艏运动时要求模型迎流方向与中心处轨迹曲线相切,来流速度U,中心处横荡速度v=Utan θ≈Uθ0sin ωt,θ0为给定模型运动初始角位移,当θ0较小时,一阶近似为简谐运动。此时后杆对前杆的滞后角ε满足:
| $ \tan \left({\frac{\varepsilon }{2}} \right)=\frac{{{l_0}\omega }}{U} $ | (3) |
通过运动分解可把测得的拘束力(力矩) 写为方程(4) 所示形式,用下标in表示惯性力(同相分量),用下标out表示阻尼力(正交分量),其余为常量:
| $ \left\{ \begin{array}{l} {F_z}\left(t \right)={Z_{{\rm{in}}}}{\rm{sin}}\left({\omega t} \right)+{Z_{{\rm{out}}}}{\rm{cos}}\left({\omega t} \right)-{Z_0}\\ {M_y}t={M_{{\rm{in}}}}{\rm{sin}}\left({\omega t} \right)+{M_{{\rm{out}}}}{\rm{cos}}\left({\omega t} \right)-{M_0} \end{array} \right. $ | (4) |
纯升沉试验目的是测定无因次加速度系数Z′ẇ、M′ẇ,纯横荡试验目的是测定无因次加速度系数Y′
垂直面纯升沉运动线性方程:
| $ \left\{ \begin{array}{l} {Z_{\dot w}}\dot w+{Z_w}w+{Z_0}+Fz\left(t \right)=m\dot w\\ {M_{\dot w}}\dot w+{M_w}w+{M_0}+My\left(t \right)=-m{x_G}\dot w \end{array} \right. $ | (5) |
模型纯升沉运动参数:
| $ \left\{ \begin{array}{l} {\zeta _1}={\zeta _2}=a{\rm{sin}}\omega \left(t \right)\\ w=\dot \zeta=a\omega {\rm{cos}}\left({\omega t} \right)\\ \dot w=-a{\omega ^2}{\rm{sin}}\left({\omega t} \right)\\ \theta=\dot \theta=0 \end{array} \right. $ | (6) |
测力天平与数据采集系统将拘束力测出并将其分解,从而求得纯升沉水动力系数:
| $ \left\{ \begin{array}{l} {Z_{\dot w}}=\frac{{{Z_{{\rm{in}}}}}}{{a{\omega ^2}}}+m, {Z_w}=\frac{{-{Z_{{\rm{out}}}}}}{{a\omega }}\\ {M_{\dot w}}=\frac{{{M_{{\rm{in}}}}}}{{a{\omega ^2}}}-m{x_G}, {M_w}=\frac{{-{M_{{\rm{out}}}}}}{{a\omega }} \end{array} \right. $ | (7) |
同理按上述方式试验,可以得到纯横荡水动力系数:
| $ \left\{ \begin{array}{l} {Y_{\dot v}}=\frac{{{Y_{{\rm{in}}}}}}{{a{\omega ^2}}}+m, {Y_v}=\frac{{-{Y_{{\rm{out}}}}}}{{a\omega }}\\ {N_{\dot v}}=\frac{{{N_{{\rm{in}}}}}}{{a{\omega ^2}}}+m{x_G}, {N_v}=\frac{{-{N_{{\rm{out}}}}}}{{a\omega }} \end{array} \right. $ | (8) |
试验得到对应阻尼力、惯性力随速度、加速度的变化趋势,经过线性拟合并结合表 1中水动力模型参数代入式(7)、(8) 可得到相应水动力系数,无因次化处理得到的水动力系数汇总于表 3中。以纯升沉为例,测试结果如图 5、6所示。

|
| 图5 纯升沉惯性力Zin-aω2试验结果 Figure 5 Test results of pure heave Zin-aω2 |

|
| 图6 纯升沉惯性力矩Min-aω2试验结果 Figure 6 Test results of pure heave Min-aω2 |
纯俯仰试验目的是测定无因次速度系数Z′q、M′q和无因次角速度系数Z′
根据垂直面纯俯仰运动线性方程为
| $ \left\{ \begin{array}{l} {Z_{\dot q}}\dot q+{Z_q}q+{Z_0}+{F_z}\left(t \right)=-mUq-m{z_G}{q^2}-m{x_G}\dot q\\ {M_{\dot q}}\dot q+{M_q}q+{M_0}- mgh\theta+My\left(t \right)={I_y}\dot q+m{x_G}\left({qU} \right) \end{array} \right. $ | (9) |
由于俯仰角速度的平方为二阶小量,忽略-mzGq2项。模型纯俯仰运动参数为
| $ \left\{ \begin{array}{l} \theta={\theta _0}{\rm{sin}}(\omega t)\\ q=\dot \theta={\theta _0}\omega {\rm{cos}}(\omega t)\\ \dot q=-{\theta _0}{\omega ^2}{\rm{sin}}(\omega t)\\ {z_a}=w=0 \end{array} \right. $ | (10) |
测力天平与数据采集系统将拘束力测出并将其分解,从而求得纯俯仰水动力系数:
| $ \left\{ \begin{array}{l} {Z_{\dot q}}=\frac{{{Z_{{\rm{in}}}}}}{{{\theta _0}{\omega ^2}}}-m{x_G}, {Z_q}=\frac{{-{Z_{{\rm{out}}}}}}{{{\theta _0}\omega }}-mU\\ {M_{\dot q}}=\frac{{{M_{{\rm{in}}}} - mgh{\theta _0}}}{{{\theta _0}{\omega ^2}}}+{I_y}, {M_q}=\frac{{ - {M_{{\rm{out}}}}}}{{{\theta _0}\omega }}+mU{x_G} \end{array} \right. $ | (11) |
同理按上述方式试验,可以得到纯摇艏水动力系数:
| $ \left\{ \begin{array}{l} {Y_{\dot r}}=\frac{{{Y_{{\rm{in}}}}}}{{{\psi _0}{\omega ^2}}}+m{x_G}, {Y_r}=\frac{{-{Y_{{\rm{out}}}}}}{{{\psi _0}\omega }}+mU\\ {N_{\dot r}}=\frac{{{N_{{\rm{in}}}}}}{{{\psi _0}{\omega ^2}}}+{I_z}, {N_r}=\frac{{-{N_{{\rm{out}}}}}}{{{\psi _0}\omega }}+mU{x_G} \end{array} \right. $ | (12) |
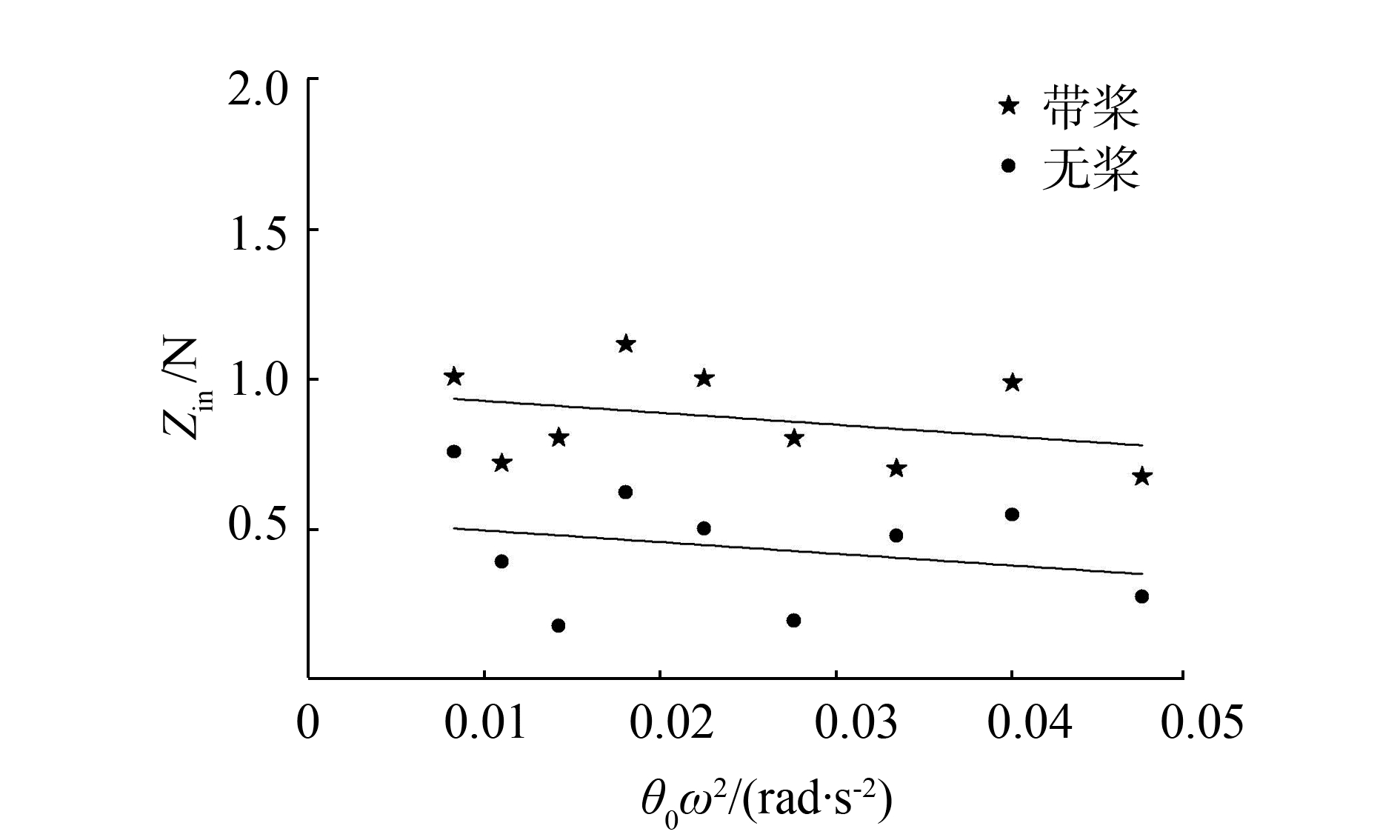
试验得到对应阻尼力、惯性力随角速度、角加速度的变化趋势,经过线性拟合并结合表 1中水动力模型参数代入式(11)、(12) 可得到相应水动力系数,无因次化处理得到的水动力系数汇总于表 3中。以纯俯仰为例,测试结果如图 7~10所示。

|
| 图7 纯俯仰阻尼力Zout-θ0ω试验结果 Figure 7 Test results of pure pitch Zout-θ0ω |
|
| 图8 纯俯仰惯性阻尼力Zin-θω2试验结果 Figure 8 Test results of pure pitch Zin-θω2 |

|
| 图9 纯俯仰阻尼力矩Mout-θ0ω试验结果 Figure 9 Test results of pure pitch Mout-θ0ω |

|
| 图10 纯俯仰惯性力矩Min-θω2试验结果 Figure 10 Test results of pure pitch Min-θω2 |
按照上述试验,所有结果汇总于表 3,一共测试得到的22个线性类水动力系数中,对比无桨与带桨值,不难发现有14个水动力系数呈减小趋势,8个呈增加趋势。
3.1 斜航与无桨相比,带桨时垂直面速度系数均减小,其中Z′w减小17.33%,M′w减小36.33%;水平面速度系数N′v增加4.37%,Y′v减小0.94%,可见螺旋桨运行产生的尾流场对垂直面水动力系数的影响大于水平面。其主要原因是:螺旋桨的抽吸和旋转加剧了艇体周围流场的流动与不对称性,漂角试验时,艇体关于中纵剖面对称;而冲角试验时,艇体关于XOY平面不对称,螺旋桨运转的扰动导致潜艇围壳后方流场不均匀性和不对称性增强,且强度大于漂角试验,故导制垂直面水动力系数变化大于水平面。
其次由于循环水槽本身尺寸的限制,导致斜航试验时,螺旋桨尾流与循环水槽壁面和自由液面的干扰势必给试验测力带来误差,且冲角试验的影响可能大于漂角试验。因为本试验是在主艇体截面积满足S/SA=2.86% < 3%条件下进行的,而如果考虑围壳等其他附体的影响,可有艇体最大横截面积SM/SA=3.9%>3%,可见围壳的存在产生了一定的阻塞效应,且阻塞效应主要发生在平行于围壳的平面内。在冲角试验时,围壳指向槽底,螺旋桨尾流场将与槽底或自由面耦合干扰加剧艇体周围流场的变化,而漂角试验时,模型绕轴x旋转90°安装,测力方向恰好正交于围壳,故影响减小。
3.2 舵角试验与无桨相比,带桨时升降舵舵角系数均减小,其中M′δs减小30.51%、Z′δs减小24.51%;方向舵舵角系数Y′δr减小为16.10%,而N′δr呈增加趋势,增加了16.45%;围壳舵舵角系数均增加,量值保持在10%以内。这是由于尾舵离螺旋桨较近,螺旋桨的抽吸和旋转作用导致尾舵周围流场不均匀性加剧,从而影响了舵效,但围壳舵较为靠前,尾流场的扰动基本只发生在艇体尾部周围,主要受到是螺旋桨的抽吸影响,故变化甚小。
3.3 简谐运动试验与无桨相比,带桨时所测得的12个水动力系数中,有8个减小,仅有4个增加。其中变化较大的是惯性类水动力系数N′
通过在循环水槽中,利用VPMM运动机构对无桨与带桨潜艇模型完成拘束模型试验,获取该潜艇模型的四自由度线性水动力系数,得到以下结论:
1) 潜艇尾部螺旋桨的存在及运转,主要导致垂直面速度系数Z′w、M′w减小,比例分别为17.33%、36.33%;尾升降舵舵舵角系数也呈减小趋势,其中M′δs减小30.51%、Z′δs减小24.51%;尾方向舵舵角系数Y′δr减小为16.10%,而N′δr增加了16.45%;
2) 其余水动力系数变化基本保持在10%以内;
3) 由于水槽尺寸的限制,试验过程中螺旋桨尾流场与水槽壁面和自由面的干扰,未免给水动力系数的测量带来影响,有待进一步改善;
4) 此研究只是定性分析了水动力系数的变化原因,故也需CFD数值模拟相互对比论证并进行流场变化物理机理的详细分析与讨论,进一步研究尾部螺旋桨的运行对操纵性水动力系数的影响。
| [1] |
姚震球, 高慧, 杨春蕾. 基于滑移网格的带螺旋桨艇体尾流场数值分析方法[J].
江苏科技大学学报:自然科学版, 2008, 22(2): 15–20.
YAO Zhenqiu, GAO Hui, YANG Chunlei. Numerical simulation of interaction between submarine and propeller based on approach of sliding mesh[J]. Journal of Jiangsu university of science and technology:natural science edition, 2008, 22(2): 15–20. |
| [2] | PAN Yucun, ZHANG Huaixin, ZHOU Qidou. Numerical Prediction of submarine hydrodynamic coefficients using CFD simulation[J]. Journal of hydrodynamics, series B, 2012, 24(6): 840–847. DOI:10.1016/S1001-6058(11)60311-9 |
| [3] | WEI Yingsan, WANG Yongsheng. Unsteady hydrodynamics of blade forces and acoustic responses of a model scaled submarine excited by propeller's thrust and side-forces[J]. Journal of sound and vibration, 2013, 332(8): 2038–2056. DOI:10.1016/j.jsv.2012.12.001 |
| [4] | ZHANG J T, MAXWELL J A, GERBER A G, et al. Simulation of the flow over axisymmetric submarine hulls in steady turning[J]. Ocean engineering, 2013, 57: 180–196. DOI:10.1016/j.oceaneng.2012.09.016 |
| [5] | ZHANG Nan, ZHANG Shengli. Numerical simulation of hull/propeller interaction of submarine in submergence and near surface conditions[J]. Journal of hydrodynamics, ser. b, 2014, 26(1): 50–56. DOI:10.1016/S1001-6058(14)60006-8 |
| [6] | SAEIDINEZHAD A, DEHGHAN A A, MANSHADI M D. Experimental investigation of hydrodynamic characteristics of a submersible vehicle model with a non-axisymmetric nose in pitch maneuver[J]. Ocean engineering, 2015, 100: 26–34. DOI:10.1016/j.oceaneng.2015.03.010 |
| [7] | CAO Liushuai, ZHU Jun, WAN Wenbin. Numerical Investigation of submarine hydrodynamics and flow field in steady turn[J]. China ocean engineering, 2016, 30(1): 57–68. DOI:10.1007/s13344-015-0076-1 |
| [8] | ZAGHI S, DI MASCIO A, BROGLIA R, et al. Application of dynamic overlapping grids to the simulation of the flow around a fully-appended submarine[J]. Mathematics and computers in simulation, 2015, 116: 75–88. DOI:10.1016/j.matcom.2014.11.003 |
| [9] | WU Xiaocui, WANG Yiwei, HUANG Chenguang, et al. An effective CFD approach for marine-vehicle maneuvering simulation based on the hybrid reference frames method[J]. Ocean engineering, 2015, 109: 83–92. DOI:10.1016/j.oceaneng.2015.08.057 |
| [10] |
高霓.微小型水下潜器近自由液面操纵性预报[D].哈尔滨:哈尔滨工程大学, 2013:68-78.
GAO Ni. Maneuverability prediction of mini underwater vehicle near free surface[D]. Harbin:Harbin Engineering University, 2013:68-78. http://cdmd.cnki.com.cn/Article/CDMD-10217-1014133957.htm |
| [11] |
丁正良, 胡瑞芝, 孙百超, 等.水平型循环水槽的水动力性能[Z].哈尔滨:哈尔滨船舶工程学院, 1985:5-10.
DING Zhengliang, HU Ruizhi, SUN Baichao, et al. Hydrodynamic performance of horizontal circulating water channel[Z]. Harbin:Harbin Shipbuilding Engineering University, 1985:5-10. |
| [12] |
王庆云, 庞永杰, 李伟坡, 等. 系列舵翼潜艇水动力系数数值计算及试验研究[J].
舰船科学技术, 2015, 37(11): 21–26.
WANG Qingyun, PANG Yongjie, LI Weipo, et al. Numerical calculation and experimental study of hydrodynamic coefficients of submarine of a series of rudder and wing[J]. Ship science and technology, 2015, 37(11): 21–26. |



