当货船航行于港口、运河、近海等位置时,货船就处于限制航道状态,船舶在浅水中有着与在深水中不同的水动力性能,研究浅水中船舶的阻力及流场特性的规律,无疑对船舶的性能预报、浅水修正有着重大的意义。
船舶在限制航道中航行的各项性能研究主要有试验方法、势流理论以及粘流 (computational fluid dynamics,CFD) 方法。1985年E.Müller利用有限水深兴波源势方法,通过在船舶纵向剖面上布置源汇,提出了薄船、线性自由表面条件下船舶水压场的计算公式[1];I.Sahin等采用有限水深格林函数方法,系统开展了潜艇、水面舰艇和气垫船水压场的理论建模和数值计算工作[2-3];郭圣汉在模型试验中采用了随车假底试验技术,该方法能够在水深吃水比h/T小于4时,对Fn<0.2的工况进行较好的预报模拟,在h/T>4时可以使用到Fn=0.35的范围[4];李一兵通过对实船与船模试验资料的分析计算,对航行于不同内河航道中船舶的航行阻力进行了分析探讨,得出对于不同航行河流应该有不同的阻力估算方法,并提出了相应的计算公式[5];缪涛等利用面元法计算了有限水深船舶在水底引起的压力分布[6];近年来,人们开始采用CFD方法进行浅水阻力的研究,与试验值进行对比发现,CFD方法能够得到较为准确的阻力计算结果[7-10]。
目前浅水航行船舶的阻力及流场特性大都采用不同水深的模型水池试验和势流理论的方法,模型试验结果需进行实尺度换算,这个过程需要消耗大量资源,并且需要进行试验次数较多,而且在换算过程中很难保证换算结果的准确性;势流理论方法忽略了粘性作用,结果准确性较差,且得不到具体的流场信息;CFD计算大多仅就浅水阻力性能进行了分析,并没有对流场信息等作进一步讨论。本文将通过CFD方法计算得到船模在深水和浅水中的阻力及流场特性,分析船舶阻力、抽吸力以及伴流场信息随水深的变换规律,探讨产生浅水效应的内在原因。
1 计算模型的建立流体流动要受物理守恒定律的支配,基本的守恒定律包括:质量守恒定律、动量守恒定律和能量守恒定律。由于水为不可压缩流体,热交换很小以至于可以忽略不计,可只对质量守恒方程和动量守恒方程进行求解。详细公式可参考文献[11]。计算中采用k-ω SST湍流模型,该模型有效集成了k-ω和k-ω模型的优点,能够较好地模拟存在流动分离和强逆压梯度的复杂流动问题。
在计算过程中监测船体阻力系数,计算初始阶段动量相、湍流动能和耗散率都使用一阶格式,观测阻力系数的变化,当阻力系数在比较小的范围内变化时改为二阶格式,当阻力系数稳定以后认定计算收敛。
1.1 计算对象本文研究对象为KCS集装箱船,如图 1所示,模型缩尺比为31.6,其船模具体参数如表 1所示。

|
| 图1 KCS船模的几何形状 Figure 1 The geometry of KCS |
| 参数 | 数值 | 参数 | 数值 |
| 垂线间长Lpp/m | 7.28 | 方型系数CB | 0.65 |
| 最大船宽Bw/m | 1.02 | 雷诺数Re | 1.4×107 |
| 吃水T/m | 0.34 | 傅汝德数Fr | 0.26 |
| 湿表面积Sw/m2 | 9.44 | 进速Vs/(m·s-1) | 2.196 |
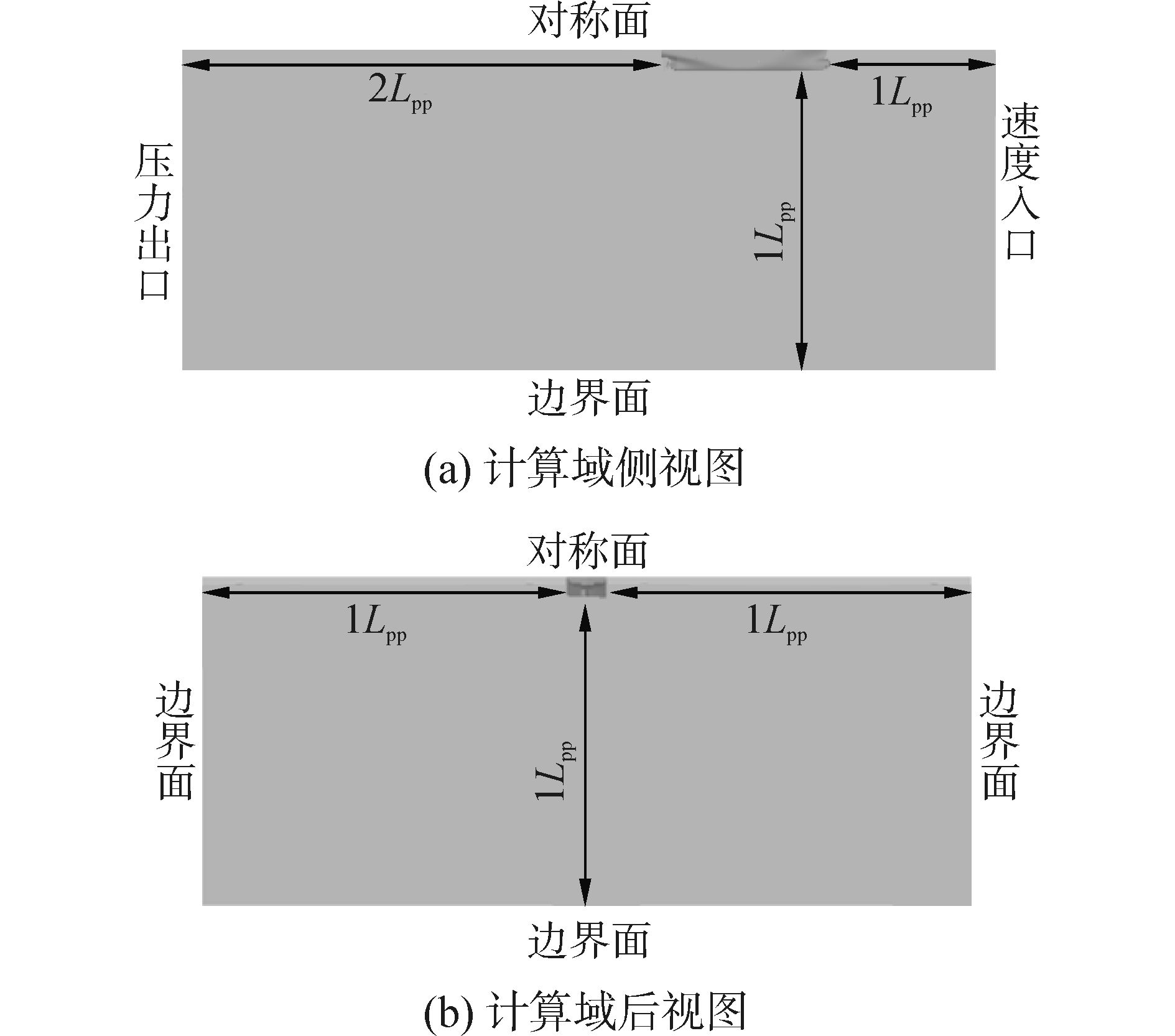
流场计算区域为:入口距船艏1Lpp,出口距船艉2Lpp,侧面和底面均距船体表面1Lpp。如图 2所示。边界条件的入口采用速度入口,速度设为2.196 m/s,侧面和底面采用与入口相同速度的移动壁面,船体表面使用固定壁面,顶面使用对称面,出口采用压力出口,设定出口压力为10 kPa。压力速度耦合迭代采用SIMPLEC方法。
|
| 图2 计算域及边界条件 Figure 2 The computational domain and boundary conditions |
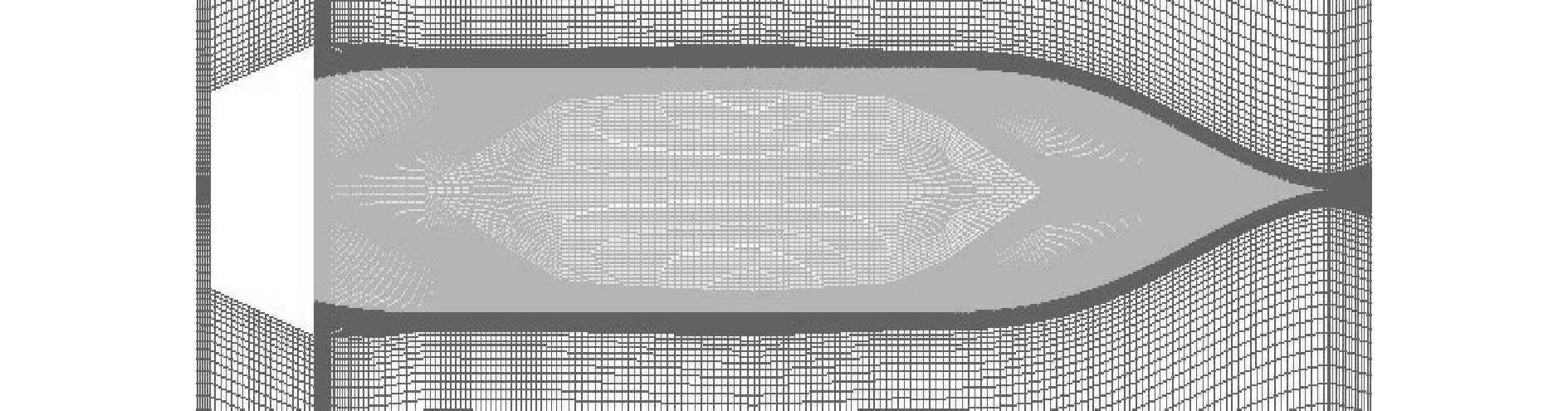
由于KCS船艉部型线较为复杂,艉部难于生成高质量的结构化网格,因此本次计算采用混合网格[12]方法,船艉小部分流域划分非结构化网格,以节省网格划分工作量,而其他部分采用六面体结构化网格,结构化网格和非结构化网格之间通过interface连接,流场通过interface插值进行信息传递。
流体的边界层区域可以分为层流底层、湍流边界层和阻流区,第一层网格的厚度对于数值模拟的结果尤为重要,因此有了无因次的第一层网格厚度y+。一般来说,模型尺度y+建议控制在60左右是合适的,对应第一层网格厚度为0.8~1 mm。结构化网格区域第一层层网格厚度可以直接用参数定义,而船艉非结构化网格则需要通过添加多层棱柱网格完成。
|
| 图3 船体周围加密网格 Figure 3 The refined mesh around ship |
对于船艉非结构网格部分,如图 4所示分别尝试使用了三种网格划分方法:方案1为常规方法,图 4(a),仅对船体表面网格进行了加密处理;方案2考虑到第一层网格厚度对于物体流体边界层的模拟比较重要,图 4(b),对船体表面附近添加棱柱网格,可以加强对船艉部分边界层细节的模拟,以利于对船艉流场计算的准确性;方案3考虑到本文计算的一个考察重点为桨盘面速度场的模拟,因此在桨盘面和桨盘面前方的位置添加密度体,图 4(c),通过使用密度体可以得到桨盘面流场更加细致伴流场信息。

|
| 图4 三种非结构网格划分方法 Figure 4 Three unstructured grid methods |
无因次化的阻力系数Ct,其公式为
| ${C_t} = \frac{{{R_T}}}{{\frac{1}{2}\rho U_0^2{S_W}}}$ | (1) |
式中:RT代表船模受到的阻力;U0代表船模航速,2.196 m/s;ρ为水的密度,998.2 kg/m3;SW为船模在正浮状态下的湿表面积,9.438 m2。
三种船艉网格划分方法的阻力系数对比如表 2所示。对比三种网格划分方法可以发现,三种方法的计算准确度依次提高,这是由于棱柱网格使船体表面网格加密,更好地模拟了物面的边界层流动,在桨盘面处添加的密度体与船体有一定的距离,密度体的添加只是使密度体位置的流场分布更加精细,对船体附近的边界层阻力等没有太大影响,这就导致了添加密度体对于阻力计算结果影响不大。
| 方法 | 网格数量 (×106) | Ct(×103) | 误差/% |
| 方案1 | 4.4 | 3.721 | 7.82 |
| 方案2 | 4.5 | 3.662 | 3.15 |
| 方案3 | 5.4 | 3.603 | 1.49 |
| 试验值 | 3.55 |
伴流的大小通常用伴流分数ω来表示,轴向伴流分数ωx的表达式为
| ${\omega _x} = 1 - \frac{{{V_x}}}{{{V_A}}}$ | (2) |
式中:ωx为桨盘面的轴向伴流分数,Vx为桨盘面的轴向速度,VA为来流速度。
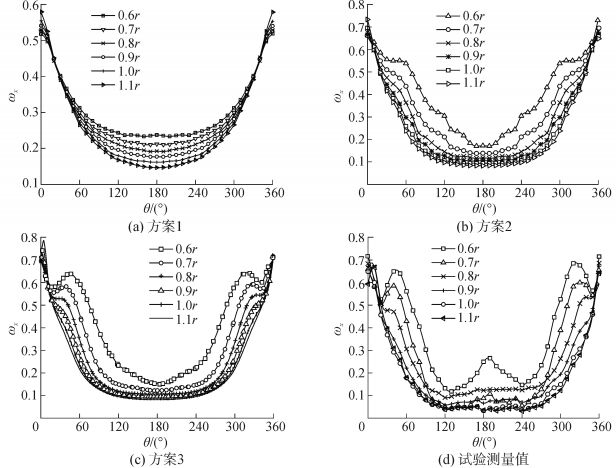
图 5为桨盘面不同半径处 (r为螺旋桨半径),三种网格方案计算结果与试验结果。将图中三种网格方案计算结果与试验测量值对比可以发现,方案1网格的计算结果最差,没有模拟出桨盘面上半部分中纵剖面附近伴流分数的一个小波峰。添加边界层后使计算结果变好,中纵剖面附近伴流分数出现变化,但不是很明显,且在内半径处,轴向伴流分数计算值与试验值偏差很大。在桨盘面处添加密度体之后,出现明显的小波峰,除了在内半径180°左右区域内的轴向伴流分数较小之外,盘面处其他区域的计算值与实验值吻合很好,为得到详细准确的船艉伴流场信息,本文考虑使用方案3划分船艉部网格。
|
| 图5 不同网格方案计算结果与试验值 Figure 5 The comparison of different grid methods between calculation and experiment |
根据国际船模试验池会议规定,试航时不产生浅水效应的水深h必须满足:
| $h > 3\sqrt {B/T} $ | (3) |
| $h > 2.75 \times {V^2}/g$ | (4) |
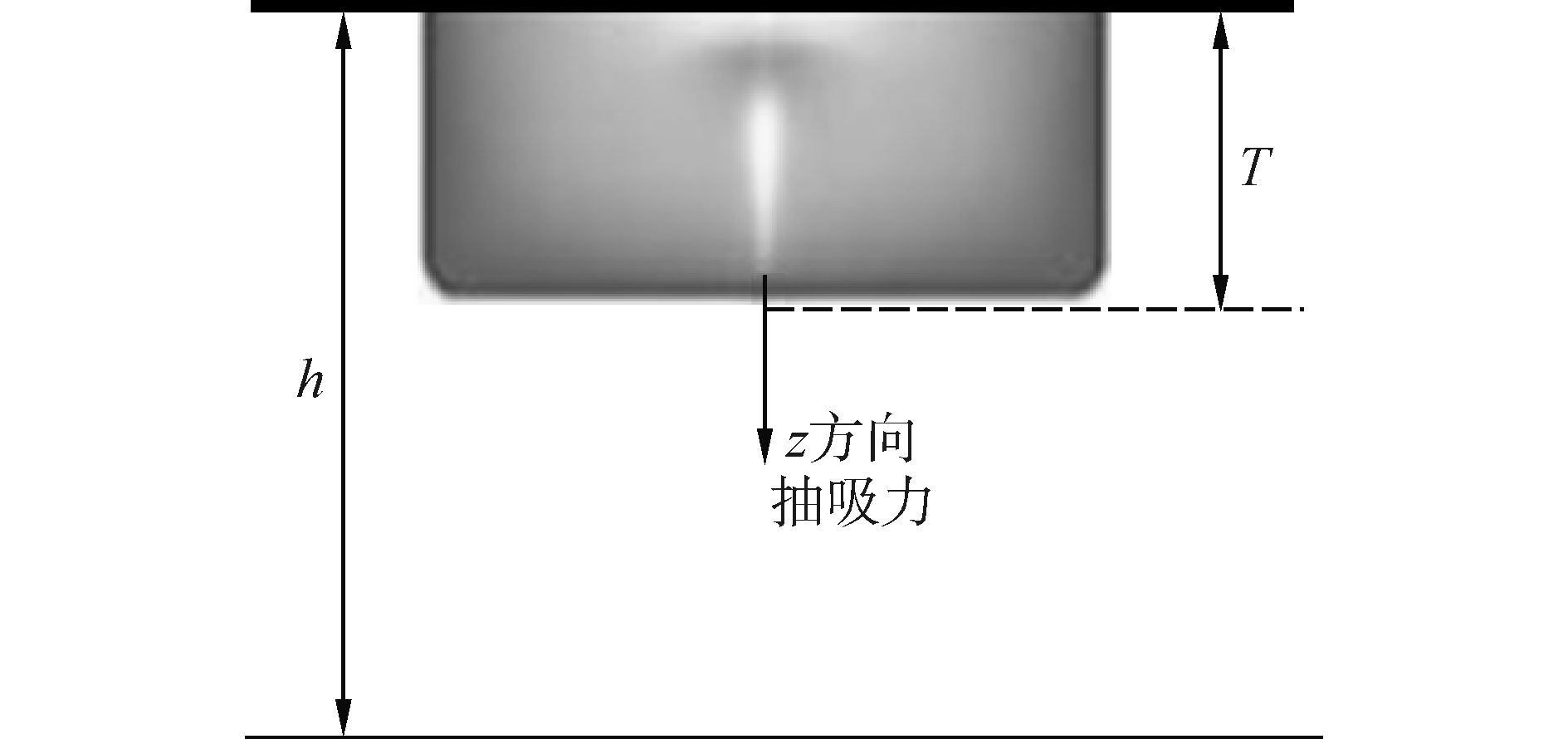
根据表 1给出的船体参数,按照式 (3) 计算得到的水深需要大于5.178 m,根据式 (4) 计算得到水深需要大于1.326 m,综合两个公式可以暂时认定水池试验水深大于5.178 m可以消除浅水的影响,h=5.178 m的情况相当于h/T=15.15。如图 6所示将计算域中的水深分别设定为h/T=21.3、h/T=15.15、h/T=10、h/T=4、h/T=3以及h/T=2六种工况,使用Fluent软件计算六种工况下的KCS船的阻力及流场特性,并进行对比分析。
|
| 图6 船体吃水与水深示意图 Figure 6 The general view of draft and depth |
船舶航行在浅水中会产生浅水效应,在浅水中航行时,船舶阻力受到的影响最大,因此首先对比六种工况的船体阻力系数。
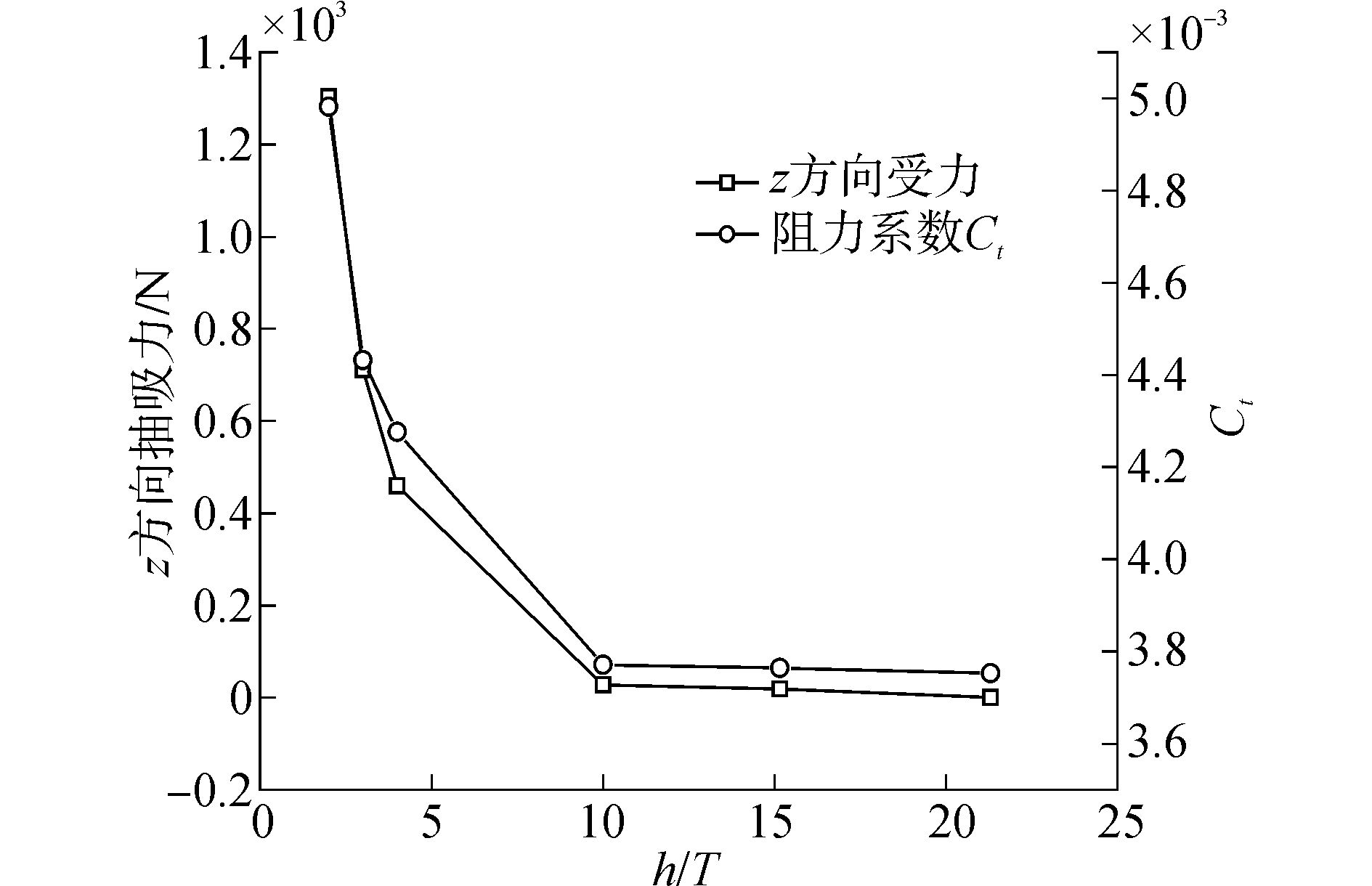
阻力系数随水深的变化曲线如图 7所示。观察图中的数据信息,当航行水深大于10倍吃水时,船舶阻力受水深变化很小,可以认为此时不发生浅水效应,根据式 (3) 国际船模水池的规定的估算公式,是足够保证避免浅水效应的。当水深小于10倍吃水时,阻力系数随吃水的减小单调增加,当水深减少到4倍吃水时,船舶阻力增幅变大,此时,船舶阻力随水深变化明显,浅水效应显著,当水深继续减小到2倍吃水时,阻力系数陡增,相比于3倍吃水时,增幅达12.4%,而相比于深水航行时 (大于10倍吃水),增加幅度达到32.7%。可见当水深较浅时,浅水效应对船舶阻力性能有较大影响。
|
| 图7 不同水深阻力系数及z向抽吸力 Figure 7 The resistance coefficient and suction force in different depth |
船舶浅水航行时,船底与航道底部间隙变窄,船底水流速度增加,由伯努利方程可知船底部的流体流速增大、压强减小,船底受到的z方向 (垂直于水线面朝下) 抽吸力增大,如图 6所示。从图 7中可以发现,z向抽吸力变化趋势与船舶阻力随水深的变化趋势基本一致:当航行水深大于10倍吃水时,z向抽吸力基本不变;当航行水深小于10倍吃水时,z向抽吸力随水深变化明显。由此可见,船舶航行于浅水航道时,船舶阻力增加与z向抽吸力的增加息息相关。
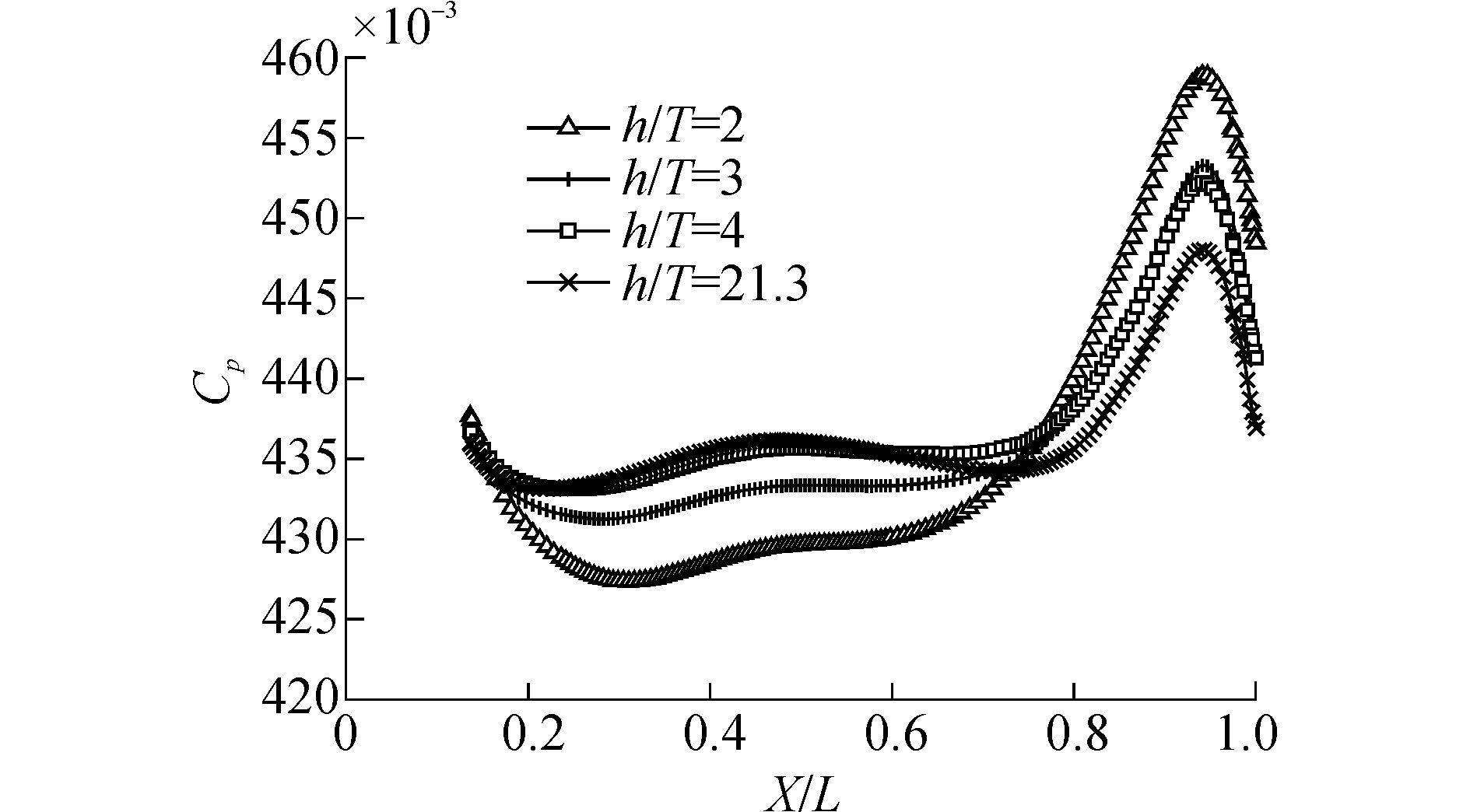
图 8给出了不同水深时,船底中纵剖线压力系数沿船长方向的变化,其中X/L=1.0为船艏位置。从图中可以看出,随着水深的减小,船艏部压力系数逐渐增大,艉部压力系数逐渐减小,艏艉的压力差逐渐增大,说明随着水深的减小,船艉尾倾现象更加明显。
|
| 图8 船底中纵剖线压力沿船长方向的变化 Figure 8 The change of pressure in the longitudinal lines along the length direction |
桨盘面伴流场信息是考察船舶裸船体水动力性能中一个重要指标,对于单桨船来说,螺旋桨工作于船的后方,其运转效果很大程度上会受到船体的影响,现在的螺旋桨设计工作多数是基于标称伴流场的螺旋桨设计,因此考察水深对桨盘面伴流场的影响就尤为重要。测量表明,与轴向伴流速度相比,周向和径向伴流是二阶小量,在螺旋桨设计中,通常不予考虑。因此本文只考虑水深变化对轴向伴流的影响。通过式 (2) 可以得到标称伴流分数[13],然后以此为基础估算船舶的实效伴流分数,实效伴流为计及了船桨之间相互干扰的船艉桨盘面处伴流,基于实效伴流分数进行螺旋桨的适伴流设计工作,适伴流设计桨的整体性能要优于图谱设计桨,达到耗能较少,减振降噪的目的。
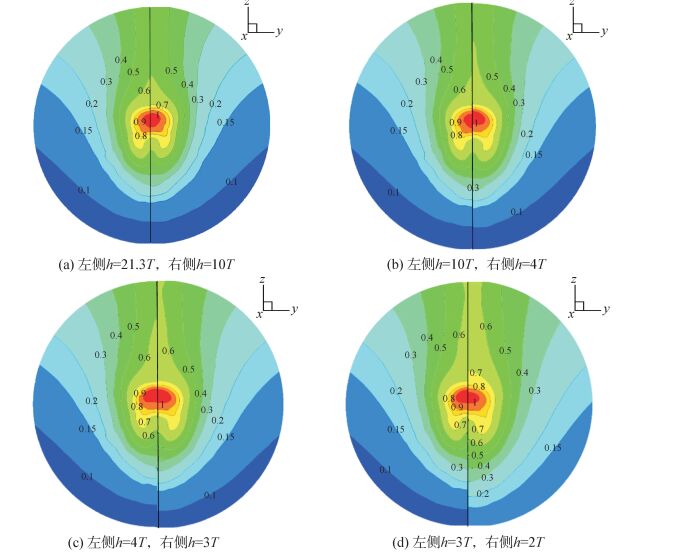
KCS为单桨船,桨盘面关于船中左右对称,为方便对比,截取如图 9所示的速度云图进行分析。对比四个水深的轴向速度可以看到在速度分布的整体趋势基本一致,在桨盘面中心形成一个封闭的高伴流区,等值线向船体方向延伸,越靠近船艉,轴向伴流越大。从图 9(a)可以观察到,水深为21.3T和10T时,桨盘面轴向伴流速度云图分布基本没有差别,说明此时没有发生浅水效应,这与之前的分析一致。从图 9(b)可以看出,当船舶从深水航行到浅水航道,伴流等值线向外扩散,在桨盘面上方ωx=0.6的等值线有一个偏上的尖锐区域,说明水深减小以后在桨盘面处的伴流分数增大,桨盘面中心与船体之间变化明显。对比图 9(c)航行水深为4T和3T时,随着水深的减小,伴流等值线继续向外扩散,曲线上方开口逐渐增大,而在上部ωx=0.6的曲线由闭合状态改变为在桨盘面边界靠近船体部分出现开口,整个盘面的平均伴流分数继续增大。继续观察图 9(d)可以看到当航行水深为2T时,桨盘面不存在ωx=0.1曲线,表明在h=2T时桨盘面的轴线伴流分数比前面三种工况有明显的扩大,与阻力系数曲线相对照可以发现伴流分数与阻力系数曲线是可以相互印证的,桨盘面上半部分具有明显特征的ωx=0.6曲线与前文分析的趋势相同,上部分的开口有所扩大。从四个水深状况的轴向伴流分数云图对比中可以分析看出,随着水深的减少,轴向伴流分数有增大的趋势,桨盘面中心与船体之间部分,伴流分数受水深影响较大,四种工况的桨盘面平均轴向伴流分数如表 3所示。
|
| 图9 不同水深下的标称伴流分数分布 Figure 9 Distribution of nominal wake fraction in different depth |
| 工况 | h/T | 平均速度/ (m·s-1) | 平均伴流分数 |
| 1 | 21.3 | 1.590 1 | 0.276 |
| 2 | 15.15 | 1.582 8 | 0.279 |
| 3 | 10 | 1.583 6 | 0.279 |
| 4 | 4 | 1.569 5 | 0.285 |
| 5 | 3 | 1.535 6 | 0.301 |
| 6 | 2 | 1.422 7 | 0.352 |
从表 3中可以看到桨盘面平均伴流分数的变化规律与前面分析过的阻力系数分布规律、桨盘面伴流场分布规律相吻合。随着水深h的减小,伴流分数逐渐增大,轴向平均伴流分数增幅最高达27.2%。受水深减小的影响,船艉流速增加,艉倾现象明显,船艉伴流相应增大。
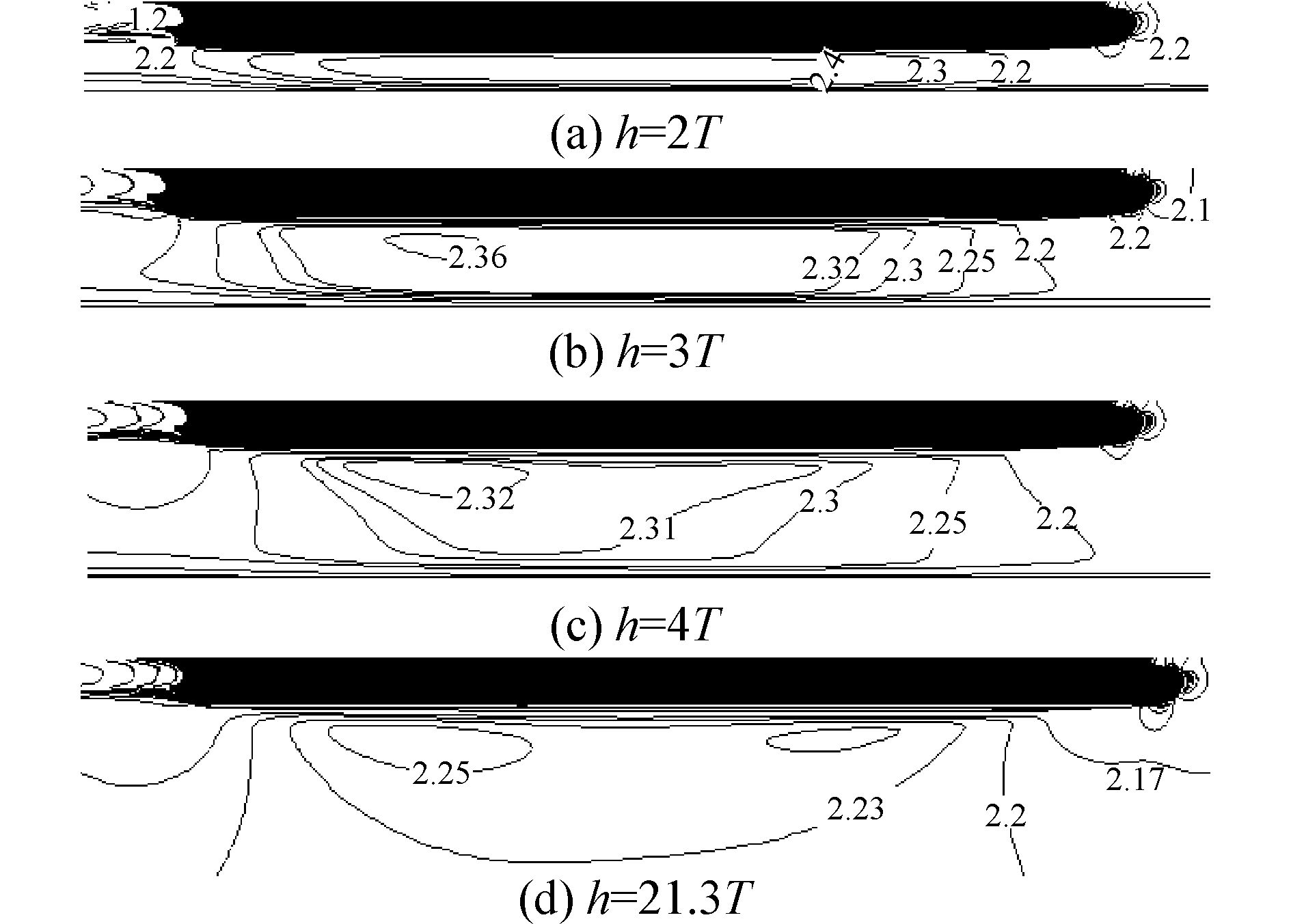
2.4 船周围流场变化分析随着水深的减小,船底速度逐渐增大,其增加的速度称为回流速度。图 10表示KCS船在浅水中航行时船底流速的变化情况。随着水深的减小,船体底部与底面边界之间形成狭窄的水道,导致船底的流速增大;另外由于水的粘性,在船底与底面边界形成边界层,使过水断面更小,导致船底的流速增大,压力降低,从而使船体下沉,吃水增加,进而导致阻力增大。
|
| 图10 不同水深处船中纵剖面速度分布 Figure 10 The distribution of velocity in different depth |
另外,从图中可以看出,船底与底面边界层厚度自船艏向船艉是逐渐增加的,导致相同水深时船艉部过水断面较船艏更小,速度更大,压力下降更甚,故船艉下沉较船艏大,产生艉倾现象。同时,随着水深的减小,水流与船体的相对速度增大,压力下降亦大,故艏艉压力差将增大,艉倾现象更加明显。且船艉与池底的间隙小,易于发生涡流,因此涡流阻力也要增大。
图 11给出了不同吃水时,船体周围的流线分布。图中可以看出,h=2T时,船侧流线分布与深水时相比更密,由于浅水航道限制,船体排开的水主要从船体两侧通过;对于船底部流线分布,浅水航行时要比深水航行时更加不均匀,分析认为浅水航行时,船底与底面边界形成的狭窄水道以及底面边界的阻碍作用造成了流线分布的不均匀。

|
| 图11 不同水深处船体周围流线分布 Figure 11 The distribution of streamline in different depth |
本文对KCS船模在不同水深下的船舶阻力及流场特性进行模拟,分析了水深变化对船舶阻力性能及流场特性的影响。分别计算了水深为h/T=21.3、h/T=15.15、h/T=10、h/T=4、h/T=3以及h/T=2六种工况,对比分析了不同工况船体的阻力系数、抽吸力、桨盘面伴流场以及边界层速度场的特点,主要得出以下结论:
1) 当水深h小于10T时,浅水效应明显,船舶各项性能随水深的减小变化较为明显,当水深h大于10T时,船舶各项性能受水深影响很小,不存在浅水效应;
2) 当水深较浅时,池底会对船体附近流场产生较大的干扰,随着水深的减小阻力系数不断增大,当水深超过10倍吃水时,阻力随水深变化不大;
3) 当水深较浅时,随着水深的减小,抽吸力不断增加,并且增加的幅度越来越大,当水深超过10倍吃水时,z方向抽吸力基本稳定,随着水深的减小,船艏艉压力差增大,艉倾现象更加明显;
4) 水深减小的过程中,桨盘面各方向伴流分数呈增大趋势;
5) 船在浅水中航行时,随着吃水的减小,船底流速增加,其摩擦阻力及涡流阻力增加。
本文计算过程中,没有考虑自由叶面及船舶六自由度运动的影响,在今后计算中需进一步探讨随着水深的变化,船周围兴波及艉倾对船舶运动性能的影响。
| [1] | MÜLLER E. Analysis of the potential flow field and of ship resistance in water of finite depth[J]. I S P, 1985(32): 266–277. |
| [2] | SAHIN I, CRANE J W, WATSON K P. Application of a singularity panel method for hydrodynamics of underwater vehicles[J]. Ocean engineering, 1997, 24(6): 501–512. DOI:10.1016/S0029-8018(96)00026-1 |
| [3] | SAHIN I, HYMAN M C. Simulation of three-dimensional finite-depth wave phenomenon for moving pressure distributions[J]. Ocean engineering, 2001, 28(12): 1621–1630. DOI:10.1016/S0029-8018(01)00025-7 |
| [4] |
郭圣汉, 刘希武. 船舶的浅水效应及随车假底浅水试验技术[J].
桥梁建设, 1990(2): 53–56.
GUO Shenghan, LIU Xiwu. Shallow water effect of ship and towing testing method in shallow water[J]. Bridge construction, 1990(2): 53–56. |
| [5] |
李一兵. 内河船舶航行阻力计算方法讨论[J].
水道港口, 2002(1): 7–11.
LI Yibing. Calculation method of riverboat navigation resistance[J]. Journal of waterway and harbor, 2002(1): 7–11. |
| [6] |
缪涛, 张志宏, 顾建农, 等. 面元法求解有限水深船舶兴波及水底压力变化[J].
计算力学学报, 2012, 29(3): 464–469.
MIAO Tao, ZHANG Zhihong, GU Jiangnong, et al. The calculation of shio wave and bottom pressure variation in finite depth by panel method[J]. Chiness journal of computational mechanics, 2012, 29(3): 464–469. DOI:10.7511/jslx20123029 |
| [7] | WANG Jinbao, YU Hai, ZHANG Yuefeng, et al. CFD-based method of determining form factor k for different ship types and different drafts[J]. Journal of marine science and application, 2016, 15(3): 236–242. DOI:10.1007/s11804-016-1372-8 |
| [8] | WU Chengsheng, ZHOU Decai, GAO Lei, et al. CFD computation of ship motions and added resistance for a high speed trimaran in regular head waves[J]. International journal of naval architecture and ocean engineering, 2011, 3: 105–110. DOI:10.2478/IJNAOE-2013-0051 |
| [9] | SENTHIL P M N, BINOD C. Numerical estimation of shallow water resistance of a river-sea ship using CFD[J]. International journal of computer applications, 2013, 71(5): 33–40. DOI:10.5120/12357-8670 |
| [10] | PHILIPP M, OULDEL M. Numerical prediction of resistance and squat for a containership in shallow water[C]//17th Numerical Towing Tank Symposium, 2014:352-359. |
| [11] |
王福军.
计算流体动力学分析-CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004: 124-126.
WANG Fujun. The analysis of computation fluid dynamics-the based theory and application of CFD[M]. Beijing: Tsing-hua University Press, 2004: 124-126. |
| [12] | HE Miao, WANG Chao, CHANG Xin, et al. Numerical analysis of propeller wake flowfield using hybrid mesh technology[J]. Journal of marine science and application, 2012, 11(3): 295–300. DOI:10.1007/s11804-012-1135-0 |
| [13] |
王超, 何苗, 郭春雨, 等. 一体化节能推进装置定常水动力性能的数值模拟分析[J].
哈尔滨工程大学学报, 2013, 34(6): 674–679.
WANG Chao, HE Miao, GUO Chunyu, et al. Steady hydrodynamic performance simulation of integrative energy-saving propulsion system[J]. Journal of Harbin Engineering University, 2013, 34(6): 674–679. |



