目前,海上航行的大多数船舶仅装备螺旋桨主推进器和舵装置,用以推进和操纵船舶。当需要依靠舵装置产生的转船力矩和螺旋桨的纵向推力,同时控制船舶水平面和航向角3个自由度的运动时,船舶控制系统便属于欠驱动系统。由于欠驱动船舶的非线性和非完整特性,要实现欠驱动船舶的精确路径跟踪控制,对传统的控制策略带来了挑战。
近年来,对船舶航迹跟踪控制问题的研究,已有很多的研究成果。Michiel使用了输出反馈的方法跟踪航迹,最后仿真在一个1:70的实际模型上实现[1]。Ghommam利用backstepping的方法,达到全局渐进稳定,实现欠驱动船舶的轨迹跟踪[2]。付明玉设计的是半全局一致指数稳定控制器[3]。文献[1-3]的不足在于都是在理想条件下,即没有干扰或者只是恒定干扰。Yang也是使用了backstepping的方法,在有时变干扰的情况下实现轨迹跟踪[4]。王昊提出了一种基于神经网络自适应动态面控制的协同路径跟踪算法,在存在未知干扰的条件下实现路径跟踪[5]。Annamalai则利用模型预测控制,在线适应环境,针对船舶受到突然的干扰进行控制,效果良好[6]。将滑模控制应用于船舶航迹跟踪的研究也有相当的研究成果,有些学者用滑模方法和迭代滑模解决参数不确定和干扰不确定的问题[7-9]。为得到更好的控制效果,邢道奇利用坐标变化,将系统转化为链式系统,设计指数控制律,在非线性模型基础上设计了滑模控制器,并在仿真过程中取得了良好的控制效果[10]。Hebertt针对气垫船设计了一种结合微分单调性与高阶滑模控制的二阶航迹控制器,在获得平滑控制效果的同时具有更强的鲁棒性[11]。随着滑模控制理论的发展,单纯的使用滑模已经不能满足人们对控制性能的要求。廖煜雷采用反演自适应和滑模相结合的方法,使船舶航迹跟踪系统指数渐近稳定[12]。朱齐丹把滑模控制和自适应鲁棒控制相结合来解决干扰不确定和参数不确定的船舶航迹跟踪问题[13]。
在上述研究中,船舶航迹跟踪控制方法的处理过程通常较为复杂,工程实现困难。为了简化计算的复杂程度,Hang采用计算复杂度较低的线性递归滑模方法获取控制量的递推算法[14]。一些学者采用非线性迭代滑模法分别对水面船舶、UUV、AUV进行了航向、航迹跟踪控制,取得了良好的控制效果,该方法一方面避免对模型线性化处理,同时也避免了估计模型中不确定量及外界的不确定干扰[15-17],然而该控制方法中参数是固定不变的,无法确保控制器参数在不同环境下取得最优值。Liu使用了自适应分层滑模控制对轨迹进行跟踪,但是鲁棒性不强[18]。
本文在文献[15-17]基础上,引入神经网络对控制参数进行自适应调节,并借鉴文献[19]的强化学习思想,提出一种基于强化学习的自适应迭代滑模控制器,应用于欠驱动船舶路径跟踪控制中。考虑抖振对实际工程的影响,在控制器设计中定义了一种抖振测量函数,用该函数输出的强化信号可评价控制参数优化效果,并对神经网络结构参数进行在线调整。最后,以5446TEU集装箱船为目标,设计基于强化学习的自适应迭代滑模控制器,在风浪等干扰环境下进行船舶路径跟踪控制仿真,并将仿真结果与迭代滑模控制器的仿真结果进行对比分析。
1 船舶路径跟踪控制问题描述目前关于船舶路径跟踪控制的研究,大都采用的是fossen模型,例如文献[1-4]、[8-11]和[13-14]。采用fossen模型所得到的控制量是船舶的横向推力、纵向推力和转船力矩,对于全驱动船舶,需要把这些控制力和力矩进行优化计算后分配到各个推进器去实现控制;而对于常规的单桨单舵欠驱动船舶,则需要将这些控制力和力矩经过进一步转换,映射为舵角和柴油机油门量,所以采用fossen模型得到的控制量与船舶控制系统的实际工程应用存在一定差距。本文采用分离型模型(mathematical model group,MMG),可直接表示出舵角和柴油机油门等控制量,与实际工程应用一致。根据文献[20],三自由度船舶运动MMG模型可表示为
| $ \left\{ \begin{array}{l} \dot u = \frac{{{X_H} + {X_P} + {X_R} + {X_{{\rm{wind}}}} + {X_{{\rm{wave}}}} + \left( {m + {m_y}} \right)vr}}{{m + {m_x}}}\\ \dot v = \frac{{{Y_H} + {Y_P} + {Y_R} + {Y_{{\rm{wind}}}} + {Y_{{\rm{wave}}}} - \left( {m + {m_x}} \right)ur}}{{m + {m_y}}}\\ \dot r = \frac{{{N_H} + {N_P} + {N_R} + {N_{{\rm{wind}}}} + {N_{{\rm{wave}}}}}}{{{I_{zz}} + {J_{zz}}}}\\ \dot x = u\cos \psi - v\sin \psi + {u_c}\cos {\psi _c}\\ \dot y = v\cos \psi - u\sin \psi + {u_c}\sin {\psi _c}\\ \dot \psi = r \end{array} \right. $ | (1) |
式中:X和Y表示坐标轴方向受力,N表示力矩,H表示裸船体,P表示螺旋桨,R表示舵机,u纵向速度,v是横向速度,r是艏揺角速度,m是船舶质量,mx是在附体坐标系下水的附加质量在X方向上的分量,my是Y方向上的分量,Jxx是附体坐标系下x轴的附加转动惯量,Jzz是附体坐标系下z轴的附加转动惯量,x、y是船舶重心在固定坐标系的位置,uc是水流的流速,ψc是水流的方向,ψ是航向角。在式(1) 中,Xwind、Ywind、Nwind表示风产生的力和力矩,由平均风和扰动风叠加而成;而Xwave、Ywave、Nwave表示浪产生的力和力矩,这里只考虑规则波浪对船舶运动的影响[20],具体如下
| $ \left\{ \begin{array}{l} {X_{{\rm{wave}}}} = 2aB\frac{{\sin b\sin c}}{c}s\left( t \right)\\ {Y_{{\rm{wave}}}} = 2aL\frac{{\sin b\sin c}}{c}s\left( t \right)\\ {N_{{\rm{wave}}}} = ak\left( {{B^2}\sin b\frac{{c\sin c - \sin c}}{{{c^2}}} - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\left. {{L^2}\sin c\frac{{b\cos b - \sin b}}{{{b^2}}}} \right)\zeta \left( t \right) \end{array} \right. $ | (2) |
式中:L为船长,k为波数,h为波高,χ为波向角,ωe为遭遇频率,ρ为海水密度,g重力加速度,d为吃水,b为船宽。其中a=ρg(1-e-kd)/k2,b=(kL/2)·cos χ,s(t)=(kh/2) sin(ωet),c=(kB/2)·sin χ,ζ(t)=(h/2) cos(ωet)。
需要注意的是,在实际的船舶操作过程中,由于受到船舶自身特性限制,常规船舶的舵角通常小于35°,最大转艏角速度通常为0.01~0.02 rad/s,满舵旋回需要5~10 min。
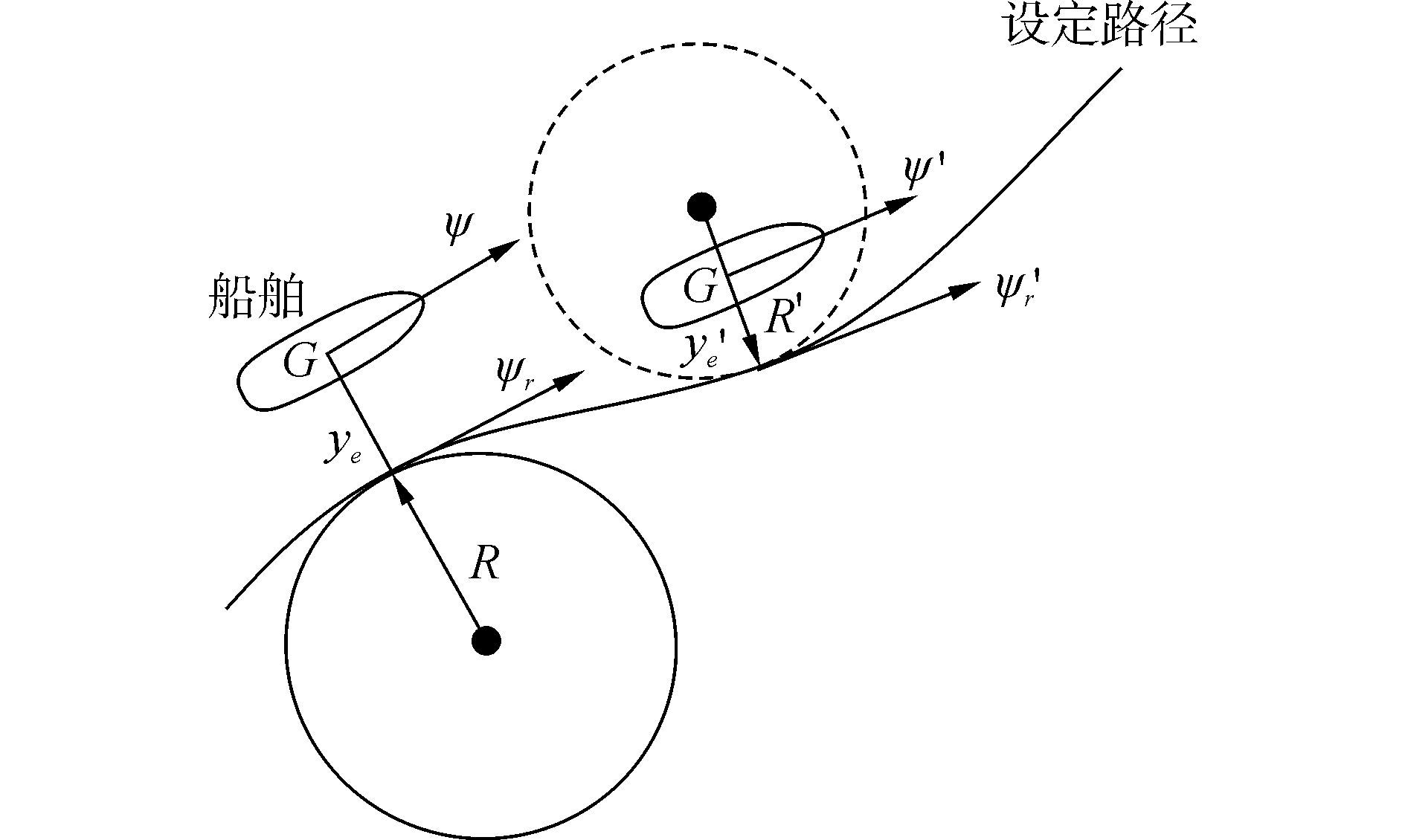
当船舶要跟踪某个光滑曲线路径时,跟踪的航迹偏差可由图 1表示。假设曲线上的任意一点都可以表示成某半径为R的圆上一点。ψ是船舶的实际航向,ψr表示期望的航向,ye表示位置偏差,带撇的量与不带撇的量分别表示两个不同时刻的值。理论上可以近似认为,只要船舶能跟踪圆路径,就可以跟踪任何光滑曲线路径。
|
| 图1 船舶路径跟踪航迹偏差示意图 Figure 1 Track error schematic on tracking ship path |
根据几何学知识可知,船舶跟踪圆弧路径的航迹偏差和航迹上的切线方向都可以用解析方程表示。圆在二维坐标系中用二元二次方程表示为(x-x0)2+(y-y0)2=R2,其中(x0,y0)是圆心坐标,R是半径。船舶航迹偏差可定义为实际位置到圆心的距离减去半径,圆周上的切线方向可以用以圆心为原点的极坐标表示:
| $ \left\{ \begin{array}{l} {y_e} = {\left[ {{{\left( {x - {x_0}} \right)}^2} + {{\left( {y - {y_0}} \right)}^2}} \right]^{1/2}} - R\\ {\psi _r} = a{\tan ^2}\left[ {\left( {y - {y_0}} \right),\left( {x - {x_0}} \right)} \right] \pm {\rm{\pi /2}} \end{array} \right. $ | (3) |
式中:ye表示航迹偏差,ψr表示切线方向,也就是期望的航向,另外因为航迹跟踪需要确定正方向,顺时针时ψr取“+”,逆时针时取“-”。定义航向偏差为ψe=ψ-ψr。
在船舶路径跟踪控制的实际操纵中,当外界干扰有界时系统是可控的,根据船舶常速航行时的特性做出如下假设:
假设1 u≫|uc|≫|v|,即船舶纵向速度(恒为正)大于流速且远大于横向速度。
假设2 系统速度、加速度以及外界干扰有界,且在t∈R+是光滑的。
系统控制目标:针对船舶运动数学模型式(1),在假设1和假设2的情况下,设计船舶路径跟踪自适应控制器,使得船舶在有限时间内,跟踪上设定的曲线路径,并且保证系统内所有信号一致最终有界。
2 船舶路径跟踪控制器设计为便于控制器设计,先给出以下定理。
定理1 考虑一零阶非线性标量系统
| $ y = f\left( {x,{u_s},t} \right) $ | (4) |
式中:y∈R为系统输出,x∈R为系统状态,us∈R为控制输入。如果
1) 状态方程为
2) f(x,us,t)是连续有界非线性函数;
3) 控制输入增益的符号已知,假设
若采用如下的增量反馈控制律
| $ {{\dot u}_s} = - {k_p}y - \varepsilon \tanh \left( y \right) $ | (5) |
式中:kp、ε∈R+,那么系统(3) 在控制律(4) 作用下能够实现一致渐近稳定。
证明:对式(4) 求导,可得
| $ \dot y = \frac{{\partial f}}{{\partial x}}\dot x + \frac{{\partial f}}{{\partial {u_s}}}{{\dot u}_s} $ | (6) |
取李亚普诺夫函数为
| $ V\left( y \right) = \frac{1}{2}{y^2} $ | (7) |
对式(7) 求导,并将式(5) 和式(6) 代入,可得
| $ \begin{array}{*{20}{c}} {\dot V\left( y \right) = y\dot y = y\left( {\frac{{\partial f}}{{\partial x}}\dot x + \frac{{\partial f}}{{\partial {u_s}}}{{\dot u}_s}} \right) = }\\ {\frac{{\partial f}}{{\partial x}}\dot xy + \frac{{\partial f}}{{\partial {u_s}}}\left[ { - {k_p}y - \varepsilon \tanh \left( y \right)} \right]y \le }\\ { - \left\{ {\frac{{\partial f}}{{\partial {u_s}}}\left[ {{k_p}\left| y \right| + \varepsilon \left| {\tanh \left( y \right)} \right|} \right] - \frac{{\partial f}}{{\partial x}}h\left( {{u_s}} \right)} \right\}\left| y \right|} \end{array} $ | (8) |
由假设(4) 有
| $ \frac{{\partial f}}{{\partial {u_s}}}\left[ {{k_p}\left| y \right| + \varepsilon \left| {\tanh \left( y \right)} \right|} \right] - \frac{{\partial f}}{{\partial x}}h\left( {{u_s}} \right) > 0 $ | (9) |
因此有
| $ \dot V\left( y \right) < 0 $ | (10) |
根据李亚普诺夫稳定性判据可知,系统(4) 一致渐近稳定,定理1成立。
2.1 非线性迭代滑模控制器的设计为实现式(1) 中船舶路径跟踪目标,利用非线性双曲正切函数设计迭代滑模函数,构造出包含航迹偏差ye和航向偏差ψe的多阶迭代滑模函数如下
| $ \left\{ \begin{array}{l} {\sigma _1} = \left( {{y_e}} \right) = {k_1}\tanh \left( {{k_0}{y_e}} \right) + {{\dot y}_e}\\ {\sigma _2} = \left( {{\sigma _1},{\psi _e}} \right) = {\psi _e} + {k_2}\int {\tanh \left( {{\sigma _1}} \right){\rm{d}}t} \\ {\sigma _3} = \left( {{\sigma _2}} \right) = {k_3}\tanh \left( {{\sigma _2}} \right) + {{\dot \sigma }_2}\\ {\sigma _4}\left( {{\sigma _3}} \right) = {k_4}\tanh \left( {{\sigma _3}} \right) + {{\dot \sigma }_3} \end{array} \right. $ | (11) |
式中:k0、k1、k2、k3、k4∈R+,并且有k3≤k4。式(11) 中一阶滑模面σ1是关于航迹偏差ye的函数,最高阶滑模面σ4包含航向偏差ψe的二阶导数项,即蕴含了滑模面σ4与控制舵角δ的关系。在滑模面σ2中加入积分项,是为了利用双曲正切函数的严格有界性限制驱动船舶转首的最大速率,以适应船舶旋回角速度和控制输入的约束条件。
以下非线性迭代滑模控制器设计的基本思想是考虑到船舶纵向速度远大于横向速度(假设1),且舵力在纵、横向的分力相对于转矩小的多,同时假设初始航向偏差角小于直角,根据双曲正切函数的严格有界,设法推导出所构造最高阶滑模面σ4与舵角δ之间的单调函数关系,再利用定理1,设计滑模面反馈控制律,并证明航迹偏差ye渐近收敛。
根据式(11) 的数学关系可以知道当σ4→0时,有σ3→0,σ2→0。而当σ2→0时,存在
| $ {\psi _e} \to - {k_2}\int {\tanh \left( {{\sigma _1}} \right){\rm{d}}t} $ | (12) |
以及
| $ {{\dot \psi }_e} \to - {k_2}\tanh \left( {{\sigma _1}} \right) $ | (13) |
根据船舶运动MMG式(1),可把σ1展开:
| $ \begin{array}{l} {\sigma _1} = {k_1}\tanh \left( {{k_0}{y_e}} \right) + v\cos {\psi _e} + \\ \;\;\;\;\;\;\;u\sin {\psi _e} + {u_c}\sin {\psi _e} \end{array} $ | (14) |
把σ1看成形如式(4) 所述的系统输出y,由于σ1受ψe控制,可将ψe作为控制量us,明显σ1是连续有界非线性函数,且可得
| $ \frac{{\partial {\sigma _1}}}{{\partial {\psi _e}}} = u\cos {\psi _e} - v\sin {\psi _e} $ | (15) |
为防止船舶反向航行,可假设初始时刻的航向偏差角ψ小于直角,即|ψe|<π/2,由假设1可知u≫|v|,再根据三角函数的性质,可得式(15) 满足大于0的条件。根据式(13) 令控制律为
| $ {{\dot u}_s} = {{\dot \psi }_e} = - {k_2}\tanh \left( {{\sigma _1}} \right) $ | (16) |
根据定理1,那么在控制律式(16) 作用下,式(14) 可以达到渐进稳定,即σ1→0,由式(11) 第一个式子可得
| $ {{\dot y}_e} \to - {k_1}\tanh \left( {{k_0}{y_e}} \right) $ | (17) |
因此航迹偏差ye也是渐近稳定的。所以只要实现σ4→0,就能确保航迹偏差ye稳定收敛。
为实现σ4→0,采用如下的滑模面反馈控制律
| $ \dot \delta = - {k_5}{\sigma _4} - \varepsilon \tanh \left( {{\sigma _4}} \right) $ | (18) |
式中:k5、ε∈R+。
根据式(11) 把σ4全部展开可得
| $ \begin{array}{*{20}{c}} {{\sigma _4} = {k_4}\tanh \left( {{\sigma _3}} \right) + }\\ {{k_3}\left[ {r + {k_2}\tanh \left( {{\sigma _1}} \right)} \right]/{{\left[ {\cosh \left( {{\sigma _2}} \right)} \right]}^2} + }\\ {{k_2}\left\{ {{k_0}{k_1}{{\dot y}_e}/{{\left[ {\cosh \left( {{k_0}{y_e}} \right)} \right]}^2} + {{\ddot y}_e}} \right\}/{{\left[ {\cosh \left( {{\sigma _1}} \right)} \right]}^2} + }\\ {\left( {{N_H} + {N_P} + {N_R} + {N_{{\rm{wind}}}} + {N_{{\rm{wave}}}}} \right)/\left( {{I_{zz}} + {J_{zz}}} \right)} \end{array} $ | (19) |
将式(19) 对δ求偏导,考虑到只有舵转矩NR、舵横向分力XR、舵纵向分力YR三项表达式与输入舵角δ有关,可得:
| $ \begin{array}{*{20}{c}} {\frac{{\partial {\sigma ^4}}}{{\partial \delta }} = \frac{\partial }{{\partial \delta }}{N_R}/\left( {{I_{zz}} + {J_{zz}}} \right) + }\\ {\frac{\partial }{{\partial \delta }}\left\{ {{k_2}{{\ddot y}_e}/{{\left[ {\cosh \left( {{\sigma _1}} \right)} \right]}^2}} \right\} = \frac{\partial }{{\partial \delta }}{N_R}/\left( {{I_{zz}} + {J_{zz}}} \right) + }\\ {{k_2}\frac{{\partial {X_R}}}{{\partial \delta }}\left[ {\sin \psi /\left( {m + {m_x}} \right)} \right]/{{\left[ {\cosh \left( {{\sigma _1}} \right)} \right]}^2}}\\ {{k_2}\frac{{\partial {Y_R}}}{{\partial \delta }}\left[ {\cos \psi /\left( {m + {m_y}} \right)} \right]/{{\left[ {\cosh \left( {{\sigma _1}} \right)} \right]}^2}} \end{array} $ | (20) |
式中:NR=h(x)cos(δ)sin(αR),αR为有效冲角,αR大小与舵角输入δ有关且符号相同,h(x)为一个恒正的函数,因此可知NR对δ求导在δ∈(-35°,35°)是恒正的。考虑实际操舵时,舵力在纵、横向的分力XR和YR及其增益相对于转矩NR小的多。根据三角函数和双曲三角函数的有界性可知,存在k2使
| $ \frac{{\partial {\sigma _4}}}{{\partial \delta }} > 0 $ | (21) |
因此,由式(18)、(21) 及定理1,可得σ4渐近收敛至0,从而确保航迹偏差ye渐近收敛,实现路径跟踪目标。
2.2 基于强化学习的控制参数优化由船舶操纵特性可知,船舶的横摇和干扰,都会使控制舵角来回波动,如果控制器设计不合理或者参数不合适,则会加大这种波动的频率和幅值。为延长设备寿命,并使控制效果接近实际操舵要求,应尽可能减少舵的抖振输出。因此所设计的非线性迭代滑模控制器器如果有自适应性,那么系统控制性能将得到提升。
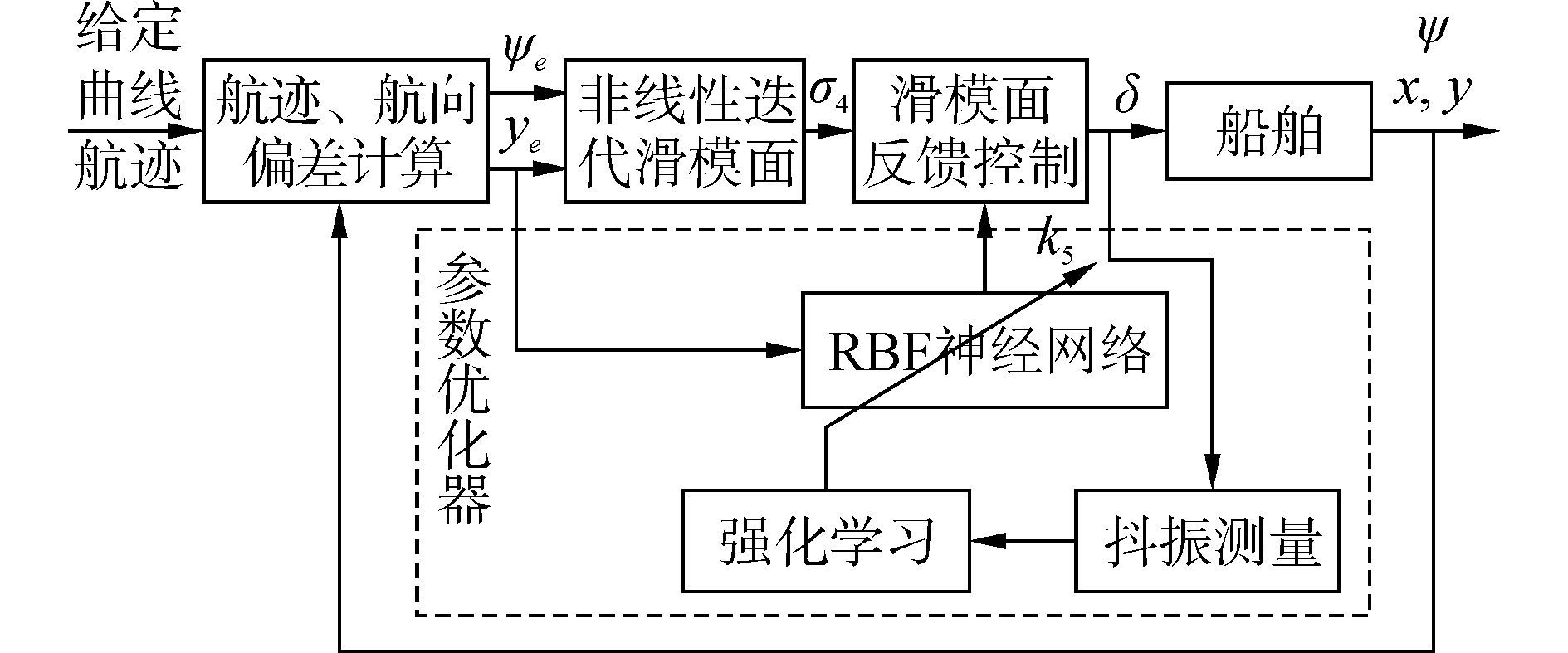
由式(18) 可看出滑模面反馈参数k5对系统的控制品质和鲁棒性有很大影响。为此,设计控制参数神经网络系统以航迹偏差为输入,根据航迹偏差变化调节控制器参数k5,同时,为了减小控制舵角的输出抖振量,定义一种抖振测量变量,并基于强化学习方法实现神经网络参数的在线学习。基于上述参数优化思想,设计出一种基于强化学习的自适应迭代滑模船舶路径跟踪控制结构,如图 2所示。
|
| 图2 基于强化学习的自适应迭代滑模船舶路径跟踪控制结构图 Figure 2 Adaptive iterative sliding mode ship path track control based on reinforcement learning |
图 2中,系统的输入是给定的船舶曲线航迹,输出是船舶实际位置坐标x、y和航向角ψ。非线性迭代滑模控制器根据反馈的航迹偏差ye和航向偏差ψe计算出控制舵角δ,并作用于船舶,从而实现船舶的路径跟踪控制。为实现控制参数k5的优化,构造了一个参数优化器,其输入是航迹偏差ye和控制舵角δ,输出是优化之后的参数值k5。在参数优化器内,设计一种RBF神经网络,以航迹偏差ye作为输入,实现控制参数k5的自适应调整;同时,为评价控制参数k5的优化效果,将控制舵角δ的抖振测量值作为强化信号,对RBF神经网络的结构参数进行在线学习,从而进一步提高参数k5的优化效果,且减小控制舵角δ的输出抖振量。
参数优化器中的神经网络采用RBF神经网络结构,其为输入层神经元数量1个,表示位置误差ye;隐含层神经元10个;输出层神经元也是1个,表示参数k5。RBF神经网络隐含层的激活函数采用高斯函数:
| $ {h_j}\left( x \right) = \exp \left( { - \frac{{{{\left\| {x - {c_j}} \right\|}^2}}}{{2\sigma _j^2}}} \right) $ | (22) |
式中:hj是第j个高斯基函数的输出值,x表示网络的输入,cj是第j个高斯基函数的中心,σj是第j个高斯基函数的宽度。
最终RBF神经网络的输出可表示为
| $ {k_5} = \mathit{\boldsymbol{W}} \cdot \mathit{\boldsymbol{h}}\left( {{y_e}} \right) $ | (23) |
式中:W是权重向量,h(ye)是隐含层输出向量。因此,所构造RBF神经网络的学习参数包括各基函数的中心cj和宽度σj,以及隐含层到输出层的权重向量W,其初始参数值选取如下
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{c}}_j} = \left[ {\begin{array}{*{20}{c}} { - 1}&{ - 0.75}&{ - 0.5}&{ - 0.3}&0&{0.2} \end{array}} \right.\\ \;\;\;\;\;\;\;\left. {\begin{array}{*{20}{c}} {0.3}&{0.5}&{0.75}&1 \end{array}} \right]\\ {\mathit{\boldsymbol{\sigma }}_j} = \left[ {\begin{array}{*{20}{c}} 2&2&{1.5}&1&1&1&1&{1.5}&2&2 \end{array}} \right]\\ \mathit{\boldsymbol{W = }}\left[ {\begin{array}{*{20}{c}} 1&1&1&1&1&1&1&1&1&1 \end{array}} \right] \end{array} \right. $ | (24) |
为实现RBF神经网络的参数学习,通常采用有导师的学习算法,但对于本结构中的输出参数k5,在不同工况下参数k5的期望值并不知道,即没有明确的导师信号。根据文献[19]可知,强化学习算法可以采用比较粗糙的训练数据,仅仅使用“评价”信号,即强化信号,通过与环境的交互来评价控制作用的优劣,采用“奖”、“罚”算法训练网络。为此,本文根据控制舵角δ的抖振测量值计算得到强化信号,采用强化学习算法实现RBF神经网络的参数学习。
在每一个学习周期中,每个神经网络的输出会对应一个权重的变化量Δwt,权重向量W将按式(25) 进行参数调整。
| $ {\mathit{\boldsymbol{W}}_{t + 1}} = {\mathit{\boldsymbol{W}}_t} + \Delta {w_t} $ | (25) |
式中:Wt表示t时刻权重,Wt+1为下一周期的权重。定义神经网络的输出误差Et为
| $ {E_t} = \frac{1}{2}{\left( {{k_5} - d} \right)^2} $ | (26) |
式中:d是参数k5的期望值,显然是不可知的,但是系统的控制效果可以间接的反应参数是否合适,故采用控制舵角的抖振情况来近似代替这个误差。即
| $ {k_5} - d \approx \frac{{M - \bar M}}{{\bar M}} $ | (27) |
式中:M表示期望的舵角抖振值,取决于设计人员对系统抖振的要求,M定义为近n次迭代周期内控制变化量绝对值的累加和,用于描述一段时间内的振荡值。若在n个周期内M值增大,则说明抖振增加;反之,若在n个周期内M值减小,则说明抖振减小。因而M的实时变化可以用于对神经网络系统的参数进行自适应调节。抖振测量变量M的表达式可描述为
| $ M\left( t \right) = \sum\limits_{l = 0}^n {{\rho _k}\left( l \right)\left| {\delta \left( {t - lT} \right) - \delta \left[ {t - \left( {l - 1} \right)T} \right]} \right|} $ | (28) |
式中:T是仿真周期,δ(t-lT)和δ[t-(l-1)T]是前后不同周期的舵角值,n表示积累的次数(取n=50),而ρk(l)定义为
| $ {\rho _k}\left( l \right) = \left\{ \begin{array}{l} 0,\;\;\;\left\{ {{\delta _k}\left( {lT} \right) - {\delta _k}\left[ {\left. {\left( {l - 1} \right)T} \right)} \right]} \right\} \cdot \\ \;\;\;\;\;\;\left\{ {{\delta _k}\left[ {\left( {l - 1} \right)T} \right] - {\delta _k}\left[ {\left( {l - 2} \right)T} \right]} \right\} \ge 0\\ 1,\;\;\;\;\;\left\{ {\delta \left( {lT} \right) - {\delta _k}\left[ {\left. {\left( {l - 1} \right)T} \right)} \right]} \right\} \cdot \\ \;\;\;\;\;\;\left\{ {{\delta _k}\left[ {\left( {l - 1} \right)T} \right] - {\delta _k}\left[ {\left( {l - 2} \right)T} \right]} \right\} < 0 \end{array} \right. $ | (29) |
在系统输出产生抖振时,输出的变化趋势会发生改变。在式(29) 中,当且仅当舵角变化量符号反向时ρk(l)记为1,否则记为0。结合式(28),即可描述最近n个周期内系统输出的抖振变化情况。因此,权重的变化量Δwt可表示为
| $ \Delta {w_t} = - {\eta _1}\frac{{\partial {E_t}}}{{\partial {w_t}}} = {\eta _1}\left( {{k_5} - d} \right)\frac{{\partial d}}{{\partial {w_t}}} = {\eta _1}\frac{{M - \bar M}}{{\bar M}}\frac{{\partial d}}{{\partial {w_t}}} $ | (30) |
式中η1是学习率。
则权重向量W的学习过程可表示为
| $ \begin{array}{l} {\mathit{\boldsymbol{W}}_{t + 1}} = {\mathit{\boldsymbol{W}}_t} + {\eta _1}\frac{{M - \bar M}}{{\bar M}}\frac{{\partial d}}{{\partial {w_t}}} = \\ \;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{W}}_t} + {\eta _1}\frac{{M - \bar M}}{{\bar M}}{h_{jt}} \end{array} $ | (31) |
同理,可得参数cj和σj的学习算法为
| $ \begin{array}{l} {\mathit{\boldsymbol{c}}_{j\left( {t + 1} \right)}} = {\mathit{\boldsymbol{c}}_{jt}} + {\eta _2}\frac{{M - \bar M}}{{\bar M}}\frac{{\partial d}}{{\partial {c_{jt}}}} = \\ \;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{c}}_{jt}} + {\eta _2}\frac{{M - \bar M}}{{\bar M}}{w_{jt}}{h_{jt}}\frac{{x - {\mathit{\boldsymbol{c}}_{jt}}}}{{\mathit{\boldsymbol{\sigma }}_{jt}^2}} \end{array} $ | (32) |
| $ \begin{array}{l} {\mathit{\boldsymbol{\sigma }}_{j\left( {t + 1} \right)}} = {\mathit{\boldsymbol{\sigma }}_{jt}} + {\eta _3}\frac{{M - \bar M}}{{\bar M}}\frac{{\partial d}}{{\partial {\mathit{\boldsymbol{\sigma }}_{jt}}}} = \\ \;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{\sigma }}_{jt}} + {\eta _3}\frac{{M - \bar M}}{{\bar M}}{w_{jt}}{h_{jt}}\frac{{{{\left\| {x - {\mathit{\boldsymbol{c}}_{jt}}} \right\|}^2}}}{{\mathit{\boldsymbol{\sigma }}_{jt}^3}} \end{array} $ | (33) |
参数优化神经网络系统根据实时测量的舵角抖振变化情况,其参数W、cj和σj按照式(31)~(33) 的学习算法进行在线学习,进而能够更准确地输出调节参数k5,从而增强控制器的自适应性。
3 船舶路径跟踪控制仿真研究本文以5446TEU集装箱船为对象进行路径跟踪控制仿真,验证所设计控制器的性能,该船的主要参数如表 1所示。
| 集装箱船物理属性 | 参数 |
| 船长/m | 280.0 |
| 船宽/m | 39.8 |
| 设计船速/kn | 24.5 |
| 总吨位/t | 65 531 |
| 空船重量/t | 24 696 |
| 设计吃水/m | 12.5 |
| 螺旋桨桨叶数 | 5 |
| 螺距 | 9.657 |
| 两柱间长/m | 267.0 |
| 型深/m | 23.6 |
| 方形系数 | 0.62 |
| 净吨位/t | 35 453 |
| 载重量/t | 69 192 |
| 满载吃水/m | 14.0 |
| 直径/m | 9.2 |
| 盘面比 | 0.668 |
在仿真验证过程中,干扰设置为风速10 m/s、流速2 m/s,方向均为110°,浪的波高为3 m,遭遇频率为0.75 Hz,船初始位置在(0,0) 点,初始船速27 kn,要跟踪的圆路径圆心在(2 000,2 000),半径是2 000 m。分别设计基于强化学习的迭代滑模控制器和迭代滑模控制器对船舶路径跟踪进行仿真。设定k0~k4分别是:0.01、3、0.05、0.005和0.01,k5的初始值是3.2,ε是0.001,Μ取0.1,η1取0.5。
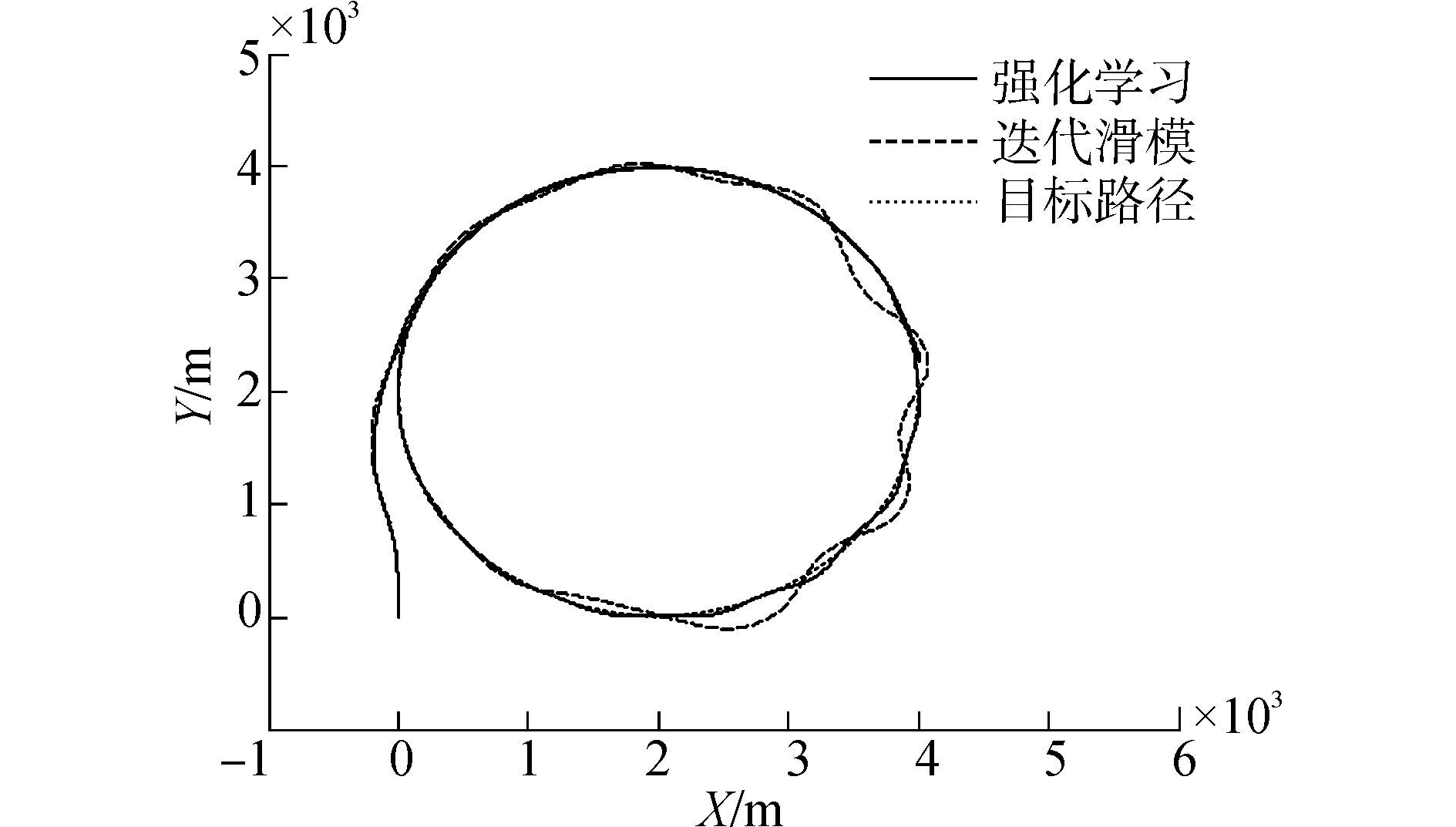
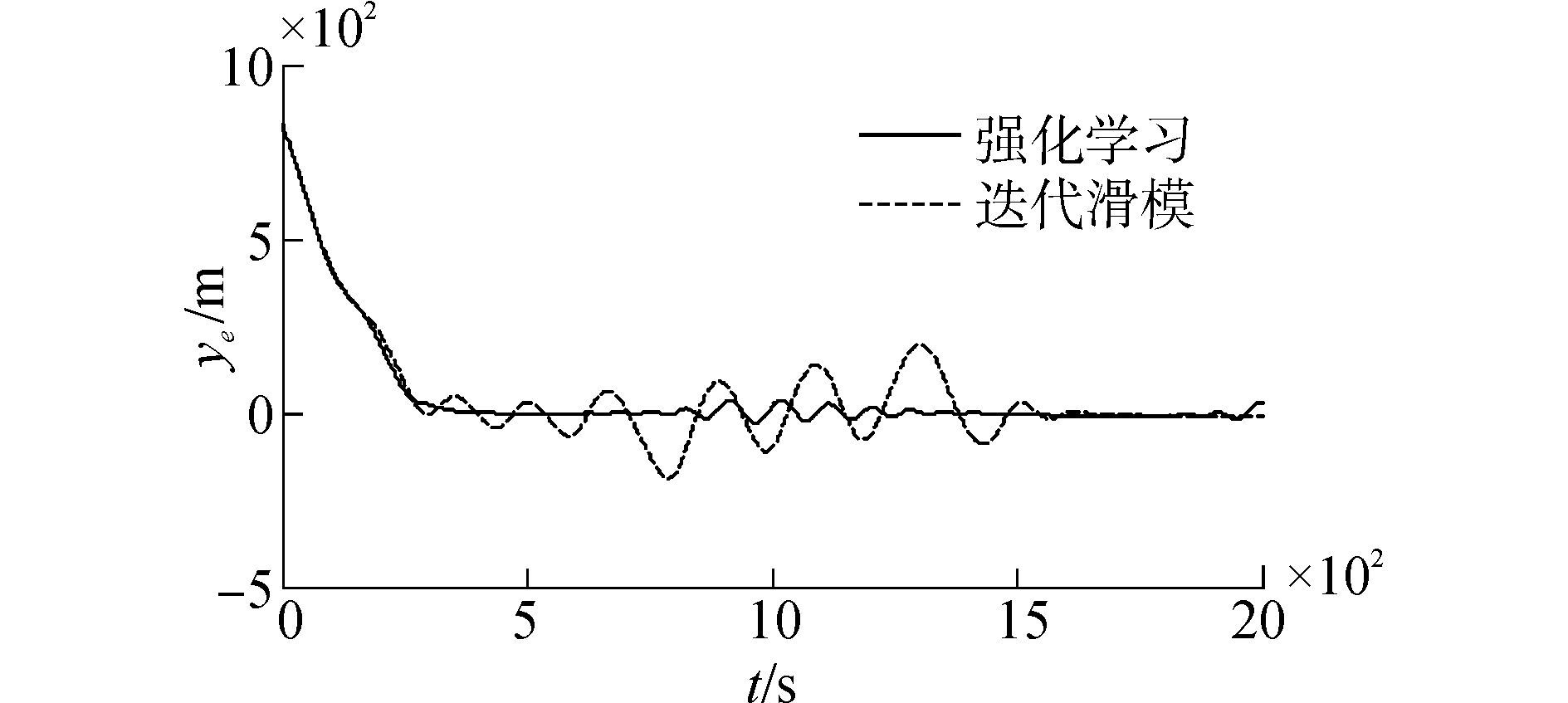
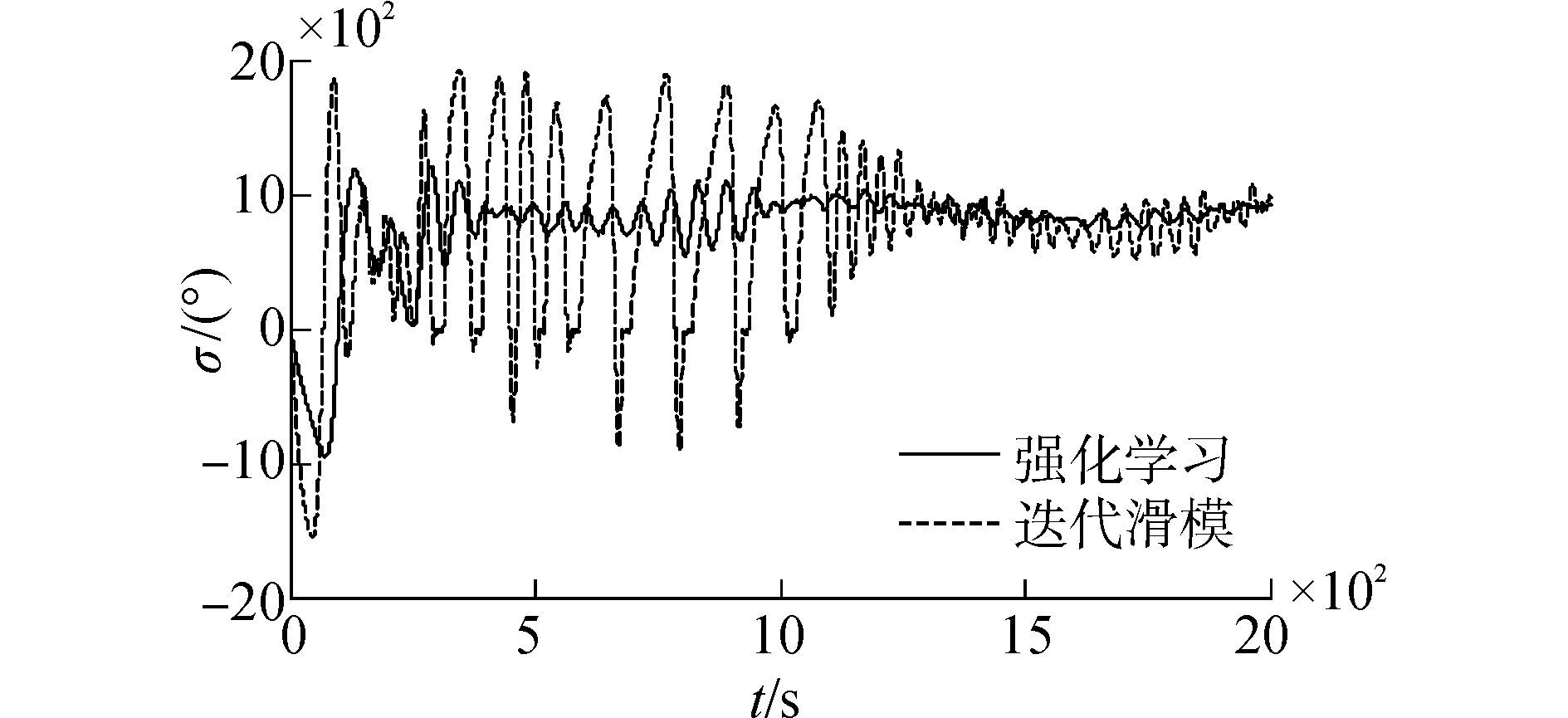
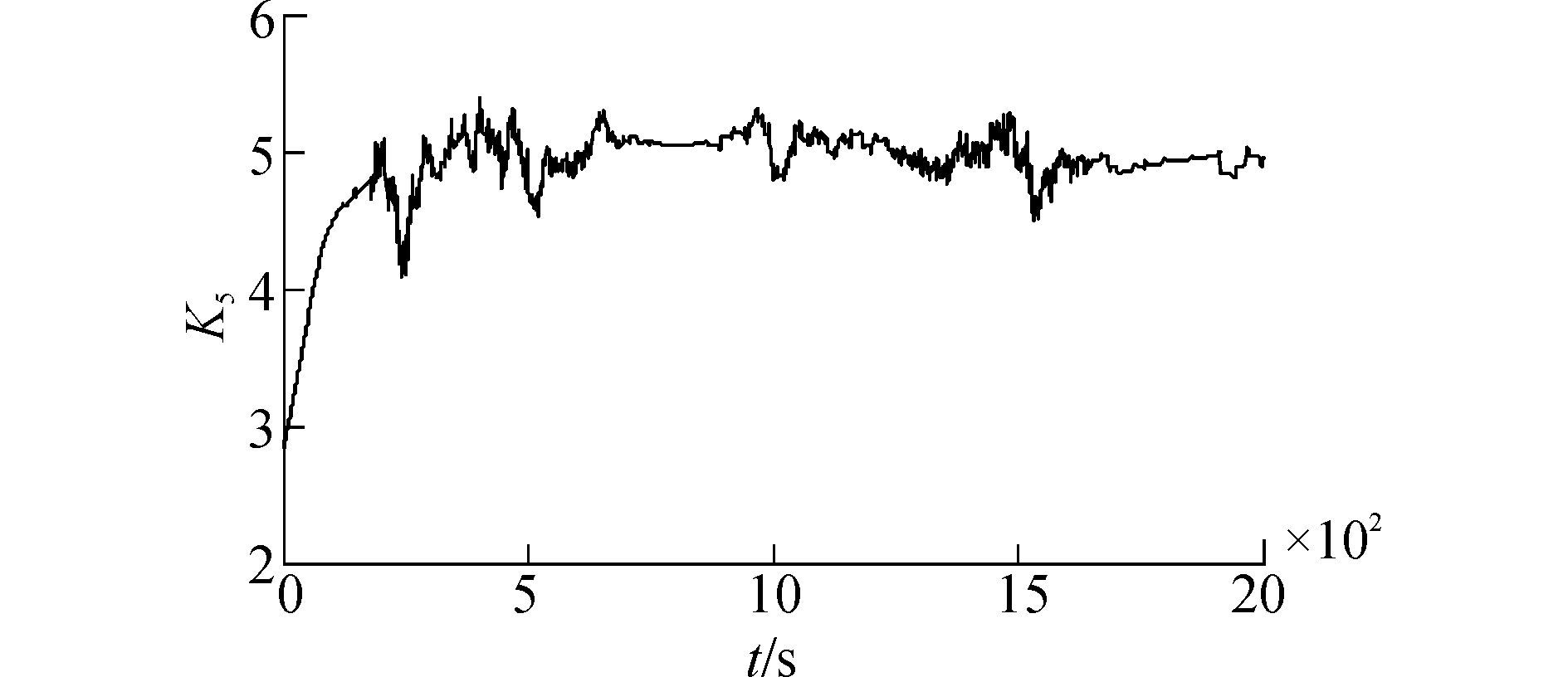
图 3~6是船舶在设定工况下跟踪圆路径,分别是跟踪路径、误差、舵角以及参数变化的曲线。从图 3可以看出用迭代滑模方法跟踪和用基于强化学习的迭代滑模算法都很快跟上了目标路径,但是迭代滑模控制算法跟踪的不准确。由图 4更能直观的看出迭代滑模控制方法和基于强化学习的迭代滑模控制算法都在300 s左右跟踪上路径,但是迭代滑模控制方法一直存在较大误差。由图 5不难发现,用迭代滑模控制算法的船舶舵角峰值为20°左右,而用基于强化学习的迭代滑模控制算法的船舶舵角峰值仅有12°,并且舵角的振荡程度更小,不会过多的损耗舵机,更符合实际的船舶航行要求。通过图 6可以发现刚开始参数k5的变化剧烈,相对幅度较大,在没有跟踪上设定路径的时候,较大幅度地去调节k5,尽快减小误差;跟踪上以后,小范围调节参数,仅是为了消除抖振,神经网络实现了对参数的动态调节。综合图 3~6可以明显看出,使用基于强化学习的迭代滑模控制算法比用迭代滑模控制算法的控制效果要更好,更稳,更准,更符合工程的实际要求。
|
| 图3 圆路径跟踪的路径跟踪曲线 Figure 3 Path tracking curves of round path tracking |
|
| 图4 圆路径跟踪的误差曲线 Figure 4 Error curves of round path tracking |
|
| 图5 圆路径跟踪的舵角变化曲线 Figure 5 Rudder angle curves of round path tracking |
|
| 图6 圆路径跟踪的参数k5变化曲线 Figure 6 The parameter k5 curve of round path tracking |
为进一步验证基于强化学习的迭代滑模控制算法的有效性,又对正弦路径进行跟踪控制仿真。仿真中干扰设置为风速10 m/s、流速2 m/s,方向均为110°,浪的波高为3 m,遭遇频率为0.75 Hz,船初始位置在(0,0) 点,初始船速27 kn,要跟踪的正弦路径方程是:y=200sin(πx/2 500)。分别设计了基于强化学习的迭代滑模控制器和迭代滑模控制器对船舶路径跟踪进行仿真。设定k0~k4分别是:0.001、10、0.2、0.000 5和0.001,k5的初始值是3.7,ε是0.001,M取1,η1取0.5。
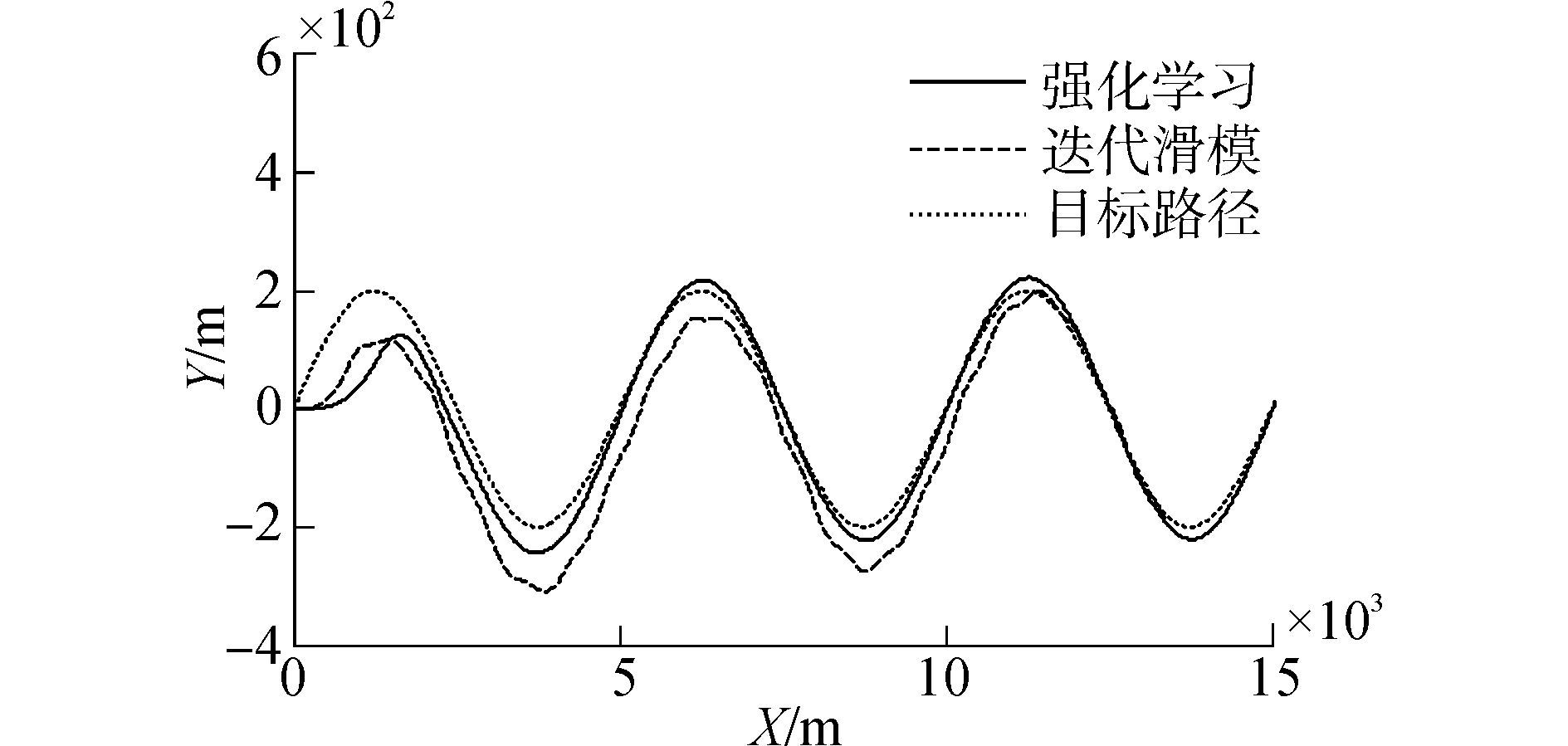
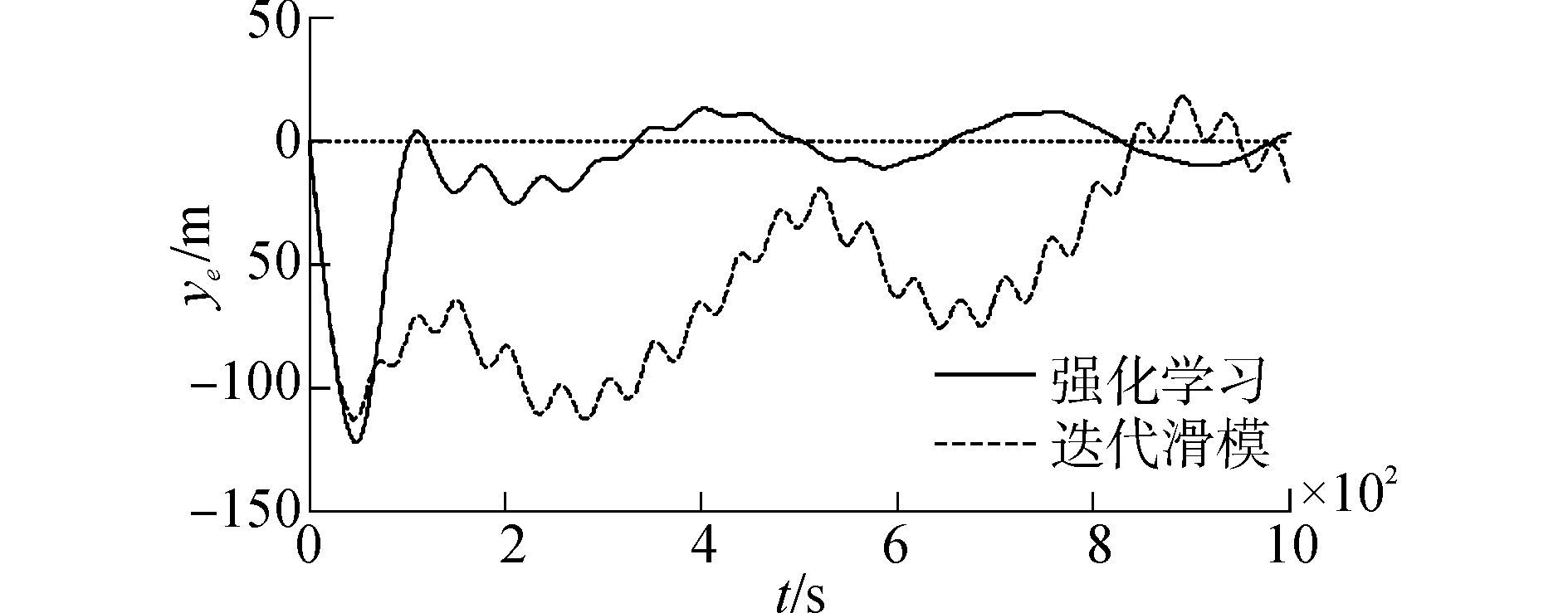
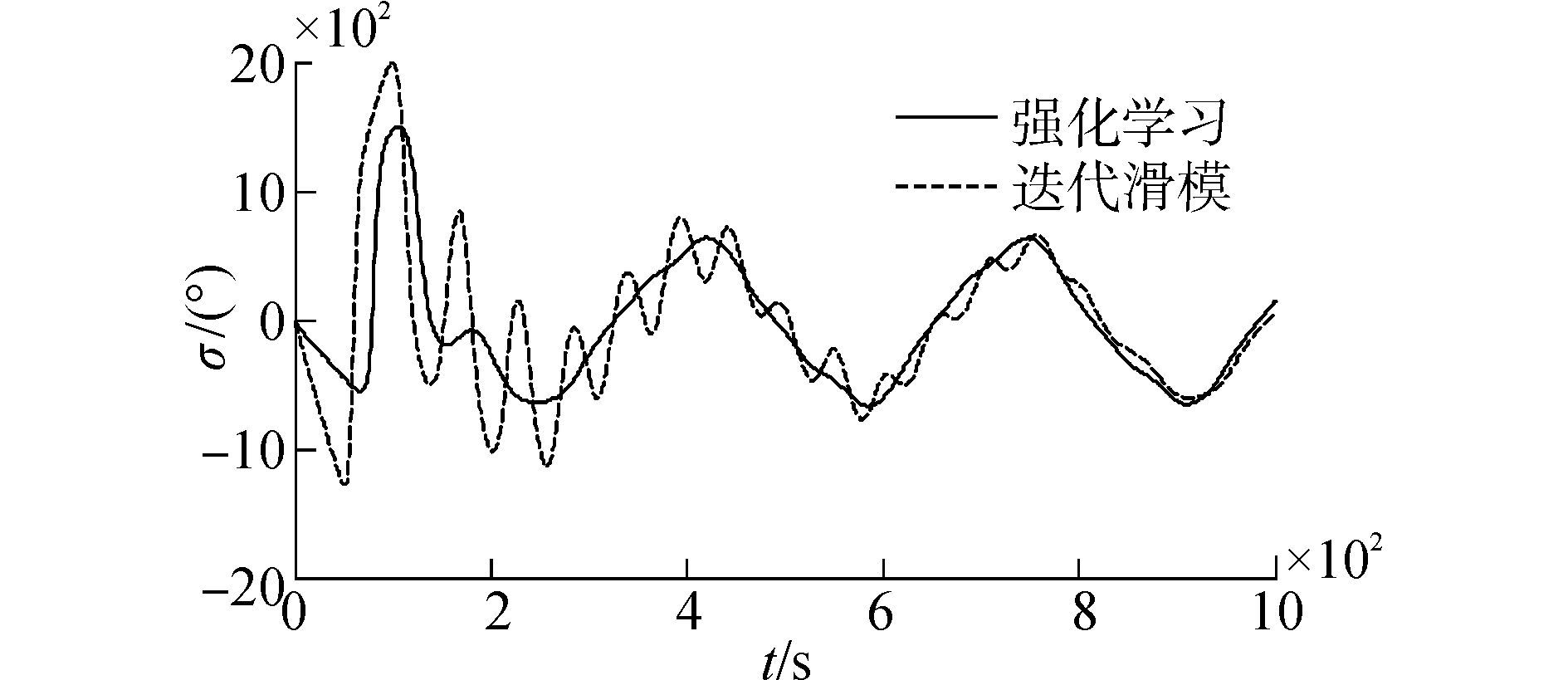
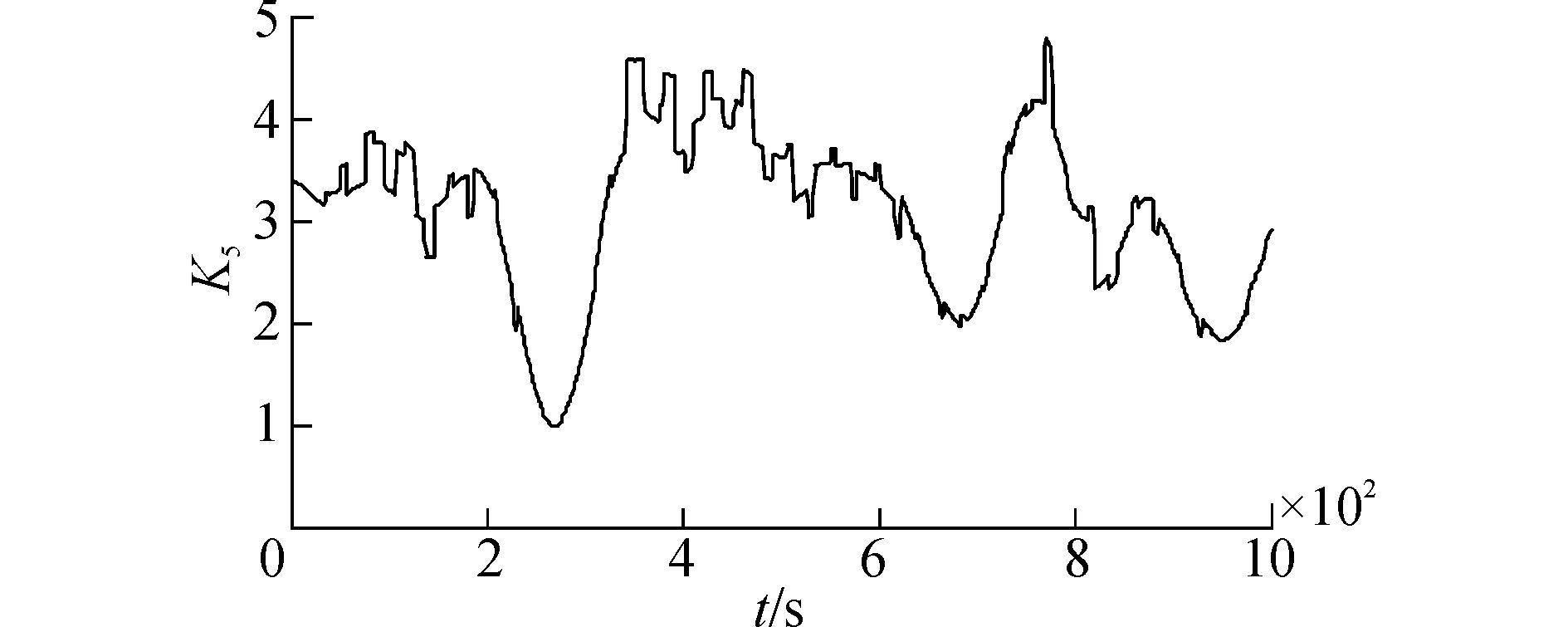
图 7~10是船舶在设定工况下跟踪正弦路径,分别是跟踪路径和舵角的变化曲线,由图 7和8可以看出用迭代滑模的控制算法跟踪效果差,不能完全跟踪上正弦路径;基于强化学习的迭代滑模控制算法在100 s左右时就几乎跟踪上了目标路径,并且相同时间内用基于强化学习的迭代滑模控制算法的跟踪距离更远,偏差更小。图 9可以发现用迭代滑模的控制算法舵角的抖振明显减小,舵角峰值也有所下降。由图 10可以看出,在600 s之前,参数k5抖动比较厉害,而这时的迭代滑模控制器的舵角抖动很大,是参数的抖动抵消了舵角的抖振。综上,可以明显看出用迭代滑模的方法跟踪速度较慢,而且一直存在偏差,跟踪不准确;用基于强化学习的迭代滑模控制算法则具有更快跟踪速度,舵角几乎没有抖振,误差更小。
|
| 图7 正弦路径跟踪的路径跟踪曲线 Figure 7 Path tracking curves of Sine path tracking |
|
| 图8 正弦路径跟踪的误差曲线 Figure 8 Error curves of Sine path tracking |
|
| 图9 正弦路径跟踪的舵角变化曲线 Figure 9 Rudder angle curves of Sine path tracking |
|
| 图10 圆路径跟踪的参数k5变化曲线 Figure 10 The parameter k5 curve of round path tracking |
1) 相较于迭代滑模控制器,基于强化学习的迭代滑模控制器的自适应性和鲁棒性更强,路径跟踪更准确,相同时间航行的更远,效率更高,有利于节省能源。
2) 使用基于强化学习的迭代滑模控制方法得到的舵角,相比较迭代滑模,舵角抖振明显下降,可以有效的保护舵机装置,更符合实际工程需求。
| [1] | WONDERGEM M, LEFEBER E, PETTERSEN K Y, et al. Output feedback tracking of ships[J]. IEEE transactions on control systems technology, 2011, 19(2): 442–448. DOI:10.1109/TCST.2010.2045654 |
| [2] | GHOMMAM J, MNIF F, DERBEL N. Global stabilisation and tracking control of underactuated surface vessels[J]. Control theory & applications, 2010, 4(1): 71–88. |
| [3] |
付明玉, 张爱华, 徐金龙. 船舶轨迹跟踪半全局一致指数稳定观测控制器[J].
控制与决策, 2013, 28(6): 920–924.
FU Mingyu, ZHANG Aihua, XU Jinlong. Semi-global uniform exponential stable observer-controller for trajectory tracking of ships[J]. Control and decision, 2013, 28(6): 920–924. |
| [4] | YANG Y, DU J, LIU H, et al. A trajectory tracking robust controller of surface vessels with disturbance uncertainties[J]. IEEE transactions on control systems technology, 2014, 22(4): 1511–1518. DOI:10.1109/TCST.2013.2281936 |
| [5] |
王昊, 王丹, 彭周华, 等. 多自主船协同路径跟踪的自适应动态面控制[J].
控制理论与应用, 2013, 30(5): 637–643.
WANG Hao, WANG Dan, PENG Zhouhua, et al. Adaptive dynamic surface control for cooperative path following of multiple autonomous surface vessels[J]. Control theory & applications, 2013, 30(5): 637–643. |
| [6] | ANNAMALAI A S K, SUTTON R, YANG C, et al. Robust adaptive control of an uninhabited surface vehicle[J]. Journal of intelligent & robotic systems, 2015, 78(2): 319–338. |
| [7] | YU R, ZHU Q, XIA G, et al. Sliding mode tracking control of an underactuated surface vessel[J]. Control theory & applications, 2012, 6(3): 461–466. |
| [8] | ASHRAFIUON H, MUSKE K R, MCNINCH L C, et al. Sliding-mode tracking control of surface vessels[J]. IEEE transactions on industrial electronics, 2008, 55(11): 4004–4012. DOI:10.1109/TIE.2008.2005933 |
| [9] |
孟威, 郭晨, 孙富春, 等. 欠驱动水面船舶的非线性滑模轨迹跟踪控制[J].
哈尔滨工程大学学报, 2012, 33(5): 585–589.
MENG Wei, GUO Chen, SUN Funchun, et al. Nonlinear sliding mode tracking control of underatuated surface vessels[J]. Journal of Harbin Engineering University, 2012, 33(5): 585–589. |
| [10] |
邢道奇, 张良欣. 船舶航迹跟踪的滑模控制[J].
船舶, 2011, 22(5): 10–14.
XING Daoqi, ZHANG Liangxin. Sliding-model control for trajectory tracking of surface vessels[J]. Ship & boat, 2011, 22(5): 10–14. |
| [11] | SIRA R H. Dynamic second-order sliding mode control of the hovercraft vessel[J]. IEEE transactions on control systems technology, 2002, 10(6): 860–865. DOI:10.1109/TCST.2002.804134 |
| [12] |
廖煜雷, 万磊, 庄佳园. 欠驱动船路径跟踪的反演自适应动态滑模控制方法[J].
中南大学学报:自然科学版, 2012, 43(7): 2655–2661.
LIAO Yulei, WAN Lei, ZHUANG Jiayuan. Back stepping adaptive dynamical sliding mode control method for path following of under actuated surface vessel[J]. Journal of central south university (science and technology), 2012, 43(7): 2655–2661. |
| [13] |
朱齐丹, 于瑞亭, 夏桂华, 等. 风浪流干扰及参数不确定欠驱动船舶航迹跟踪的滑模鲁棒控制[J].
控制理论与应用, 2012, 29(7): 959–964.
ZHU Qidan, YU Ruiting, XIA Guihua, et al. Sliding-mode robust tracking control for underactuated surface vessels with parameter uncertainties and external disturbances[J]. Control theory & applications, 2012, 29(7): 959–964. |
| [14] | HUANG Z, EDWARDS R M, LEE K Y. Fuzzy-adapted recursive sliding-mode controller design for a nuclear power plant control[J]. IEEE transactions on nuclear science, 2004, 51(1): 256–266. DOI:10.1109/TNS.2004.825100 |
| [15] |
卜仁祥, 刘正江, 李铁山. 迭代滑模增量反馈及在船舶航向控制中的应用[J].
哈尔滨工程大学学报, 2007, 28(3): 268–272.
BU Renxiang, LIU Zhengjiang, LI Tieshan. Iterative sliding mode based increment feedback control and its application to ship autopilot[J]. Journal of Harbin Engineering University, 2007, 28(3): 268–272. |
| [16] |
边信黔, 程相勤, 贾鹤鸣, 等. 基于迭代滑模增量反馈的欠驱动AUV地形跟踪控制[J].
控制与决策, 2011, 26(2): 289–292.
BIAN Xinqian, CHENG Xiangqin, JIA Heming, et al. A bottom-following controller for underactuated AUV based on iterative sliding and increment feedback[J]. Control and decision, 2011, 26(2): 289–292. |
| [17] |
贾鹤鸣, 张利军, 程相勤, 等. 基于非线性迭代滑模的欠驱动UUV三维航迹跟踪控制[J].
自动化学报, 2012, 38(2): 308–314.
JIA Heming, ZHANG Lijun, CHENG Xiangqin, et al. Three-dimensional path following control for an underactuated UUV based on nonlinear iterative sliding mode[J]. Acta automatica sinica, 2012, 38(2): 308–314. |
| [18] | LIU C, ZOU Z, HOU X. Stabilization and tracking of underactuated surface vessels in random waves with fin based on adaptive hierarchical sliding mode technique[J]. Asian journal of control, 2014, 16(5): 1492–1500. DOI:10.1002/asjc.v16.5 |
| [19] | SHEN Zhipeng, GUO Chen, ZHANG Ning. A general fuzzified CMAC based reinforcement learning control for ship steering using recursive least-squares algorithm[J]. Neurocomputing, 2010, 73: 700–706. DOI:10.1016/j.neucom.2009.03.021 |
| [20] |
贾欣乐, 杨盐生.
船舶运动数学模型:机理建模与辩识建模[M]. 大连海事大学出版社, 1999: 49-138, 328-331.
JIA Xinle, YANG Yansheng. Ship motion mathematical model: the mechanism modeling and identification modeling[M]. Dalian maritime university press, 1999: 49-138, 328-331. |



