随着加工技术的进步,椭圆柱壳在潜器、航空航天、管道输送等领域的应用日益增多。相比于圆柱壳结构,椭圆柱壳在潜器、航空器仓容及设备布置上具有更大优势,椭圆形管道相对于方形管道断面湿周面积小,密闭性更好,相对于圆形管道占用高度空间小。另一方面,即使是针对原设计的圆柱壳结构,由于制造加工工艺及深水压力等因素的影响,其横截面也无法保证为一个完美的圆形,不可避免地存在各种几何缺陷,可能会产生不可忽略的椭圆度等偏差[1]。因此,研究椭圆柱壳的振动特性具有重要意义。
目前在结构工程领域对圆柱壳体的振动特性研究较为全面,而对于椭圆柱壳振动方面的研究还相对较少,且大多关注于椭圆柱壳的自由振动。由于椭圆柱壳周向曲率的改变导致其振动方程是一个变系数的偏微分方程组,成为椭圆柱壳研究的难点,多年来学者们采取各种近似处理方法进行退化或借助于数值解法进行求解,退化等近似处理方法误差较大且计算范围受限,数值解法其方程又颇为繁琐,不便求解,对于椭圆柱壳振动机理的研究还很不充分。Klosner最早运用摄动解法对椭圆柱壳自由振动特性进行了研究,但其方法仅适用于椭圆度较小的情况,应用范围受到限制[2-3]。Sewall利用实验法对椭圆柱壳的自由振动进行了分析,将实验中具有最大椭圆度的椭圆柱壳的固有频率与圆柱壳进行了对比,发现椭圆柱壳的固有频率比圆柱壳下降了将近40%[4]。Shirakawa等则将椭圆截面视为两段圆弧组合而成,使用圆柱壳的方程来建立椭圆壳体的控制方程,但形式过于复杂,含有大量高阶偏微分形式 (最高阶偏导达到了八阶),不便应用[5]。Khalifa[6]采用传递矩阵法研究了嵌入非均匀地基上的各向异性椭圆柱壳的自由振动特性,但传递矩阵法受单元传递矩阵的计算精度、传递矩阵连乘过程中的累积误差以及计算机的舍入 (或截断) 误差影响,状态向量在传递过程中会产生一定的精度损失[7]。Tornabene等利用有限元微分法研究了复合材料椭圆柱壳的自由振动特性[8]。对于椭圆柱壳声振特性的研究,由于解析方法存在较大困难,已有文献大多采用数值仿真方法。张盛等用有限元软件对包括具有初始椭圆度在内的几种含有几何制造误差的圆柱壳的声振特性进行了仿真分析和计算[1]。倪樵等采用有限元/边界元法计算了深水中复合材料椭圆柱壳的的辐射声功率以及壳体表面、近场和远场声压,但文中并未讨论与圆柱壳声辐射特性的差异及椭圆度参数对其声辐射特性有何影响[9]。最近石焕文等采用有限元/边界元方法研究了不同类型的激励和模型结构参数对两端带有封盖的椭圆柱壳模型声振特性的影响规律[10]。Zhang提出用于求解圆柱壳的固有频率,后来该方法广泛用于求解板壳结构的振动[11-12],陈美霞等采用波传播法研究了不同激励力对圆柱壳的受迫振动特性[13],李天匀等则采用波传播法研究了静压下锥柱结合壳的自由振动特性[14],江丰采用波传播法研究了流体粘性对水下圆柱壳振动特性的影响[15],叶文兵基于波传播法研究了自由液面对水下圆柱壳声振特性的影响[16]。
本文采用波传播法将椭圆柱壳位移以双Fourier级数形式展开并结合Marguerre[17]对于非圆截面曲率半径的处理方法对椭圆柱壳的受迫振动方程进行了推导,提出了采用级数变换法将变系数的偏微分方程组转换为周向波数相互耦合的有限阶常系数线性方程组,克服了变系数偏微分方程组求解的困难,系统研究了激励力位置、壳体椭圆度及壳体厚度对椭圆柱壳输入功率流的影响。
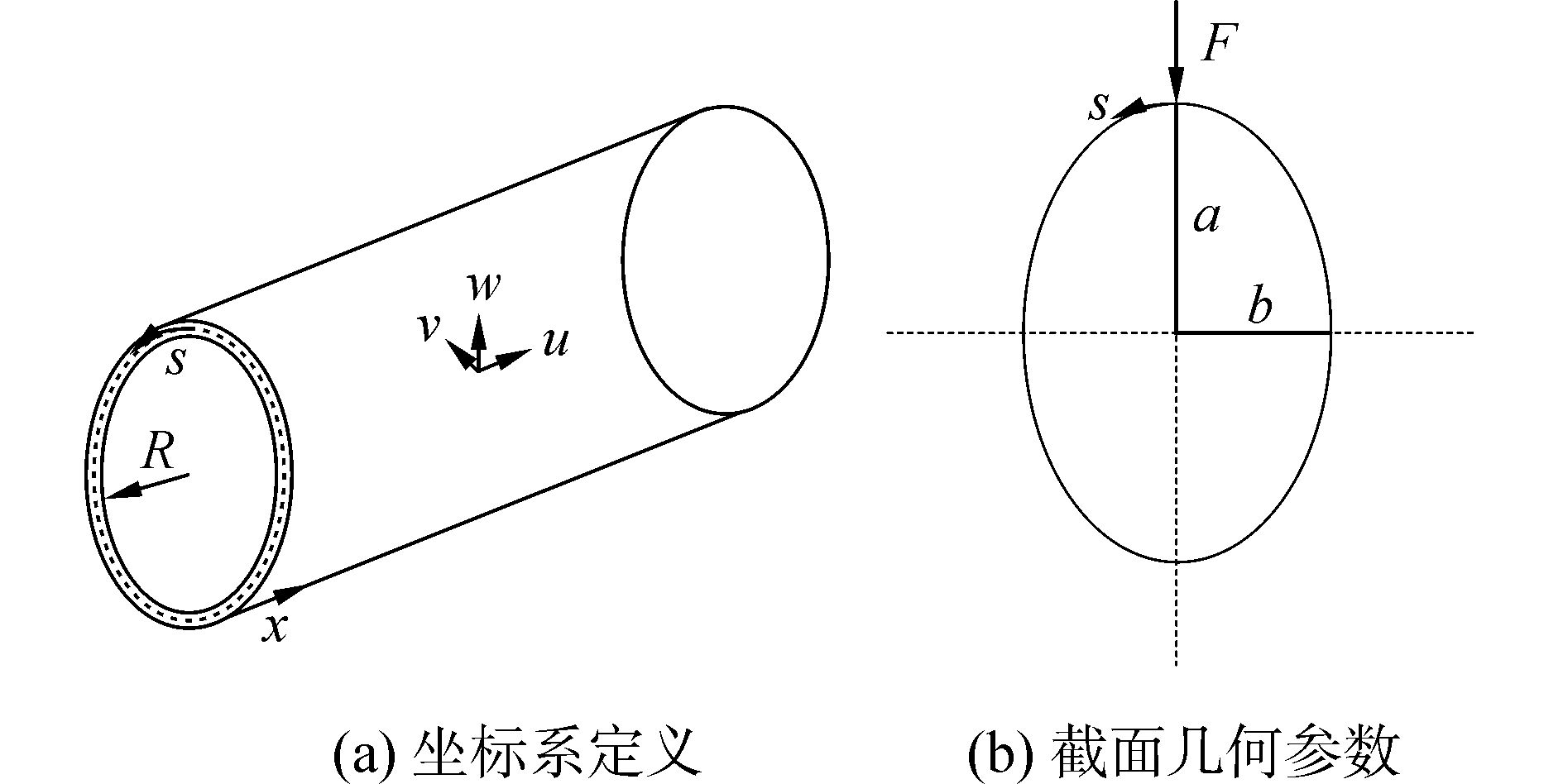
1 研究对象如图 1所示,壳体无限长,厚度为h,材料密度为ρ,杨氏模量为E,泊松比为μ。选取基础坐标系x,s,r,其中x为壳体轴线方向长度坐标,s为沿壳体截面周向的弧长坐标,r为壳体截面径向的坐标,并设u,v,w分别表示壳体中面的轴向、周向和径向位移,r0表示与椭圆柱壳截面周长相等的圆截面的半径,记为壳体截面的平均半径。R为截面中面的曲率半径,与坐标s有关,记为R=R(s)。
引入下列无量纲坐标:
| $x = \frac{{\bar x}}{{{r_0}}},s = \frac{{\bar S}}{{{r_0}}},r = \frac{{R(\bar s)}}{{{r_0}}} = r\left( s \right)$ | (1) |
|
| 图1 椭圆柱壳几何参数及坐标系 Figure 1 Geometry parameters and coordinate system of elliptic cylindrical shell |
根据Flügge薄壳理论[18],壳体的几何方程为
| $\left\{ {\begin{array}{*{20}{l}} {{\varepsilon _x} = \frac{1}{{{r_0}}}\frac{{\partial u}}{{\partial x}},}\\ {{\varepsilon _s} = \frac{1}{{{r_0}}}\frac{{\partial v}}{{\partial s}} + \frac{w}{{{r_0}r}},}\\ {{\gamma _{xs}} = \frac{1}{{{r_0}}}\frac{{\partial v}}{{\partial x}} + \frac{1}{{{r_0}}}\frac{{\partial u}}{{\partial s}},}\\ {{\kappa _x} = \frac{1}{{r_0^2}}\frac{{{\partial ^2}w}}{{\partial {x^2}}},}\\ {{\kappa _s} = \frac{1}{{r_0^2}}\frac{{{\partial ^2}w}}{{\partial {s^2}}} + \frac{w}{{r_0^2{r^2}}},}\\ {\tau = \frac{1}{{r_0^2}}\frac{{{\partial ^2}w}}{{\partial x\partial s}} + \frac{1}{{2r_0^2r}}\frac{{\partial u}}{{\partial s}} - \frac{1}{{2r_0^2r}}\frac{{\partial v}}{{\partial x}}} \end{array}} \right.$ | (2) |
式中:εx和εs为壳体中面内各点的线应变,γxs为剪应变,κx,κs和τ代表了中面内各点主曲率及扭率的改变。
壳体的物理方程为
| $\left\{ {\begin{array}{*{20}{l}} {{N_x} = K({\varepsilon _x} + \mu {\varepsilon _s})-\frac{D}{{{r_0}r}}{\kappa _x}}\\ {{N_s} = K({\varepsilon _s} + \mu {\varepsilon _x}) + \frac{D}{{{r_0}r}}{\kappa _s}}\\ {{N_{xs}} = K\frac{{1 - \mu }}{2}{\gamma _{xs}} - \frac{{D\left( {1 - \mu } \right)}}{{2{r_0}r}}(\tau - \frac{{{\gamma _{xs}}}}{{2{r_0}r}})}\\ {{N_{sx}} = K\frac{{1 - \mu }}{2}{\gamma _{xs}} + \frac{{D\left( {1 - \mu } \right)}}{{2{r_0}r}}(\tau + \frac{{{\gamma _{xs}}}}{{2{r_0}r}})}\\ {{M_x} = D({\kappa _x} + \mu {\kappa _s} - \frac{1}{{{r_0}r}}{\varepsilon _x} - \frac{\mu }{{{r_0}r}}{\varepsilon _s})}\\ {{M_s} = D({\kappa _s} + \mu {\kappa _x})}\\ {{M_{xs}} = D\left( {1 - \mu } \right)(\tau - \frac{{{\gamma _{xs}}}}{{2{r_0}r}})}\\ {{M_{sx}} = D\left( {1 - \mu } \right)\tau } \end{array}} \right.$ | (3) |
式中:K=Eh/(1-μ2) 为壳体的拉压刚度,D=Eh3/12(1-μ2) 为壳体的弯曲刚度,Nx、Ns分别为x和s方向单位宽度上的面内力,Nsx和Nxs为平面内单位宽度上的剪切力,Mx、Ms和Mxs、Msx分别为单位宽度上的弯矩和扭矩。
壳体的动力平衡方程为
| $\left\{ {\begin{array}{*{20}{l}} {\frac{1}{{{r_0}}}\frac{{\partial {N_x}}}{{\partial x}} + \frac{1}{{{r_0}}}\frac{{\partial {N_{sx}}}}{{\partial s}} + \rho h\frac{{{\partial ^2}u}}{{\partial {t^2}}} = 0}\\ {\frac{1}{{{r_0}}}\frac{{\partial {N_{xs}}}}{{\partial x}} + \frac{1}{{{r_0}}}\frac{{\partial {N_s}}}{{\partial s}} - \frac{{{Q_s}}}{{{r_0}r}} + \rho h\frac{{{\partial ^2}v}}{{\partial {t^2}}} = 0}\\ {\frac{1}{{{r_0}}}\frac{{\partial {Q_x}}}{{\partial x}} + \frac{1}{{{r_0}}}\frac{{\partial {Q_s}}}{{\partial s}} + \frac{{{N_s}}}{{{r_0}r}} - \rho h\frac{{{\partial ^2}w}}{{\partial {t^2}}} = F}\\ {\frac{1}{{{r_0}}}\frac{{\partial {M_x}}}{{\partial x}} + \frac{1}{{{r_0}}}\frac{{\partial {M_{sx}}}}{{\partial s}} - {Q_x} = 0}\\ {\frac{1}{{{r_0}}}\frac{{\partial {M_{xs}}}}{{\partial x}} + \frac{1}{{{r_0}}}\frac{{\partial {M_s}}}{{\partial s}} - {Q_s} = 0} \end{array}} \right.$ | (4) |
式中:Qx和Qs分别为x和s方向单位宽度上的横剪力,F为壳体法向受到的外力,外法线方向为正。
整理式 (4),可得到一组新的动力平衡方程:
| $\left\{ {\begin{array}{*{20}{l}} {\frac{1}{{{r_0}}}\frac{{\partial {N_x}}}{{\partial x}} + \frac{1}{{{r_0}}}\frac{{\partial {N_{sx}}}}{{\partial s}} + \rho h\frac{{{\partial ^2}u}}{{\partial {t^2}}} = 0}\\ {\frac{1}{{{r_0}}}\frac{{\partial {N_{xs}}}}{{\partial x}} + \frac{1}{{{r_0}}}\frac{{\partial {N_s}}}{{\partial s}} - \frac{1}{{r_0^2r}}\frac{{\partial {M_s}}}{{\partial s}} - \frac{1}{{r_0^2r}}\frac{{\partial {M_{xs}}}}{{\partial x}} + \rho h\frac{{{\partial ^2}v}}{{\partial {t^2}}} = 0}\\ {\frac{1}{{r_0^2}}\frac{{{\partial ^2}{M_x}}}{{\partial {x^2}}} + \frac{1}{{r_0^2}}\frac{{{\partial ^2}{M_{xs}}}}{{\partial x\partial s}} + \frac{1}{{r_0^2}}\frac{{{\partial ^2}{M_{xs}}}}{{\partial x\partial s}} + \frac{1}{{r_0^2}}\frac{{{\partial ^2}{M_s}}}{{\partial {s^2}}} + \frac{{{N_s}}}{{{r_0}r}}}\\ {\quad \quad - \rho h\frac{{{\partial ^2}w}}{{\partial {t^2}}} = F} \end{array}} \right.$ | (5) |
将方程组 (2)、(3) 代入方程 (5) 中,可得到矩阵形式表达的关于位移变量的动力平衡方程:
| $\left[ {\begin{array}{*{20}{l}} {{L_{11}}} & {{L_{12}}} & {{L_{13}}}\\ {{L_{21}}} & {{L_{22}}} & {{L_{23}}}\\ {{L_{31}}} & {{L_{32}}} & {{L_{33}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {u\left( {x,s,t} \right)}\\ {v\left( {x,s,t} \right)}\\ {w\left( {x,s,t} \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} 0\\ 0\\ F \end{array}} \right]$ | (6) |
式中各算子Lij(i,j=1,2,3) 表达式如下:
| $\begin{array}{l} {L_{11}} = \frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{1 - \mu }}{2}\frac{{{\partial ^2}}}{{\partial {s^2}}} - H\left( {1 - \mu } \right)\frac{{r_s^\prime }}{{{r^3}}}\frac{\partial }{{\partial s}} + \\ \quad \quad \quad H\frac{{1 - \mu }}{{2{r^2}}}\frac{{{\partial ^2}}}{{\partial {s^2}}} + \frac{{\rho r_0^2(1 - {\mu ^2}){\omega ^2}}}{E}\\ \quad \quad \quad \quad {L_{12}} = {L_{21}} = \frac{{1 + \mu }}{2}\frac{{{\partial ^2}}}{{\partial x\partial s}}\\ \quad \quad \quad {L_{13}} = {L_{31}} = \frac{\mu }{r}\frac{\partial }{{\partial x}} - \frac{H}{r}\frac{{{\partial ^3}}}{{\partial {x^3}}} - \\ \quad H\frac{{1 - \mu }}{2}\frac{{r_s^\prime }}{{{r^2}}}\frac{{{\partial ^2}}}{{\partial x\partial s}} + H\frac{{1 - \mu }}{2}\frac{1}{r}\frac{{{\partial ^3}}}{{\partial x\partial {s^2}}}\\ {L_{22}} = \frac{{1 - \mu }}{2}\frac{{{\partial ^2}}}{{\partial {x^2}}} + H\frac{{1 - \mu }}{2}\frac{1}{{{r^2}}}\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{{\partial ^2}}}{{\partial {s^2}}} + \\ \quad \quad \frac{H}{r}\left( {1 - \mu } \right)\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{{\rho r_0^2(1 - {\mu ^2}){\omega ^2}}}{E}\\ \quad {L_{23}} = - H\frac{{3 - \mu }}{2}\frac{1}{r}\frac{{{\partial ^3}}}{{\partial {x^2}\partial s}} - \frac{{r_s^\prime }}{{{r^2}}} + \frac{1}{r}\frac{\partial }{{\partial s}} - \\ \quad \quad \quad H\frac{{r_s^\prime }}{{{r^4}}} - H\frac{{r_s^\prime }}{{{r^2}}}\frac{{{\partial ^2}}}{{\partial {s^2}}}\\ {L_{32}} = - H\frac{{1 + \mu }}{2}\frac{1}{r}\frac{{{\partial ^3}}}{{\partial {x^2}\partial s}} - H\left( {1 - \mu } \right)\frac{{{\partial ^3}}}{{\partial {x^2}\partial s}} + \\ \quad \quad \quad \quad H\frac{{1 - \mu }}{2}\frac{{r_s^\prime }}{{{r^2}}}\frac{{{\partial ^2}}}{{\partial {x^2}}} + \frac{1}{r}\frac{\partial }{{\partial s}}\\ {L_{33}} = H\frac{{{\partial ^4}}}{{\partial {x^4}}} + 2H\frac{{{\partial ^4}}}{{\partial {x^2}\partial {s^2}}} - 2H\left( {\frac{{r_s^\prime }}{{{2^3}}}} \right){\prime _s} - 4H\frac{{r_s^\prime }}{{{r^3}}}\frac{\partial }{{\partial s}} + \\ \quad \quad \frac{{2H}}{{{r^2}}}\frac{{{\partial ^2}}}{{\partial {s^2}}} + H\frac{{{\partial ^4}}}{{\partial {s^4}}} + \frac{1}{{{r^2}}} + \frac{H}{{{r^4}}} - \frac{{\rho r_0^2(1 - {\mu ^2}){\omega ^2}}}{E} \end{array}$ |
式中:
设柱壳在点 (x0,s0) 处受到简谐点激励载荷:
| $F\left( {x,s,t} \right) = {F_0}\delta \left( s \right)\delta \left( x \right){\rm{exp}}({\rm{i}}\omega t - {\rm{i}}{k_l}x)$ | (7) |
式中:F0表示作用在 (x0,s0) 处的集中力幅值。当在椭圆柱壳上作用多个集中点激励力时,将式 (7) 中的s改写为sj(j=0,1,2,…)。式 (7) 中,令x=0,s=s0得:
| $F\left( {x,s,t} \right) = {F_0}\delta ({s_0})\delta \left( 0 \right){\rm{exp}}({\rm{i}}\omega t)$ | (8) |
对于对称位移模式,将其展开成周向波数叠加的形式:
| $F\left( {x,s,t} \right) = \sum\limits_{n = 0}^\infty {{F_n}{\rm{cos}}\left( {ns} \right)\delta \left( 0 \right){\rm{exp}}({\rm{i}}\omega t)} $ | (9) |
联立式 (8) 和 (9) 可得
| ${F_0}\delta ({s_0})\delta \left( 0 \right){\rm{exp}}({\rm{i}}\omega t) = \sum\limits_{n = 0}^\infty {{F_n}{\rm{cos}}\left( {ns} \right)\delta \left( 0 \right){\rm{exp}}({\rm{i}}\omega t)} $ | (10) |
对式 (10) 进行正交化处理可得
| ${F_n} = \frac{{{F_0}{\rm{cos}}\left( {n{s_0}} \right)}}{{{\xi _n}{\rm{\pi }}{r_0}}}$ | (11) |
对于反对称位移模式:
| ${F_n} = \frac{{{F_0}{\rm{cos}}\left( {n{s_0}} \right)}}{{{\xi _n}{\rm{\pi }}{r_0}}}$ | (12) |
式中:ξn为与周向波数n相关的系数:
| ${\xi _n} = \left\{ {\begin{array}{*{20}{l}} {2,n = 0}\\ {1,n \ne {0^ \circ }} \end{array}} \right.$ |
为求解方程 (6),需将各算子Lij(i,j=1,2,3) 转变为常系数的偏微分形式,则需要给出椭圆柱壳截面的曲率半径r(s) 的具体表达式。Marguerre[17]首先提出了用傅里叶级数表示非圆截面曲率半径的方法。随后Romano等将Marguerre的方法进行了简化[19],只取傅里叶级数的前两项来表示椭圆截面的曲率半径,其无量纲化表达式为
| $\frac{1}{{r\left( s \right)}} = 1 + \varepsilon {\rm{cos}}\left( {2s} \right)$ | (13) |
式中:s表示椭圆截面无量纲化的周向弧长坐标,0≤s≤2π;ε为截面的椭圆度参数,为了不产生负曲率,定义0≤ε≤1,改变ε的正负号只是相当于将壳体沿其对称轴转动π/2,因此,只需考虑椭圆度ε为正的情况,即0≤ε≤1。ε和椭圆长短轴a,b之间的关系为[19]
| $\varepsilon = 3Q - 36/35{Q^3}$ | (14) |
式中:
将壳体各位移在轴向和周向展开成双Fourier级数的形式。对于圆柱壳结构,由于其圆截面关于任意通过圆心的直线对称,周向对称和反对称模态可通过偏转重合,计算中可以只考虑对称模态。而椭圆柱壳,其截面只关于长轴和短轴对称,计算中需同时考虑对称振型和反对称振型 (本文中椭圆柱壳对称和反对称振型均相对于其长轴)。对于周向对称振型,其展开形式为
| $\left\{ {\begin{array}{*{20}{l}} {u\left( {x,s,t} \right) = \sum\limits_{l = 1}^\infty {\sum\limits_{n = 0}^\infty {{U_{l,n}}{\rm{cos}}\left( {ns} \right){\rm{exp}}({\rm{i}}\omega t - {\rm{i}}{k_l}x)} } }\\ {v\left( {x,s,t} \right) = \sum\limits_{l = 1}^\infty {\sum\limits_{n = 1}^\infty {{V_{l,n}}{\rm{sin}}\left( {ns} \right){\rm{exp}}({\rm{i}}\omega t - {\rm{i}}{k_l}x)} } }\\ {w\left( {x,s,t} \right) = \sum\limits_{l = 1}^\infty {\sum\limits_{n = 0}^\infty {{W_{l,n}}{\rm{cos}}\left( {ns} \right){\rm{exp}}({\rm{i}}\omega t - {\rm{i}}{k_l}x)} } } \end{array}} \right.$ | (15) |
对于周向反对称振型,其展开形式为
| $\left\{ {\begin{array}{*{20}{l}} {u\left( {x,s,t} \right) = \sum\limits_{l = 1}^\infty {\sum\limits_{n = 0}^\infty {{U_{l,n}}{\rm{sin}}\left( {ns} \right){\rm{exp}}({\rm{i}}\omega t - {\rm{i}}{k_l}x)} } }\\ {v\left( {x,s,t} \right) = \sum\limits_{l = 1}^\infty {\sum\limits_{n = 1}^\infty {{V_{l,n}}{\rm{cos}}\left( {ns} \right){\rm{exp}}({\rm{i}}\omega t - {\rm{i}}{k_l}x)} } }\\ {w\left( {x,s,t} \right) = \sum\limits_{l = 1}^\infty {\sum\limits_{n = 0}^\infty {{W_{l,n}}{\rm{sin}}\left( {ns} \right){\rm{exp}}({\rm{i}}\omega t - {\rm{i}}{k_l}x)} } } \end{array}} \right.$ | (16) |
式中:l是频散方程中轴向波数解的序号,n是周向波数,kl为壳体的轴向波数,Ul,n、Vl,n、Wl,n分别为对应于周向波数n的壳体轴向、周向和径向的位移Fourier幅值系数。
将方程 (13) 和 (15) 代入到平衡方程 (6) 中 (周向反对称振型时则将方程 (16) 代入方程 (6)),通过级数变换可将方程 (6) 中的变系数转变为常系数,得到三个关于Ul,n、Vl,n、Wl,n沿周向波数相互耦合的新的方程:
| $\left\{ {\begin{array}{*{20}{l}} {({\alpha _1} - {\mathit{\Omega }^2}){U_{l,n}} + {\alpha _2}{U_{l,n - 2}} + {\alpha _3}{U_{l,n + 2}} + {\alpha _4}{U_{l,n - 4}} + }\\ {\;{\alpha _5}{U_{l,n + 4}} + {\alpha _6}{V_{l,n}} + {\alpha _7}{W_{l,n}} + {\alpha _8}{W_{l,n - 2}} + {\alpha _9}{W_{l,n + 2}} = 0}\\ {{\alpha _{10}}{U_{l,n}} + ({\alpha _{11}} - {\mathit{\Omega }^2}){V_{l,n}} + {\alpha _{12}}{V_{l,n - 2}} + {\alpha _{13}}{V_{l,n + 2}} + }\\ {\;{\alpha _{14}}{V_{l,n - 4}} + {\alpha _{15}}{V_{l,n + 4}} + {\alpha _{16}}{W_{l,n}} + {\alpha _{17}}{W_{l,n - 2}} + {\alpha _{18}}{W_{l,n + 2}} + }\\ {{\alpha _{19}}{W_{l,n - 4}} + {\alpha _{20}}{W_{l,n + 4}} + {\alpha _{21}}{W_{l,n - 6}} + {\alpha _{22}}{W_{l,n + 6}} = 0}\\ {{\alpha _{23}}{U_{l,n}} + {\alpha _{24}}{U_{l,n - 2}} + {\alpha _{25}}{U_{l,n + 2}} + {\alpha _{26}}{V_{l,n}} + {\alpha _{27}}{V_{l,n - 2}} + }\\ {\;{\alpha _{28}}{V_{l,n + 2}} + ({\alpha _{29}} - {\mathit{\Omega }^2}){W_{l,n}} + {\alpha _{30}}{W_{l,n - 2}} + {\alpha _{31}}{W_{l,n + 2}} + }\\ {\;{\alpha _{32}}{W_{l,n - 4}} + {\alpha _{33}}{W_{l,n + 4}} + {\alpha _{34}}{W_{l,n - 6}} + {\alpha _{35}}{W_{l,n + 6}} + }\\ {\;{\alpha _{36}}{W_{l,n - 8}} + {\alpha _{37}}{W_{l,n + 8}} = \frac{{{\mathit{\Omega }^2}}}{{\rho h{\omega ^2}}}\frac{{{F_0}{\rm{cos}}(n{s_0})}}{{{\xi _n}{\rm{ \mathsf{ π} }}{r_0}}}} \end{array}} \right.$ | (17) |
式中:
方程 (17) 中的位移幅值Ul,n、Vl,n、Wl,n关于不同周向波数n相互耦合成无穷多个线性方程,需对方程组进行截断求解,即对n进行截断选取。
当n取有限项p时,可以得到3p个线性方程,并写成矩阵形式:
| $[\mathit{\boldsymbol{M}} - {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^2}\mathit{\boldsymbol{I}}]\mathit{\boldsymbol{X}} = \mathit{\boldsymbol{F}}$ | (18) |
其中,X=
[Ul,0Ul,1Ul,2…Ul,p-1Vl,0Vl,1Vl,2…Vl,p-1Wl,0Wl,1Wl,2…Wl,p-1]-1;对于对称位移形式:F=
对于反对称位移形式
| $\mathit{\boldsymbol{F}} = \frac{{{\mathit{\Omega }^2}{F_0}}}{{\rho h{\omega ^2}\pi {r_0}}}.$ |
[0 0 0… 0 sin (s0) sin (2s0)…sin ((p-1)s0)]-1。
M为3p阶方阵,由方程 (17) 中的系数循环迭代而成,I为3p阶单位矩阵,X和F均为3p阶列向量。
由方程 (18) 可得
| $\mathit{\boldsymbol{X}} = {[\mathit{\boldsymbol{M}} - {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^2}\mathit{\boldsymbol{I}}]^{ - 1}}\mathit{\boldsymbol{F}}$ | (19) |
则壳体位移幅值系数Ul,n、Vl,n、Wl,n可由方程 (19) 得到。
3 壳体输入功率流根据振动功率流的定义,因外激励力呈简谐变化,故位移响应和速度响应均呈简谐变化,设
| $F\left( t \right) = {\rm{Re}}[\bar F{\rm{exp}}({\rm{i}}\omega t)]$ | (20) |
| $V\left( t \right) = {\rm{Re}}[\bar V{\rm{exp}}({\rm{i}}\omega t)]$ | (21) |
则:
| $\begin{array}{l} \quad \quad \quad {P_{{\rm{in}}}} = \frac{1}{T}\smallint _0^TF\left( t \right)V(t){\rm{d}}t = \\ \frac{1}{T}\smallint _0^T{\rm{Re}}[\bar F{\rm{exp}}({\rm{i}}\omega t)]{\rm{Re}}[\bar V{\rm{exp}}({\rm{i}}\omega t)]{\rm{d}}t = \\ \quad \quad \quad \quad \quad \frac{1}{2}{\rm{Re}}(\bar F \cdot {{\bar V}^*}) \end{array}$ | (22) |
因此,可以求得外力输入到结构的振动功率流为
| $\begin{array}{l} \quad \quad \quad {P_{{\rm{in}}}} = \frac{1}{2}{\rm{Re}}[F\frac{{\partial {w^*}}}{{\partial t}}] = \\ \sum\limits_{l,n} {\frac{{\mathit{\Omega }{F_0}{{\cos }^2}\left( {n{s_0}} \right)}}{{{r_0}}}} \sqrt {\frac{E}{{\rho \left( {1 - {\mu ^2}} \right)}}} {\rm{Re}}\left( {W_{l,n}^*} \right) \end{array}$ | (23) |
为便于比较,将输入功率流无量纲化为
| $P_{{\rm{in}}}^\prime = \frac{{{P_{{\rm{in}}}}}}{{F_0^2\pi }}\sqrt {\rho E{R^2}(1 - {\mu ^2})} $ | (24) |
将振动功率流进行级运算可得
| ${L_p} = 10{\rm{lg}}\left( {\frac{{{P_{{\rm{in}}}}}}{{{W_0}}}} \right)$ | (25) |
式中:W0=1×10-12W。
3.1 算法收敛性及准确性验证由式 (23) 可知,要计算结构在外力作用下输入功率流,必须计算其中的无穷积分,而由于被积函数在对应于传播波的实轴上的奇点处的值为无穷大,这样积分便不能进行。这里采用文献[20]中所采用的加阻尼数值积分法,这种方法是指在求解积分时,沿着复波数域的纯实轴进行数值积分,而为了避免积分中奇点的出现,引入阻尼因子η,将材料的杨氏模量变为复模量,即E′=E(1-iη)。本文采用十点高斯积分法处理式 (23) 中的无穷积分。
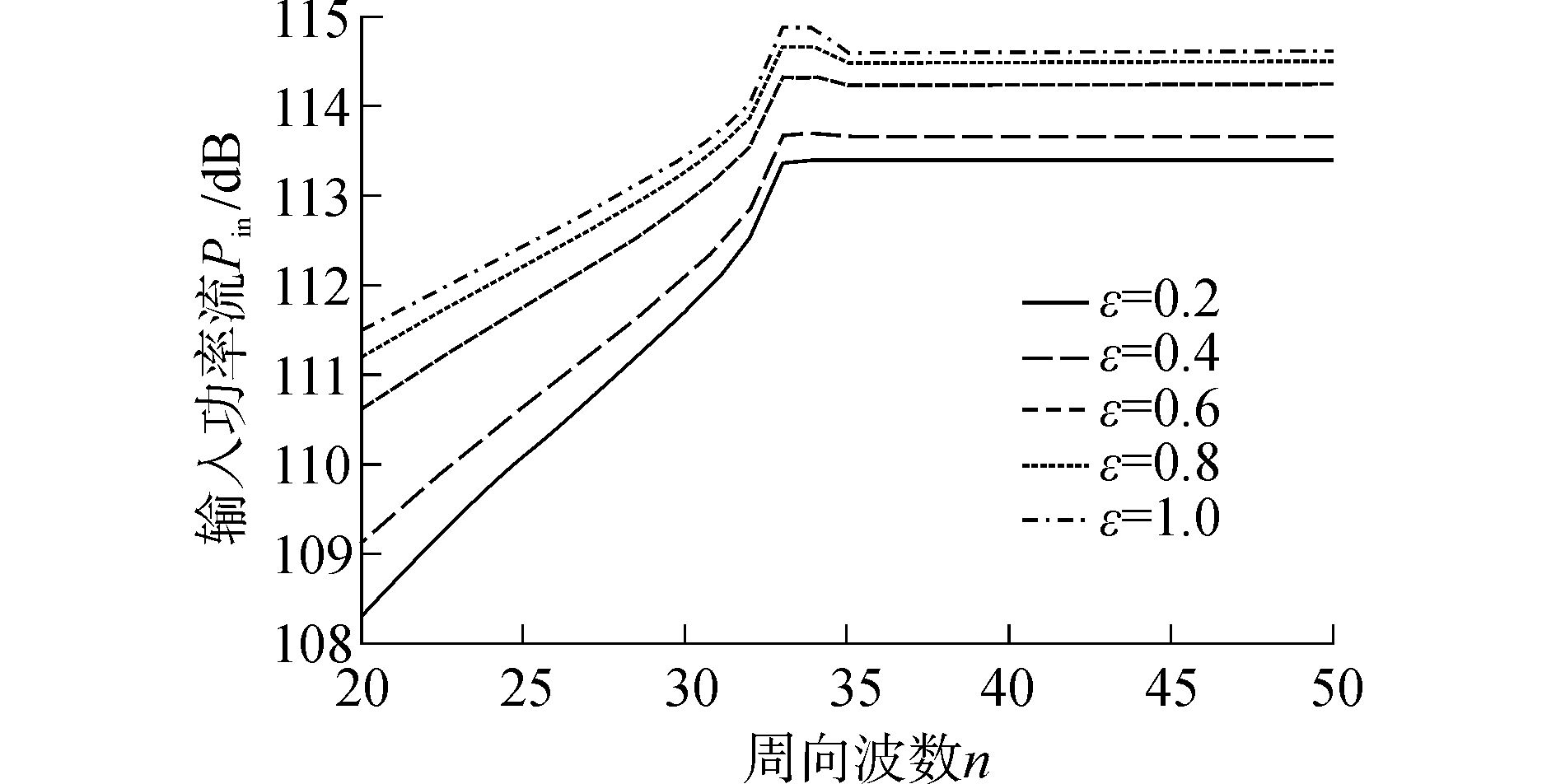
对周向波数n的截断选取进行收敛性分析,壳体输入功率流随周向波数的变化如图 2所示,壳体无限长,材料密度为ρ=7 800 kg/m3,杨氏模量为E=2.1×1011 Pa,泊松比为μ=0.3,壳体厚度为h=0.01 m,中面半径r0=1 m,纵波波速CL=5 200 m/s,点激励力幅值F0=1 N,无量纲频率Ω=3,阻尼因子取η=0.01。
|
| 图2 输入功率流随周向波数的收敛性曲线 Figure 2 Convergence curves of input power flow with circumferential wave number |
从图 2中可以看出,当椭圆度较小时,计算结果收敛所需的截断项数相对要少,当椭圆度较大时,则需取更高的截断项数以保证结果的准确性,但相差不大。随着截断项数的增加,计算结果的精度会更高,但过多的截断项数会导致计算效率的降低,从图中可以看出,在周向模态n=40下,不同椭圆度时椭圆柱壳的输入功率流均趋于稳定,在本文计算中取n=40。
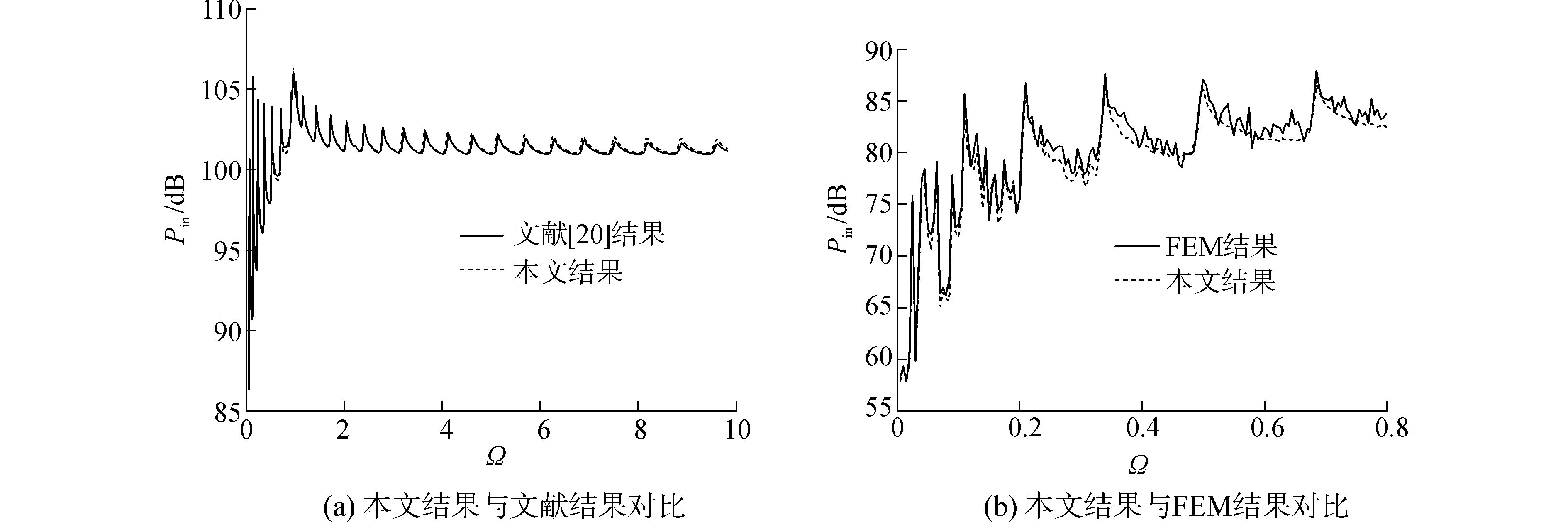
为了验证本文计算方法及程序的可靠性,在本文方法中令椭圆柱壳椭圆度ε=0,将其退化为圆柱壳,与已有文献[20]的无限长圆柱壳结果进行对比,结果如图 3(a)所示。同时选取有限长椭圆柱壳与有限元法 (finite element method,FEM) 结果进行了对比 (椭圆柱壳长度L=100m,椭圆度ε=0.5,其他参数如文献[20]),对比结果如图 3(b)所示。对于椭圆柱壳有限元模型,为满足每个振动弯曲波波长内至少6个单元,则单元尺寸约为0.06 m,单元数量为180 036个。同时还列出了采用本文算法和文献[20]及有限元法所需计算时间的对比,如表 1所示。
由图 3可见,本文计算结果与文献[20]结果和FEM结果均吻合很好,说明本文计算方法及程序准确可靠。本文计算方法中将不同周向波数的系数矩阵耦合成一个矩阵,不需要采用周向波数的循环叠加,相较文献[20]计算速度更快,计算时间约为文献方法的1/6。FEM方法在计算频率较高时,单元离散数量和计算时间均大幅增加,相较于数值仿真方法,本文方法依然具有较高的计算效率,计算时间约为FEM方法的1/50。
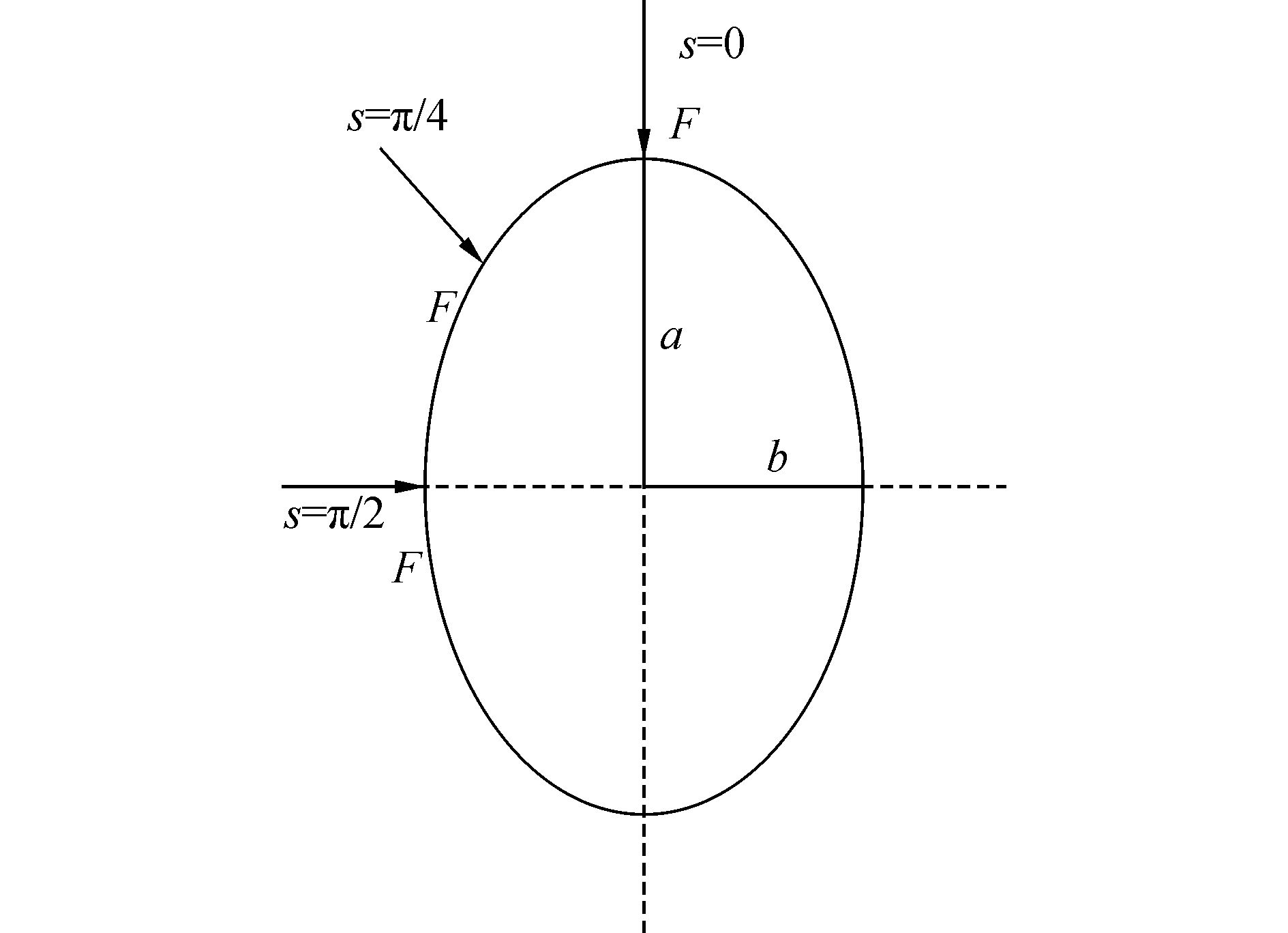
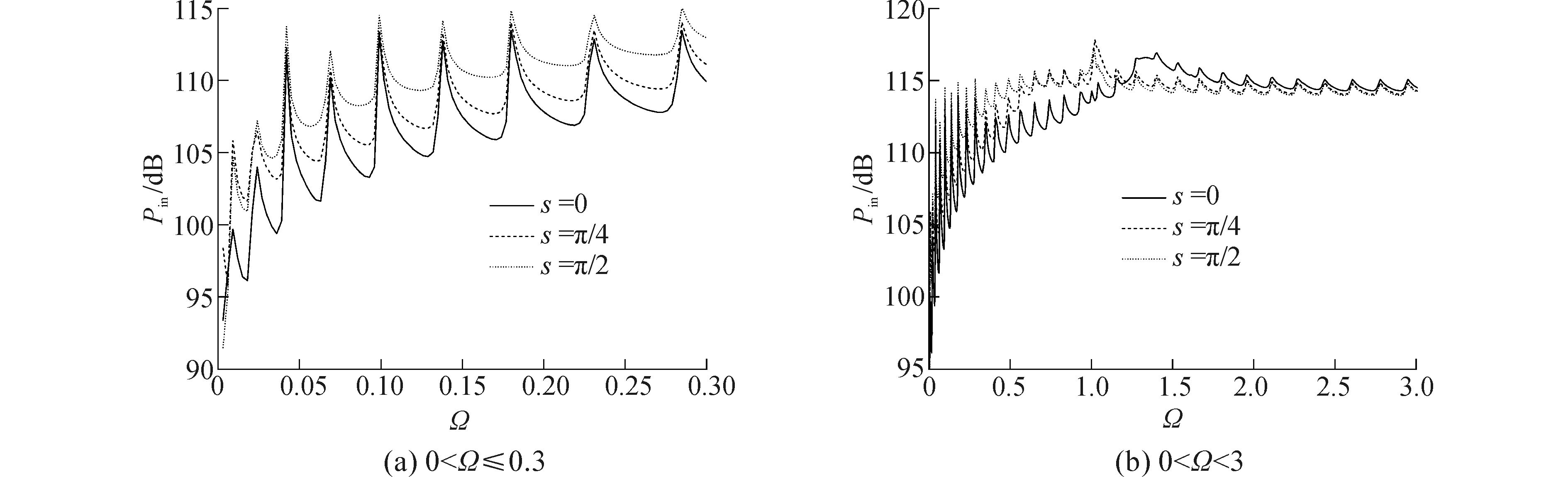
3.2 激励力位置对结构输入功率流的影响对于椭圆柱壳,截面各处的曲率沿周向是变化的,激励力施加在壳体截面不同位置也将对壳体的振动特性产生影响。本节研究了激励力分别施加在s为0、π/4、π/2位置对壳体输入功率流的影响,激励力位置如图 4所示,不同激励力下的输入功率流如图 5所示。壳体椭圆度ε=0.5,其他模型参数如上文。
|
| 图4 不同激励力周向的位置 Figure 4 Different exciting force positions in circumferential direction |
|
| 图5 不同激励力位置下椭圆柱壳输入功率流 Figure 5 Comparison of input power flow with different exciting force positions |
从图 5可以看出,激励力施加在不同位置对椭圆柱壳的输入功率流有明显的影响:在低频段 (Ω<1),激励力施加在s=0的位置壳体输入功率流相对较小,施加在s=π/2的位置输入功率流相对较大,主要由于在s=0的位置,壳体截面曲率较大,局部刚度相对也较大,激励点的位移响应较小,因此输入功率流也较小,而在s=π/2的位置,壳体截面曲率较小,局部刚度相对较小,响应较大,则输入功率流也较大。而在中高频段 (Ω>1.5),激励力施加在各位置点输入功率流差异较小,激励力施加在s=0的位置输入功率流略大,施加在s=π/2的位置输入功率流略小,主要由于在中高频段,壳体振动弯曲波波长较短,壳体曲率对结构振动弯曲波传播和振动响应的影响降低。
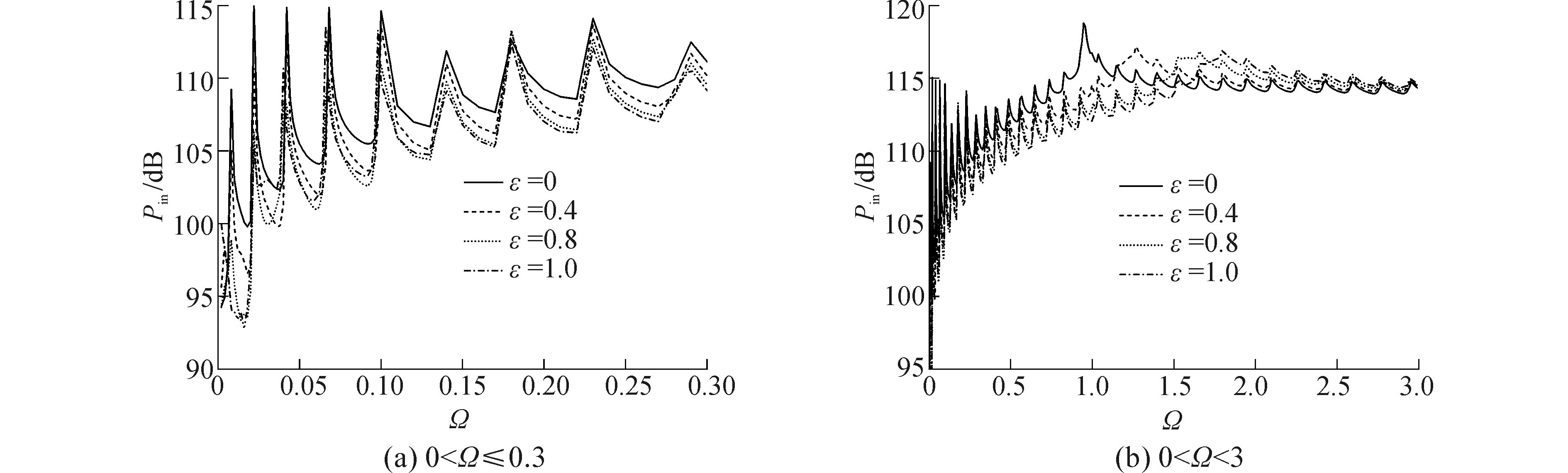
3.3 椭圆度对结构输入功率流的影响椭圆柱壳的椭圆度大小不同,对椭圆柱壳的结构刚度、振动特性等影响也不相同,因此本节研究了椭圆度对椭圆柱壳输入功率流的影响,同时也与圆柱壳 (即椭圆度ε=0) 作了对比,激励力位置取s=0。图 6给出了不同椭圆度下椭圆柱壳的输入功率流随频率变化。
|
| 图6 不同椭圆度下椭圆柱壳输入功率流对比 Figure 6 Comparison of input power flow with different ellipticities |
由图 6可以看出,不同椭圆度下椭圆柱壳的输入功率流曲线在总体趋势上有一定的相似性:输入功率流随频率的增大而不断出现峰值,峰值对应的频率差异较小,输入功率流随频率变化的总体趋势是先增大后趋于平稳。但椭圆度对椭圆柱壳的输入功率流也有一定影响:在无量纲频率Ω<1,椭圆度越大则壳体的输入功率流越小,主要是因为激励力在s=0处,椭圆度越大则壳体局部曲率较大,相对刚度也较大,因此响应和输入功率流会变小。同时,由于在低频段壳体振动波波长较大,椭圆度对振动响应的影响较明显,而较高的频率范围内 (Ω>2),壳体振动波波长较短,曲率影响较小,椭圆度对壳体输入功率流的影响也较小。
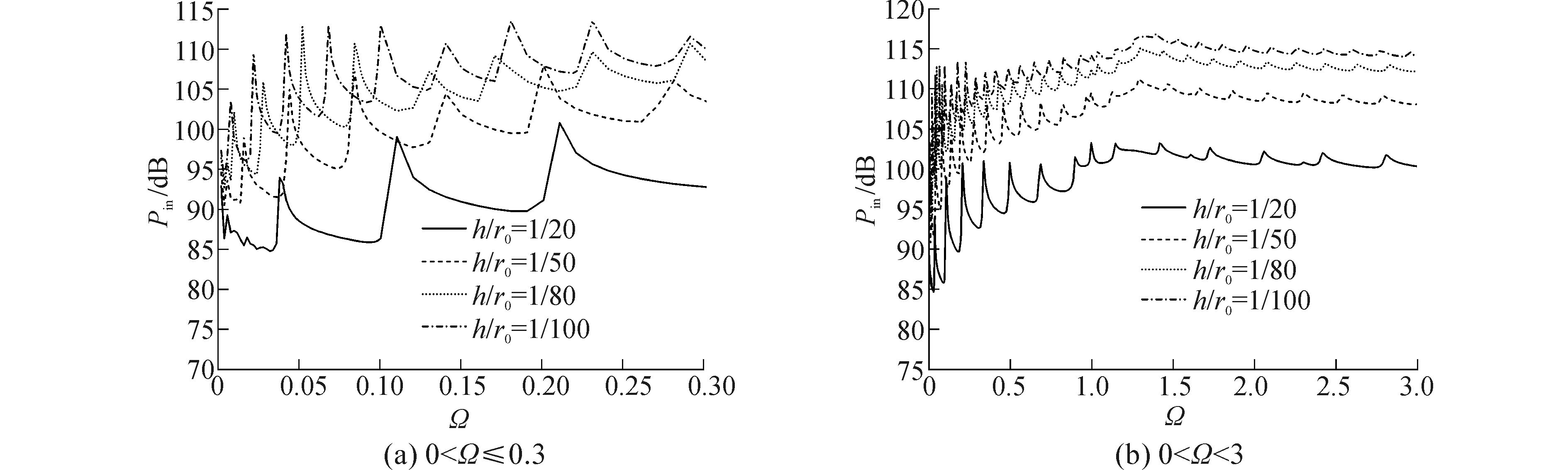
3.4 壳厚比对结构输入功率流的影响半径及壁厚作为椭圆柱壳的主要参数,研究其对椭圆柱壳振动特性的影响是必要的。由于本文采用了无量纲化参数,半径及壁厚的影响可以用无量纲化的壳厚比h/r0替代,因此,本节研究了不同壳厚比对椭圆柱壳输入功率流的影响。图 7给出了不同壳厚比椭圆柱壳的输入功率流随频率的变化曲线。
|
| 图7 不同壳厚比椭圆柱壳输入功率流对比 Figure 7 Comparison of input power flow with different thickness ratios |
由图 7可以看出,椭圆柱壳壳厚比的改变对输入功率流的大小及峰值频率均有明显影响,当壳厚比减小时,输入功率流的峰值向低频偏移且较为明显,说明壳厚比减小,椭圆柱壳的刚度降低,周向波数对应的频率降低;当壳厚比减小时,结构的输入功率流增大,说明壳厚比减小,椭圆柱壳抗振能力降低。壳厚比的改变对椭圆柱壳输入功率流最大值对应频率没有明显影响。
4 结论本文采用级数变换法将变系数的椭圆柱壳偏微分方程组转换为周向波数相互耦合的有限阶常系数线性方程组,通过求解得到椭圆柱壳受迫振动下的位移响应,分析了激励力位置、椭圆度ε和壳厚比h/r0对壳体输入功率流的影响,得到结论:
1) 本文计算方法将振动方程不同周向波数的系数矩阵耦合成一个矩阵,不需要采用周向波数循环叠加,计算速度更快,相比于数值仿真方法,本文方法的计算效率也较高。
2) 椭圆柱壳的输入功率流与激励点的位置有关,相同载荷作用下,激励沿着长半轴方向激励的输入功率流最小,沿着短半轴方向激励的输入功率流最大。
3) 椭圆度对壳体输入功率流的影响主要在低频域,当激励沿着长半轴时,椭圆度越大则壳体的输入功率流越小,在高频域振动波波长变短,椭圆度引起的曲率变化对输入功率流的影响减弱。
4) 壳厚比减小,椭圆柱壳输入功率流峰值向低频偏移且幅值增大;壳厚比的改变对椭圆柱壳输入功率流最大值对应频率没有明显影响。
| [1] |
张盛, 金翔, 周桦, 等. 加肋圆柱壳制造误差对声学性能的影响研究[J].
中国舰船研究, 2011, 6(4): 43–50.
ZHANG Sheng, JIN Xiang, ZHOU Hua, et al. Influence of construction error on sound radiation for ring-stiffened cylindrical shell[J]. Chinese journal of ship research, 2011, 6(4): 43–50. |
| [2] | KLOSNER J M, POHLE F V. Natural frequencies of an infinitely long noncircular cylindrical shell[R]. Polytechnic Institute of Brooklyn, PIBAL Report No. 478, 1958. |
| [3] | KLOSNER J M. Frequencies of an infinitely long noncircular cylindrical shell-part 2, plane strain, torsional, and flexural modes[R].Polytechnic Institute of Brooklyn, PIBAL Report No. 552, 1959. |
| [4] | SEWALL J L, THOMPSON W M, PUSEY C G. An experimental and analytical vibration study of elliptical cylindrical shells[R]. National aeronautics and space administration, TN D-6089, 1971. |
| [5] | SHIRAKAWA K, MORITA M. Vibration and buckling of cylinders of elliptical cross section[J]. Journal of sound and vibration, 1982, 84(1): 121–131. DOI:10.1016/0022-460X(82)90436-9 |
| [6] | KHALIFA M. Effects of non-uniform Winkler foundation and non-homogeneity on the free vibration of an orthotropic elliptical cylindrical shell[J]. European journal of mechanics-A/solids, 2015, 49: 570–581. DOI:10.1016/j.euromechsol.2014.09.009 |
| [7] |
曹雷, 马运义, 黄玉盈. 环肋加强变厚度圆柱壳的自由振动[J].
华中科技大学学报:城市科学版, 2007, 24(2): 63–66.
CAO Lei, MA Yunyi, HUANG Yuying. Free vibration of ring-stiffened circular cylindrical shell with variable thickness[J]. Journal of Huazhong University of science and technology:urban science edition, 2007, 24(2): 63–66. |
| [8] | TORNABENE F, FANTUZZI N, BACCIOCCHI M, et al. Dynamic analysis of thick and thin elliptic shell structures made of laminated composite materials[J]. Composite structures, 2015, 133: 278–299. DOI:10.1016/j.compstruct.2015.06.052 |
| [9] |
倪樵, 艾国庆. 深水中复合材料椭圆柱壳声辐射的数值分析[J].
华中科技大学学报, 2007, 34(12): 77–79.
NI Qiao, AI Guoqing. Numerical analysis of acoustic radiation by composite elliptic cylindrical shell submerged in deep water[J]. Journal of Huazhong University of Science and Technology, 2007, 34(12): 77–79. |
| [10] |
石焕文, 杨凯, 张玉海. 不同激励对椭圆柱壳声振特性的影响规律[C]//第十届中国CAE工程分析技术年会会议论文集. 2014: 76-81.
SHI Huanwen, YANG Kai, ZHANG Yuhai. Effect of different excitations on the vibration and sound characteristics of elliptical cylinder shells[C]//The Tenth China CAE Engineering Analysis Technology Conference.2014:76-81. |
| [11] | ZHANG X M, LIU G R, LAM K Y. Vibration analysis of thin cylindrical shells using wave propagation approach[J]. Journal of sound and vibration, 2001, 239(3): 397–403. DOI:10.1006/jsvi.2000.3139 |
| [12] | ZHANG X M. Frequency analysis of submerged cylindrical shells with the wave propagation approach[J]. International journal of mechanical sciences, 2002, 44(7): 1259–1273. DOI:10.1016/S0020-7403(02)00059-0 |
| [13] |
陈美霞, 张聪, 邓乃旗. 波传播法求解低频激励下水中加端板圆柱壳的振动[J].
振动工程学报, 2014, 27(6): 842–851.
CHEN Meixia, ZHANG Cong, DENG Naiqi, et al. Analysis of the loe frequency vibration of a submerged cylindrical shell with endplates based on wave propagation approach[J]. Journal of vibration engineering, 2014, 27(6): 842–851. |
| [14] |
李天匀, 郭文杰, 朱翔, 等. 水下圆锥壳临界载荷-频率特性分析[J].
哈尔滨工程大学学报, 2015, 36(6): 746–749.
LI Tianyun, GUO Wenjie, ZHU Xiang, et al. Frequency characteristic analysis of critical loads for a submerged conical shell[J]. Journal of Harbin Engineering University, 2015, 36(6): 746–749. |
| [15] |
江丰. 粘性流场中圆柱壳耦合系统声振特性研究[D]. 武汉: 华中科技大学, 2013.
JIANG Feng. The vibro-acoustic characteristics of circular cylindrical shells immersed in viscous fluids[D]. Wuhan:Huazhong University of Science and Technology, 2013. |
| [16] |
叶文兵. 潜浮状态下圆柱壳结构的声振特性研究[D]. 武汉: 华中科技大学, 2012.
YE Wenbing. The vibro-acoustic characteristics of cylindrical shells in the state of immersion and floating[D]. Wuhan:Huazhong University of Science and Technology, 2012. |
| [17] | MARGUERRE K. Stability of the cylindrical shells of variable curvature[R]. NASA TM 1302, 1951. |
| [18] | FLVGGE W. Stress in shells[J]. Second Edition. Berlin and New York:Spring-Verlag, 1973:204-219. |
| [19] | ROMANO F, KEMPNER J. Stresses in short noncircular cylindrical shells under lateral pressure[J]. Journal of applied mechanics, 1962, 29(4): 669–674. DOI:10.1115/1.3640652 |
| [20] |
徐慕冰. 圆柱壳-流场耦合系统的振动波传播与能量流研究[D]. 武汉: 华中科技大学, 1999.
XU Mubing. Wave propagation and power flow in a cylindrical shell-fluid coupled system[D]. Wuhan:Huazhong University of Science and Technology, 1999. |