2. School of Mechanical Engineering and Automation, Dalian Polytechnic University, Dalian 116034, China
风电主轴承的结构设计对于主轴承的综合性能有重要的影响, 风电设备的整体性能和可靠性在很大程度上也依赖于其所选用的主轴承的性能, 因此设计和制造出具有良好综合性能的风电主轴承显得格外重要。
计算滚动轴承内部载荷分布并以此为依据来预测其刚度和疲劳寿命的分析方法一般是基于赫兹弹性接触理论和和Sjovall积分的。Jones[1]提出了适用于球轴承和圆柱滚子轴承拟静力学模型的理论基础。拟静力学模型用于研究滚动轴承在外载荷、惯性效应(滚动体离心力等)、位移约束件下滚动轴承的稳态力学问题。Andréason[2]是首批研究低速圆锥滚子轴承的作者之一, 他采用基于向量的方法来描述轴承内部几何体的受力以及位移。Liu[3]考虑了离心力和陀螺力矩的因素来研究高速旋转下的圆锥滚子轴承。Tong等[4]用Liu的模型研究了单列圆锥滚子轴承在径向力和倾覆力矩作用下的受力状况。Kabus等[5]提出了一种六自由度模型来计算单列圆锥滚子轴承中接触应力沿圆锥滚子素线分布情况。罗继伟等[6]、胡浪等[7-8]对双列圆锥滚子轴承进行了一定的研究, 但是其分析模型无法求解实际复杂工况下的受力情况。Bercea等[9-10]提出了一种基于向量坐标运算的模型, 虽然能够分析复杂工况下受力情况, 但其数值计算收敛性较差。
为弥补上述不足, 本文基于坐标向量运算和旋转矩阵提出了一种分析模型, 能够快速准确计算双列圆锥滚子轴承在复杂工况下轴承内部的载荷分布情况, 且数值计算收敛性好。通过将该模型应用于风电主轴承, 得到了不同工况下的轴承内部载荷分布以及轴承整体寿命, 并得到了不同轴向游隙下轴承疲劳寿命曲线, 为风电主轴承的设计、制造提供了数据支持。
1 拟静力学模型 1.1 双列圆锥滚子轴承几何要素双列圆锥滚子轴承有背对背安装和面对面安装两种安装方式, 在背对背安装方式中, 轴承能够承受较大的弯矩, 两列滚子载荷线沿轴承的轴线分散;在面对面安装方式中, 轴向游隙具有良好的调节性, 两列滚子载荷线沿轴线收敛。
兆瓦级风电主轴承中双列圆锥滚子轴承采用背对背的安装方式, 其整体模型如图 1所示。
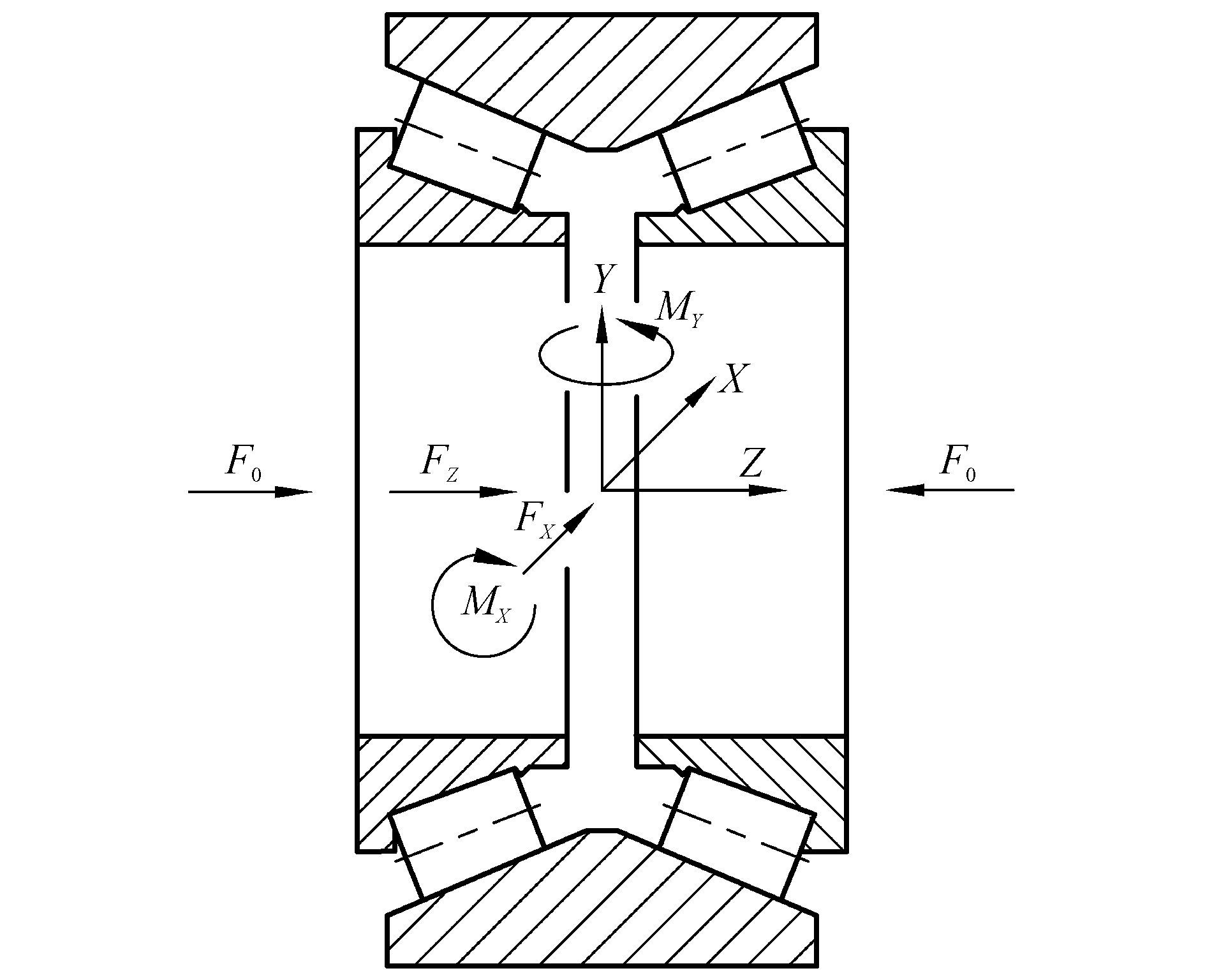
|
| 图1 双列圆锥滚子轴承模型图 Figure 1 Schematic view of a double-row tapered roller bearing |
在本文模型中, 做如下假设:
1) 轴承各部分材料均为线弹性。
2) 滚子和滚道都是直线轮廓。
3) 忽略内摩擦力和内摩擦力矩。
4) 忽略保持架的影响。
5) 外圈固定。
惯性参考系固定在轴承外圈上, 其原点在模型图中心, 坐标系的方向如图 1所示。轴承在运转过程中受到如下载荷:
1) 预紧力F0, F0沿Z轴方向;
2) 轴向力Fz, 径向力Fx和Fy;倾覆力矩Mx和My;
上述力和力矩的方向在图示坐标系中符合笛卡尔坐标系中右手螺旋法则。
轴承内圈和滚子在外部力和力矩的作用下相对于初始位置会发生平移和旋转, 平移向量和旋转向量可以在惯性坐标系中表示为
平移向量:
| ${\mathit{\boldsymbol{U}}_m} = {\left( {{\delta _{x,m}},{\delta _{y,m}},{\delta _{z,m}}} \right)^{\rm{T}}}$ | (1) |
旋转向量:
| $\mathit{\boldsymbol{ \boldsymbol{\varGamma} }} = {\left( {{\theta _x},{\theta _y},0} \right)^{\rm{T}}}$ | (2) |
式中:δx,m、δy,m、δz,m、θx、θy是内圈相对于惯性坐标系的线位移和角位移, m表示列数, m = 1 表示第一列, m = 2 表示第二列。
1.1.1 滚子质心初始位置向量由图 1所示几何关系得, 滚子质心初始位置向量为
| ${\mathit{\boldsymbol{R}}_1} = {\left( {{{{d_r}} \over 2}{\rm{sin}}\varphi i,{{{d_r}} \over 2}cos\varphi i, \mp {{{d_c}} \over 2}} \right)^{\rm{T}}}$ | (3) |
式中:dc为两列滚子质心距离在Z轴的投影长度, dr为轴承节圆直径, φi为第i个滚子与Y轴之间的夹角, “-”表示第一列滚子, “+”表示第二列滚子。
1.1.2 滚子质心最终位置向量假设双列圆锥滚子轴承在初始条件下的轴向游隙为δa0, 则每列滚子由于轴向游隙的存在而产生的位移向量为
| ${\mathit{\boldsymbol{R}}_{a0}} = {\left( {0,0, \pm {{{\delta _{a0}}} \over 2}} \right)^{\rm{T}}}$ | (4) |
式中:“+”表示第一列滚子, “-”表示第二列滚子。
在轴向预紧力F0的作用下, 每列滚子产生的位移向量为
| ${\mathit{\boldsymbol{R}}_0} = {(0,0, \pm {\delta _0})^{\rm{T}}}$ | (5) |
式中:“+”表示第一列滚子, “-”表示第二列滚子。
| ${\delta _0} = {\left( {{{0.5 \times {F_0}} \over {Z{K_{ne}}{{(sin{\alpha _e})}^{2.11}}}}} \right)^{0.9}}$ | (6) |
式中:Kne为滚子与外滚道接触处的总刚度系数[6], Le为圆锥滚子的有效接触长度:
| $\eqalign{ & {K_{ne}} = 6.24 \times {10^4}L_e^{0.82}D_w^{0.11}{[1 + c{i^{0.9}}cos({\alpha _e} - \alpha i)]^{ - 1.11}} \cr & {L_e} = l/{\rm{cos}}0.5 \times \left( {{\alpha _e} - {\alpha _i}} \right)) \cr} $ | (7) |
轴承受力平衡后, 假设轴承内圈的位移向量为Um, 旋转向量为Γ, 通过旋转矩阵, 可得到滚子质心的最终位置向量为
| ${\mathit{\boldsymbol{R}}_2} = {\mathit{\boldsymbol{R}}_y}({\theta _y})\cdot{\mathit{\boldsymbol{R}}_x}({\theta _x})\cdot({\mathit{\boldsymbol{R}}_1} + {\mathit{\boldsymbol{R}}_0} + {\mathit{\boldsymbol{U}}_m} + {\mathit{\boldsymbol{R}}_{a0}})$ | (8) |
Rx(θ), Ry(θ)为绕x轴、y轴旋转矩阵:
| $\eqalign{ & {\mathit{\boldsymbol{R}}_x}(\theta ) = \left[ \matrix{ 1 & 0 & 0 \hfill \cr 0 & {\rm{cos}}\theta & - sin\theta \hfill \cr 0 & {\rm{sin}}\theta & {\rm{cos}}\theta \hfill \cr} \right] \cr & {\mathit{\boldsymbol{R}}_y}(\theta ) = \left[ \matrix{ {\rm{cos}}\theta & 0 & {\rm{sin}}\theta \hfill \cr 0 & 1 & 0 \hfill \cr - {\rm{sin}}\theta & 0 & {\rm{cos}}\theta \hfill \cr} \right] \cr} $ |
设圆锥滚子与内、外圈滚道和内圈挡边的接触力分别为Qi、Qe、Qf, 其接触角分别为αi、αe、αf, 滚子在Qi、Qe、Qf和离心力Fc的作用下达到平衡状态, 其受力示意图如图 2所示。
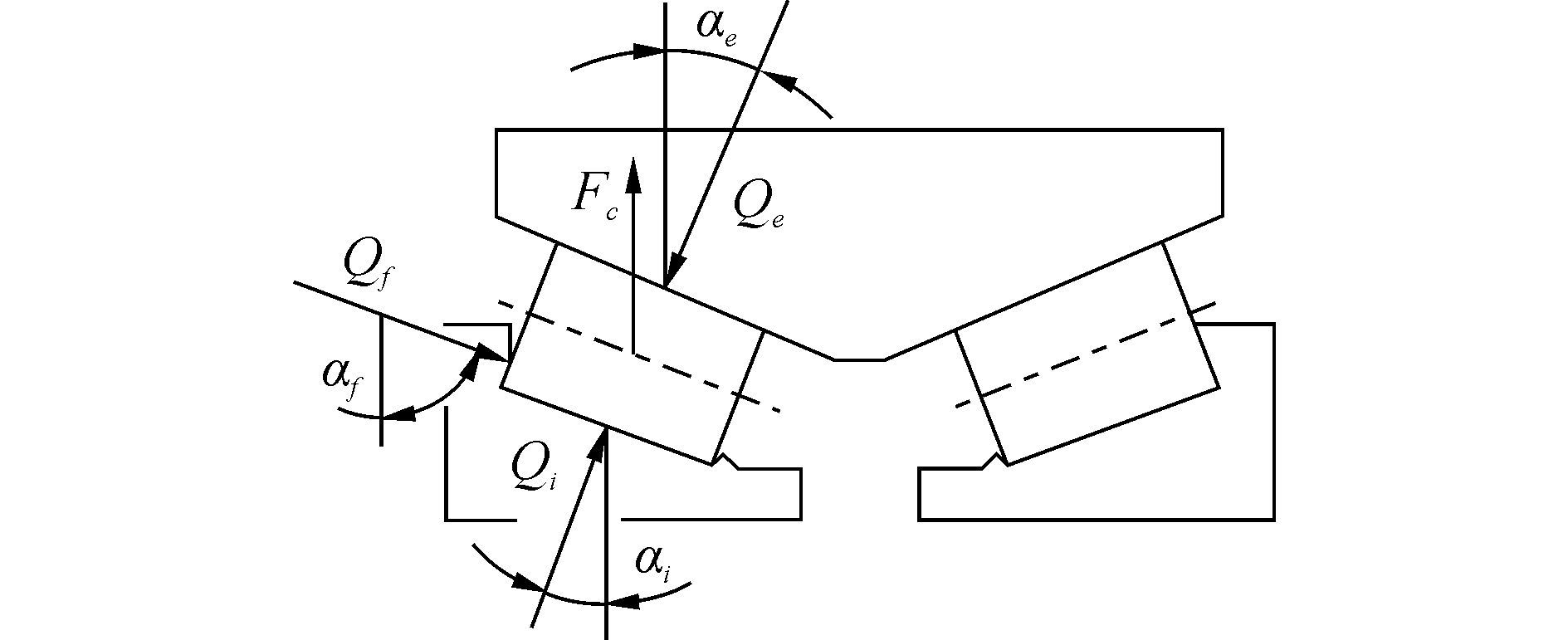
|
| 图2 圆锥滚子受力示意图 Figure 2 Forces analysis of tapered roller |
根据图 2列出圆锥滚子平衡方程:
| $\left\{ \matrix{ {Q_e}{\rm{sin}}{\alpha _e} - {Q_i}{\rm{sin}}{\alpha _i} - {Q_f}{\rm{sin}}{\alpha _f} = 0 \hfill \cr {Q_e}{\rm{cos}}{\alpha _e} - Qi{\rm{cos}}{\alpha _i} + {Q_f}{\rm{cos}}{\alpha _f} - {F_c} = 0 \hfill \cr} \right.$ | (9) |
解方程得
| ${Q_i} = {Q_e}{{{\rm{sin}}({\alpha _e} + {\alpha _f})} \over {{\rm{sin}}({\alpha _i} + {\alpha _f})}} - {F_c}{{{\rm{sin}}{\alpha _f}} \over {{\rm{sin}}(\alpha i + {\alpha _f})}}$ | (10) |
| ${Q_f} = {Q_e}{{{\rm{sin}}({\alpha _e} - {\alpha _i})} \over {{\rm{sin}}({\alpha _i} + {\alpha _f})}} + {F_c}{{{\rm{sin}}{\alpha _i}} \over {{\rm{sin}}({\alpha _e} + {\alpha _f})}}$ | (11) |
由图 2可知, 圆锥滚子与轴承外圈只有一个接触载荷Qe, 而与内圈有两个接触载荷, 因此在受力分析时可以把圆锥滚子-内圈作为力学分析的隔离体, 在求出滚子与外圈的载荷Qe后利用式(10) 和(11) 求得滚子与内圈滚道和挡边的载荷。
通过滚子质心的最终位置向量和初始位置向量, 可以求出滚子质心在滚子接触法线方向上的变形δn:
| ${\mathit{\boldsymbol{\delta }}_n} = ({\mathit{\boldsymbol{R}}_2} - {\mathit{\boldsymbol{R}}_1})\cdot{\mathit{\boldsymbol{n}}_m}$ | (12) |
式中:nm为滚子与滚道接触位置的单位法向量, m表示滚子列数:
n1=(cos αesin Φi,cos αecos Φi,sin αe)T, m = 1
n2=(cos αesin Φi,cos αecos Φi,-sin αe)T, m = 2
根据赫兹理论中接触载荷与接触刚度和变形的协调关系, 得到滚子受到外圈滚道的载荷为
| ${Q_e} = {K_{ne}}\cdot\delta _n^{10/9}$ | (13) |
由式(10) 、(11) 求出圆锥滚子与轴承内圈和挡边的接触载荷Qi和Qf。
根据受力关系, 圆锥滚子与外圈的接触载荷Qe对轴承内圈产生的力矩为
| ${T_i} = {R_2} \times {Q_e}$ | (14) |
在外部力、外部力矩、内部力和内部力矩的作用下, 轴承各部件达到平衡状态, 其整体平衡方程为
| $\left\{ \matrix{ {F_x} - \sum\limits_{i = 1}^2 {\sum\limits_{j = 1}^z {{Q_{ix}}} } = 0,{F_y} - \sum\limits_{i = 1}^2 {\sum\limits_{j = 1}^z {{Q_{iy}}} } = 0 \hfill \cr {F_z} - \sum\limits_{i = 1}^2 {\sum\limits_{j = 1}^z {{Q_{iz}}} } = 0 \hfill \cr {M_x} - \sum\limits_{i = 1}^2 {\sum\limits_{j = 1}^z {{T_{ix}}} } = 0,{M_y} - \sum\limits_{i = 1}^2 {\sum\limits_{j = 1}^z {{T_{iy}}} } = 0 \hfill \cr} \right.$ | (15) |
通过求解上述非线性方程组, 可以求得轴承内圈在所受载荷下的平移向量和旋转向量, 即可求得内圈和圆锥滚子在X、Y、Z三个方向上的线位移和X、Y两个方向上的角位移;通过圆锥滚子初始位置向量和最终位置向量可以求得圆锥滚子与外圈滚道在接触面法线方向上的变形量, 通过刚度与变形、载荷的关系, 可求得圆锥滚子与外圈滚道的接触载荷Qe, 进而可求得圆锥滚子与轴承内圈及挡边的接触载荷Qi和Qf。通过圆锥滚子与内、外圈滚道的接触载荷可以分析轴承的疲劳寿命, 同时也可以求得最大载荷滚子处的应力分布情况, 为滚子的修型提供依据。
1.4 轴承寿命目前, 轴承制造商广泛采用的滚动轴承疲劳寿命计算是基于ISO标准的[6], 而这种ISO标准是基于Lundberg和Palmgren理论。该种计算方法需要计算等效的动载荷和静载荷, 但是ISO标准在计算的过程中忽略的很多重要因素的影响,例如未考虑到倾覆力矩、轴承初始轴向游隙和预紧力的因素, 而在风电主轴承的性能分析中, 倾覆力矩是一个很重要的影响因素, 双列圆锥滚子轴承的初始轴向游隙也是风电主轴承设计的一个关键因素, 其对轴承的寿命有重要的影响, 因此单纯的用ISO标准进行计算得出的结果与实际情况是有很大偏差的。
在正常的操作情况下, 轴承内圈的挡边载荷是轻轻施加的, 并且易受到滚子滑动的影响, 其影响因素比较复杂, 因此在本文模型分析中认为内圈挡边的寿命是无穷的, 只通过前面的拟静力学分析得到的轴承内、外圈滚道载荷来分析轴承内、外圈的寿命。
对于具有线接触特征的滚子轴承[11], 其寿命计算公式为
| $L = {\left( {{{{Q_c}} \over {{Q_e}}}} \right)^4}$ | (16) |
式中:L是以百万转为单位的可靠度为90%轴承基本额定寿命, Qc是滚道的额定动载荷, Qe是与滚子实际载荷分布相关的当量载荷。
对于双列圆锥滚子轴承, 滚道额定动载荷为
| ${Q_c} = 552\lambda {{{{\left( {1 \mp \gamma } \right)}^{29/27}}} \over {{{\left( {1 \pm \gamma } \right)}^{1/4}}}}{\left( {{\gamma \over {{\rm{cos}}\alpha }}} \right)^{2/9}}{D_m}^{29/27}{L_e}^{7/9}{Z^{ - 1/4}}$ | (17) |
式中:λ为应力集中系数, 一般在0.4~0.8取值, “$ \pm $”的上、下符号分别适用于内、外滚道, α为圆锥滚子质心处的等效压力角。
相对于外部载荷旋转的内圈, 其当量载荷为
| ${Q_{e\mu }} = {\left( {{1 \over Z}\sum\limits_{j = 1}^z {Q_j^4} } \right)^{1/4}}$ | (18) |
因此, 轴承内圈的寿命为
| ${L_\mu } = {\left( {{{{Q_{c\mu }}} \over {{Q_{e\mu }}}}} \right)^4}$ | (19) |
相对于外部载荷静止的外圈, 其当量载荷为
| ${Q_{e\nu }} = {\left( {{1 \over Z}\sum\limits_{j = 1}^z {Q_j^{4.5}} } \right)^{2/9}}$ | (20) |
因此, 轴承外圈的寿命为
| ${L_\nu } = {\left( {{{{Q_{c\nu }}} \over {{Q_{e\nu }}}}} \right)^4}$ | (21) |
综上, 轴承的基本额定寿命为
| $L = {\left( {L_\mu ^{ - 9/8} + L_\nu ^{ - 9/8}} \right)^{ - 8/9}}$ | (22) |
根据轴承的类型引入修正系数bm, 则修正后的额定寿命为
| ${L_m} = b_m^4L$ | (23) |
对于双列圆锥滚子轴承, 其寿命计算公式为
| ${L_m} = {\left( {L_{m1}^{ - 9/8} + L_{m2}^{ - 9/8}} \right)^{ - 8/9}}$ | (24) |
式中:Lm1和Lm2分别为第一、第二列轴承的修正额定寿命, bm=1.1。
通过Matlab程序来实现上述计算过程, 并将拟静力学计算数据代入即可求得双列圆锥滚子轴承在外载荷下的整体疲劳寿命。
2 风电主轴承案例分析本文选用某型号3 MW风电主轴承作为研究对象, 其结构参数如表 1所示。
| 结构参数 | 值 | 单位 |
| 轴承材料泊松比, v | 0.3 | |
| 轴承材料杨氏模量, E | 2.1×105 | N/mm2 |
| 滚子与外圈接触角, αe | 47.1 | (°) |
| 滚子与内圈接触角, αi | 44.4 | (°) |
| 滚子与挡边接触角, αf | 42.3 | (°) |
| 滚子大端直径,Dw1 | 80.7 | mm |
| 两列滚子质心轴向距离, dc | 160.3 | mm |
| 滚子质心节圆直径, dm | 2 302.9 | mm |
| 滚子轴向长度,l | 110 | mm |
| 滚子个数, Z | 85 |
极限载荷工况是风电设备在工作过程中的最危险工况, 也是确定所设计主轴承能否满足使用要求的工况, 因此本文研究了极限载荷工况下风电主轴承的拟静力学特性。极限工况载荷如表 2所示, 轴承转速为20 r/min,载荷方向如图 1所示。
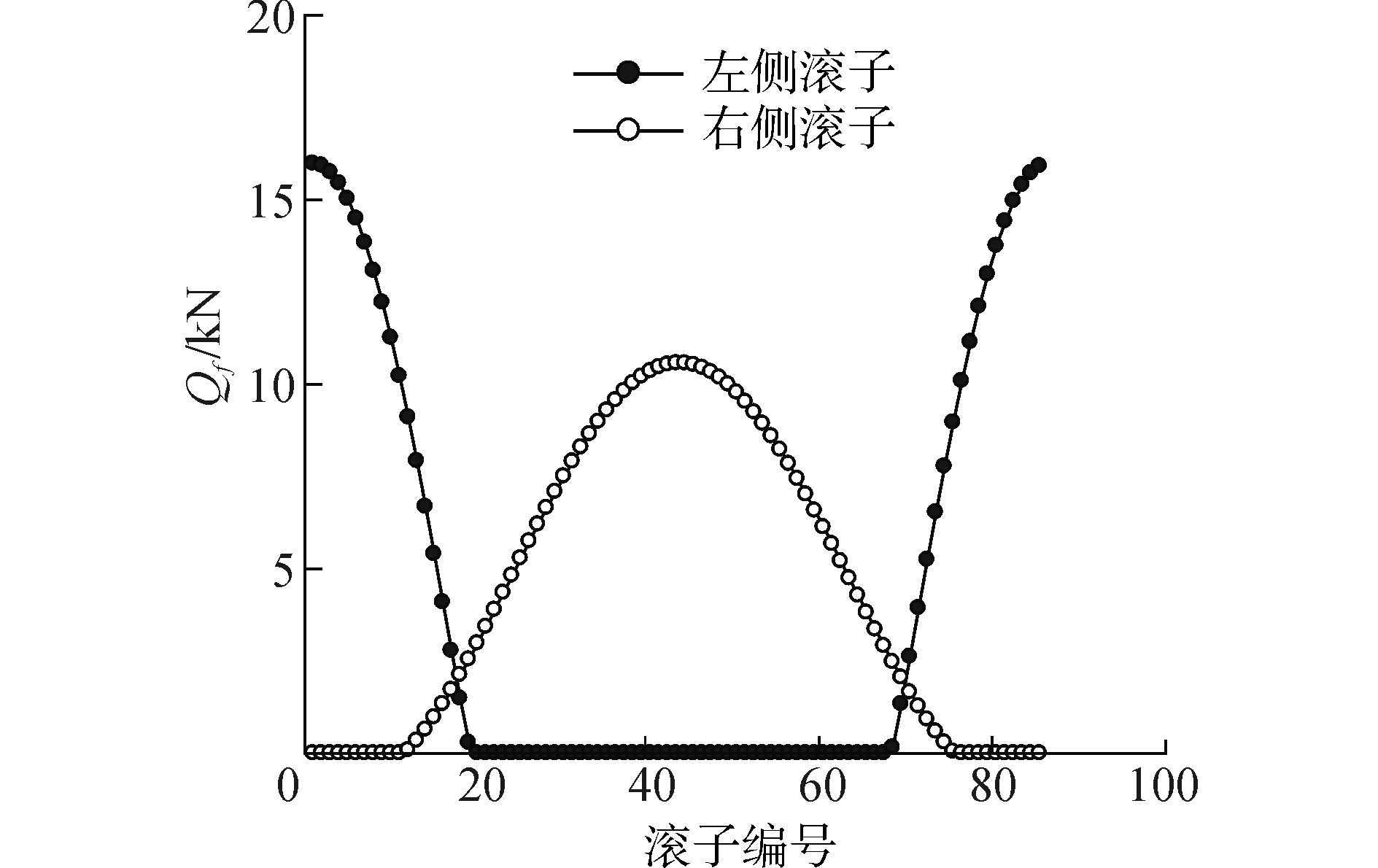
利用上述建立的拟静力学模型对其进行分析, 得到风电主轴承在极限工况下内部载荷分布, 接触载荷分布如图 3~5所示。两列圆锥滚子的最大接触载荷如表 3所示。计算得到风电主轴承内圈的转角为θx=0.013°, θy=-2.6×10-5°, X向的位移为0.001 2 mm, Y向的位移为0.129 4 mm, Z向位移为-0.083 7 mm。
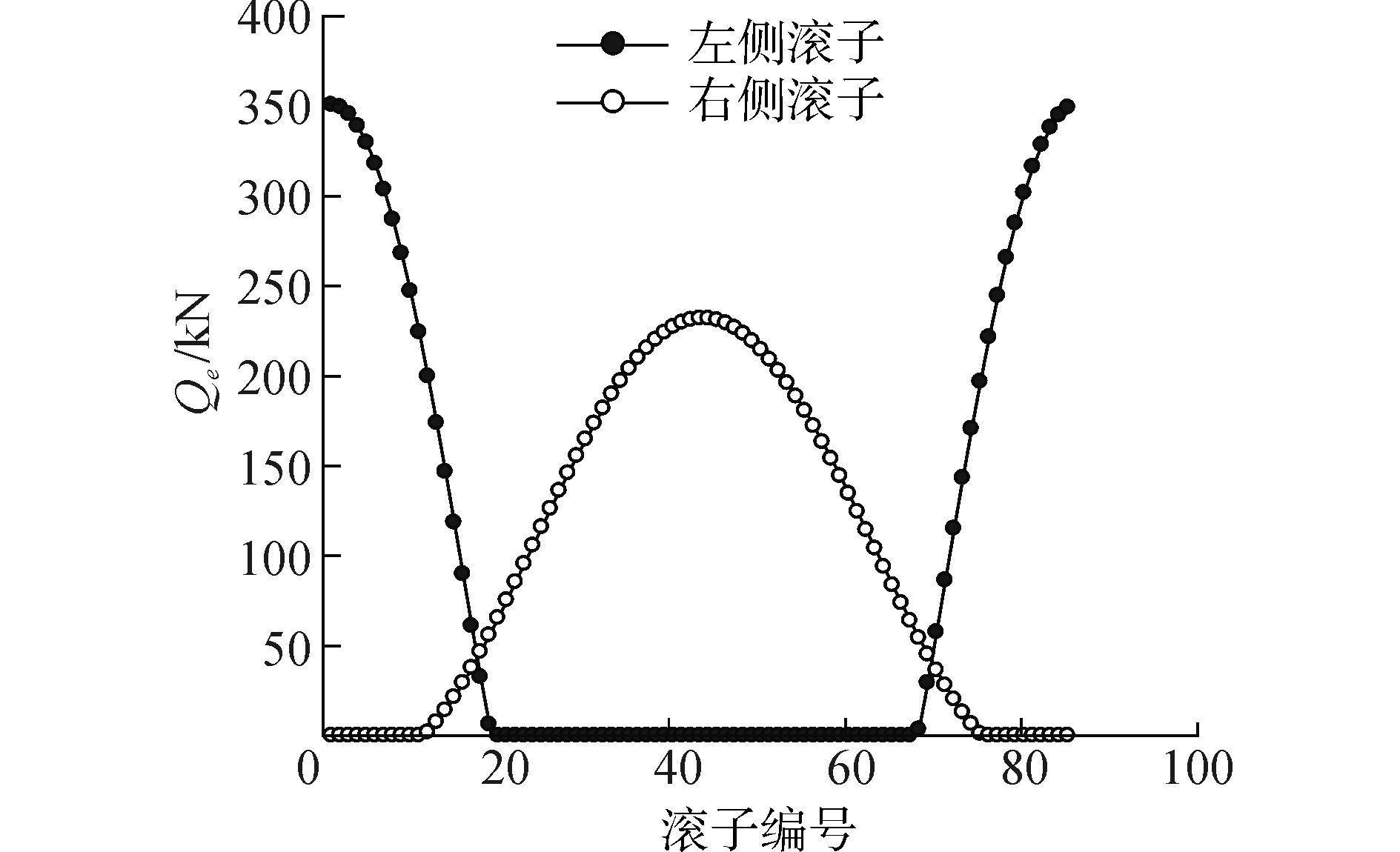
|
| 图3 滚子与外滚道接触载荷分布 Figure 3 Contact loads between tapered roller and cup |
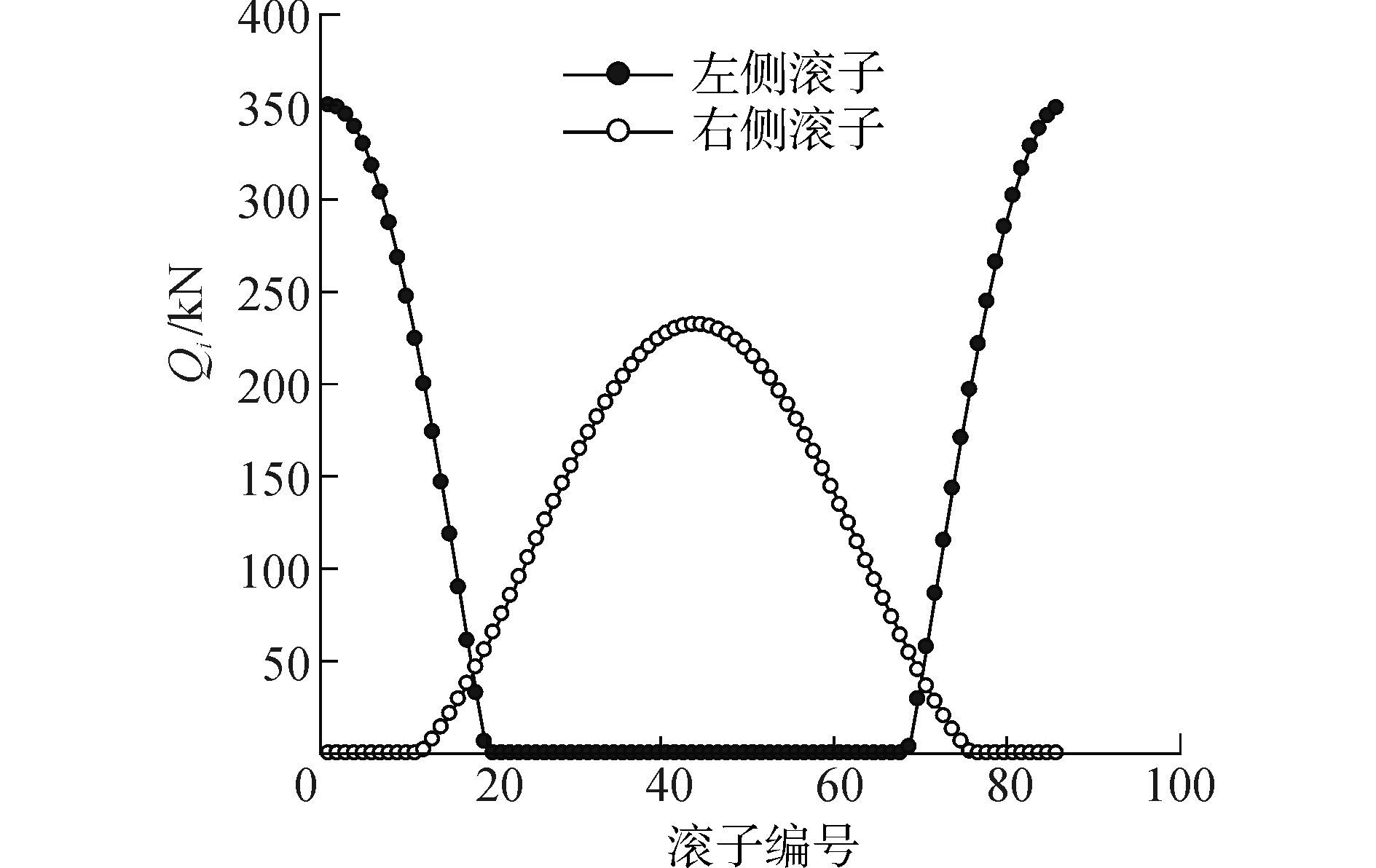
|
| 图4 滚子与内滚道接触载荷分布 Figure 4 Contact loads between tapered roller and cone |
|
| 图5 滚子与内圈挡边触载荷分布 Figure 5 Contact loads between tapered roller and flange |
| 滚子位置 | 接触部位 | 滚子最大接触载荷/kN |
| 左侧 | 外滚道 | 350.84 |
| 内滚道 | 350.84 | |
| 右侧 | 外滚道 | 232.01 |
| 内滚道 | 232.01 |
从表 3中可以看出, 由于倾覆力矩的作用, 风电主轴承中两列圆锥滚子的受力有明显的差异性, 圆锥滚子最大接触载荷为350.84 kN, 发生在左侧滚子与内、外滚道接触处。
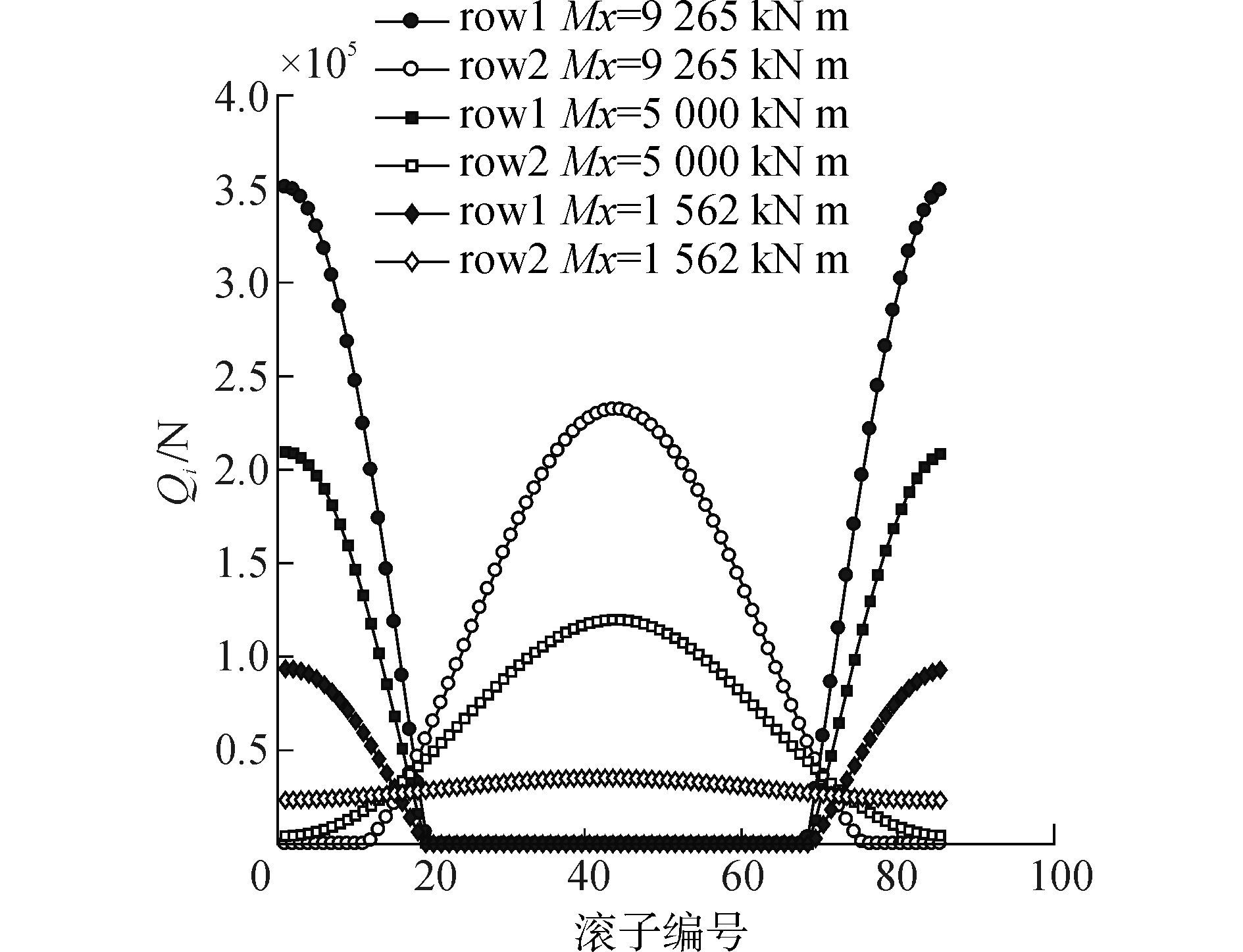
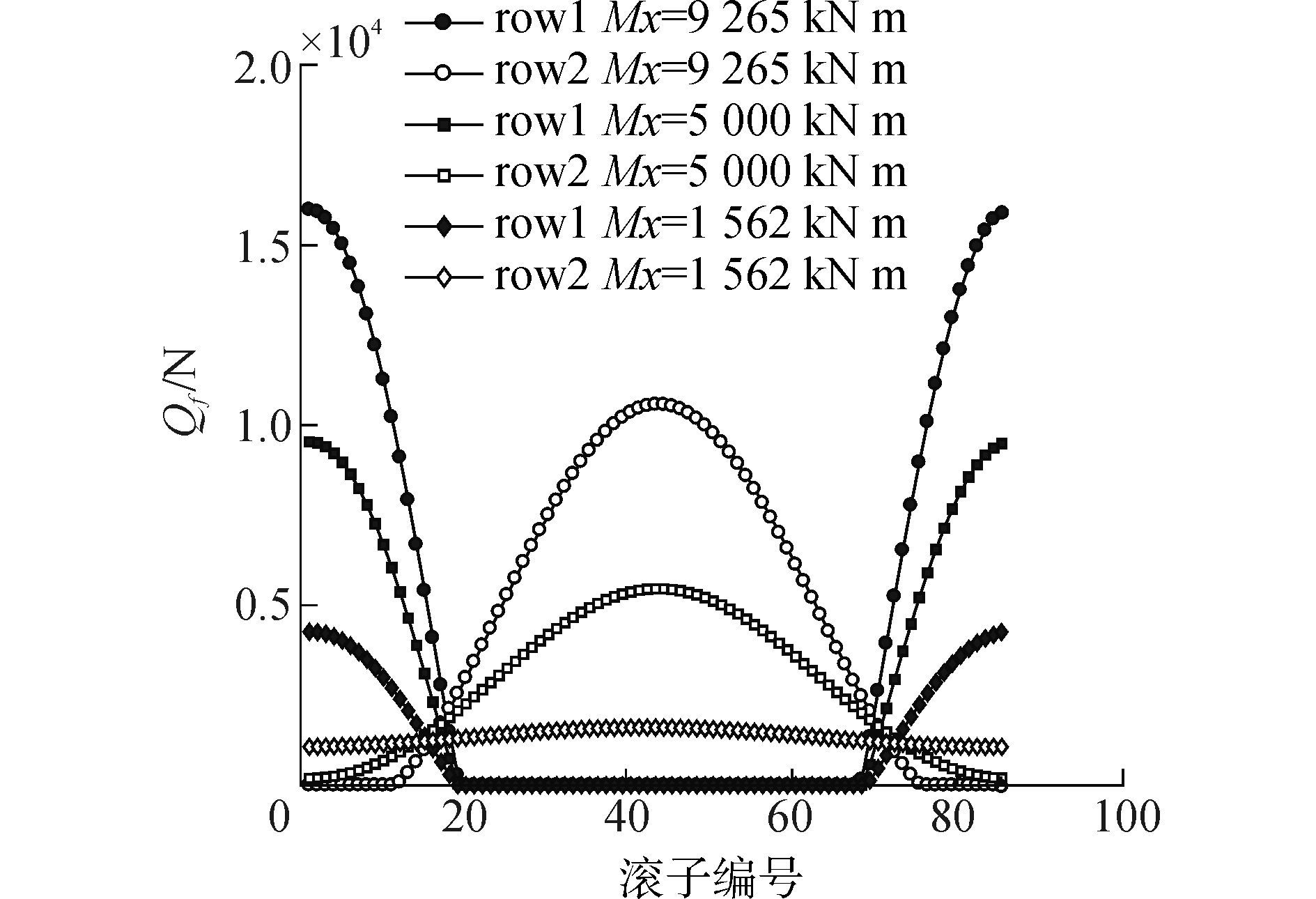
2.2 极限载荷工况下倾覆力矩的影响在风电主轴承的受力中, 倾覆力矩是一个很重要的因素, 因此本文选取极限载荷工况下的倾覆力矩作为单一变量来研究, 在分析时, 除倾覆力矩外其他因素保持不变, 应用本文所建立的分析模型, 得到的结果如图 6、7所示。可以看出, 应用所建立的分析模型, 可以准确、快速地得到不同倾覆力矩对轴承内圈滚道受力以及挡边受力的影响:在轴向力和径向分力及轴向游隙相同的情况下, 随着倾覆力矩的降低, 轴承内圈滚道和挡边受力明显降低;在倾覆力矩较大的情况下, 轴承两列滚道间的受力差异较大, 在倾覆力矩较小的情况下, 轴承两列滚道间的受力差异变小。
|
| 图6 不同倾覆力矩内圈滚道受力 Figure 6 Contact loads between tapered roller and cone under different moments |
|
| 图7 不同倾覆力矩内圈挡边受力 Figure 7 Contact loads between tapered roller and flange under different moments |
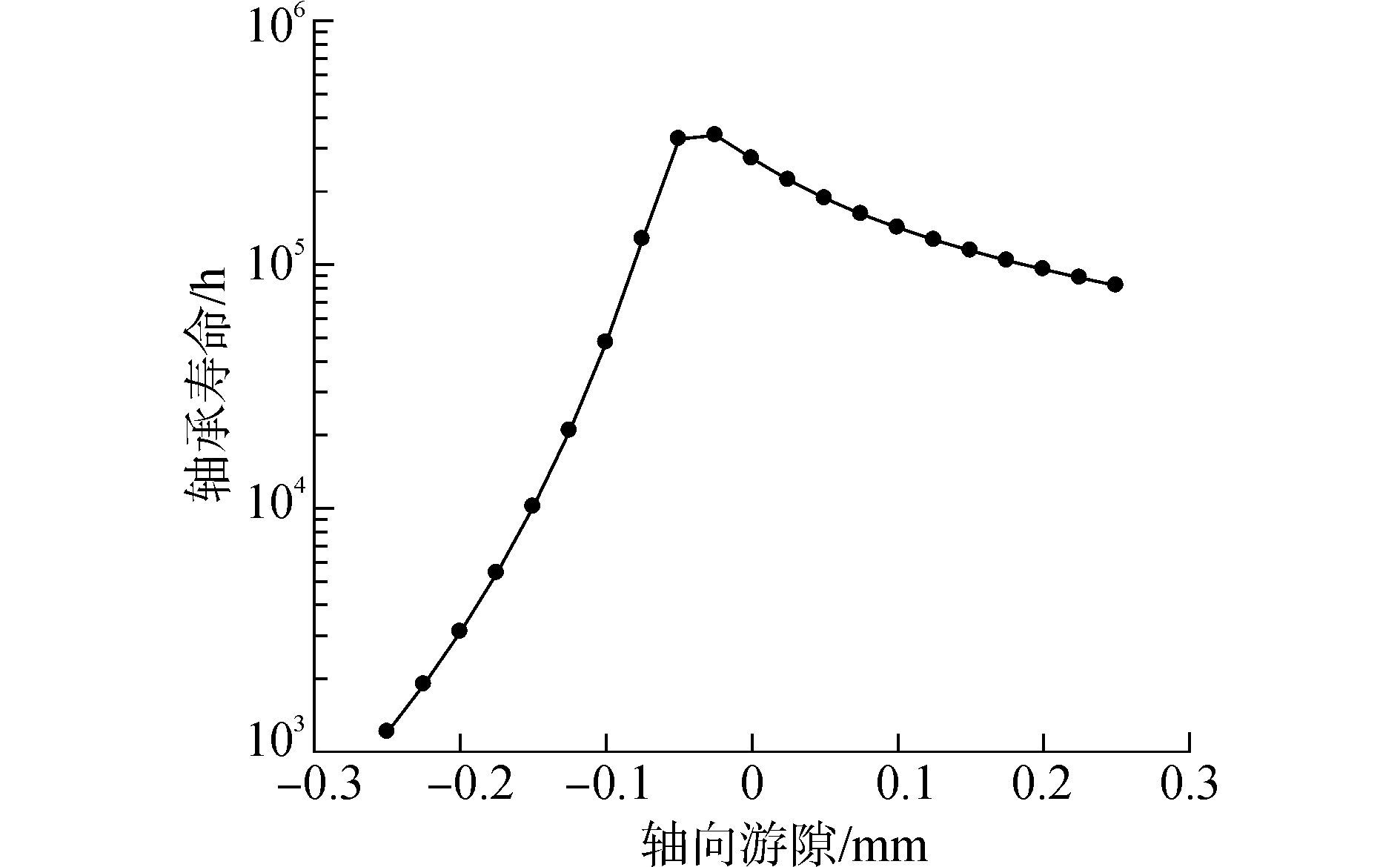
根据兆瓦级风电主轴承的技术要求, 在均载工况载荷下, 本文分析了轴向游隙在-0.25~0.25 mm时风电主轴承疲劳寿命的变化规律, 将该游隙范围-0.25~0.25 mm分为20个小段, 把游隙数据代入所建立的分析模型, 得到风电主轴承在该游隙范围内的寿命变化曲线, 如图 8所示。
|
| 图8 主轴承疲劳寿命与轴向游隙关系 Figure 8 Fatigue life of the main bearing under different axial clearance |
从图 8可以看出, 随着轴向游隙的增加, 主轴承的疲劳寿命呈现先增大后减小的趋势;当轴向游隙为-0.025 mm时轴承疲劳寿命最大,达到339 155.5 h,约为38.716 a, 相比轴向游隙为零时的额定寿命提高了24.47%,这表明可以通过调节轴向游隙来获得更高的使用寿命;某兆瓦级风电主轴承设计游隙为-0.08~0 mm, 在图 8中可以看出在该游隙范围内风电主轴承寿命处于较高的寿命阶段, 能够满足设计寿命175 200 h(20 a)的要求, 同时也说明了该模型用于预测风电主轴承设计中轴向游隙对于整体寿命影响的正确性, 也证明了该模型的准确性;在风电主轴承的设计中, 应谨慎选择轴向游隙,防止轴向游隙过小或过大而使轴承疲劳寿命急剧减小。
3 结论1) 建立了双列圆锥滚子轴承拟静力学特性分析模型, 通过该模型, 能够快速准确的分析双列圆锥滚子轴承在复杂受力(轴向力、径向力、倾覆力矩)情况下的轴承内部载荷分布和疲劳寿命。
2) 通过将该模型用于3 MW风电主轴承, 得到了极限载荷工况下风电主轴承中圆锥滚子与内、外圈滚道及挡边的受力, 并分析了极限载荷工况下倾覆力矩对于风电主轴承受力的影响。
3) 分析了均载工况下轴向游隙对轴承整体疲劳寿命的影响, 得出了轴向游隙在-0.25~0.25 mm时轴承疲劳寿命曲线, 当轴向游隙为-0.025 mm, 轴承达到最大疲劳寿命, 为339 155.5 h,约为38.716 a。
| [1] | JONES A B. A general theory for elastically constrained ball and radial roller bearings under arbitrary load and speed conditions[J]. Journal of basic engineering, 1960, 82(2): 309–320. DOI:10.1115/1.3662587 |
| [2] | ANDRÉASON S. Load distribution in a taper roller bearing arrangement considering misalignment[J]. Tribology, 1973, 6(3): 84–92. DOI:10.1016/0041-2678(73)90241-8 |
| [3] | LIU J Y. Analysis of tapered roller bearings considering high speed and combined loading[J]. Journal of lubrication technology, 1976, 98(4): 564–572. DOI:10.1115/1.3452933 |
| [4] | TONG V C, HONG S W. Characteristics of tapered roller bearing subjected to combined radial and moment loads[J]. International journal of precision engineering and manufacturing-green technology, 2014, 1(4): 323–328. DOI:10.1007/s40684-014-0040-1 |
| [5] | KABUS S, HANSEN M R, MOURITSEN O Ø. A new quasi-static multi-degree of freedom tapered roller bearing model to accurately consider non-Hertzian contact pressures in time-domain simulations[J]. Proceedings of the institution of mechanical engineers, part K:Journal of multi-body dynamics, 2014, 228(2): 111–125. DOI:10.1177/1464419313513446 |
| [6] | 罗继伟, 罗天宇. 滚动轴承分析计算与应用[M]. 北京: 机械工业出版社, 2009: 79-83. |
| [7] |
胡浪, 王文中, 赵自强, 等. 双列圆锥滚子轴承滚子大端-引导边润滑接触分析[J].
摩擦学学报, 2013, 33(1): 22–28.
HU Lang, WANG Wenzhong, ZHAO Ziqiang, et al. Lubricated contact analysis of roller large end-flange in double-row tapered roller bearing[J]. Tribology, 2013, 33(1): 22–28. |
| [8] | AI Siyuan, WANG Wenzhong, WANG Yunlong, et al. Temperature rise of double-row tapered roller bearings analyzed with the thermal network method[J]. Tribology international, 2015, 87: 11–22. DOI:10.1016/j.triboint.2015.02.011 |
| [9] | BERCEA I, CRETU S, NÉLIAS D. Analysis of double-row tapered roller bearings, Part I-model[J]. Tribology transactions, 2003, 46(2): 228–239. DOI:10.1080/10402000308982622 |
| [10] | NÉLIAS D, BERCEA I, MITU N. Analysis of double-row tapered roller bearings, Part II-results:prediction of fatigue life and heat dissipation[J]. Tribology transactions, 2003, 46(2): 240–247. DOI:10.1080/10402000308982623 |
| [11] | HARRIS T A, KOTZALAS M N. Essential concepts of bearing technology[M]. 5th ed. New York: Taylor & Francis Group, 2007: 213-231. |



