2. Key Discipline Laboratory of Nuclear Safety and Simulation Technology, Harbin Engineering University, Harbin 150001, China
作为一项重要的严重事故缓解措施,熔融物堆内滞留设计 (IVR) 在AP1000、CAP1400、华龙一号等三代核电技术中得到了广泛应用[1]。IVR设计主要利用堆腔内冷却水的自然循环实现压力容器外部冷却 (ERVC),从而带走熔融堆芯的衰变热,维持压力容器的完整[2]。现有研究中,ERVC的有效性评估多通过程序计算确定,但因自然循环具有流量较小、参数变化敏感性强[3]、容易出现流动不稳定现象[4]等特点,计算结果一般要通过台架进行试验验证。实验台架参数往往需要在原型的基础上依照模化准则进行缩比,如在AP600和AP1000的安全审评中发挥重要作用的APEX试验台架,该台架就是根据Reyes等[5]对非能动堆芯冷却系统 (PXS) 内自然循环现象模化分析的结果设计建造。
鉴于现阶段针对ERVC自然循环现象的模化较少,本文以一维漂移流模型为基础,对ERVC的自然循环过程进行了等高度、等物性模化,通过推导和选择关键无量纲准则数,实现试验台架与原型过程间最大程度的相似,为ERVC自然循环试验台架设计提供理论依据。
1 系统描述及模化分析目标在核电厂发生严重事故时,在操作员的动作下,堆腔淹没系统中的冷却水会迅速淹没反应堆堆腔,并在压力容器下封头外壁和保温层之间的环形流道内形成稳定的两相自然循环,实现压力容器外部冷却,带走熔融堆芯的衰变热,如图 1所示。
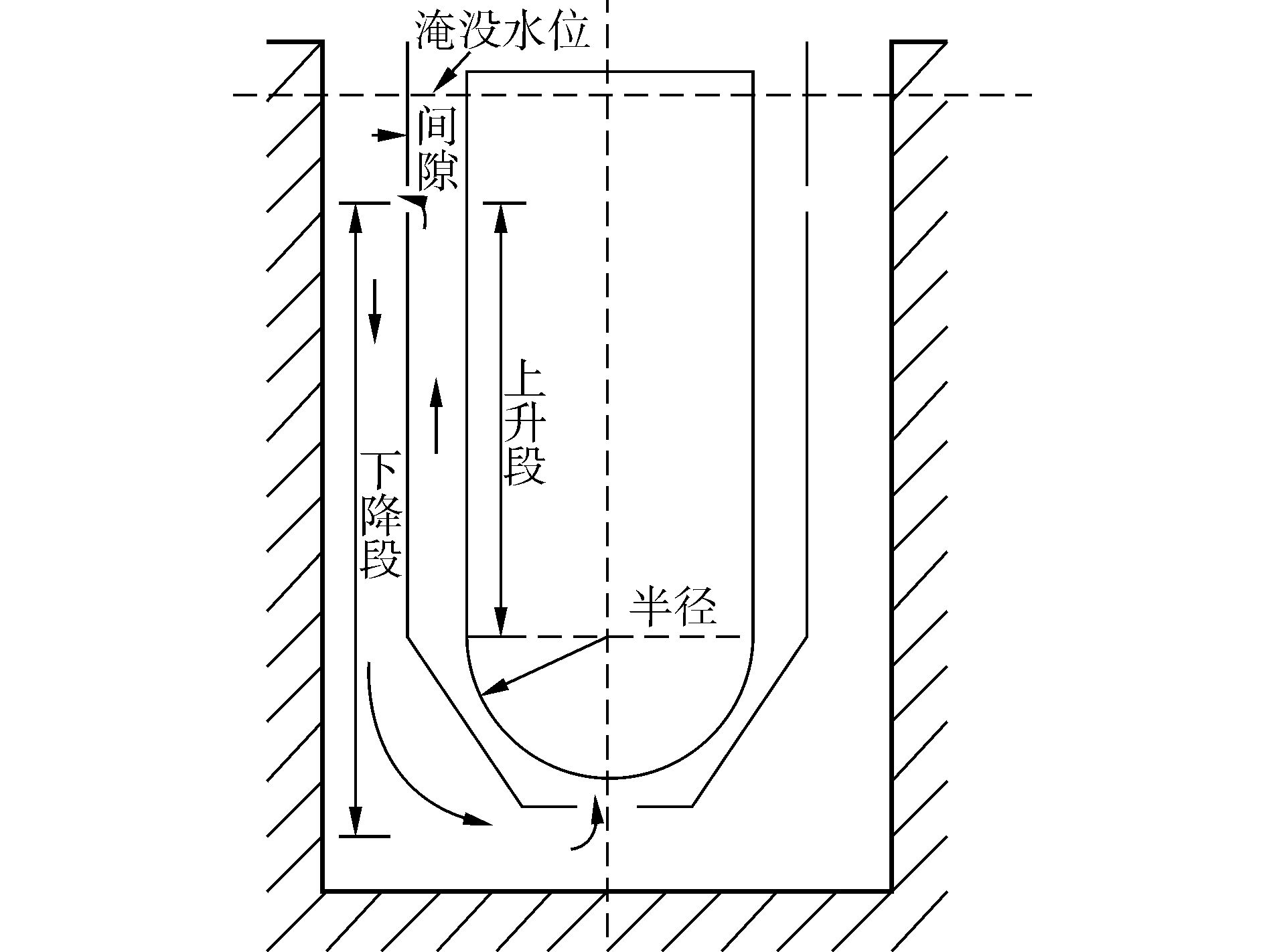
|
| 图1 ERVC自然循环示意图 Figure 1 Schematic of natural circulation for ERVC |
ERVC自然循环试验的目标是模拟ERVC系统运行时的自然循环循环流速,同时实现对RPV沸腾换热的模拟。因为ERVC系统的运行状态同时涉及两相自然循环和局部换热过程,所以本研究采用分级双向比例 (H2TS) 方法进行模化分析,H2TS方法是特别适用于综合性实验台架的一种先进的分级模化方法[6]。模化分析主要分两个层次进行,流程如图 2所示。
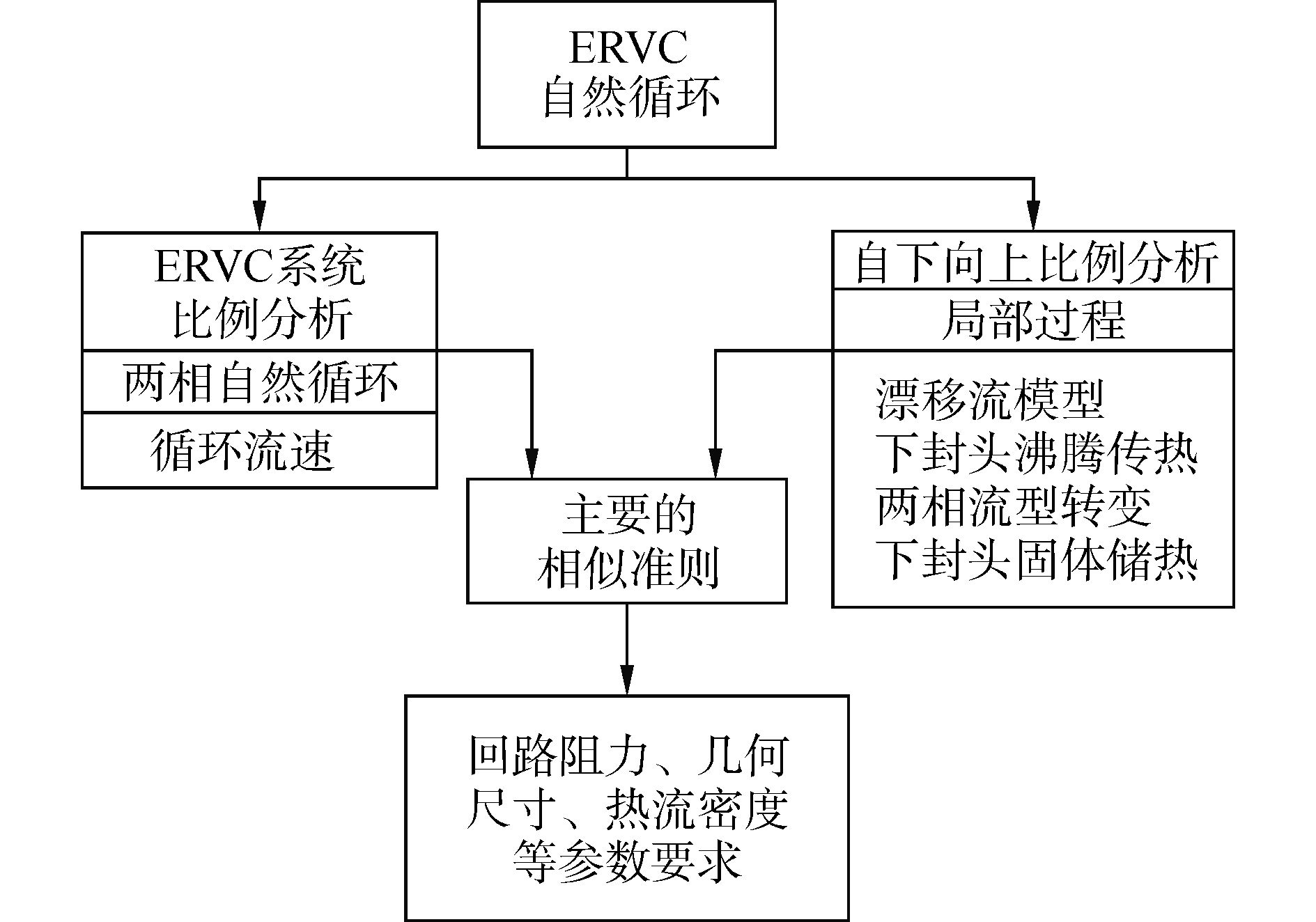
|
| 图2 ERVC自然循环比例分析流程图 Figure 2 Scaling analysis flow diagram for natural circulation of ERVC |
第一层次为ERVC系统模化分析,主要以整个自然循环回路为控制体,通过对流动换热平衡方程的处理,获得系统相似准则;第二层次主要关注局部现象的相似要求,包括漂移流模型、RPV下封头沸腾换热等内容,对系统相似准则进行补充和完善。
2 自然循环模化分析 2.1 两相自然循环控制方程ERVC系统运行时,以压力容器下封头加热面和流体作为控制体,其平衡方程如下[5]:
混合物质量守恒方程
| $\frac{\text{d}}{\text{d}t}\left( {{\rho }_{\text{TP}}}{{V}_{\text{TP}}} \right)=\Delta \left( {{\rho }_{\text{TP}}}{{Q}_{\text{TP}}} \right)-\Delta \left( \alpha A\Delta \rho {{v}_{gj}} \right)$ | (1) |
混合物动量守恒方程
| $\begin{align} & \frac{\text{d}}{\text{d}t}\left( {{\rho }_{\text{TP}}}{{u}_{\text{TP}}}{{V}_{\text{TP}}} \right)=\Delta \left( {{\rho }_{\text{TP}}}{{u}_{\text{TP}}}{{Q}_{\text{TP}}} \right)+\Delta \rho g\alpha {{V}_{\text{TP}}}~+ \\ & \Delta \left( \frac{\alpha {{\rho }_{\text{gs}}}{{\rho }_{\text{ls}}}Av_{\text{gj}}^{2}}{\left( 1-\alpha \right){{\rho }_{\text{TP}}}} \right)-\frac{{{\rho }_{\text{TPi}}}{{u}_{\text{TPi}}}{{Q}_{\text{TPi}}}}{2}\left( \frac{fl}{{{d}_{\text{h}}}}+K \right) \\ \end{align}$ | (2) |
混合物能量方程
| $\begin{align} & \frac{\text{d}\left( {{\rho }_{\text{TP}}}{{h}_{\text{TP}}}{{V}_{\text{TP}}} \right)}{\text{d}t}=\Delta \left( {{\rho }_{\text{TP}}}{{h}_{\text{TP}}}{{Q}_{\text{TP}}} \right)+ \\ & {{H}_{\text{sf}}}{{A}_{\text{s}}}\left( {{T}_{\text{s}}}-{{T}_{\text{TP}}} \right){{|}_{\text{Boundary}}}+\Delta \left( \frac{\alpha {{\rho }_{\text{gs}}}{{\rho }_{\text{ls}}}}{{{\rho }_{\text{TP}}}}A{{h}_{\text{lg}}}{{v}_{\text{gj}}} \right) \\ \end{align}$ | (3) |
固体能量方程
| $\begin{align} & {{H}_{\text{sf}}}{{A}_{\text{s}}}\left( {{T}_{\text{s}}}-{{T}_{\text{TP}}} \right){{|}_{\text{Boundary}}}+\Delta \left( \frac{\alpha {{\rho }_{\text{gs}}}{{\rho }_{\text{ls}}}}{{{\rho }_{\text{TP}}}}A{{h}_{\text{lg}}}{{v}_{\text{gj}}} \right) \\ & \frac{\text{d}}{\text{d}t}\left( {{\rho }_{\text{s}}}{{C}_{\text{vs}}}{{T}_{\text{s}}}{{V}_{\text{s}}} \right)={{H}_{\text{sf}}}{{A}_{\text{s}}}\left( {{T}_{\text{s}}}-{{T}_{\text{TP}}} \right){{|}_{\text{Boundary}}}+{{{\dot{q}}}_{\text{s}}} \\ \end{align}$ | (4) |
式中:Q为体积流率,A为流动截面积,As为换热面积,u为流体速度,α为体积含汽量,ρ为密度,Δρ为饱和水与饱和汽密度差,vgj为漂移速度,h为流体焓值,g为重力加速度,Cv为定容比热,
考虑为稳态自然循环,根据Ishii的研究,可忽略换热系数的模拟,可合并固体能量方程和能量方程为新的能量方程[7]:
| $\begin{align} & \frac{\text{d}\left( {{\rho }_{\text{TP}}}{{h}_{\text{TP}}}{{V}_{\text{TP}}} \right)}{\text{d}t}=\Delta \left( {{\rho }_{\text{TP}}}{{h}_{\text{TP}}}{{Q}_{\text{TP}}} \right)+ \\ & \frac{\text{d}\left( {{\rho }_{\text{s}}}{{C}_{\text{vs}}}{{T}_{\text{s}}}{{V}_{\text{s}}} \right)}{\text{d}t}-{{{\dot{q}}}_{\text{s}}}+\Delta \left( \frac{\alpha {{\rho }_{\text{gs}}}{{\rho }_{\text{ls}}}}{{{\rho }_{\text{TP}}}}A{{h}_{\text{lg}}}{{v}_{\text{gj}}} \right) \\ \end{align}$ | (5) |
通过分别除以稳定状态自然循环下方程中各参数的值 (以下标0表示),对方程 (1)、(2)、(5) 进行无量纲化,以无量纲数表示的方程为:
混合物质量方程
| ${{\tau }_{\text{TP,0}}}\frac{\text{d}}{\text{d}t}\left( \rho _{\text{TP}}^{+}V_{\text{TP}}^{+} \right)=\Delta \left( \rho _{\text{TP}}^{+}Q_{\text{TP}}^{+} \right)-{{\mathit{\Pi }}_{\text{Nd}}}$ | (6) |
混合物动量方程
| $\begin{align} & {{\tau }_{\text{TP,0}}}\frac{\text{d}}{\text{d}t}\left( \rho _{\text{TP}}^{+}u_{\text{TP}}^{+}V_{\text{TP}}^{+} \right)=\Delta \left( \rho _{\text{TP}}^{+}u_{\text{TP}}^{+}Q_{\text{TP}}^{+} \right)+\frac{\Delta {{\rho }^{+}}{{\alpha }^{+}}V_{\text{TP}}^{+}}{{{\mathit{\Pi }}_{\text{Fr}}}}+ \\ & {{\mathit{\Pi }}_{\rho }}\mathit{\Pi }_{\text{Nd}}^{2}\Delta {{\left( \frac{\alpha {{\rho }_{\text{gs}}}{{\rho }_{\text{ls}}}{{a}_{\text{c}}}v_{\text{gj}}^{2}}{\left( 1-\alpha \right){{\rho }_{\text{TP}}}} \right)}_{i}}-{{\mathit{\Pi }}_{\text{F}}}\frac{\rho _{\text{TP}}^{+}u_{\text{TP}}^{+}V_{\text{TP}}^{+}}{2}{{\left( \frac{fl}{{{d}_{\text{h}}}}+K \right)}^{+}} \\ \end{align}$ | (7) |
混合物能量方程
| $\begin{align} & {{\tau }_{\text{TP,0}}}\frac{\text{d}}{\text{d}t}\left( \rho _{\text{TP}}^{+}h_{\text{TP}}^{+}V_{\text{TP}}^{+} \right)=\Delta \left( \rho _{\text{TP}}^{+}h_{\text{TP}}^{+}Q_{\text{TP}}^{+} \right)+ \\ & {{\mathit{\Pi }}_{St}}\frac{\text{d}\left( \rho _{\text{s}}^{+}C_{\text{vs}}^{+}T_{\text{s}}^{+}V_{\text{s}}^{+} \right)}{\text{d}t}-{{\mathit{\Pi }}_{q}}q_{\text{s}}^{+}+{{\mathit{\Pi }}_{Nd}}{{\mathit{\Pi }}_{\rho }}{{\mathit{\Pi }}_{\text{h}}}\Delta {{\left( \frac{\alpha {{\rho }_{\text{gs}}}{{\rho }_{\text{ls}}}}{{{\rho }_{\text{TP}}}}A{{h}_{\text{lg}}}{{v}_{\text{gj}}} \right)}^{+}} \\ \end{align}$ | (8) |
上述方程中,τTP, o为流体混合物的弛豫时间,定义如下:
| ${{\tau }_{\text{TP,o}}}=\frac{{{V}_{\text{TP,o}}}}{{{Q}_{\text{TP,o}}}}$ | (9) |
各无量纲数定义如下:漂移通量数:
| ${{\mathit{\Pi }}_{\text{Nd}}}=\frac{{{v}_{\text{gj,o}}}{{\alpha }_{\text{o}}}\Delta {{\rho }_{\text{o}}}}{{{u}_{\text{TP,o}}}{{\rho }_{\text{TP,o}}}}$ | (10) |
Froude数:
| ${{\mathit{\Pi }}_{\text{Fr}}}=\frac{u_{\text{TP,o}}^{2}{{\rho }_{\text{TP}}}}{{{\alpha }_{\text{o}}}g{{l}_{\text{o}}}\Delta {{\rho }_{\text{o}}}}$ | (11) |
密度数:
| ${{\mathit{\Pi }}_{\rho }}=\frac{{{\rho }_{\text{gs,o}}}{{\rho }_{\text{ls,o}}}}{{{\alpha }_{\text{o}}}\left( 1-{{\alpha }_{\text{o}}} \right){{\left( \Delta {{\rho }_{\text{o}}} \right)}^{2}}~}$ | (12) |
Friction数:
| ${{\mathit{\Pi }}_{\text{F}}}={{\left( \frac{fl}{{{d}_{\text{h}}}}+K \right)}_{\text{o}}}$ | (13) |
修正Stanton数:
| ${{\mathit{\Pi }}_{St}}=\frac{{{\rho }_{\text{s,0}}}{{C}_{\text{vs,0}}}{{T}_{\text{s,0}}}{{V}_{\text{s,0}}}}{{{\rho }_{\text{TP,0}}}{{h}_{\text{TP,0}}}{{Q}_{\text{TP,0}}}}$ | (14) |
热源数:
| ${{\mathit{\Pi }}_{q}}=\frac{{{q}_{\text{s,0}}}}{{{\rho }_{\text{TP,o}}}{{h}_{\text{TP,o}}}{{Q}_{\text{TP,o}}}}$ | (15) |
焓升数:
| ${{\mathit{\Pi }}_{\text{h}}}=\frac{{{h}_{\text{lg,o}}}{{\left( 1-\alpha \right)}_{\text{o}}}{{\alpha }_{\text{o}}}\Delta {{\rho }_{\text{o}}}}{{{h}_{\text{TP,o}}}{{\rho }_{\text{TP,o}}}~}$ | (16) |
2.1节推导得到的无量纲数,均以稳定状态自然循环下的参数来表示,因此求解稳定条件下ERVC自然循环各参数的值,其中最为重要的参数是自然循环流速。
对ERVC系统内稳定的自然循环流动进行简化,假设两相间达到热平衡和化学平衡,忽略由于蒸发和冷凝导致的对流加速等的影响,仅在形阻损失中考虑粘性效应,采用一维均相流模型,稳定状态的控制方程为
| $\frac{\rho _{\text{in}}^{2}u_{\text{in}}^{2}}{2}\sum\limits_{i=1}^{N}{\frac{1}{{{\rho }_{i}}}}{{\left( \frac{fl}{{{d}_{\text{h}}}}+K \right)}_{i}}{{\left( \frac{{{A}_{\text{in}}}}{{{A}_{i}}} \right)}^{2}}=\left( {{{\bar{\rho }}}_{_{l}}}-{{{\bar{\rho }}}_{_{\text{TP}}}} \right){{L}_{\text{th}}}g$ | (17) |
| ${{\rho }_{i}}{{u}_{i}}{{A}_{i}}\left( {{h}_{\text{TP}}}-{{h}_{\text{in}}} \right)={{{\dot{q}}}_{\text{s}}}$ | (18) |
式中:Lth为冷热中心高度差,下标in表示RPV流道的入口,i表示通道内任意位置,l表示液相。
分别定义热平衡含汽率和两相平均密度为
| ${{\chi }_{e}}=\frac{{{h}_{\text{TP}}}-{{h}_{\text{ls}}}}{{{h}_{\text{gs}}}-{{h}_{\text{ls}}}}=\frac{{{h}_{\text{TP}}}-{{h}_{\text{ls}}}}{\gamma }~$ | (19) |
| ${{{\bar{\rho }}}_{\text{TP}}}=\frac{{{\rho }_{\text{ls}}}}{1+{{\chi }_{e}}\frac{\Delta \rho }{{{\rho }_{\text{gs}}}}~}$ | (20) |
式中:γ为汽化潜热,下标ls,gs分别表示饱和水和饱和蒸汽。
利用方程 (18) 和方程 (19),并令hsub=hls-hin,可得
| ${{\chi }_{e}}=\frac{{{{\dot{q}}}_{s}}-G{{h}_{\text{sub}}}}{G\gamma }$ | (21) |
方程 (21) 代入方程 (20) 可得
| ${{{\bar{\rho }}}_{\text{TP}}}=\frac{{{\rho }_{\text{ls}}}}{1+\frac{{{{\dot{q}}}_{s}}-G{{h}_{\text{sub}}}}{G\gamma }\frac{\Delta \rho }{{{\rho }_{\text{gs}}}~}}$ | (22) |
将方程 (22) 代入方程 (17),整理后可得
| $u_{\text{in}}^{3}+u_{\text{in}}^{2}{{\varphi }_{1}}+{{u}_{in}}{{\varphi }_{2}}-{{\varphi }_{3}}=0$ | (23) |
式中:φ1、φ2、φ3为方程的系数,由热功率、冷却水物性、摩阻损失及形阻损失确定,其计算公式为
| $\begin{align} & {{\varphi }_{1}}=\frac{{{{\dot{q}}}_{s}}\Delta \rho }{{{A}_{\text{in}}}{{\rho }_{\text{ls}}}}\cdot \\ & \left[ \frac{\left( 1+{{F}_{TP}} \right){{\rho }_{\text{gs}}}{{h}_{\text{lg}}}-2\Delta \rho {{F}_{\text{TP}}}{{h}_{\text{sub}}}}{{{F}_{T}}\rho _{\text{gs}}^{2}h_{\text{lg}}^{2}-\left( 1+{{F}_{TP}} \right){{\rho }_{\text{gs}}}{{h}_{\text{lg}}}{{h}_{\text{sub}}}\Delta \rho +{{F}_{\text{TP}}}{{\left( \Delta \rho \right)}^{2}}h_{\text{sub}}^{2}} \right] \\ & {{\varphi }_{2}}=\frac{\Delta \rho }{A_{\text{in}}^{2}\rho _{\text{ls}}^{2}}\cdot \\ & \left[ \frac{\Delta \rho {{F}_{\text{TP}}}q_{s}^{2}+2{{L}_{\text{TH}}}g\rho _{c}^{2}a_{c}^{2}{{h}_{\text{sub}}}{{\rho }_{\text{gs}}}{{h}_{\text{lg}}}}{{{F}_{T}}\rho _{\text{gs}}^{2}h_{\text{lg}}^{2}-\left( 1+{{F}_{TP}} \right){{\rho }_{\text{gs}}}{{h}_{\text{lg}}}{{h}_{\text{sub}}}\Delta \rho +{{F}_{\text{TP}}}{{\left( \Delta \rho \right)}^{2}}h_{\text{sub}}^{2}} \right] \\ & {{\varphi }_{3}}=\frac{\Delta \rho }{{{A}_{\text{in}}}{{\rho }_{\text{ls}}}}\cdot \\ & \left[ \frac{{{L}_{\text{TH}}}g{{{\dot{q}}}_{s}}\Delta \rho {{\rho }_{\text{gs}}}{{h}_{\text{lg}}}}{{{F}_{T}}\rho _{\text{gs}}^{2}h_{\text{lg}}^{2}-\left( 1+{{F}_{TP}} \right){{\rho }_{\text{gs}}}{{h}_{\text{lg}}}{{h}_{\text{sub}}}\Delta \rho +{{F}_{\text{TP}}}{{\left( \Delta \rho \right)}^{2}}h_{\text{sub}}^{2}} \right] \\ \end{align}$ | (24) |
| ${{F}_{\text{SP}}}=\sum\limits_{\text{SP}}{{{\left( f\frac{l}{{{d}_{h}}}+K \right)}_{j}}}{{\left( \frac{{{a}_{c}}}{{{a}_{i}}} \right)}^{2}}$ | (25) |
| ${{F}_{\text{TP}}}=\sum\limits_{\text{TP}}{{{\left( f\frac{l}{{{d}_{h}}}+K \right)}_{j}}}{{\left( \frac{{{a}_{c}}}{{{a}_{i}}} \right)}^{2}}$ | (26) |
| ${{F}_{T}}={{F}_{\text{SP}}}+{{F}_{\text{TP}}}$ | (27) |
方程 (23) 即为ERVC系统自然循环流速的三次多项式,可用于求解循环流速。可知,ERVC自然循环流速的相似主要与入口过冷度、流体密度、下封头加热功率、几何位置等因素有关。
方程 (25)、(26) 和 (27) 中,F为与回路阻力相关的参数,ERVC自然循环回路的阻力主要考虑入口局部损失、加热段局部损失,上升段摩阻损失、出口局部损失及下降段摩阻损失及局部损失。
2.3 自然循环比例分析Reyes证明,对于方程 (23),存在常数因子β使方程的系数严格满足比例,保证模型与原型中的流体速度相似[8],即:
| $\begin{align} & {{\beta }^{3}}\left( u_{m}^{3}+{{\varphi }_{1m}}u_{m}^{2}+{{\varphi }_{2m}}{{u}_{m}}-{{\varphi }_{3m}} \right)= \\ & u_{p}^{3}+{{\varphi }_{1p}}u_{p}^{2}+{{\varphi }_{2p}}{{u}_{p}}-{{\varphi }_{3p}} \\ \end{align}$ | (28) |
| ${{u}_{R}}=\frac{{{u}_{m}}}{{{u}_{p}}}=\frac{1}{\beta }$ | (29) |
| ${{\varphi }_{1R}}=\frac{{{\varphi }_{1m}}}{{{\varphi }_{1p}}}=\frac{1}{\beta }$ | (30) |
| ${{\varphi }_{2R}}=\frac{{{\varphi }_{2m}}}{{{\varphi }_{2p}}}=\frac{1}{{{\beta }^{2}}}$ | (31) |
| ${{\varphi }_{3R}}=\frac{{{\varphi }_{3m}}}{{{\varphi }_{3p}}}=\frac{1}{{{\beta }^{3}}}$ | (32) |
式中:下标m和p分别代表模型值和原型值。
将方程 (24)、(25)、(26) 和 (27) 代入方程 (29)~(32) 中,当ERVC稳定运行时,堆腔保温层底部入口的水温接近饱和,即过冷焓为0,于是得到:
| ${{u}_{R}}={{\left( \frac{{{{\dot{q}}}_{s}}}{{{A}_{\text{in}}}} \right)}_{R}}{{\left( \frac{\Delta \rho }{{{\rho }_{\text{ls}}}{{\rho }_{\text{gs}}}{{h}_{\text{lg}}}} \right)}_{R}}{{\left[ \frac{\left( 1+{{F}_{\text{TP}}} \right)}{{{F}_{T}}} \right]}_{R}}$ | (33) |
| $u_{R}^{2}=\left( \frac{{{{\dot{q}}}_{s}}}{{{A}_{\text{in}}}} \right)_{R}^{2}\left( \frac{\Delta \rho }{{{\rho }_{\text{ls}}}{{\rho }_{\text{gs}}}{{h}_{\text{lg}}}} \right)_{R}^{2}{{\left[ \frac{{{F}_{\text{TP}}}}{{{F}_{T}}} \right]}_{R}}$ | (34) |
| $u_{R}^{3}={{\left( \frac{{{{\dot{q}}}_{s}}}{{{A}_{\text{in}}}} \right)}_{R}}{{\left( \frac{\Delta \rho }{{{\rho }_{\text{ls}}}{{\rho }_{\text{gs}}}{{h}_{\text{lg}}}} \right)}_{R}}{{\left( {{L}_{\text{TH}}} \right)}_{R}}{{\left[ \frac{1}{{{F}_{T}}} \right]}_{R}}$ | (35) |
由于ERVC系统的工作压力接近常压,所以试验台架的工作压力及温度变化范围可选定为与原型相同,并选定相同的工质,即有
| ${{\left( \frac{\Delta \rho }{{{\rho }_{\text{ls}}}{{\rho }_{\text{gs}}}{{h}_{\text{lg}}}} \right)}_{R}}=1$ | (36) |
此外在试验台架中,可使用孔板等阻力件,保证自然循环回路中各个部件的阻力特性相等,即有
| ${{\left[ {{F}_{\text{SP}}} \right]}_{R}}={{\left[ {{F}_{\text{TP}}} \right]}_{R}}={{\left[ {{F}_{T}} \right]}_{R}}=1$ | (37) |
式 (33)、(35)、(36) 和式 (37) 结合,可得
| ${{u}_{R}}=\left( {{L}_{\text{TH}}} \right)_{R}^{1/2}$ | (38) |
将式 (38) 代入 (33) 中,得
| ${{\left( {{{\dot{q}}}_{s}} \right)}_{R}}={{\left( {{A}_{\text{in}}} \right)}_{R}}\left( {{L}_{\text{TH}}} \right)_{R}^{1/2}$ | (39) |
方程 (21) 与 (39) 结合,可得质量含汽率比为
| ${{\chi }_{e}}_{R}={{\left( \frac{1}{{{\rho }_{\text{ls}}}{{h}_{\text{lg}}}} \right)}_{R}}=1$ | (40) |
体积含汽率比为
| ${{\alpha }_{R}}={{\left[ \frac{{{x}_{e}}}{{{x}_{e}}+\left( 1-{{x}_{e}} \right){{\rho }_{\text{gs}}}/{{\rho }_{\text{ls}}}} \right]}_{R}}=1$ | (41) |
两相平均密度比为
| $\left( {{{\bar{\rho }}}_{\text{TP}}} \right){{}_{R}}={{\left( \frac{{{\rho }_{\text{ls}}}}{1+{{\chi }_{e}}\Delta \rho /{{\rho }_{\text{gs}}}} \right)}_{R}}=1$ | (42) |
可知在饱和情况下,当运行压力和自然循环回路各部分阻力满足相似时,质量含汽率、体积含汽率和两相平均密度都可满足相似要求。
系统的时间比 (即弛豫时间) 变为
| ${{\tau }_{R}}=\frac{{{l}_{R}}}{{{u}_{R}}}=\left( {{L}_{\text{TH}}} \right)_{R}^{1/2}$ | (43) |
为保证漂移通量数相等,需评估漂移速度是否满足要求,这里使用文献[9-10]提出的方程,即
| $\begin{align} & {{\left[ {{v}_{gj}} \right]}_{R}}= \\ & {{\left\{ 0.2\left[ 1-\sqrt{\frac{{{\rho }_{\text{gs}}}}{{{\rho }_{\text{ls}}}}} \right]\left[ 1+x\left( \frac{\Delta \rho }{{{\rho }_{\text{gs}}}} \right) \right]u+1.4{{\left( \frac{g\Delta \rho }{\rho _{\text{ls}}^{2}} \right)}^{\frac{1}{4}}} \right\}}_{R}} \\ \end{align}$ | (44) |
可知,漂移速度比主要与物性参数和速度有关,当采用等高度等物性模拟时,漂移通量数准则可通过速度相似和流体物性相似自动满足。
3.2 下封头沸腾换热根据文献[11]的研究,对RPV下封头沸腾换热过程的模拟,需要保证压力容器外表面上的核态沸腾过程、两相边界层中的动量传递过程以及经最小间距的蒸汽排放过程三个传递过程相似。
对于使用与ERVC系统原型中相同的的工作流体,表征热力学状态的温度范围和压力范围也基本一致的试验台架,表征沸腾过程的无量纲数Πb为
| $\left( \bar{q}_{b}^{\prime\prime } \right){{}_{\text{R}}}=\left[ \int_{0}^{\pi /2}{q_{w}^{\prime\prime }\left( \theta \right)\text{sin}\theta \text{d}\theta } \right]{{}_{\text{R}}}=1$ | (45) |
由式 (38) 可知,沸腾过程的相似可以通过在试验系统中使用与ERVC原型相同的壁面热流密度分布q″w(θ) 来满足,也可以采用与原型下封头半径相等的等宽弧形 (切片式二维试验段),并采用功率整形策略使之与原型的“瓣状”加热壁热流总量相等[10]。该类试验段一般半径与原型相同,周向宽度为原型的缩比,本文中该宽度比定义为wR。
两相边界层中流动的动量传递无量纲数Πm为
| ${{\left( {{\mathit{\Pi }}_{m}} \right)}_{\text{R}}}=\left( {{\rho }_{g}}/{{\rho }_{l}} \right)_{\text{R}}^{-0.2}=1$ | (46) |
因试验使用相同工质,上述条件能够满足。
对于经流动通道最小间距的蒸汽排放过程,当工质相同,壁面热流密度相似时,该过程的特征时间比Πv为
| ${{\left( {{\mathit{\Pi }}_{v}} \right)}_{\text{R}}}\text{=}{{\left[ \frac{{{R}^{1/2}}}{{{d}_{m}}{{\theta }_{m}}\text{sin}{{\theta }_{m}}} \right]}_{\text{R}}}\text{=}1$ | (47) |
在试验中,可保证模拟流动通道最小间距的位置与原型相同,即 (θm)R=1,则自然循环流道最小间距蒸汽排放的相似准则为
| ${{\left( {{R}^{1/2}}/{{d}_{m}} \right)}_{\text{R}}}={{\left( {{d}_{m}} \right)}_{\text{R}}}=1$ | (48) |
结合ERVC系统各部分的特点,可将自然循环回路简化为竖直下降段、下封头两相段和竖直上升段三部分,其中,竖直下降段可视为单相绝热流动过程,下封头两相段视为两相加热流动过程,竖直上升段可视为两相绝热流动过程。文献[12-13]的研究表明,ERVC中的两相沸腾主要为过冷沸腾,在下封头两相段,两相流动主要为蒸汽相偏向下封头外壁一侧的不对称流型。在竖直上升段中,主要以泡状流为主,当堆芯衰变热功率较高时,可能出现弹状流。因此ERVC系统两相流型的转变主要发生在竖直环状间隙通道中,为不均匀泡状流向均匀泡状流或弹状流的转变。根据Reyes的研究[5],流型转变相似准则主要与物性参数相关,等高等物性模拟时,可自动满足。
3.4 热源模拟体相似RPV下封头模拟体通常选用相近或相同材料的加热模拟体,即有
| ${{\left[ {{\rho }_{\text{s,0}}} \right]}_{R}}={{\left[ {{C}_{\text{vs,0}}} \right]}_{R}}=1$ | (49) |
根据最小间距和加热面宽度的比例,可以得到流道面积与加热面积的比为
| ${{\left( \frac{{{A}_{\text{in}}}}{{{A}_{\text{s}}}} \right)}_{R}}\text{=}\frac{{{\left( {{w}_{m}} \right)}_{R}}}{{{\left( {{w}_{m}} \right)}_{R}}}\text{=}1$ | (50) |
定义ds为加热段厚度,将方程 (38)、(49) 和 (50) 代入Stanton数相似准则有
| ${{\Pi }_{St,R}}={{\left[ {{T}_{\text{s,0}}} \right]}_{R}}{{\left( {{d}_{s}} \right)}_{R}}=1$ | (51) |
式 (51) 表明,试验台架的加热段固体厚度和温度应与原型相同,加热段固体厚度相似条件可通过几何相似满足;对于加热段固体温度相似条件,考虑到ERVC稳态自然循环过程中流体温度变化缓慢,当RPV换热过程相似时,换热系数也比较稳定,可认为固体温度相似可自动满足。
4 ERVC自然循环试验台架比例如前文分析所述,鉴于ERVC系统的运行特点,ERVC自然循环台架可采用等压等温同工质的模拟方式,这样可保证台架与原型间工质物性的一致。
一般来说,试验台架的几何参数越接近原型的尺寸越能反映实际工况。对于自然循环现象,模型和原型的几何比例过小可能会造成局部换热现象的失真,因此本台架将高度比选定为1:1;对压力容器下封头的模拟,选择工程上更容易实现的切片式二维试验段,半径比为1:1,流动通道间距比为1:1,综合考虑用电功率、经济性等要求,切片宽度与原型的比wR为1:100。
本文比例分析中涉及到的两相自然循环、两相流型转变、下封头换热等过程均能完全模拟。对IVR工程应用中的临界热流密度,因不是本文研究的重点,该比例分析只能对CHF现象中的核态沸腾过程进行模拟。
综上,根据前文结论,可得到等物性模拟时,试验装置主要的缩比比例,如表 1所示。
| 模化对象 | 相似条件 | |
| ERVC 自然循环回路 | 高度比 | 1:1 |
| 时间常数比 | 1:1 | |
| 循环速度比 | 1:1 | |
| 两相漂移速度比 | 1:1 | |
| 部件流通面积比 | 1:100 | |
| 保温层流道间距比 | 1:1 | |
| 热源体积释热率比 | 1:100 | |
| 回路总阻力比 | 1:1 | |
| 下封头/切片试验段 | 曲率半径比 | 1:1 |
| 周向宽度比 | 1:100 | |
| 试验段厚度比 | 1:1 | |
| 积分功率比 | 1:100 |
本文以一维漂移流模型为基础,对ERVC系统的自然循环过程进行了比例分析,通过方程无量纲化,得到了试验台架与原型ERVC两相自然循环的相似准则,主要结论如下:
1) 漂移通量数、Froude数、密度数、Friction数、修正Stanton数、焓升数、热源数、核态沸腾数、动量传递数、间隙蒸汽排放过程特征数是表征ERVC整体试验台架与核电厂原型间自然循环现象的相似准则数,ERVC整体试验装置的设计应根据相似准则数确定缩比比例和参数;
2) 结合ERVC系统自然循环的特点,当试验采用等压等物性模拟时,Froude数、密度数、焓升数和热源数相似准则均能得到满足,且所有台架参数的比值均可以写为冷热芯高差比值函数的形式;
3) 当下封头模拟体的半径、热流密度分布、加热段厚、流道最小间距的位置和尺寸均与原型一致,且热源的加热面积与热源处流通面积缩比比例一致时,修正Stanton数和表征RPV局部换热过程的准则数可得到满足。
| [1] |
徐红, 周志伟. 大型先进压水堆熔融物堆内滞留初步研究[J].
原子能科学技术, 2013, 47(6): 969–974.
XU Hong, ZHOU Zhiwei. Preliminary study on in-vessel retention in large-scale advanced PWR[J]. Atomic energy science and technology, 2013, 47(6): 969–974. |
| [2] |
金越, 鲍晗, 刘晓晶, 等. 大功率先进压水堆IVR有效性评价分析[J].
核动力工程, 2015, 36(3): 135–141.
JIN Yue, BAO Han, LIU Xiaojing, et al. Assessment of in-vessel retention for advanced large size PWRs[J]. Nuclear power engineering, 2015, 36(3): 135–141. |
| [3] |
周涛, 刘亮, 李宇, 等. 矩形窄缝自然循环密度波不稳定特性实验研究[J].
原子能科学技术, 2015, 49(5): 848–851.
ZHOU Tao, LIU Liang, LI Yu, et al. Experiment study of density wave instability of natural circulation in narrow rectangle channel[J]. Atomic energy science and technology, 2015, 49(5): 848–851. |
| [4] |
周涛, 李精精, 琚忠云, 等. 非能动自然循环技术的发展与研究[J].
核安全, 2013, 12(3): 32–36.
ZHOU Tao, LI Jingjing, JU Zhongyun, et al. The development and study on passive natural circulation[J]. Nuclear safety, 2013, 12(3): 32–36. |
| [5] | REYES Jr J N, HOCHREITER L. Scaling analysis for the OSU AP600 test facility (APEX)[J]. Nuclear engineering and design, 1998, 186(1/2): 53–109. |
| [6] | ZUBER N, WILSON G E, ISHII M, et al. An integrated structure and scaling methodology for severe accident technical issue resolution:Development of methodology[J]. Nuclear engineering and design, 1998, 186(1/2): 1–21. |
| [7] |
卢冬华, 肖泽军, 陈炳德. 压水堆自然循环比例模化基本方程及相似准则数的研究[J].
核动力工程, 2009, 30(3): 72–84.
LU Donghua, XIAO Zejun, CHEN Bingde. Investigation on basic equations and scaling criteria of PWR natural circulation[J]. Nuclear power engineering, 2009, 30(3): 72–84. |
| [8] | REYES Jr J N. Scaling single-state variable catastrophe functions:an application to two-phase natural circulation[J]. Nuclear engineering and design, 1994, 151(1): 41–48. DOI:10.1016/0029-5493(94)90032-9 |
| [9] | HIBIKI T, ISHII M. One-dimensional drift-flux model and constitutive equations for relative motion between phases in various two-phase flow regimes[J]. International journal of heat and mass transfer, 2003, 46(25): 4935–4948. DOI:10.1016/S0017-9310(03)00322-3 |
| [10] |
闫超星, 阎昌琪, 孙立成, 等. 基于漂移流模型的矩形通道内泡状流-弹状流转变准则[J].
原子能科学技术, 2013, 47(10): 1718–1722.
YAN Chaoxing, YAN Changqi, SUN Licheng, et al. Transitional criterion from bubbly flow to slug flow in vertical rectangular channels based on drift-flux model[J]. Atomic energy science and technology, 2013, 47(10): 1718–1722. |
| [11] | CHEUNG F, LIU Y. Critical heat flux experiments to support in-vessel retention feasibility study for an evolutionary advanced light water reactor, Technical Results 1003101[R]. Palo Alto, CA:EPRI, 2001. |
| [12] | CHU T Y, BENTZ J H, SLEZAK S E, et al. Ex-vessel boiling experiments:laboratory-and reactor-scale testing of the flooded cavity concept for in-vessel core retention Part II:Reactor-scale boiling experiments of the flooded cavity concept for in-vessel core retention[J]. Nuclear engineering and design, 1997, 169(1/2/3): 89–99. |
| [13] |
李永春, 刘晓晶, 程旭. ERVC流道内两相局部分布实验研究[J].
核动力工程, 2014, 35(5): 153–156.
LI Yongchun, LIU Xiaojing, CHENG Xu. Experimental study on local two phase distributions in ERVC flow channel[J]. Nuclear power engineering, 2014, 35(5): 153–156. |



