2. Department of Industrial Engineering and Logistics Management, Shanghai Jiao Tong University, Shanghai 200240, China
生产活动使设备可靠性下降、故障率提升, 而预防性维护能改善设备状态并降低故障率, 因此合理的设备维护计划决策对企业提高生产效率及降低成本具有重要意义。以往的研究主要集中在单设备预防性维护建模, 并取得了丰富的成果[1-3]。通常多部件系统考虑的关联性包括三种:经济关联性、结构关联性和随机关联性。多设备系统与多部件系统类似, 但在考虑经济与结构关联性时更多地受到生产活动的影响。多部件串联系统通常假设一个部件停止运作会导致整个系统停机, 即“一停全停”;而在多设备串联生产系统中往往会有在制品中间缓冲, 上下游之间存在生产结构关联性, 一台设备的停机可能不会立即导致整个系统停机, 即“一停不停”。
序号不对对于多部件单设备或多设备系统的建模和决策大致可分为维护计划与维护策略两种。维护计划一般将有限计划期分成若干时间区间, 优化决策各部件在每个时间区间的预防性维护活动。Moghaddam等[4]引入设备有效役龄作为中间变量反映部件状态变化, 以此建立了多部件系统决策维护/换新的两种计划模型。Ahmad等[5]以比例强度模型来描述系统状态, 建立了多部件系统检查及换新计划模型。维护策略指先决策各部件的维护方案, 再考虑各部件间的关联性, 运用成组维护或机会维护策略对系统中各部件的预防性维护进行调整。Horenbee等[6]以长期平均成本为最小化目标决策各部件不完全维护时点, 考虑了多部件系统的三种关联性, 并运用滚动周期法进行更新。Van[7]考虑多部件的经济关联性, 提出了成组维护及动态更新策略。Hai[8]考虑了串联系统的两种经济关联性:准备成本和停机成本, 且关键部件停机会导致生产损失而非关键设备不牵涉该成本。Zhou等[9]在进行预防性维护决策时考虑了车间加工作业活动的影响, 以工件的完成时刻作为维护机会提出成组维护策略。Tambe等[10]建立了多部件系统的机会维护模型, 利用部件因故障及物料配送等原因而停机产生的维护机会, 以可用性及作业延迟因子为约束, 目标为总成本最小化。Xia等[11]以生产换模时间作为维护机会, 对串并联生产系统提出机会维护策略以优化目标成本。
上述研究均以成本为决策目标, 且考虑“一停全停”的情况, 而本文研究对象为在实际生产中普遍存在的具有中间在制品缓冲的多设备串联生产系统, 其预防性维护计划决策问题不再符合“一停全停”假设。引入中间缓冲后的系统, 其实际生产情形更符合“一停不停”情形。采用预防性维护计划方法来对上述系统的预防性计划问题进行建模, 针对设备故障随机性与系统“一停不停”带来的复杂结构关联性, 提出了基于蒙特卡洛方法的遗传算法对模型进行优化求解。
1 串联系统维护计划问题描述 1.1 问题假设与符号定义以N台设备构成的多设备串联系统为对象, 在具有J个相等时间区间的计划期T上, 优化决策每个时间区间结束时刻是否对各设备进行维护(不完全维护)、换新(完全维护), 或无操作, 使得在整个计划期系统维护相关总成本最小化。问题假设及相关符号定义如下:
1) 多设备生产系统为纯串行结构, 工件依次通过各台设备进行加工, 假设串行生产线完全平衡, 即各设备i平均加工一个零件的时间Pi相等。
2) 设备在加工过程中都可能发生故障, 故障率随时间递增, 记为h(t)。假设h(t)服从非齐次泊松分布, 即h(t)=λ·β·tβ-1, 其中t表示时间, λ和β为设备的寿命参数和形状参数。设备发生故障后需要进行小修, 小修不改变设备有效役龄, 即“修旧如旧”, 设备i一次小修成本为cif, 一次小修时间为τif。
3) 设备间有中间缓冲, 因此当一台设备因故障、预防性维护或饥饿而停机时, 串联系统“一停不停”, 即单位时间系统生产损失并非定值, 而是受随机故障影响的随机变量。记τd为系统在计划期T间的生产停机时间, 即第N台设备无产出时间, cd为系统在计划期T间总的生产停机损失成本, 根据定义可得cd=V·τd, 其中V为系统无停顿连续生产时的单位时间产出。另可推得系统产出率为1-τd/T。
4) 生产活动会使得设备故障率增加, 而维护、换新则会改善设备状态, 减少故障率。记设备i一次维护成本为常数cip、一次维护时间为τip、一次换新成本为常数cir、一次维护时间为τir。
5) 引入有效役龄来反映设备状态, 记xij和x′ij分别表示区间j开始和结束时设备i的有效役龄, 生产活动会使得设备役龄增加, 而维护、换新能减少设备的有效役龄。
如果设备i在区间j结束时进行维护, 则对设备有效役龄的影响为
| ${x_{i,j + 1}} = \alpha \cdot x{\prime _{ij}},i = 1, \ldots ,N,j = 1, \ldots ,J - 1$ | (1) |
式中:α为修复因子0≤α≤1, 反映维护修复程度, α=0表示系统还原到初始状态, 即修复如新, α=1相当于维持原状, 即修旧如旧。
如果设备i在区间j结束时进行换新, 则对设备有效役龄的影响为
| ${x_{i,j + 1}} = 0,i = 1,2, \ldots ,N,j = 1,2,, \ldots ,J - 1$ | (2) |
相当于设备修复如新, 即为换新作业。
如果设备i在区间j结束时维持原状, 则
| ${x_{i,j + 1}} = x{\prime _{ij}},i = 1,2, \ldots ,N,j = 1,2, \ldots ,J - 1$ | (3) |
即设备有效役龄不发生改变。
1.2 数学模型定义决策变量mij和rij, 分别表示维护决策与换新决策, 均为0/1变量, 部件i在区间j结束时进行维护则mij为1, 否则为0;部件i在区间j结束时进行换新则rij为1, 否则为0。
成本最小化和产出率最大化通常是两个互相矛盾的指标, 要满足较高的设备产出率必须及时维修/换新部件, 因而投入较高昂的成本;而一味节省维护成本也将导致产出率过低, 本模型将在满足系统产出率条件的基础上使得总成本最小化。记总成本为TC, 考虑设备维护成本、换新成本、故障后小修成本、系统生产停机损失成本、设备进行维护/换新损失的剩余价值成本。
1) 维护/换新成本。
已知各设备单次维护或换新的成本, 则总的维护/换新成本为
2) 小修成本。
记设备i在区间j期间的故障次数为nij, 期望故障次数为Enij, 根据可靠性理论[12]:
| $\eqalign{ & E{n_{ij}} = \smallint _{{x_{ij}}}^{x{\prime _{ij}}}{h_i}\left( t \right){\rm{d}}t = \smallint _{{x_{ij}}}^{x{\prime _{ij}}}{\lambda _i}{\beta _i}{t^{{\beta _i} - 1}}{\rm{d}}t = \cr & {\lambda _i}\left[ {{{\left( {x{\prime _{ij}}} \right)}^{{\beta _i}}} - {{\left( {{x_{ij}}} \right)}^{{\beta _i}}}} \right] \cr} $ | (4) |
因此设备i在区间j期间的故障后小修成本为cifλix′ijβi-xijβi, 总的小修成本为
3) 系统生产停机损失成本。
由前述可知系统生产停机损失成本为cd=Vτd, 其中随机变量τd的具体求解过程在本文2.2节中详述。
4) 设备进行维护/换新后剩余价值损失成本。
Tambe(2013) 提出在计算成本时需考虑设备换新造成的设备剩余价值损失, 并给出了设备在役龄为t′时换新的剩余价值损失成本, 记为rvir(t′)[8]:
| $r{v_i}^r\left( {t\prime } \right) = c_i^r\cdot{{{1 \over {{R_i}\left( {t\prime } \right)}}\int_{t\prime }^\infty {{R_i}} \left( t \right){\rm{d}}t} \over {\int_{t\prime }^\infty {{R_i}} \left( t \right){\rm{d}}t}}$ | (5) |
式中Ri(t)为设备i在时刻t的可靠度。式(5) 中并未考虑维护对设备剩余价值的影响, 在本文中的假设中预防性维护相当于换新一部分设备零件, 因此有必要考虑设备维护所损失的部分剩余价值。记rvipt′为设备在役龄为t′时进行预防性维护的剩余价值损失成本, 其占换新后剩余价值损失的比重等于维护与换新成本的比值, 即
| $rv_i^pt\prime = rv_i^rt\prime \cdot c_i^p/c_i^r$ | (6) |
综上, 预防性维护计划决策的数学模型如下:
| $\eqalign{ & {\rm{min}}TC = \sum\limits_{j = 1}^J {\sum\limits_{i = 1}^N \{ } c_i^f{\lambda _i}\left[ {{{\left( {x{\prime _{ij}}} \right)}^{{\beta _i}}} - {{\left( {{x_{ij}}} \right)}^{{\beta _i}}}} \right] + \cr & c_i^p\cdot\left( {{m_{ij}} + rv_i^p(x{\prime _{ij}})} \right) + \left( {c_i^r\cdot{r_{ij}} + rv_i^r(x{\prime _{ij}})} \right) + {c^d}\} \cr} $ | (7) |
s.t.
| ${x_{i,1}} = {X_{0i}},i = 1, \ldots ,N,j = 1, \ldots ,J - 1$ | (8) |
| $\eqalign{ & {x_{ij}} = 1 - {m_{i,j - 1}}1 - {r_{i,j - 1}}x{\prime _{i,j - 1}} + {m_{i,j - 1}}{\alpha _i}x{\prime _{i,j - 1}}, \cr & i = 1, \ldots ,N,j = 2, \ldots ,J \cr} $ | (9) |
| $x{\prime _{ij}} = {x_{ij}} + {T^*}/J,\forall i,\forall j$ | (10) |
| ${m_{ij}} + {r_{ij}} \le 1,\forall i,\forall j$ | (11) |
| $1 - {\tau ^d}/T \ge {A_{{\rm{req}}}}$ | (12) |
| ${m_{ij}},{r_{ij}} = 0/1,\forall i,\forall j$ | (13) |
| ${x_{ij}},x{\prime _{ij}} \ge 0,\forall i,\forall j$ | (14) |
式中:X0i表示计划期初设备i的有效役龄, Areq为多设备串联生产系统的产出率要求。
式(8) 表示初始设备有效役龄, 式(9) 说明有效役龄与预防性维护决策的关系, 如部件i在批次j加工完成后进行维护, 则mij=1, xij=αix′i,j-1;如部件i在区间j结束时进行换新, 则rij=1, xij=0。式(10) 为各时间区间开始和结束时各设备有效役龄的递推关系;其中, T*为有效作业时间, 具体计算方式在下文中有所体现。式(11) 表示每当区间j结束时对部件i只能采取预防性维修、换新或维持原状中的一种。式(12) 为系统产出率需求约束。式(13) 表示决策变量只能取0或1。
2 基于蒙特卡洛的遗传算法设计由于设备发生故障的随机性, 上述数学模型中的系统生产停机时间τd难以通过确定的表达式来进行推算, 为求得有效τd以获得系统产出率与生产停机损失成本, 本文采用蒙特卡洛方法进行估计。另一方面, 由于模型的规模以及故障随机性使得模型求解变得复杂, 无法使用Cplex等商业软件进行直接求解, 鉴于遗传算法的优化机理及求解大规模问题的优越性, 本文的算法采用自适应遗传算法框架。
2.1 自适应遗传算法框架1) 染色体编码。
由于维护/换新决策为0/1变量, 故采用二进制编码, 如图 1所示, 染色体总长度为2N·J, 前N·J个基因代表维护决策, 后N·J个基因代表换新决策。

|
| 图1 染色体编码示例 Figure 1 Chromosome coding example |
2) 初始种群生成。
种群数量G是影响算法最优化性能和效率的因素之一, 目前常用的种群数目范围为20~200, 考虑到染色体长度与运算时间, 本文取G为100。初始种群随机生成, 即每条染色体中随机生成维护/换新概率, 再根据概率随机生成基因, 需要注意的是, 如果第k个基因与第N·J+k个基因都等于1, 说明其在同一时刻对同一台设备同时进行维护及换新, 违背式(11) , 随机使第k个和第N·J+k个基因之一等于0。
3) 解的评价(适应度函数设计)。
采用目标成本作为适应度函数, 记为f=TC, TC中的生产停机时间利用蒙特卡洛方法求得, 详见2.2节。不满足系统产出率约束的染色体在适应度值上加入惩罚值, 即f=TC+M(M为一个很大的数), 使其在竞争中淘汰。
4) 选择算子。
采用轮盘赌法进行选择。为了保证每一代的最优染色体不被破坏, 运用跨世代精英策略, 将父代种群与通过交叉、变异产生的子代种群混合起来, 从中选择较优的G个染色体直接进入下一代。
5) 交叉算子。
采用均匀交叉法, 随机选择不定数量的交叉位置, 使对应位置基因进行互换。交叉概率Pc通过自适应法求得:
| ${P_{\rm{c}}} = \left\{ \matrix{ {P_{{\rm{c}}1}} - {{\left( {{P_{{\rm{c}}1}} - {P_{{\rm{c2}}}}} \right)\left( {{f_{{\rm{max}}}} - f\prime } \right)} \over {{f_{{\rm{max}}}} - {f_{{\rm{avg}}}}}},f \ge {f_{{\rm{avg}}}} \hfill \cr {P_{{\rm{c1}}}},f < {f_{{\rm{avg}}}} \hfill \cr} \right.$ | (15) |
式中:fmax为种群中最大适应度值, favg为种群平均适应度值, f′为交叉的两条染色体中较大的适应度值, 通过数值试验调试, 取Pc1=0.9, Pc2=0.6。若交叉后染色体的基因位出现冲突(对应的两个维护位置都为1) , 则随机令一个基因位为0。
6) 变异算子。
采用二进制变异法, 随机选择变异位置, 使其对应位置基因进行翻转。变异概率Pm通过自适应法求得:
| ${P_m} = \left\{ \matrix{ {P_{m1}} - {{\left( {{P_{m1}} - {P_{m2}}} \right)\left( {{f_{{\rm{max}}}} - f\prime } \right)} \over {{f_{{\rm{max}}}} - {f_{{\rm{avg}}}}}},f \ge {f_{{\rm{avg}}}} \hfill \cr {P_{m1}},f < {f_{{\rm{avg}}}}{\rm{ }} \hfill \cr} \right.$ | (16) |
通过数据调试, 取Pm1=0.1, Pm2=0.001。如果变异后第k个基因与第N·J+k个基因都等于1, 随机使第k个或第N·J+k个基因等于0。交叉概率和变异概率的选取采用了自适应遗传算法相关技术, 可根据种群的总体表现自动选取合适的值, Pc1、Pc2、Pm1、Pm2为基本参数。
7) 终止条件。
为控制嵌套了蒙特卡洛抽样估计过程的遗传算法运行时间,本文限制最大的迭代步数tmax, 通过数值试验调试, 取tmax=300。
2.2 基于蒙特卡洛方法的系统产出损失估计蒙特卡洛方法是通过某种“试验”进行抽样以求得随机变量的期望值的方法, 本文设计的“试验”过程如图 2所示。

|
| 图2 蒙特卡洛方法示意图 Figure 2 Diagram of Monte Carlo method |
以遗传算法迭始代中的可行维护计划、初始时刻、初始中间缓冲以及设备有效役龄作为输入;以各台设备加工各工件的开始与结束时间, 以及设备前库存最早可用时间作为中间变量模拟工件的加工;以设备故障概率分布模拟随机故障的发生;根据可行维护计划进行预防性维护;以此得到生产停机时间的期望值, 从而推导获得系统生产损失。随机故障的模拟通过随机生成故障间隔时间得到, 记设备i在有效役龄为t′时发生故障后距下一次故障的间隔时间为tbfi, 根据可靠性与维修性相关理论[12]:
| ${\rm{tb}}{{\rm{f}}_i} = \root \beta \of {{{\left( {{x_i}} \right)}^\beta } - {{{\rm{ln}}U} \over \lambda }} - t\prime $ | (17) |
式中:U为随机数, U∈0,1。
具体步骤及说明如下:记计划期初时刻为tcur, 假设设备间库存容量无限制, 各设备前实时库存为WIPi, 系统原材料充足, 第一台设备从不因缺货停机, 即WIP1=∞, 记各设备初始有效役龄为xi。给定抽样总次数samp。
1) 设定初始状态。复制xi, 记为xxi,∀i;复制决策变量mij和rij, 记为mmij和rrij, ∀i。xxi、mmij和rrij仅用于蒙特卡洛方法的迭代中, 保证初始值未被覆盖。记产出为TH, TH=WIPN+1=0, 设备i最新工件的开始加工时为sti, 结束加工时间为eti, 设备后库存的最早可用时间为etiWIP, 初始状态sti=eti=etiWIP=tcur,∀i, 或另给定。记当前累计无故障时间为APTi=0, 根据式(17) 随机生成各设备故障间隔tbfi, 记当前累计抽样次数为samptemp=1。
2) 判断仿真是否结束, 若满足∀eti≤tcur+T,i=1,2,…,N, 则i=1, 转到3) ;否则转到10) 。
3) 判断eti≤tcur+T是否成立, 成立则转到4) ;否则转到9) 。
4) 判断设备能否开始加工, 即etiWIP≤eti是否成立, 成立则sti=eti, 不成立则sti=etiWIP。转到5) 。
5) 模拟设备i加工工件, WIPi=WIPi-1, APTi=APTi+Pi 。判断该工件加工期间是否发生故障, 即APTi>tbfi成立则假设发生故障, eti=sti+Pi+τif, APTi=tbfi-APTi, 根据式(17) 重新生成tbfi;不成立则eti=sti+Pi。转到6) 。
6) WIPi+1=WIPi+1+1, xxi=xxi+Pi。判断设备后是否有在制品库存, 即WIPi+1=1是否成立, 是则eti+1WIP=eti;否则eti+1WIP不变。转到7) 。
7) 检验是否需要进行维护, 满足eti≥jT/J&mmij=1,∀j, 则进行维护, eti=eti+τip, mmij=0, xxi=0;否则eti不变。转到8) 。
8) 检验是否需要进行换新, 满足eti≥jT/J&rrij=1,∀j, 则进行换新, eti=eti+τir, rrij=0, xxi=αi·xxi ;否则eti不变。转到9) 。
9) i=i+1。i≤N则转到3) , 否则转到2) 。
10) τd=τd+T-tcur-WIPi+1·minPi, samptemp=samptemp+1, 如果samptemp≤samp, 转到2) , 否则转到11) 。
11) τd=τd/samp, 根据cd=Vτd求得cd。
“试验”的重复抽样次数samp关系到解的解的精度, 抽样次数太少则统计值不能代表期望值, 而太多则会使计算时间过长, 本文采用置信区间法求解抽样次数, 取显著水平5%, 得samp约为30。
3 数据实验与对比分析运用VS C#编程进行数据实验, 以5台设备的实际串联生产系统为例, 各设备参数如表 1所示, 计划期为12周, 以周为长度将计划期分成等间隔时间区间, 决策每个区间结束时的预防性维护计划, 系统每天生产8 h, 要求系统产出率Areq不小于0.85, 计划期初系统无中间缓冲, 系统无停顿连续生产时单位时间产出V为8千元/h。
| 参数 | 取值 |
| 修复因子αi | 0.5 |
| 寿命参数λi | [0.000 1 0.000 5] |
| 形状参数βi | [1.5 2.5] |
| 单次小修成本cif/千元 | [1 2] |
| 单次维护成本cip/千元 | [10 20] |
| 单次换新成本cir/千元 | [20 40] |
| 单次小修时间τif/h | 1 |
| 单次维护/换新时间τip/τir/h | 1 |
| 平均加工一个零件时间Pt/h | 0.67 |
Moghaddam(2011) [4]在建立预防性维护计划模型时假设“一停全停”, 即单位时间内各台设备的系统停机损失为常数, 且假设设备故障瞬时修复, 记TRA1为其对应的模型, τtra1d为其对应的系统生产停机时间:
| $\tau _{{\rm{tra1}}}^d = \sum\limits_{j = 1}^J \{ 1 - \prod\limits_{i = 1}^N {\left[ {1 - \left( {{m_{ij}} + {r_{ij}}} \right)} \right]} \} $ | (18) |
记tra2为“一停全停”这一前提下考虑故障后小修时间时所对应的模型, τtra2d为其对应的生产停机时间, 即
| $\eqalign{ & \tau _{{\rm{tra2}}}^d = \sum\limits_{j = 1}^J \{ 1 - \prod\limits_{i = 1}^N {\left[ {1 - \left( {{m_{ij}} + {r_{ij}}} \right)} \right]} + \cr & \sum\limits_{i = 1}^N {{\lambda _i}} \left[ {{{\left( {x{\prime _{ij}}} \right)}^{{\beta _i}}} - {{\left( {{x_{ij}}} \right)}^{{\beta _i}}}} \right]\} \cr} $ | (19) |
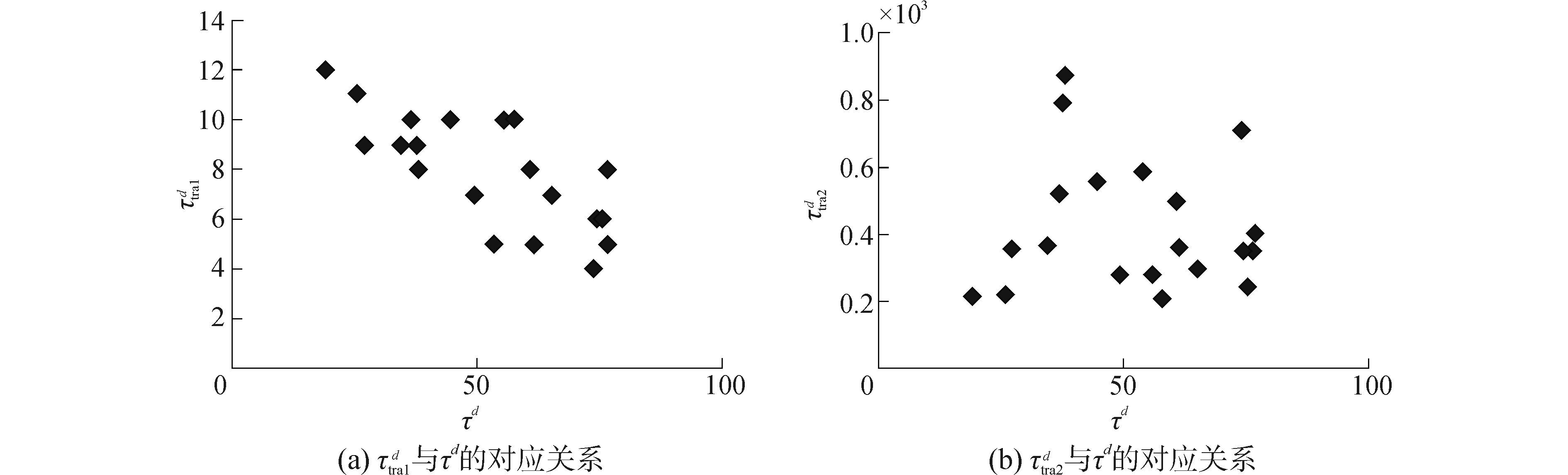
“一停不停”时的τd由蒙特卡洛方法求得, 具有统计学意义, 能反应实际情况, 而传统“一停全停”时的τtra1d和τtra2d则是以确定表达式(18) 和(19) 求得。图 3为同一算例下随机生产20组不同的预防性维护计划, 其中τtra1d未考虑随机故障的影响, 与τd有很大出入且不呈线性关系, 因此并不能有效反映故障率变化对系统生产停机时间乃至总成本造成的影响;图 3(b)中τtra2d为在“一停全停”的前提下考虑故障后小修时间, 过高地估计了随机故障对系统损失的影响, 所得值比τd大。由此可以看出“一停全停”这一假设下的生产停机损失均不能准确对应目标成本中的生产损失, 因而在决策预防性维护时运用蒙特卡洛方法求得生产停机时间, 进而求得实际系统产出率与停机生产损失是有必要的。
|
| 图3 不同算例下蒙特卡洛方法与传统方法求得的系统生产停机时间比较 Figure 3 Comparison between Monte Carlo method and traditional ones under different examples |
不同数据规模下本文模型(记为PRO)与tra1及tra2运用2.1算法所求得解的成本如表 2所示, 从中可以看出本文模型由于综合考虑了生产停机损失成本与预防性维护成本, 能获得更低的总成本。tra1未考虑随机故障对系统停机的影响, 所得解的实际停机损失cd较大, 虽然节省了预防性维护以及相对应的剩余价值损失成本, 但依然抬高了总成本;TRA2假设一台设备故障即导致整个系统停机, 其得到的解虽然有较低的cd, 但因过高估计了随机故障的影响, 预防性维护成本大大增加, 使总成本增加。综上, 本文模型考虑系统产出率及停机生产损失更贴近实际, 且比传统模型解的总成本更低。
3.2 参数敏感性分析在表 2所述实验参数下, 以5台设备为例, 依次改变系统产出率要求Areq、连续生产时单位时间产出V, 及设备小修时间τif, 保持其余参数不变, 考虑各参数变化对总成本的影响。
| n | 5 | 10 | 15 | ||||||||
| PRO | tra1 | tra2 | PRO | tra1 | tra2 | PRO | tra1 | tra2 | |||
| cd | 390.13 | 1071.42 | 408.40 | 767.51 | 1 062.58 | 700.71 | 1 044.00 | 1 348.76 | 1 080.76 | ||
| cp | 182.00 | 238.00 | 296.00 | 630.00 | 758.00 | 1484.00 | 900.00 | 1 000.00 | 1 712.00 | ||
| cr | 306.00 | 28.00 | 506.00 | 414.00 | 192.00 | 1 172.00 | 762.00 | 440.00 | 1 964.00 | ||
| cf | 160.74 | 274.74 | 103.09 | 335.20 | 458.23 | 200.90 | 876.08 | 1 047.40 | 932.77 | ||
| rvp | 19.14 | 16.07 | 66.33 | 82.78 | 38.67 | 302.99 | 110.94 | 91.89 | 380.74 | ||
| rvr | 67.86 | 3.10 | 142.00 | 64.30 | 18.75 | 493.56 | 127.26 | 70.39 | 766.54 | ||
| TC | 1 125.87 | 1 631.33 | 1 521.82 | 2 293.79 | 2 528.23 | 4 354.16 | 3 820.28 | 3 998.44 | 6 836.81 | ||
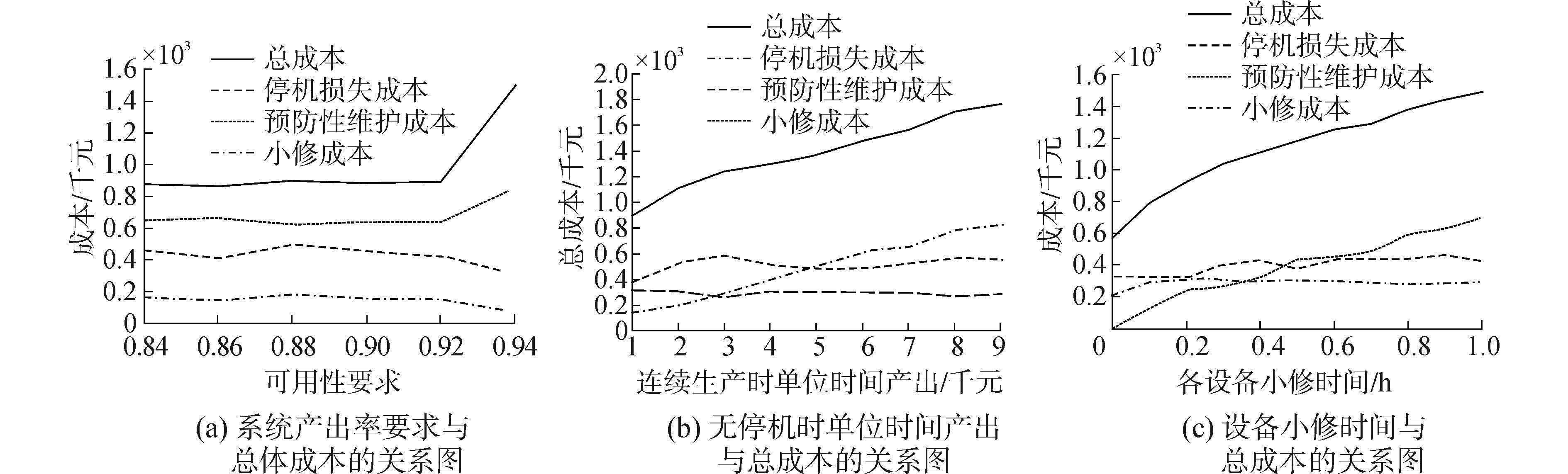
从图 4(a)中可以看出当Areq不大于0.92时, Areq对总成本几乎没有影响, 这是因为在目标函数中考虑了生产停机损失成本, 系统产出率过低则生产停机损失成本也会上升, 因此优化解需满足一定系统产出率;而当要求的系统产出率从0.92上升到0.94时, 对设备的可靠性要求更为严格, 预防性维护成本增加, 预防性维护后寿命损失成本也随之增加, 虽小修成本及生产停机损失成本略有下降, 但总成本仍显著上升;由于存在设备故障与维护, 系统产出率几乎不可能达到100%, 当需求产出率大于0.94时, 未搜索到可行解。
|
| 图4 不同参数与总成本的关系图 Figure 4 Diagram of different parameters and total cost |
图 4(b)反映了在其余参数均不变的情况下, 生产停机损失成本及总成本随单位时间产出V的增加呈递增趋势, 预防性维护成本在V为1~3千元时随V缓慢上升, 随后趋于平缓, 对应小修成本先略有下降后趋于平缓, 说明在V较小时, 预防性维护随着V的增加而略有增多, 而当V增大到一定数值时将不再影响预防性维护决策。图 4(c)与图 4(b)类似, 生产停机损失成本及总成本随设备小修时间的增加而增加, 当小修时间增大到一定程度时, 将不再影响预防性维护决策。
4 结论本文研究了多设备串联生产系统预防性维护计划优化问题。
1) 考虑串联系统的“一停不停”因素, 综合分析各种成本构成, 可使得企业总成本更低;
2) 在与传统模型相比较的算例以及敏感性分析的算例中, 未发现异常值, 验证了模型与算法的有效性;
3) 模型不仅考虑维护/换新成本、故障小修成本, 还引入了维护/换新造成的设备剩余价值损失成本以及实际生产停机损失成本;
4) 考虑“一停不停”的假设与系统产出率约束, 更加符合车间实际, 同时也使得数学模型在理论上更加复杂, 因此设计了基于蒙特卡洛抽样的遗传算法进行优化求解;
5) 未来研究可以从实时反应策略着手, 以机器故障所产生的生产停机时间作为可能的维护机会对设备进行更加科学合理的预防性维护安排。
| [1] | XIA Tangbin, XI Lifeng, LEE J, et al. Optimal CBPM policy considering maintenance effects and environmental condition[J]. The international journal of advanced manufacturing technology, 2011, 56(9-12): 1181–1193. DOI:10.1007/s00170-011-3235-4 |
| [2] | NAKAGAWA T, MIZUTANI S. A summary of maintenance policies for a finite interval[J]. Reliability engineering & system safety, 2009, 94(1): 89–96. |
| [3] | CLAVAREAU J, LABEAU P E. Maintenance and replacement policies under technological obsolescence[J]. Reliability engineering & system safety, 2009, 94(2): 370–381. |
| [4] | MOGHADDAM K S, USHER J S. Preventive maintenance and replacement scheduling for repairable and maintainable systems using dynamic programming[J]. Computers & industrial engineering, 2011, 60(4): 654–665. |
| [5] | AHMADI R. Optimal maintenance scheduling for a complex manufacturing system subject to deterioration[J]. Annals of operations research, 2014, 217(1): 1–29. DOI:10.1007/s10479-014-1543-4 |
| [6] | VAN HORENBEEK A, PINTELON L. A dynamic predictive maintenance policy for complex multi-component systems[J]. Reliability engineering & system safety, 2013, 120: 39–50. |
| [7] | DO VAN P, BARROS A, BÉRENGUER C, et al. Dynamic grouping maintenance with time limited opportunities[J]. Reliability engineering & system safety, 2013, 120: 51–59. |
| [8] | VU H C, DO P, BARROS A, et al. Maintenance grouping strategy for multi-component systems with dynamic contexts[J]. Reliability engineering & system safety, 2014, 132: 233–249. |
| [9] | ZHOU Xiaojun, LU Zhiqiang, XI Lifeng. Preventive maintenance optimization for a multi-component system under changing job shop schedule[J]. Reliability engineering & system safety, 2012, 101: 14–20. |
| [10] | TAMBE P P, MOHITE S, KULKARNI M S. Optimisation of opportunistic maintenance of a multi-component system considering the effect of failures on quality and production schedule:a case study[J]. The international journal of advanced manufacturing technology, 2013, 69(5-8): 1743–1756. DOI:10.1007/s00170-013-5122-7 |
| [11] | XIA Tangbin, JIN Xiaoning, XI Lifeng, et al. Production-driven opportunistic maintenance for batch production based on MAM-APB scheduling[J]. European journal of operational research, 2015, 240(3): 781–790. DOI:10.1016/j.ejor.2014.08.004 |
| [12] |
EBELING C E. 可靠性与维修性工程概论[M]. 康锐, 李瑞莹, 王乃超, 等译. 北京:清华大学出版社, 2010.
EBELING C E. Reliability and maintainability engineering[M]. KANG Rui, LI Ruiying, WANG Naichao, trans. Beijing:Tsinghua University Press, 2010. |



