海洋油气开采及海洋可再生能源开发利用过程中,海底悬空管道、海洋立管以及海洋浮式风机系泊缆等柔性圆柱结构十分常见。在海流的作用下,圆柱结构两侧会出现交替的漩涡脱落,产生周期变化的流体力,促使结构振动,结构振动又反作用于流场,这种典型的流-固耦合现象称为“涡激振动(vortex-induced vibrations, VIV)”。近年来,人们针对垂直来流作用下柔性圆柱涡激振动开展了广泛的理论和实验研究,并取得了大量成果[1-4]。
实验是探究柔性圆柱涡激振动现象最有效的手段之一。Trim等[5]开展了垂直均匀流作用的柔性立管涡激振动实验,发现顺流向涡激振动对结构疲劳损伤的贡献与横流向同等重要。Song等[6]设计了大长径比柔性立管涡激振动实验,研究表明柔性圆柱立管振动存在多个模态,并存在3倍、4倍和5倍频率等高频现象。Huera-Huarte等[7]开展了垂直阶梯流作用下低质量比(1.1、2.7) 柔性圆柱涡激振动实验,观测发现低质量比情况下柔性圆柱响应幅值显著增大,横流向与顺流向最大幅值可分别达到3倍和1.5倍结构直径。
上述研究的来流条件均与圆柱轴向垂直。实际工程应用中,圆柱结构与来流方向并不完全垂直,常存在不同的倾斜角度。为了简化问题,学术界提出了不相关原则[8-9],认为倾斜圆柱涡激振动问题等效为与圆柱轴向垂直的来流速度分量引起的涡激振动。现阶段,倾斜圆柱涡激振动研究才刚刚起步,不相关原则的合理性仍存在争议。Franzini等[10]开展了倾斜刚性圆柱的涡激振动实验,结果表明:倾角小于20°时,不相关原则成立,倾角大于20°时则不完全成立。Bourguet等[11]采用直接数值模拟研究了倾角为60°,长径比为50柔性圆柱涡激振动,发现在低轴向力条件时倾斜圆柱涡激振动特性与垂直圆柱差异较大,不相关原则不合理,高轴向力时不相关原则合理。
由于轴向二次流的存在,柔性圆柱在倾斜来流条件下的涡激振动十分复杂,已开展的研究不能完全反映柔性圆柱在倾斜来流作用下的涡激振动行为,缺乏大长径比、小质量比、高雷诺数条件下的倾斜圆柱涡激振动实验研究。基于此,本文设计开展了小倾角倾斜柔性圆柱涡激振动实验,目的是探究不相关原则的适用性,并观测小倾角倾斜圆柱涡激振动特性。
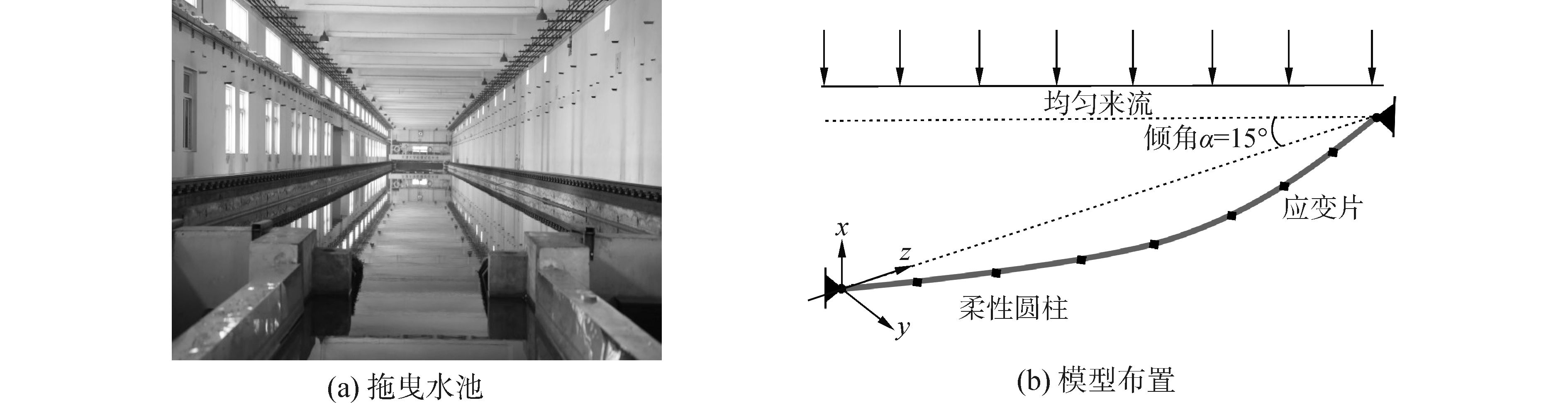
1 小倾角柔性圆柱VIV实验实验在天津大学水利工程仿真与安全国家重点实验室的拖曳水池中完成。图 1为实验水池及装置示意图。拖曳水池长137.0 m,宽7.0 m,深3.3 m,柔性圆柱模型通过万向节安装在与拖车相连钢架上,圆柱结构轴向力为500 N。调整钢架和拖车的相对位置可实现垂直来流条件和15°倾角来流条件。实验中拖车速度范围为0.05~1.00 m/s,间隔为0.05 m/s,雷诺数范围近似800~16 000。拖车采用模拟控制和数字控制两套系统,可保证速度精度为0.1%,如图 1所示。
|
| 图1 实验示意图 Figure 1 Schematic of the experimental set-up |
柔性圆柱模型内芯材料为铜管,铜管沿轴向被7个截面等分8段,应变片粘贴于上述7个截面的横流向和顺流向,用于采集振动信息,应变片采用半桥接法,测量导线沿铜管端部引出。铜管外部包裹硅胶管,目的是使柔性圆柱模型外表面规则光滑,同时保护内部的应变片和测量导线,并起到防水和绝缘的作用。
拖车匀速拖动柔性圆柱模型,实现均匀来流条件,待圆柱振动达到稳定开始数据采集,采样频率为100 Hz,稳定段采集时间为50 s。本文实验完成了两个工况:一为柔性圆柱模型轴向与来流方向垂直(即倾角为0) ,二为柔性圆柱模型倾角为15°。共计开展40组观测与测量。详细的圆柱模型结构参数如表 1所示。
| 参数 | 数值 |
| 长度L /m | 5.6 |
| 外径 D/m | 0.016 |
| 弯曲刚度 EI/(N·m2) | 17.45 |
| 轴向力 T/N | 500 |
| 质量(内部为空气)m/(kg·m-1) | 0.3821 |
| 质量比4m/(πρD2) | 1.9 |
| 长径比 L/D | 350 |
运用模态法处理实验采集的应变数据,模态法可以根据柔性圆柱模型上离散点应变信息获得整个圆柱模型上任一点的位移信息[12-13]。下面以横流向(CF)为例详细说明模态法的运用过程,顺流向(IL)与之类似不再赘述。
建立坐标系:x轴对应IL方向, y轴对应CF方向, z轴对应圆柱模型轴向(如图 1(b)所示)。圆柱模型CF方向的曲率Cy(z, t)可表示为
| ${{C}_{y}}(z,t)=\frac{\varepsilon (z,t)}{R}$ | (1) |
式中:t为时间,ε(z, t)为应变信号, R为圆柱模型的半径。对于长度为L的圆柱振动问题,根据模态法可以将其CF振动位移表示为
| $U(z,t)=\sum\limits_{1}^{N}{{{A}_{n}}(}t){{\varphi }_{n}}(z)$ | (2) |
式中:U(z, t)为圆柱CF方向振动位移,n为模态阶次, L为圆柱模型总长度, An(t)为权重系数,φn(z)为模态函数。本实验中柔性圆柱模型两端为简支条件,因此φn(z)为
| ${{\varphi }_{n}}(z)=\sin \frac{n\text{ }\!\!\pi\!\!\text{ }z}{L}$ | (3) |
根据力学关系,曲率Cy(z, t)还可表示为
| ${{C}_{y}}(z,t)={U}''(z,t)=-\sum\limits_{1}^{\infty }{{{A}_{n}}(}t){{(\frac{n\text{ }\!\!\pi\!\!\text{ }}{L})}^{2}}\sin \frac{n\text{ }\!\!\pi\!\!\text{ }z}{L}$ | (4) |
若在圆柱模型上布置M个应变片,其振动位移采用N阶模态的线性叠加来表示,式(4) 可写成矩阵形式:
| ${{\mathit{\boldsymbol{C}}}_{y}}=\mathit{\boldsymbol{ }}\!\!\Phi\!\!\rm{ A}$ | (5) |
其中,
| ${{\mathit{\boldsymbol{C}}}_{y}}=\left[ \frac{\varepsilon (t,{{z}_{1}})}{R}\ \ \ \frac{\varepsilon (t,{{z}_{1}})}{R}\cdots \frac{\varepsilon (t,{{z}_{n}})}{R} \right]$ | (6) |
| $\mathit{\boldsymbol{ }}\!\!\Phi\!\!\rm{ =}\left[ \begin{matrix} \sin \frac{\rm{ }\!\!\pi\!\!\rm{ }{{z}_{1}}}{L} & {{2}^{2}}\sin \frac{\rm{2 }\!\!\pi\!\!\rm{ }{{z}_{1}}}{L} & \cdots & {{N}^{2}}\sin \frac{N\rm{ }\!\!\pi\!\!\rm{ }{{z}_{1}}}{L} \\ \sin \frac{\rm{ }\!\!\pi\!\!\rm{ }{{z}_{2}}}{L} & {{2}^{2}}\sin \frac{\rm{2 }\!\!\pi\!\!\rm{ }{{z}_{2}}}{L} & \cdots & {{N}^{2}}\sin \frac{N\rm{ }\!\!\pi\!\!\rm{ }{{z}_{1}}}{L} \\ \cdots & \cdots & \cdots & \cdots \\ \sin \frac{\rm{ }\!\!\pi\!\!\rm{ }{{z}_{M}}}{L} & {{2}^{2}}\sin \frac{\rm{2 }\!\!\pi\!\!\rm{ }{{z}_{M}}}{L} & \cdots & {{N}^{2}}\sin \frac{N\rm{ }\!\!\pi\!\!\rm{ }{{z}_{M}}}{L} \\ \end{matrix} \right]$ | (7) |
| $\mathit{\boldsymbol{A}}={{[{{A}_{1}}(t)\ \ \ {{A}_{2}}(t)\cdots {{A}_{N}}(t)]}^{T}}$ | (8) |
数据处理时权重系数采用最小二乘法确定:
| $\mathit{\boldsymbol{A=}}{{[{{\mathit{\boldsymbol{ }}\!\!\Phi\!\!\rm{ }}^{T}}\mathit{\boldsymbol{ }}\!\!\Phi\!\!\rm{ }]}^{-1}}{{\mathit{\boldsymbol{ }}\!\!\Phi\!\!\rm{ }}^{T}}{{\mathit{\boldsymbol{C}}}_{y}}$ | (9) |
将式(9) 代入式(2) ,可得到CF方向振动位移。
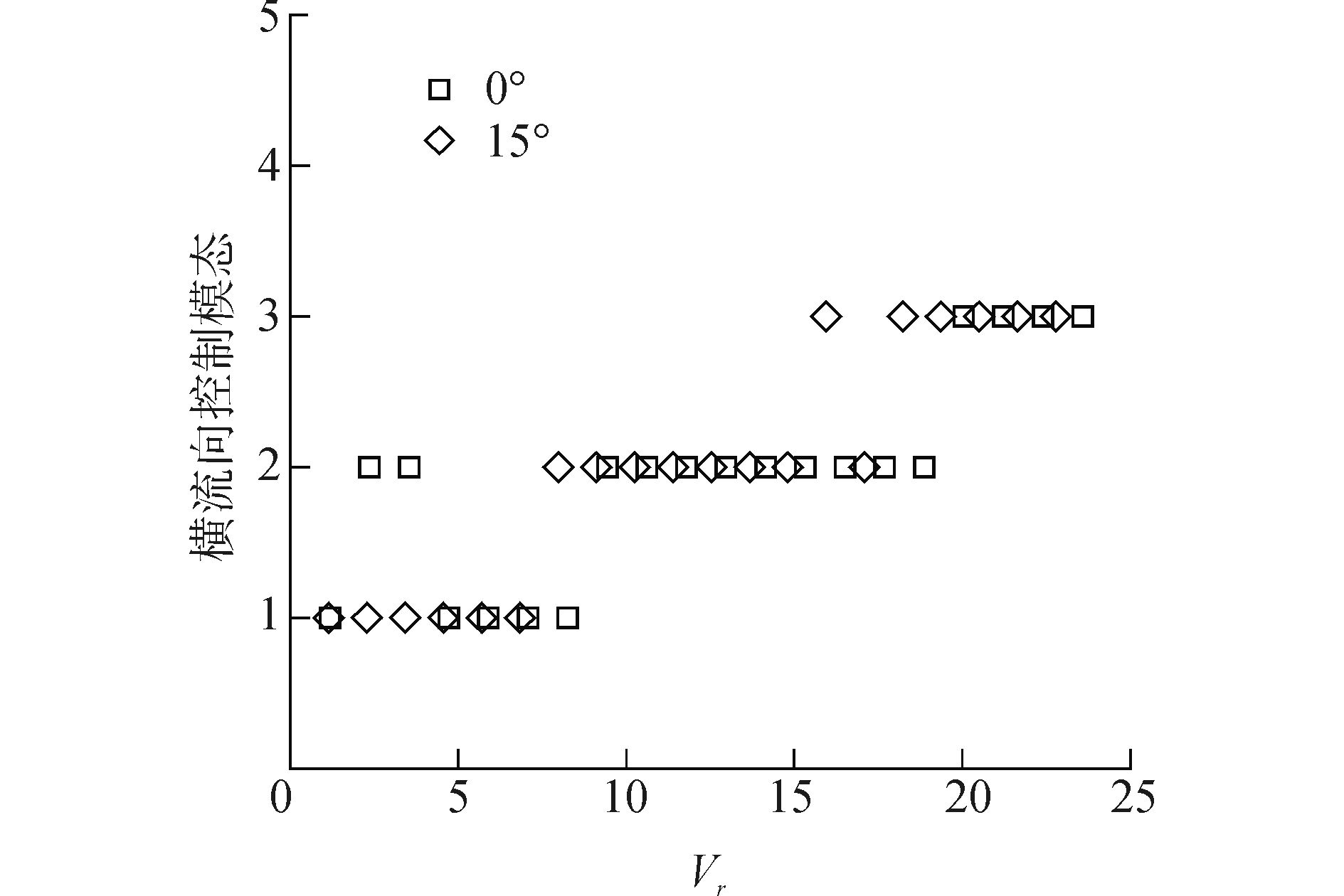
3 小倾角柔性圆柱涡激振动特性控制模态是描述柔性圆柱涡激振动特性的一个重要的指标。图 2和图 3分别绘制了圆柱横流向和顺流向振动控制模态随约化速度变化情况。其中横坐标为约化速度Vr=Vcos(α)/(f1D), V是来流速度, a表示倾斜角度,垂直时为0,倾斜时为15°,f1为结构一阶固有频率,本实验测量了圆柱结构静水中的固有频率,发现测量的结果与式(10) 得到的理论结果误差非常小。考虑到柔性圆柱垂直和倾斜时测量结果存在微小差异,为了方便分析,统一采用式(10) 得到的理论值计算约化速度:
|
| 图2 横流向控制模态随流速变化 Figure 2 CF dominate mode number versus reduced velocity |
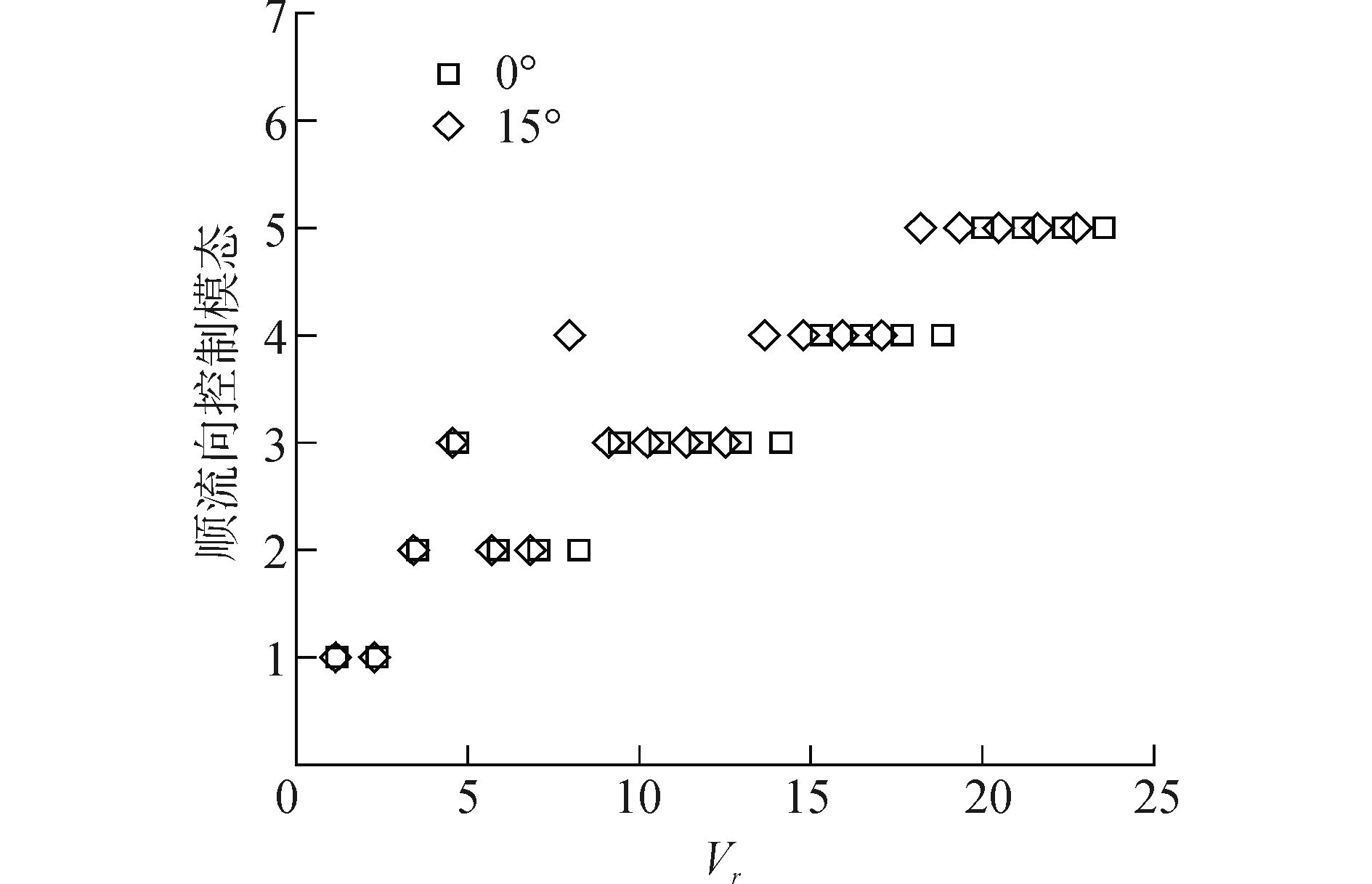
|
| 图3 顺流向控制模态随流速变化 Figure 3 IL dominate mode number versus reduced velocity |
| ${{f}_{n}}=\frac{n}{2L}\sqrt{\frac{T}{m}+{{\left( \frac{n\text{ }\!\!\pi\!\!\text{ }}{L} \right)}^{2}}\frac{EI}{m}}$ | (10) |
从图 2和图 3中可发现无论是横流向还是顺流向涡激振动,垂直与倾斜圆柱两者的控制模态变化规律基本一致。横流向涡激振动最高控制模态为3阶,顺流向为5阶。在不同控制模态转化区域,如约化速度Vr在8.0、18.0附近范围,相比于垂直柔性圆柱,倾斜柔性圆柱更容易被激发更高阶模态。产生上述现象的原因是轴向二次流引起的,这也充分证明了倾斜柔性圆柱涡激振动的复杂性。
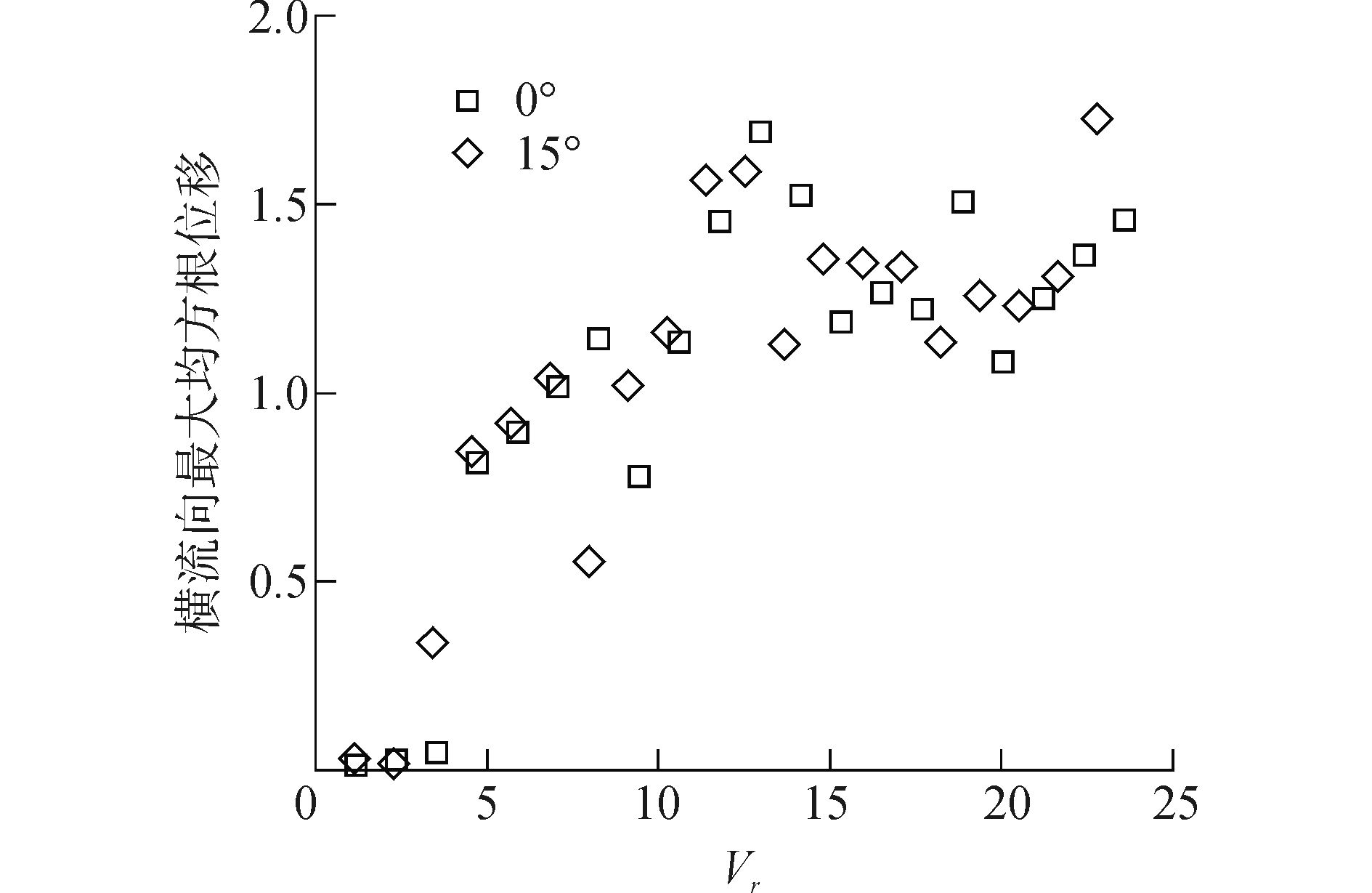
|
| 图4 横流向最大均方根位移幅值随约化速度变化 Figure 4 Max RMS CF displacement versus reduced velocity |
|
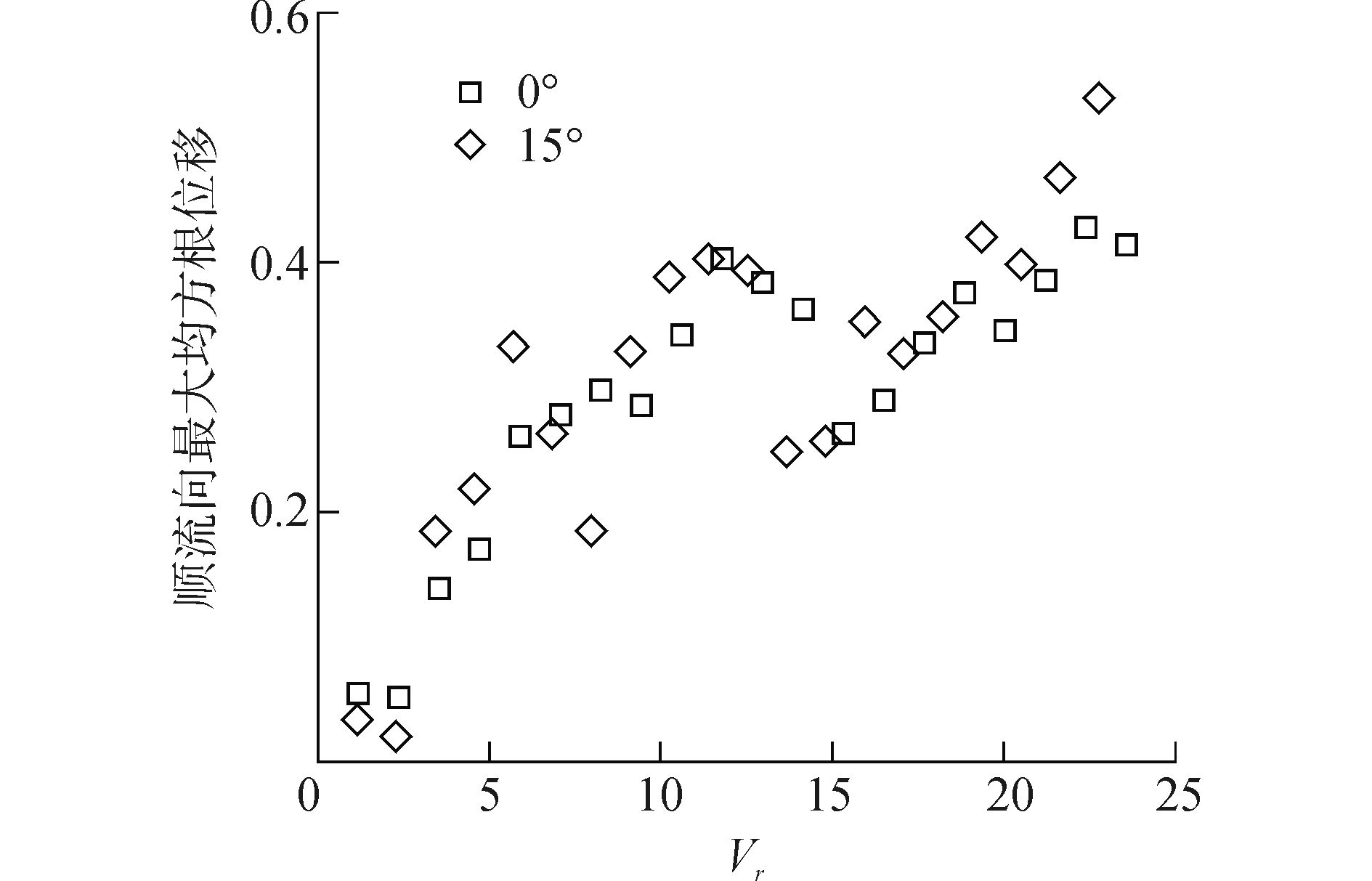
| 图5 顺流向最大均方根位移幅值随约化速度变化 Figure 5 Max RMS IL displacement versus reduced velocity |
由图 4、5可以看出在模态转化区域外,垂直圆柱与倾斜圆柱横流向和顺流向的最大位移均方根基本接近。但在模态转化区域,倾斜圆柱得到的响应幅值,无论是横流向还是顺流向均会更小。由于实验所用的圆柱模型质量比为1.9,垂直圆柱和小倾角圆柱均出现了较大响应幅值现象,这与近期Huera-Huarte等[7]的研究成果一致。
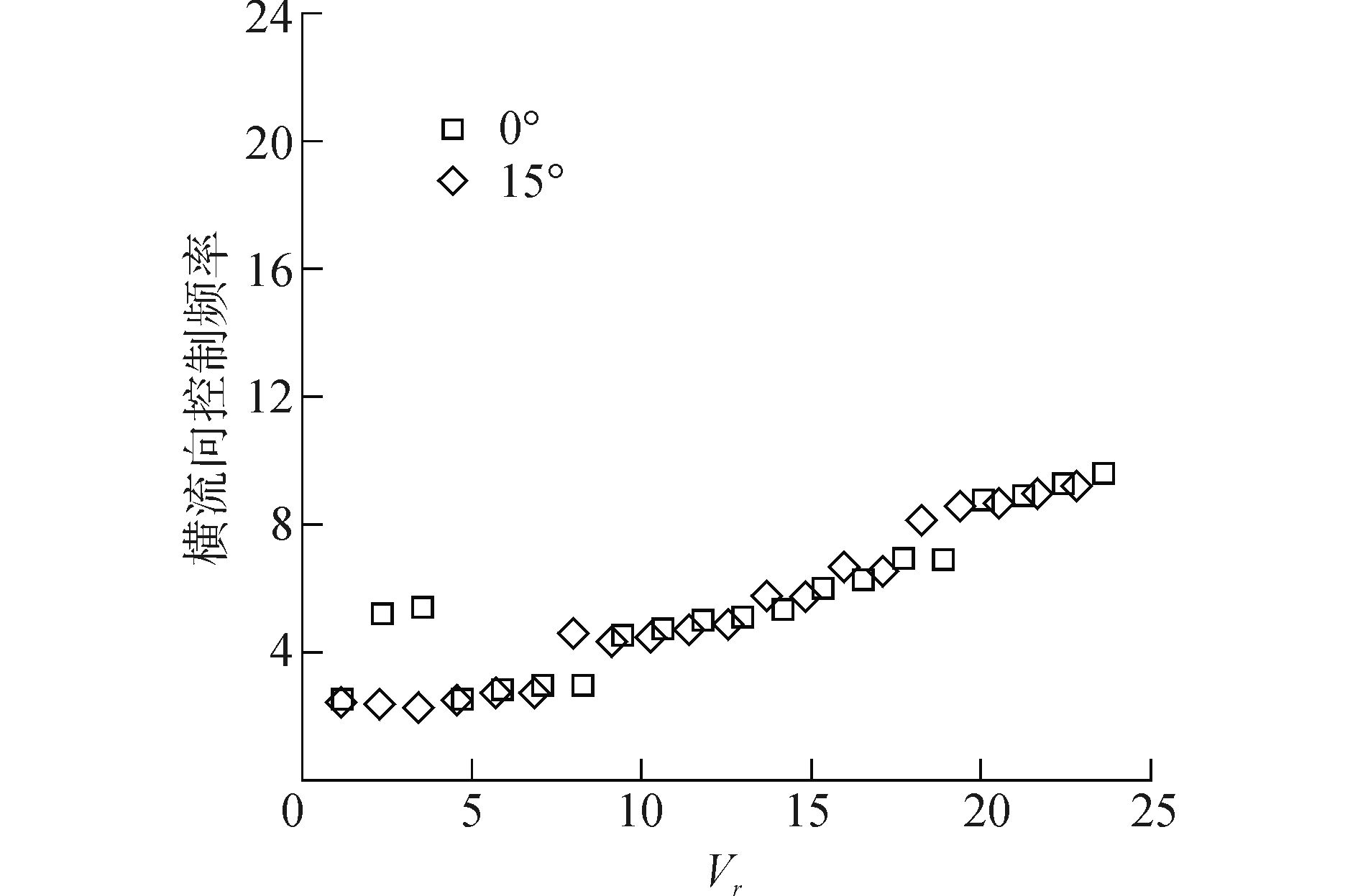
柔性圆柱涡激振动的控制频率是评估结构疲劳寿命的重要参数。横流向与顺流向控制频率随约化速度变化情况如图 6和图 7所示。观测发现控制频率随约化速度变化呈线性增长,0与15°倾角工况下,圆柱涡激振动控制频率变化规律基本相同。但在低阶模态向高阶模态转化的区域,倾斜圆柱的控制频率高于垂直圆柱,再次说明倾斜柔性圆柱更容易激发高阶模态。
|
| 图6 横流向控制频率随约化速度变化 Figure 6 CF dominate frequency versus reduced velocity |

|
| 图7 顺流向控制频率随约化速度变 Figure 7 IL dominate frequency versus reduced velocity |
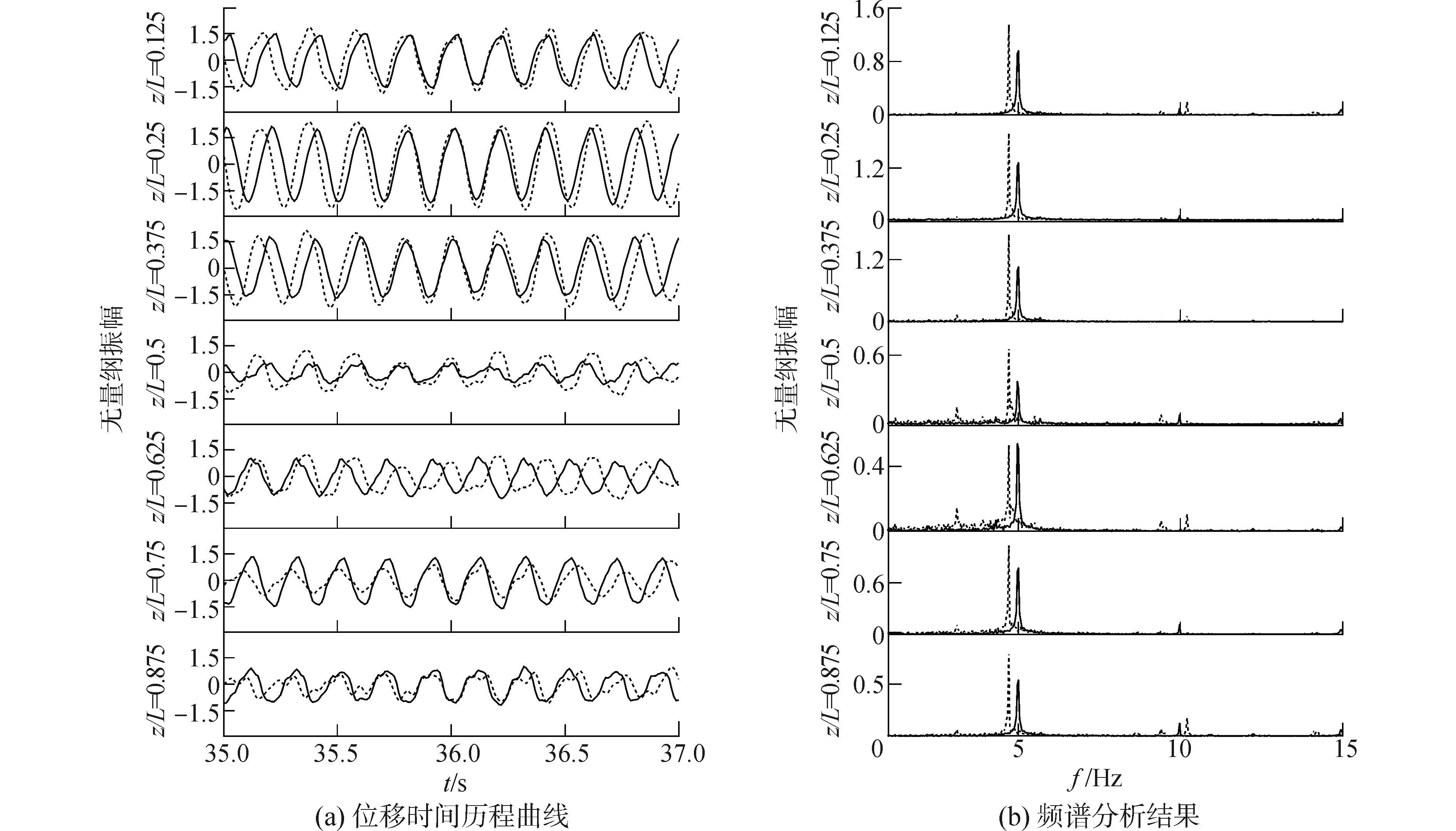
图 8给出了中等来流速度(V=0.5 m/s)时七个测点处横流向位移时间历程曲线和对应的频谱图。
|
| 图8 测点处横流向位移时间历程曲线和频谱分析结果(V=0.5 m/s) Figure 8 CF displacement history and its spectra at measured positions (V=0.5 m/s) 注:实线为垂直圆柱,虚线为倾斜圆柱 |
V=0.5 m/s位于模态转化区域外,垂直圆柱和倾斜圆柱的位移历程曲线两者之间几乎无差异,证明在模态转化区域范围外,不相关原则对于小倾角倾斜柔性圆柱是适用的。从横流向位移的频谱分析图中可以看出倾斜圆柱控制频率为4.7 Hz,而垂直圆柱为5.0 Hz,均出现了2倍频和3倍频等高频谐波成分。
图 9给出了较大来流速度(V=0.8 m/s)时垂直圆柱和倾斜圆柱在的测点处的横流向位移时间历程曲线和对应的频谱图。V=0.8 m/s时正好处于模态转化区域,从位移历程曲线可看出,垂直圆柱和倾斜圆柱测点处的位移差异较大,因此在模态转化区域内不相关原则并不能很好的适用于小倾角倾斜柔性圆柱。从频谱分析图中可以看出,倾斜圆柱横流向的控制频率为8.13 Hz,垂直圆柱横流向的控制频率为6.90 Hz,均出现了高频的成分。

|
| 图9 测点处横流向位移时间历程曲线和频谱分析结果(V=0.8 m/s) Figure 9 CF displacement history and its spectra at measured positions(V=0.8 m/s) 注:实线为垂直圆柱,虚线为倾斜圆柱 |
本文对小倾角倾斜柔性圆柱涡激振动进行了实验研究,采用了大长径比、小质量比的圆柱实验模型,雷诺数最大可达到16 000,通过与垂直柔性圆柱的涡激振动实验结果对比得到了如下结论:
1) 小倾角倾斜圆柱与垂直圆柱测点处的位移在模态转化区域外差异很小,而在模态转化区域内差异较大,并且均发现了高频的成分。
2) 通过分析小倾角倾斜圆柱和垂直圆柱的响应幅值,发现在模态转化区域外,两者的最大位移均方根差异很小。由于柔性圆柱模型质量比较小,均出现了大响应幅值现象。
3) 根据小倾角倾斜圆柱和垂直圆柱的控制模态、控制频率、响应幅值、测点处的位移观测结果,发现在模态转化区域内倾斜圆柱比垂直圆柱更容易激发高阶模态,不相关原则在模态转化区域范围外适用于小倾角柔性圆柱的涡激振动。
| [1] | SARPKAYA T. A critical review of the intrinsic nature of vortex-induced vibrations[J]. Journal of fluids and structures, 2004, 19(4): 389–447. DOI:10.1016/j.jfluidstructs.2004.02.005 |
| [2] | GABBAI R D, BENAROYA H. An overview of modeling and experiments of vortex-induced vibration of circular cylinders[J]. Journal of sound and vibration, 2005, 282(3/4/5): 575–616. |
| [3] | WILLIAMSON C H K, GOVARDHAN R. A brief review of recent results in vortex-induced vibrations[J]. Journal of wind engineering and industrial aerodynamics, 2008, 96(6/7): 713–735. |
| [4] | WU Xiaodong, GE Fei, HONG Youshi. A review of recent studies on vortex-induced vibrations of long slender cylinders[J]. Journal of fluids and structures, 2012, 28: 292–308. DOI:10.1016/j.jfluidstructs.2011.11.010 |
| [5] | TRIM A D, BRAATEN H, LIE H, et al. Experimental investigation of vortex-induced vibration of long marine risers[J]. Journal of fluids and structures, 2005, 21(3): 335–361. DOI:10.1016/j.jfluidstructs.2005.07.014 |
| [6] | SONG Jining, LU Lin, TENG Bin, et al. Laboratory tests of vortex-induced vibrations of a long flexible riser pipe subjected to uniform flow[J]. Ocean engineering, 2011, 38(11/12): 1308–1322. |
| [7] | HUERA-HUARTE F J, BANGASH Z A, GONZÁLEZ L M. Towing tank experiments on the vortex-induced vibrations of low mass ratio long flexible cylinders[J]. Journal of fluids and structures, 2014, 48: 81–92. DOI:10.1016/j.jfluidstructs.2014.02.006 |
| [8] | HANSON A R. Vortex shedding from yawed cylinders[J]. AIAA journal, 1966, 4(4): 738–740. DOI:10.2514/3.3531 |
| [9] | VAN ATTA C W. Experiments on vortex shedding from yawed circular cylinders[J]. AIAA journal, 1968, 6(5): 931–933. DOI:10.2514/3.4630 |
| [10] | FRANZINI G R, GONÇALVES R T, MENEGHINI J R, et al. One and two degrees-of-freedom vortex-induced vibration experiments with yawed cylinders[J]. Journal of fluids and structures, 2013, 42: 401–420. DOI:10.1016/j.jfluidstructs.2013.07.006 |
| [11] | BOURGUET R, KARNIADAKIS G E, TRIANTAFYLLOU M S. On the validity of the independence principle applied to the vortex-induced vibrations of a flexible cylinder inclined at 60°[J]. Journal of fluids and structures, 2015, 53: 58–69. DOI:10.1016/j.jfluidstructs.2014.09.005 |
| [12] | LIE H, KAASEN K E. Modal analysis of measurements from a large-scale VIV model test of a riser in linearly sheared flow[J]. Journal of fluids and structures, 2006, 22(4): 557–575. DOI:10.1016/j.jfluidstructs.2006.01.002 |
| [13] | CHAPLIN J R, BEARMAN P W, HUERA HUARTE F J, et al. Laboratory measurements of vortex-induced vibrations of a vertical tension riser in a stepped current[J]. Journal of fluids and structures, 2005, 21(1): 3–24. DOI:10.1016/j.jfluidstructs.2005.04.010 |



