对于敏感潜艇运动的导航系统而言,在装备前要对其进行性能鉴定,需要尽可能地遍历潜艇出海时的各种运动,包括各种海洋环境干扰。实艇试验成本高、风险大[1],而且由于复杂海况的不可预见性,造成潜艇的短周期运动具有不可控性,海况(尤其是复杂海况) 干扰造成的潜艇受迫运动无法实现人为控制,无法全面考察设备性能。这使得全面分析潜艇在海洋环境干扰下的六自由度运动十分有意义。利用陆地上建立的真实的潜艇模拟仿真环境,一定程度上弥补实际海试时条件的局限性,是一种很好的解决办法。
本文研究了海况干扰下的潜艇运动,首先介绍了描述潜艇运动时所用到的坐标系,然后以格特勒的潜艇标准运动方程为基础,进行适当简化,结合海洋环境干扰模型,建立海况干扰下的潜艇六自由度运动方程。以某潜艇为研究对象,进行静水和海况干扰下的直航、回转运动仿真分析,最后得出潜艇六自由度运动的速度和姿态的变化特点。
1 坐标系描述潜艇六自由度运动时采用了固定坐标系(或称地面坐标系) 及运动坐标系(或称艇体坐标系),按研究惯例,一律采用右手坐标系,参数、符号体系与国际水池会议(ITTC) 及造船和轮机工程学会(SNAME) 术语公报推荐的一致[2]。
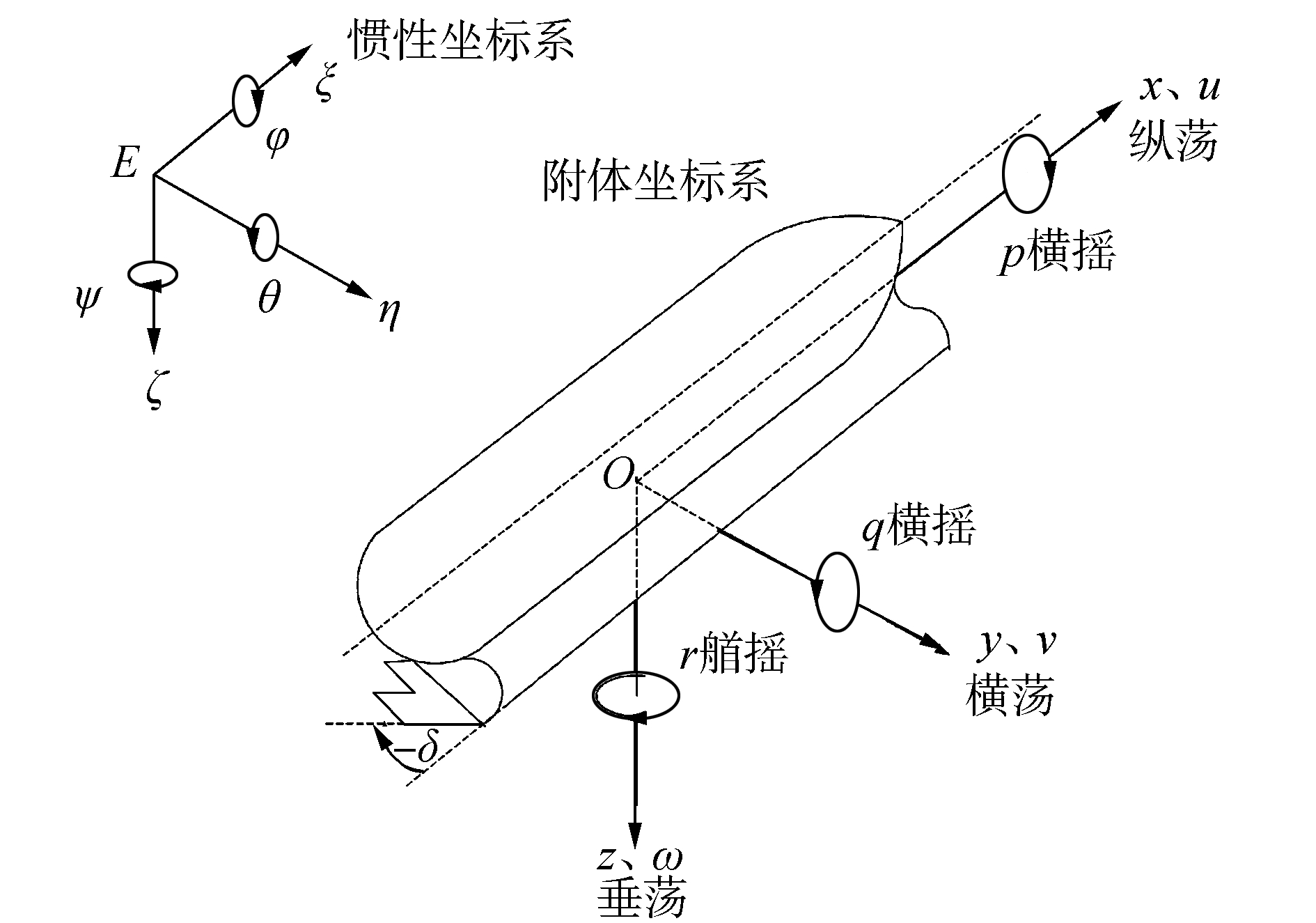
固定坐标系的原点E可以任意选取海面或海中的某一点,本文将t=0时刻潜艇重心所在位置定为坐标原点,Eξ轴沿水平方向,以潜艇的主航向作为正向,Eη轴位于Eξ轴所在的水平面,且由Eξ轴顺时针旋转90°得到,Eζ轴垂直于Eη轴和Eξ轴构成的平面,其正向符合右手定则。
运动坐标系的坐标原点O通常选取在艇体的重心G处,Ox轴位于艇体纵中剖面内,沿水平线指向船艏方向为正,Oy轴与纵中剖面垂直,以指向右舷方向为正,Oz轴垂直于Ox轴与Oy轴所在的平面,以指向船底方向为正,固定坐标系及运动坐标系如图 1所示。
|
| 图1 固定坐标系及运动坐标系 Figure 1 Fixed coordinate system and moving coordinate system |
设两个坐标系原点重合,则固定坐标系可以通过三次正交旋转与动系完全重合。表 1中列出了本文在描述潜艇运动时常用参量的符号表示。
| 参量 | Ox轴 | Oy轴 | Oz轴 |
| 线速度U | u | v | w |
| 角速度Ω | p | q | r |
| 力F | X | Y | Z |
| 力矩T | K | M | N |
潜艇六自由度空间运动方程[3-4]以1967年泰勒海军潜艇研究和发展中心发表的格特勒《用于潜艇模拟研究的标准运动方程》为基础,该方程含108个水动力系数,实际中由于试验的困难很难全部得到,在不影响潜艇六自由度运动的主要特性下,可对标准方程进行简化处理,假设条件主要有[5-6]:1) 潜艇左右对称;2) 潜艇重心与原点重合;3) 潜艇运动状态对舵力没有影响,且不考虑舵之间的相互耦合;4) 忽略对潜艇运动影响非常小的二阶水动力系数及其耦合系数;5) 忽略潜艇垂直面的速度对水平面的运动耦合。
根据以上简化条件,得到简化后的潜艇六自由度运动力与力矩的方程如式(1)~(6),其中前三个方程为力的方程,后三个方程为力矩方程。
轴向力方程:
| $ \begin{align} & m\left[ \dot{u}-vr+wq \right]=\frac{1}{2}\rho {{L}^{4}}\left[ X{{\prime }_{qq}}{{q}^{2}}+X{{\prime }_{rr}}{{r}^{2}}+X{{\prime }_{rp}}rp \right]+ \\ & \ \ \ \ \ \ \ \ \frac{1}{2}\rho {{L}^{3}}Y{{\prime }_{vr}}vr+\frac{1}{2}\rho {{L}^{2}}\left[ X{{\prime }_{uu}}{{u}^{2}}+X{{\prime }_{vv}}{{v}^{2}} \right]+ \\ & \ \ \ \ \frac{1}{2}\rho {{L}^{2}}{{u}^{2}}\left[ X{{\prime }_{{{\delta }_{r}}{{\delta }_{r}}}}{{\delta }^{2}}_{r}+X{{\prime }_{{{\delta }_{s}}{{\delta }_{s}}}}^{2}{{\delta }_{s}}~+X{{\prime }_{{{\delta }_{b}}{{\delta }_{b}}}}\delta _{b}^{2} \right]+{{X}_{T}} \\ \end{align} $ | (1) |
横向力方程:
| $ \begin{align} & m\left[ \dot{v}-wp+ur \right]=\ \frac{1}{2}\rho {{L}^{4}}\left[ Y{{\prime }_{pq}}pq+Y{{\prime }_{qr}}qr \right]+\ \\ &\frac{1}{2}\rho {{L}^{2}}Y{{\prime }_{v}}uv+\ \frac{1}{2}\rho {{L}^{2}}Y{{\prime }_{{{\delta }_{r}}}}{{u}^{2}}{{\delta }_{r}}+ \\ & \frac{1}{2}\rho {{L}^{3}}\left[ Y{{\prime }_{r}}ur+Y{{\prime }_{p}}up+Y{{\prime }_{vq}}vq+Y{{\prime }_{wp}}wp+Y{{\prime }_{wr}}wr \right] \\ \end{align} $ | (2) |
垂向力方程:
| $ \begin{align} & m\left[ \dot{w}-uq+vp \right]=\ \frac{1}{2}\rho {{L}^{4}}\left[ Z{{\prime }_{pp}}{{p}^{2}}+Z{{\prime }_{rr}}{{r}^{2}}+Z{{\prime }_{rp}}rp \right]+ \\ & \frac{1}{2}\rho {{L}^{3}}\left[ Z{{\prime }_{q}}uq+Z{{\prime }_{vr}}vr+Z{{\prime }_{vp}}vp+\text{ }Z{{\prime }_{w|q|}}\frac{w}{\left| w \right|}\left| {{\left( {{v}^{2}}+{{w}^{2}} \right)}^{\frac{1}{2}}} \right|\left| q \right| \right]+ \\ & \frac{1}{2}\rho {{L}^{2}}\left[ Z{{\prime }_{0}}{{u}^{2}}+Z{{\prime }_{w}}uw+Z{{\prime }_{vv}}{{v}^{2}}+Z{{\prime }_{{{\delta }_{s}}}}{{u}^{2}}{{\delta }_{s}}+Z{{\prime }_{{{\delta }_{b}}}}{{u}^{2}}{{\delta }_{b}} \right] \\ \end{align} $ | (3) |
横倾力矩方程:
| $ \begin{align} & \ \ \ {{I}_{x}}\dot{p}+\left( {{I}_{z}}-{{I}_{y}} \right)qr=\frac{1}{2}\rho {{L}^{5}}\left[ K{{\prime }_{qr}}qr+K{{\prime }_{pq}}pq \right]+ \\ & \frac{1}{2}\rho {{L}^{4}}\left[ K{{\prime }_{p}}up+K{{\prime }_{r}}ur+K{{\prime }_{vq}}vq+K{{\prime }_{wp}}wp+K{{\prime }_{wr}}wr \right]+ \\ & \ \ \ \ \ \ \ \frac{1}{2}\rho {{L}^{3}}\left[ K{{\prime }_{v}}uv+K{{\prime }_{{{\delta }_{r}}}}{{u}^{2}}{{\delta }_{r}} \right]-mgh\text{cos}~\theta \text{sin}~\varphi \\ \end{align} $ | (4) |
纵倾力矩方程:
| $ \begin{align} & \ \ \ \ {{I}_{y}}\dot{q}+\left( {{I}_{x}}-{{I}_{z}} \right)rp=\frac{1}{2}\rho {{L}^{5}}\left[ M{{\prime }_{pp}}{{p}^{2}}+M \right[{{\prime }_{rr}}{{r}^{2}}+ \\ & \left. \ \ \ \ M{{\prime }_{rp}}rp \right]+\frac{1}{2}\rho {{L}^{4}}\left[ M{{\prime }_{q}}uq+ \right.M{{\prime }_{vr}}vr+M{{\prime }_{vp}}vp+ \\ & M{{\prime }_{w\left| q \right|}}|\left( {{v}^{2}}+{{w}^{2}} \right)\left. ^{12}|q \right]+\frac{1}{2}\rho {{L}^{3}}[M{{\prime }_{0}}{{u}^{2}}+M{{\prime }_{w}}uw]+ \\ & \ \ \ \frac{1}{2}\rho LM{{\prime }_{vv}}{{v}^{2}}+\frac{1}{2}\rho {{L}^{3}}\left[ M{{\prime }_{{{\delta }_{s}}}}{{u}^{2}}{{\delta }_{s}}+M{{\prime }_{{{\delta }_{b}}}}{{u}^{2}}{{\delta }_{b}} \right]-mgh\text{sin}~\theta \\ \end{align} $ | (5) |
偏航力矩方程:
| $ \begin{align} & \ \ \ \ \ {{I}_{z}}\dot{r}+\left( {{I}_{y}}-{{I}_{x}} \right)pq=\frac{1}{2}\rho {{L}^{5}}\left[ N{{\prime }_{pq}}pq+N{{\prime }_{qr}}qr \right]+ \\ & \frac{1}{2}\rho {{L}^{4}}\left[ N{{\prime }_{p}}up+N{{\prime }_{r}}ur+N{{\prime }_{wr}}wr+N{{\prime }_{wp}}wp+N{{\prime }_{vq}}vq \right]+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{1}{2}\rho {{L}^{3}}\left[ N{{\prime }_{v}}uv+N{{\prime }_{{{\delta }_{r}}}}{{u}^{2}}{{\delta }_{r}} \right] \\ \end{align} $ | (6) |
结合潜艇六自由度运动辅助方程为[7]
| $ \left\{ \begin{align} & \dot{\varphi }=p+q\text{tan}~\theta \text{sin}~\varphi +r\text{tan}~\theta \text{cos}~\varphi \\ & \dot{\theta }=q\text{cos}~\varphi -r\text{sin}~\varphi \\ & \dot{\psi }=(q\text{sin}~\varphi +r\text{cos}~\varphi )/\text{cos}~\theta \\ & \dot{\xi }=u\text{cos }\!\!~\!\!\text{ }\psi \text{cos }\!\!~\!\!\text{ }\theta +v(\text{cos}~\psi \text{sin}~\theta \text{sin}~\varphi -\text{sin}~\psi \text{cos }\!\!~\!\!\text{ }\varphi )+ \\ & \ \ \ \ \ \ w\left( \text{cos}~\psi \text{sin}~\theta \text{cos}~\varphi +\text{sin}~\psi \text{sin}~\varphi \right) \\ & \dot{\eta }=u\text{sin }\!\!~\!\!\text{ }\psi \text{cos}~\theta +v(\text{sin}~\psi \text{sin}~\theta \text{sin}~\varphi +\text{cos }\!\!~\!\!\text{ }\psi \text{cos }\!\!~\!\!\text{ }\varphi )+ \\ & \ \ \ \ \ \ w\left( \text{sin }\!\!~\!\!\text{ }\psi \text{sin}~\theta \text{cos}~\varphi -\text{cos}~\psi \text{sin}~\varphi \right) \\ & \dot{\zeta }=-u\text{sin }\!\!~\!\!\text{ }\theta +u\text{cos}~\theta \text{sin}~\varphi +w\text{cos}~\theta \text{cos}~\varphi \\ \end{align} \right. $ | (7) |
若已知潜艇水动力系数,对于任何操纵信息(包括舵、桨等),采用四阶龙格-库塔积分算法对潜艇六自由度运动模型进行求解,可快速得到舰潜艇动状态的数值解,包括潜艇的三维速度、角速度、姿态及轨迹。
2.2 海洋环境干扰模型潜艇的战术任务主要是在近水面完成的,如水深十多米处发射导弹等,不可避免地受到海浪和海流的影响而产生摇荡[8],为了更真实的模拟潜艇在海洋中的运动状况,本文对海浪和海流干扰下的潜艇运动进行了仿真研究。
2.2.1 作用在潜艇上的海浪干扰模型为了提高仿真模型的精度,同时满足实时仿真的需求,本文采用十二届ITTC提供的双参数随机海浪频谱来实时仿真长峰波随机海浪。
ITTC提供的双参数海浪谱为[9]
| $ S\left( \omega \right)=\frac{A}{{{\omega }^{5}}}\text{exp}(-\frac{B}{{{\omega }^{4}}}) $ | (8) |
式中:
根据能量等效原则,遭遇频率能量谱密度函数与自然频率能量密度函数之间的关系为
| $ {{S}_{\alpha }}({{\omega }_{e}})={{S}_{\alpha }}\left( \omega \right)/(1-\frac{2\omega }{g}V\text{cos}~\beta ) $ | (9) |
式中:V为潜艇航速,β为浪向角,g为重力加速度。
潜艇在海浪作用下所受到力及力矩可主要考虑为横摇力矩,纵摇力矩及垂向作用力,其受力模型分别介绍如下:
1) 潜艇受海浪作用横摇力矩
作用于潜艇上的海浪横摇力矩[10]:
| $ {{K}_{w}}=Dh{{\alpha }_{e}}+2{{K}_{{\dot{\varphi }}}}{{{\dot{\alpha }}}_{e}}+{{J}_{xx}}{{{\ddot{\alpha }}}_{e}} $ | (10) |
式中:Jxx为潜艇绕x轴的附加转动惯量,
海浪作用下潜艇横摇的波倾角仿真模型为
| $ {{\alpha }_{e}}=\left\{ \sum\limits_{i=1}^{n}{(\sqrt{2{{S}_{\alpha }}({{\omega }_{i}})\Delta \omega \text{cos}({{\omega }_{ei}}t+{{\varepsilon }_{i}})})} \right\}\text{ sin}~\beta $ | (11) |
式中:n为谐波个数,ωi为第i个海浪谐波的频率,Δω为频率增量,Sα(ωi) 为第i个谐波波倾角能量谱密度。
2) 潜艇受海浪作用纵摇力矩
作用于潜艇上的海浪纵摇力矩[10]:
| $ {{M}_{w}}=DH{{\alpha }_{e}}+2{{M}_{{\dot{\theta }}}}{{{\dot{\alpha }}}_{e}}+{{J}_{yy}}{{{\ddot{\alpha }}}_{e}} $ | (12) |
式中:Jyy为潜艇绕y轴的附加转动惯量,
本文中所用到的海浪作用下的潜艇纵摇的波倾角仿真模型为
| $ {{\alpha }_{e}}=\left\{ \sum\limits_{i=1}^{n}{(\sqrt{2{{S}_{\alpha }}({{\omega }_{i}})\Delta \omega \text{cos}({{\omega }_{ei}}t+{{\varepsilon }_{i}})})} \right\}\text{cos}~\beta $ | (13) |
3) 潜艇垂向受海浪的作用力
本文采用Hirom近似公式来计算作用于潜艇垂向上的海浪一阶垂荡力[11],当潜艇深度变化值和纵摇角都较小的情况下,潜艇在近水面所受的波浪力为
| $ {{Z}_{\text{wave}}}=\left( 780-145\sum\limits_{i=1}^{n}{{{F}_{1i}}}\text{sin}({{\omega }_{ei}}t) \right)\sum\limits_{i=1}^{n}{{{F}_{1i}}}\text{sin}({{\omega }_{ei}}t) $ | (14) |
式中:F1i=aiωi2exp (-ωi2(h+Δh(t))/g);ai=
海流的处理,采用均匀定常流的假设,对于非高速运动的潜艇,只是从运动学上考虑其对潜艇的影响。若VC为流速,ψC为流向,则流速VC在附体坐标轴上的分量为
| $ \left\{ \begin{align} & {{u}_{C}}={{V}_{C}}\text{cos}({{\psi }_{C}}-\psi ) \\ & {{v}_{C}}={{V}_{C}}\text{sin}({{\psi }_{C}}-\psi ) \\ \end{align} \right. $ | (15) |
潜艇运动对水流的相对速度的投影ur、vr:
| $ \left\{ \begin{align} & {{u}_{r}}=u-{{u}_{c}} \\ & {{v}_{r}}=v-{{v}_{c}} \\ \end{align} \right. $ | (16) |
将海浪模型中的力和力矩加入到潜艇六自由度运动方程,引入海浪干扰信息,而对于海流,由于只考虑运动学上的影响,故按上式进行处理。
3 某潜艇六自由度运动仿真试验水下回转是潜艇转向运动的重要研究内容[12],本文根据上小节中建立的潜艇六自由度运动模型及海洋环境干扰模型,以某潜艇为仿真对象,给出了该潜艇在静水中、海洋环境干扰下的直航及回转运动情况。
3.1 静水中潜艇回转静水中潜艇直航相对较简单,本文仅给出静水中回转运动的仿真,设定初始航速20 kn,航向角为0°,即正北向航行,调整螺旋桨推力以固定航速,方向舵角分别给为10°、20°、30°,艏艉升降舵角为0,即不进行定深控制。
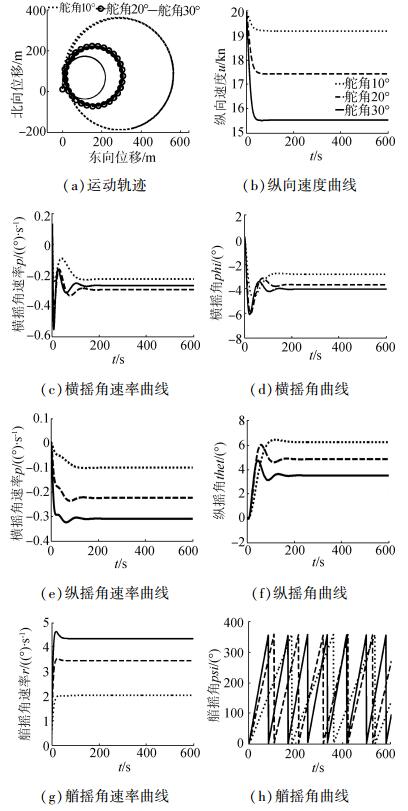
图 2为该潜艇在静水中固定航速改变方向舵角进行的回转运动,图中列出了某潜艇的轨迹、轴向速率、三维角速率以及三维姿态角图。由图中可以看出,潜艇方向舵角由10°、20°、30°依次增大时,潜艇在回转过程中的漂角也相应增大,其回转圈的半径越小;潜艇纵向阻力依次增大,其速降越严重;潜艇定常回转时的向心力也依次增大,其横向力应等于向心力在横向的投影,横向力对重心的力矩与扶正力矩平衡,潜艇定常回转时的横倾角也相应的增大。
|
| 图2 固定航速改变舵角 Figure 2 Fix speed and change rudder angle |
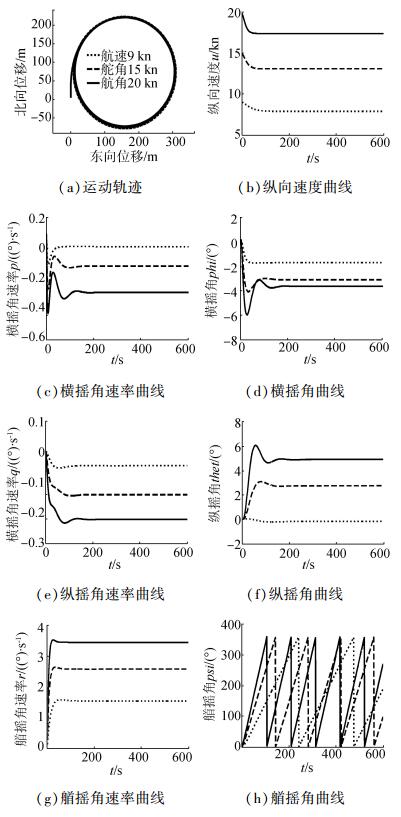
如果方向舵角固定为20°,调节螺旋桨推力使潜艇的速度分别固定在9、15、20 kn,其运动状态如图 3。
|
| 图3 固定舵角改变航速 Figure 3 Fix rudder angle and change speed |
图 3为潜艇在静水中固定舵角改变航速进行的回转运动,从三种速度下的航迹图可以看出,航速对潜艇定常回转直径的影响不大;潜艇定常回转时其横倾角与航速的平方存在正比关系,因而随着航速增大,横倾角也相应增大,稳态时的横倾角也越大,当航速为20 kn时,稳定横倾角达3.8°。纵倾角也随着航速的增大而增大,当航速为20 kn时,稳定纵倾角达到5°。
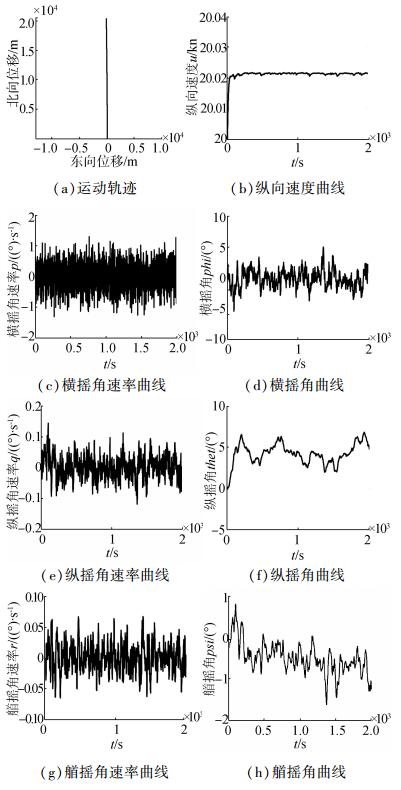
3.2 海浪对潜艇运动的干扰作用海浪的大小决定了海面的粗糙程度,进一步影响了潜艇的运动,本节在静水的基础上加上海浪干扰对潜艇运动影响进行仿真。设潜艇航速20 kn,航向角为0°,即正北向航行,初始深度为5 m,方向舵角为0°,首尾升降舵角为0°,不进行定深控制。按实际海域统计得到的海浪参数对仿真模型进行修正,其中海浪浪高为1.28 m,浪向角为30°,潜艇的轨迹及横摇和纵摇曲线如图 4所示。
|
| 图4 海浪干扰下潜艇直航运动 Figure 4 Direct motion under ocean wave interference |
图 4中给出了在海浪干扰下潜艇直航运动的状态。受海浪干扰力的作用,潜艇在水下直航运动时存在纵横摇,其中横摇角最大达到6°,纵倾角达7°。
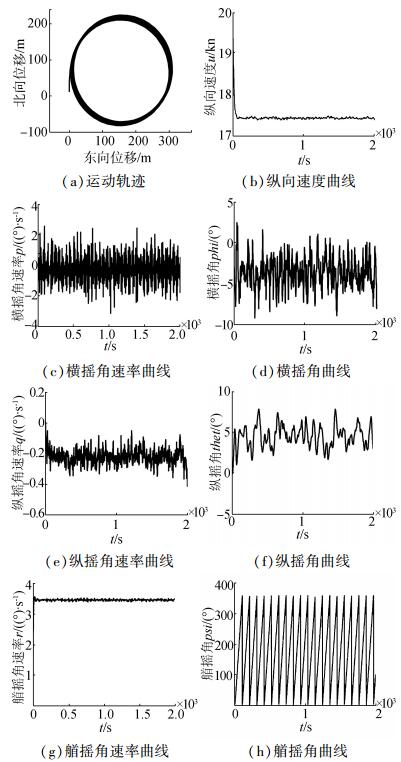
保持上述仿真条件不变,将方向舵角改为20°,进行海浪干扰下,潜艇回转运动的仿真,其运动轨迹及横纵摇曲线如图 5所示。对比潜艇在静水中回转运动时的角速率及姿态角参数,在海浪干扰下,潜艇的横向、纵向以及垂向角速度出现高频的震荡,相应的,其三维姿态角随之变化,横摇、纵摇较为明显。与图 4中的直航运动状态比较,潜艇受回转力和力矩的作用,其三维角速率变大,横摇角不再以0°为中心上下震荡,而是以-4°为中心上下震荡,纵倾角出现高频变化量。
|
| 图5 海浪干扰下的潜艇回转运动 Figure 5 Rotary motion under ocean wave interference |
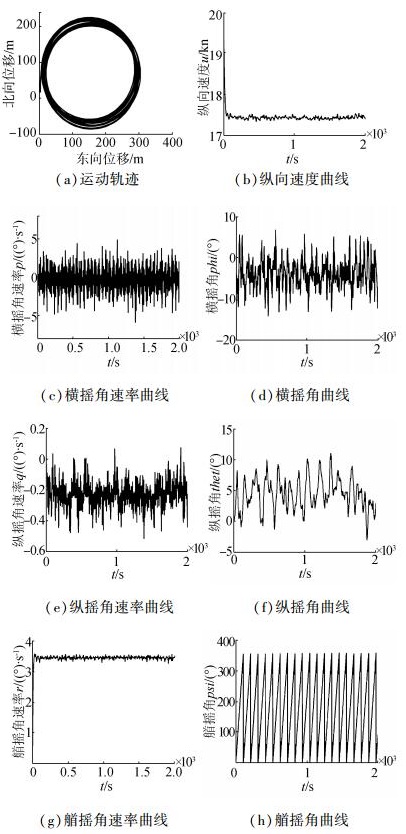
为了更进一步体现海浪对潜艇的作用效果,加强海浪干扰,将波高设置为3.25 m,潜艇的轨迹及横纵摇曲线如图 6所示。
|
| 图6 增大海浪干扰下潜艇回转运动 Figure 6 Rotary motion under increased ocean wave interference |
对比图 5,海浪的浪向保持不变,波高由1.28 m变为3.25 m,潜艇的三维角速率以及三维姿态角明显变大,横摇角及纵倾角高达11°。
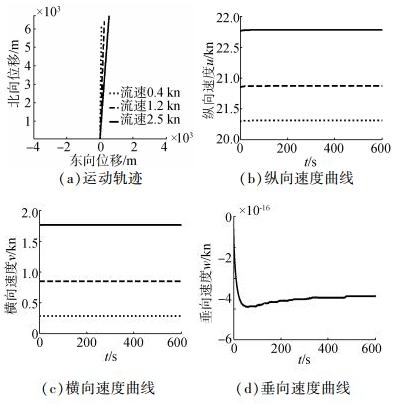
3.3 海流对潜艇运动的干扰作用本小节仿真了潜艇在不同等级海流下的直航和回转运动。潜艇初始航速20 kn,调整螺旋桨推力使潜艇航速保持不变,航向角0°,正北航向,方向舵角为0°,首尾升降舵角设置为平衡,取首舵角为0.231 8°,尾舵角0.446 6°。其轨迹与速度曲线如图 7。
|
| 图7 不同流速干扰下潜艇直航运动 Figure 7 Direct motion under different ocean current interference |
对于匀速运动的潜艇,海流的作用只是运动学上的。潜艇的初始速度是潜艇相对于海流的速度,潜艇相对固定坐标系的速度为潜艇相对于海流的速度加上海流的速度。根据海流方向及大小,流速1.20 kn,流向角45°时,可计算流速在船体纵向分量为0.849 kn,横向分量为0.849 kn。潜艇纵向速度和横向速度增量为流速的分量,由图 7可看出,潜艇横向和纵向速度分量与流速在船体坐标系投影相等。对于潜艇的角速度及姿态角与静水匀速直航时相同,海流不会引起它们的变化。
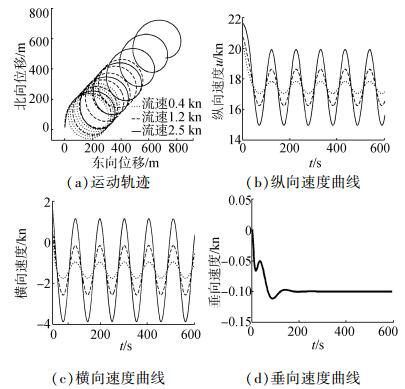
在上述仿真条件下,若将方向舵角设置为20°,对潜艇在不同海流下的回转运动进行仿真,则其速度及运动轨迹如图 8所示。
|
| 图8 不同流速干扰下潜艇回转运动 Figure 8 Rotary motion under different ocean current interference |
潜艇做回转运动时,海流速度在艇体坐标系上的分量随航向角的变化而做周期性的变化,故潜艇的纵向速度与横向速度在速降后稳定在某一值处不断周期变化。此外,由于潜艇相对于固定坐标系具有沿海流方向的速度,大小等于流速,故潜艇在做回转运动时的回转圈会沿海流方向漂移。
4 结束语本文结合已有的经过实际试验修正过的部分水动力系数,对潜艇在静水及海况干扰下的回转运动进行了仿真,通过定量设定仿真条件,定性分析了其运动轨迹、三维速率、角速率及三维姿态角的变化,将各种条件设置下的潜艇运动结果应用到敏感潜艇运动的导航系统的陆上性能鉴定中,从而为全面分析导航系性能提供了条件,一定程度上补充了实际海试条件的局限性。文中所用到的仿真对象某潜艇,因水动力系数有限,建立在许多假设条件上,是基于简化的潜艇六自由度运动模型进行的仿真研究;对于海浪干扰的处理,采用海浪等级表中相关海浪参数,定性描述海浪大小;对于海流干扰的处理,因为缺少数据,只从运动学上考虑其对潜艇运动造成的影响,并不适用于潜艇高速运动,有待进一步研究改进。
| [1] |
李玉东, 胡大斌, 陈勇, 等. 潜艇操纵控制系统仿真平台设计与实现[J].
舰船科学技术, 2013, 35(5): 123–127.
LI Yudong, HU Dabin, CHEN Yong, et al. Design and realization of the submarine maneuver controlling system simulation platform[J]. Ship science and technology, 2013, 35(5): 123–127. |
| [2] |
施生达.
潜艇操纵性[M]. 北京: 国防工业出版社, 1995: 48-59.
SHI Shengda. Submarine maneuverability[M]. Beijing: National Defence Industry Press, 1995: 48-59. |
| [3] |
吴秀恒, 刘祖源, 施生达, 等.
船舶操纵性[M]. 北京: 国防工业出版社, 2005: 60-62.
WU Xiuheng, LIU Zuyuan, SHI Shengda, et al. Ship maneuverability[M]. Beijing: national defence industry press, 2005: 60-62. |
| [4] |
林雄伟, 胡大斌, 戴余良, 等. 潜艇操纵控制方法[J].
舰船科学技术, 2013, 35(5): 7–10.
LIN Xiongwei, HU Dabin, DAI Yuliang, et al. Survey for maneuver control of submarine[J]. Ship science and technology, 2013, 35(5): 7–10. |
| [5] |
时俊宇.基于潜器空间运动的惯导系统适应性问题研究[D].哈尔滨:哈尔滨工程大学, 2011:23-26.
SHI Junyu. The research of inertial navigation system adaptability based on underwater vehicle space motion[D]. Harbin:Harbin Engineering University, 2011:23-26. |
| [6] |
朱怡.潜艇航行训练模拟器模型简化与参数优化研究[D].哈尔滨:哈尔滨工程大学, 2009:45-47.
ZHU Yi. The research on model simplification and coefficient optimization for submarine training simulator[D]. Harbin:Harbin Engineering University, 2009:45-47. |
| [7] |
金涛, 杨枫, 王京齐, 等. 大攻角情况下破损进水潜艇水下机动性[J].
华中科技大学学报:自然科学版, 2008, 36(12): 79–82.
JIN Tao, YANG Feng, WANG Jingqi, et al. Submerged maneuverability of flooded submarine with large angle of attack[J]. Journal of Huazhong university of science and technology:nature science edition, 2008, 36(12): 79–82. |
| [8] |
王彦磊, 袁博, 朱尚卿, 等. 海洋环境对潜艇活动的影响[J].
舰船科学技术, 2010, 32(6): 52–55.
WANG Yanlei, YUAN Bo, ZHU Shangqing, et al. The influence of marine environment on submarine activities[J]. Ship science and technology, 2010, 32(6): 52–55. |
| [9] | OSTAFICHUK P M. AUV hydrodynamics and modelling for improved control[D]. Vancouver, Canada:The University of British Columbia, 2004:78-81. |
| [10] |
戴余良. 潜艇在随机海浪中摇荡运动的仿真研究[J].
计算机仿真, 2001, 18(5): 42–45.
DAI Yuliang. Simulation study on swaying movement of a submarine in random ocean waves[J]. Computer simulation, 2001, 18(5): 42–45. |
| [11] | SEO M G, KIM Y. Effects of ship motion on ship maneuvering in waves[C]//Proceedings of the 26th International Workshop on Water Waves and Floating Bodies. Athens, Greece, 2011. |
| [12] |
丰少伟, 戴余良, 陈志法. 潜艇水下回转运动稳定性分析[J].
指挥控制与仿真, 2015, 37(1): 74–79.
FENG Shaowei, DAI Yuliang, CHEN Zhifa. Analysis of motion stability of submarine s underwater rotational movement[J]. Command control & simulation, 2015, 37(1): 74–79. |



