永磁直线电机兼有永磁电机和直线电机的优良特性, 具有功率密度高、损耗小、效率高、大推力等优点, 其在高性能伺服驱动系统中具有广阔的应用前景。然而, 齿槽效应、边端效应和纹波推力引起的推力波动是其主要缺陷, 直接影响伺服控制系统的定位精度及低速运行的稳定性, 严重时引起振动和噪声[1]。因此, 对产生推力波动的机理及有效抑制推力波动技术措施的研究是提高永磁直线电机性能的关键课题。
国内外学者针对永磁直线电机的推力波动进行了大量了研究工作, 主要由变极弧系数、合适的初级长度、增加辅助槽、合适的极槽配合、斜极、斜槽及合适的控制策略等方法来抑制电机的推力波动[2-6]。文献[7]对齿槽效应和边端效应做了定性分析, 提出了改善永磁同步直线电机推力波动的技术措施, 但是没有给出具体的模型和理论分析。文献[8]以12/11和12/10两种极槽配合为例, 分别建立了这两种极槽配合的不同绕组形式、单双边模型, 给出了单边与双边型分数槽集中绕组永磁同步直线电机推力波动与推力比值的最小化方案。文献[9-10]采用有限元法对齿槽力及边端力进行了仿真分析, 建立了半无限单端结构模型, 分析了定子铁心长度对边端力的影响, 并探讨了永磁体宽度对整体磁阻力的影响, 但将定子铁芯等效为一个没有齿槽的方块, 没有给出电机内部结构对磁阻力的影响。文献[11-12]采用磁极偏移法消弱圆筒型永磁直线电机的齿槽力, 给出了磁极偏移的计算公式, 但圆筒型永磁直线电机轴向充磁结构很难采用该方法。文献[13]采用哈佛阵列磁极结构来消弱磁阻力, 该种磁极结构复杂, 有时很难实现。文献[14]采用磁极分段方法消弱电机的齿槽力, 文献[15]采用双初级及动子磁极偏移的方法抑制推力波动, 文献[16]提出在初级铁芯两端增加辅助槽及辅助铁芯的方法。上述方案虽然能够实现抑制推力波动的目的, 但其主要缺点是增加了结构复杂性或大大增加了制造费用。同时, 斜极法的缺点是存在横向窜动力, 需要采用人字形磁极布置或采取合适的支承结构。
上述消弱永磁直线推力波动的方法大多针对平板型永磁直线电机, 有些方法很难在圆筒型永磁直线电机上实现, 本文提出定、动子不等极距的方法来抑制整数槽圆筒型永磁直线电机的推力波动, 分析了定、动子不等极距法抑制齿槽力和纹波推力的机理, 给出了动子极距选取的计算公式, 有限元分析与试验验证表明:采用合适的动子极距能够有效的消弱电机的推力波动, 为消弱圆筒型永磁直线电机的推力波动提供了一种简单有效的方法。
1 齿槽力研究永磁直线电机的齿槽力是永磁磁极和定子齿相互作用产生的作用力, 齿槽力的特性只和电机结构及永磁磁极与定子齿的相对位置有关。当永磁直线的定子与动子相对运动时, 每极下定子齿与永磁磁极间的磁导发生变化, 引起磁场储能的变化, 从而产生齿槽力。旋转永磁电机齿槽转矩的定义为磁场储能W相对于位置角α的负倒数, 即:
| ${T_{{\rm{cog}}}} = - {{\partial W} \over {\partial \alpha }}$ | (1) |
由于永磁直线电机可视为旋转永磁电机在结构上的一种演变, 忽略边端效应, 永磁直线电机定子与动子直线的相对位移对应于旋转永磁电机中的位置角α,因此, 永磁直线的齿槽力可定义为磁场储能W相对于位移x的负倒数, 即:
| $\alpha = {{2\pi x} \over L}$ | (2) |
| ${F_{{\rm{cog}}}} = - {{\partial W} \over {\partial \alpha }}{{\partial \alpha } \over {\partial x}}$ | (3) |
式中:L为初级定子长度, L=Zts, 其中Z为定子槽数, ts为齿距。
1.1 齿槽力解析分析由于定子铁芯开槽, 导致磁路介质不连续, 当定、动子相对运动时, 引起磁场储能变化, 从而产生齿槽力, 由于齿槽力只与永磁磁极和定子齿的相对位置有关, 永磁直线电机的齿槽力可视为每个永磁磁极与定子齿相互作用所产生的齿槽力之和。因此每个永磁磁极产生的齿槽力可以采用Fourier级数进行描述, 则第i个永磁磁极与定子齿相互产生的齿槽力为
| ${F_{{\rm{cog}},i}}\left( x \right) = \sum\limits_{k = 1}^\infty {{F_{k,i}}} {\rm{sin}}(k{{2\pi {x_c}} \over {{\tau _s}}} + {\varphi _{k,i}})$ | (4) |
式中:τs为齿距, xc为动子所在的位置, Fk,i是第k次谐波齿槽力的幅值, φk,i为第i个磁极第次谐波齿槽力的初始相角:
| ${\varphi _{k,i}} = {\varphi _{k,0}} + j2\pi {q_p}$ | (5) |
式中:qp为每极下定子槽数。
由式(5) 可知, 每极下定子槽数qp决定了谐波齿槽力的初始相角φk,i。当qp为整数且定子极距与动子极距相等时, 各磁极齿槽效应所产生的k谐波齿槽力幅值相等且具有相同的初始相角, 由此可知, 电机总的齿槽力为单个磁极所产生的齿槽力的2p倍, 电机的齿槽力可表示为
| ${F_{{\rm{cog}}}}\left( x \right) = 2p\sum\limits_{k = 1}^\infty {{F_{k,i}}} {\rm{sin}}(k{{2\pi {x_c}} \over {{\tau _s}}} + {\varphi _{k,i}})$ | (6) |
当qp为分数或整数槽电机且定、动子极距不等时, 使各磁极所产生的同次谐波齿槽力初始相角不同, 从而使电机的齿槽力能够得到有效的消弱, 总的齿槽力可表示为
| ${F_{{\rm{cog}}}}\left( x \right)\sum\limits_{i = 0}^{2p - 1} {\sum\limits_{k = 1}^\infty {{F_{k,i}}} {\rm{sin}}(k{{2\pi {x_c}} \over {{\tau _s}}} + {\varphi _{k,i}})} $ | (7) |
由式(7) 可知, 采用合理的极槽配合, 使一个齿距内齿槽力的周期数增多或采用分数槽绕组, 可有效消弱电机的齿槽力。一个齿距电机的齿槽力周期数NP:
| ${N_p} = {{2p} \over {{\rm{GCD}}\left( {Z,2p} \right)}}$ | (8) |
式中:GCD(Z,2p)为定子槽数Z与极对数2p的最大公约数。
1.2 定动子不等极距齿槽力研究由式(7) 可知, 当定、动子极距不等时, 使各磁极所产生的同次谐波齿槽力具有不同的初始相角, 实现了同次谐波齿槽力的分布, K次谐波齿槽力幅值之和可表示为
| ${F_{{\rm{cog}},k\sum }} = 2p{K_{{\rm{cog}},k}}{F_k}$ | (9) |
式中:Kcog,k为k次谐波齿槽力的分布系数。
| ${K_{{\rm{cog}},k}} = {{{\rm{sin}}(2mqpk\Delta \theta )} \over {2p{\rm{sin}}(mqk\Delta \theta )}}$ | (10) |
| $\left| {\Delta \theta } \right| = \left| {{{{\tau _p} - {\tau _a}} \over {{\tau _p}}}} \right|\pi $ | (11) |
由式(10) 、(11) 可知, 当定子、动子极距不等, 理论上当
| ${\tau _p} = {{6p{\tau _a}} \over {6p \pm 1}}$ | (12) |
理想情况下, 忽略齿槽效应和边端效应, 空载反电动势为正弦波, 定子绕组通入三相对称正弦交流电流:
| $\left\{ \matrix{ {i_a} = {I_m}{\rm{sin}}(\omega t + {\theta _0}) \hfill \cr {i_b} = {I_m}{\rm{sin}}(\omega t + {\theta _0} - 2\pi /3) \hfill \cr {\rm{ }}{i_c} = {I_m}{\rm{sin}}(\omega t + {\theta _0} - 4\pi /3) \hfill \cr} \right.$ | (13) |
式中:Im为电流幅值, ω为角频率, θ0为电流初始相角。
同时假设气隙磁密正弦, 无谐波含量, 坐标原点位于磁极的中心线上, 则气隙磁密为
| $B\left( x \right) = {B_m}{\rm{cos}}(\pi x/{\tau _p})$ | (14) |
式中:Bm为气隙磁密幅值, x为纵向绝对坐标, τp为极距。
永磁直线电机的电磁推力可表示为
| ${F_x} = {{{e_a}{i_a} + {e_b}{i_b} + {e_c}{i_c}} \over {{v_s}}}$ | (15) |
式中:ea、eb、ec为三相反电动势, vs为动子运行速度。
三相电流转换到dq轴坐标系上, 采用直轴电流为零(id=0)的电流矢量控制时, 电机的电磁推力为
| ${F_x} = {{3\pi } \over {2\tau }}({\psi _d}{i_q} + {\psi _q}{i_d}) = {{3\pi } \over {2\tau }}{\psi _d}{i_q}$ | (16) |
式中:τ为极距, ψd、ψq分别为d、q轴磁链, id、iq分别为d、q轴电流。
由式(15) ~(16) 可知, 理想情况下, 采用直轴电流等于零的电流矢量控制时, 永磁直线电机的电磁推力正比于交轴电流, 因此只要控制交轴电流就能实现电磁推力的输出, 电磁推力基本上无波动。
实际上, 输入电流及反电动势中均含有高次谐波成分, 均为非标准的正弦波。对于采用无中线星型连接的三相永磁直线电机, 输入电流中不含3次倍次谐波成分, 忽略齿槽效应及边端效应, 采用电流矢量控制id=0, 假设电流的初始相角为0, 三相电流可表示为
| $\left\{ \matrix{ {i_a} = {I_{m1}}{\rm{sin}}(\omega t) + {I_{m5}}{\rm{sin}}(\omega t) + {I_{m7}}{\rm{sin}}(\omega t) \ldots \hfill \cr {i_b} = {I_{m1}}{\rm{sin}}(\omega t - 2\pi /3){\rm{ }} + {I_{m5}}{\rm{sin}}(\omega t - 2\pi /3){\rm{ }} + \hfill \cr {\rm{ }}{I_{m7}}{\rm{sin}}(\omega t - 2\pi /3){\rm{ }} \ldots \hfill \cr {i_c} = {I_{m1}}{\rm{sin}}(\omega t - 4\pi /3){\rm{ }} + {I_{m5}}{\rm{sin}}(\omega t - 4\pi /3){\rm{ }} + \hfill \cr {\rm{ }}{I_{m7}}sin(\omega t - 4\pi /3){\rm{ }} \ldots \hfill \cr} \right.$ | (17) |
三相空载反电动势可表示为
| $\left\{ \matrix{ {e_a} = {E_{m1}}{\rm{sin}}(\omega t) + {E_{m5}}{\rm{sin}}(\omega t) + {E_{m7}}{\rm{sin}}(\omega t) \ldots \hfill \cr {e_b} = {E_{m1}}{\rm{sin}}(\omega t - 2\pi /3){\rm{ }} + {E_{m5}}{\rm{sin}}(\omega t - 2\pi /3){\rm{ }} + {\rm{ }} \hfill \cr {E_{m7}}{\rm{sin}}(\omega t - 2\pi /3){\rm{ }} \ldots \hfill \cr {e_c} = {E_{m1}}{\rm{sin}}(\omega t - 4\pi /3){\rm{ }} + {E_{m5}}{\rm{sin}}(\omega t - 4\pi /3){\rm{ }} + \hfill \cr {\rm{ }}{E_{m7}}{\rm{sin}}(\omega t - 4\pi /3){\rm{ }} \ldots \hfill \cr} \right.$ | (18) |
则永磁同步直线电机的电磁推力为
| $\eqalign{ & {F_x} = {{{e_a}{i_a} + {e_b}{i_b} + {e_c}{i_c}} \over {{v_s}}} = {{3\pi } \over {2\tau \omega }} \times ({F_0} + {F_6}{\rm{cos}}(6\omega t) + \cr & {F_{12}}{\rm{cos}}(12\omega t) + {F_{18}}{\rm{cos}}(18\omega t) + \ldots ) \cr} $ | (19) |
式中:τ为极距, ω为电流角频率, F0为电磁推力平均值, F6n(n≥1) 为纹波电磁推力幅值。由式(19) 纹波电磁力只包含6倍次基波电流谐波, F0-F18纹波电磁推力可表示为
| $\left[ \matrix{ {F_0} \hfill \cr {F_6} \hfill \cr {F_{12}} \hfill \cr {F_{18}} \hfill \cr} \right] = \left[ \matrix{ {E_{m1}} & {E_{m5}} & {E_{m7}} & {E_{m11}} \hfill \cr {E_{m7}} - {E_{m5}} & {E_{m11}} - {E_{m1}} & {E_{m13}} + {E_{m1}} & {E_{m17}} + {E_{m5}} \hfill \cr {E_{m13}} - {E_{m11}} & {E_{m17}} - {E_{m7}} & {E_{m19}} - {E_{m5}} & {E_{m23}} - {E_{m1}} \hfill \cr {E_{m19}} - {E_{m17}} & {E_{m23}} - {E_{m13}} & {E_{m25}} - {E_{m11}} & {E_{m29}} - {E_{m7}} \hfill \cr} \right]\left[ \matrix{ {I_{m1}} \hfill \cr {I_{m5}} \hfill \cr {I_{m7}} \hfill \cr {I_{m11}} \hfill \cr} \right]$ | (20) |
由式(20) 可知, 如果空载反电动势中存在谐波分量, 即使输入电流为三相对称标准正弦波, 电磁推力中也包含谐波分量。对于三相整数槽永磁同步直线电机, 由电机绕组理论可知, 绕组的极距为短距或长距时, 能够降低反电动势中的谐波成分含量。因此, 对于单层整距永磁直线电机。当定、动子极距不等时, 使各磁极下线圈的感应电动势在时间产生相位差, 从而实现抑制谐波电动势的目的。
由此可知, 当永磁直线电机定、动子极距不等, 且选取合适的动子极距时, 即使主极气隙磁场含有谐波成分, 也可消弱绕组谐波电动势, 从而实现对纹波推力的抑制。
3 不等极距有限元分析 3.1 齿槽力分析针对上文所提出的定、动子不等极距消弱齿槽力的方法, 本文对36槽12极圆筒型永磁直线电机进行有限元分析, 样机的主要结构参数如表 1所示。
| 参数 | 值 |
| 初级长度/mm | 364 |
| 初级外径/mm | 104 |
| 次级外径/mm | 50 |
| 气隙长度/mm | 1.5 |
| 槽距/mm | 10 |
| 动子极距mm | 30 |
| 槽数 | 36 |
| 槽宽/mm | 6 |
| 齿宽/mm | 4 |
| 充磁方式 | 轴向 |
| 磁钢 | SmCo30H |
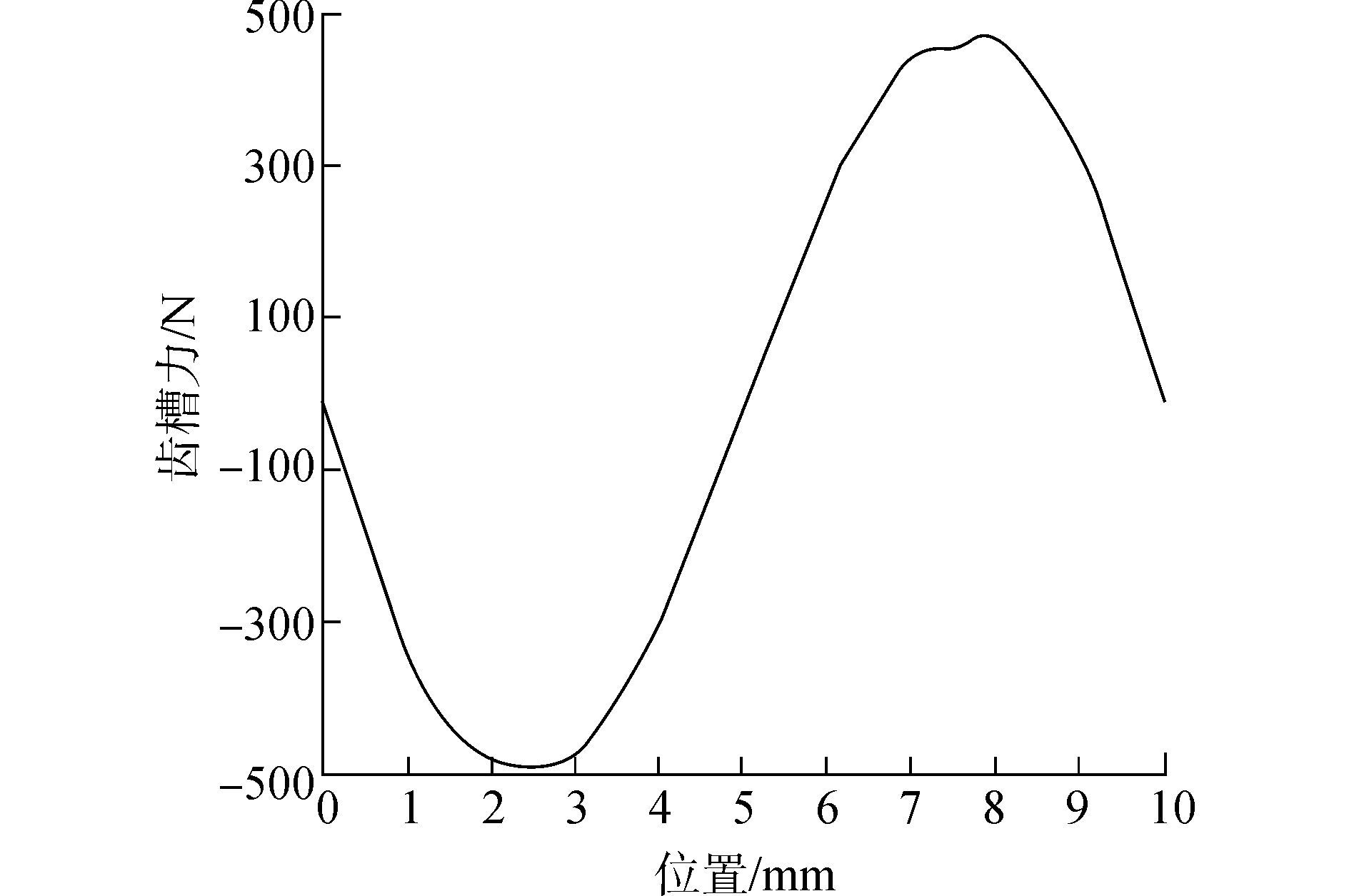
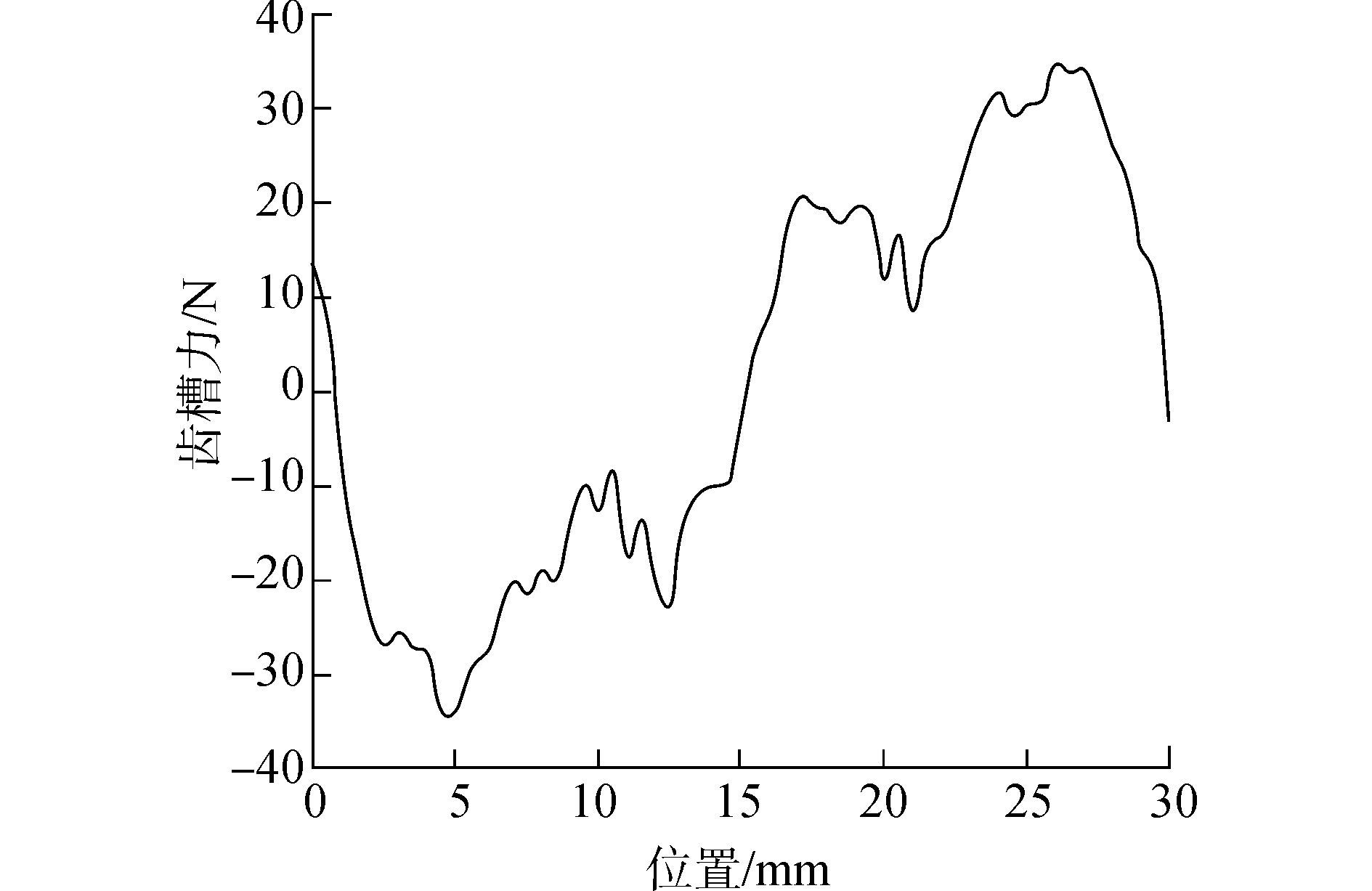
忽略边端力的影响, 图 1为定、动子等距时电机的齿槽力, 由图 1可知, 电机的齿槽力峰-峰值为940 N, 齿槽力较大(额定电磁推力设计值为1 850 N)。由式(10) 所确定的动子极距为29.2 mm时, 电机的齿槽力波形如图 2所示, 由图 2可看出电机的齿槽力峰-峰值较等距时减小了91.7%, 为78 N。
|
| 图1 定、动子等距齿槽力 Figure 1 Cogging force of equal pole-pitch |
|
| 图2 动子极距为29.2 mm齿槽力 Figure 2 Cogging force of unequal pole-pitch(29.2 mm) |
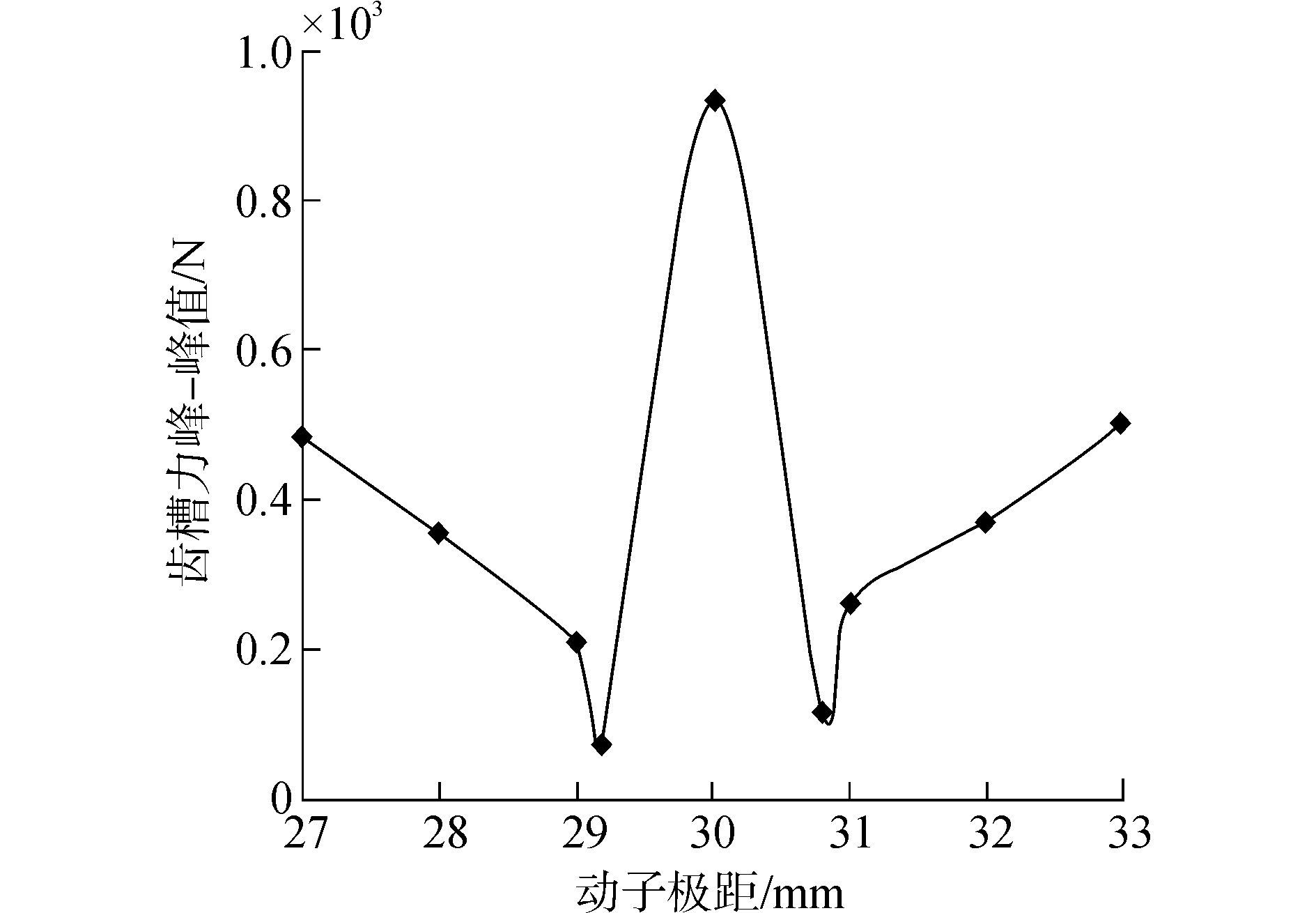
由图 1和图 2可看出, 按式(10) 选取的动子极距, 电机的齿槽力得到了有效的消弱。定子极距保持30 mm不变, 永磁体充磁高度不变, 改变动子极距, 电机的齿槽力峰-峰值如图 3所示。
|
| 图3 不同动子极距下的齿槽力 Figure 3 Cogging force of the mover pole-pitch |
由图 3可看出电机的齿槽力与动子极距的关系, 动子极距为29.2 mm时电机的齿槽力最小, 由此可知本文所提出的定、动子不等极距消弱齿槽力的方法可行的, 同时表明动子极距的计算公式是正确的。
3.2 推力波动分析空载反电动势波形对永磁同步直线电机的电磁推力波动具有较大的影响, 因此要抑制电机的推力波动就必须有效的降低空载反电动势中的谐波含量。当定、动子不等极距时, 各磁极下的线圈感应的空载电动势在时间上产生相位差, 等效于定子绕组短距或长距。因此, 选择合适的动子极距能够有效的消弱空载谐波电动势。
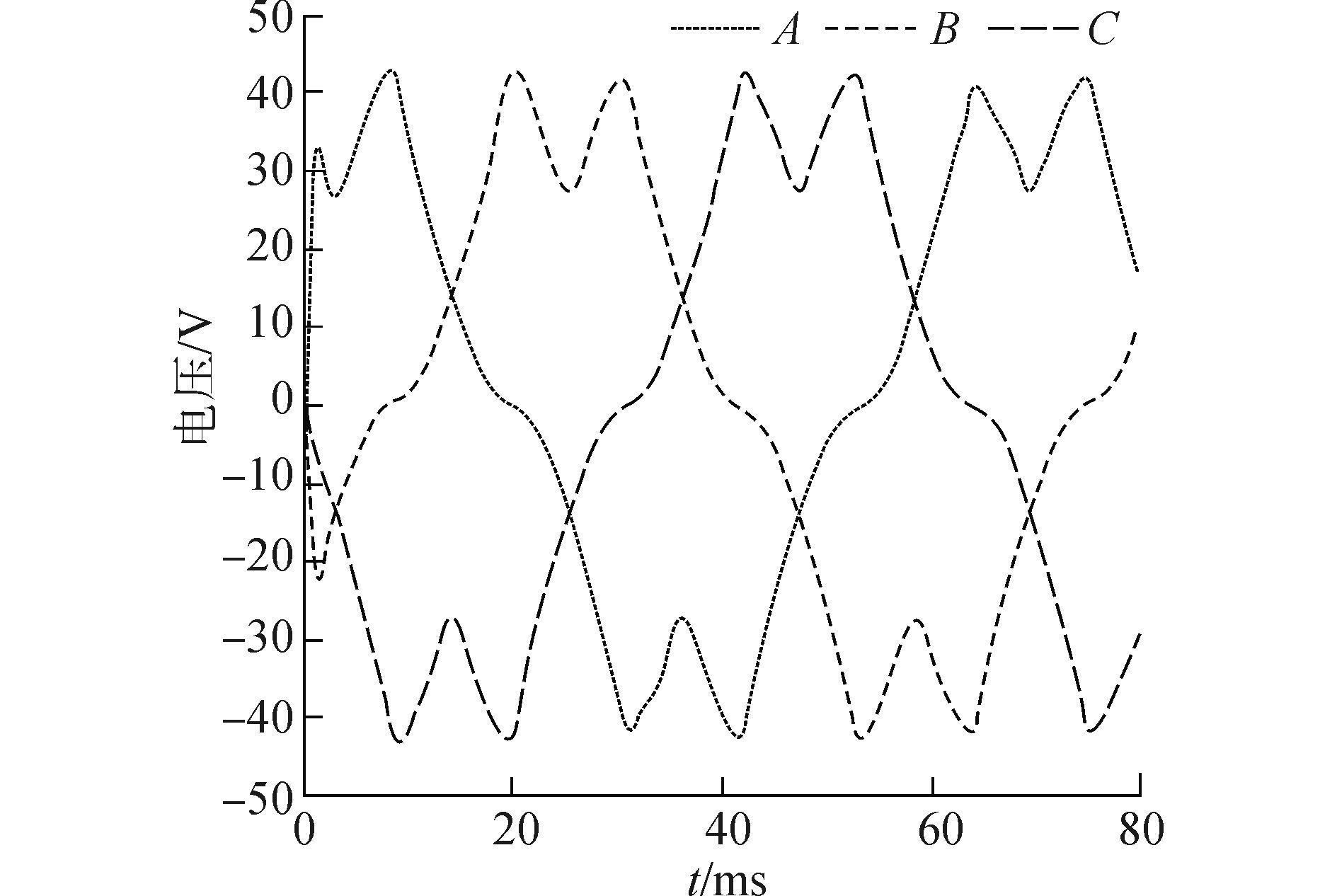
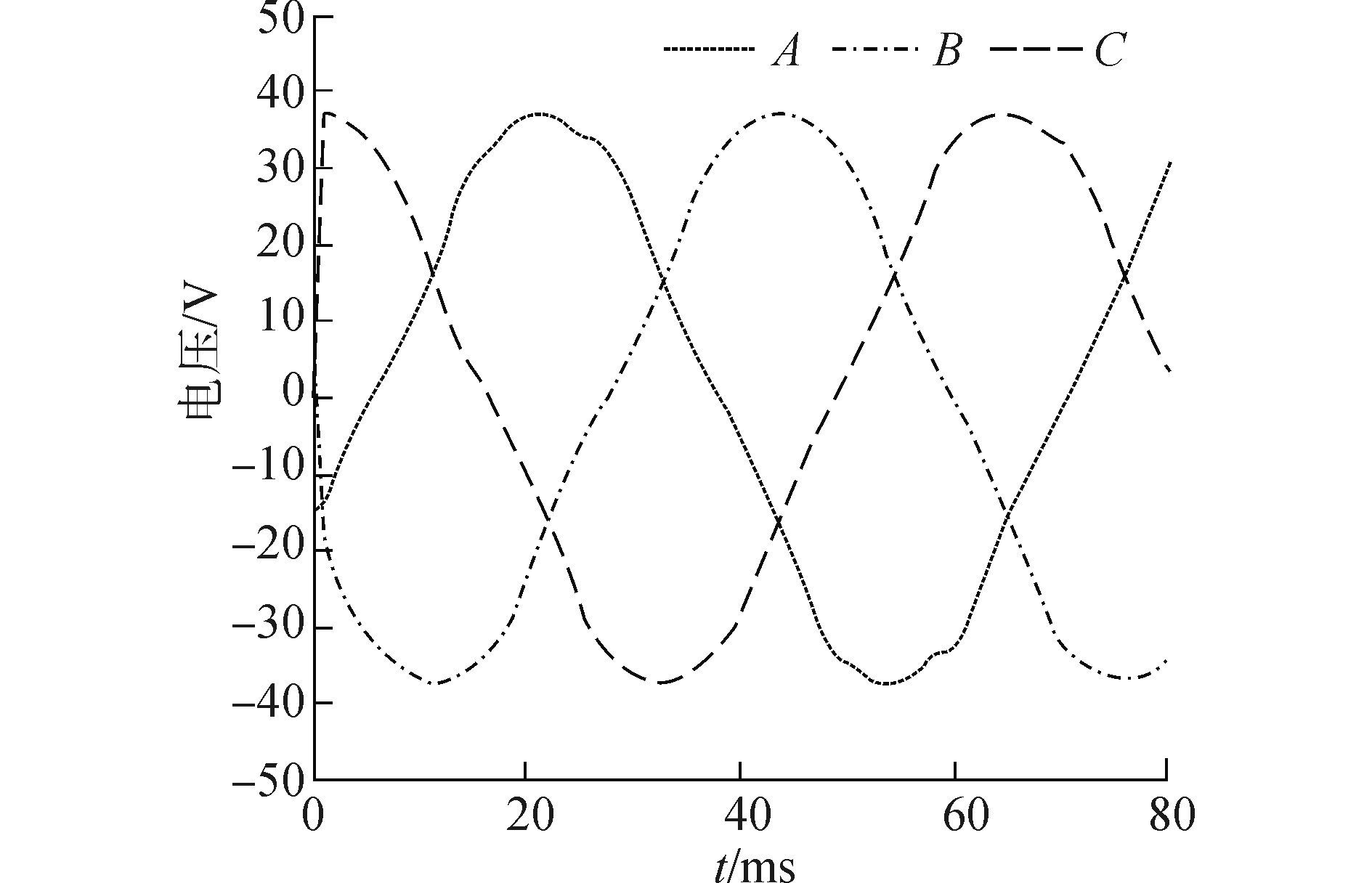
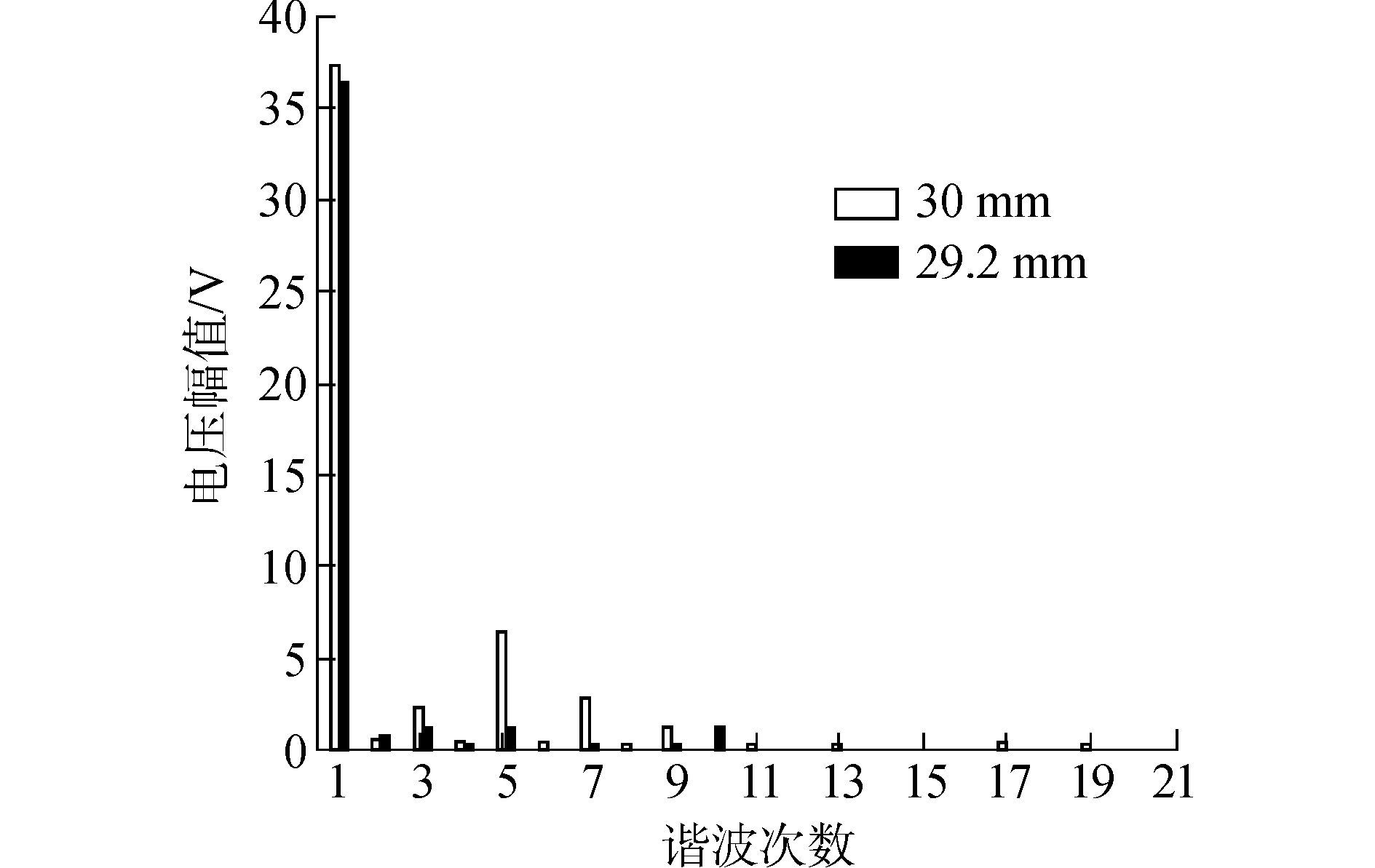
根据表 1分别建立定、动子等极距(定、动子极距为30 mm)和不等极距(定子极距为30 mm、动子极距为29.2 mm)有限元分析模型, 空载反电动势波形分别如图 4和图 5所示, 空载反电动势谐波分析频谱如图 6所示。由图 4和图 5可看出, 定、动子等距时, 空载反电动势谐波含量较大, 不等极距时, 空载反电动势正弦性较好, 能够保持三相反电动势对称性。由图 6可看出, 采用不等极距时, 空载反电动势各次谐波成分均得到了有效的消弱, 等距时电机的空载反电动势幅值为37.6 V, 不等距时空载反电动势幅值为36.8 V, 反电动势幅值的降低是由不等距时各磁极下线圈的感应电动势在时间上存在相位差造成的。
|
| 图4 等极距三相空载反电动势 Figure 4 The three-phase no-load back-EMF of the equal pole-pitch |
|
| 图5 不等极距三相空载反电动势 Figure 5 The three-phase no-load back-EMF of the unequal pole-pitch |
|
| 图6 空载反电动势谐波分析频谱 Figure 6 The harmonic spectrum of the no-load Back-EMF |
由此可知, 当选取合适的动子极距时能够有效的降低空载反电动势中的谐波含量, 对基波反电动势的大小影响较小。
采用电流矢量控制(id=0), 输入电流为标准正弦波, 电流有效值为30 A,速度为0.9 m/s。根据表 1分别建立动子极距为30 mm和29.2 mm的模型。
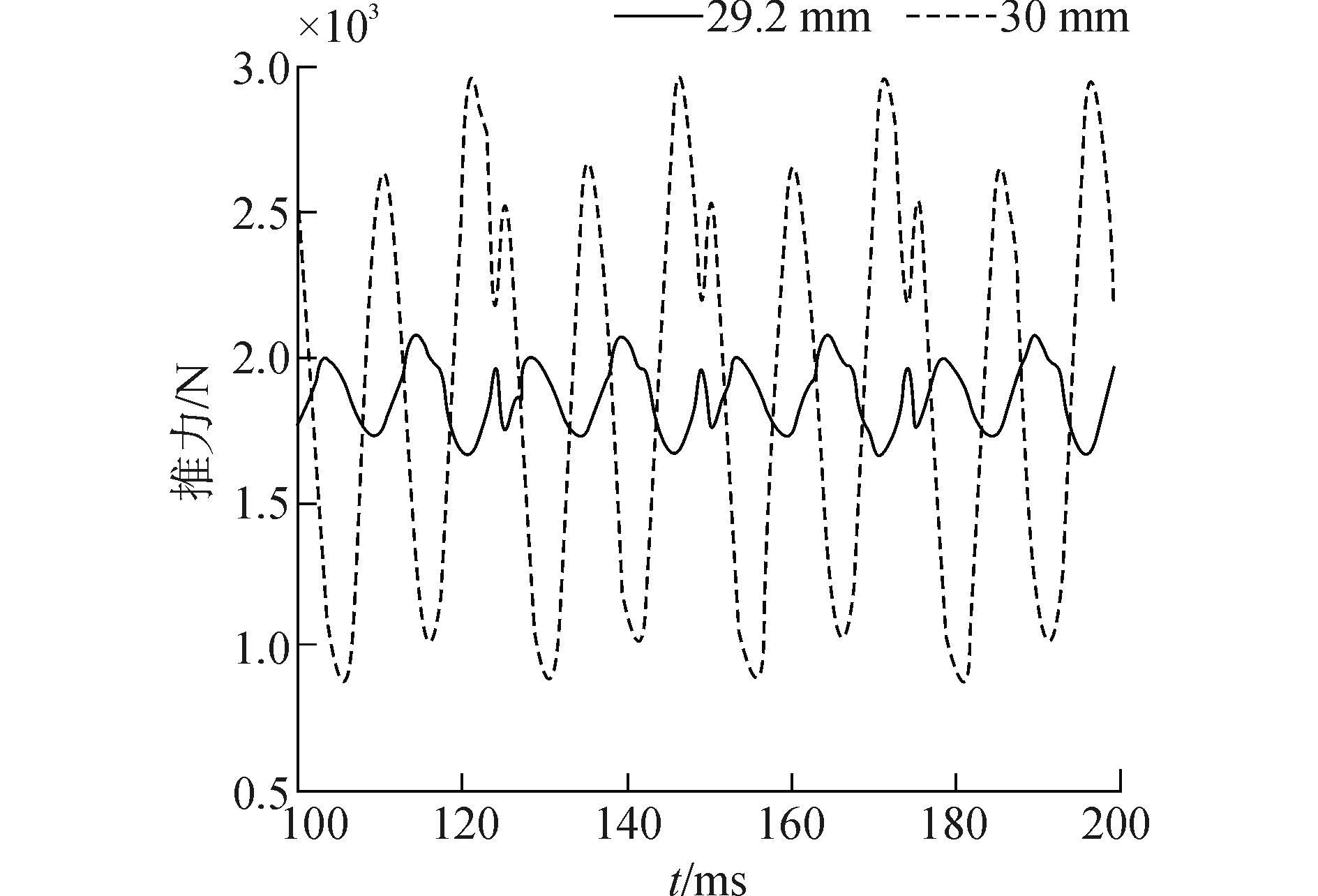
图 7为定、动子等距与不等极距的瞬态电磁推力曲线。
|
| 图7 瞬态推力波动曲线 Figure 7 The transient thrust curve |
由图 7可看出, 不等极距时电机的电磁推力波动明显优于等距, 动子极距为29.2 mm时, 对反电动势基波影响较小, 不等距时基本不影响额定电磁推力输出, 其中:等距时平均电机推力分析值为1 861 N,动子极距为29.2 mm时平均电机推力分析值为1 856 N。
4 试验分析本文对不等极距圆筒型永磁直线电机进行了齿槽力和空载反电动势实验分析。样机的主要结构参数如上述表 1所示, 样机动子极距为29.2 mm,实验平台如图 8所示。

|
| 图8 样机实验平台 Figure 8 TPMLSM and experimental platform |
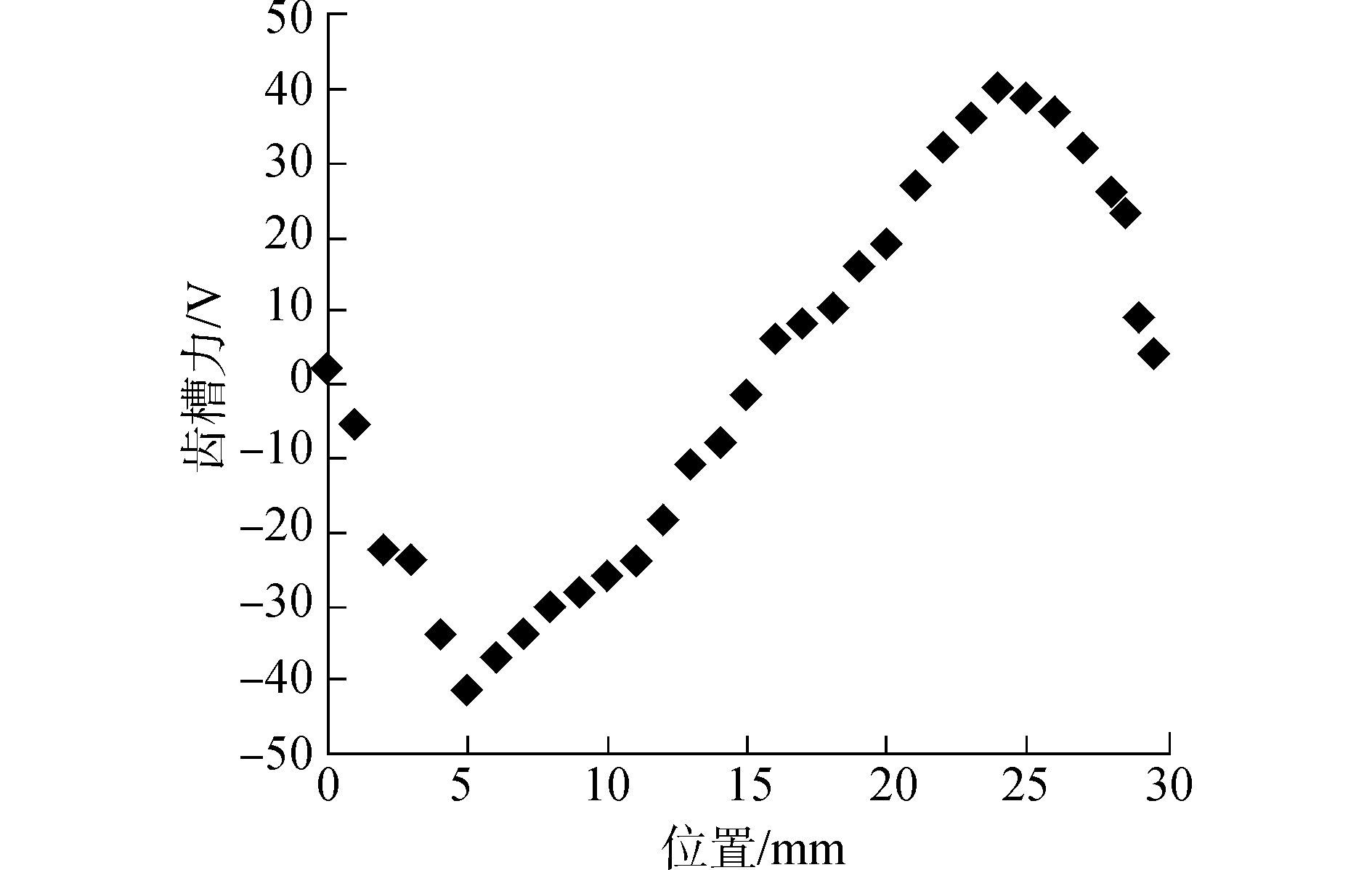
采用静态位移法逐点测量样机的齿槽力, 齿槽力实测值如图 9所示, 样机在0.9 m/s速度时的空载反电动势测试值如图 10所示。
|
| 图9 齿槽力实验值 Figure 9 Measured cogging force |
|
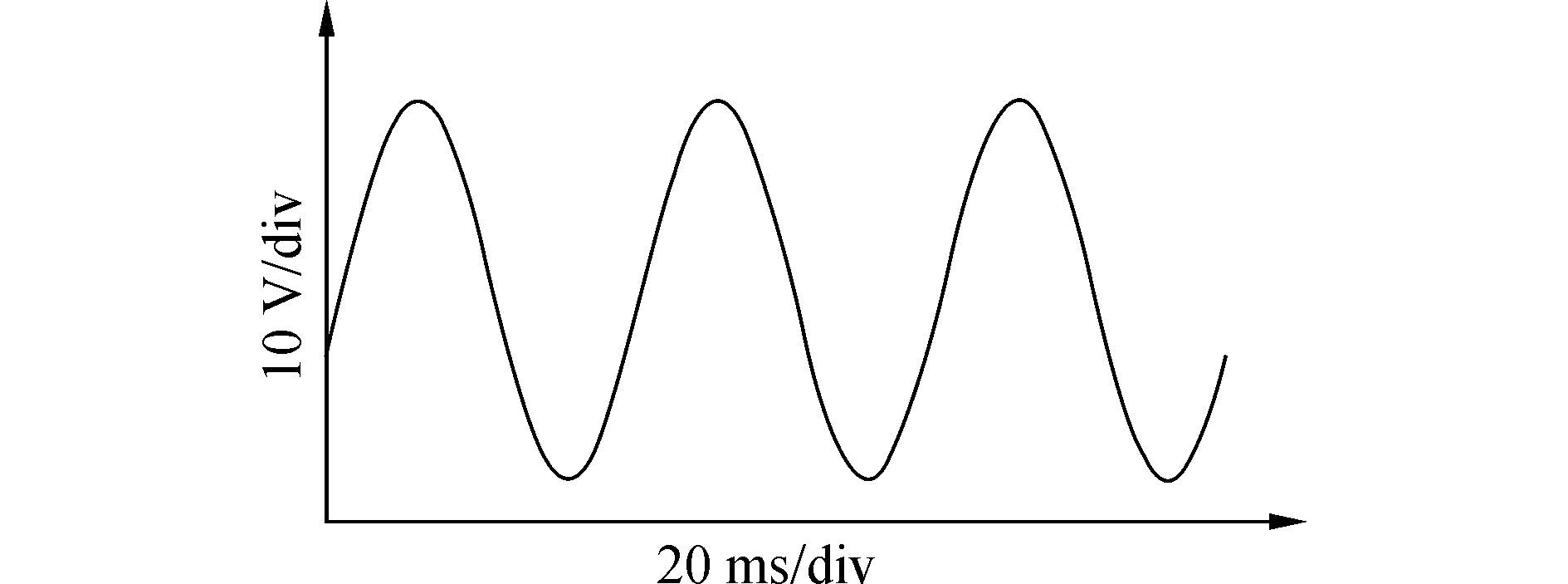
| 图10 空载反电动势实验波形 Figure 10 Measured No-load Back-EMF curve |
由图 9可看出, 齿槽力峰-峰值实验结果为87 N, 实验值与有限元分析结果基本吻合, 额定电磁推力设计值为1 850 N, 由此可知样机的齿槽力较小, 同时也验证了不等极距法消弱齿槽力的有效性。由图 10可看出样机的空载反电动势波形正弦性较好, 实测电压幅值为36.3 V(横坐标轴每格50 ms,纵坐标轴每格10 V), 有限元分析值为36.8 V。
5 结论本文提出定、动子不等极距的方法抑制永磁直线电机的推力波动, 仿真分析及试验得出如下结论:
1) 采用本文给出的动子极距计算公式, 选取合适的动子极距, 电机的齿槽力能够得到有效的消弱, 该方法简单有效;
2) 定、动子不等极距时, 对每极下绕组感应电动势存在相位差, 从而实现了每相绕组的等效分布, 能够有效的消弱空载反电动势中的谐波含量, 达到抑制电机纹波推力的目的;
3) 由于各极下线圈的感应电动势存在相位差, 并联之路数不是1时, 使支路电压不均衡, 该方法适用于多极且定子绕组并联支路数为1的永磁直线电机。
| [1] | ZHU Z O, XIA Z P, HOWE D, et al. Reduction of cogging force in slotless linear permanent magnet motors[J]. IEE proceedings-electric power applications, 1997, 144(4): 277–282. DOI:10.1049/ip-epa:19971057 |
| [2] | CAI Jiongjiong, LU Qinfen, HUANG Xiaoyan, et al. Thrust ripple of a permanent magnet LSM with step skewed magnets[J]. IEEE transactions on magnetics, 2012, 48(11): 4666–4669. DOI:10.1109/TMAG.2012.2198437 |
| [3] | WANG Mingyi, LI Liyi, PAN Donghua. Detent force compensation for PMLSM systems based on structural design and control method combination[J]. IEEE transactions on industrial electronics, 2015, 62(11): 6845–6854. DOI:10.1109/TIE.2015.2443096 |
| [4] | LEE S G, KIM S A, SAHA S, et al. Optimal structure design for minimizing detent force of PMLSM for a ropeless elevator[J]. IEEE transactions on magnetics, 2014, 50(1): 1–4. |
| [5] | ZHU Yuwu, LEE S G, CHUNG K S, et al. Investigation of auxiliary poles design criteria on reduction of end effect of detent force for PMLSM[J]. IEEE transactions on magnetics, 2009, 45(6): 2863–2866. DOI:10.1109/TMAG.2009.2018778 |
| [6] |
黄克峰, 李槐树, 周羽. 利用辅助槽削弱齿槽力的方法研究[J].
电机与控制学报, 2014, 18(3): 54–59.
HUANG Kefeng, LI Huaishu, ZHOU Yu. Method research for reducing the cogging force by auxiliary slots[J]. Electric machines and control, 2014, 18(3): 54–59. |
| [7] |
李庆雷, 王先逵, 吴丹, 等. 永磁同步直线电机推力波动分析及改善措施[J].
清华大学学报:自然科学版, 2000, 40(5): 33–36.
LI Qinglei, WANG Xiankui, WU Dan, et al. Thrust fluctuation analysis and reduction of PMSLM[J]. Journal of Tsinghua university:science & technology, 2000, 40(5): 33–36. |
| [8] |
卢琴芬, 程传莹, 叶云岳, 等. 每极分数槽永磁直线电机的槽极数配合研究[J].
中国电机工程学报, 2012, 32(36): 68–74.
LU Qinfen, CHENG Chuanying, YE Yunyue, et al. Slot/Pole number combination research of-PM linear motors with fractional slots per pole[J]. Proceedings of the CSEE, 2012, 32(36): 68–74. |
| [9] | INOUE M, SATO K. An approach to a suitable stator length for minimizing the detent force of permanent magnet linear synchronous motors[J]. IEEE transactions on magnetics, 2000, 36(4): 1890–1893. DOI:10.1109/20.877814 |
| [10] |
徐月同, 傅建中, 陈子辰. 永磁直线同步电机推力波动优化及实验研究[J].
中国电机工程学报, 2005, 25(12): 122–126.
XU Yuetong, FU Jianzhong, CHEN Zichen. Thrust ripple optimization and experiment for PMLSM[J]. Proceedings of the CSEE, 2005, 25(12): 122–126. |
| [11] | BIANCHI N, BOLOGNANI S, CAPPELLO A D F. Reduction of cogging force in PM linear motors by pole-shifting[J]. IEE proceedings-electric power applications, 2005, 152(3): 703–709. DOI:10.1049/ip-epa:20045082 |
| [12] |
崔皆凡, 秦超. 基于磁极偏移圆筒永磁直线电机齿槽力的削弱[J].
沈阳工业大学学报, 2014, 36(2): 133–137.
CUI Jiefan, QIN Chao. Reduction of cogging force of tubular permanent magnet linear synchronous motors based on permanent magnet shifting[J]. Journal of Shenyang university of technology, 2014, 36(2): 133–137. |
| [13] | JANG S M, LEE S H, YOON I K. Design criteria for detent force reduction of permanent-magnet linear synchronous motors with Halbach array[J]. IEEE transactions on magnetics, 2002, 38(5): 3261–3263. DOI:10.1109/TMAG.2002.802129 |
| [14] | SHABAN M A, MILIMONFARED J, TAGHIPOU S. Cogging force mitigation of tubular permanent magnet machines with magnet dividing[C]//Proceedings of International Conference on Electrical Machines and Systems. Seoul, Korea:IEEE, 2007:810-814. |
| [15] | KIM S A, ZHU Yuwu, LEE S G, et al. Electromagnetic normal force characteristics of a permanent magnet linear synchronous motor with double primary side[J]. IEEE transactions on magnetics, 2014, 50(1): 1–4. |
| [16] | LIU Chunyuan, YU Haitao, Hu Minqiang, et al. Detent force reduction in permanent magnet tubular linear generator for direct-driver wave energy conversion[J]. IEEE transactions on magnetics, 2013, 49(5): 1913–1916. DOI:10.1109/TMAG.2013.2242873 |



