2. School of Information Science and Technology, Dalian Maritime University, Dalian 116026, China
多传感器融合技术已经广泛应用于目标跟踪、监控、导航、通信以及信号和图像处理等领域。信息融合主要包括集中式融合、分布式融合以及混合式融合。集中式融合是融合本地端的测量数据来获得全局最佳状态估计。许多学者在集中式融合[1-4](centralised fusion,CF)问题上已经做了大量的工作,而且融合算法大部分都是以高斯逼近滤波器作为基本的滤波。由于高斯假设固有的缺陷,这些算法不适用于非线性动态系统。近年来,粒子滤波(particle filtering,PF)在解决非线性滤波问题上已经取得了巨大的成就[5-6],其优点在于可以有效解决噪声为非高斯分布的组合导航系统的最优估计问题,然而,粒子滤波算法较难选取合适的重要性采样密度,从而导致滤波精度不高以及严重的粒子退化的问题。为了克服粒子滤波的不足,Eric Wan等人提出了Unscented粒子滤波,虽然可以克服粒子滤波的缺点,滤波精度高,适应于非线性、非高斯的系统,但是其精度与粒子数成正比,粒子数越多其精度越高,而实时性会随着粒子数的增多而下降[7-8]。Torma[9]等提出了基于似然分布的自适应调整的粒子滤波算法,算法将重要性密度函数选取为先验密度,而且忽略了最新量测信息在系统中的影响。虽然在一定程度上提高了滤波的稳定性,但是当满足非归一化的似然度函数值超过预先设定的阈值的条件时,才产生新的粒子,而且需要考虑到最新的量测信息。薛丽[10]等提出一种新的权值自适应调整Unscented粒子滤波算法,在考虑最新量测影响的基础上,利用UT(unscented transformation)变换获得重要性密度函数,并且对粒子权值进行了自适应的调整,提高了滤波精度。但是当似然分布位于转移先验分布尾部或者观测模型具有很高精度时,很多样本由于归一化权重很小而成为无效样本,过低的采样率,很可能导致粒子滤波失败。
综上所述,相对于标准粒子滤波,针对不同具体的应用背景其算法的滤波精度获得一定程度的改善。但以上方法的共同缺陷在于算法构建原理局限在单传感器量测系统。熊伟[11]等提出的多传感器顺序粒子滤波算法能够明显提高多传感器系统状态估计精度,并且随着传感器数增多,改善的效果越好。但是由于多传感器信息仅仅能够影响粒子的权重,对状态值没有影响,从而导致低质量粒子的出现[12]。这些问题源于粒子滤波及其特有的以粒子滤波为基础的融合算法。因此,本文建立一种二阶自适应权值信息融合算法来解决此问题。将多传感器的信息融合过程分为两个阶段,将多传感器数据送入与之对应的粒子滤波计算模块中,达到以优化粒子分布为目的对建议分布密度(proposal density,PD)的更新。而后,在最终的自适应权值粒子滤波模块中对多传感器数据构造完整的似然函数,通过欧氏距离和反映量测噪声统计特性的精度因子进行自适应权值分布调整,得到最终的估计。
1 粒子滤波的多传感器信息融合算法 1.1 集中式融合的标准粒子滤波考虑以下的多传感器非线性离散系统[12]:
| $\left\{ \begin{array}{*{35}{l}} {{x}_{t}}={{f}_{t}}({{x}_{t-1}})+{{v}_{t-1}} \\ z_{_{t}}^{^{(m)}}=h_{_{t}}^{^{(m)}}({{x}_{t}})+w_{_{t}}^{^{(m)}} \\ \end{array} \right.$ | (1) |
其中,m=1,2,…,M;t和m是时间指数和传感器指数,xt和zt(m)为状态矢量和量测矢量。过程噪声vt-1和量测噪声wt(m)是零均值并且相互独立。f(·)为状态转移方程,h(·)为观测方程。我们的目的是根据所有的量测值z1:t:={zτ}τ=1t递归估计出xt,其中zτ:={zτ(m)}m=1M。
在粒子滤波中,后验概率密度p(xt|z1:t)=$\sum\limits_{i=1}^{n}{\omega _{_{t}}^{^{i}}\delta ({{x}_{t}}-x_{_{t}}^{^{i}})}$,xti是带有权重ωti的第i个粒子。根据多传感器测量的独立假设的基础上,似然函数p(zt|xt)能够被分解为$\prod\limits_{m=1}^{M}{p(z_{t}^{(m)}|{{x}_{t}})}$。在每一个滤波周期中,根据式(2)计算权重ωti:
| $\omega _{t}^{i}\propto \frac{p(x_{t}^{i}|x_{_{t-1}}^{^{i}})\prod\limits_{m=1}^{M}{p(z_{_{t}}^{^{(m)}}|x_{t}^{i})}}{q(x_{t}^{i}|x_{_{t-1}}^{^{i}},{{z}_{t}})}$ | (2) |
式中:q(xti|xt-1i,zt)是PD,用于产生粒子xti并且评价q(xti|xt-1i,zt)。由于很难获得最优采样分布,本文将先验概率密度函数p(xti|xt-1i)作为PD,因此,权重计算可以表示为简化形式ωti∝$\prod\limits_{m=1}^{M}{p(z_{t}^{(m)}|x_{_{t}}^{i})}$。
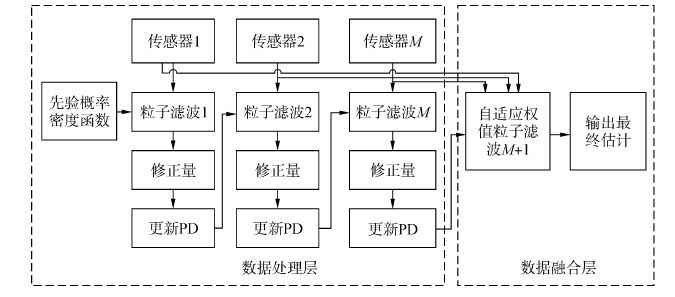
1.2 二阶集中式粒子滤波提高滤波估计精度的基本方式之一就是有效地使用多传感器数据。然而,在集中式融合的标准粒子滤波算法中,多传感器数据仅仅在似然模型中融合,因而忽视了重要性采样过程。为此提出了基于粒子滤波框架下的二阶数据融合方法,如图 1所示。
|
| 图1 PF框架下提出的二阶融合方法 Figure 1 Two order fusion method proposed in PF framework |
在第一阶段的数据处理层中,多传感器数据发送给粒子滤波计算模块,在状态空间中以优化粒子分布为目的相应地更新PD。在此状态中有M个粒子滤波模块,其中第n个模块标记为PF_n。第二阶段的数据融合层中包括标记PF_M+1的自适应权值粒子滤波模块,此模块中的多传感器数据用于构造完整的似然函数$\prod\limits_{m=1}^{M}{p(z_{t}^{(m)}|{{x}_{t}})}$,之后利用欧氏距离和反映量测噪声统计特性的精度因子来自适应的调整权值的分布,达到降低粒子退化程度,保持粒子的多样性的目的,进而得到状态估计${{\hat{x}}_{t}}$。
从图 1可以看出,每一个滤波周期需要M个基本的粒子滤波模块和一个自适应权值粒子滤波模块。第n个模块中使用的PD表示为qn(xt|xt-1i,zt),n∈{1,2,…,M+1}。采用文献[13]中算法确定qn(xt|xt-1i,zt),可以得到式(3)~(4)的更新系统方程:
| ${{x}_{t}}=f({{x}_{t-1}})+{{c}_{n}}({{z}_{t}})+{{v}_{t-1}}$ | (3) |
| ${{q}_{n}}({{x}_{t}}|x_{_{t-1}}^{^{i}},{{z}_{t}}):={{p}_{v}}({{x}_{t}}-f(x_{_{t-1}}^{^{i}})-{{c}_{n}}({{z}_{t}}))$ | (4) |
因此,cn(zt)为修正项,初始设置为零向量并且随着n增加而更新。根据式(4),在‘PF_1’中,c1(zt)=0意味着q1(xt|xt-1i,zt)=p(xt|xt-1i),使用第一个传感器数据来定义本地似然函数p(zt(1)|xt)并且通过运行‘PF_1’获得估计${{{\hat{x}}}_{t,1}}$。根据式(4),在‘PF_2’使c2(zt)=${{{\hat{x}}}_{t,1}}-f\left( {{{\hat{x}}}_{t-1}} \right)$并且定义q2(xt|xt-1i,zt),使用第二个传感器数据来定义本地似然函数p(zt(2)|xt)并且获得估计${{{\hat{x}}}_{t,2}}$,而后被用于获得q3(xt|xt-1i,zt)。整个过程持续到所有传感器数据用完为止,得出的估计${{{\hat{x}}}_{t,n}}$,n∈{1,2,…,M}只是用于优化PD的中间结果。
1.3 二阶自适应权值粒子滤波的多传感器信息算法一个周期的算法如下:
第一阶段:
1) 初始化。n=1并且cn(zt)=0;
FOR n=1∶M
2) 更新。由式(4)定义的PD为qn(xt|xt-1i,zt)产生粒子xti;使用ωti∝p(xti|xt-1i)p(zt(n)|xti)/qn(xti|xt-1i,zt)更新粒子权值。并且归一化ωti=$\omega _{_{t}}^{^{i}}/\sum\limits_{i=1}^{N}{\omega _{_{t}}^{^{i}}}$。给出估计${{{\hat{x}}}_{t,n}}=\sum\limits_{i=1}^{n}{\omega _{t}^{i}x_{t}^{i}};{{c}_{n+1}}\left( {{z}_{t}} \right)={{{\hat{x}}}_{t,n}}-f\left( {{{\hat{x}}}_{t-1}} \right)$,而后n:=n+1。
END FOR
第二阶段:
1) 初始化。已知cM+1(zt),定义PD为q(xt|xt-1i,zt)=qM+1(xt|xt-1i,zt),产生出粒子群{xti}i=1N。
2) 根据式(2)进行权值ωti更新后,分别用ωt-maxi*和ωt-mini*表示最大权值和最小权值,同时计算出量测新息zt-maxi、zt-mini,以及欧式距离Lmax和Li表示为
| ${{L}_{\max }}={{(z_{t-\min }^{^{i}}-z_{t-\max }^{i})}^{T}}\cdot (z_{t-\min }^{^{i}}-z_{t-\max }^{i})$ | (5) |
| ${{L}^{i}}={{(z_{t}^{i}-z_{t-\max }^{i})}^{T}}\cdot (z_{t}^{i}-z_{t-\max }^{i})$ | (6) |
式中:量测新息为zt-maxi=zt-h(xt-maxi)、zt-mini=zt-h(xt-mini),imax、imin表示最大权值ωt-maxi*和最小权值ωt-mini*对应粒子的序号。则权值可以表示为
| $\omega _{_{t}}^{^{i*}}=\omega _{_{t}}^{^{i*}}+(\frac{\omega _{_{t-\max }}^{^{i*}}}{N})\cdot sin(\frac{{{L}^{i}}}{{{L}_{\max }}\cdot (\pi /2)})\cdot \beta $ | (7) |
式中:β为由量测噪声统计特性决定的自适应系数:
| $\beta =\left\{ \begin{array}{*{35}{l}} K/\alpha & \alpha \le \varepsilon \\ 0 & \alpha >\varepsilon \\ \end{array} \right.$ | (8) |
式中:α为量测噪声统计特性的精度因子,α的改变可以实现自适应调整粒子对应权值的分布,增加有用粒子的权值。α越大,则量测精度较低;反之,量测精度较高。ε为由经验确定的阙值,K为常数,且K/α>0。当存在较低量测噪声时,β=0,不调整似然分布;反之,当似然分布呈尖峰状态或位于转移先验分布尾部时,β=K/α,人为扩展似然分布[14]。而后权值归一化处理为ωti*=$\omega _{t}^{i*}=\sum\limits_{i=1}^{N}{\omega _{t}^{i*}}$。
3) 在判断粒子退化程度时使用估计式Neff=$1/{{\sum\limits_{i=1}^{n}{\left( \omega _{0}^{i*} \right)}}^{2}}$,若退化严重则必须进行重采样。根据以上得到的后验密度进行重采样,可以得到新的M个粒子,之后,对每个粒子进行赋权值。
4) 进行马尔可夫链蒙特卡罗(MCMC)移动,目的是增加粒子的多样性,消除重采样过程引起的粒子枯竭现象。
5) 给出状态量的估计值${{{\hat{x}}}_{t,n}}=\sum\limits_{i=1}^{n}{\omega _{t}^{i*}}x_{t}^{i}$。返回第1)步,按新观测量递归计算下一时刻的状态估计值。
2 仿真结果与实验分析 2.1 仿真结果本文按照式(9)及(10)的状态空间模型进行[11]仿真:
| ${{x}_{t+1}}=1+sin(0.04\pi t)+0.5{{x}_{t}}+{{v}_{t}}$ | (9) |
| $\left\{ \begin{array}{*{35}{l}} z_{_{t}}^{^{(1)}}=\frac{x{{\left( t \right)}^{2}}}{20}+\frac{{{x}_{t}}}{3}+w_{t}^{(1)} \\ z_{t}^{(2)}=\left\{ \begin{array}{*{35}{l}} 0.2x_{t}^{2}+w_{t}^{(2)},t\le 30 \\ 0.5{{x}_{t}}-2+w_{t}^{(2)},t>30 \\ \end{array} \right. \\ \end{array} \right.$ | (10) |
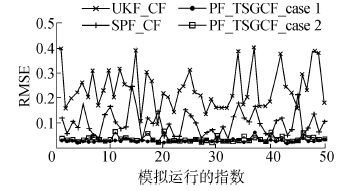
vt为根据gamma(3,2)分布建模的过程噪声;wt(1)~N(0,10-1)和wt(2)~N(0,10-3)是量测噪声。包括三个滤波,无味卡尔曼滤波(UKF_CF)、粒子滤波(SPF_CF)和二阶自适应权值粒子滤波(PF_TSAWCF),估计出状态序列xt(t=1,2,…,60)。二阶自适应权值粒子滤波分为两个阶段,PF_TSAWCF_case1为数据处理层、PF_TSAWCF_case2为数据融合层。使用均方根误差(RMSE)测量出估计精度。每一个算法运行1 000次。图 2中只取前50次的RMSEs的独立运行。
|
| 图2 各种滤波下的均方根误差 Figure 2 RMSE of different filter |
表 1总结了各种算法的总体性能。两个PF_TSAWCF的估计精度比其他滤波方法明显高,但是以时间作为代价来实现的。而且PF_TSAWCF_case2的精度比PF_TSAWCF_case1的精度稍高,根据数据处理层提供的优化粒子的状态估计,通过欧氏距离和反映量测噪声统计特性的精度因子自适应的调整粒子对应权值的分布,增加了有用粒子的权值,进而提高了估计的精度,多传感器应用到重要性采样过程也提高了最终的估计精度。PF_TSAWCF的性能依靠数据处理层中传感器数据的使用顺序。一般来讲,由粗到细的策略有助于提高估计精度,因此优先使用来自低精度传感器的数据。
| 滤波种类 | 均值 | 方差 | 时间/s |
| UKF_PF | 0.272 1 | 1.421×10-2 | — |
| SPF_CF | 0.097 2 | 4.751×10-3 | 0.454 |
| PF_TSAWCF_case1 | 0.019 8 | 5.697×10-6 | 0.631 |
| PF_TSAWCF_case2 | 0.018 7 | 4.986×10-6 | 0.864 |
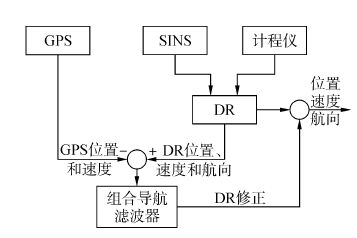
将UKF_CF、SPF_CF以及PF_TSAWCF应用于GPS/SINS/LOG的船舶组合导航系统中,见图 3所示。
|
| 图3 组合导航系统的结构图 Figure 3 Diagram of integrated navigation system |
为了验证本文算法的性能,以大连海事大学“育鲲”轮实验数据为例,按照图 3所示的组合导航系统进行试验的设计,其中GPS定位设备采用Kongsberg公司的MX420接收机,SINS为Mti-G-700的导航级设备,计程仪为Skipper DL850多普勒计程仪。组合导航的试验设计分为两部分:一是原始数据的采集;二是根据本文提出的算法对原始数据进行仿真试验研究并分析结果。
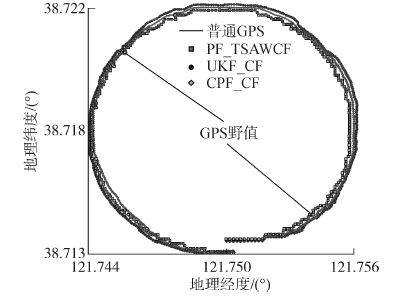
图 4为船舶右旋回测试的位置结果。位置曲线的X轴为地理经度,Y轴为地理纬度。可以看出UKF_CF和SPF_CF在整个阶段的位置误差都较大,而PF_TSAWCF算法在初始阶段时位置误差较大,但随着船舶航行,融合算法的曲线基本稳定。同时,可以看出当GPS数据存在野值跳变时,PF_TSAWCF算法能够有效地抑制野值的影响从而减小定位误差。
|
| 图4 位置结果 Figure 4 Result of position |
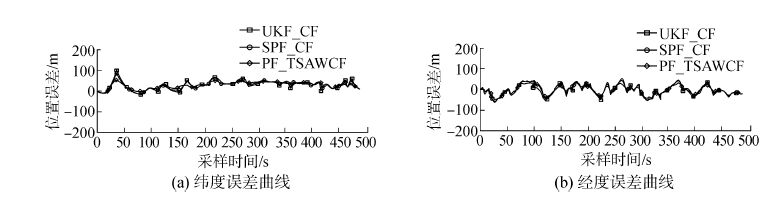
图 5为三种滤波的位置误差曲线。图 5(a)为三种算法的纬度误差,其中UKF_CF的误差在-20~100m;SPF_CF的误差在-20~90m;PF_TSAWCF的误差在-10~70m。图 5(b)为三种算法的经度误差,UKF_CF的误差在-70~50m,SPF_CF的误差在-70~50m,PF_TSAWCF的误差在-60~40m。由误差曲线也能明显看出:在初始阶段和转向时UKF_CF和SPF_CF的定位误差均较大;但是PF_TSAWCF相比UKF_CF和SPF_CF整体上系统定位误差较小,基本稳定。
|
| 图5 三种滤波的位置误差曲线 Figure 5 Variance curve of position error of three type of filters |
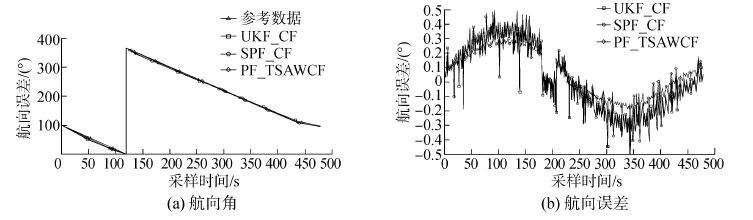
图 6为航向和航向误差曲线,航向对于船舶的控制是一个很重要的参数,因此航向的估计对整个组合导航控制系统都有影响,图 6(a)为三种算法的航向角,其中PF_TSAWCF最接近参考航向值;由图 6(b)中可看出,UKF_CF和SPF_CF的航向角误差范围是±0.5°,PF_TSAWCF的航向角误差范围是±0.3°,因此,本方法能够较好地估计出船舶的航向。
|
| 图6 航向和航向误差曲线 Figure 6 Variance curve of heading and heading error |
图 7为三种算法的速度曲线,由图 7(a)和(b)可以看出,UKF_CF和SPF_CF总体上速度曲线波动较大,PF_TSAWCF在前期加速运动期间和船舶转向时速度的有一定的波动,但是总体上速度较平稳。

|
| 图7 速度曲线 Figure 7 Speed curve |
本文提出了以粒子滤波为框架的二阶自适应权值数据融合算法。通过使用多传感器数据来更新建议分布密度,多传感器数据能够体现在重要性采样的过程中,在数据融合层构造完整的似然函数,根据自适应权值的分布调整,并且利用欧氏距离和反映量测噪声统计特性的精度因子自适应的调整粒子对应权值的分布,增加有用粒子的权值。同时重采样和马尔可夫链蒙特卡罗过程,保留了权值较大的粒子,又避免了粒子耗尽问题,进一步保持粒子的多样性,提高了滤波精度,进而得到最终的估计值。主要结论包括:
1) 根据模拟实验结果,对提出的算法同无味卡尔曼滤波、粒子滤波进行了比较分析,得出本文提出的算法的估计精度比其他滤波方法明显高,但是以时间作为代价来实现的。
2) 根据实船试验的数据进行了验证,将提出的算法应用于GPS/SINS/LOG组合导航系统进行仿真计算,并且同无味卡尔曼滤波、粒子滤波进行了比较分析,本文提出的算法能够得到精确的位置、速度和航向信息,而且也能有效改善滤波性能,提高组合导航系统的解算精度,能够满足船舶高精度导航定位的要求。
本文算法会增大计算量,需要作者下一步进行深入研究,对算法进行改进,使其性能更加完善。
| [1] | GOH S T, ABDELKHALIK O, ZEKAVAT S A. A weighted measurement fusion Kalman filter implementation for UAV navigation[J]. Aerospace science and technology, 2013, 28(1): 315–323. DOI:10.1016/j.ast.2012.11.012 |
| [2] | WANG Yuru, TANG Xianglong, CUI Qing. Dynamic appearance model for particle filter based visual tracking[J]. Pattern recognition, 2012, 45(12): 4510–4523. DOI:10.1016/j.patcog.2012.05.010 |
| [3] | ERDEM E, DUBUISSON S, BLOCH I. Fragments based tracking with adaptive cue integration[J]. Computer vision and image understanding, 2012, 116(7): 827–841. DOI:10.1016/j.cviu.2012.03.005 |
| [4] | VURAL R A, YILDIRIM T, KADIOGLU T, et al. Performance evaluation of evolutionary algorithms for optimal filter design[J]. IEEE transactions on evolutionary computation, 2012, 16(1): 135–147. DOI:10.1109/TEVC.2011.2112664 |
| [5] | WANG Yuru, TANG Xianglong, CUI Qing. Dynamic appearance model for particle filter based visual tracking[J]. Pattern recognition, 2012, 45(12): 4510–4523. DOI:10.1016/j.patcog.2012.05.010 |
| [6] | YIN Shen, ZHU Xiangping. Intelligent particle filter and its application to fault detection of nonlinear system[J]. IEEE transactions on industrial electronics, 2015, 62(6): 3852–3861. |
| [7] | DINI D H, MANDIC D P, JULIER S J. A widely linear complex unscented Kalman filter[J]. IEEE signal processing letters, 2011, 18(11): 623–626. DOI:10.1109/LSP.2011.2166259 |
| [8] | JOHANSEN A M, DOUCET A. A Note on auxiliary particle filters[J]. Statistics & probability letters, 2008, 78(12): 1498–1504. |
| [9] | TORMA P, SZEPESVáRI C. Local importance sampling: a novel technique to enhance particle filtering[J]. Journal of multimedia, 2006, 1(1): 32–43. |
| [10] |
薛丽, 高社生, 赵岩. 权值自适应调整Unscented粒子滤波及其在组合导航中的应用[J].
中国惯性技术学报, 2012, 20(4): 459–463.
XUE Li, GAO Shesheng, ZHAO Yan. Unscented particle filtering with adaptive adjusted weight and its application in integrated navigation[J]. Journal of Chinese inertial technology, 2012, 20(4): 459–463. |
| [11] |
熊伟, 何友, 张晶炜. 多传感器顺序粒子滤波算法[J].
电子学报, 2005, 33(6): 1116–1119.
XIONG Wei, HE You, ZHANG Jingwei. Multisensor sequential particle filter[J]. Acta electronica sinica, 2005, 33(6): 1116–1119. |
| [12] | ZHANG Wei, ZUO Junyi, GUO Qing, et al. Multisensor information fusion scheme for particle filter[J]. Electronics letters, 2015, 51(6): 486–488. DOI:10.1049/el.2014.3051 |
| [13] | HU Zhentao, LIU Xianxing, HU Yumei. Particle filter based on the lifting scheme of observations[J]. IET radar, sonar & navigation, 2015, 9(1): 48–54. |
| [14] | ZUO J Y, JIA Y N, ZHANG Y Z, et al. Adaptive iterated particle filter[J]. Electronics letters, 2013, 49(12): 742–744. DOI:10.1049/el.2012.4506 |
| [15] |
薛丽, 高社生, 胡高歌. 自适应Sage-Husa粒子滤波及其在组合导航中的应用[J].
中国惯性技术学报, 2013, 21(1): 84–88.
XUE Li, GAO Shesheng, HU Gaoge. Adaptive Sage-Husa particle filtering and its application in integrated navigation[J]. Journal of Chinese inertial technology, 2013, 21(1): 84–88. |



