普通舵位于螺旋桨后面,舵面呈对称形式,未考虑到螺旋桨引起的旋转尾流,从而导致普通舵一般会产生比较严重的空泡现象,引起舵面空化剥蚀,空化后舵效也会明显降低,另外,舵的空化还会产生较大的噪音,引起舵和尾部结构振动等一系列不利影响,因此研究提高舵的抗空化性能,对提高舵效和操纵性、抑制空化剥蚀、降低舵引起的振动和噪音是非常必要的。
最早提出扭曲舵思想的是J. Tutin,其基本思想是充分利用螺旋桨尾流的能量,提高推进效率。现在国内对扭曲舵在节能增效方面的研究进行得较多。董国祥[1]用升力面方法计算了扭曲舵的水动力性能,徐一军[2]对扭曲舵的节能可行性进行了探讨,黄胜、郭春雨、王超等[3-6]采用面元法计算桨后扭曲舵的水动力性能,助推效率可以达到3%,刘登成[7]用CFD方法对不同扭曲舵设计方案的节能效果进行计算比较。
对于高速舰船,处于螺旋桨后工作的舵的振动和空化剥蚀也越来越严重,因此对舵性能的考虑也越来越全面。20世纪90年代美国海军进行了一项实船航行空泡观测试验[8-9],试验表明,即便是中等海况条件下保持航向航行,23 kn航速时舵表面即出现空泡,舵空化引起的空化剥蚀在后来的船坞检修中也被证实。究其原因,主要是因为普通舵未考虑到螺旋桨旋转尾流的特点,从而导致普通舵一般会产生比较严重的空泡现象。舵发生空化后舵效会明显降低,还会对舵面引起严重的剥蚀作用,从而影响舵的水动力性能和使用寿命。根据螺旋桨尾流场特点将舵设计成扭曲舵可以有效解决舵上的空化剥蚀问题[10],美国海军科学办公室通过实验发现扭曲舵对于补偿由推进器与船体引起的来流攻角非常有效,同时,其升力性能并不亚于常规舵,目前这种扭曲舵已用于阿利伯克导弹驱逐舰上。本文对桨后舵水动力性能进行计算,重点考查两种舵的压力分布特性,通过压力分布特性比较分析两种舵的空化性能,对两种舵的舵空化起始航速进行计算评估,分析扭曲舵抗空化的效果。
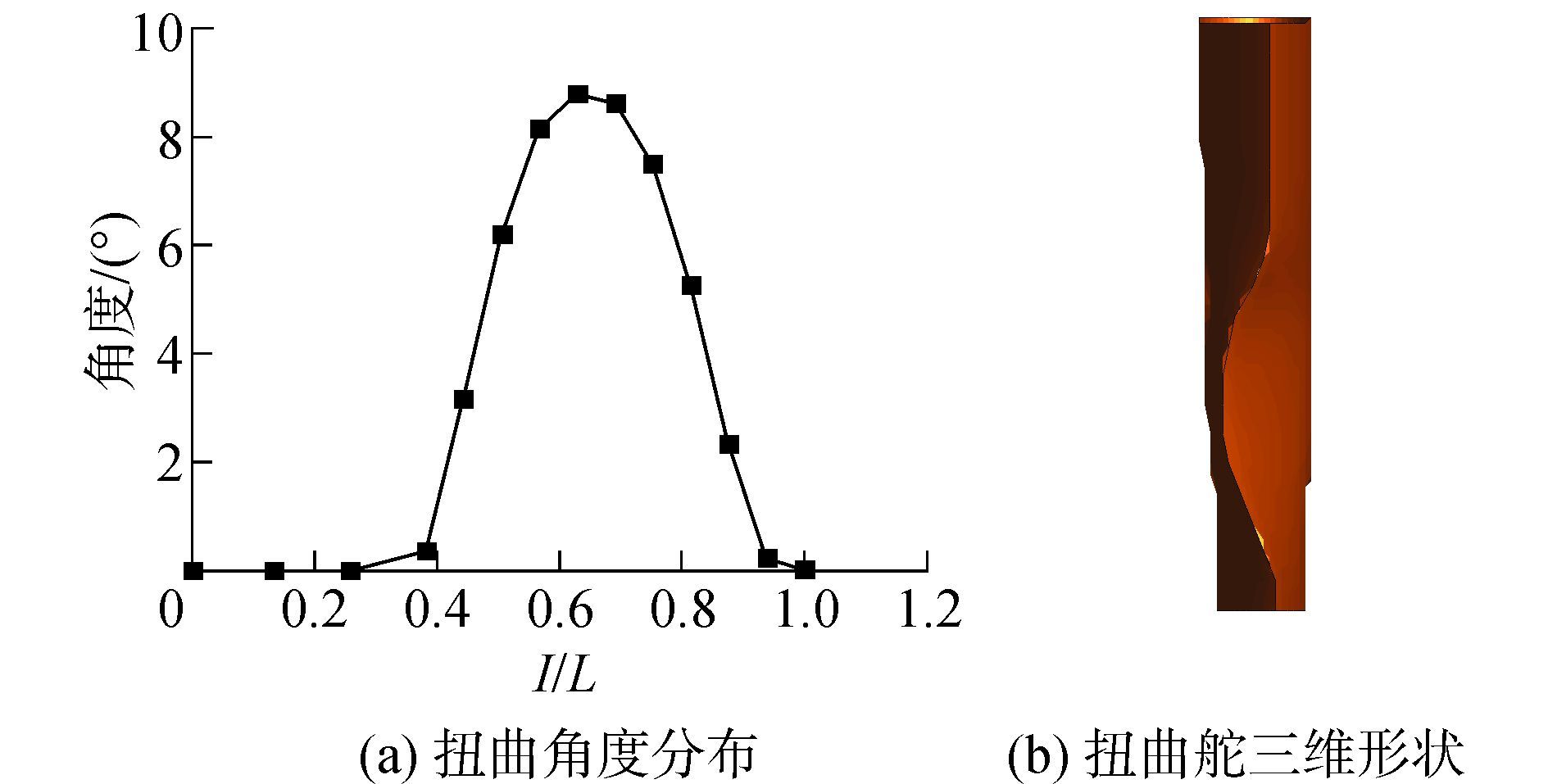
1 桨后舵压力分布数值计算 1.1 扭曲舵基本设计方法扭曲舵的设计,就是根据螺旋桨尾流场的速度分布,在舵攻角为0时,尽量使来流的攻角与舵角相同,从而减小舵面所受横向力,优化空化性能即舵面的压力差分布情况,也提高舰船的操作性。通过面元法计算出舵面的扭曲角度,设计扭曲舵时,舵的弦长与安装位置均不改变,只改变舵面上各展向位置的扭曲角度。用面元法计算得到的某型船螺旋桨后在舵轴盘面处各半径的流体速度,进而可以得到与之匹配的扭曲舵扭曲角度,具体的设计过程见文献[11]。设计扭曲舵的扭曲角与三维视图如图 1所示,其中,L为舵的展长,l为舵各剖面的展向位置,l/L表示各剖面相对于舵展长的无因次展向位置。
|
| 图1 设计扭曲舵几何特征 Figure 1 Geomety features of twisted rudder |
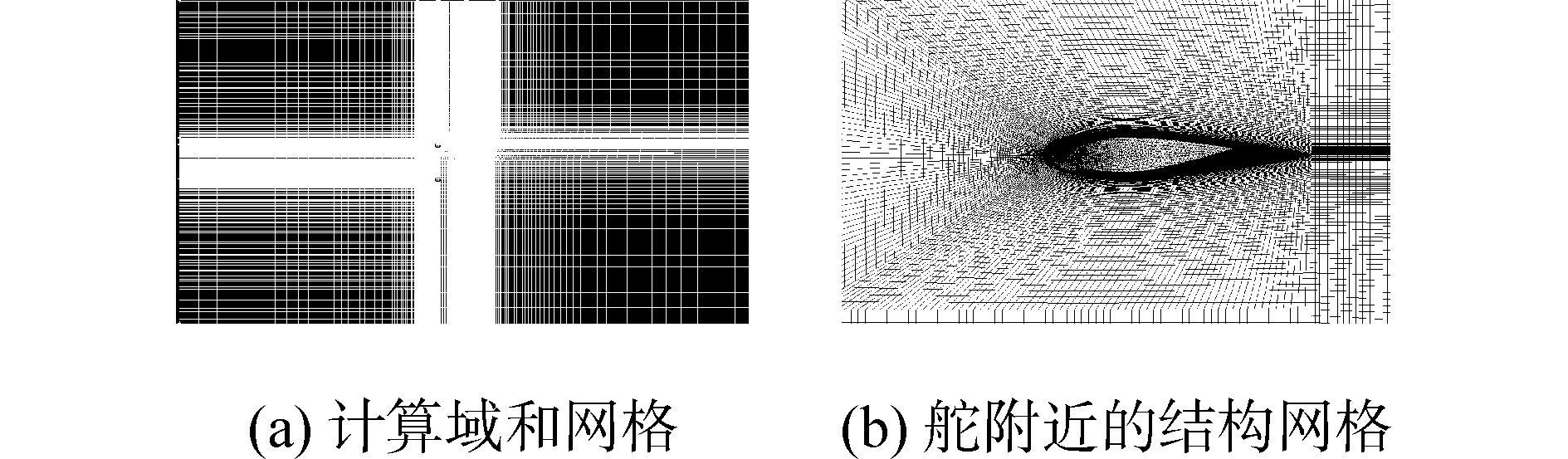
建立某型船模型尺度下螺旋桨和舵的整体计算模型,为了使网格数量较少,同时又保证网格质量和计算精度,采用结构网格和非结构混合型网格划分方法,在螺旋桨附近的区域内采用非结构网格,网格划分较密,而在其他区域采用网格质量很高的结构网格,整个计算域分为静止部分和旋转部分,两个部分都有自己独立的网格形式和分界面(如图 2),整个计算网格数为810万,采用k-ω SST湍流模型。
|
| 图2 计算网格划分情况 Figure 2 Mesh distribution of calculation domain |
根据实船在31.5、24、18 kn三个航速工况,确定了自航模试验的航速,再根据自航模自航试验,得到了自航模各航速下对应的螺旋桨转速分别为107、802、590 r/min,对3种航速工况下舵角为0°和10°的普通舵与扭曲舵的水动力性能进行计算,比较两种舵压力分布的特点,由此分析两种舵的空化起始航速。
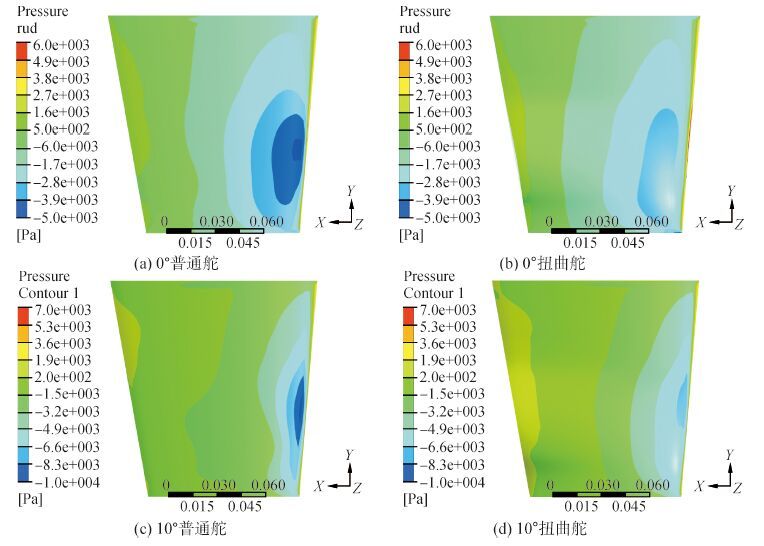
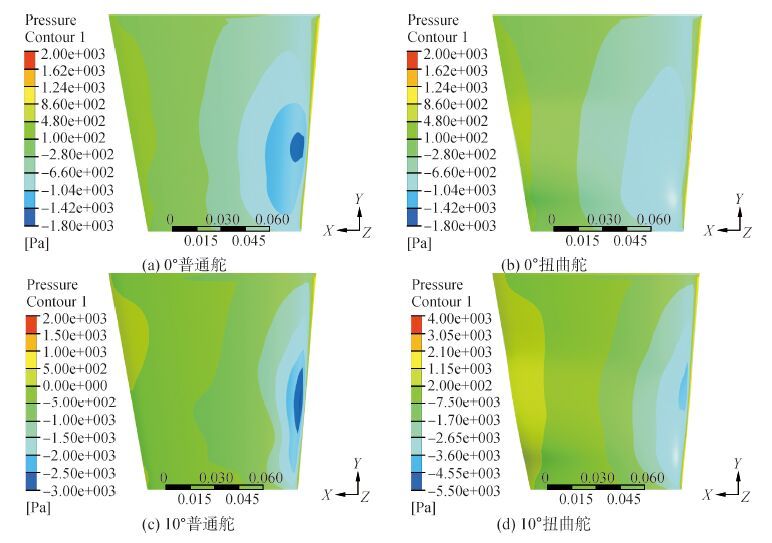
1.3 压力分布计算结果在3种航速工况下,两种舵面在各舵角时叶背(吸力面)压力分布云图如图 3~5所示。从图形中可以看出,在各工况条件下扭曲舵的负压力峰值比普通舵明显小,有利于抑制舵上的空化。
|
| 图3 1 070 r/min工况条件下压力分布比较图 Figure 3 Cloud pictures of pressre ditribution at 1 070 r/min |
|
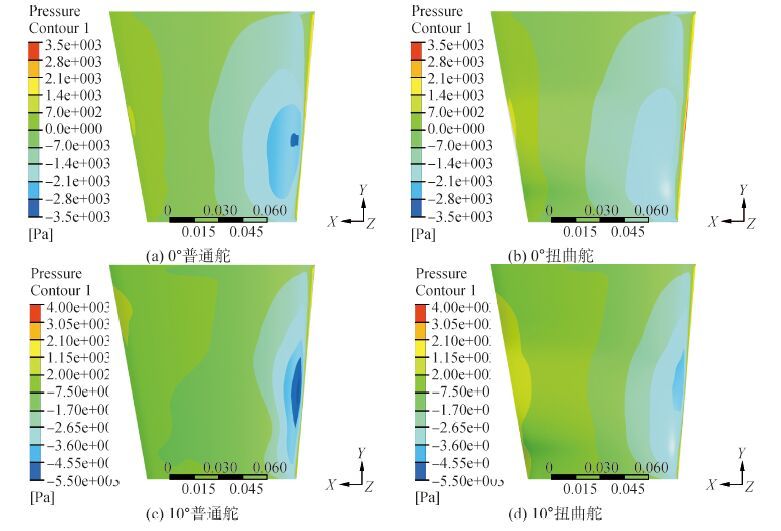
| 图4 802 r/min工况条件下压力分布比较图 Figure 4 Cloud pictures of pressre ditribution at 802 r/min |
|
| 图5 590 r/min工况条件下压力分布比较图 Figure 5 Cloud pictures of pressre ditribution at 590 r/min |
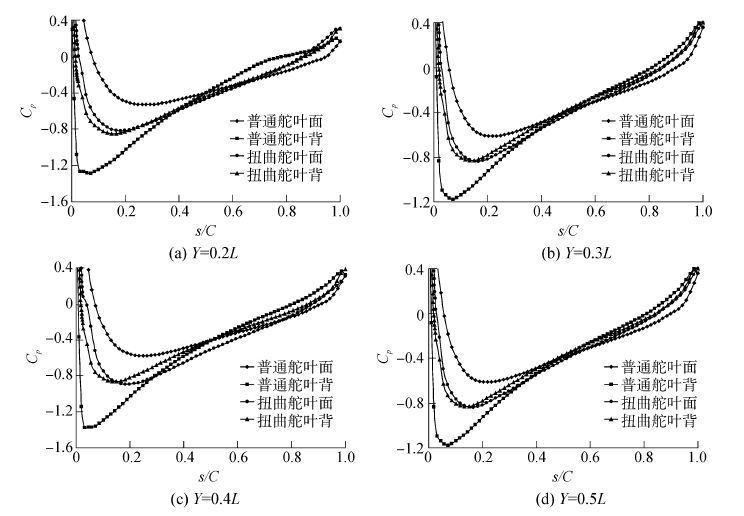
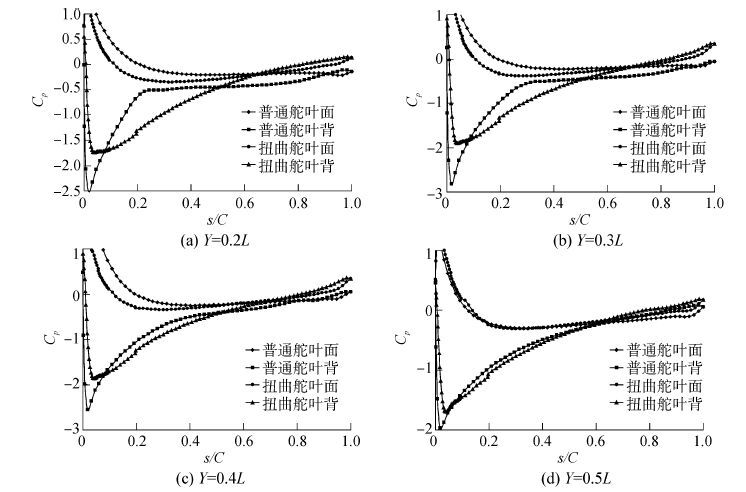
为了更清楚地区分普通舵和扭曲舵上的压力分布情况,取舵上各展向位置的压力分布进行比较,分别取Y=0.2L,Y=0.3L,Y=0.4L,Y=0.5L等4个展向位置的截面上的压力分布进行比较(舵的下端面Y=0,L为舵的展长)。其中1 070 r/min工况下普通舵与扭曲舵在0°、10°舵角时4个截面上压力分布系数比较如图 6、7。
|
| 图6 0°舵角时普通舵与扭曲舵各截面压力分布曲线 Figure 6 Ppressure distribution curves of twisted rudder and ordinary rudder at 0° rudder angle |
|
| 图7 10°舵角时普通舵与扭曲舵各截面压力分布曲线 Figure 7 Ppressure distribution curves of twisted rudder and ordinary rudder at 10° rudder angle |
从压力分布的比较结果可以看出,扭曲舵4个截面在各航速各舵角下负压力峰值均比普通舵明显减小,以1 070 r/min工况下的0°舵角Y=0.3L剖面为例,普通舵的最大负压力系数为-1.287,扭曲舵的负压力峰值为-0.848,负压力幅值明显降低,降幅达34%,这说明扭曲舵可以有效果抑制舵空化,提高舵上的空化起始航速。
2 扭曲舵空化性能评估 2.1 扭曲舵负压力峰值通过扭曲舵与普通舵压力分布的比较,可以看出扭曲舵上的负压力峰值较小,为了进一步分析两种舵的空泡起始航速,将普通舵和扭曲舵在各航速工况条件下各舵角时4个截面上的负压力系数峰值取出进行对比,如表 1~3所示。
| 角度/(°) | 舵类型 | 截面Y | |||
| 0.2L | 0.3L | 0.4L | 0.5L | ||
| 0 |
普通舵 扭曲舵 |
-1.09 -0.823 |
-1.2151 -0.805 |
-1.304 -0.877 |
-1.13 -0.82 |
| 10 |
普通舵 扭曲舵 |
-2.021 -1.571 |
-2.338 -1.626 |
-2.66 -1.809 |
-2.437 -1.78 |
| 角度/(°) | 舵类型 | 截面Y | |||
| 0.2L | 0.3L | 0.4L | 0.5L | ||
| 0 |
普通舵 扭曲舵 |
-1.041 -0.783 |
-1.129 -0.779 |
-1.225 -0.855 |
-1.076 -0.797 |
| 10 |
普通舵 扭曲舵 |
-1.949 -1.491 |
-2.205 -1.516 |
-2.525 -1.7 |
-2.334 -1.687 |
| 角度/(°) | 舵类型 | 截面Y | |||
| 0.2L | 0.3L | 0.4L | 0.5L | ||
| 0 |
普通舵 扭曲舵 |
-1.14 -0.862 |
-1.287 -0.848 |
-1.376 -0.895 |
-1.178 -0.839 |
| 10 |
普通舵 扭曲舵 |
-2.145 -1.646 |
-2.513 -1.74 |
-2.817 -1.903 |
-2.550 -1.86 |
从表 1~3可以看出,无论是扭曲舵还是普通舵,各工况下Y=0.4L截面的负压力系数峰值最大。两种舵各航速工况各舵角时负压力系数峰值如表 4所示,可以看出,各航速各舵角下,扭曲舵的负压力系数峰值均比普通舵小,0°和10°舵角时峰值降低30%以上。
| 角度 | 舵类型 | 航速/(r·min-1) | ||
| 1 070 | 802 | 590 | ||
| 0° |
普通舵 扭曲舵 变化幅度 |
-1.376 -0.895 35.0% |
-1.304 -0.877 32.7% |
-1.225 -0.855 30.2% |
| 10° |
普通舵 扭曲舵 变化幅度 |
-2.817 -1.903 32.4% |
-2.66 -1.809 32.0% |
-2.525 -1.7 32.7% |
忽略模型和实船的尺度效应,假设模型和实船之间的水动力具有相似性,对应工况下对应位置处,模型和实船的压力系数相等,即
| ${{\left( {{C}_{p}} \right)}_{m}}=\frac{{{\left( p-{{p}_{0}} \right)}_{m}}}{0.5\rho V_{m}^{2}}={{C}_{p}}_{S}=\frac{{{\left( p-{{p}_{0}} \right)}_{S}}}{0.5\rho V_{S}^{2}}$ | (1) |
因此可以直接将模型尺度的压力系数看成是实船尺度下的压力系数,为了方便,模型尺度的压力系数Cpm和实船压力系数CpS的下标可以省去,统一写成Cp,根据压力系数的定义:
| ${{C}_{p}}=\frac{p-{{p}_{0}}}{0.5\rho V_{S}^{2}}=\frac{p-({{p}_{a}}+\rho gh)}{0.5\rho V_{S}^{2}}$ | (2) |
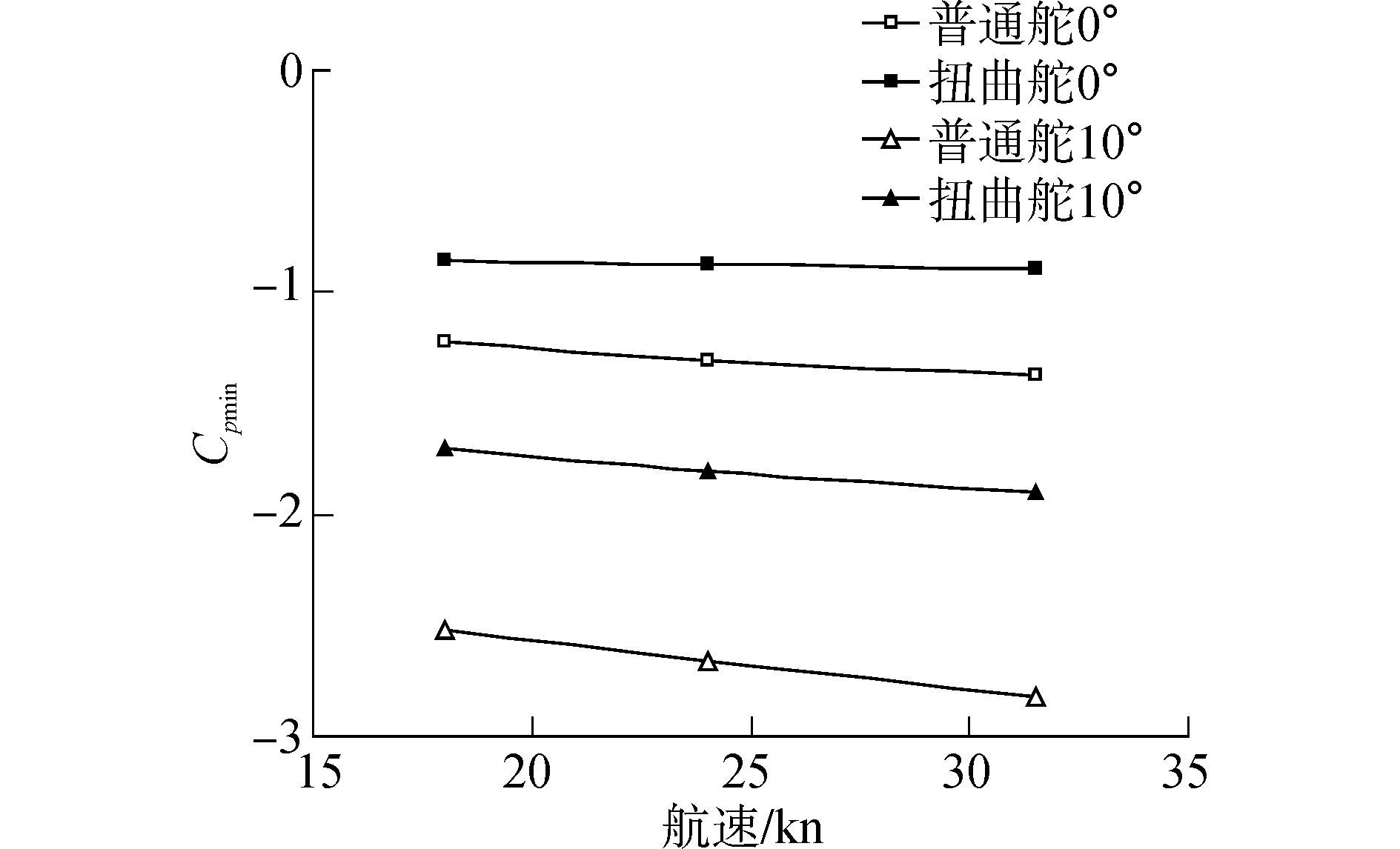
因此根据表 4可以得到实船尺度下两种舵各舵角时负压力系数峰值随航速的变化,如图 8所示,可以看出,无论是扭曲舵还是普通舵,同一舵角负压力系数峰值随航速的变化不大,且负压力系数峰值随航速近似呈线性变化。
|
| 图8 舵负压力系数峰值随航速变化的关系图 Figure 8 Relationship between presure peak and ship speed |
定义舵面上的空泡数:
| ${{\sigma }_{V}}=\frac{{{p}_{a}}+\rho gh-{{p}_{V}}}{0.5\rho V_{S}^{2}}$ |
式中:VS为实船航速,h为舵负压力峰值处的水深,pV为空化压力(15°C时空化压力为2 332 N/m2)。
根据舵面最低压力系数和空泡数的相对关系,可以判断舵面上有无发生空泡:
当-Cpmin <σV 时,即舵面最低压力pmin>pV,无空泡发生;
当-Cpmin≥σV 时,即舵面最低压力pmin≤pV,会发生空泡。
根据同一舵角各航速工况条件下的负压力系数峰值变化不大,且负压力系数峰值随航速近似呈线性变化这一规律,将扭曲舵和普通舵的负压力系数峰值-Cpmin可以表示成航速的线性函数:
| $-{{C}_{pmin}}({{V}_{S}})=-{{C}_{pmin}}({{V}_{S0}})+k({{V}_{S}}-{{V}_{S0}})$ |
根据表 4可以得到上式中扭曲舵和普通舵各舵角下的系数k,普通舵和扭曲舵在0°舵角时负压力系数峰值-Cpmin随航速的关系可以分别表示为
普通舵0°:-Cpmin(VS)=1.376+0.009 6(VS-31.5)
扭曲舵0°:-Cpmin(VS)=0.895+0.002 4(VS-31.5)
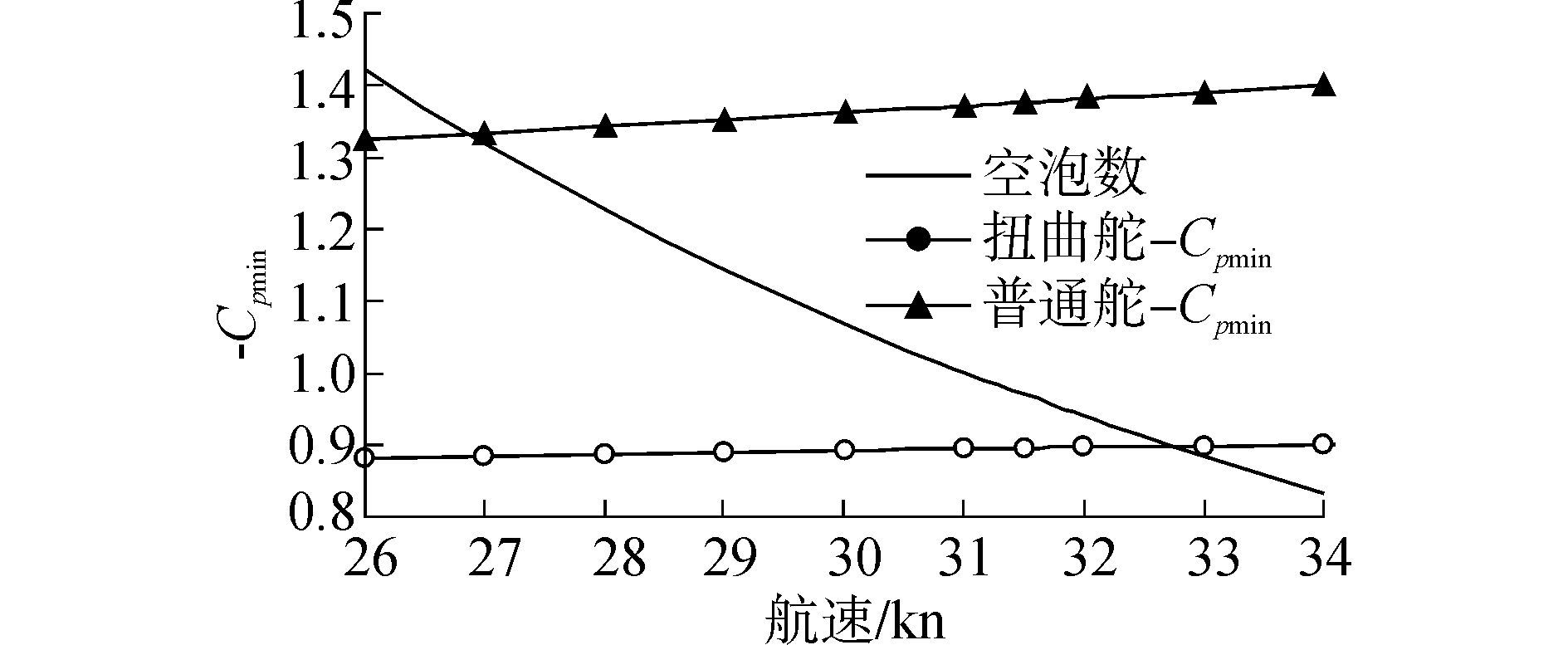
将空泡数、普通舵和扭曲舵在0°舵角时负压力系数峰值-Cpmin随航速的关系曲线画到一张图上,空泡数随航速的关系曲线与负压力系数峰值随航速的关系曲线的交点即为空化起始点,如图 9所示。从图 10可以看出普通舵在0°舵角时的空泡起始航速为26.8 kn,而扭曲舵在0°舵角时空泡起始航速为32.7 kn,0°舵角时,扭曲舵的空化起始航速比普通舵提高5.9 kn。
|
| 图9 0°舵角空泡起始航速分析图 Figure 9 Analysis on inception speed of rudder cavitation at 0° rudder angle |
|
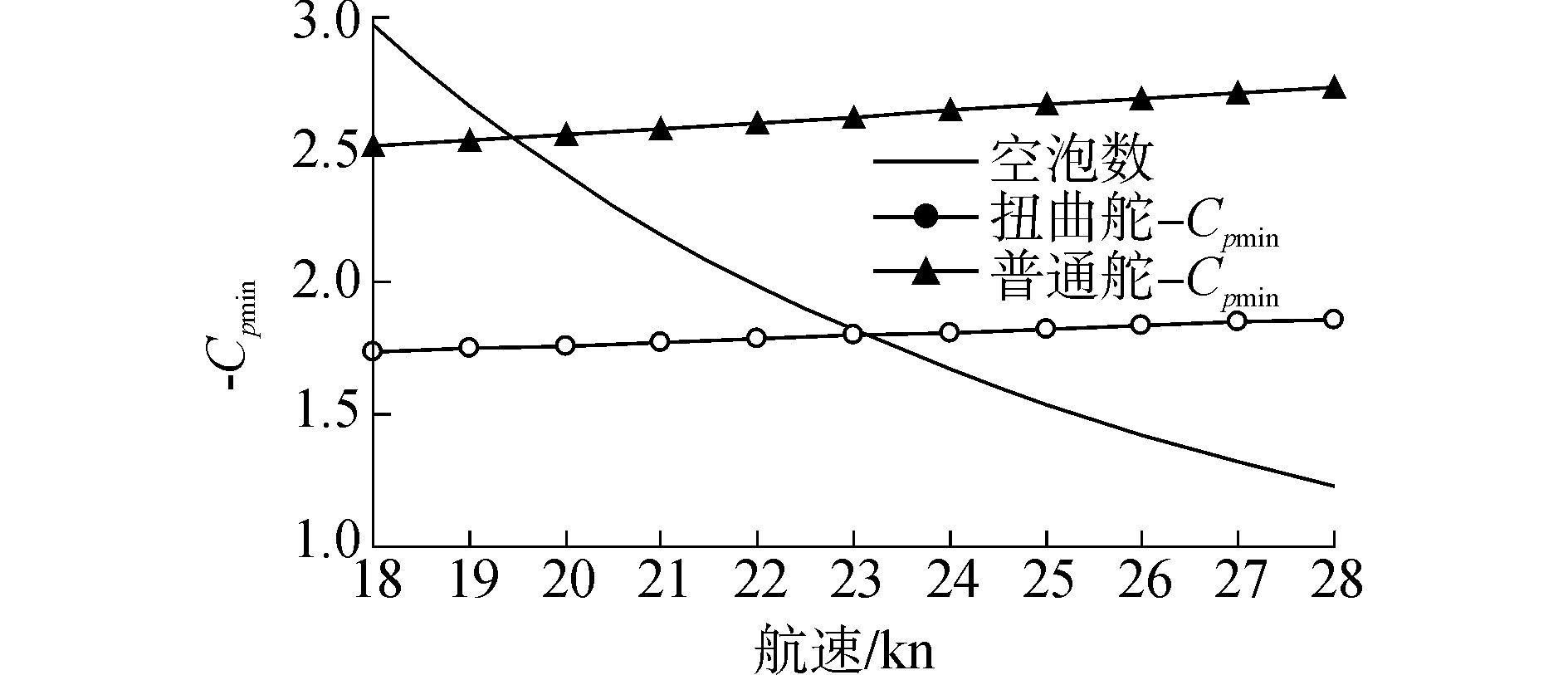
| 图10 10°舵角空泡起始航速分析图 Figure 10 Analysis on inception speed of rudder cavitation at 10° rudder angle |
用相同的方法可得到普通舵和扭曲舵在10°舵角时负压力系数峰值-Cpmin随航速的关系可以分别表示为
普通舵10°:-Cpmin(VS)=2.660+0.022 5(VS-31.5)
扭曲舵10°:-Cpmin(VS)=1.809+0.012 5(VS-31.5)
将空泡数、普通舵和扭曲舵在10°舵角时负压力系数峰值随航速的关系曲线在一张图上给出,如图 10所示。从图 10可以看出普通舵在10°舵角时的空泡起始航速为19.4 kn,而扭曲舵在10°舵角时空泡起始航速为23.2 kn,扭曲舵的空化起始航速比普通舵提高4.8 kn。
通过以上分析可以看出,扭曲舵可以大幅提高舵的空化起始航速,在0°舵角时,扭曲舵的空化起始航速比普通舵提高5.9 kn,在10°舵角时,扭曲舵的空化起始航速比普通舵提高4.8 kn;扭曲舵在0°舵角时,在整个设计航速范围内均不产生空泡,扭曲舵抗空化效果比较明显。
3 结论通过CFD方法,对桨后舵水动力性能进行了数值计算,得到普通舵和扭曲舵的压力分布特性并进行了比较,结果显示,扭曲舵在各航速各舵角下负压力峰值比普通舵明显减小,扭曲舵有较好的空化性能。
通过比较两种舵的压力分布特性,对普通舵和扭曲舵的空化起始航速进行了计算评估。在0°舵角时扭曲舵的空化起始航速比普通舵提高5.9 kn左右,在10°舵角时扭曲舵的空化起始航速比普通舵提高4.8 kn左右,因此,通过抗空化设计,扭曲舵可以大幅提高舵的空化起始航速,减小舵上空化剥蚀和振动,有利于提高舵的使用寿命。
| [1] |
董国祥. 助推节能扭曲舵性能的理论预报[J].
船舶, 1994(6): 58–63.
DONG Guoxiang. Theory prediction on performance of Energy Saving twisted rudder[J]. Journal of ship, 1994(6): 58–63. |
| [2] |
徐一军. 扭曲反应舵节能功效的可行性探讨[J].
船舶设计通讯, 2010(S1): 21–24.
XU Yijun. Feasibility Discussion on Energy Saving Efficiency of twisted rudder[J]. Journal of ship design, 2010(S1): 21–24. |
| [3] |
祝享元, 黄胜, 郭春雨, 等. 桨后扭曲舵的理论设计及水动力性能计算[J].
哈尔滨工程大学学报, 2008, 29(2): 126–129.
ZHU Xiangyuan, HUANG Sheng, GUO Chunyu, et al. Design and performance of a skew rudder behind a propeller[J]. Journal of Harbin Engineering University, 2008, 29(2): 126–129. |
| [4] | WANG Chao, HE Miao, WANG Guoliang, et al. Design and performance analysis of twisted rudder based on the maximum reduction of rudder resistance[J]. Journal of ship mechanics, 2014, 18(3): 238–247. |
| [5] |
郭春雨, 赵庆新, 吴铁成, 等. 船舶附加水动力组合节能技术研究进展[J].
舰船科学技术, 2014, 36(4): 1–10.
GUO Chunyu, ZHAO Qingxin, WU Tiecheng, et al. Research and development of marine hydrodynamic compounded energy-saving[J]. Ship science and technology, 2014, 36(4): 1–10. |
| [6] |
齐慧博. 扭曲舵的水动力性能研究[D]. 哈尔滨:哈尔滨工程大学, 2011:9-67.
QI Huibo. A hydrodynamic performance analysis of skew rudder[D]. Harbin:Harbin Engineering University, 2011:9-67. http://cdmd.cnki.com.cn/Article/CDMD-10217-1012264258.htm |
| [7] |
刘登成, 黄国富. 高效扭曲舵水动力特性数值分析[C]//第十一届全国水动力学学术会议暨第二十四届全国水动力学研讨会并周培源诞辰110周年纪念大会文集. 无锡, 中国, 2012:1074-1081.
LIU Dengcheng, HUANG Guofu. Numerical analysis on hydrodynamic performance of hign efficiency twisted rudder of ship[C]//Eleventh Symposium on Hydrodynamics of china, Wuxi, China, 2012:1074-1081. |
| [8] | SHEN Y T, JIANG C W, REMMERS K D. A twisted rudder for reduced cavitation[J]. Journal of ship research, 1997, 41(4): 260–272. |
| [9] | SHEN Y T, REMMERS K D, JIANG C W. Effects of ship hull and Propeller on rudder cavitation[J]. Journal of ship research, 1997, 4: . |
| [10] | KOOP A H, HOEIJMAKERS H W, SCHNERR G H, et al. Design of twisted cavitating hydrofoil using a barotropic flow method[C]//Proceedings of the Sixth International Symposium on Cavitation. Wageningen, The Netherlands, 2006:1-13. |
| [11] |
叶金铭, 王威, 李渊, 等. 抗空化扭曲舵设计及力学特性分析[C]//2015年船舶水动力学学术会议论文集. 哈尔滨, 中国, 2015:328-335.
YE Jinming, WANG Wei, LI Yuan, et al. Research on Hydrodynamic performance of anti-cavitation twisted rudder[C]//2015 Symposium on ship hydrodynamics. Harbin, China, 2015:328-335. |



