多输入多输出(multiple-input multiple-output, MIMO)雷达是由国外学者将通信领域的MIMO思想引入雷达领域所提出的一种新体制雷达[1]。MIMO雷达通过多个发射阵元同时发射相互正交的波形,且利用多个接收阵元同时接收目标的回波信号,具有可利用波形分级和空间分级增益,以及更高的自由度等优点,因而受到了广泛的关注。有关MIMO雷达的波离角(DOD)和波达角(DOA)估计的研究是研究热点之一,相关研究主要围绕经典测向算法展开[2-10]。文献[2-6]研究了基于ESPRIT的相关算法,文献[2-4]基于双基地MIMO雷达,分别提出了EPSRIT算法[2]、共轭EPSRIT算法[3]和酉ESPRIT算法[4],算法的效率和性能都得到一定的提升,但只有酉ESPRIT算法具有解相干能力,其他算法的性能在存在相干信源时急剧恶化。文献[5-6]基于单基地MIMO雷达分别提出了采用非圆信号的ESPRIT算法和降维酉EPSRIT算法。文献[7]利用最大似然的方法估计MIMO雷达的波达方向,该方法虽然可以用于相干信源的角度估计,但计算量非常大。文献[8-10]则研究了MUSIC算法在双基地MIMO雷达中的应用,文献[8]将二维谱峰搜索MUSIC算法转换为只需一维搜索的降维MUSIC算法,分别估计出DOA和DOD,计算量显著降低,但不具备解相干能力;文献[9]提出了基于MIMO雷达的求根MUSIC方法,通过将传统求根MUSIC算法应用于MIMO雷达,分两步分别估计出DOD和DOA,避免了计算量巨大的谱峰搜索,其计算量相对于文献[8]的方法有所降低,但计算效率仍有待提升,且当目标相关或相干时性能严重恶化,算法失效。考虑到实际噪声环境的复杂性,文献[10]研究了基于双基地MIMO雷达的四阶累积量,提出了可以用于色噪声环境下的估计方法,该方法需要二维谱峰搜索,计算量巨大,且只能估计相互独立的信源。
针对双基地MIMO雷达中现有角度估计算法计算量大及无法估计相干信源的问题,提出一种酉求根MUSIC方法。该方法将信号协方差矩阵进行实值化处理,将复运算转换为实运算,构造实值求根方程,分两步分别估计DOA和DOD,结果自动配对。
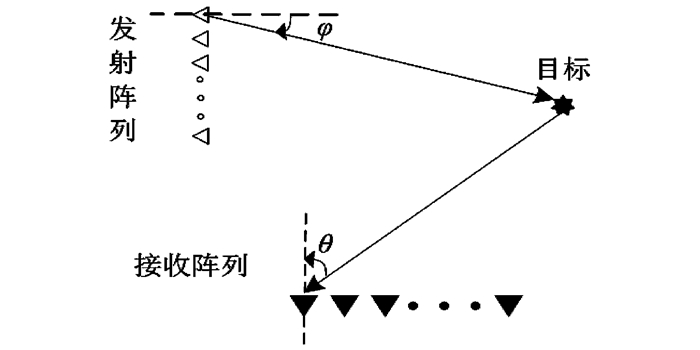
1 双基地MIMO雷达数据模型图 1所示为双基地MIMO雷达模型。
|
| 图1 双基地MIMO雷达示意图 Figure 1 Structure of bistatic MIMO radar |
考虑如图 1所示双基地MIMO雷达,发射阵列和接收阵列分置,均为阵元间距为半波长的均匀线阵,分别由M个和N个全向的阵元组成。M个发射阵元同时发射M种具有相同载频和带宽的正交波形,接收端通过匹配滤波器将M种波形分开。假设在同一距离存在P个相互独立的远场信源,第t个快拍接收端全部匹配滤波器的输出信号为
| $ \boldsymbol{x}\left( t \right) = \boldsymbol{As}\left( t \right) + \boldsymbol{n}\left( t \right) $ | (1) |
式中:A=[a1 a2 … aP]为MN×P维的目标导向矢量矩阵,ar(θp)=[1 e-jπsin θp … e-j(N-1)πsin θp]T为接收导向矢量,at(φp)=[1 e-jπsin φp … e-j(M-1)πsin φp]T为发射导向矢量,ap=ar(θp)⊗ at(φp)为第p个目标的导向矢量,⊗表示Kronecker积,θp表示第p个目标的波达方向,即DOA,φp表示第p个目标的波离方向,即DOD;s(t)=[s1(t) s2(t) … sP(t)]T表示为P×1维信号反射复幅度向量,sp(t)=βpej2πfdt,βp表示幅度,fd表示多普勒频移;n(t)表示MN×1维的复高斯白噪声向量,其均值为零,协方差矩阵为σ2IMN,其中σ2表示噪声功率,IMN表示MN×MN维的单位矩阵。
由L个快拍构成的数据矩阵为
| $ \boldsymbol{X} = \left[ {x\left( 1 \right)\;x\left( 2 \right) \cdots x\left( L \right)} \right] = \boldsymbol{As + N} $ | (2) |
式中:X=[x(1) x(2) … x(L)]表示MN×L维接收快拍矩阵,S=[s(1) s(2) … s(L)]为P×L维回波矩阵,N=[n(1) n(2) … n(L)]为MN×L维噪声矩阵。
2 实值协方差矩阵的构造由L个快拍的数据矩阵X计算协方差矩阵的最大似然估计可得
| $ \boldsymbol{R} = {\text{E}}\left[ {\boldsymbol{x}\left( t \right){\boldsymbol{x}^{\text{H}}}\left( t \right)} \right] = \boldsymbol{X}{\boldsymbol{X}^{\text{H}}} = \boldsymbol{A}{\boldsymbol{R}_5}{\boldsymbol{A}^{\text{H}}} + {\sigma ^2}{\boldsymbol{I}_{MN}} $ | (3) |
式中:R5=E[s (t)sH(t)]=SSH为回波矩阵的协方差矩阵。只有当R5为对角矩阵时,R才具有中心Hermite对称性质[12],即
| $ \boldsymbol{R} = {\boldsymbol{J}_{MN}}{\boldsymbol{R}^*}{\boldsymbol{J}_{MN}} $ | (4) |
式中:JMN表示MN×MN维的交换矩阵,其副对角线位置上的元素均为1,其他位置上的元素均为0;(·)*表示复共轭; JMN满足JMN2=IMN。当Rs不是对角矩阵时,常使用R的前后向平均形式RFB[4, 11, 12],用来增强其中心Hermite对称性质和增加虚拟快拍数,RFB可表示为
| $ {\boldsymbol{R}_{{\text{FB}}}} = \frac{1}{2}\left( {\boldsymbol{R} + {\boldsymbol{J}_{MN}}{\boldsymbol{R}^*}{\boldsymbol{J}_{MN}}} \right) = \boldsymbol{A}{{\boldsymbol{\tilde R}}_S}{\boldsymbol{A}^{\text{H}}} + {\sigma ^2}{\boldsymbol{I}_{MN}} $ | (5) |
式中:${\boldsymbol{\tilde R}_s}$s=12(Rs+ DRs*DH),D为P×P维的导向矢量转换矩阵,表示为
| $ \begin{array}{l} \boldsymbol{D}{\rm{ = diag(}}\exp \left[ {{\rm{j}}\left( {N - 1} \right)\pi {\rm{sin }}{\theta _1} + {\rm{j}}\left( {M - 1} \right)\pi {\rm{sin }}{\varphi _i}} \right],\\ \;\;\;\exp \left[ {{\rm{j}}\left( {N - 1} \right)\pi {\rm{sin }}{\theta _2} + {\rm{j}}\left( {M - 1} \right)\pi {\rm{sin }}{\varphi _2}} \right], \cdots \\ \;\;\;\;\;\exp \left[ {{\rm{j}}\left( {N - 1} \right)\pi {\rm{sin }}{\theta _{\rm{P}}} + {\rm{j}}\left( {M - 1} \right)\pi {\rm{sin }}{\varphi _P}} \right]) \end{array} $ | (6) |
且D满足
| $ \boldsymbol{AD} = {\boldsymbol{J}_{MN}}{\boldsymbol{A}^*} $ | (7) |
由于任意的中心Hermite对称矩阵经过酉变换均可以得到实值矩阵[12]。因此对中心Hermite对称矩阵RFB进行实值变换,可以获得实值协方差矩阵:
| $ \begin{array}{1} \;\;{\boldsymbol{R}_{\text{U}}} = \boldsymbol{Q}_{{\text{MN}}}^{\text{H}}{\boldsymbol{R}_{{\text{FB}}}}{\boldsymbol{Q}_{{\text{MN}}}} = \hfill \\ \boldsymbol{Q}_{{\text{MN}}}^{\text{H}}\boldsymbol{A}{{\boldsymbol{\tilde R}}_S}{\boldsymbol{A}^{\text{H}}}{\boldsymbol{Q}_{MN}} + {\sigma ^2}{\boldsymbol{I}_{{\text{MN}}}} \hfill \\ \end{array} $ | (8) |
式中:QMN为一稀疏的酉转换矩阵,满足如下性质:
| $ {\boldsymbol{J}_K}{\boldsymbol{Q}_K} = \boldsymbol{Q}_K^* $ | (9) |
| $ \boldsymbol{Q}_{\text{K}}^{\text{H}}{\boldsymbol{J}_K} = {\left( {\boldsymbol{Q}_{\text{K}}^{\text{H}}} \right)^*} $ | (10) |
根据以上性质可以将QMN根据MN的奇偶不同选取如下不同形式[12]:
| $ {\boldsymbol{Q}_{2K}} = \frac{1}{{\sqrt 2 }}\left[ {\begin{array}{*{20}{l}} {{\boldsymbol{I}_K}}&{{\text{j}}{\boldsymbol{I}_K}} \\ {{\boldsymbol{J}_K}}&{ - {\text{j}}{\boldsymbol{J}_K}} \end{array}} \right] $ | (11) |
| $ {\boldsymbol{Q}_{2K + 1}} = \frac{1}{{\sqrt 2 }}\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{I}_K}}&0&{{\text{j}}{\boldsymbol{I}_K}} \\ {{0^{\text{T}}}}&{\sqrt 2 }&{{0^{\text{T}}}} \\ {{\boldsymbol{J}_K}}&0&{ - {\text{j}}{\boldsymbol{J}_K}} \end{array}} \right] $ | (12) |
考虑式(5),RU可进一步改写为
| $ \begin{array}{1} {\boldsymbol{R}_{\text{U}}} = \frac{1}{2}\left( {\boldsymbol{R}_{MN}^{\text{H}}\boldsymbol{R}{\boldsymbol{Q}_{MN}} + \boldsymbol{Q}_{MN}^{\text{H}}\boldsymbol{J}_{MN}^{\text{H}}{\boldsymbol{R}^*}\boldsymbol{J}_{MN}^{\text{H}}{\boldsymbol{Q}_{MN}}} \right) = \hfill \\ \;\;\;\;\;\;\;\frac{1}{2}\left( {\boldsymbol{Q}_{MN}^{\text{H}}\boldsymbol{R}{\boldsymbol{Q}_{MN}} + {{\left( {\boldsymbol{Q}_{MN}^{\text{H}}} \right)}^*}{\boldsymbol{R}^*}\boldsymbol{Q}_{MN}^{\text{*}}} \right) = \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\operatorname{Re} \left\{ {\boldsymbol{Q}_{MN}^{\text{H}}\boldsymbol{R}{\boldsymbol{Q}_{MN}}} \right\} \hfill \\ \end{array} $ | (13) |
对比式(8)和式(13)发现,RU有两种构成方式,一种可以直接使用协方差矩阵R进行酉转换,然后取其实部,另一种为使用协方差矩阵的前后向平均形式RFB进行酉变换获得,二者均可用于实值协方差矩阵的构造。
3 酉求根MUSIC算法对协方差矩阵的前后向平均RFB和实值协方差矩阵RU进行特征分解可得:
| $ {\boldsymbol{R}_{{\text{FB}}}} = {\boldsymbol{E}_{{\text{FB}}}}{\mathit{\Sigma} _{\text{S}}}\boldsymbol{E}_{{\text{FB}}}^{\text{H}} + \sigma {\boldsymbol{V}_{{\text{FB}}}}\boldsymbol{V}_{{\text{FB}}}^{\text{H}} $ | (14) |
| $ {\boldsymbol{R}_{\text{U}}} = {\boldsymbol{E}_{\text{U}}}{\mathit{\prod} _{\text{S}}}\boldsymbol{E}_{\text{U}}^{\text{H}} + \sigma {\boldsymbol{V}_{\text{S}}}\boldsymbol{V}_{\text{U}}^{\text{H}} $ | (15) |
式中: EFB和VFB分别代表RFB的信号子空间和噪声子空间,EU和VU分别代表RU的信号子空间和噪声子空间,EFB和EU为MN×P维矩阵,VFB和VU为MN×(MB-P)维矩阵,ΣS和ΠS分别为由RFB和RU的P个大特征值构成的特征值矩阵。
下面通过分析RFB和RU的特征方程来获得二者的信号子空间和噪声子空间之间的关系。RFB的特征方程可表示为
| $ {\boldsymbol{R}_{{\text{FB}}}}{\boldsymbol{\xi} _p} = {\boldsymbol{\lambda} _p}{\boldsymbol{\xi} _p} $ | (16) |
式中:λp和ξp分别代表RFB对应第p个信号的特征值和特征向量。由于QMN QMNH=IMN,因此对式(16)左乘QMNH可得
| $ \begin{array}{l} \boldsymbol{Q}_{MN}^{\text{H}}{\boldsymbol{R}_{{\text{FB}}}}{\boldsymbol{\xi} _p} = \boldsymbol{Q}_{MN}^{\text{H}}{\boldsymbol{R}_{{\text{FB}}}}{\boldsymbol{Q}_{MN}}{\boldsymbol{R}_{{\text{FB}}}}{\boldsymbol{Q}_{MN}}Q_{MN}^{\text{H}}{\boldsymbol{\xi} _p} = \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\boldsymbol{\lambda} _p}\boldsymbol{Q}_{MN}^{\text{H}}{\boldsymbol{\xi} _p} = {\boldsymbol{R}_{\text{U}}}\boldsymbol{Q}_{MN}^{\text{H}}{\boldsymbol{\xi} _p} \hfill \\ \end{array} $ |
观察式(17)可知,RFB和RU具有相同的特征值,且其对应特征向量,即特征子空间之间的关系可表示为
| $ {\boldsymbol{E}_{\text{U}}} = \boldsymbol{Q}_{MN}^{\text{H}}\boldsymbol{E}_{EB}^{\text{H}} $ | (18) |
| $ {\boldsymbol{V}_{\text{U}}} = \boldsymbol{Q}_{MN}^{\text{H}}{\xi _p}{\boldsymbol{V}_{FB}} $ | (19) |
由传统root-MUSIC的原理可以求得双基地MIMO雷达的求根多项式:
| $ {f_{{\text{root - MUSIC}}}} = \boldsymbol{A}{\left( {z_t^{ - 1},z_r^{ - 1}} \right)^{\text{T}}}{\boldsymbol{V}_{{\text{FB}}}}\boldsymbol{V}_{{\text{FB}}}^{\text{H}}\boldsymbol{A}\left( {{z_t},{z_r}} \right) $ | (20) |
式中:A(zt, zr)=ar(zr)⊗ at(zr), ar(zr)=[1, zr, …, zrN-1]T, at(zr)=[1, zt, …, ztN-1]T, zt=e-jπsin φ, zr=e-jπsin θ。根据信号子空间和噪声子空间的正交关系可知,当φ和θ分别对应某一目标的真实DOD和DOA时,froot-MUSIC=0。
基于式(20)所示求根多项式以及式(18)、(19)所示的关系式,双基地MIMO雷达的酉求根(URM)多项式可表示为
| $ \begin{array}{1} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{f_{URM}} = \hfill \\ A{\left( {z_t^{ - 1},z_r^{ - 1}} \right)^{\text{T}}}{\boldsymbol{Q}_{MN}}\boldsymbol{Q}_{MN}^{\text{H}}{\boldsymbol{V}_{{\text{FB}}}}\boldsymbol{V}_{{\text{FB}}}^{\text{H}}{\boldsymbol{Q}_{{\text{MN}}}}\boldsymbol{Q}_{{\text{MN}}}^{\text{H}}\boldsymbol{A}\left( {{z_t},{z_r}} \right) = \hfill \\ {\boldsymbol{a}_t}{\left( {z_t^{ - 1}} \right)^{\text{T}}}{\left[ {{\boldsymbol{a}_r}\left( {z_r^{ - 1}} \right) \otimes {\boldsymbol{I}_M}} \right]^{\text{T}}}{\boldsymbol{Q}_{MN}}{\boldsymbol{V}_{\text{U}}}\boldsymbol{V}_{\text{U}}^{\text{H}}\boldsymbol{Q}_{{\text{MN}}}^{\text{H}} \hfill \\ {\left[ {{\boldsymbol{a}_r}\left( {{z_r}} \right) \otimes {\boldsymbol{I}_M}} \right]^{\text{T}}}{a_t}\left( {{z_t}} \right) = {\boldsymbol{a}_t}{\left( {z_t^{ - 1}} \right)^{\text{T}}}\prod \left( {{z_r}} \right){\boldsymbol{a}_t}\left( {{z_t}} \right) \hfill \\ \end{array} $ | (21) |
式中:∏(zr)为一M×M维的矩阵,∏(zr)=[ar (zr-1)⊗IM]T QMN VU VUH QMNH [ar(zr) ⊗IM], 用于DOA估计。计算使∏(zr)的行列式获得最小值的zr,即令
| $ \det \left[ {\prod \left( {{z_r}} \right)} \right] = 0 $ | (22) |
所得的所有根中,P对离单位圆最近的根zr(p)|p=1, …, p即为对应的DOA,实际计算时不妨取位于单位圆内的离单位圆最近的P个解作为DOA的估计值。
将由式(22)求得的每个zr(p)分别代入式中,可得对应DOD的求根多项式:
| $ \prod \left( {{z_t}} \right) = \left( {{\boldsymbol{a}_t}{{\left( {z_t^{ - 1}} \right)}^{\text{T}}}} \right)\prod \left( {{z_r}\left( p \right)} \right){\boldsymbol{a}_t}\left( {{z_t}} \right) $ | (23) |
再次利用信号子空间和噪声子空间的正交关系,令
| $ \det \left[ {\prod \left( {{z_r}} \right)} \right] = 0 $ | (24) |
所得的根中离单位圆最近的一对根zt(p)即为与相应DOA对应的DOD。不妨与DOA的选取类似,取位于单位圆内的根作为DOD的估计值。
DOA和DOD与zr(p)和zt(p)的转换关系式为
| $ {\theta _p} = - \arcsin \left( {{\text{angle}}\left( {{z_r}\left( p \right)} \right)/{\pi }} \right) $ | (25) |
| $ {\varphi _p} = - \arcsin \left( {{\text{angle}}\left( {{z_t}\left( p \right)} \right)/{\pi }} \right) $ | (26) |
由式(25)、(26),可估计出第p个目标的DOA和DOD,且无需额外的配对算法即可进行自动配对。
4 仿真实验和结果分析为了证明所提方法的有效性和优越性,分别在不同场景下进行了系统的计算机仿真实验。
定义均方误差公式为
| $ {\text{RMSE = }}\sqrt {E{{\left( {\hat \theta - \theta } \right)}^2} + E{{\left( {\hat \varphi - \varphi } \right)}^2}} $ | (27) |
式中:E($\hat \theta $-θ)2=
考虑一双基地MIMO雷达,其结构如图 1所示,发射阵元数M=8,接收阵元数N=6。假设在同一距离单元内存在P=3个远场点目标,其收发角分别为(φ1, θ1)=(5°, -10°),(φ2, θ2)=(27°, 8°), (φ3, θ3)=(13°, 25°),快拍数为L=100。
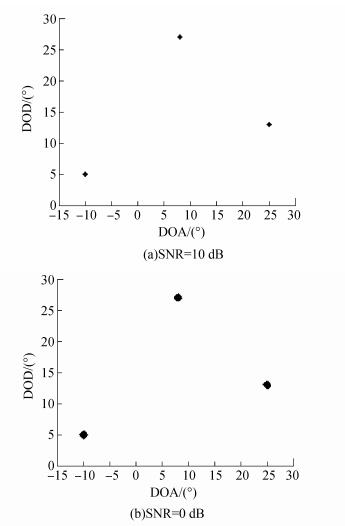
实验1 3个目标相互独立时,分别在信噪比SNR=10 dB和SNR=0 dB的情况下进行100次蒙特卡罗仿真,图 2(a)、(b)分别给出了所提算法的三个目标在SNR=10 dB、SNR=0 dB时的角度估计计算结果。可以看出,所提算法的角度估计结果正确,且在信噪比较低的情况下仍能有效配对。
|
| 图2 文中所提URM算法在不同SNR下的角度估计 Figure 2 Angel estimation of the URM algorithm proposed in the paper versus SNR |
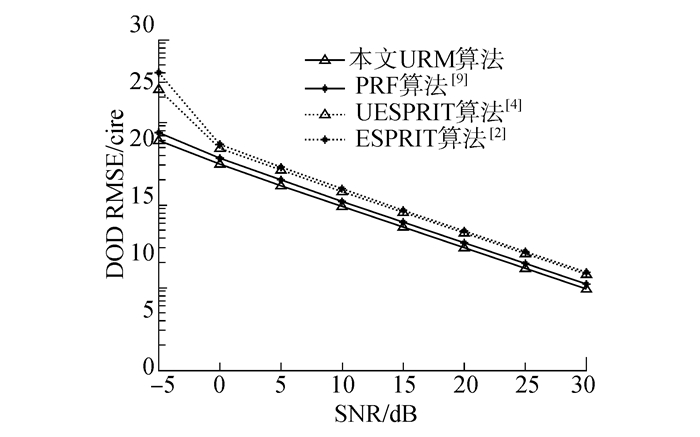
实验2 3个目标相互独立,信噪比SNR由-5 dB变化至30 dB,间隔为5 dB。图 3给出了所提算法与文献[9]中所提出的PRF算法、文献[4]中的酉ESPRIT算法和文献[2]中的ESPRIT算法的RMSE随信噪比的变化趋势。可见,所提算法的偏差更小,更稳定,在信噪比较低的情况下优势明显。
|
| 图3 基于独立信源的均方误差随信噪比的变化 Figure 3 The RMSE for independent sources versus SNR |
实验3 第2个和第3个目标相干时,进行100次蒙特卡罗仿真。图 4分别给出了所提算法与PRF算法[9]、酉ESPRIT算法[4]的角度估计结果。可以看出,所提算法仍能成功估计和配对,其解相干能力得到证实,而文献[9]中的方法配对失效,文献[4]中方法虽具一定的解相干能力,但性能较差。

|
| 图4 基于相干信源的不同算法估计结果 Figure 4 Angel estimations in different algorithms based on independent sources |
实验4 本次实验系统的对比分析了所提算法和文献[4]中算法的解相干能力。本实验中假设存在P=5个远场点目标,分别位于(φ1, θ1)=(-25°, -27°),(φ2, θ2)=(23°, -13°),(φ3, θ3)=(-6°, 5°),(φ4, θ4)=(33°, 21°)和(φ5, θ5)=(-14°, 35°),其中第1个和第2个目标相干,第4个和第5个目标相干。图 5给出了所提算法与文献[4]中的酉ESPRIT算法的RMSE随信噪比的变化趋势。可以看出,所提算法的性能优于文献[4]中的酉ESPRIT算法,结果与实验3中的结果吻合。

|
| 图5 相干信源的均方误差随信噪比的变化 Figure 5 The RMSE for coherent sources versus SNR |
实验5 文中所提URM方法由于采用了酉变换,将协方差矩阵转化为实值矩阵,较之复数矩阵大大降低了运算量,因此其复杂度比文献[4, 9]中的方法都较低。1次复数乘积相当于4次实数乘积,而酉变换将复数运算转换为实数运算,因此大大缩短运算时间。在计算机仿真中,记录下文中所提URM算法和文献[4、9]在相同条件下的计算运行时间进行对比,如图 6所示。

|
| 图6 相同条件下几种算法运行时间结果 Figure 6 Running time in the same conditions |
1) 提出了一种基于双基地MIMO雷达的酉求根MUSIC算法,根据中心Hermite对称矩阵的性质,采用酉变换将协方差矩阵变换为实值矩阵,对实值协方差矩阵进行分解得到噪声子空间,因此降低了计算量。
2) 文中所采用的实值处理与空间平滑具有相似效果,但不会降低阵列孔径,算法的解相干能力得到提升。
3) 对所提算法和以往算法进行了复杂度分析和实验仿真分析,结果表明,该方法不仅在信号相互独立时估计性能优于现有算法,而且具有良好的解相干能力,符合测向的实际要求。
| [1] | FISHLER E, HAIMOVICH A, BLUM R S, et al. MIMO radar:an idea whose time has come[C]//Proceedings of the IEEE Radar Conference. Philadelphia, PA, USA:IEEE, 2004:71-78. |
| [2] | CHEN Duofang, CHEN Baixiao, QIN Guodong. Angle estimation using ESPRIT in MIMO radar[J]. Electronics letters, 2008, 44(12): 770–771. DOI:10.1049/el:20080276 |
| [3] | YANG M L, CHEN B X, YANG X Y. Conjugate esprit algorithm for bistatic MIMO radar[J]. Electronics letters, 2010, 46(25): 1692–1694. DOI:10.1049/el.2010.2306 |
| [4] | ZHENG Guimei, CHEN Baixiao, YANG Minglei. Unitary ESPRIT algorithm for bistatic MIMO radar[J]. Electronics letters, 2012, 48(3): 179–181. DOI:10.1049/el.2011.3657 |
| [5] |
胡彤, 张弓, 李建峰, 等. 非圆实信号MIMO雷达中基于实值ESPRIT的角度估计[J].
航空学报, 2013, 34(8): 1953–1959.
HU Tong, ZHANG Gong, LI Jianfeng, et al. Angle estimation in MIMO radar with non-circular signals based on real-valued ESPRIT[J]. Acta aeronautica et astronautica sinica, 2013, 34(8): 1953–1959. |
| [6] |
文才, 王彤. 单基地MIMO雷达降维酉ESPRIT算法[J].
系统工程与电子技术, 2014, 36(6): 1062–1067.
WEN Cai, WANG Tong. Reduced-dimensional unitary ESPRIT algorithm for monostatic MIMO radar[J]. Systems engineering and electronics, 2014, 36(6): 1062–1067. |
| [7] |
张娟, 张林让, 刘楠. MIMO雷达最大似然波达方向估计方法[J].
系统工程与电子技术, 2009, 31(6): 1292–1294.
ZHANG Juan, ZHANG Linrang, LIU Nan. Maximum likelihood DOA estimation of MIMO radar[J]. Systems engineering and electronics, 2009, 31(6): 1292–1294. |
| [8] | ZHANG Xiaofei, XU Lingyun, XU Lei, et al. Direction of departure (DOD) and direction of arrival (DOA) estimation in MIMO radar with reduced-dimension MUSIC[J]. IEEE communications letters, 2010, 14(12): 1161–1163. DOI:10.1109/LCOMM.2010.102610.101581 |
| [9] | BENCHEIKH M L, WANG Yide, HE Hongyang. Polynomial root finding technique for joint DOA DOD estimation in bistatic MIMO radar[J]. Signal processing, 2010, 90(9): 2723–2730. DOI:10.1016/j.sigpro.2010.03.023 |
| [10] |
徐定杰, 李沫璇, 王咸鹏, 等. 色噪声环境下双基地MIMO雷达收发角度估计[J].
哈尔滨工程大学学报, 2013, 34(5): 623–627.
XU Dingjie, LI Moxuan, WANG Xianpeng, et al. Joint DOD and DOA estimation for bistatic MIMO radar in colored noise[J]. Journal of Harbin engineering university, 2013, 34(5): 623–627. |
| [11] | PESAVENTO M, GERSHMAN A B, HAARDT M. Unitary root-MUSIC with a real-valued eigendecomposition a theoretical and experimental performance study[J]. IEEE transactions on signal processing, 2000, 48(5): 1306–1314. DOI:10.1109/78.839978 |
| [12] | HAARDT M, NOSSEK J A. Unitary ESPRIT:how to obtain increased estimation accuracy with a reduced computational burden[J]. IEEE transactions on signal processing, 1995, 43(5): 1232–1242. DOI:10.1109/78.382406 |



