海洋中存在连续流体分层,当潜体在分层流中运动时受到分层的作用,产生异于均匀环境的流动现象,如在低傅汝德数条件下可以明显观察到尾迹中Lee波的存在。尾迹的这些特征会引起自由面短重力波及表面张力波辐聚辐散,在自由面及自由面附近流场形成持续较长时间的小尺度或微尺度皱褶波纹[1-3]。Miles[4]在Long[5]及Lighthill[6]提出的弥散波模型的基础上用渐近分析的方法研究了不同傅汝德数条件下圆柱绕流形成Lee波,Stevenson[7-8]、Boyer[9-10]用试验的方法,研究了线性分层流中圆柱绕流的流动现象。对分层流体中圆柱绕流的研究较少,尤其缺少基于数值方法的仿真研究,姚志崇等[11]提出了基于多相流混合模型的连续分层流中源致内波的CFD模拟方法,并且对不同傅汝德数条件下拖曳小球的内波增阻进行了数值计算,数值结果与试验结果基本相符。但该研究对分层流中的流场特征并没有进行描述,尤其对这种方法在高傅汝德数条件下的应用并没有进行讨论。
本文基于多相流混合模型对线性分层流中圆柱绕流进行了数值模拟,对低傅汝德数及高傅汝德数下的情形分别进行了讨论。考虑到分层流体的各向异性特性,对不同湍流模型下的流动也展开了讨论。
1 数值方法文中用的无量纲参数:内傅汝德数Fr=U/Nd,雷诺数Re=Ud/v,无量纲时间t'=tU/d。其中U为来流速度,d为圆柱直径,t在数值模拟条件下为计算时间,无量纲时间用t'n表示,在试验条件下为拖曳时间,无量纲时间用t'e表示,v为流体的运动粘性系数,N为浮频率,N=(g△ρ/ρ0H)1/2,其中g为重力加速度,其他参数含义如图 1所示。
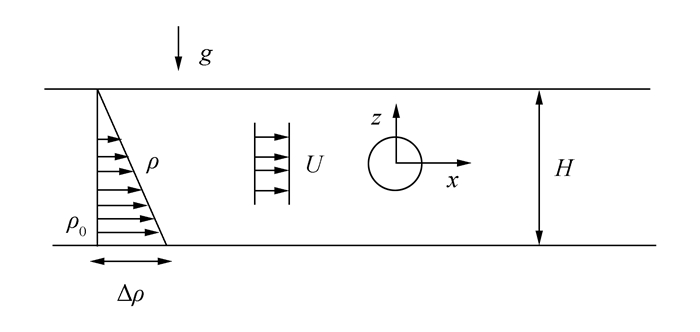
|
| 图1 计算域示意图 Figure 1 Domain diagram |
混合模型假定了各相在短空间尺度上局部的平衡,通过求解混合相的动量、连续性方程,次相的体积分数方程来实现对互相贯通各相流动的数值求解。第p次相的体积分数通过解第p次相的连续方程获得:
| $ \frac{\partial }{{\partial t}}\left( {{\alpha _p}{\rho _p}} \right) + \nabla \cdot \left( {{\alpha _p}{\rho _p}{\boldsymbol{v}_m}} \right) = 0 $ | (1) |
式中:vm是各相速度的平均值,在本例中各相具有相同的速度;αp为第p相的体积分数。
设运动粘性系数相同密度不同的两种水分别为主相和次相,通过指定不同垂向位置各相的体积分数,可以实现连续分层。两种相的体积分数分布如下(ρ2 > ρ1):
| $ \left\{ \begin{array}{l} {V_1} = \left( {z + H/2} \right)/H\\ {V_2} = 1 - \left( {z + H/2} \right)/H \end{array} \right. $ | (2) |
式中:ρ1、ρ2分别为主相及次相的密度;V1、V2分别为主相及次相的体积分数。各个位置处的密度:
| $ \rho = \left( {{\rho _1} - {\rho _2}} \right)z/H + \left( {{\rho _1} + {\rho _2}} \right)/2 $ | (3) |
这时分层为线性分层。
利用商业软件Fluent进行数值模拟,分层的设置通过式(2)以udf形式实现。由于流体域比较简单,网格不再赘述,二维及三维的网格规模分别为15万、150万。利用RANS方法计算时通过PISO求解器进行计算,利用LES方法计算时通过SIMPLE求解器进行计算,时间及空间的离散均采用二阶离散格式。为了与试验条件保持一致,流体域的高度设置为20 cm,圆柱直径设置为2.4 cm,入口及出口边界足够远。ρ0=998 kg/m3,△ρ=20.58 kg/m3,此时N=1 rad/s。
理论认为,当傅汝德数较小时,尾迹中会出现明显的Lee波,当傅汝德数较大时,尾迹中的涡结构起主导作用。通过试验[9]发现,当Fr=0.4时,尾迹中Lee波已经不是尾迹的主要特征,这时尾迹中出现明显的涡结构。规定当Fr > 0.4时为高傅汝德数,Fr < 0.4时为低傅汝德数。对低傅汝德数下的情形,可通过RANS方法予以模拟实现,对高傅汝德数下的情形,则应通过LES方法实现。在高傅汝德数条件下,尾迹中湍流脉动成份的水动力作用会增强,而雷诺平均的方法抹去了瞬时脉动成份,因此无法获得满意的计算结果,LES方法则没有这种弊端。主要工况设置如表 1, 数值结果均与Boyer[9]的试验结果进行对比。
| 编号 | 傅汝德数 | Fr | Re | 流动状态 |
| 1 | 低傅汝德数 | 0.018 | 12 | 层流 |
| 2 | 0.08 | 1 500 | 湍流 | |
| 3 | 高傅汝德数 | 0.88 | 480 | 湍流 |
| 4 | 1.77 | 960 | 湍流 |
对Fr=0.018,Re=12的分层流圆柱绕流进行数值模拟。数值及试验条件下的流线如图 2所示,可以看出数值结果与试验结果基本一致,不同的是在数值条件下,在圆柱的后方形成对称的波动图案,这种图案是由于圆柱的体积效应形成的Lee波,Lee波波峰线只有上下对称的两列,在流动方向上没有形成新的Lee波。

|
| 图2 Fr=0.018,Re=12时流线图对比 Figure 2 Streamline for Fr=0.018, Re=12 |
图 3为数值条件下x=±7.5d处,t'n=11、22、54时的速度剖面曲线。绕流图形表明上游速度剖面曲线速度波峰值及下游速度剖面的速度波谷值均随时间的增大而增大。在分层流中形成的流动是一种准稳态的现象,在不同的时刻圆柱上下游的速度剖面略有不同,在试验条件下也观察到了相同的规律。图 4为试验条件下,x=±7.5d处t'e=21、42、62时的速度剖面曲线。下游速度剖面曲线并没有作出相对速度大于1的两段,而研究表明[9]下游速度剖面曲线在轴线附近是一段相对速度小于1的波谷,在紧邻波谷段的上下两侧是相对速度大于1的两段波峰,形状与数值条件下的结果一致,数值结果与试验结果定性一致。
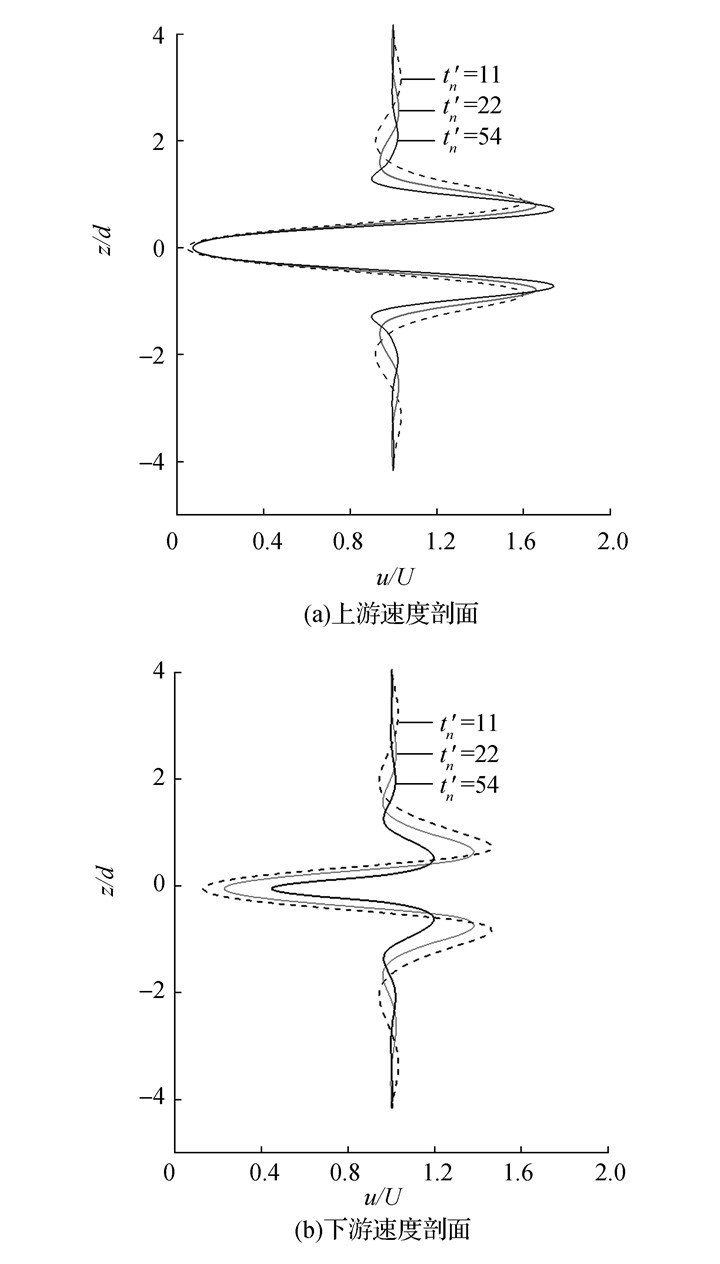
|
| 图3 数值条件下不同时刻圆柱绕流上下游速度剖面图 Figure 3 Numerical results of velocity profiles upstream and downstream of cylinder |
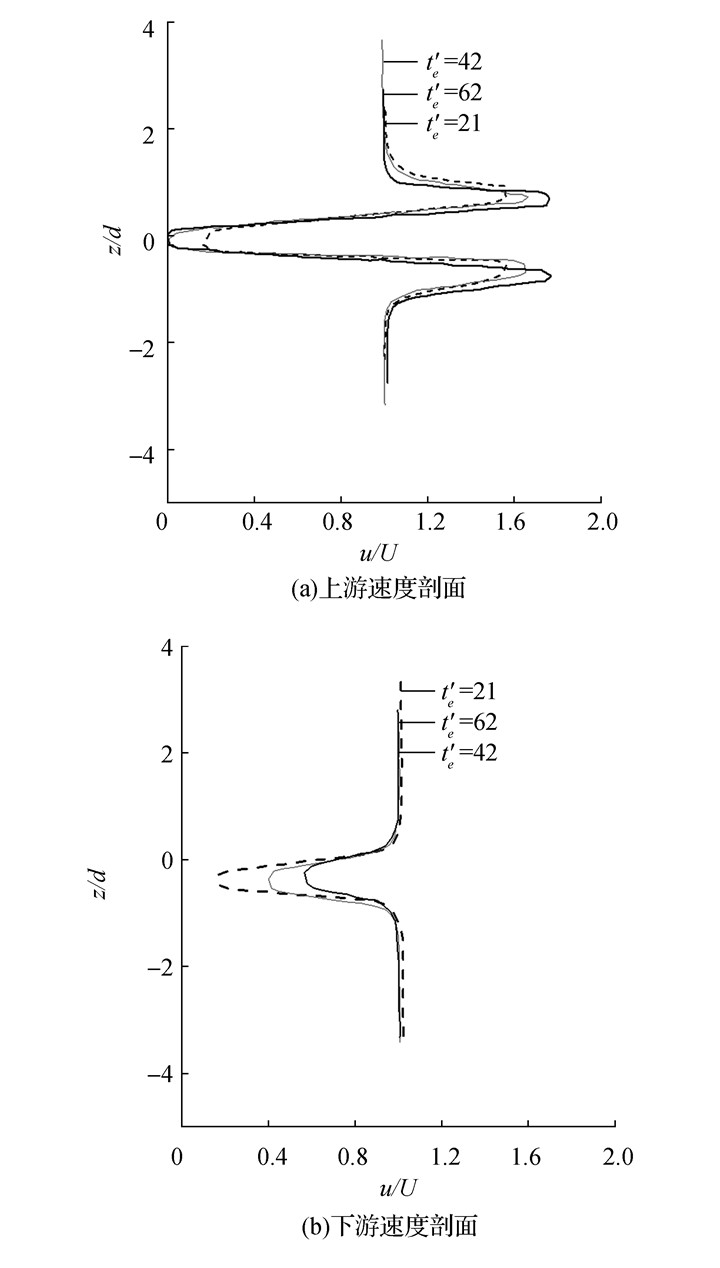
|
| 图4 试验条件下不同时刻圆柱绕流上下游速度剖面图 Figure 4 Experimental results of velocity profiles upstream and downstream of cylinder |
数值时间并不能与试验时间相对应,但在某数值时刻,若上游速度剖面曲线与某一试验时刻结果相对应,同时刻下游速度剖面数值结果也应与同试验时刻的结果对应。图 5为两对时刻下数值及试验条件下上下游速度剖面曲线(x=±7.5d),数值时刻t'n=15、67的数值结果,分别与试验时刻为t'e=21、62的试验结果进行对比。速度曲线的极值代表该剖面处速度的最大值或最小值,在上游速度剖面曲线吻合的时刻,下游速度剖面基本吻合,两组结果中波谷值的相对误差最大为2%,数值结果与试验结果定量基本吻合,基于混合模型模拟低傅汝德分层流流动是行之有效的方法。
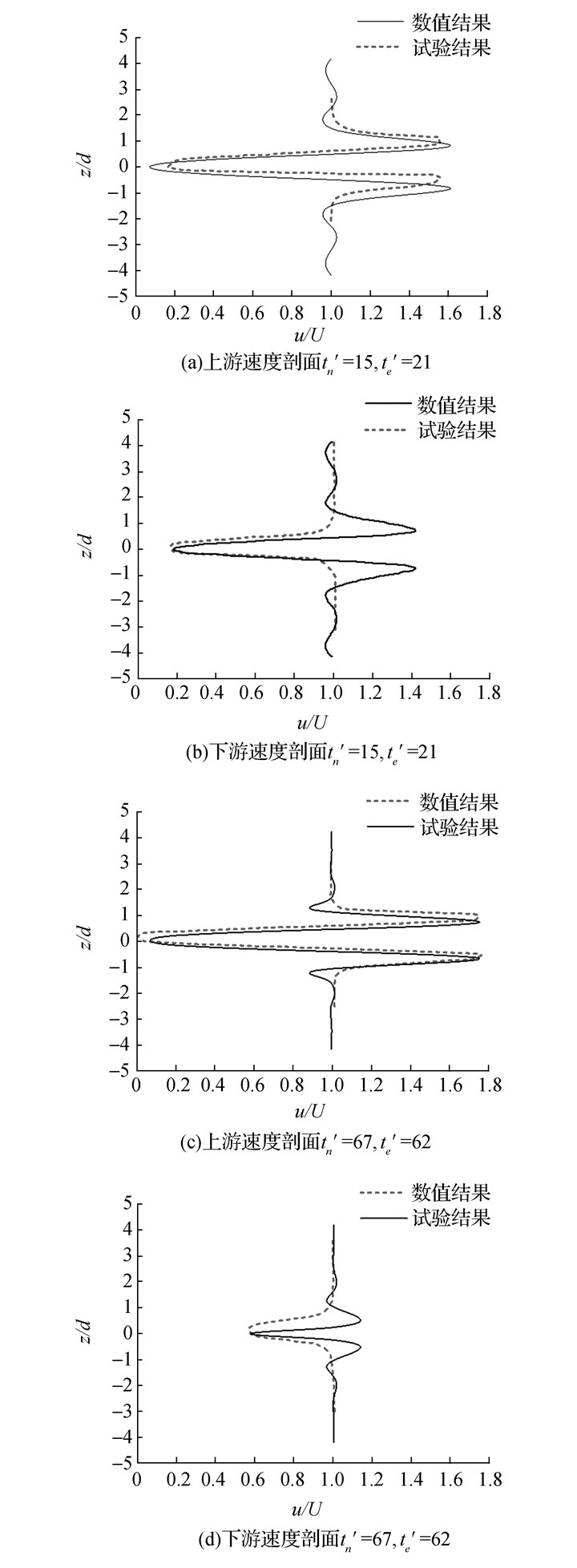
|
| 图5 数值及试验条件下上下游速度剖面对比图 Figure 5 Velocity profiles upstream and downstream of cylinder under numerical and experimental conditions |
在层流模型下同时改变速度及特征长度,保持傅汝德数不变为0.08,数值模拟雷诺数为240、540、960、1 500、6 000条件下的分层流圆柱绕流,发现当Re≥240时尾迹特征都与Fr=0.17,Re=98.7条件下的尾迹特征类似,在轴线附近流线以葫芦状形状出现,而且尾迹中伴随有Lee波的产生。由于缺少较高雷诺数下的试验结果,而低雷诺数条件下基于层流模型的模拟结果与相应试验结果吻合得很好,不妨结合湍流度(初始扰动大小)以雷诺数为1 500时基于层流模型的模拟结果为参考,对不同湍流模型下的圆柱绕流进行数值模拟,以推敲基于各个湍流模型模拟分层湍流的合理性。不同湍流模型下的圆柱绕流尾迹如图 6所示。可以发现对于尾迹中的葫芦状流线特征在RSM模型下的结果与层流模型下的结果最为贴近;SST模型下的结果比较贴近;k-ε模型下的结果与层流模型下的结果相差最远。对于尾迹中的Lee波特征在RSM模型下的结果与层流模型下的结果符合得很好;k-ε模型下的结果只有一对Lee波;SST模型下Lee波很快衰减,只有两对。事实上,湍流模型均建立在涡粘系数各向同性的假设上,在分层流体中,密度并不是各向同性的,因此用不受各向同性假设限制的RSM模型是合理的。值得一提的是图 6中RSM模型条件下的结果对近壁面的处理用的是壁面函数的方法,同样条件下用增强壁面函数处理的方法,结果与SST模型下的结果类似。对于k-ε模型及SST模型用壁面函数的方法与用增强壁面函数处理的方法结果并没有什么不同。在Re=6 000时结论与Re=1 500时相同。
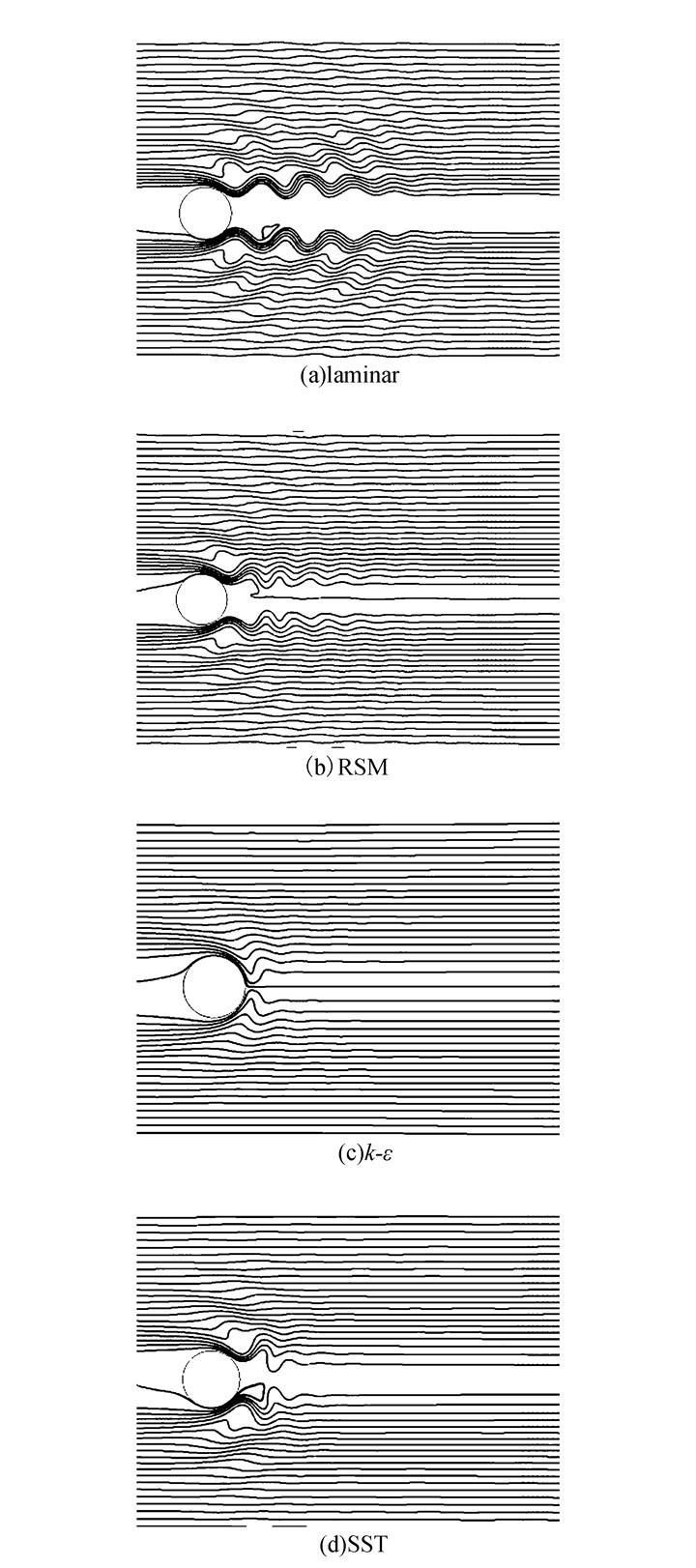
|
| 图6 不同流动模型下的模拟结果 Figure 6 The numerical results under different viscous models |
图 7为Fr=0.88,Re=480条件下圆柱绕流的试验结果及数值结果。二者尾迹流线形状大致趋势相同,在圆柱的后方都有一对涡的出现,在距离圆柱中心6倍直径处形成第一个波包,在16倍直径处形成第二个波包。不同的是第一个波包及第二个波包的大小较试验结果小些,事实上这两处波包的大小是随时间不断震荡变化的,数值结果与试验结果基本吻合。
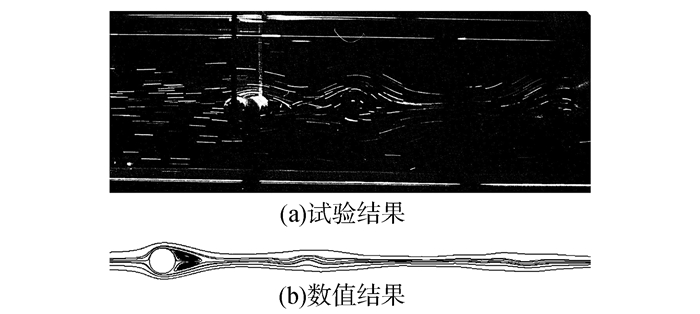
|
| 图7 圆柱绕流试验结果及数值结果(Fr=0.88,Re=480) Figure 7 Experimental and numerical results for Fr=0.88, Re=480 |
图 8为Fr=1.77,Re=960条件下圆柱绕流的试验结果及数值结果。在这种条件下尾迹的典型特征是尾迹进入了完全湍流的状态,且在靠近圆柱处尾迹有很强的涡结构。显然数值方法成功模拟出了这些特征。
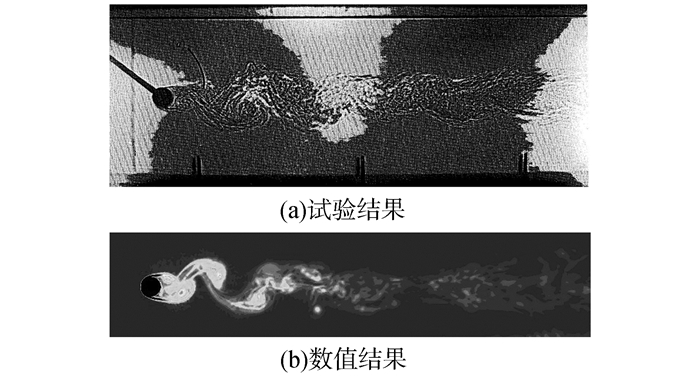
|
| 图8 圆柱绕流试验结果及数值结果(Fr=1.77,Re=960) Figure 8 Experimental and numerical results for Fr=1.77, Re=960 |
基于多相流混合模型,对线性分层流体中圆柱绕流进行了数值模拟,并且讨论了利用这种方法数值研究分层流体尾迹的可行性。
1)当Fr=0.018,Re=12时,尾迹流线图数值结果与试验结果定性一致,x=±7.5d处的上下游速度剖面曲线随时间的变化规律定性一致,数值结果与试验结果上下游速度剖面定量上对应,峰值的误差在2%以内。基于多相流混合模型,利用RANS方法可以很好地模拟低傅汝德数条件下的分层流尾迹。
2)在湍流范围内,用不受各向同性假设限制的RSM模型模拟分层流动是最合理的,而且对近壁面的处理要用壁面函数的方法。
3)利用LES对Fr=0.88及Fr=1.77条件下的圆柱绕流进行模拟,尾迹特征与试验条件下的尾迹特征基本相符,基于多相流混合模型,利用LES可以很好地模拟高傅汝德数条件下的分层流尾迹。
基于多相流混合模型建立了傅汝德数从低到高,雷诺数从层流至湍流各个取值段模拟连续分层流动的数值方法可以有效地模拟水下航行潜体的尾迹,从而为水下航行潜体的探测研究提供依据。
| [1] |
王进, 尤云祥, 胡天群, 等. 密度分层流体中不同长径比拖曳潜体激发内波特性实验[J].
科学通报, 2012, 57(8): 606–617.
WANG Jin, YOU Yunxiang, HU Tianqun, et al. The characteristics of internal waves excited by towed bodies with different aspect ratios in a stratified fluid[J]. Chinese science bulletin, 2012, 57(8): 606–617. DOI:10.1360/972011-1361 |
| [2] | OUCHI K. Recent trend and advance of synthetic aperture radar with selected topics[J]. Remote sensing, 2013, 5(2): 716–807. DOI:10.3390/rs5020716 |
| [3] | SPEDDING G R. Wake signature detection[J]. Annual review of fluid mechanics, 2014, 46: 273–302. DOI:10.1146/annurev-fluid-011212-140747 |
| [4] | MILES J W, HUPPERT H E. Lee waves in a stratified flow. Part 2. Semi-circular obstacle[J]. Journal of fluid mechanics, 1968, 33(4): 803–814. DOI:10.1017/S0022112068001680 |
| [5] | LONG R R. Some aspects of the flow of stratified fluids:Ⅲ. continuous density gradients[J]. Tellus, 1955, 7(3): 341–357. DOI:10.1111/tus.1955.7.issue-3 |
| [6] | LIGHTHILL M J. On waves generated in dispersive systems to travelling forcing effects, with applications to the dynamics of rotating fluids[M]//FROISSART P M. Hyperbolic Equations and Waves. Berlin Heidelberg:Springer, 1970:124-152. http://link.springer.com/10.1007/978-3-642-87025-5 |
| [7] | STEVENSON T N. Some two-dimensional internal waves in a stratified fluid[J]. Journal of fluid mechanics, 1968, 33(4): 715–720. DOI:10.1017/S0022112068001631 |
| [8] | STEVENSON T N, CHANG W L, LAWS P. Viscous effects in Lee waves[J]. Geophysical & astrophysical fluid dynamics, 1979, 13(1): 141–151. |
| [9] | BOYER D L, DAVIES P A, FERNANDO H J S, et al. Linearly stratified flow past a horizontal circular cylinder[J]. Philosophical transactions of the royal society of London A:mathematical, physical and engineering sciences, 1989, 328(1601): 501–528. DOI:10.1098/rsta.1989.0049 |
| [10] | XU Yunxiu, FERNANDO H J S, BOYER D L. Turbulent wakes of stratified flow past a cylinder[J]. Physics of fluids, 1995, 7(9): 2243–2255. DOI:10.1063/1.868472 |
| [11] | 姚志崇, 赵峰, 洪方文.连续分层流中源致内波的CFD模拟方法[C]//第二十三届全国水动力研讨会暨第十届全国水动力学学术会议论文集.西安, 2011. |



