随着海洋开发进程的加快,水下设备的研发越来越受到重视[1],基于试压容器的深海环境模拟实验装置可在实验室条件下模拟深海环境,为研制水下设备提供便捷、可靠的陆地实验平台,对缩短设备研究周期、降低研制成本、减少海试造成意外损失等具有重要的研究意义和实际价值[2]。
本文针对水下设备工作在不同水深的需求,研制了一套模拟压力可在大范围连续变化的深海环境模拟实验装置。针对系统固有惯性以及闭环系统延迟特性的影响问题,提出一种对目标函数进行相位补偿的方法,以改善系统压力动态控制性能;针对模拟实验装置内压力突降的问题,研究了一种压力快速补偿方法。通过对模拟实验装置进行相关实验,验证本文所提出方法的可行性与有效性。
1 深海环境模拟实验装置总体方案 1.1 深海环境模拟实验装置组成分析深海环境模拟实验装置需要能够模拟水下设备做复杂升沉运动所对应承压环境的变化,同时当舱体类实验试件爆破造成系统压力突降时应使系统压力快速恢复。针对这些要求,本文研制了一套深海环境模拟实验装置,其组成如图 1所示。本实验装置的基本工作原理为:控制器根据目标压力曲线,控制压力动态控制模块,升高试压容器内压力,当试压容器内某个试验舱爆炸时,试压容器内压力陡降,此时压力快速补偿模块启动,使其快速升压,达到接近爆炸前的压力。

|
| 图1 深海环境模拟实验装置组成图 Figure 1 The composition diagram of deep sea environment simulation experiment device |
压力动态控制模块的作用是模拟不同水深的外部环境压力。文献[3]研制了一套压力控制模块,该模块的压力控制精度较高,但由于受电机、减速器和丝杠等启动惯性的影响,其频响速度较慢。文献[4]基于电液比例阀设计的压力动态控制方案,其仿真结果能满足设计指标,但没有考虑深海环境模拟实验装置通常使用水介质,易造成电液比例阀内部锈蚀,从而影响其控制性能和使用寿命。
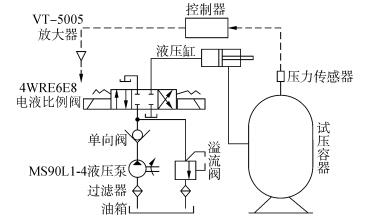
针对上述问题,本文研究并设计了压力动态控制方案。针对文献[3]中电机驱动方式频响速度慢的问题,本文改进为液压驱动方式;针对文献[4]中电液比例阀不适于水介质的问题,本文提出在电液比例阀出油口和试压容器之间串联一只液压缸,通过其活塞阻隔作用实现油水转换的解决方案。本文设计的压力动态控制模块工作原理如图 2所示。
|
| 图2 压力动态控制模块的工作原理图 Figure 2 The working schematic diagram of pressure dynamic control module |
图 2中,压力动态控制模块工作过程为:电液比例阀根据放大器接收信号的幅值和极性调节阀口的开度和方向,控制油路的流量和方向,进而控制水路中进出试压容器的液体流量和方向,实现模拟实验装置的压力动态控制。
本文基于PID控制算法进行动态压力补偿控制,具体如下:
1)推导传递函数
基于文献[1]的方法,通过图 2压力动态控制模块的工作原理图,结合本文所选择的具体元件,推导出压力动态控制模块的开环传递函数为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;{G_k}\left( s \right) = \frac{{{P_a}\left( s \right)}}{{{U_0}\left( s \right)}} = \\ \frac{{{K_{sv}}{K_0}{E_V}{A_2}/{A_1}{V_0}}}{{s\left( {\frac{{{s^2}}}{{\omega _{sv}^2}} + \frac{{2{\xi _{sv}}}}{{{\omega _{sv}}}}s + 1} \right)\left( {\frac{{{s^2}}}{{\omega _y^2}} + \frac{{2{\xi _y}}}{{{\omega _y}}}s + 1} \right)}} \end{array} $ | (1) |
式中:Pa(s)为压力模块输出量;U0(s)为控制电压信号;Ksv为电液比例阀的流量增益,m3/(s·A);K0为比例放大器增益,A/V;EV为液体的体积弹性模量;A1为液压缸的有效作用面积,m2;A2为活塞杆面积,m2;V0为试压容器容积,m3;ωsv为电液比例阀固有频率,rad/s;ξsv为电液比例阀阻尼比;ωy为液压缸一负载质量系统的固有频率,rad/s;ξy为液压缸一负载质量系统的阻尼比。
压力动态控制模块的闭环传递函数为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{G_b}\left( s \right) = \\ \frac{{{K_0}{K_{sv}}{E_V}{A_2}/{A_1}{V_0}}}{{\left( {\frac{{{s^2}}}{{\omega _{sv}^2}} + \frac{{2{\xi _{sv}}}}{{{\omega _{sv}}}}s + 1} \right)\left( {\frac{{{s^2}}}{{\omega _y^2}} + \frac{{2{\xi _y}}}{{{\omega _y}}}s + 1} \right) + {K_0}{K_{sv}}{E_V}{A_2}/{A_1}{V_0}}} \end{array} $ | (2) |
式中:Ky为压力传感器比例系数。
2)确定PID控制器参数
本文参考文献[14]的方法,通过式(2)建立仿真模型,并采用Simulink Design Optimization工具对PID控制器参数进行寻优,最终得到参数的具体值为:Kp=3.50、Ki=0.01、Kd=2.20。
1.3 压力快速补偿方法研究压力突降是影响深海环境模拟实验装置工作性能的一个不确定因素,舱体类试件在爆破时造成试压容器内压力突降,为模拟真实海洋环境的要求,希望压力突降后能够快速恢复。对于压力突降后快速恢复问题,国内外研究不多。文献[5]通过闭环机械加载进行压力突降后快速补偿,但受电机启动特性和机械惯性影响,实际补偿速度慢。
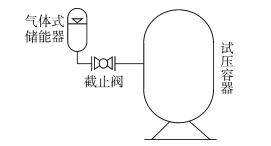
针对以上问题,本文首先对压力补偿源进行研究。文献[6]针对工程机械液压系统在复杂工况时受较大压力冲击问题,提出在液压回路中安装气体式蓄能器对压力冲击进行吸收,仿真结果表明,选用合适参数的气体式蓄能器可对压力冲击具有良好的吸收效果,但该方式存在如何优选蓄能器的问题。本文借鉴文献[6]的思路,采用蓄能器在压力突降后快速补偿,压力快速补偿方法工作原理如图 3。
|
| 图3 压力快速补偿方法工作原理图 Figure 3 The working schematic diagram of pressure fast compensation method |
压力快速补偿方法的工作原理为:蓄能器气腔内为高压气体,当试压容器内试件发生爆破造成系统压力突降时,在气腔和液腔压差的作用下,蓄能器液腔内的液体快速补充给试压容器,使得系统压力迅速恢复。
2 压力快速补偿方法关键技术研究本节分析蓄能器的数学模型,通过仿真研究其主要参数与吸收压力冲击效果之间的关系,以提高压力快速补偿性能。
2.1 蓄能器系统模型分析试压罐内压力突变与试验舱容积和试压罐容积相关。即,试验舱容积越大,压力突变值越大,试压罐容积越大,压力突变值越小。因此,单纯取试压罐容积突变来研究深海环境模拟实验装置的压力补偿能力不能充分说明问题。本文选取压力突变来验证本文研制的深海环境模拟实验装置的压力补偿能力。
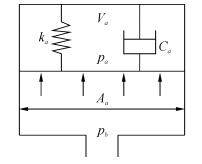
已有文献表明:初始压力p0越大,蓄能器的快速补偿能力越好,但是气体体积V0并不是越大越好,V0的优选值涉及到输出流量振荡、吸收压力耗时等因素。为了分析蓄能器在压力快速补偿方法中的性能,本节研究蓄能器的主要结构参数V0和工作参数p0对其性能的影响。文献[7]指出,气体式蓄能器为一个模型复杂的二阶系统,影响其工作性能的参数较多,对此,本文采用机理分析法对其工作原理进行分析[8],参考文献[9, 19]简化气体式蓄能器本体模型,如图 4所示。
|
| 图4 气体式蓄能器等效力学模型 Figure 4 The equivalent mechanical model of gas accumulator |
本文基于牛顿第二定律,对蓄能器液腔对蓄能器模进行力学分析,得到以蓄能器液腔内液体为研究对象的数学模型[10, 15-16]:
| $ \left( {{P_a}-{P_b}} \right){A_a} = \frac{{{m_a}\frac{{{{\rm{d}}^2}{V_a}}}{{{\rm{d}}{t^2}}} + {B_b}\frac{{{\rm{d}}{V_a}}}{{{\rm{d}}t}} + {C_a}\frac{{{\rm{d}}{V_a}}}{{{\rm{d}}t}} + {k_a}{V_a}}}{{{A_a}}} $ | (3) |
式中:Aa为蓄能器内腔的横截面积;pa为试件爆破时蓄能器气腔内气体的压强;pb为试件爆破时蓄能器液腔的压强;Va为试件爆破时蓄能器气腔内气体的体积;ma为蓄能器液腔内液体的质量;Bb为液腔中液体的阻尼系数;Ca为气体阻尼系数[11];ka气体的等效弹簧刚度。
对式(3)进行拉氏变换,得到气体式蓄能器的传递函数:
| $ G\left( s \right) = \frac{{{Q_1}\left( s \right)}}{{{P_b}\left( s \right)}} = \frac{{A_a^2}}{{{k_a} + k{p_0}A_a^2/{V_0}}}\frac{{\omega _n^2s}}{{{s^2} + 2\xi {\omega _n}s + \omega _n^2}} $ | (4) |
式中:Q1(s)为蓄能器液腔的液体输出流量,Pb(s)为蓄能器液腔压力,k为气体多变指数,ka为气体等效刚度系数。
本文蓄能器工作时其液腔放液速度快,近似为绝热过程,因此取k=1.4[12];刚度系数ka等效为气体压强变化量与体积变化量的比值,其表达式为[12]
| $ {k_a} = \frac{{\Delta F}}{{\Delta {x_p}}} = \frac{{\Delta {p_a}{A_a}}}{{\Delta {V_a}/{A_a}}} $ | (5) |
根据蓄能器各结构参数之间的关系,对ka表达式进行整理得:
| $ {k_a} = \frac{{k{\rm{ \mathsf{ π} }}{\mathit{d}^4}{p_a}}}{{16{V_0}}}{\left( {\frac{{{p_a}}}{{{p_0}}}} \right)^{\frac{1}{k}}} $ | (6) |
分析式(4)、(6),蓄能器系统的固有特性与其横截面积Aa、初始充气压力p0、初始充气体积V0和系统工作压力p2等参数有关。
2.2 蓄能器系统仿真研究本文的研究背景是深海环境(水深大于4 000 m),基于上述分析,压力罐加压应该大于40 MPa。考虑到40 MPa压力陡降时进行快速补偿有一定的危险性,同时由于试验条件有限(已有的压力罐最大耐压7 MPa),为了探讨本文所提出方法的可行性,本文在仿真和实验中都选择4.5 MPa (对应水深450 m)。
综合考虑深海环境模拟实验技术研究现状,并结合水下作业设备研制工作的实际应用需求,爆破试件的容积约占整体容积的1%左右,本系统试压器总容积是253 L,因此本文研制的目标爆破试件容积ΔV为0.3 L,爆破压力pb为4.5 MPa,应用MATLAB软件对公称容积V0分别为4、6.3、10 L的蓄能器进行仿真。参考文献[11, 17-18],蓄能器气腔的初始充气压力p0设为4.0 MPa,通过仿真分析蓄能器公称容积V0对于其吸收压力冲击效果的影响。
为建立蓄能器系统的仿真模型,本文将式(6)代入式(4),得到蓄能器系统的阻尼系数ξ和无阻尼固有频率ωn的表达式:
| $ \xi = \frac{{8{\rm{\pi }}{\mu _a}\frac{{{V_0}}}{{{A_a}}}{{\left( {\frac{{{p_0}}}{{{p_a}}}} \right)}^{\frac{1}{k}}} + 8{\rm{\pi }}\mu \left[{{V_0}-{{\left( {\frac{{{p_0}}}{{{p_a}}}} \right)}^{\frac{1}{k}}}} \right]/{A_a}}}{{2\sqrt {\left[{kA_a^2{{\left( {\frac{{{p_0}}}{{{p_a}}}} \right)}^{\frac{1}{k}}}{p_a}V_0^{-1} + \frac{{k{p_0}A_a^2}}{{{V_0}}}} \right]\left[{{V_0}-{{\left( {\frac{{{p_0}}}{{{p_a}}}} \right)}^{\frac{1}{k}}}{V_0}} \right]\rho } }} $ | (7) |
| $ {\omega _n} = \sqrt {\frac{{kA_a^2{{\left( {\frac{{{p_a}}}{{{p_0}}}} \right)}^{\frac{1}{k}}}{p_a}V_0^{- 1} + \frac{{k{p_0}A_a^2}}{{{V_0}}}}}{{\left[{{V_0}-{{\left( {\frac{{{p_a}}}{{{p_0}}}} \right)}^{\frac{1}{k}}}{V_0}} \right]\rho }}} $ | (8) |
参考蓄能器标准系列手册,并根据压力快速补偿方法的实际参数,对不同公称容积时蓄能器的ξ、ωn进行求解,得到数据如表 1所示。
| 容积/L | d/m | Aa/m2 | ξ | ωn/rad |
| 4 | 0.152 | 1.81×10-2 | 0.471 | 706 |
| 6.3 | 0.152 | 1.81×10-2 | 0.747 | 445 |
| 10 | 0.219 | 3.76×10-2 | 0.092 | 583 |
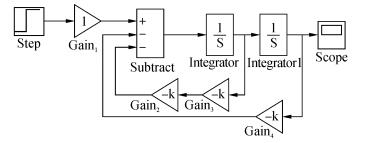
根据式(2)在MATLAB软件Simulink环境中建立蓄能器系统吸收压力冲击的仿真模型,如图 5所示,并将表 1的数据代入图 5对应位置。
|
| 图5 蓄能器系统仿真模型 Figure 5 Accumulator system simulation model |
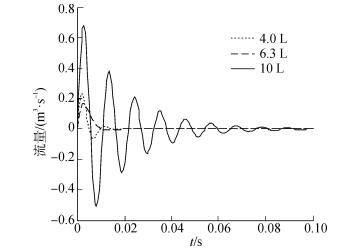
图 5中,输入量单位阶跃信号Step表示为试件发生爆破时系统压力突降值,其值的选取是基于作者之前的实验数据,输出量表示压力快速补偿模块工作时蓄能器液腔流量Q1的变化。Gain1为蓄能器液腔中液体质量的倒数1/ma,Gain2为Ba/ma,Gain3对应为Ca/ma,Gain2与Gain3之和即为蓄能器传递函数中的2ζωn,Gain4表示ka+kp0Aa/V0,即为系统无阻尼固有频率的平方ωn2。进行仿真实验,得到横截面积Aa和初始充气压力p0相同而公称容积不同的蓄能器吸收压力冲击效果的曲线,如图 6所示。
|
| 图6 不同公称容积蓄能器吸收压力冲击效果 Figure 6 The absorbing pressure impact effect of different nominal volume accumulator |
分析图 6公称容积V0为4.0 L、6.3 L、10 L的曲线可知,随着公称容积V0增大,蓄能器系统的响应速度减慢,但稳定性增强,输出流量的振荡情况减小,当V0从4.0 L依次增加至6.3 L和10 L时,蓄能器吸收相同压力冲击所耗时间分别为0.015 s、0.013 s、0.10 s。可以看出,V0并不是越大越好,也不是越小越好,对于本文深海环境模拟实验装置的具体参数,当V0为6.3 L时,蓄能器具有良好的吸收压力冲击效果,输出流量的振荡最小,吸收压力冲击的时间最短。基于仿真结果,本文选定V0为6.3 L的气体式蓄能器。
3 实验研究为了验证本文设计的压力动态控制模块和压力快速补偿方法的可行性,验证在试压容器和蓄能器之间串联液压缸的压力快速补偿的效果,作者搭建了深海环境模拟实验装置进行相关实验研究。
3.1 压力动态模拟实验研究本文搭建了深海环境模拟实验装置如图 7所示。

|
| 图7 深海环境模拟实验装置 Figure 7 Deep sea environment simulation experiment device |
为了验证本文研制的深海环境模拟实验装置模拟水下设备工作在不同水深时的水压变化情况,参考我国“蛟龙号”载人潜器7 000 m海试时的下潜速度(约0.84 m/s)[13],本文设计斜率为0.01 MPa/s斜坡函数跟踪实验。考虑到水下装备因地形限制或工作需求,可能往复升沉运动,本文又设计了频率为0.025 Hz、0.05 Hz、0.1 Hz的正弦曲线跟踪实验。
1)斜坡函数跟踪效果
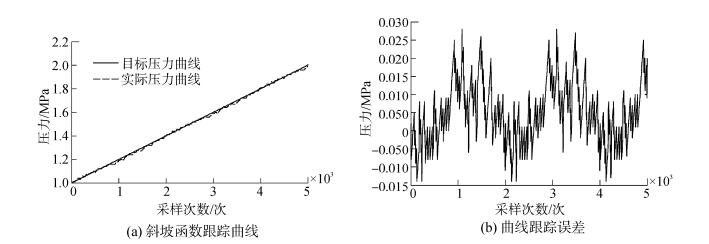
压力动态控制模块跟踪斜率为0.01 MPa/s斜坡函数的实际压力曲线及其跟踪误差如图 8所示。
|
| 图8 斜坡函数跟踪曲线及跟踪误差 Figure 8 Slop function tracking curves and tracking error |
由图 8可知,跟踪绝对误差小于±0.02 MPa (对应水深±2 m),能保持目标曲线特征,反映出压力动态控制模块可较好地跟踪0.01 MPa/s的斜坡函数。
2)正弦曲线跟踪效果
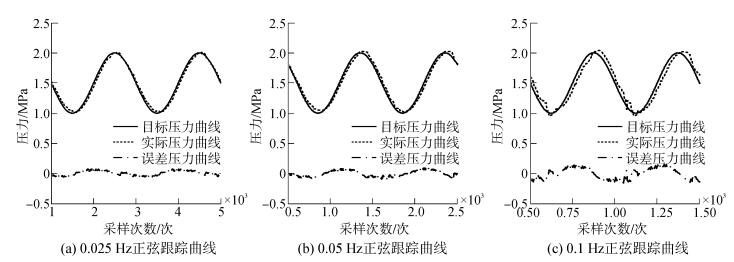
频率为0.025、0.05、0.1 Hz,幅值为0.5 MPa的正弦实际跟踪曲线及跟踪误差如图 9所示。
|
| 图9 正弦信号跟踪曲线及跟踪误差 Figure 9 Sinusoidal signal tracking curves and tracking error |
分析图 9可知,压力动态控制模块可以较好地跟踪目标曲线的形状特征。斜坡函数和正弦曲线跟踪实验结果,验证了本文研制的压力动态控制模块的可行性。实验过程中电液比例阀工作良好,系统升压过程稳定,表明本文提出在液压回路中串联液压缸来实现油水转换方案的有效性,将图 9不同频率正弦曲线跟踪数据整理为表 2。
| 曲线频率/Hz | 幅值超调/MPa | 跟踪误差/MPa | 相位滞后/(°) | 时间延迟/s |
| 0.025 | 0 | 0.05 | 4 | 0.44 |
| 0.05 | 0.05 | 0.1 | 8 | 0.44 |
| 0.1 | 0.1 | 0.18 | 15 | 0.42 |
分析表 2数据,目标曲线频率分别为0.025 Hz、0.05 Hz、0.1 Hz时,最大跟踪误差分别为0.05 MPa、0.10 MPa、0.18 MPa,相位滞后分别为4°、8°、15°。分析其原因主要是受液压、机械系统的惯性以及闭环系统延迟特性影响,造成跟踪曲线相位滞后,对此,本文接下来研究相位滞后问题。
3.2 针对相位滞后的改进算法及其实验验证本文目标曲线为Y1=Asin2πft+B,根据图 9实验可知,实际跟踪曲线表达式为Y1=Asin (2πft+θ)+B,即实际跟踪曲线与目标曲线之间存在θ的相移,θ具体数值可由实验得到的时间延迟t1、目标函数频率f来求得,三者的关系为θ=2πft1。为了得到理想的压力跟踪曲线,本文根据目标函数的频率f特征,对上述目标函数表达式Y1补偿一定的相角-θ,得到经处理后的表达式Y2=Asin (2πft-θ)+B,控制系统根据表达式Y2进行控制,从而实现相位补偿的目的。
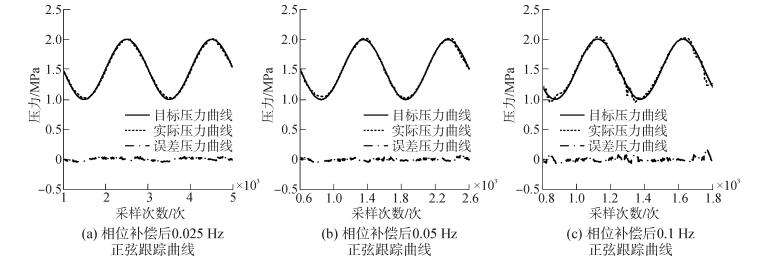
根据表 2中跟踪曲线的参数,由θ=2πft1得到本文频率为0.025 Hz、0.05 Hz、0.1 Hz时目标曲线的补偿相角θ分别为π/45、2π/45、π/12,根据Y2进行实验,如图 10所示。
|
| 图10 相位补偿后正弦跟踪曲线及跟踪误差 Figure 10 The sine tracking curves after phase compensation and tracking error |
为了方便分析相位补偿算法的实际效果,将图 9和图 10中,跟踪不同频率正弦曲线、有无相位补偿算法的跟踪效果整理成表 3。
| 曲线频率/Hz | 最大跟踪误差/MPa | 改善效果/% | |
| 无补偿 | 有补偿 | ||
| 0.025 | 0.05 | 0.02 | 150 |
| 0.05 | 0.10 | 0.04 | 150 |
| 0.1 | 0.18 | 0.07 | 152 |
分析表 3,有相位补偿时,对应0.025 Hz、0.05 Hz、0.1 Hz频率的正弦曲线,最大跟踪误差分别为0.02 MPa、0.04 MPa、0.07 MPa,相比无补偿时,分别减小了150%、150%、152%,反映出本文提出的相位补偿方法的有效性。
3.3 压力快速补偿实验研究为了验证本文研制的压力快速补偿方法的可行性,本文进行压力快速补偿实验研究。
实验时试压容器容积为253 L,实验试件容积为0.3 L,蓄能器公称容积为6.3 L。为了研究初始充气压力对于蓄能器工作性能的影响,本文设定蓄能器初始充气压力分别为2.0 MPa、3.0 MPa、4.0 MPa[11],得到压力快速补偿方法的数据如表 4所示。
| 初始压力/MPa | 压力恢复值/MPa | 压力差值/MPa | 压力补偿能力/% | 补偿时间/s |
| 无补偿 | 3.21 | 1.28 | - | - |
| 2.0 | 4.09 | 0.40 | 68.7 | 0.32 |
| 3.0 | 4.19 | 0.30 | 76.0 | 0.28 |
| 4.0 | 4.27 | 0.22 | 82.2 | 0.24 |
分析表 4可知,当试压容器内加压到4.49 MPa (爆炸压力值)时,舱体类试件发生爆破,无压力快速补偿时,系统压力迅速下降至3.21 MPa。理论上,需要尽快将压力由3.21 MPa补偿到爆炸压力4.49 MPa,即“需要补偿压力”为1.28 MPa。
有压力快速补偿时,本文以初始充气压力2.0 MPa为例,经过0.32 s后,压力恢复至4.09 MPa,压力补偿能力为4.09 MPa-3.21 MPa=0.88 MPa,占需要补偿压力1.28 MPa的68.7%,本文将68.7%称为压力补偿能力。其他充气压力的压力补偿能力见表 4。
比较文献[5]的补偿时间11.76 s,本文方法的补偿时间很小。实验结果验证了本文研制的压力快速补偿方法的可行性及其迅速性。进一步分析表 4,本文方法对压力突降后快速补偿问题有较好效果,但压力恢复值与爆破时的压力值仍存在一定差值。
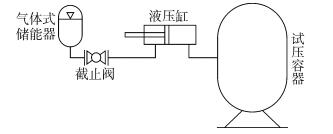
3.4 压力快速补偿方法改进方案及其实验验证在基于气体式蓄能器的压力快速系统中,该系统工作完成后,试压容器内的压力仍与目标压力存在一定差值。本文针对小容积蓄能器系统压力补偿能力有限的问题,提出在压力快速补偿方法中气体式蓄能器和试压容器之间串联液压缸的方式进行改进。改进方案如图 11所示。
|
| 图11 压力快速补偿方法改进方案 Figure 11 Improved scheme for pressure fast compensation method |
图 11中,液压缸的有杆腔与蓄能器液腔出口相连,无杆腔与试压容器直接相连,对于试压容器内同等ΔV液体补充量的需求,该方式通过间接减小蓄能器气腔内气体体积变化量,从而达到提高其压力补偿能力的目的。为了检验改善方案的效果,本文在深海环境模拟实验装置上进行压力快速补偿实验。实验中液压缸的参数为:内径63 mm,活塞杆直径45 mm,行程为500 mm,最大容积为1 550 ml。液压缸有杆腔压力为4.0 MPa,得到压力快速补偿方法的相关数据如表 5所示。
| 状态 | 改进前 | 改进后 |
| 压力恢复值/MPa | 4.27 | 4.35 |
| 与目标压力差值/MPa | 0.23 | 0.14 |
| 压力补偿能力/% | 82.2 | 89.1 |
| 补偿时间/s | 0.24 | 0.30 |
由表 5中数据可知,改进前后,压力恢复值增加了0.08 MPa,与目标压力的差值减小了0.09 MPa,压力补偿能力由82.2%提高至89.1%,相对提高了6.9%。补偿时间增加了0.06 s。以上实验结果反映出,本文提出的串联液压缸的方案,对于改善压力快速补偿方法的压力补偿能力有较好的效果,不足的是补偿时间稍有增加,可以根据实验对补偿压力和补偿时间的不同要求,选择是否采用该方法。
4 结论1)针对深海环境模拟实验装置模拟外部复杂压力环境的要求,研制了一套压力动态控制模块。针对电液比例阀不适合水介质的问题,提出串联液压缸实现油水转换的方法,函数跟踪实验结果验证了本文研制的压力动态控制模块以及串联液压缸实现油水转换方法的可行性。
2)针对液压系统滞后特性影响压力动态模块性能的问题,本文提出采用相位补偿的方法,跟踪实验结果表明,相位补偿方法具有很好的改善效果。
3)针对模拟实验装置在实验过程中压力突降后快速恢复问题,本文研究了压力快速补偿方法。压力快速补偿实验结果表明,当蓄能器初始充气压力为4.0 MPa时,突降后的压力由3.21 MPa快速恢复至4.27 MPa,耗时0.24 s,压力补偿能力为82.2%。反映出较好的压力快速补偿效果。
4)针对经过快速补偿后,系统压力与目标压力仍存在一定差值的问题,本文提出串联液压缸的改善方法。实验结果表明,采用该方法后,压力补偿能力达到89.1%,反映出较好的补偿效果。
| [1] |
孙小辉, 李维嘉, 曹和云. 基于模糊PID的压力筒动态保压系统[J].
中国舰船研究, 2014, 9(1): 127–131.
SUN Xiaohui, LI Weijia, CAO Heyun. A dynamic pressure packing system based on fuzzy PID[J]. Chinese journal of ship research, 2014, 9(1): 127–131. |
| [2] | DUNN P M. The navy unmanned undersea vehicle master plan[J]. Naval undersea warfare center, 2006: 15–23. |
| [3] |
李维嘉, 李绍安, 罗兴桂. 高精度压力筒试验系统[J].
中国造船, 2008, 49(1): 72–76.
LI Weijia, LI Shao'an, LUO Xinggui. The pressure vessel experiment system with high precision[J]. Shipbuilding of China, 2008, 49(1): 72–76. |
| [4] |
谭宗柒, 戴浩林, 汪云峰. 基于AMESim的深度模拟器液压系统设计与仿真[J].
机床与液压, 2009, 37(2): 150–152.
TAN Zongqi, DAI Haolin, WANG Yunfeng. Design and simulation of hydraulic depth simulator based on AMESim[J]. Machine tool & hydraulics, 2009, 37(2): 150–152. |
| [5] |
李天.深海压力环境模拟试验装置及其恒压控制系统研究[D].哈尔滨:哈尔滨工程大学, 2013: 40-50.
LI Tian. Research on the deep-sea pressure environmental simulation test device and its constant pressure control system[D]. Harbin: Harbin Engineering University, 2013: 40-50. http://cdmd.cnki.com.cn/Article/CDMD-10217-1014132375.htm |
| [6] | CHO D O, WHITCOMB M A. A review of the ocean science and technology partnership between US and Korea[J]. Marine policy, 2008, 32(3): 502–513. DOI:10.1016/j.marpol.2007.09.015 |
| [7] |
李浪, 王海涛, 龚烈航. 皮囊式蓄能器吸收压力脉动的参数分析与试验[J].
液压与气动, 2012(7): 3–6.
LI Lang, WANG Haitao, GONG Liehang. The parameter analysis and experiment of the bladder accumulator absorbing pressure pulsation[J]. Chinese hydraulics & pneumatics, 2012(7): 3–6. |
| [8] |
吕少力. 波义耳定律在液压缸加载系统中的应用[J].
液压与气动, 2010(11): 63–64.
LYU Shaoli. Application of boyle's law in loading system of hydraulic cylinder[J]. Chinese hydraulics & pneumatics, 2010(11): 63–64. |
| [9] | OHISHI K, NAKAO M, OHNISHI K, et al. Microprocessor-controlled DC motor for load-insensitive position servo system[J]. IEEE transactions on industrial electronics, 1987, IE-34(1): 44–49. DOI:10.1109/TIE.1987.350923 |
| [10] |
柳俊忻, 马彪, 李和言, 等. 基于吸收压力冲击的蓄能器参数设计及其仿真研究[J].
车辆与动力技术, 2009(2): 6–11.
LIU Junxin, MA Biao, LI Heyan, et al. Study on parameters design and hydraulic shock reduction of hydraulic accumulator for hydrostatic transmission system[J]. Vehicle & power technology, 2009(2): 6–11. |
| [11] |
马登成, 杨士敏, 陈筝, 等. 蓄能器对工程机械液压系统影响的仿真与试验[J].
中国公路学报, 2013, 26(2): 183–190.
MA Dengcheng, YANG Shimin, CHEN Zheng, et al. Simulation and experimental study on impact of accumulator on engineering machinery hydraulic system[J]. China journal of highway and transport, 2013, 26(2): 183–190. |
| [12] |
孔祥东, 权凌霄, 姚静, 等. 基于力学分析的蓄能器数学模型建立及实验研究[J].
液压与气动, 2006(7): 31–34.
KONG Xiangdong, QUAN Lingxiao, YAO Jing, et al. Accumulator is modeled on its stressing model and experiments research[J]. Chinese hydraulics & pneumatics, 2006(7): 31–34. |
| [13] |
崔维成, 刘峰, 胡震, 等. 蛟龙号载人潜水器的7000米级海上试验[J].
船舶力学, 2012, 16(10): 1131–1143.
CUI Weicheng, LIU Feng, HU Zhen, et al. 7000 m sea trials test of the deep manned submersible "JIAOLONG"[J]. Journal of ship mechanics, 2012, 16(10): 1131–1143. |
| [14] | 熊世和. 机电系统计算机控制工程[M]. 成都: 电子科技大学出版社, 1999: 115 -122. |
| [15] | MURAKAMI P, HIROAKI, NAOKA Y. Multiplier-accumulator macro for a 45 MIPS embedded RISC processor[J]. IEEE journal of solid-state circuits, 1996, 31(7): 1067–1071. DOI:10.1109/4.508224 |
| [16] | SUNG P, KYEONGCHEOL Y. Multi-rate parity accumulator accumulator codes[J]. IEEE vehicular technology conference, 2003, 57(4): 551–740. |
| [17] |
杨燕芳.不同工况下皮囊式蓄能器工作参数的选择与计算[D].秦皇岛:燕山大学, 2011:25-26.
YANG Yangfang. Working parameters selection and calculation of bladder-type accumulator under the different conditions[D]. Qinhuangdao: Yanshan University, 2011:25-26. http://cdmd.cnki.com.cn/Article/CDMD-10216-1011282327.htm |
| [18] |
战兴群, 张炎华. 二次调节系统中液压蓄能器数学模型的研究[J].
中国机械工程, 2001, 12(3): 45–46.
ZHAN Xingqun, ZHANG Yanhua. Research on the mathematical model of hydraulic accumulator in the two regulation system[J]. China mechanical engineering, 2001, 12(3): 45–46. |
| [19] |
宋孝臣.入口特性蓄能器性能影响的研究[D].秦皇岛:燕山大学, 2006:12.
SONG Xiaochen. Research on the influence of inlet characteristics on the performance of accumulator[D]. Qinhuangdao: Yanshan University, 2006:12. http://www.cnki.com.cn/Article/CJFDTOTAL-YYQD199002000.htm |



