2. Suzhou Branch, China Nonferrous Metals Processing Technology Co., Ltd., Suzhou 215000, China
结构布置时,矩形墙肢通常被组合成了箱形、T形、工字形等带翼缘剪力墙形式。而这类构件在受横向荷载作用时,由于受到翼缘剪切变形影响,翼缘端部的正应力势必小于翼缘与腹板交界处,产生剪力滞后现象[1]。剪滞效应的存在不但会减小构件的承载力和有效刚度,同时会增大翼缘与腹板交界处的正应力,不利于构件抗震性能的发挥。目前各国规范通过引入有效翼缘宽度来考虑剪滞效应的影响。但各国规范对有效翼缘宽的取值差异较大,并且取值方法相对粗糙,所以有必要寻求一种具有一定工程精度的有效翼缘宽度计算方法,在保证计算简便的同时,又能在计算公式中体现出不同设计参数的影响。
目前常见的有效翼缘宽度的计算方法主要有弹性解析法[2-5]、基于试验数据的经验法[6-9]、基于规范取值的改进法[10]以及基于剪滞效应的量化计算和截面应力分布的半理论半经验法[11]。解析法所得公式较为繁琐,不便于工程应用。经验法和改进法又很难保证结果的精确性和广泛适用性,半理论半经验法在确保有效翼缘宽度取值精确性和理论性的同时,所得公式也相对简化。
国内外对剪滞效应影响下正应力的分布及有效翼缘宽度的研究主要集中在箱形梁、组合梁、框架梁、框筒结构以及核心筒结构[12-16],而对于工程中常见的T形截面带翼缘剪力墙的研究却很少涉足。本文采用解析法对弹性阶段有效翼缘宽度进行求解;采用半理论半经验法对弹塑性阶段有效翼缘宽度的表达式进行推导计算,并采用放大系数法推导了承载力极限状态下的有效翼缘宽度。
1 弹性阶段有效翼缘宽度的解析解 1.1 变分方程的推导在应用最小势能原理分析带翼缘剪力墙受弯挠曲问题时,因为翼缘截面剪切变形的存在,需要引入两个广义位移:剪力墙的水平侧移w(x) 和纵向位移u(x, y) 来描述构件的变形:
| $ w = w\left( x \right) $ | (1) |
| $ u\left( {x,y} \right) = {h_a}\left[ {\frac{{{\rm{d}}w}}{{{\rm{d}}x}} + \left( {1 - \frac{{{y^3}}}{{{b^3}}}} \right)u\left( x \right)} \right] $ | (2) |
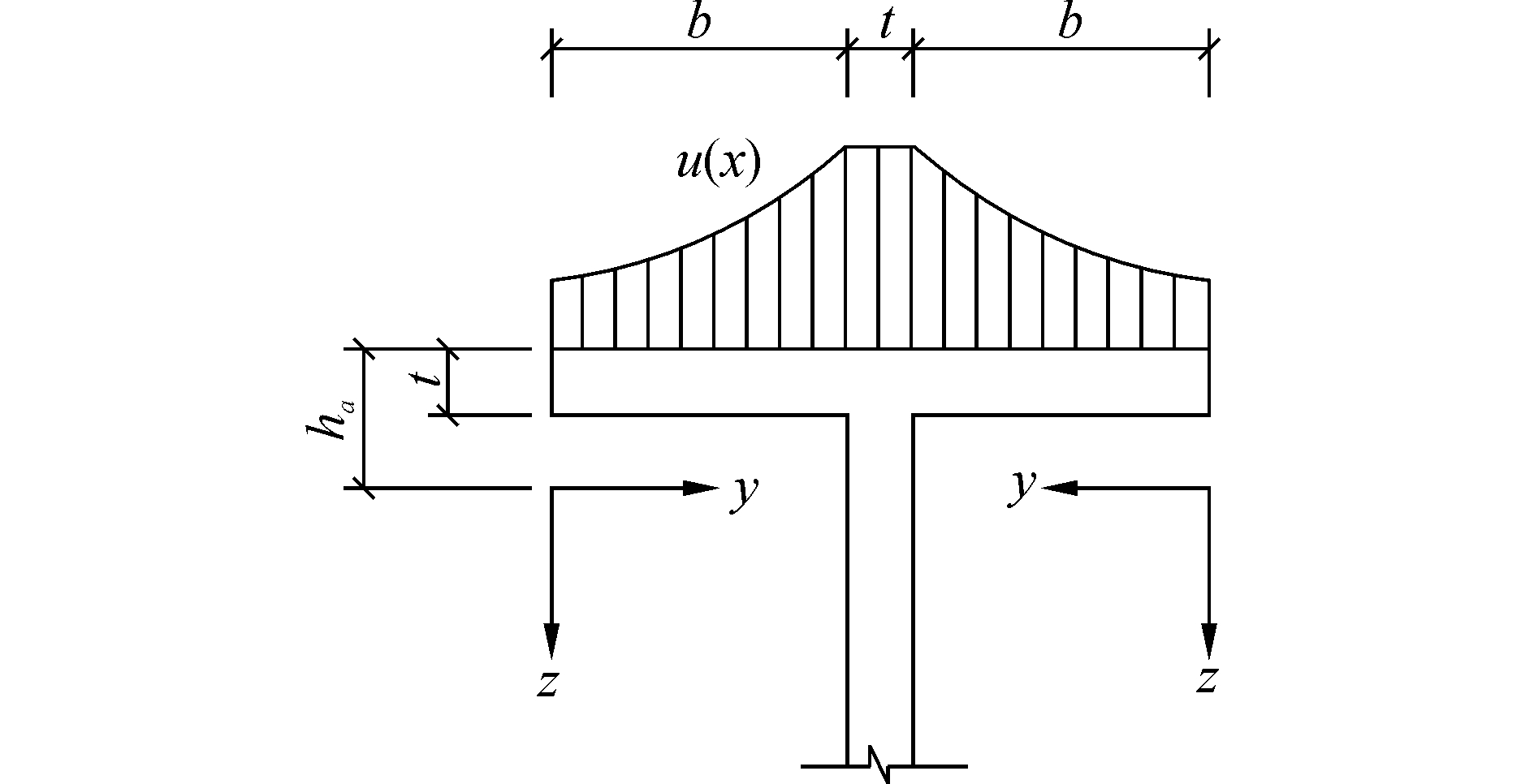
式中:b为一侧翼缘净宽度,ha为翼缘中心截面到形心轴的距离,u(x) 为翼缘最大剪滞转角,其具体定义见图 1。式 (2) 是郭金琼[2]提出的修正位移函数,即假定翼缘的纵向位移沿横向为三次抛物线分布。
|
| 图1 翼缘纵向位移意图 Figure 1 Longitudinal displacement of flange |
根据最小势能原理,结构在外力作用下处于平衡状态时,当产生虚位移时,其总位能的变分为零:
| $ \partial \prod = \partial \left( {\bar V - \bar W} \right) = 0 $ | (3) |
其中,剪力墙的外力势能为
| $ \bar W = - \smallint M\left( x \right)\frac{{{{\rm{d}}^2}w}}{{{\rm{d}}{x^2}}}{\rm{d}}x $ | (4) |
腹板部分仍采用平截面假定,只考虑其弯曲应变能,而翼缘则考虑纵向纤维的正应变和剪应变,腹板应变能为
| $ {{\bar V}_w} = \frac{1}{2}\int {E{I_w}{{\left( {\frac{{{{\rm{d}}^2}w}}{{{\rm{d}}{x^2}}}} \right)}^2}{\rm{d}}x} $ | (5) |
翼缘应变能为
| $ {{\bar V}_f} = \frac{1}{2}\iint {t\left( {E\varepsilon _x^2 + G{\gamma ^2}} \right){\text{d}}x{\text{d}}y} $ | (6) |
其中
| $ {\varepsilon _x} = \frac{{\partial u\left( {x,y} \right)}}{{\partial x}} $ | (7) |
| $ \gamma = \frac{{\partial u\left( {x,y} \right)}}{{\partial y}} $ | (8) |
将式 (2) 代入式 (7)、(8),可得:
| $ {\varepsilon _x} = {h_a}\left[ {w'' + \left( {1 - \frac{{{y^3}}}{{{b^3}}}} \right)u'\left( x \right)} \right] $ | (9) |
| $ \gamma = - \frac{{3{y^3}}}{{{b^3}}}{h_a}u\left( x \right) $ | (10) |
再将式 (9)、(10) 代入式 (6),可得翼缘应变能:
| $ \begin{array}{l} {{\bar V}_f} = \frac{1}{2}{I_f}\int {\left\{ {E\left[ {{{\left( {w''} \right)}^2} + \frac{3}{2}w''u'\left( x \right) + \frac{9}{{14}}{{\left[ {u'\left( x \right)} \right]}^2}} \right]} \right.} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\frac{{9G}}{{5{b^2}}}{{\left[ {u\left( x \right)} \right]}^2}} \right\}{\rm{d}}x \end{array} $ | (11) |
式中:Iw为腹板截面惯性矩,If为翼缘对截面形心的面积距,即If=2tbha2。
将各部分相加可得体系总势能:
| $ \begin{array}{*{20}{c}} {\prod = \int {M\left( x \right)\frac{{{{\rm{d}}^2}w}}{{{\rm{d}}{x^2}}}{\rm{d}}x} + \frac{1}{2}\int {E{I_w}{{\left( {\frac{{{{\rm{d}}^2}w}}{{{\rm{d}}{x^2}}}} \right)}^2}{\rm{d}}x} + }\\ {\frac{1}{2}{I_u}\int {\left\{ {E\left[ {{{\left( {w''} \right)}^2} + \frac{3}{2}w''u'\left( x \right) + \frac{9}{{14}}{{\left[ {u'\left( x \right)} \right]}^2}} \right] + \frac{{9G{u^2}}}{{5{b^2}}}} \right\}} {\rm{d}}x} \end{array} $ | (12) |
将式 (12) 代入式 (3),即可得到剪力滞基本微分方程:
| $ EIw'' + M\left( x \right) + \frac{3}{4}E{I_f}u'\left( x \right) = 0 $ | (13) |
| $ E{I_u}\left[ { - \frac{9}{{14}}u''\left( x \right) - \frac{3}{4}w'' + \frac{{9Gu\left( x \right)}}{{5E{b^2}}}} \right] = 0 $ | (14) |
| $ E{I_u}\left[ {\frac{9}{{14}}u' + \frac{3}{4}w''} \right]\delta u\left| {_{{x_1}}^{{x_2}}} \right. = 0 $ | (15) |
整理式 (13)~(15),并令
| $ \left\{ \begin{array}{l} n = \frac{1}{{1 - \frac{{7{I_u}}}{{8I}}}}\\ k = \frac{1}{b}\sqrt {\frac{{14Gn}}{{5E}}} \end{array} \right. $ | (16) |
可得到关于翼缘最大剪滞转角u(x) 的二阶常微分方程:
| $ u'' - {k^2}u = \frac{{7nQ\left( x \right)}}{{6EI}} $ | (17) |
求得其通解:
| $ u\left( x \right) = \frac{{7n}}{{6EI}}\left( {{c_1}\sinh x + {c_2}\cosh x + {u^ * }} \right) $ | (18) |
式中:c1、c2可由边界条件确定,u*为与Q(x) 有关的特解。
1.2 应力及有效翼缘宽度的求解对于剪力墙顶部受一水平集中力的情况,将边界条件代入式 (18),可求得翼缘最大剪滞转角:
| $ u\left( x \right) = \frac{{7nP}}{{6EI}}\left( {\frac{{\cosh \left( {kx} \right)}}{{{k^2}\cosh \left( {kl} \right)}} - \frac{1}{{{k^2}}}} \right) $ | (19) |
又因为翼缘截面正应力分布函数为
| $ {\sigma _x} = E\frac{{\partial u\left( {x,y} \right)}}{{\partial x}} $ | (20) |
将式 (2)、(19) 代入式 (20),可得
| $ {\sigma _x} = E{h_a}\left[ {w'' + \frac{{7nP}}{{6kEI}}\left( {1 - \frac{{{y^3}}}{{{b^3}}}} \right)\frac{{\sinh \left( {kx} \right)}}{{\cosh \left( {kl} \right)}}} \right] $ | (21) |
由式 (13) 可得
| $ w'' = - \left( {\frac{{M\left( x \right)}}{{EI}} + \frac{{3{I_f}}}{{4I}}u'} \right) $ | (22) |
代入式 (21) 即可得到翼缘截面正应力分布函数表达式:
| $ {\sigma _x} = - \frac{{{h_a}}}{I}\left[ {M\left( x \right) - \frac{{7nP}}{{6k}}\left( {1 - \frac{{{y^3}}}{{{b^3}}} - \frac{{3{I_f}}}{{4I}}} \right)\frac{{\sinh \left( {kx} \right)}}{{\cosh \left( {kl} \right)}}} \right] $ | (23) |
在墙肢底部x=l处,即剪力墙剪滞效应最显著截面的正应力为
| $ {\sigma _x} = - \frac{{{h_a}}}{I}\left[ {Pl - \frac{{7nP}}{{6k}}\left( {1 - \frac{{{y^3}}}{{{b^3}}} - \frac{{3{I_f}}}{{4I}}} \right)\tanh \left( {kl} \right)} \right] $ | (24) |
从图 1可以看出,在y=b时,应力达到最大值σmax,即
| $ {\sigma _{\max }} = - \frac{{{h_a}}}{I}\left[ {Pl + \frac{{7nP}}{{6k}}\frac{{3{I_f}}}{{4I}}\tanh \left( {kl} \right)} \right] $ | (25) |
根据应力等效原则,剪力墙有效翼缘宽度可按下式计算:
| $ {b_e} = \left( {\int_{ - b}^b {{\sigma _x}{\rm{d}}y} } \right)/{\sigma _{\max }} $ | (26) |
将式 (25)、(26) 代入式 (27),即可得到弹性阶段带翼缘的解析解:
| $ {b_e} = 2\frac{{ - \int_0^b {\frac{{{h_a}}}{I}\left[ {Pl - \frac{{7nP}}{{6k}}\left( {1 - \frac{{{y^3}}}{{{b^3}}} - \frac{{3{I_f}}}{{4I}}} \right)\tanh \left( {kl} \right)} \right]{\rm{d}}y} }}{{ - \frac{{{h_a}}}{I}\left[ {Pl + \frac{{7nP}}{{6k}}\frac{{3{I_f}}}{{4I}}\tanh \left( {kl} \right)} \right]}} + t $ | (27) |
式 (27) 经积分化简可得
| $ {b_e} = 2b\frac{{l - \frac{{7n}}{{8k}}\left( {1 - \frac{{{I_f}}}{I}} \right)\tanh \left( {kl} \right)}}{{l + \frac{{7n{I_f}}}{{8kI}}\tanh \left( {kl} \right)}} + t $ | (28) |
由文献[17]中剪滞效应的参数分析可知,该式基本考虑了有效翼缘宽度取值的所有影响因素,可认为,该解析解是弹性阶段有效翼缘宽度的精确解。但该式需要计算的参数较多,计算量偏大,不便于工程设计的应用。因此还需进一步研究有效翼缘宽度的简化计算方法。
2 弹性阶段有效翼缘宽度的数值计算 2.1 模型验证为了验证有限元模型的合理性,采用非线性有限元分析软件ABAQUS模拟了文献[18]中RC剪力墙TW2的拟静力加载试验。采用塑性损伤模型模拟混凝土的非线性行为。混凝土受压本构选用Saenz[19]提出的表达式,受拉本构选用文献[20]的表达式。混凝土采用8节点、6面体线性非协调模式三维实体单元-C3D8I。考虑到本文的研究对象为截面应变,故在翼缘厚度方向划分四个单元,长度及高度方向单元长度取0.5倍的墙厚,以保证塑性铰区内应力分布的准确性和连续性。模拟加载时,采用位移控制模式单调加载,墙体底部也与一刚性体板相连接,约束其全部六个自由度。
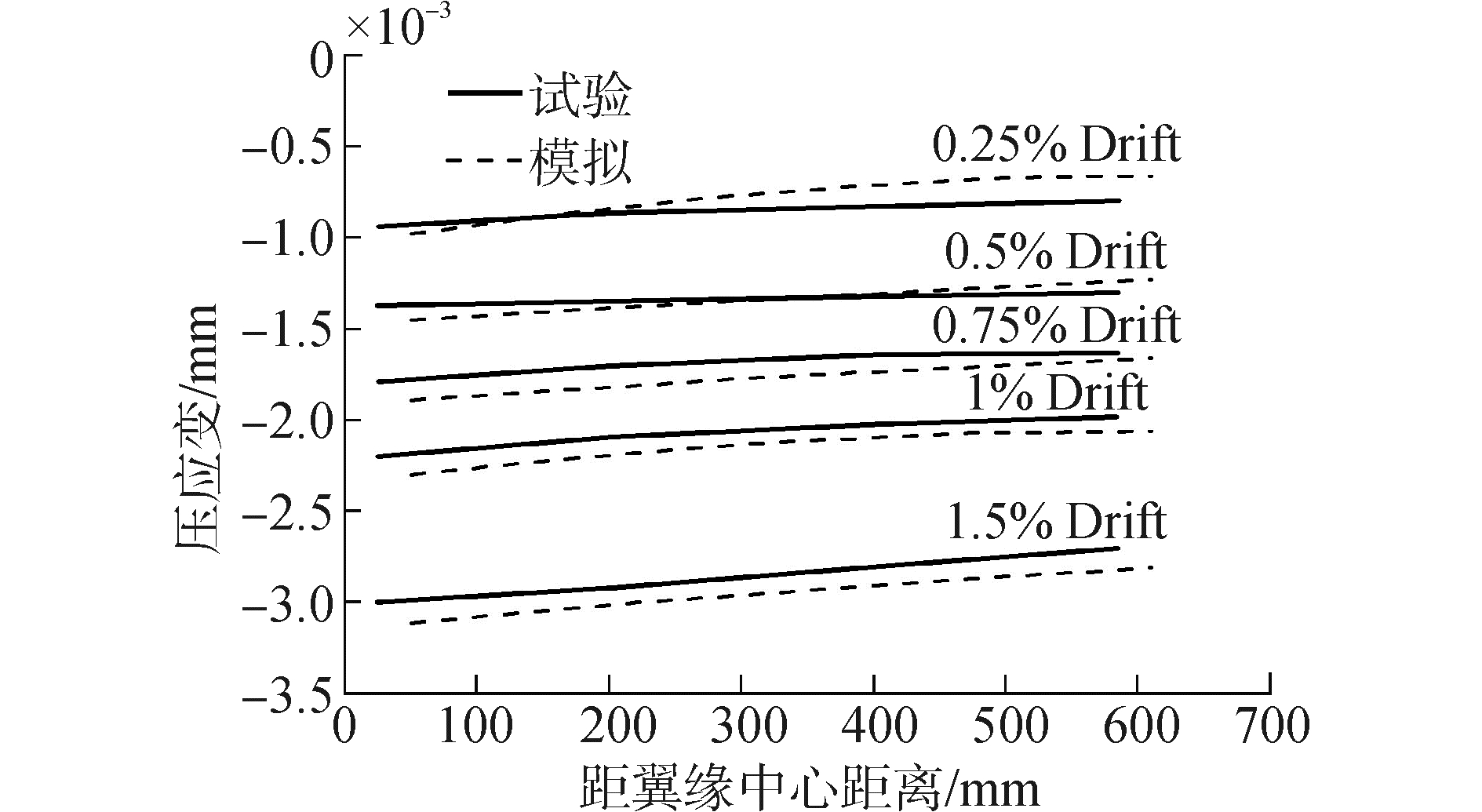
图 2给出了试验骨架曲线与模拟单调荷载位移曲线对比图,可见模拟结果与试验基本吻合。图 3比较了试验中测量的翼缘外皮混凝土压应变与有限元计算所得应变,可以看出试验数据与模拟结果均显示混凝土压应变在腹板翼缘交界处达到最大,验证了所建立的有限元模型及参数选取的准确性。

|
| 图2 试验与模拟荷载-位移曲线 Figure 2 Load-displacement curves of experiment and simulation |
|
| 图3 翼缘混凝土压应变分布 Figure 3 Concrete compressive strain distribution of flange |
将上述试验模型进行简化,所用材性与试验相同。以翼缘宽度与腹板高度比 (a/b)、墙高与翼缘宽度比 (H/b)、墙高与翼缘宽度比 (H/a) 作为模型参数,对15个不同几何参数下的剪力墙模型进行有限元分析,具体的几何参数及弹性阶段计算结果见表 1。
| 模型 | a:b:H | 剪滞系数β |
| 1 | 3:1:5 | 0.179 |
| 2 | 3:1:10 | 0.104 |
| 3 | 3:1:20 | 0.038 |
| 4 | 2:1:5 | 0.145 |
| 5 | 2:1:10 | 0.075 |
| 6 | 2:1:20 | 0.029 |
| 7 | 1:1:5 | 0.133 |
| 8 | 1:1:10 | 0.056 |
| 9 | 1:1:20 | 0.020 |
| 10 | 1:2:5 | 0.293 |
| 11 | 1:2:10 | 0.133 |
| 12 | 1:2:20 | 0.046 |
| 13 | 1:3:5 | 0.442 |
| 14 | 1:3:10 | 0.219 |
| 15 | 1:3:20 | 0.124 |
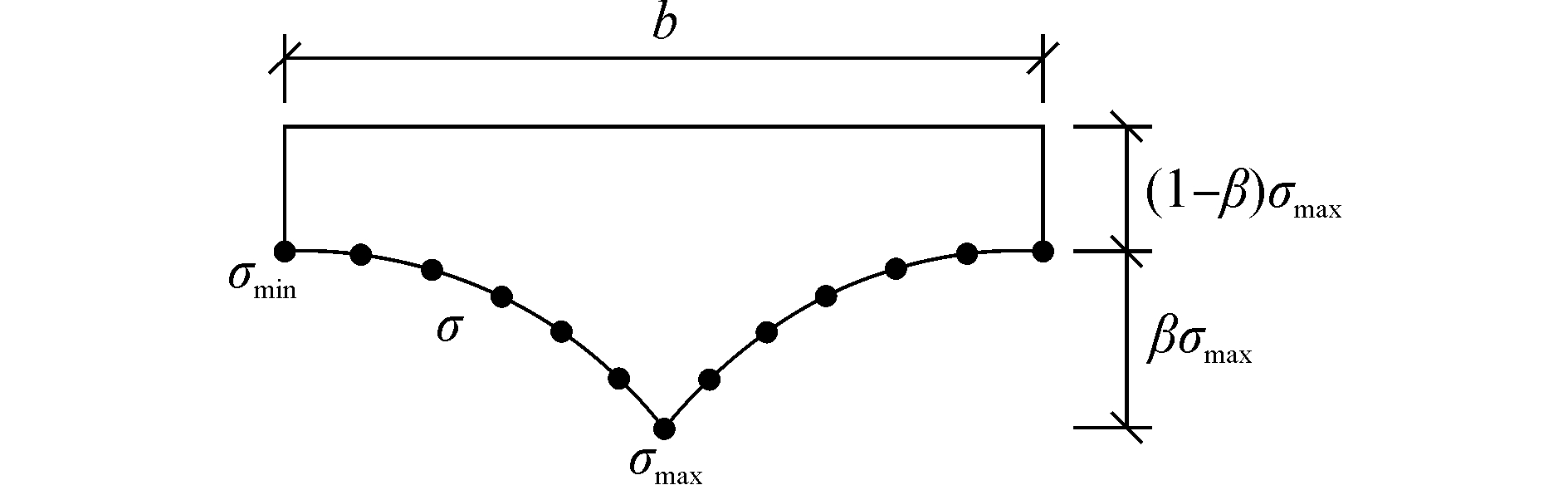
考虑到进一步研究剪滞效应的需要,本文引入无量纲剪滞系数β来定量描述剪滞效应。图 4给出了剪滞效应影响下翼缘截面的正应力分布及剪滞系数β的定义。可以看出正应力σ在翼缘中部达到最大值σmax,向两侧σ逐渐递减,剪滞系数β的引入就是来定量描述翼缘端部正应力的减小程度,剪滞效应较小时β趋于0,剪滞效应明显时β趋于1。
|
| 图4 剪滞系数定义 Figure 4 Definition of shear lag coefficient |
由有限元分析结果可知,剪滞效应沿墙肢高度方向逐渐衰减,并在墙肢底部达到最大,因此选取翼缘底部混凝土单元的正应力作为研究对象,不同位置处正应力取墙体厚度方向的四个混凝土单元形心处的正应力之和。由表 1可以看出,剪滞系数β的大小主要依赖于墙高与翼缘宽度比 (H/b) 的变化,随着H/b的减小,剪滞系数β相应增大。分析其原因是墙肢高度H越小,剪跨比越小,剪力墙的破坏形态从弯曲型向剪切型转化,从而正应力在翼缘的传递过程中产生的剪切变形增大,使得翼缘端部传递到的正应力较翼缘与腹板交界处有很大程度的减少。而翼缘宽度b的增大使得翼缘截面正应力的传递路线增长,在剪力传递过程中正应力衰减程度增大,剪滞效应增强。
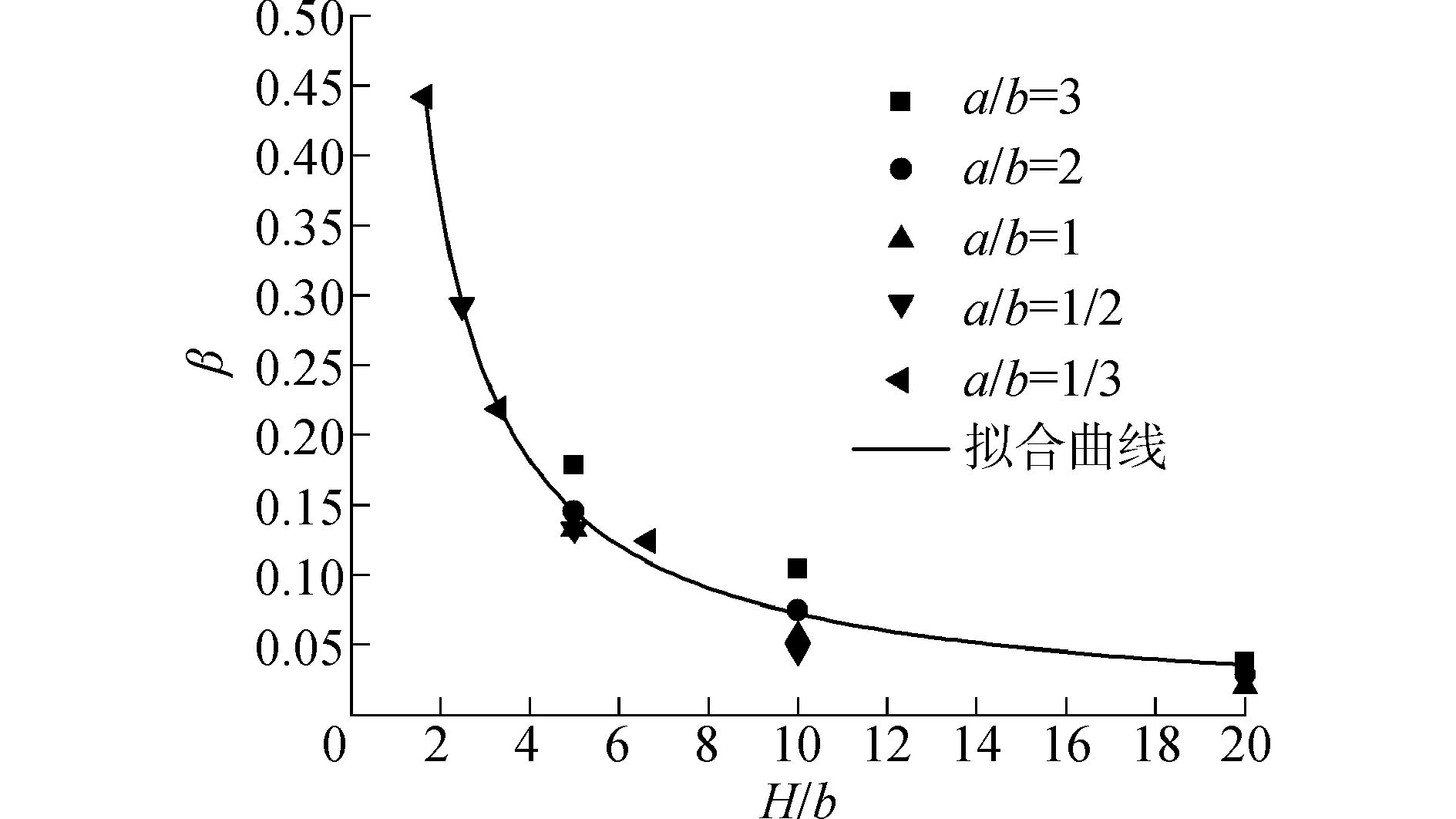
腹板高度与翼缘宽度比 (a/b) 对剪滞系数也有影响,当a=b时,β达到最小;当a/b>1或a/b < 1时,β增大,并且a与b相差越悬殊β值越大。然而相比墙高与翼缘宽度比,腹板高度与翼缘宽度比对β的影响较小,因此在β值的计算中可忽略a/b的影响。取相同H/b时不同a/b有限元计算出的β的平均值,来拟合β与H/b的关系曲线,拟合结果见图 5。比较不同类型函数的拟合结果,同时考虑计算的简便性,发现幂函数与计算结果吻合较好,可得到如下弹性阶段β值的经验计算式:
|
| 图5 弹性阶段剪滞系数与墙高与翼缘高宽比关系曲线 Figure 5 Curve for shear lag coefficient versus height/flange width ratio in elastic stage |
| $ \beta = 0.74{\left( {H/b} \right)^{ - 1.01}} $ | (29) |
Kwan[11]曾提出用四次多项式来描述核心筒翼缘截面的正应力分布。根据本文有限元计算出的正应力分布曲线,同时考虑边界条件的约束,发现五次多项式能较好的吻合有限元计算结果,可以得到如下的应力分布函数表达式:
| $ \sigma = {\sigma _{\max }}\left[ {1 - \beta + \beta {{\left( {\frac{{b/2 - x}}{{b/2}}} \right)}^5}} \right] $ | (30) |
式中:x=0时,即位于翼缘与腹板交界处,正应力达到最大值σmax;当x=b/2时,即位于翼缘端部,正应力达到最小值 (1-β)σmax,这一结果与图 5有关剪滞系数的定义相一致。
根据应力等效原则,有效翼缘宽度可按式 (26) 计算。考虑到正应力σx在翼缘左右两侧对称分布,即be是关于x的偶函数。因此可将式 (26) 简化为
| $ {b_e} = 2\left( {\int_0^{b/2} {{\sigma _x}{\rm{d}}z} } \right)/{\sigma _{\max }} $ | (31) |
再将构造出的应力分布函数表达式 (30) 代入式 (31):
| $ {b_e} = 2\left\{ {\int_0^{b/2} {{\sigma _{\max }}\left[ {1 - \beta + \beta {{\left( {\frac{{b/2 - x}}{{b/2}}} \right)}^5}} \right]{\rm{d}}x} } \right\}/{\sigma _{\max }} $ | (32) |
式 (32) 经过积分化简可得
| $ {b_e} = b - 0.83b\beta $ | (33) |
将之前拟合出的剪滞系数β的经验计算式 (29) 代入式 (33)。即可得到弹性阶段有效翼缘宽度的简化计算公式:
| $ {b_{e0}} = b - 0.62b{\left( {H/b} \right)^{ - 1.01}} $ | (34) |
因此,在设计计算中,只要知道了墙高H与翼缘截面宽度b,就可以通过上式来计算有效翼缘宽度。这相比规范中查表所得的结果的准确性更高。同时式 (34) 只需要通过计算器计算即可得到有效翼缘宽度,确保了在实际设计计算中应用的可行性。
2.4 弹性阶段有效翼缘宽度取值对比为了比较解析法与有限元法计算结果的差异性,将弹性阶段两者计算出的有效翼缘宽度值列于表 2。可以看出两者的差值基本在10%以内,进一步验证了有限元法的准确性。同时发现解析解基本均大于有限元计算值,这首先是因为是解析法假定应力分布为三次抛物线形状,而有限元计算出的应力分布曲线更接近于五次多项式,所以解析法一定程度上低估了剪滞效应。其次解析法不仅忽略了腹板中的剪滞效应,同时在计算中忽略了翼缘横向和竖向应变 (εy, εz) 以及平面外剪切变形 (γxz, γyz),所以解析解与有限元计算值存在一定偏差。
| 模型 | a:b:H | 解析法/m | 有限元法/m | 误差值/% |
| 1 | 3:1:5 | 0.923 | 0.850 | 7.98 |
| 2 | 3:1:10 | 0.961 | 0.912 | 5.16 |
| 3 | 3:1:20 | 0.980 | 0.968 | 1.31 |
| 4 | 2:1:5 | 0.921 | 0.877 | 4.83 |
| 5 | 2:1:10 | 0.956 | 0.937 | 2.35 |
| 6 | 2:1:20 | 0.980 | 0.976 | 0.43 |
| 7 | 1:1:5 | 0.922 | 0.891 | 3.42 |
| 8 | 1:1:10 | 0.961 | 0.953 | 0.75 |
| 9 | 1:1:20 | 0.980 | 0.983 | -0.29 |
| 10 | 1:2:5 | 1.648 | 1.515 | 8.11 |
| 11 | 1:2:10 | 1.819 | 1.782 | 1.87 |
| 12 | 1:2:20 | 1.906 | 1.925 | -1.01 |
| 13 | 1:3:5 | 2.219 | 1.915 | 13.68 |
| 14 | 1:3:10 | 2.582 | 2.469 | 4.39 |
| 15 | 1:3:20 | 2.783 | 2.675 | 3.89 |
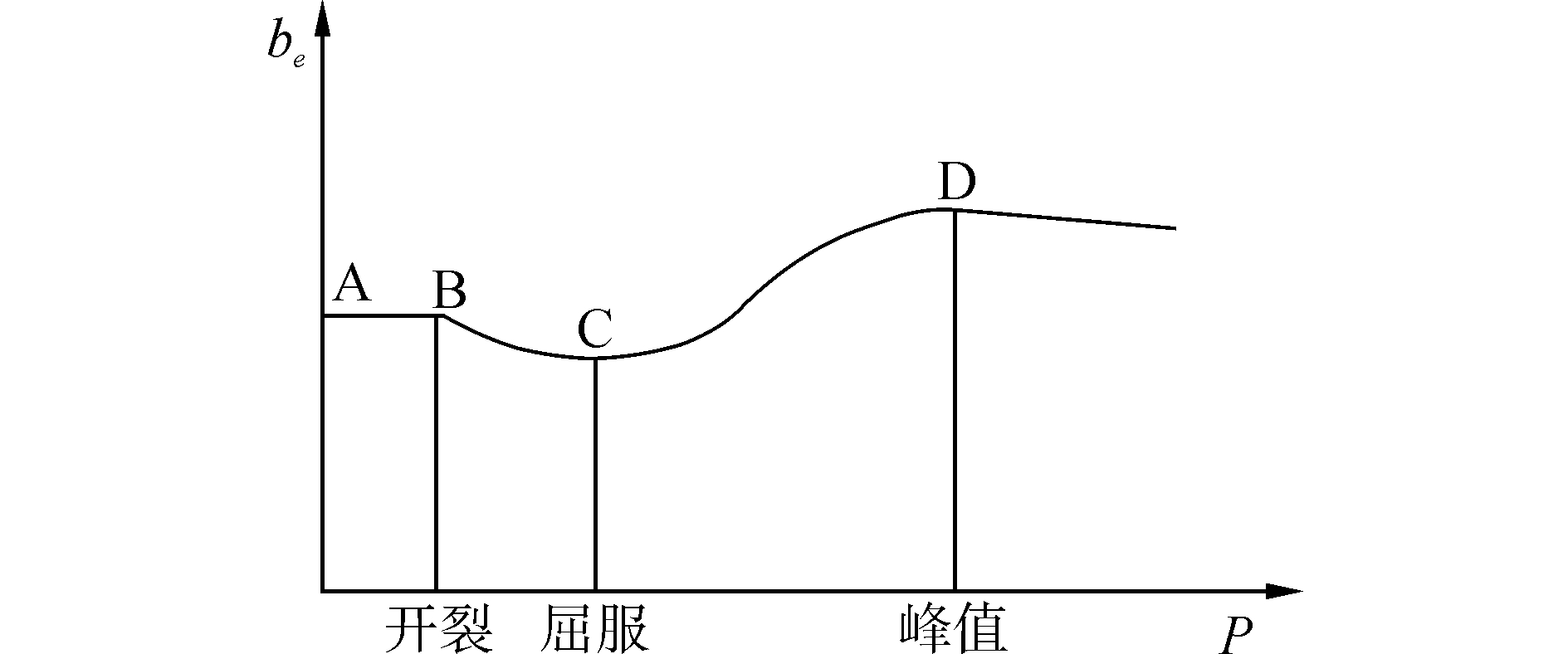
目前各国规范中有效翼缘宽度的取值都是基于线弹性的分析结果,适用于计算正常使用极限状态下剪力墙刚度和变形。而由文献[17]可知有效翼缘宽度在加载过程中是不断变化的,通过对带翼缘剪力墙剪滞效应的全过程模拟,图 6给出了有效翼缘宽度随加载过程的变化规律。
|
| 图6 有效翼缘宽度随加载过程的变化 Figure 6 Variation of effective flange width along loading |
可以看出剪力墙屈服时有效翼缘宽度达到最小,为工程设计的最不利情况。为了给结构中的关键部件和薄弱部位留有一定的安全储备,有必要推导剪力墙屈服时有效翼缘宽度的简化计算公式。而在计算剪力墙承载力时,需要用相应的承载能力极限状态下的有效翼缘宽度进行分析,因此还需推导出承载力极限状态下有效翼缘宽度的简化计算公式。
3.2 剪力墙屈服时有效翼缘宽度的简化计算沿用弹性阶段的数值计算方法,对15组不几何同参数的剪力墙进行非线性有限元分析。表 3给出了剪力墙屈服时的有限元计算结果。
| 模型 | a:b:H | 剪滞系数β |
| 1 | 3:1:5 | 0.420 |
| 2 | 3:1:10 | 0.325 |
| 3 | 3:1:20 | 0.220 |
| 4 | 2:1::5 | 0.400 |
| 5 | 2:1:10 | 0.321 |
| 6 | 2:1:20 | 0.219 |
| 7 | 1:1:5 | 0.367 |
| 8 | 1:1:10 | 0.295 |
| 9 | 1:1:20 | 0.217 |
| 10 | 1:2:5 | 0.563 |
| 11 | 1:2:10 | 0.351 |
| 12 | 1:2:20 | 0.281 |
| 13 | 1:3:5 | 0.681 |
| 14 | 1:3:10 | 0.519 |
| 15 | 1:3:20 | 0.356 |
由表 3可以看出,剪力墙屈服时翼缘剪滞系数β的大小同样主要依赖于墙高与翼缘宽度比值 (H/b) 的变化,取相同H/b时不同a/b有限元计算出的平均值,来拟合β与H/b的关系曲线,拟合结果见图 7。发现幂函数与有限元计算结果吻合较好,从而可以得到以下剪力墙屈服时β值的经验计算式:

|
| 图7 屈服时剪滞系数与墙高与翼缘高宽比关系曲线 Figure 7 Curve for shear lag coefficient versus height/flange width ratio at yield |
| $ \beta = 0.85{\left( {H/b} \right)^{ - 0.46}} $ | (35) |
屈服时有限元计算出的正应力分布曲线仍然可用2.3节构造出的五次多项式来表示。将本节拟合出的屈服时剪滞系数β的经验计算式 (35) 代入式 (33),即可得剪力墙屈服时即工程最不利情况下有效翼缘宽度的简化计算公式:
| $ {b_{ey}} = b - 0.71b{\left( {H/b} \right)^{ - 0.46}} $ | (36) |
由3.1节全过程分析可知,在极限状态下翼缘截面的应力分布不再符合图 5所示的典型分布,3.2节所采用的方法不再适用。而由前述分析可知极限状态下有效翼缘宽度相比弹性阶段有所提高,故本节将采用基于弹性阶段有效翼缘宽度的放大系数法来计算承载力极限状态下的有效翼缘宽度。表 4给出了15组不同参数下承载力极限状态的有效翼缘宽度值相对于弹性阶段取值的放大系数。
| 模型 | a:b:H | 放大系数γ |
| 1 | 3:1:5 | 1.038 |
| 2 | 3:1:10 | 1.024 |
| 3 | 3:1:20 | 1.007 |
| 4 | 2:1:5 | 1.036 |
| 5 | 2:1:10 | 1.021 |
| 6 | 2:1:20 | 1.009 |
| 7 | 1:1:5 | 1.044 |
| 8 | 1:1:10 | 1.026 |
| 9 | 1:1:20 | 1.011 |
| 10 | 1:2:5 | 1.202 |
| 11 | 1:2:10 | 1.049 |
| 12 | 1:2:20 | 1.029 |
| 13 | 1:3:5 | 1.237 |
| 14 | 1:3:10 | 1.133 |
| 15 | 1:3:20 | 1.027 |
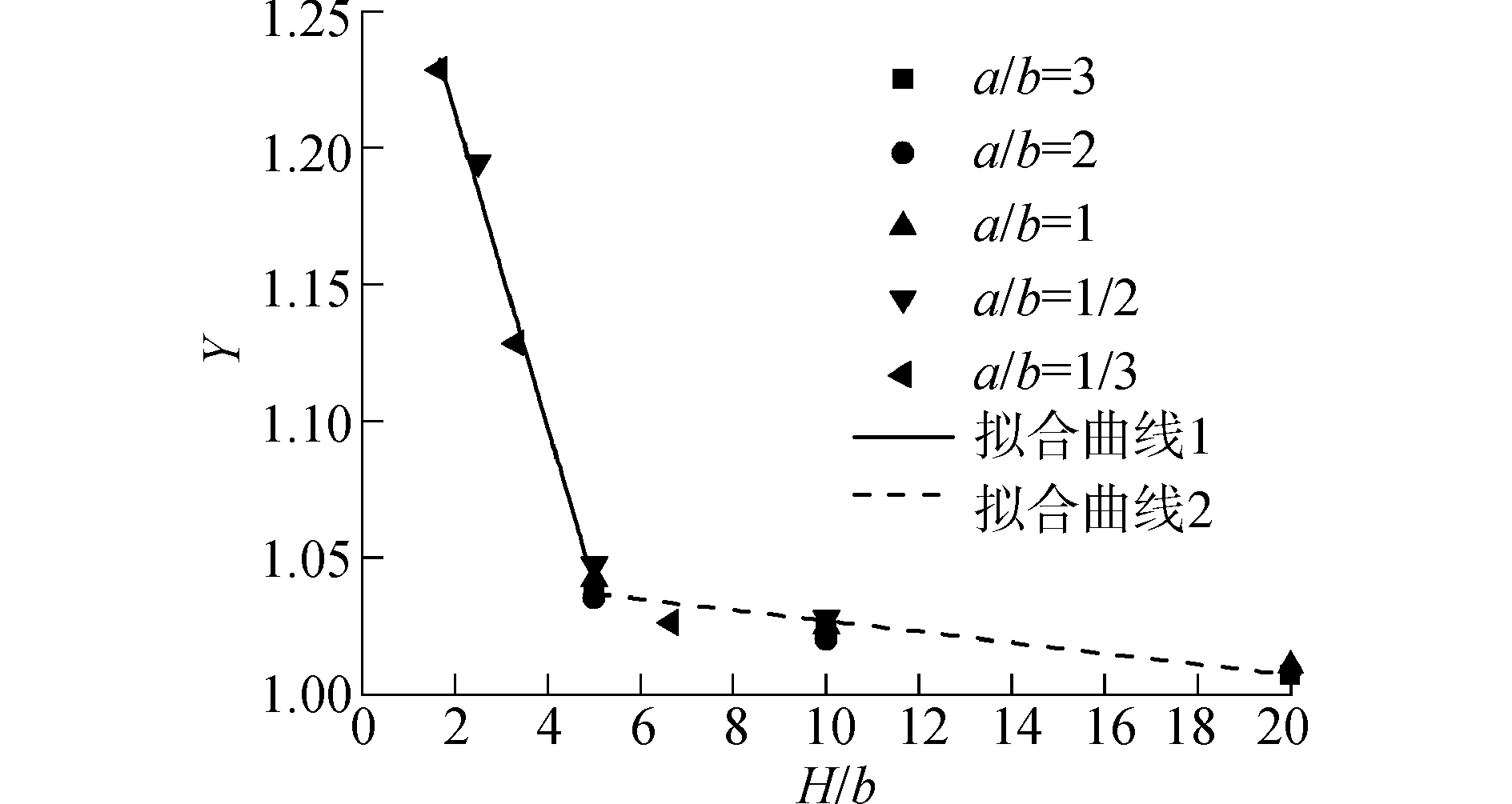
从表 4可以看出,放大系数γ值主要依赖于墙高与翼缘宽度比 (H/b) 的变化,取相同H/b时不同a/b的放大系数的平均值,来拟合γ与H/b的关系曲线,拟合结果见图 8,发现分段线性函数拟合效果较好,可得到承载力极限状态下γ的经验计算式:
|
| 图8 承载极限状态放大系数与翼缘高宽比关系曲线 Figure 8 Curve for amplification coefficient versus height/flange width ratio at ultimate limit state. |
| $ \gamma = \left\{ \begin{array}{l} 1.34 - 0.059\left( {H/b} \right)\;\;\;\;\left( {H/b \le 5} \right)\\ 1.05 - 0.002\left( {H/b} \right)\;\;\;\;\left( {H/b \ge 5} \right) \end{array} \right. $ | (37) |
代入式 (32) 即可得到承载力极限状态下有效翼缘宽度的简化计算公式:
| $ {b_{eu}} = \gamma {b_{e0}} $ | (38) |
为了验证本文所推导出的有效翼缘宽度简化计算公式的准确性,运用上述简化计算公式计算出的不同参数下有效翼缘宽度的取值,与有限元计算结果进行比较,比较结果见表 5。可以看出,本文提出的简化计算公式与有限元计算结果吻合良好,最大误差绝对值基本控制在10%以内,充分验证了简化计算公式的精确性,可为工程设计提供参考。
| 模型 | 弹性阶段 | 屈服时 | 极限状态 | |||||
| 简化 公式 |
有限元 分析 |
简化 公式 |
有限元 分析 |
简化 公式 |
有限元 分析 |
|||
| 1 | 0.878 | 0.850 | 0.661 | 0.622 | 0.913 | 0.882 | ||
| 2 | 0.939 | 0.912 | 0.754 | 0.733 | 0.968 | 0.934 | ||
| 3 | 0.970 | 0.968 | 0.821 | 0.813 | 0.980 | 0.974 | ||
| 4 | 0.878 | 0.877 | 0.661 | 0.651 | 0.913 | 0.909 | ||
| 5 | 0.939 | 0.937 | 0.754 | 0.731 | 0.968 | 0.957 | ||
| 6 | 0.970 | 0.976 | 0.821 | 0.847 | 0.980 | 0.984 | ||
| 7 | 0.878 | 0.891 | 0.661 | 0.696 | 0.913 | 0.930 | ||
| 8 | 0.939 | 0.953 | 0.754 | 0.757 | 0.968 | 0.978 | ||
| 9 | 0.970 | 0.983 | 0.821 | 0.818 | 0.980 | 0.993 | ||
| 10 | 1.509 | 1.515 | 1.068 | 1.058 | 1.799 | 1.820 | ||
| 11 | 1.756 | 1.782 | 1.323 | 1.240 | 1.826 | 1.870 | ||
| 12 | 1.879 | 1.925 | 1.508 | 1.516 | 1.935 | 1.981 | ||
| 13 | 1.890 | 1.915 | 1.316 | 1.333 | 2.346 | 2.369 | ||
| 14 | 2.449 | 2.469 | 1.776 | 1.662 | 2.780 | 2.797 | ||
| 15 | 2.726 | 2.675 | 2.110 | 2.087 | 2.826 | 2.747 | ||
1) 基于能量变分原理,采用解析法推导了剪力墙翼缘截面的正应力分布,进一步计算了弹性阶段有效翼缘宽度的解析解。
2) 采用有限元法对一组带翼缘剪力墙进行了参数分析,发现剪滞系数β的大小主要依赖于墙高与翼缘宽度比值的变化,随着其比值的减小,剪滞系数β增大。在腹板高度与翼缘宽度相等时,剪滞系数β达到极小值。
3) 根据有限元计算结果,拟合出了剪滞系数的经验计算式。并推导出了弹性阶段和剪力墙屈服时有效翼缘宽的简化公式,采用放大系数法推导了承载力极限状态下有效翼缘宽度的简化公式,通过与有限元结果的比对验证了简化公式的准确性。
| [1] | LIN Z B, ZHAO J. Modeling inelastic shear lag in steel box beams[J]. Engineering structures, 2012, 41: 90–97. DOI:10.1016/j.engstruct.2012.03.018 |
| [2] | REISSNER E. Analysis of shear lag in box beam by the principle of minimum potential energy[J]. Quarterly of applied mathematics, 1946, 5(4): 268–278. |
| [3] | KRISTEK V. Folded plate approach to analysis of shear wall systems and frame structures[J]. ICE Proceedings, 1979, 67(2): 1065–1075. |
| [4] |
郭金琼, 房贞政, 罗孝登. 箱型梁桥剪滞效应分析[J].
土木工程学报, 1983, 16(1): 1–13.
GUO Jinqiong, FANG Zhenzheng, LUO Xiaodeng. Analysis of shear lag in box beams[J]. China civil engineering journal, 1983, 16(1): 1–13. |
| [5] |
张彦玲, 李运生, 樊健生, 等. 钢-混凝土组合梁负弯矩区有效翼缘宽度的研究[J].
工程力学, 2010, 27(2): 178–185.
ZHANG Yanling, LI Yunsheng, FAN Jiansheng, et al. Study of the shear lag effective flange width at negative moment zone of steel-concrete composite beams[J]. Engineering mechanics, 2010, 27(2): 178–185. |
| [6] |
聂建国, 田春雨. 简支组合梁板体系有效宽度分析[J].
土木工程学报, 2005, 38(2): 8–12.
NIE Jianguo, TIAN Chunyu. Effective widths of simply supported composite beams with transverse end girders[J]. China civil engineering journal, 2005, 38(2): 8–12. |
| [7] | NIE J G, TAO M X. Slab spatial composite effect in composite frame systems. Ⅰ:Effective widthfor ultimate loading capacity[J]. Engineering structures, 2012, 38: 171–184. DOI:10.1016/j.engstruct.2011.11.034 |
| [8] |
保蓓蓓, 陈中汉, 陈德荣. 承载极限状态下组合梁的有效翼缘宽度[J].
苏州科技学院学报:工程技术版, 2008, 21(1): 8–12.
BAO Beibei, CHEN Zhonghan, CHEN Derong. Research on effective width of composite beams in plastic stage[J]. Journal of University of Science and Technology of Suzhou:Engineering and Technology, 2008, 21(1): 8–12. |
| [9] |
黄远, 聂建国, 易伟建. 钢-混凝土组合框架梁变形计算的有效翼缘宽度[J].
土木工程学报, 2012, 45(8): 33–40.
HUANG Yuan, NIE Jianguo, YI Weijian. Effective flange width for calculation of the deformation of steel-concrete composite frame beams[J]. China Civil Engineering Journal, 2012, 45(8): 33–40. |
| [10] |
聂建国, 田春雨. 钢-混凝土简支组合梁塑性阶段有效宽度分析[J].
铁道科学与工程学报, 2004, 1(1): 39–43.
NIE Jianguo, TIAN Chunyu. Plastic analysis of effective composite beam width[J]. Journal of railway science and engineering, 2004, 1(1): 39–43. |
| [11] | KWAN A K H. Shear lag in shear/core walls[J]. Journal of structure engineering, 1996, 122: 1097–1104. DOI:10.1061/(ASCE)0733-9445(1996)122:9(1097) |
| [12] | ZHANGY H. Improved finite-segment method for analyzing shearlag effect in thin-walled box girders[J]. Journal of structure engineering, 2012, 138: 1279–1284. DOI:10.1061/(ASCE)ST.1943-541X.0000552 |
| [13] | HAJI-KAZEMI H, COMPANY M. Exact method of analysis of shear lag in framed tube structures[J]. The structural design of tall and special buildings, 2001, 11: 375–388. |
| [14] | CASTRO J M, ELGHAZOULI A Y, IZZUDDIN. Assessment of effective slab widths in composite beams[J]. Journal of constructional steel research, 2007, 63: 1317–1327. DOI:10.1016/j.jcsr.2006.11.018 |
| [15] |
王素裹. 考虑板参与作用的RC框架有效翼缘宽度简化公式[J].
华南理工大学学报:自然科学版, 2014, 42(11): 99–105.
WANG Suguo. A simplified formula of effective flange width of RC frame considering slab reinforcement participation[J]. Journal of South China university of technology:Natural Science Edition, 2014, 42(11): 99–105. |
| [16] |
信瑛佩. 考虑剪力滞后的复杂截面剪力墙配筋研究[D]. 哈尔滨: 哈尔滨工业大学, 2011.
XIN Yingpei. Research on reinforcement design of shear walls of complex cross section considering shear lag effect[D]. Harbin:Harbin Insstitute, 2011. |
| [17] |
史庆轩, 王斌, 郑晓龙, 等. T形截面带翼缘剪力墙剪滞效应分析及有效翼缘宽度谈论[J].
建筑结构, 2014, 44(22): 67–71.
SHI Qingxuan, WANG Bin, ZHENG Xiaolong, et al. Shear lag effect analysis and effective flange width study of the T-shaped shear wall with flange[J]. Building structure, 2014, 44(22): 67–71. |
| [18] | THOMSEN J H, Ⅳ, WALLACE J W. Displacement-based design of slender reinforced concretestructural walls-experimental verification[J]. Journal of structure engineering, 2004, 130: 618–630. DOI:10.1061/(ASCE)0733-9445(2004)130:4(618) |
| [19] | SAENZ L P. Discussion of equation for the stress-steain curve of concrete by Desayi and Krisbnan[J]. ACI structure journal, 1964, 61(9): 1229–1235. |
| [20] |
GB 50010, 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2010.
GB 50010, Code for design of concrete structures[S]. Beijing:Architecture Industry Press, 2010. |



