玄武岩纤维是一种具有突出力学性能的新型纤维材料,掺入混凝土后,混凝土的力学性能将会受到一定影响[1]。目前国内外对玄武岩纤维混凝土的研究已经获得一些成果:Jiang[2]、Ali[3]、Borhan[4]等人研究了短切玄武岩纤维混凝土的基本力学性能和微观结构,证明了玄武岩纤维能够较大幅度地提高混凝土基本力学性能;El等[5]在大量实验的基础上给出了7 d和28 d龄期的玄武岩纤维最优体积率;Gu 等[6]研究了纤维与基体混凝土的粘结滑移问题。然而,目前对玄武岩纤维混凝土的断裂力学性能研究还相对较少。本文通过不同纤维掺量和长径比的玄武岩纤维混凝土的三点弯曲实验,分析获得的断裂能、断裂韧性和延性指数这三种重要的断裂参数,探讨玄武岩纤维影响混凝土断裂性能的机理,以期为更加全面的研究玄武岩纤维混凝土的断裂性能提供基础。
1 实验概述 1.1 原材料实验采用P.O 42.5级普通硅酸盐水泥,石子为最大粒径20 mm的石灰石碎石,连续级配。细骨料为中粗河砂,细度模数3.47。玄武岩纤维直径为15 μm,抗拉强度为3 300~4 500 MPa,伸长率为3.3%,密度为2.63 kg/cm3。
1.2 实验配比为尽可能减少试件制作过程中造成的离散性,本实验所有试件采用相同的基体并在相同环境下一次浇筑成型。由于纤维混凝土基体一般要求较高强度,因此实验基体采用C40级混凝土、水泥、水、砂、石、减水剂按照质量比427∶196∶717∶1 150∶3配置。共设置31个实验组,其中A0组为基体混凝土。其余各组分别以纤维长径比和体积率为变量,编号规则见下表 1。
| lf/df | ρf | ||||||
| 0 | 0.25 | 0.50 | 0.75 | 1.00 | 1.25 | 1.50 | |
| 333 | A25 | A50 | A75 | A100 | A125 | A175 | |
| 667 | B25 | B50 | B75 | B100 | B125 | B175 | |
| 1 000 | A0 | C25 | C50 | C75 | C100 | C125 | C175 |
| 1 333 | D25 | D50 | D75 | D100 | D125 | D175 | |
| 1 667 | E25 | E50 | E75 | E100 | E125 | E175 | |
| 注:ρf为掺入纤维体积率百分比,lf /df为纤维长径比。 | |||||||
按砂、石、水泥、纤维的顺序加入料斗,干搅30 s后加入预先混入外加剂的拌合水,搅拌3 min后每组成型4个515 mm×100 mm×100 mm三点弯曲试件(图 1)和3个150 mm×150 mm×150 mm标准立方体试件。三点弯曲试件用5 mm 厚端部尖的薄钢板形成一个小于15°的V形缺口(a0=40 mm),待浇筑完毕5 h后取出钢板,24 h后拆模,标准条件下养护28 d。

|
| 图1 试件几何尺寸及加载示意图 Figure 1 Loading sketch with specimen sizes |
本文采用RILEM三点弯曲实验方法进行实验[7]。弯曲试验采用INETRON4505型电子万能试验机开展,最大加载量程100 kN,采用的夹持式引伸计标距12.5 mm,量程5 mm。实验前2天将试件取出晾干,称量每个试件重量(精确到1 N),实验加载速率为0.02 mm/s、跨距S=400 mm。每次加载前检查校核支座距离,以消除由于跨距不同带来的影响。
2 混凝土的断裂参数与计算方法基于断裂力学分析理论,材料的断裂能、断裂韧性和延性指数是三个从不同角度衡量材料断裂性能的重要指标,具有重要的理论和实际意义。
2.1 断裂韧度弹塑性条件下,裂纹失稳扩展而导致材料断裂所对应的应力强度因子即断裂韧度(KIC)。它反映了混凝土对裂纹扩展的抵抗能力。对于中心裂纹三点弯曲实验,一般采用ASTM推荐的公式计算[7]
| ${{K}_{IC}}=\frac{{{P}_{max}}S}{b{{h}^{3/2}}}fa/h$ | (1) |
| $fa/h=2.9a/{{h}^{1/2}}-4.6a/{{h}^{3/2}}+21.8a/{{h}^{5/2}}+37.6a/{{h}^{7/2}}+38.7a/{{h}^{9/2}}$ | (2) |
式中:Pmax为三点弯曲试验最大荷载,S为跨距(本文实验中S=400 mm),b 、h为试件的宽和高。
a定义为混凝土试件的临界有效裂纹长度,对于A组(ρf=0),a=a0。其余各组通过几何关系近似推求[8],详见式(3)、(4)及图 2,其中δt、δm为V型缺口张开出和尖端位移,通过引伸计实测。
| $e=\sqrt{\frac{{{a}_{0}}}{{{\delta }_{m}}/{{\delta }_{t}}-1}-{{\left( {{\delta }_{t}}/2 \right)}^{2}}}$ | (3) |
| $a=e+{{a}_{0}}$ | (4) |

|
| 图2 试件有效长度裂纹计算示意图 Figure 2 Sketch of effective crack length calculation |
断裂能(GF)是基于Hillerborg虚拟裂纹模型并考虑混凝土软化特性的断裂参数[9-10],表征了形成断裂区单位面积所需消耗的能量大小。图 3为B100组获得的典型荷载-挠度曲线(F-δ曲线),断裂能即为该曲线与坐标轴围成的阴影部分面积,断裂能一般采用三点弯曲实验测定,按式(5)计算。
| ${{G}_{F}}=\left( {{W}_{0}}+m\delta \right)/A$ | (5) |

|
| 图3 实测的 B10组典型F-δ曲线 Figure 3 Typical F-δ curve obtained by group B10 |
式中:W0是外载对梁做的功;m为实验支点之间梁重量m1和测量附件的重量m2之和,本实验认为梁重量沿着梁长方向均匀分布,因此有m1=0.777mb,m2实测;δ为压头位移;A为梁的断裂区面积。
2.3 延性指数Chiaia等[11]指出断裂能GF 或者材料的断裂韧度KIC并不能完全衡量材料的断裂性能,因此提出采用延性指数Du(如式6)来衡量混凝土的开裂变形的特征。实际上,延性指数是一个反映材料脆性程度的参数,延性指数越小,材料越脆。
| ${{D}_{u}}={{G}_{F}}/{{P}_{max}}$ | (6) |
图 4是实验获得的一组典型的玄武岩纤维混凝土实测的荷载-裂纹张开位移( F-CMOD)曲线。分析可知,F-CMOD曲线大致可以分为以下3个阶段:近似直线上升的OA段,非直线上升的AB段和非直线下降的BC段。OA段发生在加载的初始阶段,该阶段荷载较小,试件基本处于弹性工作阶段。外载F与裂纹张开位移CMOD之间基本呈线性关系。随着荷载的增加,预制裂纹尖端应力强度因子逐渐增大,跨过某一临界阈值之后,F-CMOD曲线出现第一个拐点A,荷载与裂纹张口位移之间关系由线性转变成非线性。在该拐点和荷载极值点之间的一段曲线范围内,混凝土内部的玄武岩纤维将会通过产生桥连应力的形式发挥作用。随着加载的继续进行,裂纹张开位移的进一步增大,荷载继续呈非线性增加,直至达到峰值荷载,此时F-CMOD曲线出现第二个拐点B,随后开始卸载,此阶段由于纤维被拔出而形成的孔洞将会加速卸载过程,因而曲线趋于陡峭。

|
| 图4 实验获得典型F-CMOD曲线 Figure 4 Typical F-CMOD curve obtained by experimental group B50,C75 and D125 |
由前文分析可知玄武岩纤维混凝土试件的裂纹裂纹扩展过程可以分为以下三个阶段:第一阶段即加载初期的裂纹不扩展阶段。该阶段的试件处于弹性工作状态,玄武岩纤维与混凝土共同工作,裂纹张开位移与荷载近似成线性关系;第二阶段即裂纹的稳定扩展阶段。荷载达到一定阈值后,预制裂纹尖端处的混凝土起裂,裂纹进入稳定扩展阶段。在该阶段,纤维桥产生的桥连应力将延缓裂纹的扩展,裂纹张口位移和荷载之间不再成线性变化关系;第三阶段即裂纹失稳扩展阶段。该阶段始于荷载峰值点,作用于截面上的弯矩、纤维产生的桥连应力以及黏聚力共同作用下在裂纹尖端处产生的净应力强度因子达到混凝土的所能承受之极限,表现为F-CMOD曲线的下降段。
3.2 纤维体积率对混凝土断裂性能的影响定义玄武岩纤维断裂韧度(KIC,ρf)与基体混凝土断裂韧度(KIC,0.00%)比值为断裂韧度增益比CKIC(下文立方体抗压强度、断裂能和延性指数增益比意义类似),它反映了纤维对混凝土断裂韧度的影响。实验获得的各组断裂参数及增益比如表 2所示。
| ${{C}_{{{K}_{IC}}}}={{K}_{IC,{{\rho }_{f}}}}/{{K}_{IC,0.00%}}$ | (7) |
| ${{C}_{{{G}_{F}}}}={{G}_{F,{{\rho }_{f}}}}/{{G}_{F,0.00%}}$ | (8) |
| ${{C}_{{{D}_{u}}}}={{D}_{u,{{\rho }_{f}}}}/{{D}_{u,0,00%}}$ | (9) |
| 组号 | a0/h | fcu /MPa | Cfcu | KIC/(N·m-1) | CKIC | GF/(MPa·m-2) | CGF | Du | CDu |
| A0 | 0.4 | 42.19 | 1.000 | 0.857 | 1.000 | 247.25 | 1.000 | 0.038 4 | 1.000 |
| A25 | 0.4 | 45.79 | 1.085 | 0.913 | 1.065 | 267.10 | 1.080 | 0.041 5 | 1.080 |
| A50 | 0.4 | 47.07 | 1.116 | 1.005 | 1.173 | 276.83 | 1.120 | 0.042 1 | 1.097 |
| A75 | 0.4 | 47.34 | 1.122 | 1.044 | 1.218 | 288.30 | 1.166 | 0.042 6 | 1.111 |
| A100 | 0.4 | 47.94 | 1.136 | 1.057 | 1.234 | 298.71 | 1.208 | 0.042 7 | 1.113 |
| A125 | 0.4 | 48.81 | 1.157 | 1.074 | 1.253 | 305.50 | 1.236 | 0.043 2 | 1.124 |
| A150 | 0.4 | 49.15 | 1.165 | 0.954 | 1.221 | 294.46 | 1.191 | 0.042 8 | 1.114 |
| B25 | 0.4 | 44.56 | 1.056 | 1.040 | 1.114 | 276.87 | 1.120 | 0.042 1 | 1.097 |
| B50 | 0.4 | 44.64 | 1.058 | 1.083 | 1.214 | 292.23 | 1.182 | 0.042 4 | 1.103 |
| B75 | 0.4 | 45.09 | 1.069 | 1.119 | 1.264 | 301.18 | 1.218 | 0.043 5 | 1.132 |
| B100 | 0.4 | 47.21 | 1.119 | 1.143 | 1.306 | 306.38 | 1.239 | 0.043 7 | 1.137 |
| B125 | 0.4 | 49.44 | 1.172 | 1.137 | 1.334 | 316.72 | 1.281 | 0.044 7 | 1.164 |
| B150 | 0.4 | 49.71 | 1.178 | 0.954 | 1.327 | 309.93 | 1.254 | 0.043 5 | 1.132 |
| C25 | 0.4 | 50.60 | 1.199 | 0.972 | 1.135 | 293.42 | 1.187 | 0.043 4 | 1.129 |
| C50 | 0.4 | 48.43 | 1.148 | 1.109 | 1.294 | 308.59 | 1.248 | 0.043 8 | 1.141 |
| C75 | 0.4 | 50.49 | 1.197 | 1.112 | 1.298 | 315.67 | 1.277 | 0.045 8 | 1.192 |
| C100 | 0.4 | 51.44 | 1.219 | 1.181 | 1.378 | 319.48 | 1.292 | 0.044 9 | 1.168 |
| C125 | 0.4 | 51.63 | 1.224 | 1.160 | 1.354 | 326.50 | 1.321 | 0.043 5 | 1.134 |
| C150 | 0.4 | 51.94 | 1.231 | 1.148 | 1.340 | 316.88 | 1.282 | 0.043 1 | 1.123 |
| D25 | 0.4 | 52.78 | 1.251 | 1.040 | 1.213 | 305.30 | 1.235 | 0.041 7 | 1.086 |
| D50 | 0.4 | 52.85 | 1.253 | 1.108 | 1.292 | 316.48 | 1.280 | 0.043 2 | 1.126 |
| D75 | 0.4 | 50.70 | 1.202 | 1.169 | 1.364 | 330.26 | 1.336 | 0.045 1 | 1.176 |
| D100 | 0.4 | 51.23 | 1.214 | 1.236 | 1.442 | 339.20 | 1.372 | 0.043 7 | 1.138 |
| D125 | 0.4 | 51.27 | 1.215 | 1.149 | 1.341 | 335.89 | 1.359 | 0.043 4 | 1.131 |
| D150 | 0.4 | 52.12 | 1.235 | 1.087 | 1.268 | 322.80 | 1.306 | 0.042 9 | 1.118 |
| E25 | 0.4 | 53.15 | 1.260 | 0.974 | 1.136 | 285.05 | 1.153 | 0.042 0 | 1.094 |
| E50 | 0.4 | 53.40 | 1.266 | 1.022 | 1.193 | 292.40 | 1.183 | 0.042 8 | 1.114 |
| E75 | 0.4 | 51.81 | 1.228 | 1.030 | 1.201 | 300.02 | 1.213 | 0.043 4 | 1.131 |
| E100 | 0.4 | 49.92 | 1.183 | 1.109 | 1.294 | 313.16 | 1.267 | 0.042 6 | 1.108 |
| E125 | 0.4 | 50.48 | 1.197 | 1.036 | 1.209 | 323.60 | 1.309 | 0.041 5 | 1.081 |
| E150 | 0.4 | 51.74 | 1.226 | 0.995 | 1.161 | 312.10 | 1.262 | 0.040 0 | 1.041 |
由表 2知,基体混凝土的立方体抗压强度接近配比强度,因此有效。纤维的掺入使得其立方体抗压强度有了一定提高,但是这种提高并不与各自组的变量(纤维体积率或者长径比)成线性增长关系。
图 5给出了实验各组在以纤维体积率为变量时的断裂参数增益曲线。从整体趋势上看,纤维的掺入使得断裂韧度、断裂能以及延性指数都有了不同程度的提高。但是三种断裂参数的增益比都不是纤维体积率的单调函数,更不成简单的线性增长关系,而是经历了一个先上升后下降的过程。其次,各断裂参数在相同长径比和体积率下的增益比互不相同,总体上断裂韧度提高最大,断裂能次之,延性指数最低。再者,各断裂参数对同一纤维长度的敏感度不相同。并且,各断裂参数的增益比最大值对应的体积率也不相同。

|
| 图5 增益比关于体积率的变化曲线 Figure 5 The increment ratio curve affected by volume percentage |
掺入纤维之后,断裂韧度的提高最为明显。实验各组的增益比在1.065~1.442。在长径比为1333、体积率为1.00%情况下断裂韧度增益比达到最大值1.442。增益比最小值在长径比333、体积率0.25%时达到。说明纤维的掺入能够有效提高混凝土抵抗裂纹失稳扩展的能力。而纤维长径比不同,断裂韧度极值增益比所对应的纤维掺量(实验最优体积率)也不同,在长径比为333和666情况下的实验最优体积率为1.25%,其余3组的实验最优体积率为1.00%,这表明断裂韧度的最优纤维体积率不是一个定值,其取值与纤维长径比有关。
玄武岩纤维较大幅度的提高了混凝土的断裂能。D100组的增益比1.372为各实验组最大。其余各组断裂能增益比都随着纤维掺量的增加而增加并在1.25%情况下达到最大值。此后,增益比随着纤维体积率的增加而降低。
玄武岩纤维对混凝土延性指数的提高并不明显。各实验组的延性指数的增益比最大值也只有1.192,这要小于断裂韧度和断裂能的最大增益比。并且延性指数的实验最优体积率较离散,长径比333和667对应的实验最优体积率是分别为1.25%和1.00%,其余3组的实验最优体积率为0.75%。
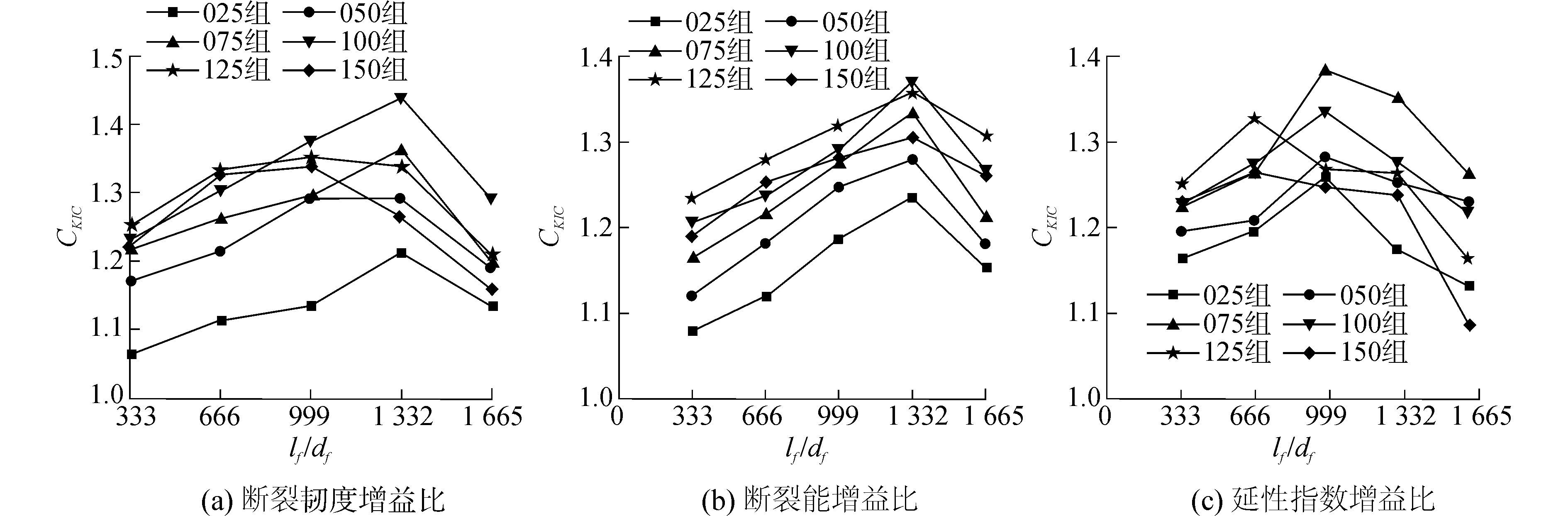
3.3 纤维体积率对混凝土断裂性能的影响纤维长径比指纤维单丝直径与纤维长度的比值。图 6给出了不同长径比下的断裂参数的增益比曲线。从整体上看,增益曲线随着长径比的增大经历了一个先增长后下降的过程,并且在这个过程中峰值之前增益比均为长径比的单调增函数,增益比后为其单调减函数。各参数增益比最大值以及最大值对应的长径比(实验最优长径比)均不相同,不存在一个最佳长径比使得各个参数均取得最大值。
|
| 图6 增益比关于长径比的变化曲线 Figure 6 The increment ratio curve affected by slenderness ratio |
对于不同长径比的纤维,实验结果显示,在纤维体积率不高于1.00%的各组,组内增益比在长径比为1 333时取得最大值,分别是1.213、1.292、1.364和1.442。当纤维体积率为1.25%和1.50%时,实验最优长径比为1 000,增益比分别为1.354和1.340。
对于断裂能,其实验最优长径比情况与断裂韧度相同。当体积率为0.25%、0.5%、0.75%和1.00%情况下,长径比为1333时各组的增益比最大,分别是1.235、1.280、1.336、1.372。纤维体积率在1.25%和1.50%时,最大值出现在长径比为999处,增益比分别为1.359和1.360。
虽然延性指数的增益比也出现上述趋势,但是前四组的实验最优长径比为999,后两组为667。所对应的增益比也较前者小的多,分别只有1.129、1.141、1.192、1.168、1.124和1.114。
3.4 玄武岩纤维影响混凝土断裂性能的机理由实验结果可知,掺入纤维的混凝土的断裂性能,首先无论是断裂韧度还是断裂能或者是延性指数来看,比之于素混凝土都有了一定程度上的提高,但这种提高并不同步。再者,这种提高并不与纤维掺量或者长径比成简单的单调递增或递减关系,而是经历了一个先上升后下降的过程,并且出现了纤维体积较大者其实验最优长径比较小,长径比较小者所对应的最优纤维体积率较大的现象。
纤维作为一种混凝土的掺入物,主要通过桥连应力来影响混凝土的断裂性能。在玄武岩纤维混凝土的桥联区,基体混凝土与纤维之间的界面脱粘、摩阻滑移和倾角效应消耗了一部分能量,换言之,在裂纹前段存在着一定区域的纤维咬合区,该区域增大了裂纹扩展阻力,使裂纹需要扩展不仅要克服主裂纹平面上的阻力还要克服由于纤维拔出所产生的非主裂纹平面上的阻力[12]。因此,从这一方面来说,掺入纤维的确能有效提高混凝土的断裂性能,实验结果也体现了这一点。并且,对于钢纤维这类与基体混凝土粘结和锚固较好的纤维而言,在一定范围内这种促进作用与纤维的特征系数λf成近似的线性关系[10]:
| ${{f}_{f}}={{f}_{0}}\left( 1+\alpha {{\lambda }_{f}} \right)$ | (10) |
| ${{\lambda }_{f}}={{\rho }_{f}}\times {{l}_{f}}/{{d}_{f}}$ | (11) |
式中:ff是纤维混凝土的断裂力学参数(断裂韧度、断裂能或者延性指数),f0是同配比的基体混凝土的相对应参数,α是纤维对强度的影响系数,ρf、lf、df分别是纤维的体积率、长度和单丝直径。
然而,本次实验并未得到与钢纤维混凝土类似的结果。事实上,国内外大量关于玄武岩纤维混凝土的力学性能(包括基本力学性能和断裂力学性能)研究结果也都显示玄武岩纤维混凝土的力学性能不与纤维特征系数成简单线性关系[1-7, 11-12]。一方面,玄武岩纤维柔软纤细,因此在搅拌过程中较易结团,结团将可能导致基体内部形成孔洞,进而产生薄弱界面,降低纤维—水泥石界面力学性能[13];另一方面,玄武岩纤维有吸水性,在拌制和养护过程中玄武岩纤维吸收了其周围原本用于水泥水化的水,从而影响了混凝土基体强度的产生和发展。再者,玄武岩纤维单丝过于纤细,既无法进行有效的表面工艺处理,也无法像钢纤维那样做成弓形加强锚固。因此在加载过程中,纤维与基体的粘结力将远小于纤维的抗拉强度,导致纤维被大量拔出,而由此造成的孔洞将加速试件的破坏过程,导致F-CMOD曲线达到峰值之后快速下降,曲线趋于陡峭。这也是延性指数增益比要小于其余两者增益比的一个重要原因。从这个层面来说,纤维对于混凝土断裂性能又是一种削弱作用。
对于玄武岩纤维混凝土而言,由纤维带来的增强和削弱是同时存在并贯穿于试件的整个工作阶段的。在纤维体积率较低,长径比较小情况下,结团和吸水以及由此带来的孔洞较小,此时增强作用显著,并占据主导地位,断裂性能也随之出现较为显著的增长,而且在一定范围内,这种增强将随着体积率和长径比的增加而增加。当跨过一定阈值之后,结团、吸水和孔洞带来的削弱将逐渐增强并逐渐占据主导地位,从而导致了增益比在上升一段后又出现了下降的现象。
4 断裂参数的数据拟合 4.1 拟合形式如前所述,对玄武岩纤维混凝土而言,由纤维带来的促进和削弱是同时存在的,并且贯穿于混凝土试件的整个工作过程。结合实验获得的增益曲线随着体积率和长径比均呈现先增长后下降的特点,考虑纤维掺入后对混凝土的力学性能削弱也与纤维的特征系数近似成线性关系,定义β为纤维对强度的削弱系数,那么引入削弱函数g(λf):
| $g\left( {{\lambda }_{f}} \right)=1-\beta {{\lambda }_{f}}$ | (12) |
进而玄武岩纤维混凝土的断裂力学参数表示为
| ${{f}_{f}}={{f}_{0}}(1+\alpha {{\lambda }_{f}})\left( 1-\beta {{\lambda }_{f}} \right)$ | (13) |
此时,纤维混凝土的断裂参数将与纤维的特征系数成二次曲线关系,符合试验结果曲线走势。
4.2 拟合结果将实验得到的数据用最小二乘法拟合,得到断裂韧度、断裂能以及延性指数关于纤维体积率和长径比的表达式(14)~(16)。表 3给出了各影响系数的拟合值及其标准差
| ${{K}_{IC}}=0.857(1+0.000\text{ }809{{\rho }_{f}}\frac{{{l}_{f}}}{{{d}_{f}}})(1-0.000\text{ }257{{\rho }_{f}}\frac{{{l}_{f}}}{{{d}_{f}}})$ | (14) |
| ${{G}_{F}}=247.25(1+0.000\text{ }679{{\rho }_{f}}\frac{{{l}_{f}}}{{{d}_{f}}})(1-0.000\text{ }223{{\rho }_{f}}\frac{{{l}_{f}}}{{{d}_{f}}})$ | (15) |
| ${{D}_{u}}=0.0384(1+0.000\text{ }495{{\rho }_{f}}\frac{{{l}_{f}}}{{{d}_{f}}})(1-0.000\text{ }223\text{ }1{{\rho }_{f}}\frac{{{l}_{f}}}{{{d}_{f}}})$ | (16) |
| 参数/系数 | KIC | GF | Du | |||||
| α | β | α | β | α | β | |||
| 拟合值 | 8.09 | 2.57 | 6.79 | 2.23 | 4.95 | 2.23 | ||
| 标准差 | 0.354 | 0.088 4 | 0.350 | 0.010 5 | 0.237 | 0.083 2 | ||
根据拟合函数反算得各组拟合值,按式(17)计算实验值和拟合值的相对误差,得到断裂韧度、断裂能和延性指数相对误差的最大值分别是13.65%、7.95%和13.09%,考虑到混凝土本身存在一定的离散性,因此认为拟合是有效的。
| $\delta =\frac{\left| {{f}_{f,fitting}}-{{f}_{f,experimental}} \right|}{{{f}_{f,experimental}}}$ | (17) |
对于实际工程,纤维和长径比都具有较大可选择性,因此寻求最佳配比就显得尤为总要,根据前文拟合的公式,断裂参数是关于纤维体积率和长径比的曲面,拟合后的曲面断裂韧度,断裂能和延性指数的峰值能到达1.157 N/m,340 MPa/m2和0.050 0,图 7给出了各断裂参数关纤维体积率和长径比的等值曲线,深色部分为最优的纤维体积率和长径比范围,可为实际应用提高参考。

|
| 图7 拟合后的断裂参数关于纤维体积率和长径比的等值曲线 Figure 7 Contour curve of fracture parameters affected by fiber volume ratio and slenderness ratio |
1) 玄武岩纤维混凝土的裂纹扩展过程大致可以分为三个阶段,即加载初期的裂纹不扩展阶段,裂纹稳定扩展阶段和裂纹失稳扩展阶段。
2) 纤维的掺入对各断裂参数均有不同程度的提高。总体而言,断裂韧度提高最显著,断裂能次之,延性指数最差。三者的最大增益比分别为1.442、1.372和1.192。纤维对混凝土断裂性能的提高与纤维体积率和长径比都不成简单的线性关系而是无一例外的经历了一个先增加后降低的过程。
3) 讨论了纤维对断裂性能的增强和削弱机理,据此引入了以纤维特征系数为变量的削弱函数,拟合建立了与实验结果符合较好的各断裂参数关于特征系数的表达式。
4) 根据拟合的函数讨论了玄武纤维混凝土的断裂性能的配比优化问题。给出了各断裂参数关于纤维掺量和长径比的等高分布,可以为实际应用和理论分析提供参考。
| [1] | HIGH C, SELIEM H M, EL-SAFTY A, et al. Use of basalt fibers for concrete structures[J]. Construction and building materials, 2015, 96: 37–46. |
| [2] | JIANG Chaohua, FAN Ke, WU Fei, et al. Experimental study on the mechanical properties and microstructure of chopped basalt fibre reinforced concrete[J]. Materials & design, 2014, 58: 187–193. |
| [3] | ALI N M, WANG Xin, WU Zhisen, et al. Basalt fiber reinforced polymer grids as an external reinforcement for reinforced concrete structures[J]. Journal of reinforced plastics and composites, 2015, 34(19): 1615–1627. |
| [4] | BORHAN T M, BAILEY C G. Structural behaviour of basalt fibre reinforced glass concrete slabs[J]. Materials and structures, 2014, 47(1/2): 77–87. |
| [5] | EL REFAI A, ABED F, ALTALMAS A. Bond durability of basalt fiber-reinforced polymer bars embedded in concrete under direct pullout conditions[J]. Journal of composites for construction, 2015, 19(5): 1943–5614. |
| [6] | GU Xingyu, DONG Qiao. Laboratory test and numerical simulation of bond performance between basalt fiber reinforced polymer rebar and concrete[J]. Journal of testing and evaluation, 2012, 40(7): 1–8. |
| [7] | ASTM. E647-11, Standard test method for measurement of fatigue crack growth rates[S]. United States:ASTM, 2011. |
| [8] | 1GAODanying, ZHANGTingyi. Fracture energy of steel fiber reinforced high strength concrete under the three-point bending[J]. Journal of hydraulic engineering, 2007, 38(9): 1115–1120. |
| [9] | HILLERBORG A, MODÉER M, PETERSSON P E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements[J]. Cement and concrete research, 1976, 6(6): 773–781. |
| [10] | HILLERBORG A. The theoretical basis of a method to determine the fracture energy GF of concrete[J]. Materials and structures, 1985, 18(4): 291–296. |
| [11] | CHIAIA B, VAN MIER J G M, VERVUURT A. Crack growth mechanisms in four different concretes:microscopic observations and fractal analysis[J]. Cement and concrete research, 1998, 28(1): 103–114. |
| [12] | LIPATOV Y V, GUTNIKOV S I, MANYLOV M S, et al. High alkali-resistant basalt fiber for reinforcing concrete[J]. Materials & design, 2015, 73: 60–66. |
| [13] | MA Gao, LI Hui. Experimental study of the seismic behavior of predamaged reinforced-concrete columns retrofitted with basalt fiber-reinforced polymer[J]. Journal of composites for construction, 2015, 19(6): 1943–5614. |



