激光跟踪仪是一种高精度的便携式三维坐标测量设备, 用于超大空间几何量精密测量和动态轨迹测量[1]。激光跟踪仪的工作原理是在目标点上安置一个靶镜, 激光跟踪仪发出的测量光入射到靶镜上, 又返回到跟踪仪。当测量光入射到靶镜的中心位置, 则激光原路返回照射在四象限传感器的中心;当靶镜移动, 激光偏离靶镜中心时, 回到激光跟踪仪的反射光会照射在四象限传感器上偏离中心的位置, 光斑偏离中心的距离即光斑偏移量。控制系统会根据光斑偏移量控制电机转动以调整光束方向直到光斑偏移量为零, 实现对靶镜的跟踪[2-3]。光斑偏移量的高精度实时测量对于提高激光跟踪仪的跟踪精度具有重大的意义。根据四象限传感器的工作原理, 传感器的输出信号与光斑偏移量存在等量关系。但这种关系是非线性的超越函数关系, 为解出光斑偏移量, 常用的解算方法有查表法、迭代法和分段线性插值法等。查表法是非常直接、简单的方法, 但对系统存储空间要求较高。迭代法程序存储量小, 但迭代需要对反函数进行多次计算, 计算量较大, 对于实时性要求较高的场合不适用, 并且迭代次数越多计算结果的累积误差越大[4]。分段线性插值法就是在小范围内用分段的直线去拟合曲线, 并用直线段来代替曲线作近似处理的方法, 这种方法在计算精度与分段范围上很难平衡, 而且分段越细运算量越大[2]。
本文结合激光光斑的特性, 提出了采用泰勒级数展开算法解算光斑偏移量, 并基于此设计了光斑偏移量测量系统, 进行了相应的验证实验。
1 光斑偏移量的测量原理 1.1 光斑偏移量的推导四象限传感器作为一种常用的位置敏感器件, 当入射光斑落在器件感光面的不同位置时, 四象限传感器的每个象限输出不同幅度的电流信号, 通过对这些信号的幅度进行计算, 可以确定入射光斑中心在感光面上的位置[5-6]。
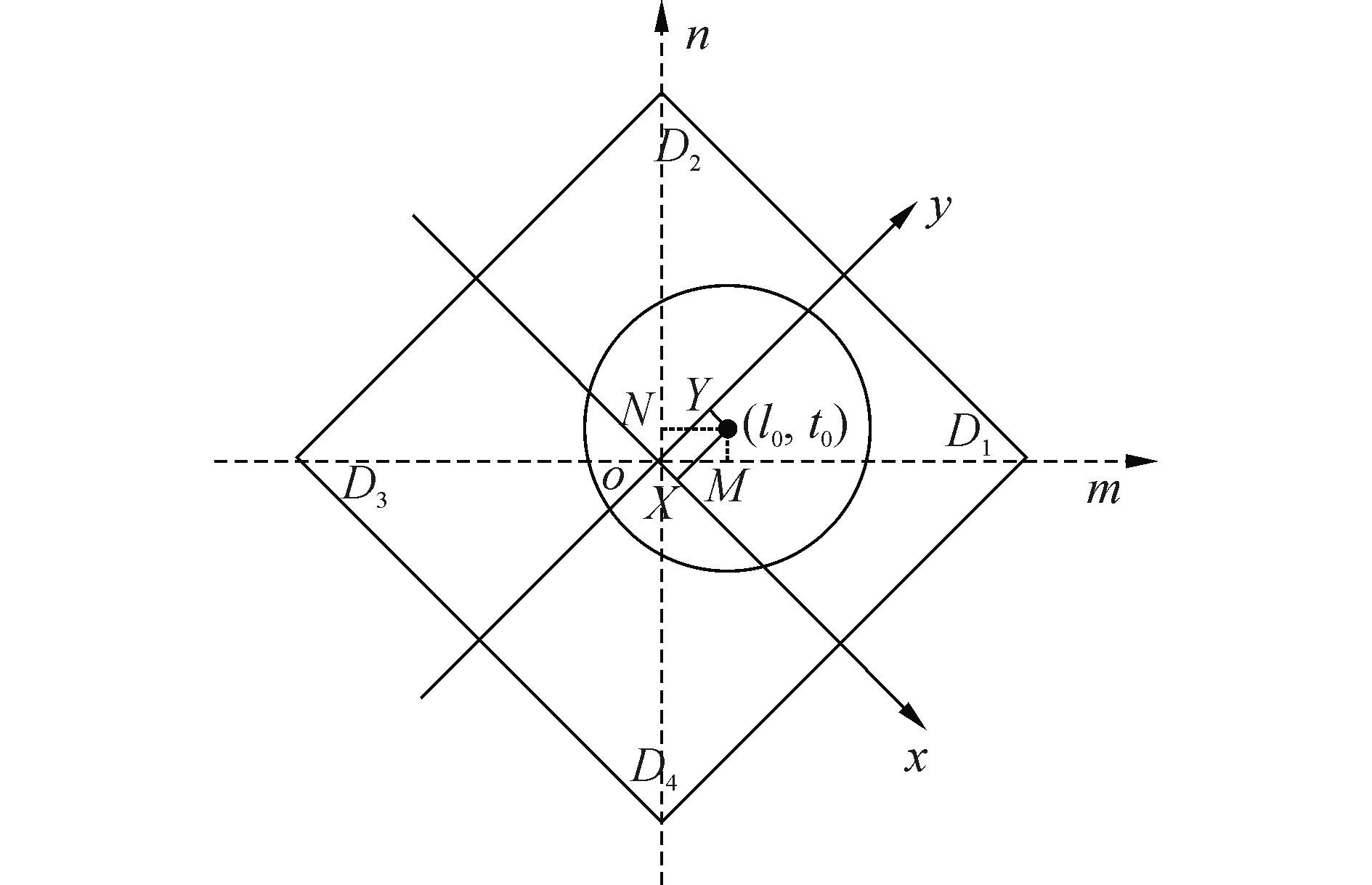
在本系统中将四象限传感器采用如图 1所示对角线法布置, 即将四象限传感器的坐标轴相对于系统位置坐标轴顺时针旋转45°。保持激光垂直照射在四象限传感器上, 当激光光斑在系统坐标系内沿水平(竖直)方向移动时, 光斑相应地在四象限传感器坐标系内沿对角线方向移动[6-7]。对角线算法有利于扩展线性区的范围, 其线性区的范围是常规加减算法的$\sqrt 2 $倍[7-8]。设系统的坐标系为mon, 四象限传感器坐标系为xoy, 激光光斑中心在四象限坐标系下的坐标为(X,Y), 激光光斑中心在系统坐标系下的坐标为(M,N), 激光光斑的半径为r, 则光斑边界围成的圆在四象限传感器坐标系下的方程为
|
| 图1 四象限传感器光斑几何关系示意图 Figure 1 Quadrant photodiode geometry |
| ${{\left( x-X \right)}^{2}}+{{\left( y-Y \right)}^{2}}={{r}^{2}}$ | (1) |
根据极坐标与直角坐标的转换公式:
| $\left\{ \matrix{ x = l{\rm{cos }}t,y = l{\rm{sin }}t \hfill \cr X = {l_0}{\rm{cos }}{t_0},Y = {l_0}{\rm{sin }}{t_0} \hfill \cr} \right.$ | (2) |
式中:l是四象限传感器坐标系下圆上任意一点的极径, t是圆上任意一点的极角, l0 是圆心的极径, t0 是圆心的极角。将式(1) 转换成极坐标系下的方程为
| ${l^2} + {l_0}^2 - 2l{l_0}{\rm{cos}}t - {t_0} = {r^2}$ | (3) |
由于四象限传感器输出光电流很小, 要对每个象限的输出信号进行放大处理。设I1、I2、I3、I4表示按逆时针顺序排列的4个象限的输出光电流,U1、U2、U3、U4分别表示各路电流经过放大后的输出电压值, 则:
| ${U_k} = \beta {I_k}$ | (4) |
式中:β为4路放大电路的增益。
由四象限传感器工作原理, 四象限传感器得到的电流信号与光斑投射在传感器光敏面上的面积成正比, 设比例系数为A, 则式(4) 表示为
| ${U_k} = \beta {I_k} = \beta A{S_k}$ | (5) |
式中:Sk是光斑在每个象限Dk上的光照面积。
激光光斑沿系统坐标系水平x方向的原始偏差信号, 也即光斑沿四象限传感器坐标系对角线m方向的原始偏差信号Em , 可以由相对象限D1、D3 上的光照面积求出:
| ${E_m} = \beta A\left( {{S_1} - {S_3}} \right) = {U_1} - {U_3}$ | (6) |
同理, 激光光斑沿竖直方向的原始偏差信号, 也即光斑沿四象限传感器坐标系对角线n方向的原始偏差信号En为
| ${E_n} = \beta A\left( {{S_2} - {S_4}} \right) = {U_2} - {U_4}$ | (7) |
对两个方向的原始偏差信号Em、En进行归一化处理得到Km、Kn:
| $\eqalign{ & {K_m} = {{{S_1} - {S_3}} \over {{S_1} + {S_2} + {S_3} + {S_4}}} = {{{U_1} - {U_3}} \over {{U_1} + {U_2} + {U_3} + {U_4}}} \cr & {K_n} = {{{S_2} - {S_4}} \over {{S_1} + {S_2} + {S_3} + {S_4}}} = {{{U_2} - {U_4}} \over {{U_1} + {U_2} + {U_3} + {U_4}}} \cr} $ | (8) |
每个象限的光照面积在极坐标系下利用二重积分来计算, 则第一象限D1的光照面积S1为
| ${S_1} = \smallint _0^{\pi /2}\smallint _0^{lt}l{\rm{d}}l{\rm{d}}t = \smallint _0^{\pi /2}{{l{{\left( t \right)}^2}} \over 2}{\rm{d}}t$ | (9) |
由式(3) 得到极坐标系下的l(t)为
| $l\left( t \right) = {l_0}{\rm{cos}}\left( {t - {t_0}} \right) + \sqrt {{{\left( {{l_0}{\rm{cos}}\left( {t - {t_0}} \right)} \right)}^2} - l_0^2 + {r^2}} $ | (10) |
对于第二、三、四象限D2、D3、D4上的光照面积, 只需要分别把式(9) 中的极角t的积分限分别换成π/2, π、π,3π/2、3π/2,2π, 然后将式(9) 、(10) 代入式(8) 分别得到m、n方向上光斑归一化后的偏移信号:
| $\eqalign{ & {K_m}X,Y = {{\left( {X/r} \right)\sqrt {1 - {{\left( {X/r} \right)}^2}} + {\rm{arcsin}}\left( {X/r} \right)} \over \pi } + \cr & {{\left( {Y/r} \right)\sqrt {1 - {{\left( {Y/r} \right)}^2}} + {\rm{arcsin}}\left( {Y/r} \right)} \over \pi } \cr} $ | (11) |
| $\eqalign{ & {K_n}\left( {X,Y} \right) = {{\left( {Y/r} \right)\sqrt {1 - {{\left( {Y/r} \right)}^2} + {\rm{arcsin}}\left( {Y/r} \right)} } \over \pi } - \cr & {{\left( {X/r} \right)\sqrt {1 - {{\left( {X/r} \right)}^2}} + {\rm{arcsin}}\left( {X/r} \right)} \over \pi } \cr} $ | (12) |
进行和差变换, 得到四象限传感器输出信号与四象限传感器坐标系中的光斑偏移量的方程为
| $\eqalign{ & \left[ \matrix{ {K_m}\left( {X,Y} \right) - {K_n}\left( {X,Y} \right) \hfill \cr {K_m}\left( {X,Y} \right) + {K_n}\left( {X,Y} \right) \hfill \cr} \right] = \cr & 2\left[ \matrix{ {{\sqrt {\left( {X/r} \right)\sqrt {1 - {{\left( {X/r} \right)}^2}} + {\rm{arcsin}}\left( {X/r} \right)} } \over \pi } \hfill \cr {{\left( {Y/r} \right)\sqrt {1 - {{\left( {Y/r} \right)}^2}} + {\rm{arcsin}}\left( {Y/r} \right)} \over \pi } \hfill \cr} \right] \cr} $ | (13) |
由等式(13) 可以看出, 光斑偏移量的解算方程是超越函数方程, 直接求解异常繁锁, 采用下述方式给予解决:
在激光跟踪仪工作过程中, 由于光斑中心离开坐标原点的距离X、Y均远小于光斑的半径r, 对式(13) 取一级近似得到:
| $\left[ \matrix{ {K_m}\left( {X,Y} \right) - {K_n}\left( {X,Y} \right) \hfill \cr {K_m}\left( {X,Y} \right) + {K_n}\left( {X,Y} \right) \hfill \cr} \right] \approx 2\left[ \matrix{ {X \over {\pi r}} \hfill \cr {Y \over {\pi r}} \hfill \cr} \right]$ | (14) |
根据从传感器信号处理电路得到的光斑偏移信号KmX,Y、KnX,Y和已知的光斑半径r按照式(14) 求出一组光斑中心在四象限传感器坐标系的近似值X0,Y0。再对式(13) 在X0,Y0处取泰勒展开, 有
| $\eqalign{ & \left[ \matrix{ {K_m}\left( {X,Y} \right) - {K_n}\left( {X,Y} \right) \hfill \cr {K_m}\left( {X,Y} \right) + {K_n}\left( {X,Y} \right) \hfill \cr} \right] = \sqrt 2 \cr & \left[ \matrix{ {{\left( {{{{X_0}} \over r}} \right)\sqrt {1 - {{\left( {{{{X_0}} \over r}} \right)}^2}} + {\rm{arcsin}}\left( {{{{X_0}} \over r}} \right)} \over \pi } + {{2\left( {{{\sqrt {{r^2} - X_0^2} } \over {{r^2}}}} \right)} \over \pi }\Delta X - {{{X_0}} \over {{{{r^2}\sqrt {{r^2} - X_0^2} } \over \pi }}}\Delta {X^2} \hfill \cr {{\left( {{{{Y_0}} \over r}} \right)\sqrt {1 - {{\left( {{{{Y_0}} \over r}} \right)}^2}} + {\rm{arcsin}}\left( {{{{Y_0}} \over r}} \right)} \over \pi } + {{2\left( {{{\sqrt {{r^2} - Y_0^2} } \over {{r^2}}}} \right)} \over \pi }\Delta Y - {{{{{Y_0}} \over {{{\sqrt {{r^2} - Y_0^2} } \over {{r^2}}}}}} \over \pi }\Delta {Y^2} \hfill \cr} \right] \cr} $ | (15) |
式(15) 是两个关于ΔX、ΔY的一元二次方程, 利用求根公式求出光斑中心坐标的修正值(ΔX、ΔY)。把光斑中心坐标的近似值(X0,Y0)与修正值(ΔX、ΔY)相加, 得到光斑中心在当前位置四象限传感器坐标系中的准确坐标(X,Y)。
转换四象限传感器坐标系xoy下的光斑中心坐标到系统坐标系mon下, 如图 1所示, 两个坐标系间的夹角是45°, 根据坐标变换公式, 光斑中心在系统坐标系mon中的坐标表达式为
| $\left[ \matrix{ M \hfill \cr N \hfill \cr} \right] = \left[ {\matrix{ {{{\sqrt 2 } \over 2}} & {{{\sqrt 2 } \over 2}} \cr { - {{\sqrt 2 } \over 2}} & {{{\sqrt 2 } \over 2}} \cr } } \right]\cdot\left[ \matrix{ X \hfill \cr Y \hfill \cr} \right] = {{\sqrt 2 } \over 2}\left[ \matrix{ X + Y \hfill \cr Y - X \hfill \cr} \right]$ | (16) |
最后, 根据式(16) 得到光斑在当前位置系统坐标系中水平和垂直方向上准确的偏移量M和N, 进而控制偏摆和俯仰方向的电机准确进行跟踪。
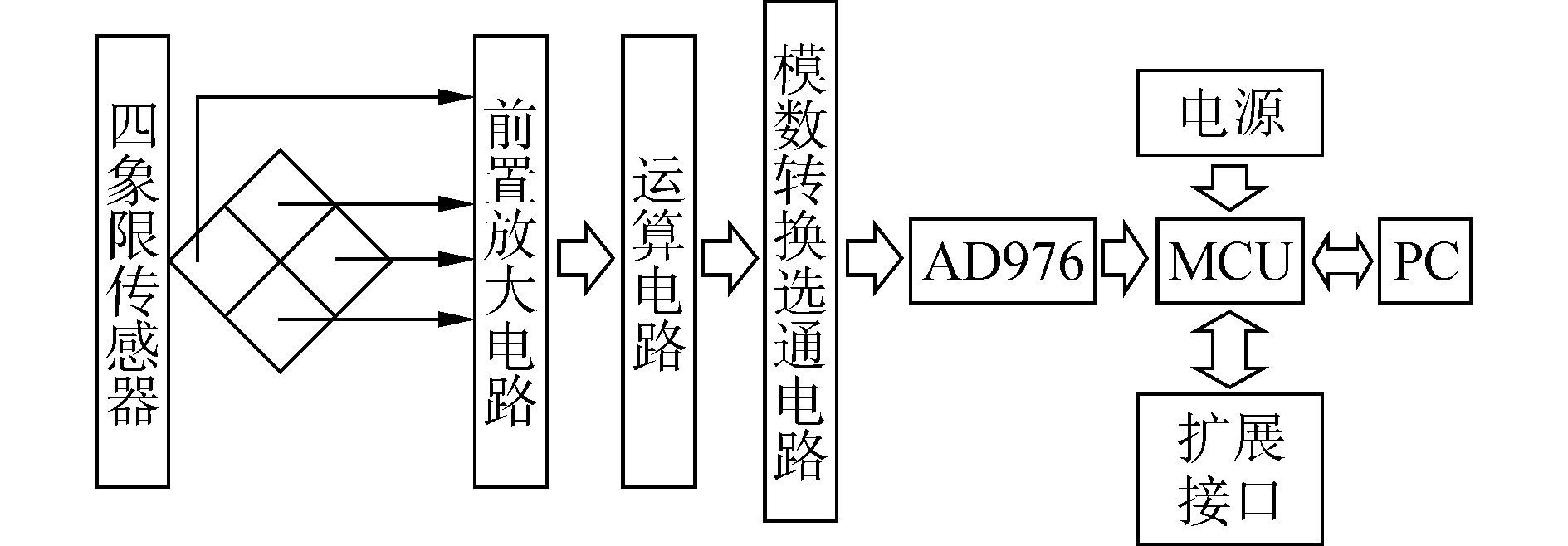
2 光斑偏移量测量系统设计激光跟踪仪的工作过程是一个随动过程, 目标靶镜运动不规则, 速度变化范围较大, 尤其是在靶镜运动的加速和减速阶段及靶镜高速运动时, 对跟踪控制机构的动态性能要求较高[9]。这就要求发现靶镜运动和反映靶镜位移的四象限传感器的信号处理电路具有快速、准确的动态响应[10]。因此, 设计了以STC15F2K60S2芯片为核心的抗干扰性能优越的数字信号处理电路。整个系统的硬件结构框图如图 2所示。
|
| 图2 光斑偏移量测量系统框图 Figure 2 Block diagram of spot offset measurement system |
激光照射在四象限传感器表面, 传感器会输出四路与光能大小相关的弱电流信号, 经I/V转换、放大滤波后, 将信号调理为-10~+10 V的标准信号, 送入16位模数转换器AD976进行模数转换。处理器通过对数字量的分析计算得到光斑偏移量信息, 并将偏移量数据发送至上位机进行实时显示。
为提高程序的可读性和可维护性, 软件设计采用自顶向下、模块化设计的思想。程序主要包括AD976采集模块、定时器延时模块、平均滤波模块、光斑偏移量计算模块以及串口发送模块等。
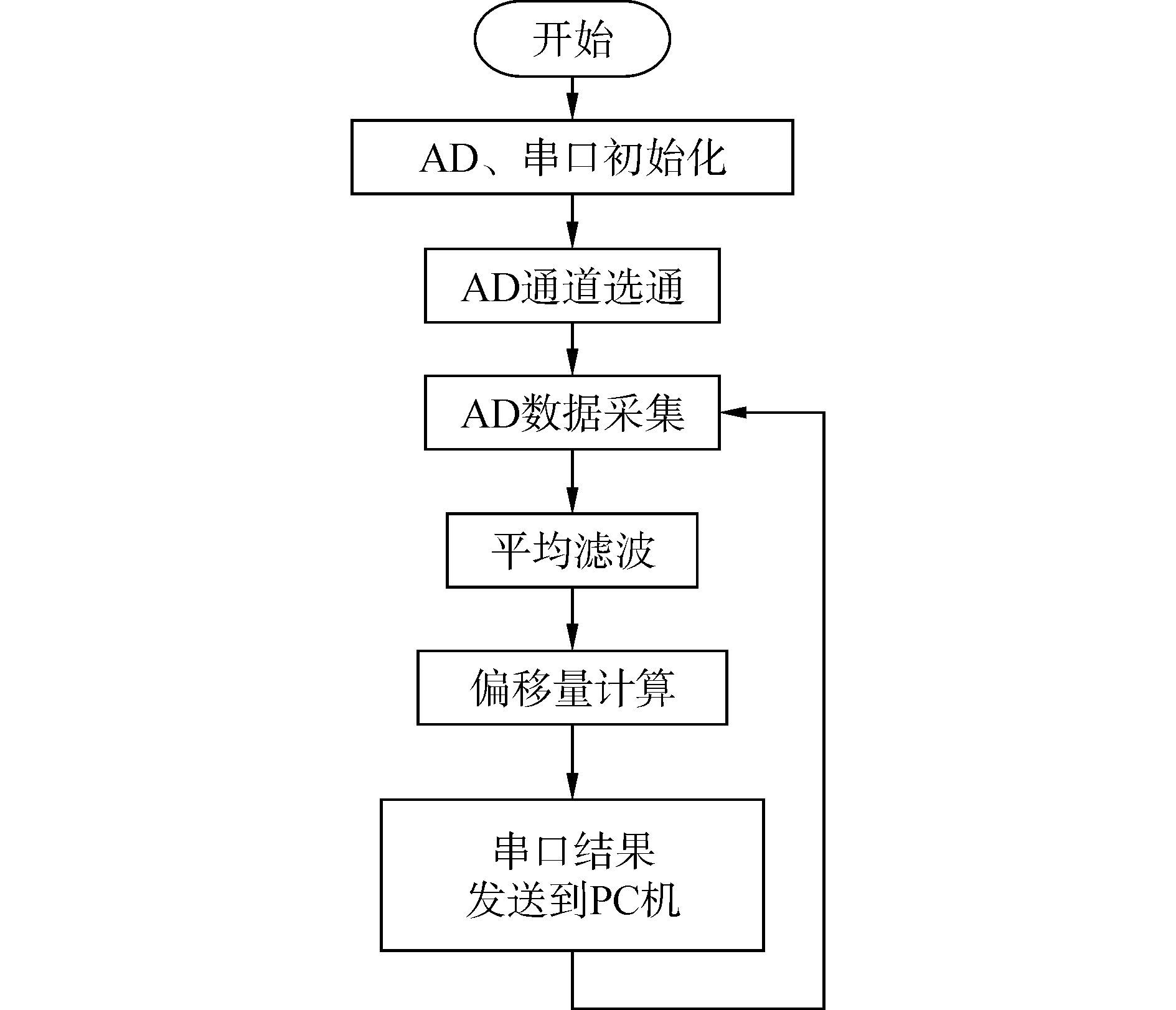
在Keil uVision4中对光斑偏移量测量进行仿真, 完成一次光斑偏移量的测量需要0.000 951 56 s, 即一秒钟可以测量1 050次光斑偏移量, 达到了对光斑偏移量的实时测量。软件设计主程序流程图如图 3所示。
|
| 图3 主程序流程图 Figure 3 Flow chart of main program |
为了测试基于文中所提出算法的光斑偏移量测量系统, 在FormFree300上完成了相关实验, 并对实验数据进行了分析[11-12]。实验所用的光源为德国SIOS Meβtechnik GmbH公司的激光干涉仪, 其经过耦合的输出功率大约800 μW左右, 激光光斑直径为2 mm。FormFree300是一台高精度的柱式直角坐标测量机, 它的测量工作平台通过气浮装置安装在基座平面上, 并通过H型机构导向实现X方向和Y方向的直线运动, 其中X轴的定位精度经过调试达到0.717 μm, Y轴的定位精度为2.451 μm。四象限传感器采用的是日本滨松公司的S5980。实验装置如图 4所示。

|
| 图4 实验装置图 Figure 4 Experimental equipment |
把SIOS激光干涉仪固定在三角架上, 四象限传感器固定在Formfree300的测量工作台上。然后垂直方向上调节三角架, 水平方向上调节气浮平台, 让四象限传感器输出的偏差信号为零, 此时激光光斑位于四象限传感器中心。保持SIOS激光干涉仪不动, 控制Formfree300 X轴上的气浮平台从中心位置向两边以50 μm为步距各移动10次, 同时上位机接收处理器输出的传感器信号和光斑偏移量数据。每个位置下四象限传感器输出偏差信号Km、Kn, 及根据偏差信号求出的光斑偏移量如表 1所示。
| 平台位移/μm | Km | Kn | 光斑偏移量/μm |
| -500 | -0.563 1 | -0.011 3 | -493.619 0 |
| -450 | -0.524 6 | -0.013 0 | -441.541 0 |
| -400 | -0.475 1 | -0.008 0 | -392.894 0 |
| -350 | -0.424 8 | -0.007 0 | -344.628 0 |
| -300 | -0.373 6 | -0.006 4 | -298.587 0 |
| -250 | -0.316 7 | -0.004 7 | -250.828 0 |
| -200 | -0.259 0 | -0.004 9 | -202.510 0 |
| -150 | -0.196 9 | -0.005 6 | -151.443 0 |
| -100 | -0.133 0 | -0.003 0 | -102.466 0 |
| -50 | -0.065 6 | -0.001 3 | -50.544 0 |
| 0 | 0.000 7 | -0.002 3 | 2.356 0 |
| 50 | 0.065 9 | -0.001 2 | 52.749 0 |
| 100 | 0.132 1 | 0.005 7 | 99.608 0 |
| 150 | 0.197 3 | 0.008 5 | 149.432 0 |
| 200 | 0.250 5 | 0.007 2 | 193.645 0 |
| 250 | 0.313 0 | 0.006 3 | 246.341 0 |
| 300 | 0.374 5 | 0.004 8 | 300.803 0 |
| 350 | 0.425 2 | 0.005 0 | 346.886 0 |
| 400 | 0.475 6 | 0.005 6 | 395.884 0 |
| 450 | 0.523 0 | 0.003 0 | 451.582 0 |
| 500 | 0.565 9 | 0.001 3 | 513.161 0 |
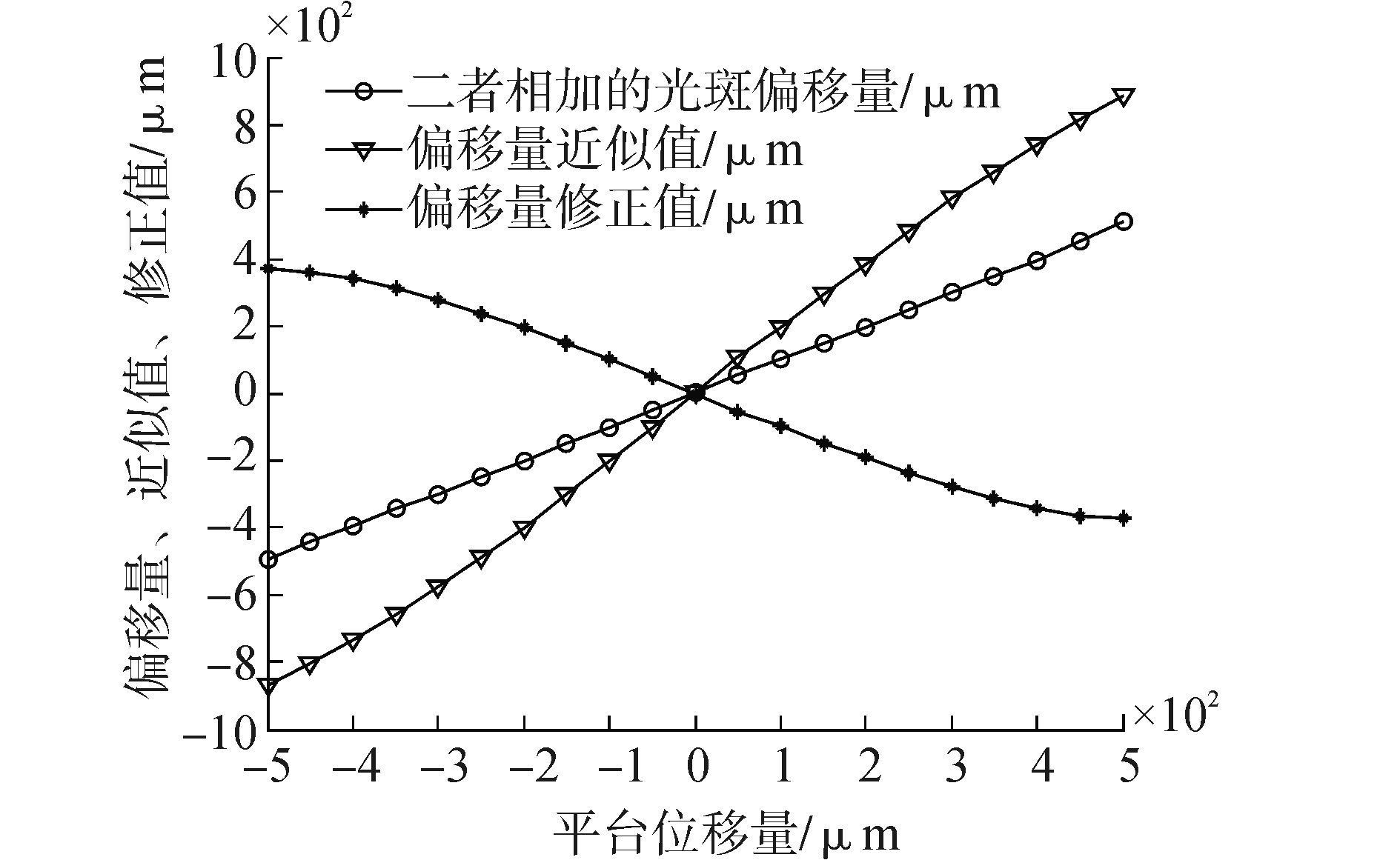
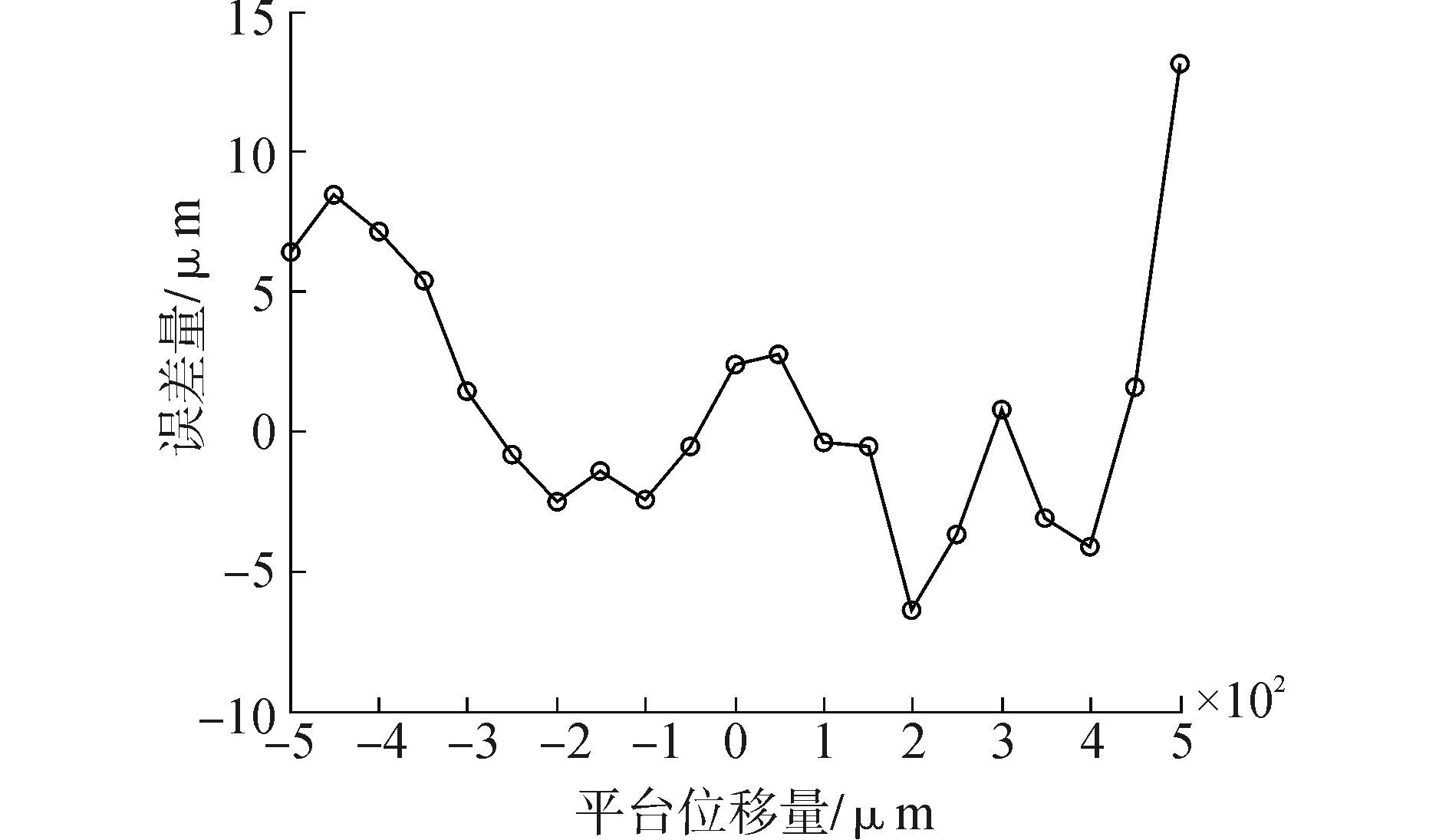
同时把计算过程中的系统坐标系下偏移量近似值与偏移量修正值绘制如图 5所示的曲线图。把平台位移量与系统坐标系下光斑偏移量间的误差绘制如图 6所示曲线图。在图 5中, 通过泰勒级数展开求出的光斑偏移量修正值对根据光斑特性求出的偏移量估计值有修正作用, 使其能很快接近真实的光斑偏移量。结合误差曲线图 6, 距离传感器的中心的距离越近, 测量误差越小;距离传感器中心的距离越远, 测量误差越大。在±400 μm的范围内, 测量误差在6 μm;在±500 μm的范围内, 测量误差在13.2 μm以内。
|
| 图5 计算出的偏移量、偏移量近似值、偏移量修正值 Figure 5 Curve of offset calculated,approximate value of offset and correction value of offset |
|
| 图6 平台位移与计算出光斑偏移量间的误差曲线图 Figure 6 Error curve between displacement of platform and spot offset |
在通常情况下, 随着背景光所占比例的增大, 四象限传感器的检测范围有所降低, 检测灵敏度也有一定程度的降低[13]。根据式(8) , 背景光的存在, 使得分母上的S1+S2+S3+S4在很大程度上增加了, 但是对于分子上的S1-S3和S2-S4几乎没有影响, 这就使得Km和Kn在一定程度上减小, 从而降低了量程范围。在±400 μm以外的范围, 测量误差突然增大是因为这一区域在四象限传感器线性区域的边缘[14], 超出了传感器测量范围。
4 结论1) 采用泰勒级数展开算法可以解算四象限传感器输出信号与光斑偏移量之间准确的等量关系;
2) 通过搭建用于激光跟踪的光斑偏移量测量系统进行实验, 表明该测量系统测量速度快、测量精度高。
| [1] | ZHOU Guofeng, LI Xiaoxing, LI Dongsheng, et al. Large-scale compact range on-site alignment based on laser tracker measurement network[J]. Measurement, 2015, 68: 143–154. DOI:10.1016/j.measurement.2015.02.036 |
| [2] |
周培松, 卢荣胜, 周维虎, 等. 四象限探测器用于激光跟踪仪目标脱靶量测量[J].
光电技术应用, 2014, 29(1): 75–79.
ZHOU Peisong, LU Rongsheng, ZHOU Weihu, et al. Measurement system for laser tracker's target-missing quantity based on four-quadrant detector[J]. Electro-optic technology application, 2014, 29(1): 75–79. |
| [3] | ACERO R, BRAU A, SANTOLARIA J, et al. Verification of an articulated arm coordinate measuring machine using a laser tracker as reference equipment and an indexed metrology platform[J]. Measurement, 2015, 69: 52–63. DOI:10.1016/j.measurement.2015.03.023 |
| [4] |
郭绍忠, 许瑾晨, 陈建勋. 一种改进的超越函数通用算法[J].
计算机工程, 2012, 38(15): 31–34.
GUO Shaozhong, XU Jinchen, CHEN Jianxun. Improved transcendental function general algorithm[J]. Computer engineering, 2012, 38(15): 31–34. |
| [5] | BARBARIĈŽP, MANOJLOVIĈ S M, BONDŽULIĈB P, et al. New relationship of displacement signal at quadrant photodiode:Control signal analysis and simulation of a laser tracker[J]. Optik-international journal for light and electron optics, 2014, 125(4): 1550–1557. DOI:10.1016/j.ijleo.2013.10.012 |
| [6] | LU Chao, ZHAI Yusheng, WANG Xinjie, et al. A novel method to improve detecting sensitivity of quadrant detector[J]. Optik-international journal for light and electron optics, 2014, 125(14): 3519–3523. DOI:10.1016/j.ijleo.2014.01.059 |
| [7] | HAO Xiang, KUANG Cuifang, KU Yulong, et al. A quadrant detector based laser alignment method with higher sensitivity[J]. Optik-international journal for light and electron optics, 2012, 123(24): 2238–2240. DOI:10.1016/j.ijleo.2011.10.031 |
| [8] |
余峰, 何烨, 李松, 等. 四象限光电检测系统的定位算法研究及改进[J].
应用光学, 2008, 29(4): 493–497.
YU Feng, HE Ye, LI Song, et al. Improvement of positioning algorithm for four-quadrant optoelectronic detection system[J]. Journal of applied optics, 2008, 29(4): 493–497. |
| [9] |
王为农, 苏永昌, 任国营. 激光跟踪仪的动态特性研究[J].
计量学报, 2007, 28(1): 34–36.
WANG Weinong, SU Yongchang, REN Guoying. A study on dynamic character of laser tracker[J]. Acta metrologica sinica, 2007, 28(1): 34–36. |
| [10] | YAN Z S, LIN Wenhan, LIU C H. Measurement of the thermal elongation of high speed spindles in real time using a cat's eye reflector based optical sensor[J]. Sensors and actuators a:physical, 2015, 221: 154–160. DOI:10.1016/j.sna.2014.11.003 |
| [11] | LEE H W, CHEN C L, LIU C H. Development of an optical three-dimensional laser tracker using dual modulated laser diodes and a signal detector[J]. Review of scientific instruments, 2011, 82(3): 035101. DOI:10.1063/1.3549138 |
| [12] | MISSOFFE A, CHASSAGNE L, TOPÇU S, et al. New simple optical sensor:From nanometer resolution to centimeter displacement range[J]. Sensors and actuators A:physical, 2012, 176: 46–52. DOI:10.1016/j.sna.2012.01.007 |
| [13] |
陈琳. 影响四象限探测器探测结果的若干因素的研究[J].
仪器仪表用户, 2010, 17(4): 56–57.
CHEN Lin. Studies processes in the result of QD detection[J]. Electronic instrumentation customers, 2010, 17(4): 56–57. |
| [14] | ZHANG Leihong, YANG Yan, XIA Wenbing, et al. Linearity of quadrant avalanche photodiode in laser tracking system[J]. Chinese optics letters, 2009, 7(8): 728–731. DOI:10.3788/COL |



