多自治水下机器人(autonomous underwater vehicle,AUV)系统的任务分配算法涵盖两方面:任务分配和路径规划,即指依据一定的算法控制一组AUV,各自沿着运动学约束条件下的优化路径到达目标的技术。其中任务分配是指将任意数目的目标分配给多AUV系统,在保证所有目标被遍历的前提下,整个多AUV系统的代价最小[1]。路径规划技术是指在全局任务分配后,针对单一AUV的路径规划方法。
任务分配算法的研究目前已经有不少的理论和研究成果,市场机制[2-3]算法是解决多任务分配作业中最常见的方法;另一种常见任务分配算法就是蚁群算法[4],主要研究动态环境下多机器人系统在动态环境下自主任务分配问题。在此基础上文献[5]进一步提出了适合于大规模多机器人集群的任务分配算法。自组织神经网络算法也可以应用于多任务分配,该算法是由Kohonen[6]于20世纪80年代提出的,文献[7-9]将自组织神经网络应用于多移动机器人系统的任务分配与路径规划中。文献[10]采用了自组织映射(self-organizing map,SOM)神经网络算法,提出了在二维海洋环境下的多AUV系统的动态任务分配。在此基础上文献[11]进一步将自组织映射(SOM)神经网络的多AUV多目标分配策略推广应用到三维海洋环境中。虽然多任务分配问题已经得到了广泛的研究,但是,以往的研究均未考虑AUV水下运动学约束和障碍物问题。实际环境中的AUV水下任务分配与路径规划,不能忽略运动学约束和障碍物环境的实际存在,本文主要对此进行深入研究。
路径规划则是AUV需要具备的智能行为之一。所谓路径规划,是在具有障碍物的环境中,AUV按照一定的评价标准,找到一条从起始状态到达目标状态的无碰撞路径[12-14]。传统的路径规划方法主要有:可视图法[15]、人工势场法[16]、遗传算法[17]、模糊逻辑法[18]等。这些路径规划方法都有各自的适用范围,但是,AUV的水下运动具有局限性,它的转向性能受到方向舵最大偏角的制约,因此其转向时的最小转向半径为R,AUV的转弯半径无法比R更小,在运动上就受到约束,传统的路径规划方法并没有考虑这一点。能够处理运动学约束的路径规划方法是Dubins路径规划方法[19],该方法主要基于以下定理:在运动方向已知和转向半径最小的情况下,从初始向量到终止向量的最短的路径是由直线和最小半径转向圆弧组成的。AUV在任务分配和路径规划时,采用最短路径可以有效的节约能量。
本文研究二维环境中运动学约束条件下的多AUV系统的任务分配和路径规划问题,并考虑了障碍物等干扰因素。通过将Dubins Path算法与改进的自组织特征映射(SOM)神经网络算法相结合,本文提出一种新型的任务分配与路径规划算法。
1 运动学约束下任务分配算法设计本文针对多AUV、多目标点,采用一种基于SOM神经网络和Dubins路径的方法,处理多AUV系统的多任务分配及相应的路径规划问题。在该方法中,AUV运动规划集成在任务分配当中,从而一旦总体任务给出,AUV就可以开始运动。此外,多AUV系统可以自动安排总任务,并根据环境的变化动态实时调整运动规划。
对于不考虑运动学约束的静态多AUV任务分配与路径规划,AUV的路径只是简单的点对点的规划,当遇到障碍物直线路径被阻断时,则需要规划曲线路径甚至更换AUV去执行任务。但是,在真实的水下工作空间内,AUV不可能实现任意拐角转向的任务。第一,AUV在运动过程中受到惯性的制约,导致其不可能在需要转向时先紧急制动停下来,然后再直线向目标前进。第二,对于某一个具体的水下AUV而言,巡航的过程中总是会受到方向舵最大偏角的制约。考虑运动学限制的AUV路径规划算法的基本思想是:在有限的工作空间内,将AUV和目标点视为质点,保持AUV运动速度不变,控制其沿着Dubins路径到达目标点。Dubins路径算法是实现从一个向量到另外一个向量的最短的路径,使一个向量经过一定的平滑转弯能够与另一个向量方向一致。平滑转弯曲线有很多种,但最小半径圆弧转弯是最短的路径。用C表示圆弧,L表示直线,已经证明,为保证最短路径的要求,CLC路径是一种理想的方式[20]。
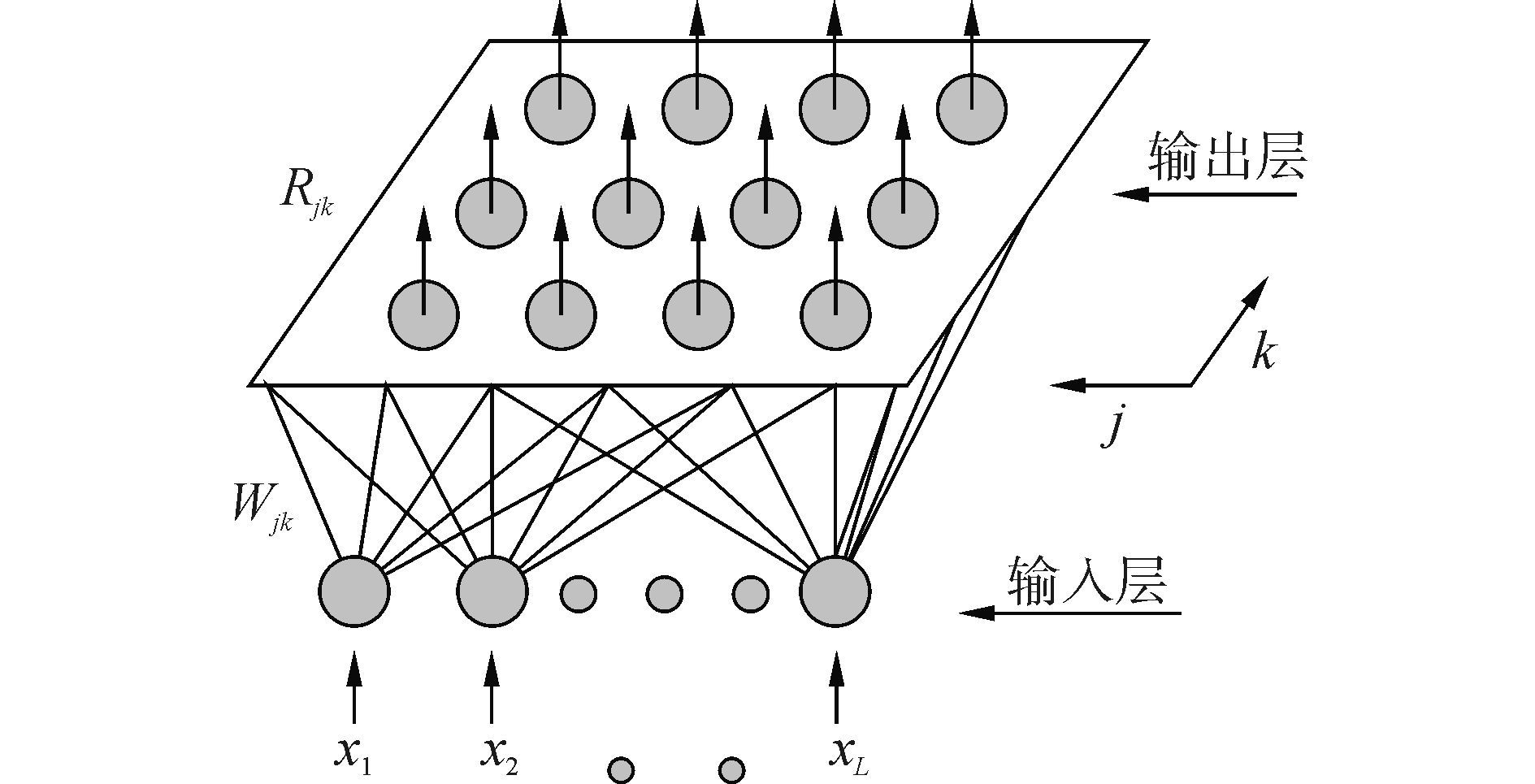
1.1 SOM神经网络SOM算法最大的特点之一就是能够使相似输入产生相似的输出,输入信号的特征越相近,输出映射也越接近。SOM网络由输入层和输出层组成,其中输出层也即竞争层。输入层通过权向量将外界信息汇集到输出层各神经元,竞争层负责对输入模式进行“比较”,“分析”,寻找规律,并归类。如图 1所示,输入层可以是一维的神经元,竞争层可以是二维的神经元,输入层的神经元和输出层的神经元有权值连接。
|
| 图1 AUV编队与虚拟结构的位置关系 Figure 1 Position relationship between AUV formation and virtual structure |
由于自组织映射算法是一种无导师的聚类法,它能将任意维输入模式在输出层映射成一维或二维离散图形,具有聚类功能、自组织功能、自学习功能。SOM神经网络采用的算法是在“胜者为王”(winner-take-all,WTA)学习规则基础上加以改进的。这种竞争学习规则的生理学基础是神经细胞的侧抑制现象,当一个神经细胞兴奋后,会对其周围的神经细胞产生抑制作用。
SOM神经网络的学习按如下步骤进行:
1) 初始化,即对输出层各权向量赋值并进行归一化处理;
2) 接受输入,即从训练集中随机取一个输入模式并进行归一化处理;
3) 寻找获胜节点,按照竞争规则计算;
4) 定义优胜邻域,确定t时刻的权值调整域,一般初始邻域较大,训练过程中优胜邻域随训练时间收缩;
5) 调整权值,对优胜邻域内的所有节点调整权值;
6) 结束判定,当学习率小于最小学习率时,训练结束,不满足结束条件时,转到2)继续进行。
1.2 SOM应用于多AUV系统假定在一个有限的工作区域内分布着一组AUV,同时在此区域分布着任意数目的目标。每个目标都需要一个AUV在该点完成特定的任务。对于每个AUV来讲,其代价是由从起始位置坐标点运动到目标位置坐标点所移动的距离来衡量。总代价定义为所有单个AUV代价的总和。当所有目标点都被访问过一次后,任务完成。这种访问目标点的过程与SOM算法是一致的[10]。
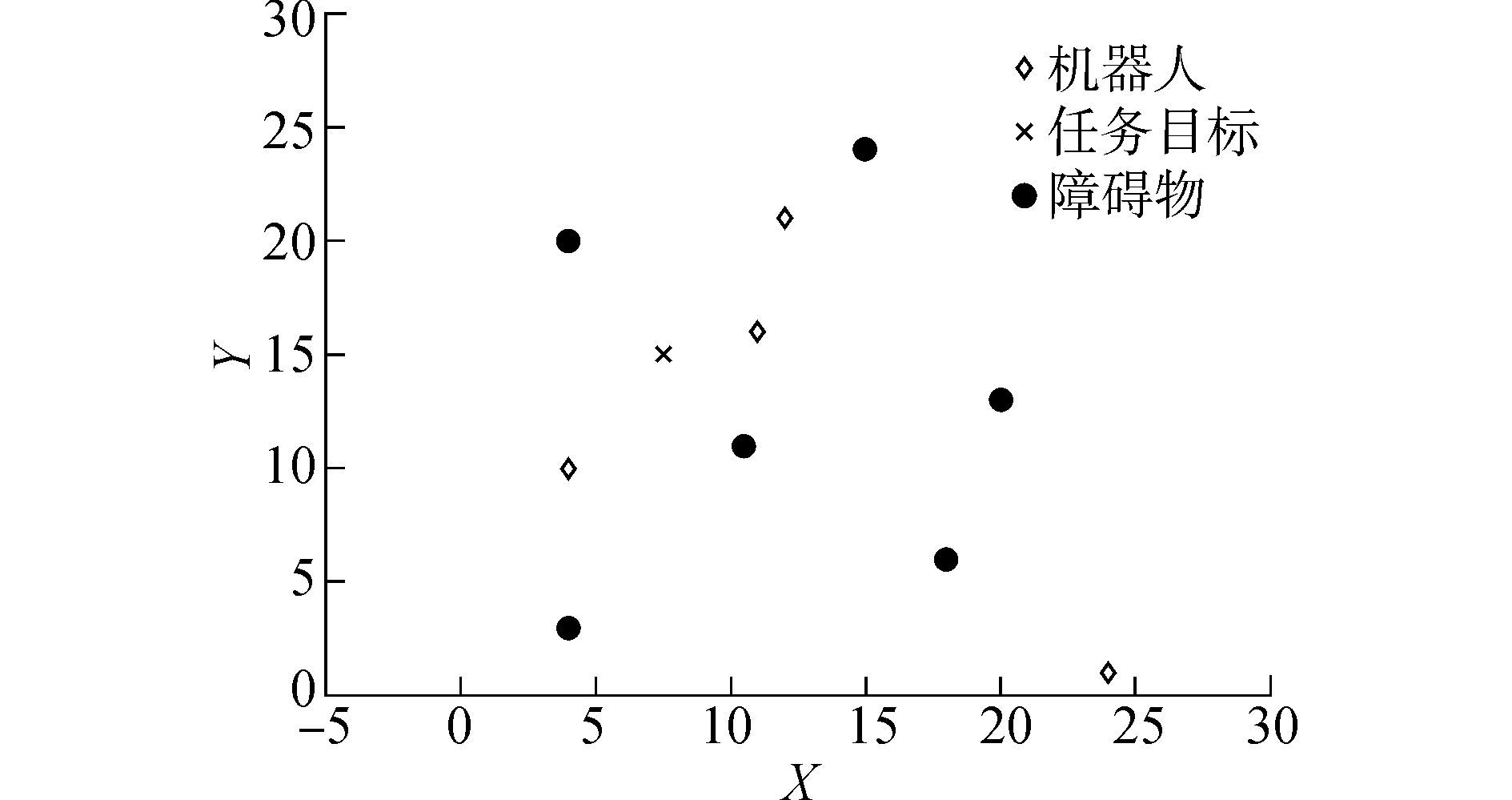
本文采用有限的二维平面作为多AUV系统的工作空间。如图 2所示,在该工作空间内,红色的菱形代表AUV,绿色的圆点代表目标,黑色的叉代表障碍物。假定所有AUV都是相同的,具备基本的导航、避障和位置识别功能。
|
| 图2 多AUV系统的工作区域 Figure 2 Workspace of multi-AUV system |
在该工作空间内,有4个AUV需要遍历5个目标,同时存在1个障碍物。基于两点之间直线最短的原理,认为AUV的初始位置坐标到目标点的位置坐标之间的直线为最优路径。
单纯依靠目标点坐标与AUV坐标最近原则分配任务,有时可能出现某个AUV被分配太多任务的现象,使其在动力耗尽前还无法完全到达所有分配的目标,而另外的AUV却得不到任务目标;以及由于障碍物而使一开始分配的任务在实际规划路径中无法完成。为了保证每个AUV携带的能源得到最大限度的利用,同时避免AUV在向目标运动的过程中因为能源不足而停止,所以在算法中要考虑AUV的负载均衡。假定,AUV具有相同的水下巡航能力且携带同样的能源,所能行走的距离相同。在算法设计中,根据AUV个数,在分配任务前初始化矩阵,矩阵阶数与AUV数量一致。在算法中,首先计算N=NT/NR,其中,NT是目标点数量,NR是AUV数量,则任务负载的上限设置为
| ${{N}_{MAX}}=\left\{ \begin{align} & N,N\in {{N}^{+}} \\ & \left\lfloor N \right\rfloor +1,N\notin {{N}^{+}} \\ \end{align} \right.$ | (1) |
当本次任务执行后超过任务数量上限时,则不分配该任务给获胜AUV,选择次优AUV执行任务。将AUV系统的负载均衡考虑进SOM任务分配算法是在文献[10-11]的基础上对传统神经网络的有效改进,使其更适合多AUV多任务分配的实际情况。
1.3 Dubins路径规划算法实现二维环境下的多AUV系统的任务分配与路径规划主要运用了两个算法:改进的自组织神经网络算法(SOM)和Dubins Path算法。其中,自组织神经网络算法用来实现多目标的分配策略,包括神经网络的输入层和输出层定义、领域函数的确定以及权值的更新等几个过程;Dubins Path算法用于实现运动学约束下AUV到目标点的最短有效的路径规划。
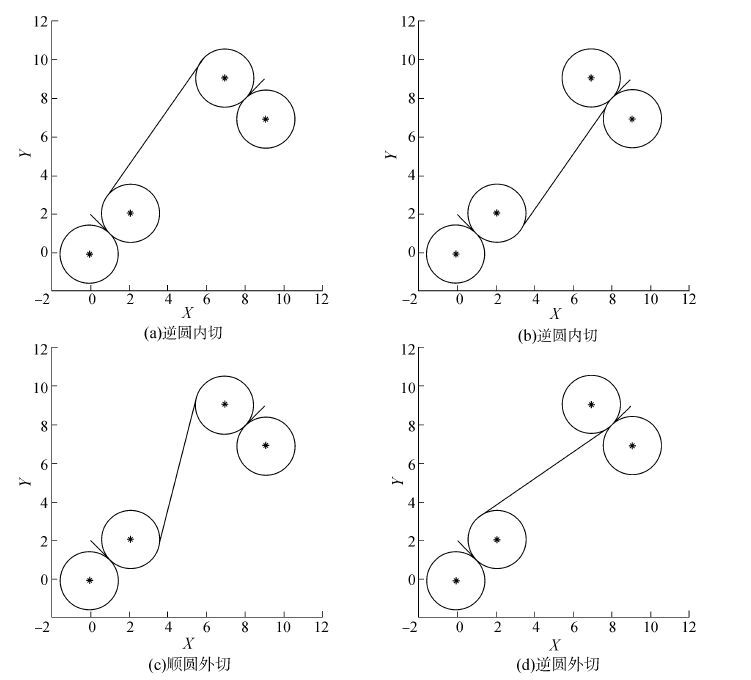
对于具有初始和终止速度向量的AUV到目标点的路径规划,设AUV最小转向半径为R,当确定起始点和终止点后,对速度向量可以各做两个切圆。起始向量的两个圆和终止向量的两个圆,两两组合后共有4种情况,而两个相离的圆又可以做四条切线。相对于传统的圆和直线,通过相切关系联立方程组求解,求出四个解后判断舍解,本文将采用更为简便的旋转与相似来进行求解,使用这种求解方法将使本来需要通过讨论来确定的切点的复杂情况变得极为简单。文中以向量的起始方向开始画圆,若画圆轨迹为顺时针则称该圆为该向量的顺时针圆,简称顺圆,反之则称为逆圆。图 3给出了两个圆切线的的4种位置关系。
|
| 图3 圆与切线的关系 Figure 3 Circles and the corresponding tangents |
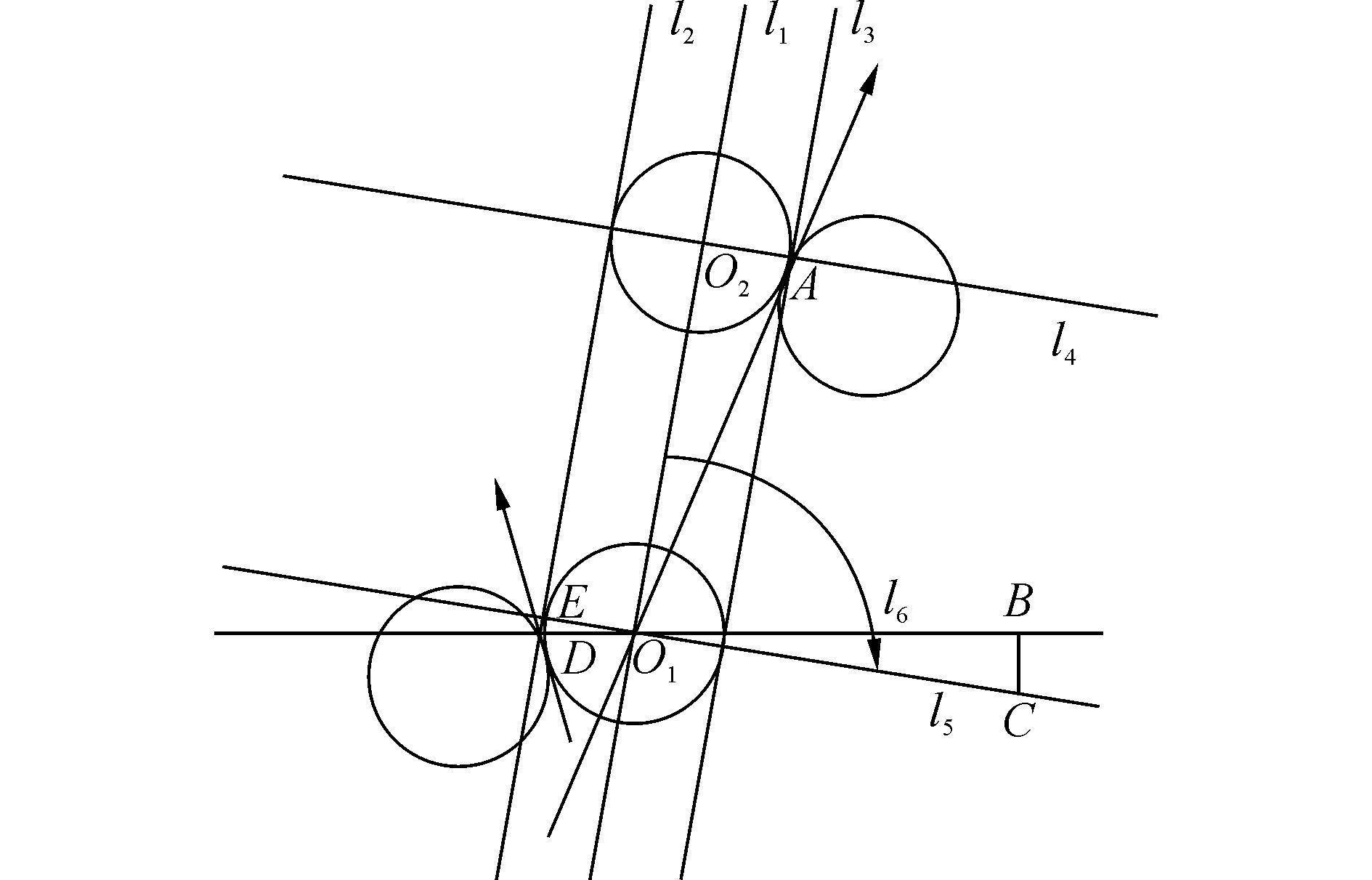
如图 4所示,由起始向量和终止向量,根据转弯半径R可以求出圆心点O1和点O2的坐标,l2为圆O1、O2的切线,与圆O1相切于点E。过圆心O1、O2做l1,过O2做l4垂直于l2,其中l4与圆的另一侧交于点A。过点E和O1做l5垂直于l2,再过点O1做一条平行于X轴的l6。O1O2为圆心距,顺时针旋转到O1C处(逆时针旋转亦可),过C作垂线交l6于点B,同时过点E作垂线交l6于D。O2的坐标经过旋转到点C,其中旋转角度为π/2,这样点C的坐标即可以求出,同时三角形ΔO1DE与三角形ΔO1BC相似,通过相似即可求出点E的坐标,至此l2与圆O1的切点E坐标已经求出,类似的也可以求出l2与圆O2的切点。设l2与圆O1的切点坐标为(xa,ya),l2与圆O2的切点坐标为(xb,yb),圆心O1坐标为(a1,b1),圆心O2坐标为(a2,b2),则有:
| $\begin{array}{l} \left| \begin{array}{l} {x_b}\\ {y_b} \end{array} \right| = \left| \begin{array}{l} {a_1}\\ {b_1} \end{array} \right| + \left| \begin{array}{l} \begin{array}{*{20}{c}} {cos\theta }&{ - sin\theta } \end{array}\\ \begin{array}{*{20}{c}} {sin\theta }&{cos\theta } \end{array} \end{array} \right| \cdot \\ \left| \begin{array}{l} {a_2} - {a_1}\\ {b_2} - {b_1} \end{array} \right| \cdot R/{O_1}{O_2} \end{array}$ | (2) |
| $\begin{array}{l} \left| \begin{array}{l} {x_a}\\ {y_a} \end{array} \right| = \left| \begin{array}{l} {a_2}\\ {b_2} \end{array} \right| + \left| \begin{array}{l} \begin{array}{*{20}{c}} {cos\phi }&{ - sin\phi } \end{array}\\ \begin{array}{*{20}{c}} {sin\phi }&{cos\phi } \end{array} \end{array} \right| \cdot \\ \left| \begin{array}{l} {a_1} - {a_2}\\ {b_1} - {b_2} \end{array} \right| \cdot R/{O_1}{O_2} \end{array}$ | (3) |
|
| 图4 圆与外切线的关系求解图 Figure 4 Solution graph of the outer tangent line |
式中:θ=π/2,φ=θ+π。另一侧的外切线与圆O1和O2的切点亦可以通过这种方法求解。实际上即是第一种情况的镜像对称。设l3与圆O1的切点坐标为(xc,yc),l3与圆O2的切点坐标为(xd,yd),则有:
| $\begin{array}{l} \left| \begin{array}{l} {x_d}\\ {y_d} \end{array} \right| = \left| \begin{array}{l} {a_1}\\ {b_1} \end{array} \right| + \left| \begin{array}{l} \begin{array}{*{20}{c}} {cos\theta }&{ - sin\theta } \end{array}\\ \begin{array}{*{20}{c}} {sin\theta }&{cos\theta } \end{array} \end{array} \right| \cdot \\ \left| \begin{array}{l} {a_2} - {a_1}\\ {b_2} - {b_1} \end{array} \right| \cdot R/{O_1}{O_2} \end{array}$ | (4) |
| $\begin{array}{l} \left| \begin{array}{l} {x_c}\\ {y_c} \end{array} \right| = \left| \begin{array}{l} {a_2}\\ {b_2} \end{array} \right| + \left| \begin{array}{l} \begin{array}{*{20}{c}} {cos\phi }&{ - sin\phi } \end{array}\\ \begin{array}{*{20}{c}} {sin\phi }&{cos\phi } \end{array} \end{array} \right| \cdot \\ \left| \begin{array}{l} {a_1} - {a_2}\\ {b_1} - {b_2} \end{array} \right| \cdot R/{O_1}{O_2} \end{array}$ | (5) |
式中:θ=-π/2,φ=θ+π。通过比较两种情况的θ角可以发现其互为相反数,这也体现了旋转对称的特性。内切线的求解原理与外切线相同,限于篇幅在此不再赘述。
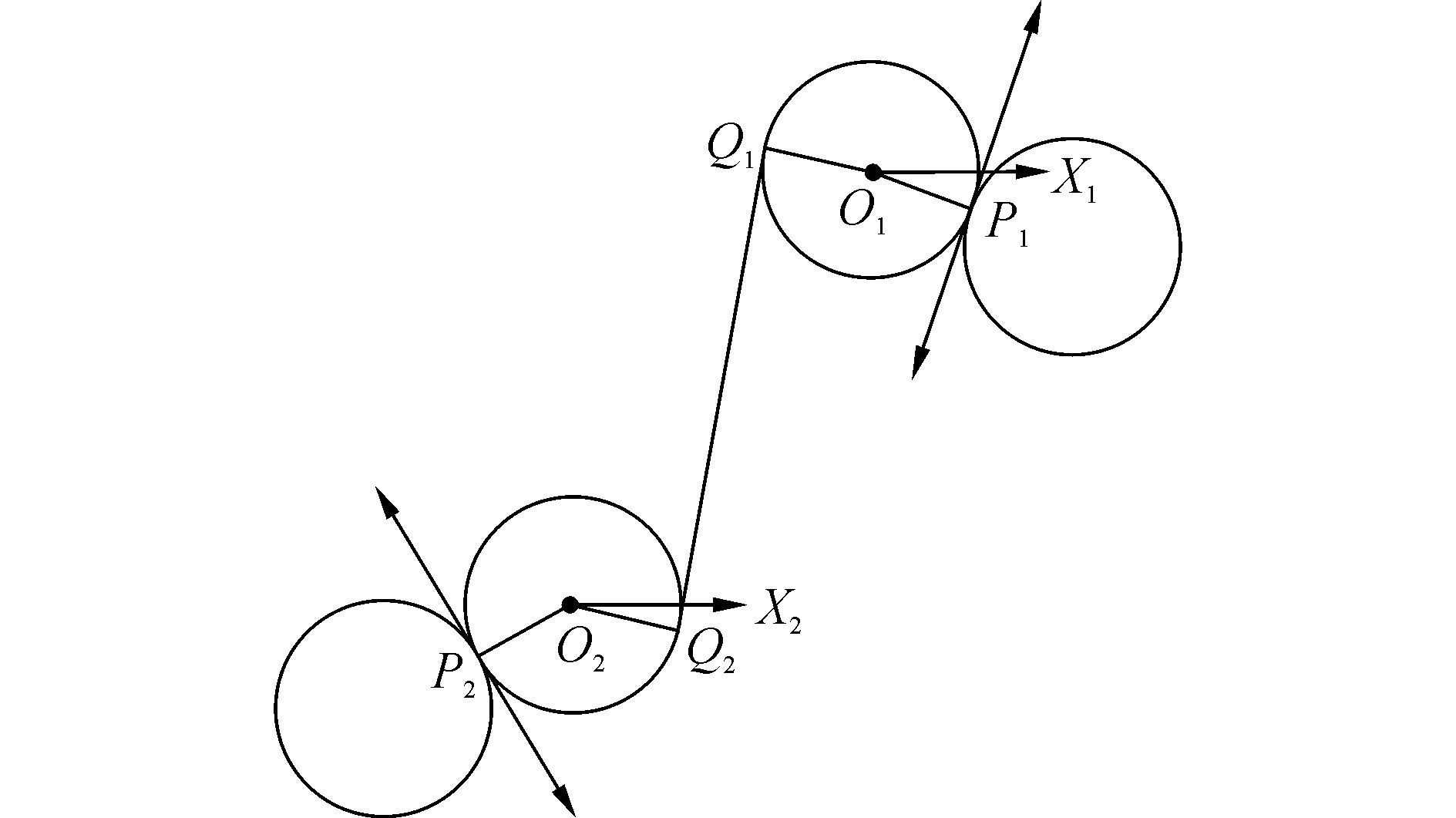
图 5是Dubin路径弧线规划的求解,红色的平箭头向量为初始向量,绿色的凹箭头向量为终止向量。切点为P1,P2,Q1,Q2。
|
| 图5 Dubins Path弧线部分规划 Figure 5 The planning of arc part of Dubins Path |
当初始向量在0到π之间,通过比较圆心O1和起点P1,若O1的横坐标大于P1的横坐标,则说明圆O1为顺圆,反之则为逆圆。当为顺圆时,以P1为起点沿圆弧P1Q1顺时针运动;当为逆圆时,以P1为起点沿圆弧P1Q1逆时针运动。当初始向量在π到2π之间,通过比较圆心O2和起点P2,若O2的横坐标大于P2的横坐标,则说明圆O1为逆圆,反之则为顺圆。当为顺圆时,以P2为起点沿圆弧P2Q2顺时针运动;当为逆圆时,以P2为起点沿圆弧P2Q2逆时针运动。
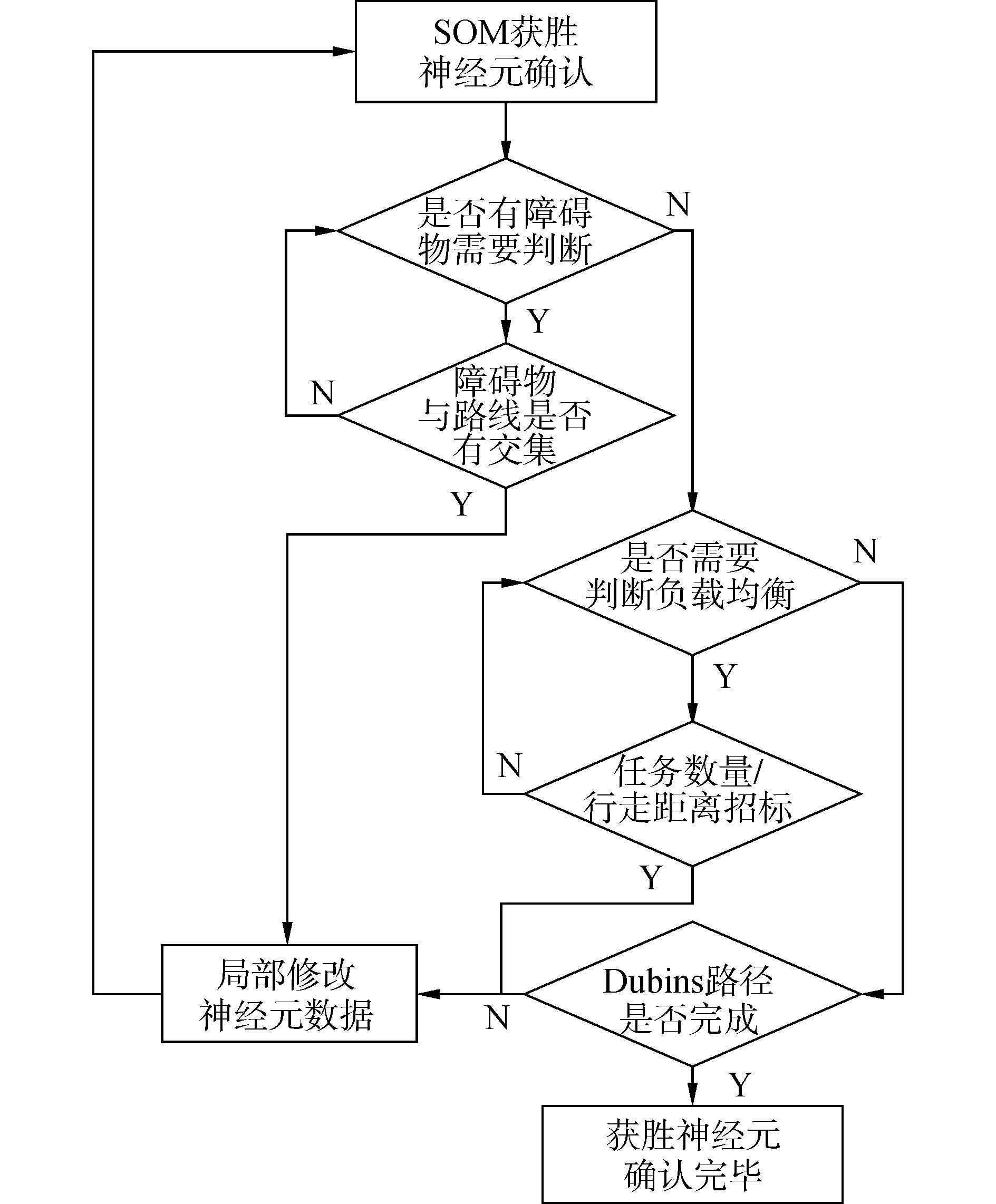
当终止向量在0到π之间,通过比较圆心O2和终点P2,若O2的横坐标大于P2的横坐标,则说明圆O2为顺圆,反之则为逆圆。当为顺圆时,以Q2为起点沿圆弧Q2P2逆时针运动;当为逆圆时,以P2为起点沿圆弧Q2P2顺时针运动。当终止向量在π到2π之间,通过比较圆心O1和P1,若O1的横坐标大于P1的横坐标,则说明圆O1为逆圆,反之则为顺圆。当为顺圆时,以Q1为起点沿圆弧Q1P1逆时针运动;当为逆圆时,以Q1为起点沿圆弧Q1P1顺时针运动。程序总体算法流程图如图 6所示。
|
| 图6 算法流程图 Figure 6 Flow chart of the algorithm |
为了验证该算法在解决二维工作空间内多AUV多任务分配与相应路径规划问题的有效性,仿真在MATLAB R2011a上实现。
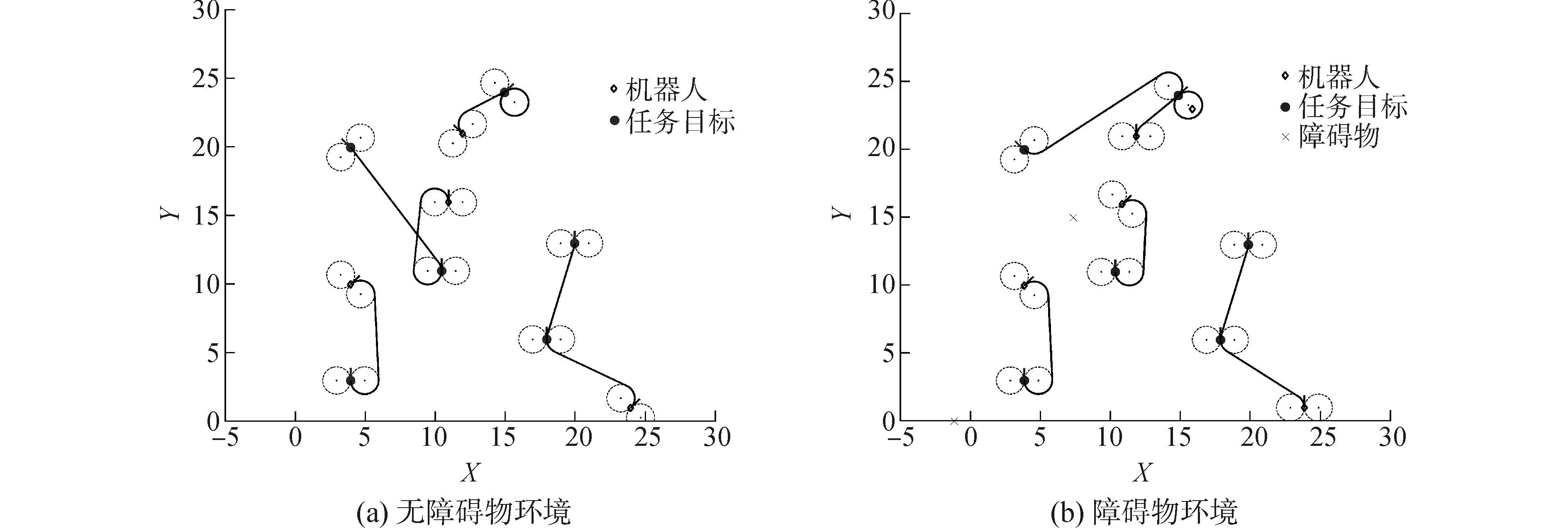
2.1 障碍物环境下的多任务分配与路径规划如图 7(a)所示,在多AUV系统的工作空间内,有4个AUV需要访问随机分布的6个目标点,蓝色的线表示向量的切圆,红色的线表示AUV的运动轨迹,绿色点是目标。AUV受到运动学约束,具有初始速度向量,其最小转弯半径为R,初始速度向量和终止任务向量是预先随机设定的。在完成任务分配后,每个AUV都能沿着Dubins路径到达离各自最近的目标点,而Dubins路径已经证明是在运动学约束条件下的最优路径。在图 7(b)中,4个AUV和 6个目标点在工作空间内位置不变,只是在进行任务分配时,路线被障碍物挡住路径无法规划时,此时则算法不选用当前获胜神经元,而是针对次优神经元进行路线规划,重新分配任务,最后路径规划成功。仿真结果证明,障碍物的情况下该算法是有效的。
|
| 图7 障碍物环境下的多任务分配仿真 Figure 7 Simulation of task assignment in the obstacle environment |
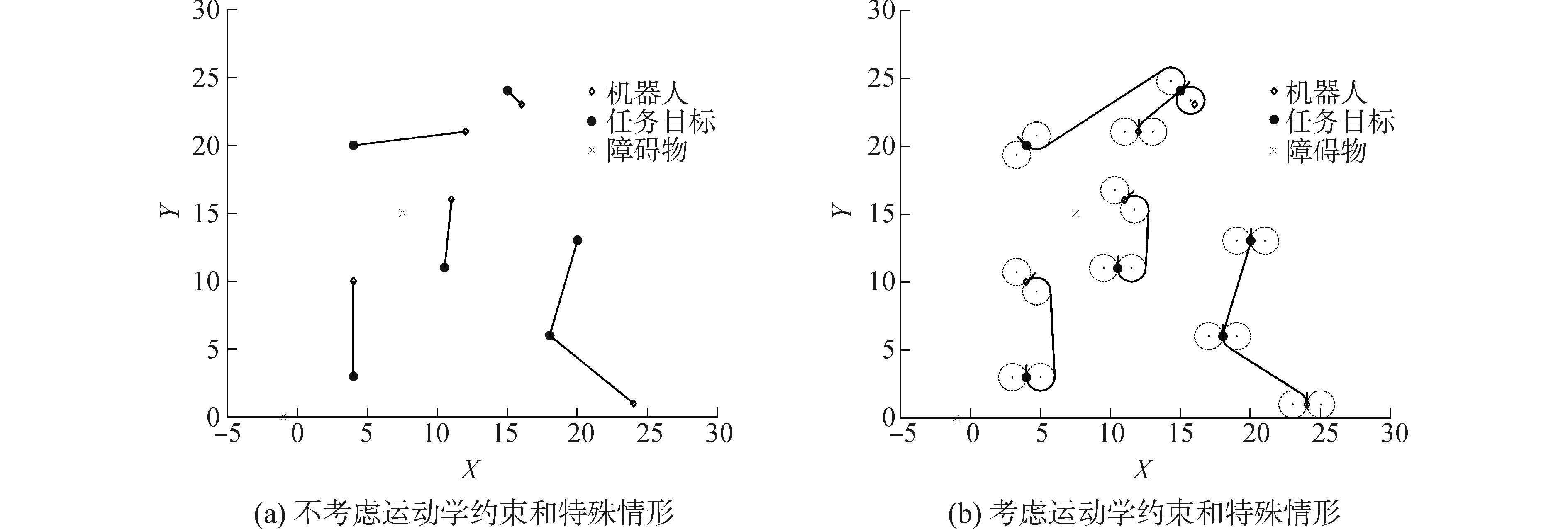
当获胜AUV与任务点之间距离小于两倍最小转弯半径时,无法规划出Dubins路径,算法则不选用该AUV为当前获胜神经元。如图 8(a)所示,在多AUV系统的工作空间内,有5个AUV需要访问随机分布的6个目标。不考虑运动学约束时,采用SOM方法任务分配完成后,每个AUV都能沿着最优路径到达离各自最近的目标点。图 8(a)中的任务分配为直线路径,其中蓝色的线表示路径轨迹。所有的路径都是直线,每条路径都是最优的。但是在实际条件下,完全使用直线路径是不能实现的。图 9(b)的仿真结果是运动学约束下的最优任务分配和路径规划,其中虚线的圆表示向量切圆,红色的线表示Dubins路径轨迹。对比图 8(a)和图 8(b)可以发现,最上方的任务点附近存在1个AUV,在直线路径规划中其被选为获胜AUV进行路径规划,而在Dubins路径中则没有被选为获胜AUV。这是因为在该特殊情形下,获胜AUV与任务点之间距离小于两倍最小转弯半径,无法规划出Dubins路径。算法选取次优神经元进行任务分配并作路径规划。
|
| 图8 特殊情况下的多任务分配仿真 Figure 8 Simulation of task assignment in the special situation |
|
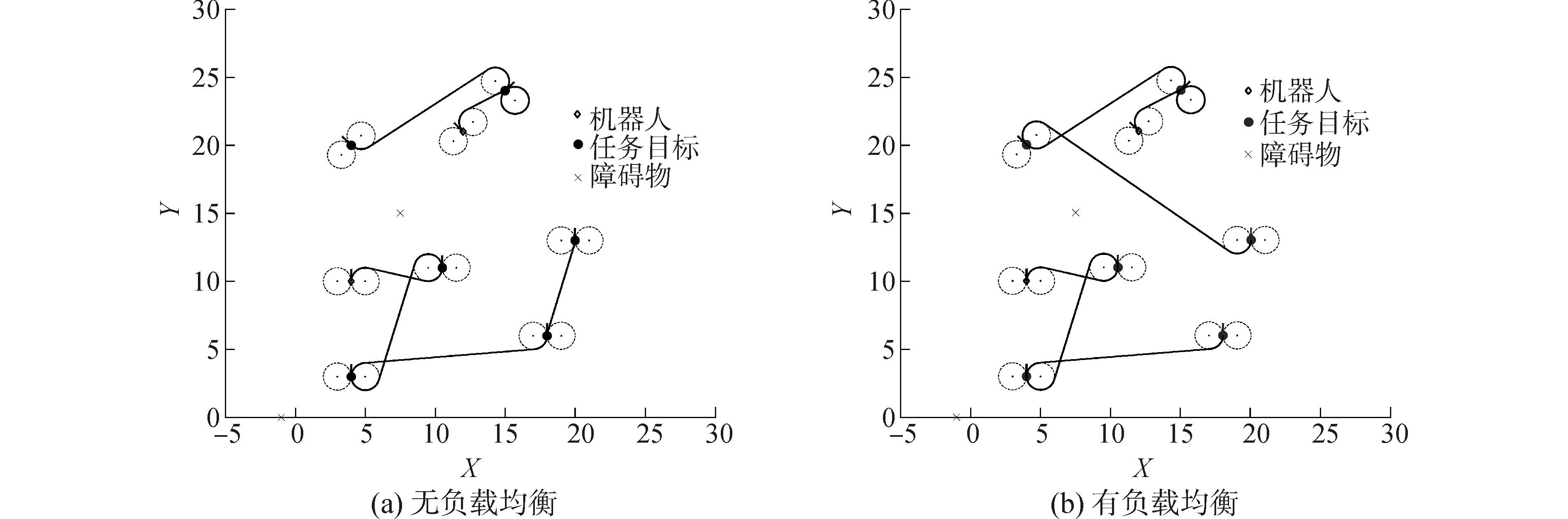
| 图9 任务负载均衡下的多任务分配 Figure 9 Task assignment under load balancing |
如图 9(a)所示,在多AUV系统的工作空间内,有2个AUV需要访问随机分布的6个目标。在没有任务负载设置的情况下进行的任务分配和路径规划,其中一个AUV访问4个目标点,另一个AUV访问2个目标点。图 9(b)则是根据2.2节中的负载均衡方法进行算法调整和参数设置,在任务负载NMAX=3时进行任务分配和路径规划,2个AUV各自访问了3个任务点,能源的消耗相对平衡,从而证明了该算法的有效性。
3 结论本文研究了二维工作空间中多AUV系统在速度和最小转向半径受约束的条件下的多任务分配。首先,本文将SOM神经网络算法思想应用到多AUV任务分配过程中。在此基础上,考虑到AUV的实际运动学特性,将Dubins路径结合到多任务分配算法当中,解决了运动学约束的问题。最后,通过仿真实验进行验证,考虑了障碍物环境下的任务分配、获胜AUV与任务点之间距离小于两倍最小转弯半径时的特殊情况,以及任务负载均衡下的任务分配。仿真结果表明,本文所提出的算法在多AUV任务分配中具有一定的特点和优势,这是传统的多任务分配算法不能实现的。尽管如此,本论文的研究还停留在理论层面,多AUV系统本身动力学特性复杂,工作所在的水下环境复杂多变,存在海流的影响等不确定因素,这也是未来的研究方向。
| [1] | LUO Lingzhi, CHAKRABORTY N, SYCARA K. Distributed algorithm design for multi-robot generalized task assignment problem[C]//Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems. Tokyo, Japan, 2013:4765-4771. |
| [2] | SARIEL S, BALCH T, STACK J. Distributed multi-AUV coordination in naval mine countermeasure missions[R]. Atlanta, Georgia:Georgia Institute of Technology, 2006:25-31. |
| [3] | AKKIRAJU R, KESKINOCAK P, MURTHY S, et al. An agent-based approach for scheduling multiple machines[J]. Applied intelligence, 2001, 14(2): 135–144. DOI:10.1023/A:1008363208898 |
| [4] |
曹宗华, 吴斌, 黄玉清, 等. 基于改进蚁群算法的多机器人任务分配[J].
组合机床与自动化加工技术, 2013(2): 34–37.
CAO Zonghua, WU Bing, HUANG Yuqing, et al. The multi-robot task allocation study based on improved ant colony algorithm[J]. Modular machine tool & automatic manufacturing technique, 2013(2): 34–37. |
| [5] |
刘淑华, 张嵛, 吴洪岩, 等. 基于群体智能的多机器人任务分配[J].
吉林大学学报:工学版, 2010, 40(1): 123–129.
LIU Shuhua, ZHANG Yu, WU Hongyan, et al. Multi-robot task allocation based on swarm intelligence[J]. Journal of Jilin University:engineering and technology edition, 2010, 40(1): 123–129. |
| [6] | KOHONEN T. Analysis of a simple self-organizing process[J]. Biological cybernetics, 1982, 44(2): 135–140. DOI:10.1007/BF00317973 |
| [7] | ZHU A, YANG S X. A neural network approach to dynamic task assignment of multirobots[J]. IEEE transactions on neural networks, 2006, 17(5): 1278–1287. DOI:10.1109/TNN.2006.875994 |
| [8] | ZHU Anmin, YANG S X. An improved SOM-based approach to dynamic task assignment of multi-robots[C]//Proceedings of the 8th World Congress on Intelligent Control and Automation. Jinan, China:IEEE, 2010:2168-2173. |
| [9] | HUANG Huan, ZHU Daqi, DING Feng. Dynamic task assignment and path planning for multi-AUV system in variable ocean current environment and movable targets[J]. Journal of intelligent & robotic systems, 2014, 74(3/4): 999–1012. |
| [10] |
朱大奇, 李欣, 颜明重. 多自治水下机器人多任务分配的自组织算法[J].
控制与决策, 2012, 27(8): 1201–1205.
ZHU Daqi, LI Xin, YAN Mingzhong. Task assignment algorithm of multi-AUV based on self-organizing map[J]. Control and decision, 2012, 27(8): 1201–1205. |
| [11] | ZHU Daqi, HUANG Huan, YANG S Y. Dynamic task assignment and path planning of multi-AUV system based on an improved self-organizing map and velocity synthesis method in three-dimensional underwater workspace[J]. IEEE transactions on cybernetics, 2013, 43(2): 504–514. DOI:10.1109/TSMCB.2012.2210212 |
| [12] | JIANG Kaichun, SENEVIRATNE L D, EARLES S W E. A shortest path based path planning algorithm for nonholonomic mobile robots[J]. Journal of intelligent and robotic systems, 1999, 24(4): 347–366. DOI:10.1023/A:1008070923246 |
| [13] | MANSOR M A, MORRIS A S. Path planning in unknown environment with obstacles using virtual window[J]. Journal of intelligent and robotic systems, 1999, 24(3): 235–251. DOI:10.1023/A:1008047425796 |
| [14] |
冷静, 刘健, 徐红丽. 实时避碰的无人水面机器人在线路径规划方法[J].
智能系统学报, 2015, 10(3): 343–348.
LENG Jing, LIU Jian, XU Hongli. Online path planning of an unmanned surface vehicle for real-time collision avoidance[J]. CAAI transactions on intelligent systems, 2015, 10(3): 343–348. |
| [15] |
陈超, 唐坚, 靳祖光, 等. 一种基于可视图法导盲机器人路径规划的研究[J].
机械科学与技术, 2014, 33(4): 490–495.
CHEN Chao, TANG Jian, JIN Zuguang, et al. A path planning algorithm for seeing eye robots based on V-Graph[J]. Mechanical science and technology for aerospace engineering, 2014, 33(4): 490–495. |
| [16] | KHATIB O. Real-time obstacle avoidance for manipulators and mobile robots[J]. Robotics research, 1986, 5(1): 90–98. DOI:10.1177/027836498600500106 |
| [17] | SUGIHARA K. GA-based on-line path planning for SAUVIM[M]//DEL POBIL A P, MIRA J, ALI M. Tasks and Methods in Applied Artificial Intelligence:Lecture Notes in Artificial Intelligence. Berlin Heidelberg:Springer, 1998:329-338. |
| [18] | LI T H S, CHIANG M S, JIAN S S. Motion planning of an autonomous mobile robot by integrating GAs and fuzzy logic control[C]//Proceedings of the 9th IEEE International Conference on Fuzz Systems. San Antonio, TX, USA:IEEE, 2000:933-936. |
| [19] |
吴友谦, 裴海龙. 基于Dubins曲线的无人直升机轨迹规划[J].
计算机工程与技术, 2011, 32(4): 1426–1429.
WU Youqian, QIU Hailong. Trajectory planning for unmanned helicopter based on Dubins curves[J]. Computer engineering and design, 2011, 32(4): 1426–1429. |
| [20] |
梁勇, 张友安, 雷军委. 一种基于Dubins路径的在线快速航路规划方法[J].
系统仿真学报, 2013, 25(S1): 291–296.
LIANG Yong, ZHANG You'an, LEI Junwei. New method of online fast path planning based Dubins path[J]. Journal of system simulation, 2013, 25(S1): 291–296. |



