工程结构或机械设备的疲劳破坏是材料内部疲劳损伤逐渐累积的结果。随着载荷循环次数的增加, 材料内部的损伤逐渐累积, 当累积的损伤达到某一临界值时, 结构或构件便发生疲劳破坏。疲劳累积损伤理论研究的是循环载荷作用下结构或构件的损伤累积规律及疲劳破坏准则, 它对于产品疲劳寿命的预测而言是十分重要的[1]。
对于疲劳累积损伤理论的研究经历了漫长的过程, 早在1924年Palmgren就首先提出了疲劳累积损伤与应力循环次数成线性关系的假设, 随后于1945年Miner又将此理论公式化, 于是便形成了著名的Palmgren-Miner线性疲劳累积损伤理论(简称Miner理论)[2]。自Miner理论被提出以来, 针对其不足, 国内外许多学者开展了大量的研究, 在过去的几十年中相继提出了多种疲劳累积损伤理论[3]。根据累积损伤规律的不同, 可将现有的疲劳累积损伤理论分为两大类:线性疲劳累积损伤理论[4-7]和非线性疲劳累积损伤理论[8-11]。
对于这些现有的累积损伤模型, 有的是宏观的或唯象的, 其虽然形式简单, 使用方便, 但对损伤变量的定义缺乏明确的物理含义, 或模型的建立缺乏基础性的理论依据;有的则是微观的或物理的, 其虽然具有较好的数学或力学基础, 但模型过于复杂, 且须进行大量的疲劳试验才能确定模型参数, 使其目前难以在工程上推广。因此, 迄今为止, 还没有一个统一的、实用的、能够较好揭示疲劳损伤内在演化机理的累积损伤模型。相对来说, Miner理论由于其形式简单, 使用方便, 且大量试验统计事实表明:Miner理论能够较好地预测结构或构件在循环载荷作用下的均值寿命。所以, 尽管在过去的几十年中相继提出了多种疲劳累积损伤理论, 但Miner理论仍然是工程界广泛采用的抗疲劳设计准则[12]。
然而, 由于各种随机因素(如材料微观结构、制造工艺、载荷和服役环境等)的影响, 致使疲劳累积损伤伴随着固有的分散性。而Miner理论是基于“确定性”基础之上的, 它没有考虑由于材料和载荷等的不确定性对瞬时累积损伤造成的分散性。
事实上, 金属材料的疲劳损伤主要属于机械损伤, 造成损伤的外因主要是应力幅, 而导致损伤的内因是材料本身的固有属性[8]。因此, 本文利用应力与寿命之间的映射关系, 推导出随机恒幅载荷下结构疲劳寿命的概率分布, 并基于传统的Miner理论建立了适用于结构可靠性评估及疲劳寿命预测的疲劳累积损伤的概率模型。
1 产品疲劳寿命的分布特征 1.1 S-N曲线产品疲劳寿命预测的前提是拥有必要的疲劳试验统计数据(包括材料的、载荷的及各种影响因素的), 其中S-N曲线最为关键。S-N曲线作为疲劳寿命预测的基础, 其描述的是循环应力S与失效循环数(疲劳寿命)N之间的对应关系。材料S-N曲线最常用的是幂函数表达式[13]:
| ${S^m}N = C$ | (1) |
式中:m和C为材料疲劳性能参数。
1.2 疲劳寿命分布特征对于产品疲劳寿命分布类型的选择或拟合而言, 传统上大多采用粗放的、非精确的概率统计方法(例如, 对数正态分布、Weibull分布等), 其统计学的假设与检验也未必十分严格[14]。事实上, 对于由特定材料制成的结构或构件, 疲劳寿命的分布特征是由其在服役周期内所承受的载荷唯一确定的, 疲劳寿命N可以看作是在载荷激励S作用下的响应。因此, 根据产品的载荷分布特征来推断其疲劳寿命的分布特征不失为一种有效途径。
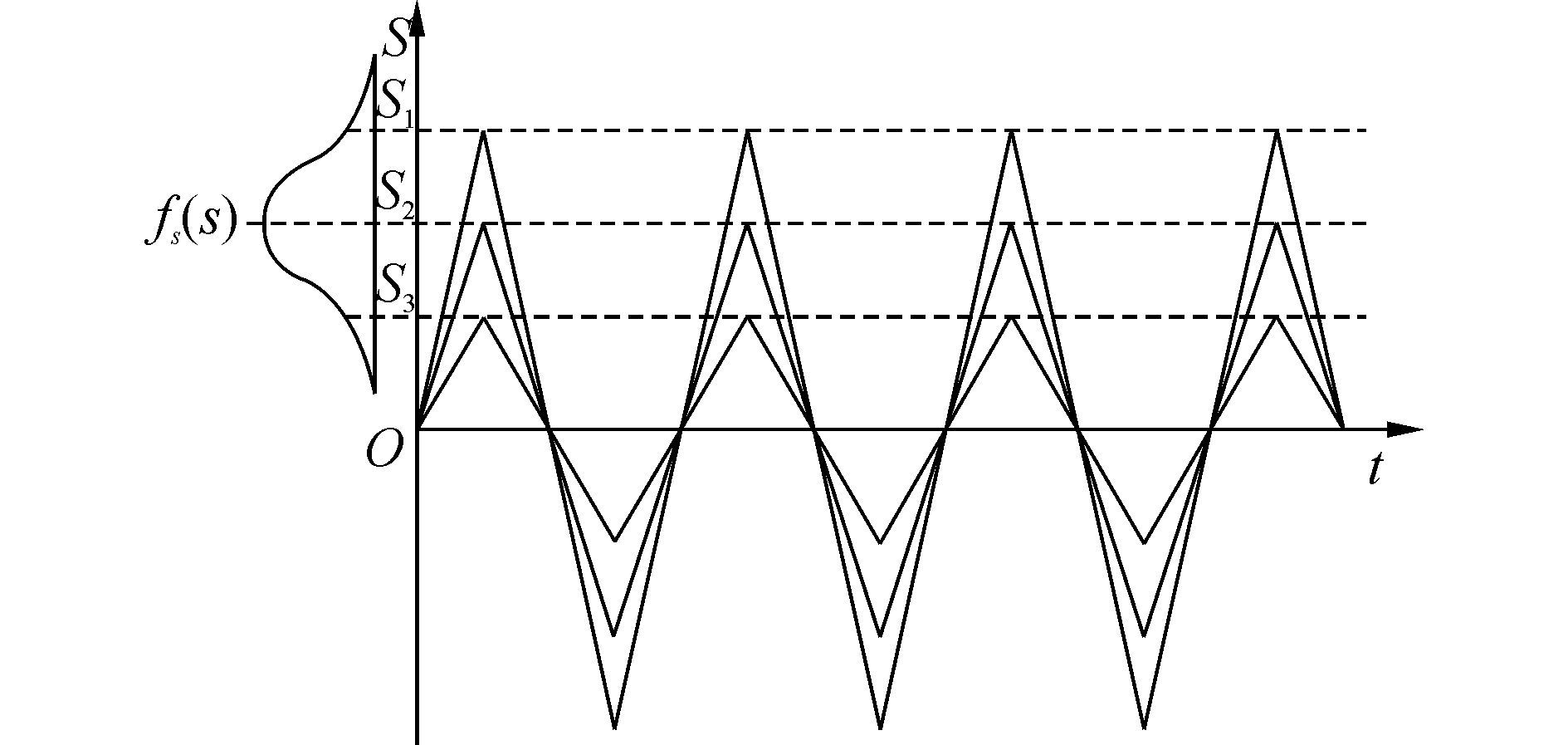
本文仅考虑随机恒幅载荷下产品的寿命分布问题。所谓随机恒幅载荷, 指的是载荷为恒幅循环应力, 应力幅服从某一概率分布[15], 如图 1所示。在图 1中, S为一随机变量, 对应的概率密度函数为fS(s), 代表应力幅值的概率分布;S1, S2和S3是S中的三个载荷样本, 分别代表三种不同幅值下的恒幅循环应力。
|
| 图1 随机恒幅循环载荷示意图 Figure 1 Schematic diagram of uncertain cyclic load |
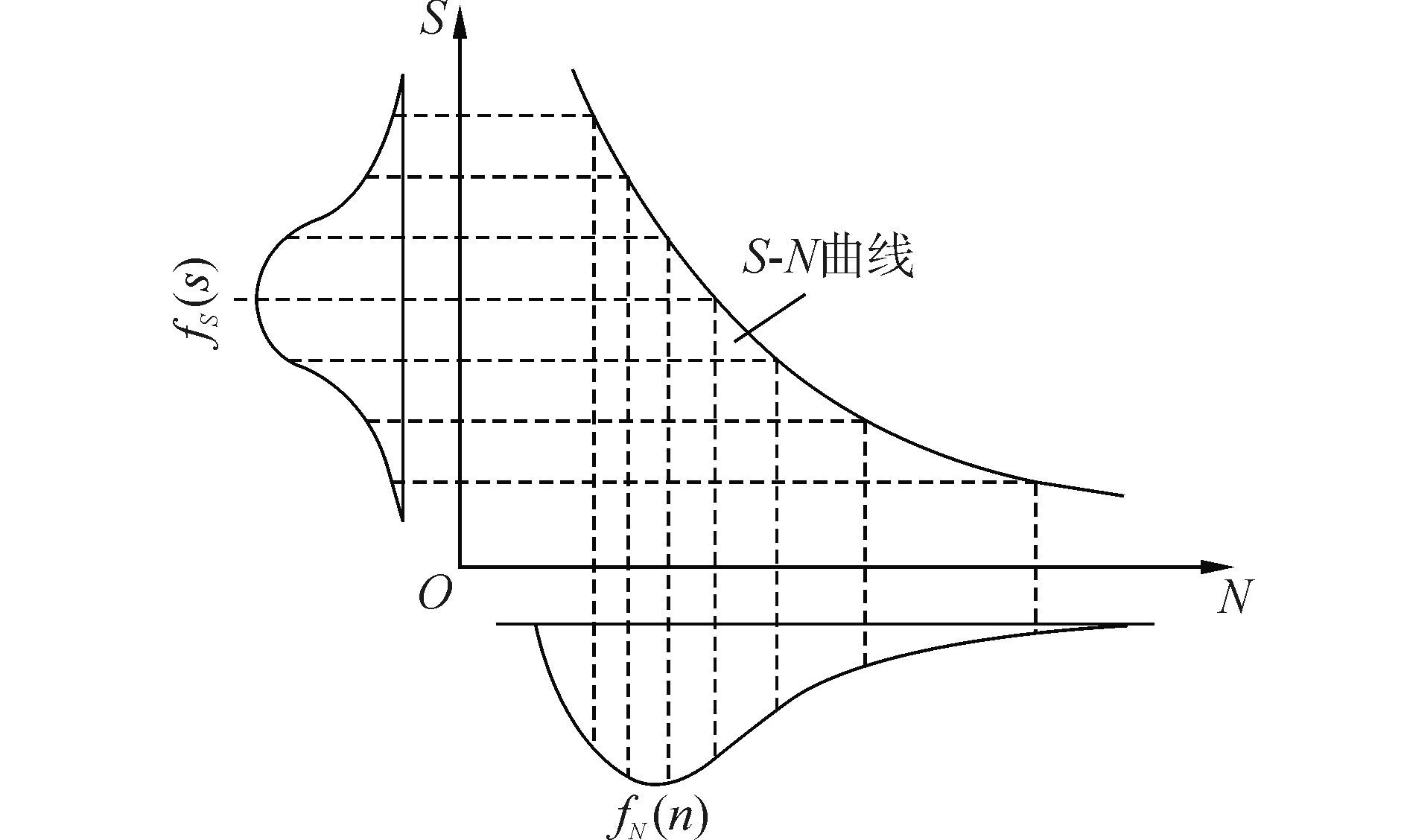
在应力S作用下, 疲劳寿命N的分布特征fN(n)与应力S的分布特征fS(s)之间存在一种类似于函数映射关系的纽带(如图 2所示), 这种映射关系可用S-N曲线方程表示。因此, 根据随机变量函数的概率密度函数与其自变量的概率密度函数之间的关系, 便可由应力S(激励)的分布特征fS(s)确定出疲劳寿命N(响应)的分布特征fN(n)。
|
| 图2 应力分布与寿命分布的关系 Figure 2 Relationship between stress distribution and fatigue life distribution |
设应力S的累积分布函数为FS(s), 在应力S作用下, 疲劳寿命N的概率密度函数与累积分布函数分别记为fN(n)和FN(n)。由随机变量分布函数的定义可知, 疲劳寿命N的累积分布函数FN(n)可表示为
| ${F_N}\left( n \right) = {\rm{Pr}}\left\{ {N \le n} \right\}$ | (2) |
式中:Pr{·}表示概率。
由S-N曲线的幂函数表达式可得
| $N = {C \over {{S^m}}}$ | (3) |
将式(3) 代入式(2) , 可得FS(s)与FN(n)之间的关系:
| $\eqalign{ & {F_N}\left( n \right) = {\rm{Pr}}\left\{ {N \le n} \right\} = {\rm{Pr}}\{ {C \over {{S^m}}} \le n\} = {\rm{Pr}}\{ S \ge {\left( {{C \over n}} \right)^{1m}}\} = \cr & 1 - {\rm{Pr}}\{ S < {\left( {{C \over n}} \right)^{1m}}\} = 1 - {F_S}[{\left( {{C \over n}} \right)^{1m}}] \cr} $ | (4) |
对式(4) 两边求导, 可得fS(s)与fN(n)之间的关系:
| $\eqalign{ & {f_N}\left( n \right) = {{d{F_N}\left( n \right)} \over {{\rm{d}}n}} = - {f_S}[{\left( {{C \over n}} \right)^{{1 \over m}}}\left] \cdot \right[{\left( {{C \over n}} \right)^{{1 \over m}}}]' = \cr & - {f_S}[{\left( {{C \over n}} \right)^{{1 \over m}}}\left] \cdot \right[{1 \over m}\cdot{\left( {{C \over n}} \right)^{1m - 1}}\cdot( - {C \over {{n^2}}})] = \cr & {1 \over {mn}}\cdot{\left( {{C \over n}} \right)^{{1 \over m}}}\cdot{f_S}[{\left( {{C \over n}} \right)^{{1 \over m}}}] \cr} $ | (5) |
式(5) 便是随机恒幅载荷下产品疲劳寿命的概率密度函数表达式。从式(5) 可以看出, 疲劳寿命N的分布特征随着应力S(外因)的分布特征及材料疲劳性能参数C和m(内因)取值的不同而变化。该模型用简洁的数学表达式阐述了外因(应力)及内因(材料疲劳性能参数)对产品疲劳寿命分布规律的影响, 克服了传统采用的概率统计方法在寿命分布拟合过程中产生的误差。
2 概率疲劳累积损伤模型Miner理论是一个确定性模型, 它与实际疲劳问题存在的分散性不符, 不能满足疲劳可靠性设计的要求。因此, 建立一个适用的概率疲劳累积损伤模型对产品的疲劳可靠性评估至关重要。
本文基于Miner理论, 建立了随机恒幅载荷作用下产品的概率疲劳累积损伤模型。具体过程如下:
1) 一个循环造成的损伤D(1) 。
| $D\left( 1 \right) = {1 \over N}$ | (6) |
式中:N为应力S作用下产品的疲劳寿命, 此处它是一个随机变量, 其累积分布函数FN(n)与概率密度函数fN(n)分别由式(4) 和式(5) 确定。
2) n个循环造成的损伤D(n)。
产品在疲劳载荷作用n后造成的损伤D(n)称为瞬时累积损伤:
| $D\left( n \right) = {n \over N}$ | (7) |
式中:n为载荷循环次数, 是一个确定量。
理论和试验结果表明, 瞬时累积损伤D(n)是个随机变量, 它由内在分散性(材料疲劳性能参数)和外在分散性(载荷特性)共同决定。根据随机变量分布函数的定义, 瞬时累积损伤D(n)的累积分布函数FD(d)可表示为
| ${F_D}\left( d \right) = P\left\{ {D\left( n \right) \le d} \right\}$ | (8) |
将式(7) 代入式(8) , 可得疲劳寿命N的累积分布函数FN(n)与瞬时累积损伤D(n)的累积分布函数FD(d)之间的关系:
| $\eqalign{ & {F_D}\left( d \right) = P\left\{ {D\left( n \right) \le d} \right\} = P\left\{ {{n \over N} \le d} \right\} = P\left\{ {N \ge {n \over d}} \right\} = \cr & 1 - P\{ N < {n \over d}\} = 1 - {F_N}\left( {{n \over d}} \right) \cr} $ | (9) |
对式(9) 两边求导, 可得疲劳寿命N的概率密度函数fN(n)与瞬时累积损伤D(n)的概率密度函数fD(d)之间的关系:
| $\eqalign{ & {f_D}\left( d \right) = {{d{F_D}\left( d \right)} \over {{\rm{d}}d}} = - {f_N}\left( {{n \over d}} \right)\cdot\left( {{n \over d}} \right)\prime = \cr & - {f_N}\left( {{n \over d}} \right)\cdot( - {n \over {{d^2}}}) = {n \over {{d^2}}}\cdot{f_N}\left( {{n \over d}} \right) \cr} $ | (10) |
将式(5) 代入式(10) 可得:
| $\eqalign{ & {f_D}\left( d \right) = {n \over {{d^2}}}\cdot{f_N}\left( {{n \over d}} \right) = {n \over {{d^2}}}\cdot1m\cdot{n \over d}\cdot{\left( {{C \over n}} \right)^{{1 \over m}}}\cdot{f_S}\left[ {{{\left( {{C \over n}} \right)}^{{1 \over m}}}} \right] = \cr & {n \over {{d^2}}}\cdot{d \over {mn}}\cdot{\left( {{C \over n}} \right)^{{1 \over m}}}\cdot{f_S}\left[ {{{\left( {{C \over n}} \right)}^{{1 \over m}}}} \right] = {1 \over {md}}\cdot{\left( {{C \over n}} \right)^{{1 \over m}}}\cdot{f_S}\left[ {{{\left( {{C \over n}} \right)}^{{1 \over m}}}} \right] \cr} $ | (11) |
式(11) 便是随机恒幅载荷下的概率疲劳累积损伤模型。由式(11) 可知, 瞬时累积损伤D(n)的概率分布特征是内在分散性(材料疲劳性能参数C和m的不同取值)和外在分散性(应力S的概率分布)的综合体现。该模型用清晰的数学表达式阐述了外因(应力)及内因(材料疲劳性能参数)对产品瞬时累积损伤分布规律的影响, 克服了传统Miner理论的不足。
3) 临界损伤Dcr。
目前, 对于临界损伤Dcr的统计特性有两种观点:一种观点认为Dcr是一个确定量, 即Dcr=1;另一种观点认为Dcr是一个随机变量, 即服从某一概率分布。事实上, 对于两级或者很少几级的加载情况, 试件发生疲劳破坏时的临界损伤值Dcr偏离1很大。例如在实际工程中, 对于承受两级加载的材料, 在高—低加载情况下其临界损伤Dcr<1, 而在低-高加载情况下其临界损伤Dcr>1, 即是所谓的“锻炼”效应[16]。材料的“锻炼”效应说明将临界损伤Dcr看作一个随机变量似乎更加合理。其中文献[12]认为临界损伤Dcr是一个均值为1, 变异系数与疲劳寿命变异系数近似相等的随机变量。鉴于此, 本文假设临界损伤Dcr服从均值为1, 变异系数CDcr由正态分布表示:
| ${C_{{D_{{\rm{cr}}}}}} \approx {C_N} = {{{\sigma _N}} \over {{\mu _N}}}$ | (12) |
式中:CN为疲劳寿命的变异系数, μN和σN分别为疲劳寿命的均值与方差:
| ${\mu _N} = \smallint _0^{ + \infty }n\cdot{f_N}\left( n \right){\rm{d}}n$ | (13) |
| $\sigma _N^2 = \smallint _0^{ + \infty }{(n - {\mu _N})^2}\cdot{f_N}\left( n \right){\rm{d}}n$ | (14) |
至此, 随机恒幅载荷下的概率疲劳累积损伤模型建立完毕。其中, 瞬时累积损伤D(n)的概率分布特征由式(11) 确定, 临界损伤Dcr服从均值为1, 变异系数由式(12) 确定的正态分布。
3 实例分析以机械工业中常用的齿轮材料20CrMnTi钢的接触疲劳试验为例, 对本文所建模型的有效性进行验证和分析。试验条件及试验数据如下[17]:
1) 试验条件:矩形试样, 920℃加热渗碳直接油淬, 200℃回火2 h, 空冷;JPM-1型试验机进行, 滑差率5%。
2) P-S-N曲线参数估计结果如表 1所示。
| P | m | C |
| 0.99 | 28.571 4 | 1.082 2×10102 |
| 0.95 | 21.886 6 | 7.099 0×1079 |
| 0.90 | 20.242 5 | 3.207 0×1074 |
| 0.50 | 14.044 9 | 1.160 4×1054 |
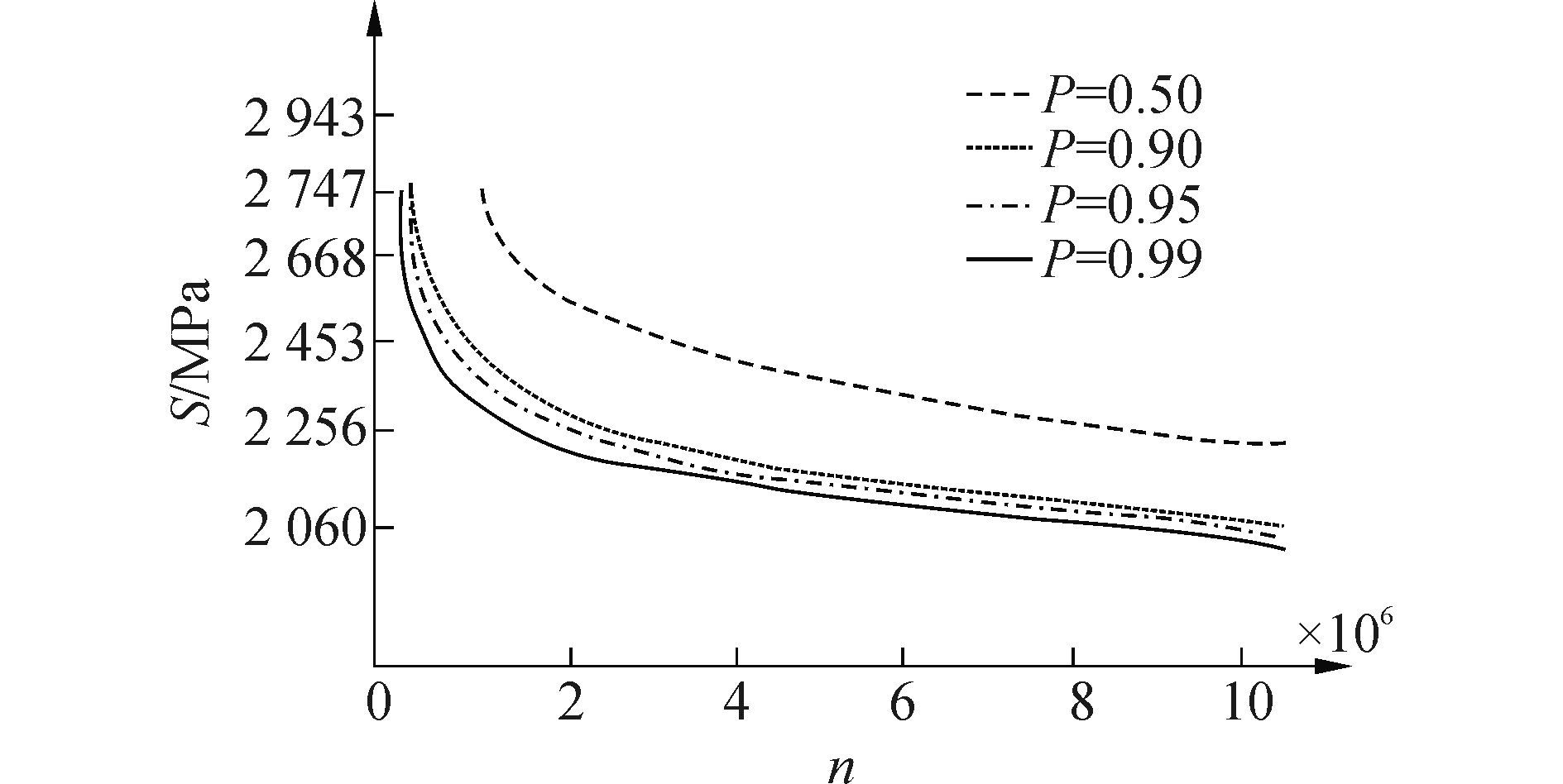
3) P-S-N曲线如图 3所示。
|
| 图3 20CrMnTi钢P-S-N曲线 Figure 3 P-S-N curves of 20CrMnTi steel |
设应力S服从均值μ=245 3 MPa, 标准差σ=20 MPa的正态分布。以表 1中存活率P=0.50的S-N曲线(C=1.160 4×1054, m=14.044 9) 为例。在应力S作用下, 由式(5) 可得存活率P=0.50时20CrMnTi钢试样的疲劳寿命概率密度函数:
| $\eqalign{ & {f_N}\left( n \right) = {1 \over {mn}}\cdot{\left( {{C \over n}} \right)^{{1 \over m}}}\cdot{f_S}[{\left( {{C \over n}} \right)^{{1 \over m}}}] = \cr & {1 \over {14.0449n}}{\rm{ }}\cdot{({{1.160{\rm{ }}4 \times {{10}^{54}}} \over n})^{{1 \over {14.044{\rm{ }}9}}}}\cdot \cr & {f_S}\left[ {{{\left( {1.160{\rm{ }}4 \times {{10}^{54}}} \right)}^{{1 \over {14.044{\rm{ }}9}}}}} \right] \cr} $ | (15) |
式中:
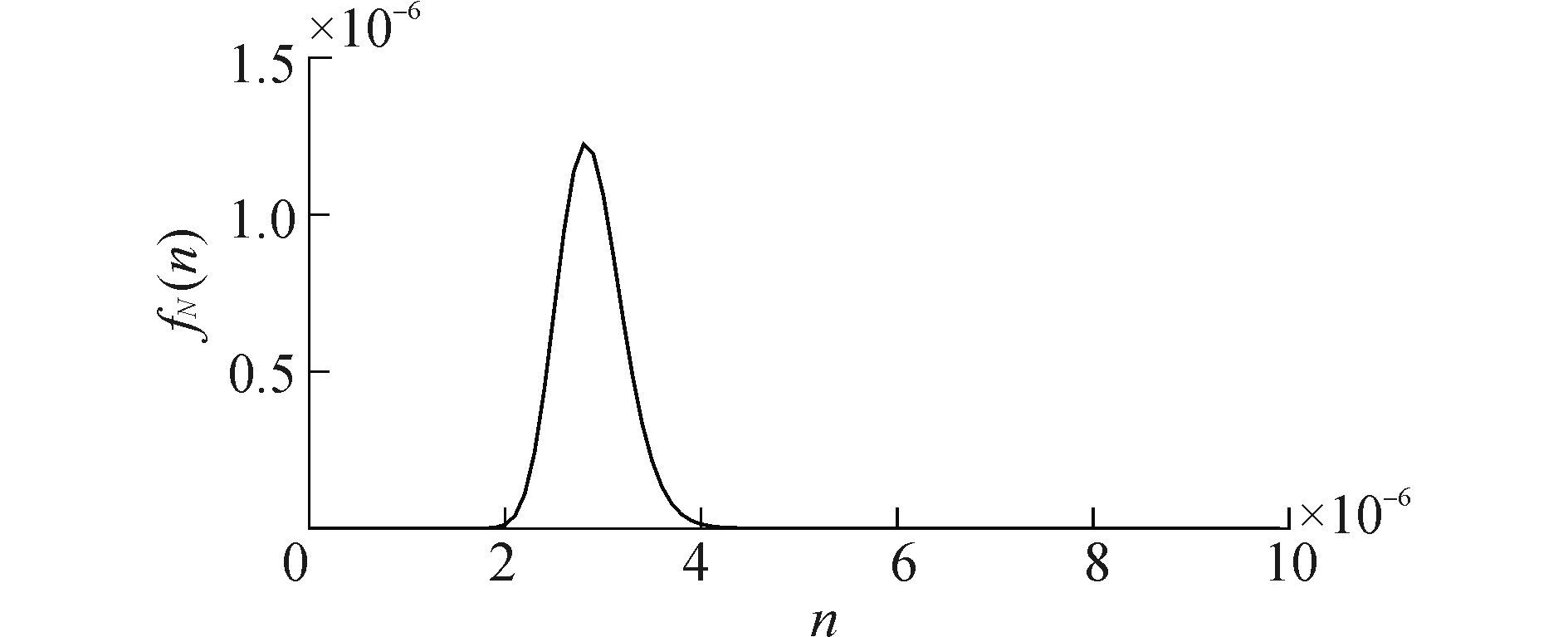
根据式(15) , 可得20CrMnTi钢试样的疲劳寿命概率密度函数曲线, 如图 4所示。
|
| 图4 20CrMnTi钢试样疲劳寿命概率密度函数曲线 Figure 4 Probability density function curve of fatigue life of 20CrMnTi steel specimen |
从图 4可以看出, 在应力S作用下, 20CrMnTi钢试样的疲劳寿命N服从如图 4所示的偏态分布。事实上, 当应力S(外因)的概率分布特征或材料疲劳性能参数C和m(内因)的取值发生变化时, 20CrMnTi钢试样的疲劳寿命概率密度函数曲线也将发生相应的变化。也就是说, 20CrMnTi钢试样的疲劳寿命分布特征是由外因(载荷特性)及内因(材料疲劳性能参数)共同决定的, 而不拘泥于传统方法所采用的对数正态分布或Weibull分布等。
3.2 20CrMnTi钢试样疲劳累积损伤的分布特性同样, 以表 1中存活率P=0.50的S-N曲线(C=1.160 4×1054, m=14.044 9) 为例。在应力S作用下, 由式(11) 可得20CrMnTi钢试样瞬时累积损伤D(n)的概率密度函数:
| $\eqalign{ & {f_D}\left( d \right) = {1 \over {md}}\cdot{\left( {{{Cd} \over n}} \right)^{{1 \over m}}}\cdot{f_S}[{\left( {{{Cd} \over n}} \right)^{{1 \over m}}}] = {1 \over {14.044{\rm{ }}9d}}\cdot \cr & {({{1.160{\rm{ }}4 \times {{10}^{54}}d} \over n})^{{1 \over {14.044{\rm{ }}9}}}}\cdot{f_S}[{({{1.160{\rm{ }}4 \times {{10}^{54}}d} \over n})^{{1 \over {14.044{\rm{ }}9}}}}] \cr} $ | (16) |
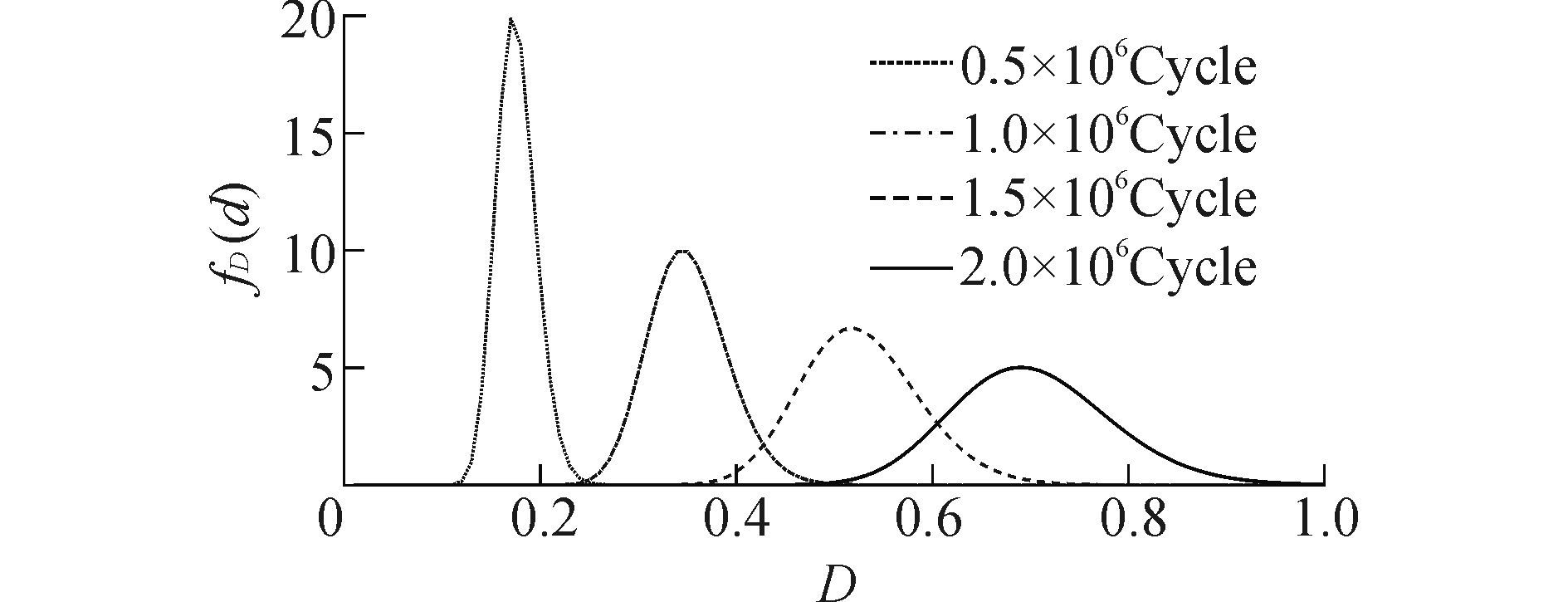
由式(16) 可知, 瞬时累积损伤D(n)的概率密度函数fD(d)随着载荷作用次数n的变化而变化。例如, 当n分别取0.5×106、1.0×106、1.5×106、2.0×106时, 20CrMnTi钢试样瞬时累积损伤D(n)的概率密度函数曲线如图 5所示。
从图 5可以看出:1) 当载荷作用次数n为某一确定值时, 20CrMnTi钢试样的瞬时累积损伤D(n)是一个随机变量, 且服从某一特定的概率分布, 满足疲劳累积损伤规律的随机性;2) 随着载荷作用次数n的增加, 20CrMnTi钢试样瞬时累积损伤D(n)的概率密度函数曲线fD(d)逐渐向右移动, 满足疲劳累积损伤规律的不可逆性。
|
| 图5 20CrMnTi钢试样瞬时累积损伤概率密度函数曲线 Figure 5 Probability density function curve of instantaneous cumulative damage of 20CrMnTi steel specimen |
以上是20CrMnTi钢试样瞬时累积损伤D(n)的概率分布特性, 下面对其临界损伤Dcr的分布特性进行分析。根据式(13) 和式(14) , 可分别计算出20CrMnTi钢试样疲劳寿命的均值和方差:
| ${\mu _N} = \smallint _0^{ + \infty }n\cdot{f_N}\left( n \right)dn = 2.882{\rm{ }}0 \times {10^6}$ | (17) |
| $\sigma _N^2 = \smallint _0^{ + \infty }{(n - {\mu _N})^2}\cdot{f_N}\left( n \right)dn = 1.099{\rm{ }}7 \times {10^{11}}$ | (18) |
根据式(12) , 可得20CrMnTi钢试样临界损伤Dcr的变异系数:
| ${C_{{D_{{\rm{cr}}}}}} \approx {C_N} = {{{\sigma _N}} \over {{\mu _N}}} = {{3.316{\rm{ }}1 \times {{10}^5}} \over {2.882{\rm{ }}0 \times {{10}^6}}} = 0.115{\rm{ }}1$ | (19) |
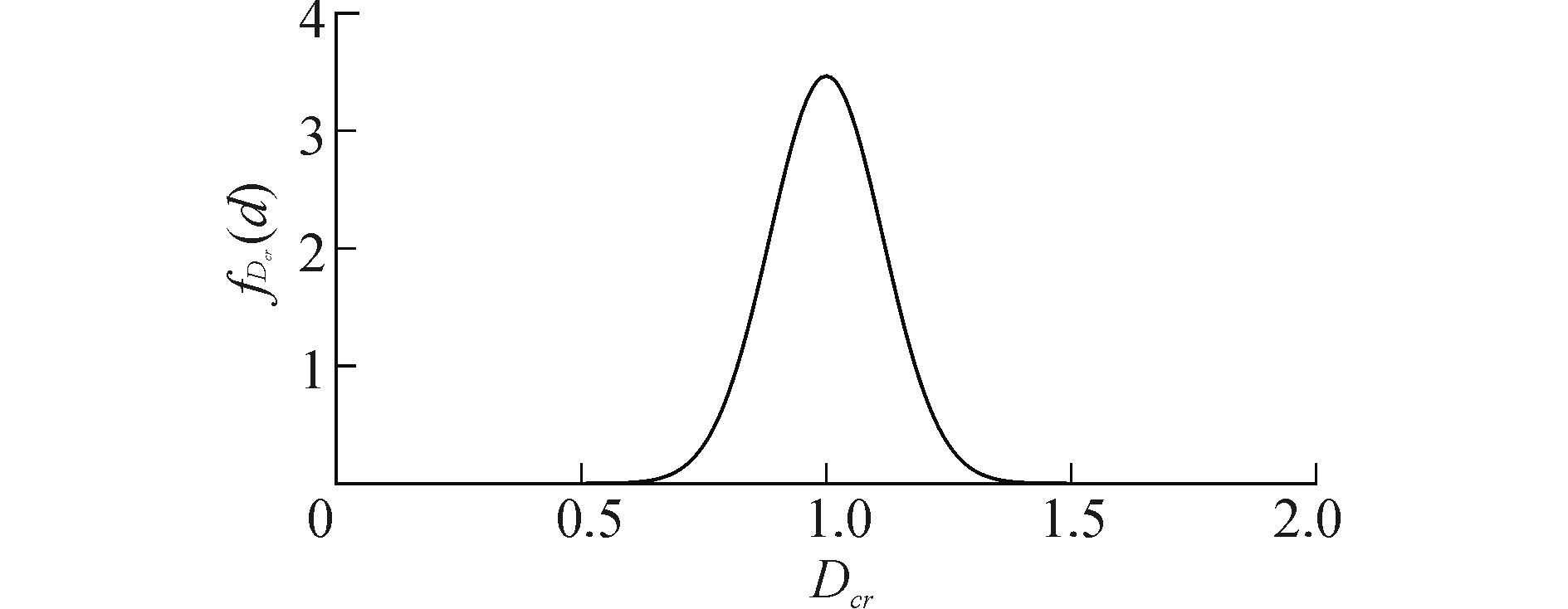
因此, 20CrMnTi钢试样临界损伤Dcr服从均值为1, 变异系数为0.115 1的正态分布, 其概率密度函数曲线如图 6所示。
|
| 图6 20CrMnTi钢试样临界损伤概率密度函数曲线 Figure 6 Probability density function curve of critical damage of 20CrMnTi steel specimen |
为研究材料属性对20CrMnTi钢试样疲劳累积损伤分布特性的影响, 以表 1中不同存活率P下的S-N曲线为例, 探究材料疲劳性能参数(C和m)对累积损伤规律的影响。
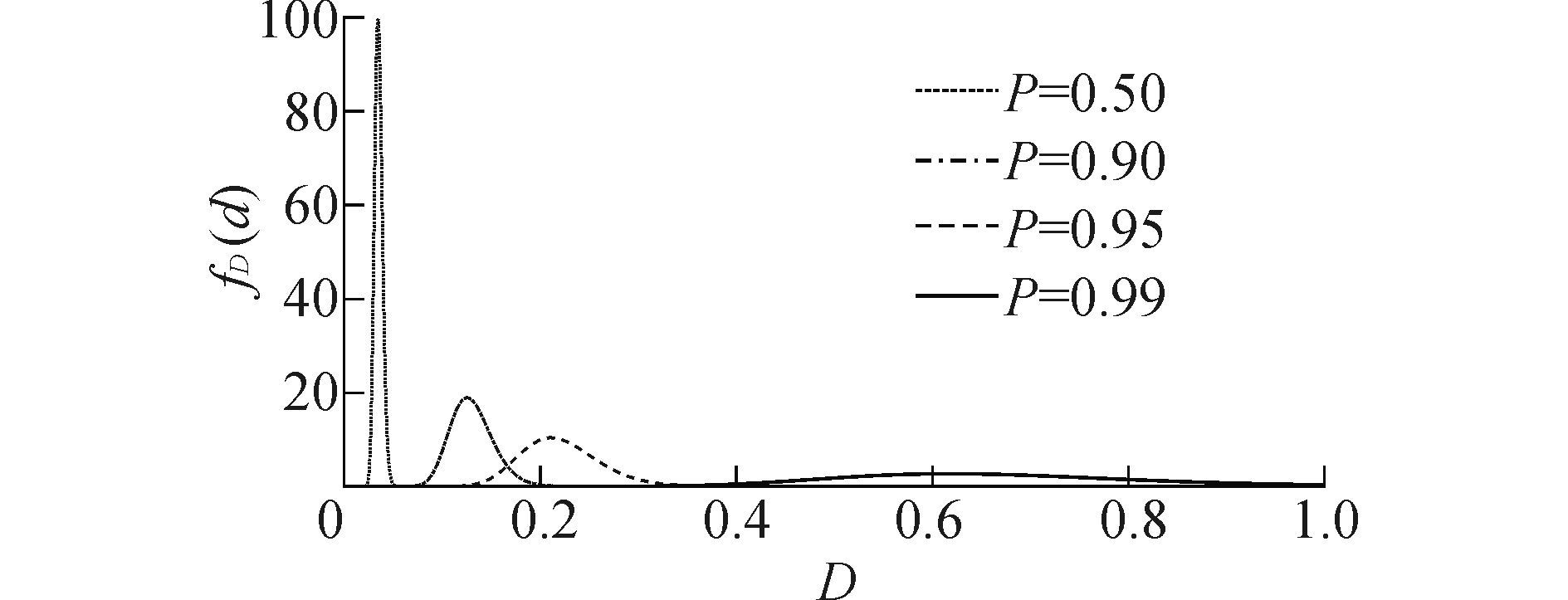
当载荷作用次数n为某一确定值时, 例如n=0.1×106。根据式(11) 可得不同存活率P下20CrMnTi钢试样疲劳累积损伤的概率分布, 如图 7所示。
|
| 图7 材料属性对疲劳累积损伤分布特性的影响 Figure 7 Distribution of fatigue cumulative damage effected by material properties |
由图 7可知, 不同存活率P下20CrMnTi钢试样疲劳累积损伤的概率分布差异很大, 说明材料疲劳性能参数(内因)对疲劳累积损伤分布特性的影响很大。因此, 在产品的加工制造过程中, 应及时修订或改善工艺过程, 避免加工过程中因材料微观结构或内部缺陷等的不均匀性对产品疲劳性能造成的影响。
3.4 载荷特性对疲劳累积损伤分布特性的影响1) 应力均值对疲劳累积损伤分布特性的影响。
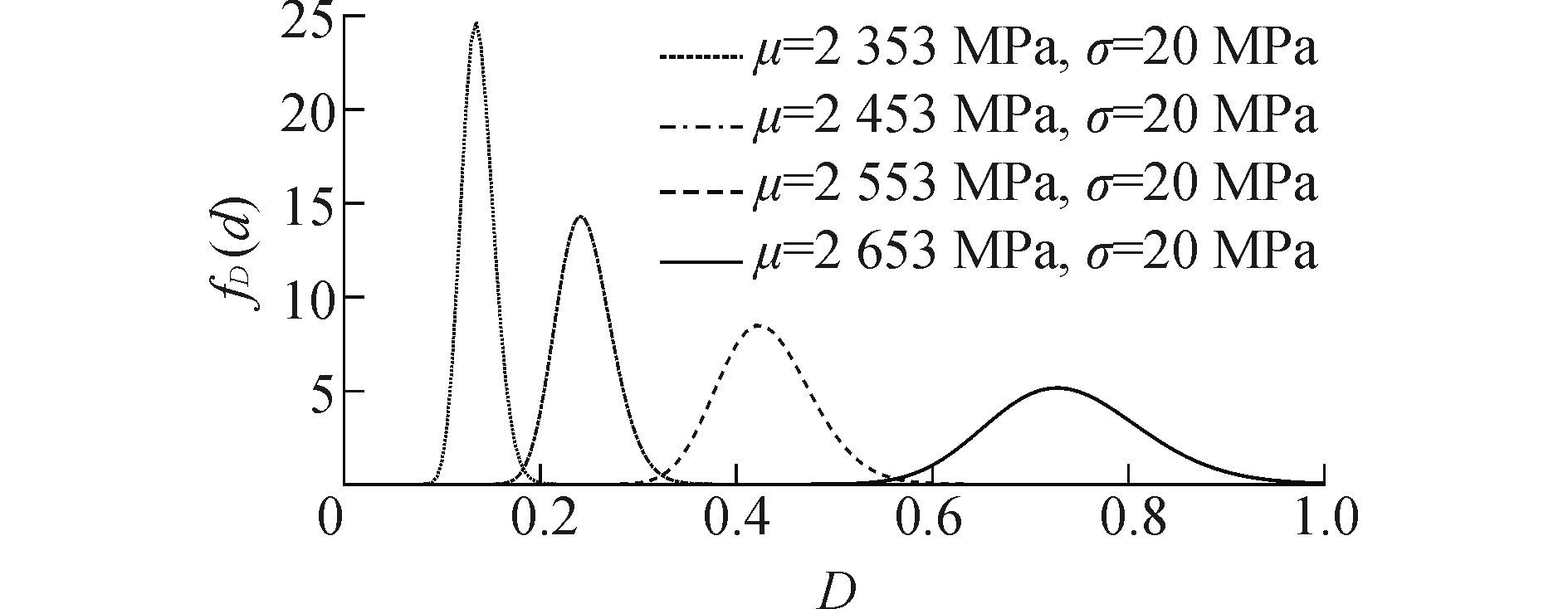
当载荷作用次数n为某一确定值时, 例如n=0.7×106。在应力标准差σ=20 MPa保持不变, 应力均值μ分别取2 353、2 453、2 553、2 653 MPa时, 20CrMnTi钢试样疲劳累积损伤的概率分布如图 8所示。
|
| 图8 应力均值对疲劳累积损伤分布特性的影响 Figure 8 Distribution of fatigue cumulative damage effected by mean stress |
由图 8可知, 在应力方差保持不变的情况下, 一方面, 随着应力均值的降低, 20CrMnTi钢试样疲劳累积损伤的均值逐渐增大;另一方面, 随着应力均值的降低, 20CrMnTi钢试样疲劳累积损伤的分散性逐渐增大, 这种现象符合“随着应力水平的降低, 产品疲劳寿命的分散性逐渐增大[18-19]”的一般规律。
2) 应力方差对疲劳累积损伤分布特性的影响。
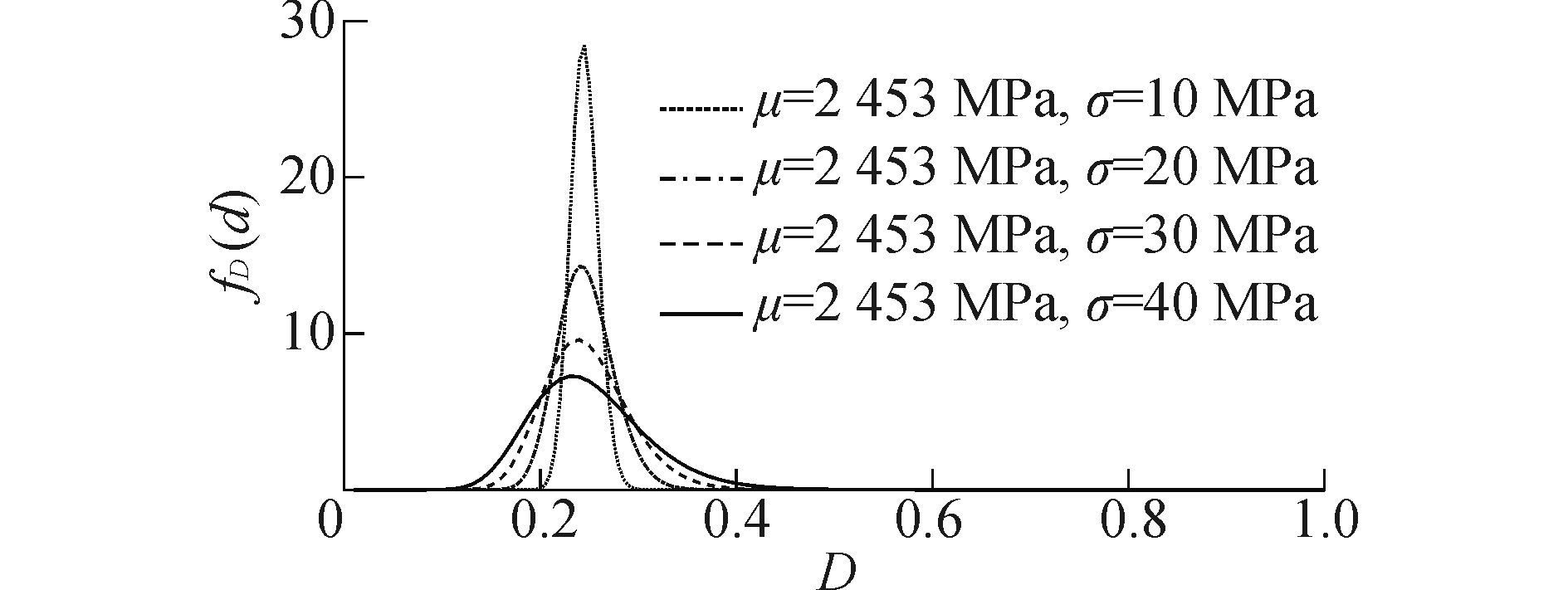
同样, 当载荷作用次数n为某一确定值时, 例如n=0.7×106。在应力均值μ=2 453 MPa保持不变, 应力标准差σ分别取10、20、30、40 MPa时, 20CrMnTi钢试样疲劳累积损伤的概率分布如图 9所示。
|
| 图9 应力方差对疲劳累积损伤分布特性的影响 Figure 9 Distribution of fatigue cumulative damage effected by variance of stress |
由图 9可知, 在应力均值保持不变的情况下, 20CrMnTi钢试样疲劳累积损伤的分散性随着应力方差的增大而增大。因此, 若要通过试验的方法来研究产品疲劳损伤的内在演化机理时, 在试验过程中就应严格控制应力的波动范围, 避免因应力的随机波动对疲劳损伤演化规律造成的影响。
根据以上分析可以看出, 材料属性(内因)及载荷特性(外因)对结构疲劳累积损伤分布规律都有影响, 相比之下, 前者(材料属性)对结构疲劳累积损伤分布规律的影响更为显著。因此, 若要从本质上改善结构的抗疲劳特性, 则应在加工制造过程中及时修订和改善工艺, 避免材料微结构或内部缺陷等的不均匀性对结构疲劳性能产生影响。
4 结论1) 在实例分析中, 通过对20CrMnTi钢试样瞬时累积损伤及临界损伤分布特征及演化规律的分析, 结果表明本文所建模型能够表征疲劳损伤累积的一般规律(随机性和不可逆性)。
2) 该模型是基于Miner理论建立的, 形式简单、参数少, 便于工程应用, 并且能够很好的反映外因(载荷环境)和内因(材料疲劳性能参数)对产品疲劳累积损伤分布特性的影响, 为产品的可靠性设计和疲劳寿命预测提供了理论依据。
| [1] |
许金泉, 郭凤明. 疲劳损伤演化的机理及损伤演化律[J].
机械工程学报, 2010, 46(2): 40–46.
XU Jinquan, GUO Fengming. Mechanism of fatigue damage evolution and the evolution law[J]. Journal of mechanical engineering, 2010, 46(2): 40–46. DOI:10.3901/JME.2010.02.040 |
| [2] | MINER M A. Cumulative damage in fatigue[J]. Journal of applied mechanics, 1945, 12: A159–A164. |
| [3] |
杨晓华, 姚卫星, 段成美. 确定性疲劳累积损伤理论进展[J].
中国工程科学, 2003, 5(4): 81–87.
YANG Xiaohua, YAO Weixing, DUAN Chengmei. The review of ascertainable fatigue cumulative damage rule[J]. Engineering science, 2003, 5(4): 81–87. |
| [4] | CHRISTENSEN R M. An evaluation of linear cumulative damage (Miner's law) using kinetic crack growth theory[J]. Mechanics of time-dependent materials, 2002, 6(4): 363–377. DOI:10.1023/A:1021297914883 |
| [5] |
朱正浩, 沈秋伊, 刘毅. 基于双线性损伤本构的复合材料修理后强度数值分析方法[J].
科学技术与工程, 2014, 14(29): 130–134.
ZHU Zhenghao, SHEN Qiuyi, LIU Yi. A numerical analysis method for strength of scarf-repaired composite structure based on a bilinear damage constitutive model[J]. Science technology and engineering, 2014, 14(29): 130–134. |
| [6] | LI Wei, LI Qiang, WANG Ping. Statistical evaluation on cumulative damage property of aluminum alloy welded joint under multi-stage loading[J]. Advanced materials research, 2010, 118-120: 522–526. DOI:10.4028/www.scientific.net/AMR.118-120 |
| [7] | SUGIMOTO T, SASAKI Y. Fatigue life of structural plywood under two-stage panel shear load:a new cumulative fatigue damage theory[J]. Journal of wood science, 2007, 53(3): 211–217. DOI:10.1007/s10086-006-0855-7 |
| [8] |
姜风春, 刘瑞堂, 张德驺. 一个基于能量原理的疲劳损伤函数[J].
哈尔滨船舶工程学院学报, 1994, 15(2): 25–30.
JIANG Fengchun, LIU Ruitang, ZHANG Dezou. A fatigue damage function based on energy analysis[J]. Journal of Harbin Shipbuilding Engineering Institute, 1994, 15(2): 25–30. |
| [9] | SHANG Deguang, SUN Guoqin, DENG Jing, et al. Nonlinear cumulative damage model for multiaxial fatigue[J]. Frontiers of mechanical engineering in China, 2006, 1(3): 265–269. DOI:10.1007/s11465-006-0035-x |
| [10] | HAN Zhongying, HUANG Xiaoguang, CAO Yuguang, et al. A nonlinear cumulative evolution model for corrosion fatigue damage[J]. Journal of Zhejiang University science A, 2014, 15(6): 447–453. DOI:10.1631/jzus.A1300362 |
| [11] | PÁLMAI Z. A model of non-linear cumulative damage to tools at changing cutting speeds[J]. The international journal of advanced manufacturing technology, 2014, 74(5/6/7/8): 973–982. |
| [12] | 姚卫星. 结构疲劳寿命分析[M]. 北京: 国防工业出版社, 2003: 199-205. |
| [13] |
谢里阳, 刘建中. 样本信息聚集原理与P-S-N曲线拟合方法[J].
机械工程学报, 2013, 49(15): 96–104.
XIE Liyang, LIU Jianzhong. Principle of sample polymerization and method of P-S-N curve fitting[J]. Journal of mechanical engineering, 2013, 49(15): 96–104. DOI:10.3901/JME.2013.15.096 |
| [14] |
谢里阳. 机械可靠性理论、方法及模型中若干问题评述[J].
机械工程学报, 2014, 50(14): 27–35.
XIE Liyang. Issues and commentary on mechanical reliability theories, methods and models[J]. Journal of mechanical engineering, 2014, 50(14): 27–35. DOI:10.3901/JME.2014.14.027 |
| [15] |
谢里阳, 王正. 随机恒幅循环载荷疲劳可靠度异量纲干涉模型[J].
机械工程学报, 2008, 44(1): 1–6.
XIE Liyang, WANG Zheng. Dissimilar-dimension interference model of fatigue reliability under uncertain cyclic load[J]. Chinese journal of mechanical engineering, 2008, 44(1): 1–6. DOI:10.3901/JME.2008.01.001 |
| [16] | MILLER K J, ZACHARIAH K P. Cumulative damage laws for fatigue crack initiation and stage I propagation[J]. Journal of strain analysis for engineering design, 1977, 12(4): 262–270. DOI:10.1243/03093247V124262 |
| [17] | 机械工程材料性能数据手册编委会. 机械工程材料性能数据手册[M]. 北京: 机械工业出版社, 1995: 163-166. |
| [18] | ZHAI Jianming, LI Xiaoyang. A methodology to determine a conditional probability density distribution surface from S-N data[J]. International journal of fatigue, 2012, 44: 107–115. DOI:10.1016/j.ijfatigue.2012.05.008 |
| [19] | XIE Luyang, LIU Jianzhong, WU Ningxiang, et al. Backwards statistical inference method for P-S-N curve fitting with small-sample experiment data[J]. International journal of fatigue, 2014, 63: 62–67. DOI:10.1016/j.ijfatigue.2014.01.006 |



