预应力混凝土桥梁在目前桥梁建设中占据着重要的地位,已经成为主要的桥梁体系,但是桥梁预应力损失一直以来是人们关注的重点问题[1]。预应力桥梁在服役阶段,由于各种因素的影响,均存在不同程度的预应力损失。一方面,预应力损失会引起桥梁结构变形增大,梁体结构出现裂缝,缩短了桥梁的使用寿命,甚至会引起桥梁坍塌;另一方面,预应力损失会引起桥梁结构受力状态的改变,影响桥梁结构静动力特性,进而影响桥梁结构的状态评估[2-3]。相关研究表明,预应力桥梁在服役期间,其预应力损失可达到30%左右,预应力箱梁腹板竖向预应力的损失能达到45%甚至更高[4-5]。近年来,国内外学者在预应力损失方面进行了大量研究,理论计算方法主要是依据国内外规范进行[6-7],主要有“时-步”分析法;分项预应力损失法;预应力总损失法。然而由于材料特性的时变性和外界环境的复杂性,规范中的计算方法很难客观准确地反应实际预应力损失,同时需要的参数较多,计算复杂。基于试验的预应力损失测量方法主要有[8-12]:1)静力测试法,通过测试预应力筋的应力大小来预测预应力损失;2)动力测试方法,基于结构动力特性与预应力大小之间的关系,通过测试桥梁动力特性的变化实现预应力损失的检测;3)基于磁力偏振场原理的测试技术;4)应力释放技术;5)超声波技术。
然而以上预应力测量方法大部分都是基于试验进行的,应用于实际工程的很少,对于实际桥梁预应力测试的可行性和准确性还有待进一步研究。本文基于光纤光栅传感技术,以实际工程为依托,研究了光纤光栅传感技术应用于实际桥梁预应力测试的可行性,提供一种新的预应力检测计算方法,对于预应力损失计算和预应力测试方法有一定的参考价值。
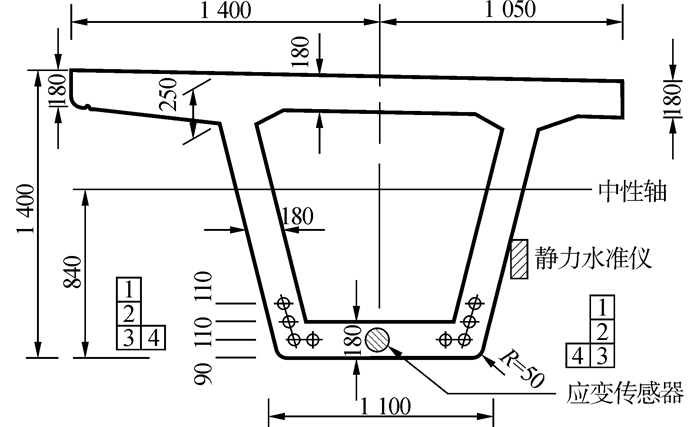
1 工程概况该桥是国道102线安龙泉互通立交桥匝道桥的一部分,为三片组合小箱梁结构的预应力混凝土简支梁桥,桥梁跨径25 m,梁高1.4 m,桥面宽8 m,主梁混凝土设计强度50 MPa,预应力钢绞线的锚下控制应力σcon=1 350 MPa。光纤光栅应变传感器埋设在简支梁边梁跨中底板中间,距离箱梁截面中性轴0.75 m,数量1个,测量桥梁内部纵向应变;光纤光栅静力水准仪安装在桥梁跨中腹板外缘,距离底板下缘0.70 m,数量1个,用于测量桥梁跨中竖向位移。箱梁横截面如图 1所示。图中1号、2号钢绞线为4Φs15.2,3号、4号钢绞线为5Φs15.2。
|
| 图1 箱梁边跨跨中横截面 Figure 1 Side span cross section of box girder |
光纤光栅传感技术是利用光纤光栅反射的光学频谱对温度、应力的敏感特性,通过光学频谱分析和物理量换算,给出各监测点的温度、应变、位移、压力等物理量信息。其测量原理为:宽带光入射时与光场发生耦合作用,反射回一个窄带光,反射回的窄带光的中心波长值随着作用于光纤光栅的温度和应变的改变而线性变化,从而使光纤光栅成为性能优异的应变测量敏感元件。
通过光纤光栅应变传感器计算应变如下
| $ \varepsilon = K\left( {{\lambda _1} - {\lambda _0}} \right) + B\left( {{\lambda _{t1}} - {\lambda _{t0}}} \right) $ | (1) |
式中:ε为所测应变,正值为拉应变,负值为压应变,με;K、B为应变传感器应变系数和温度修正系数,με/nm,每个传感器在出厂时该参数已被标定;λ1、λ0为应变光栅当前波长和初始波长,nm;λt1、λt0为温补光栅当前波长和初始波长,nm。
通过光纤光栅静力水准仪计算位移如下
| $ \nabla H = K\left[ {\left( {{\lambda _1} - {\lambda _0}} \right) - \left( {{\lambda _{t1}} - {\lambda _{t0}}} \right)} \right] $ | (2) |
式中:
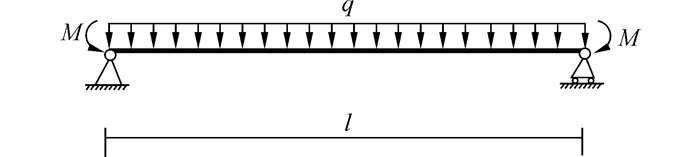
利用等效思想,将简支箱梁在自重荷载和预应力长期荷载作用下的变形等效为弹性杆件在两端支撑条件下的变形,桥梁结构自重简化为均布荷载q,包括一期二期恒载;预应力对结构的作用简化为弯矩M,计算简图如图 2所示。
|
| 图2 预应力简支梁受力计算简图 Figure 2 Stress calculation of prestress simple-supported beam |
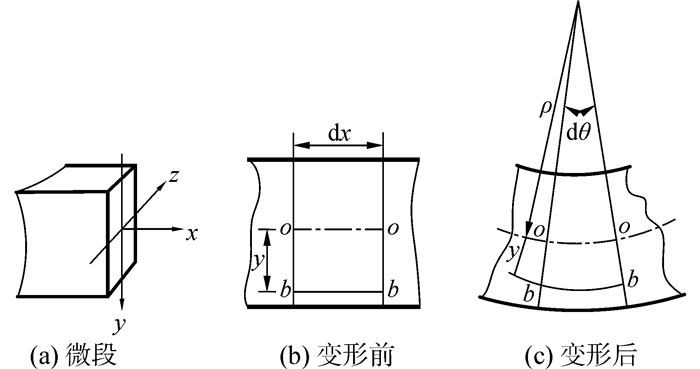
通过力学分析,图 2中简支梁跨中截面属于纯弯曲截面,取该截面的微段进行变形几何分析,所取微段及其变形前后如图 3所示。
|
| 图3 所取微段及其变形图 Figure 3 Micro-section and its deformation |
由力学知识可知,距中性轴y处的纤维应变为
| $ \varepsilon =\frac{\overset\frown{bb}-\overline{bb}}{\overline{bb}}=\frac{\left( \rho +y \right)\text{d}\theta \text{-}\rho \text{d}\theta }{\rho \text{d}\theta }=\frac{y}{\rho } $ |
基于弹性理论,由静力学关系可知,荷载作用下该截面处的曲率半径和弯矩之间的关系为
| $ \frac{1}{\rho } = \frac{{{M_e}}}{{EI}} = \frac{{\frac{1}{8}q{l^2}-M}}{{EI}} $ |
另外,简支梁的最大挠度f出现在跨中截面,且最大挠度为
由以上公式可以求得简支梁跨中挠度f和应变ε的关系为
| $ f = \frac{{48M{l^2}-5q{l^4}}}{{48\left( {q{l^2}-8M} \right)y}}\varepsilon $ |
对上式作进一步的公式变换,得出预应力引起的截面弯矩M的表达式为
| $ M = \frac{{48yq{l^2}\frac{f}{\varepsilon } + 5q{l^2}}}{{48{l^2} + 384y\frac{f}{\varepsilon }}} $ | (3) |
从式(3)可以看出,一旦桥梁结构确定,均布荷载q、桥梁跨径l和y(所测截面到中性轴的距离)都将成为常量,弯矩M只是变量
| $ M = \frac{{AQ + B}}{{C + DQ}} $ | (4) |
式中:A=48yql2,B=5ql4,C=48l2,D=384y,Q=
预应力损失率记为L(%),则其表达式为
| $ L = \left( {1 - \frac{M}{{{M_0}}}} \right) \times 100\% $ | (5) |
式中:M0表示预应力简支梁由初始预应力引起的桥梁弯矩,由初始预应力大小、预应力筋数量和面积、跨中截面预应力筋位置到该中性轴的距离计算求得。将式(4)代入式(5),则预应力损失率L的表达式为
| $ L = \frac{{\left( {{M_0}D - A} \right)Q + \left( {{M_0}C - B} \right)}}{{{M_0}C + {M_0}DQ}} \times 100\% $ | (6) |
令:A′=M0D-A,B′=M0C-B,C′=M0C,D′=M0D,则式(6)进一步简化为
| $ L = \frac{{A'Q + B'}}{{C' + D'Q}} \times 100\% $ | (7) |
式中:A′、B′、C′、D′是和桥梁自身结构有关的参数,Q是和实测桥梁跨中纵向应变和跨中竖向位移有关的参数,该式就是预应力简支梁跨中预应力损失计算的基本公式。
从该公式的建立过程可以看出,公式的推导都是基于弹性理论而进行的,所以该式对于已经开裂的预应力桥梁结构并不适用。
4 预应力损失计算 4.1 基于本文方法的预应力损失分析 4.1.1 参数测定为了测量桥梁跨中的应变和竖向位移,在浇筑箱梁混凝土时将光纤光栅应变传感器埋入箱梁跨中底板,同时在桥梁跨中位置安装静力水准仪,并在桥梁竣工时测量应变传感器和静力水准仪应变中心波长和温补波长平均值作为初始值。此时的波长数据为桥梁预应力筋张拉完成后的数据,这也是进行预应力损失计算的基准波长数据。箱梁竣工时间为2011年4月,初始波长平均值为:
1)应变传感器初始波长:
λ0=1 540.015 2 nm,λt0=1 527.822 7 nm
2)静力水准仪初始波长:
λ0=1 552.054 0 nm,λt0=1 530.426 0 nm
桥梁运营4年后,测量应变传感器和静力水准仪的应变中心波长和温补波长,并取测量时间段内平均值作为计算值,测量时间为2015年12月。取12月份一个月内约2.6×106个波长数据的平均值作为测量值:
1)应变传感器测量时段平均波长:
λ1=1 540.256 4 nm,λt1=1 527.840 5 nm
2)静力水准仪测量时段平均波长:
λ1=1 551.268 7 nm,λt1=1 530.768 3 nm
简支梁跨中应变传感器各参数测量值如下:
B=-907.758 035 8 με/nm
λ1=1 540.256 4 nm, λ0=1 540.015 2 nm
K=829.460 015 8 με/nm
λt1=1 527.840 5 nm, λt0=1 527.822 7 nm
简支梁跨中静力水准仪各参数测量值如下:
K=32.224 361 mm/nm
λ1=1 551.268 7 nm, λ0=1 552.054 0 nm
λt1=1 530.768 3 nm, λt0=1 530.426 0 nm
将简支梁跨中应变传感器各参数测量值代入到式(1)中,求得应变ε=184,将简支梁跨中静力水准仪各参数测量值代入到式(2)中,求得位移ΔH=-36.3 mm。
4.1.2 预应力损失计算初始预应力引起的桥梁弯矩M0按图 1中预应力筋对截面中性轴的矩进行计算,其中预应力筋初始应力取张拉控制应力1 350 MPa,Φs15.2预应力钢绞线公称面积为139 mm2,各预应力筋到中性轴的距离见图 1。经计算M0=4 571 kN·m。桥梁跨径l=25 m,应变测量点到截面中性轴的距离为y=0.75 m,均布荷载q=42.14 kN/m,求得各参数后代入到式(7)中求得预应力损失率,各参数值及预应力损失率如下:
A′=368 298 kN·m2,B′=54 825 313 kN·m3
C′=173 130 000 kN·m3,D′=1 316 448 kN·m2
Q=-197.282 6 m,L=14.6%
4.2 基于我国公路桥规的预应力损失分析我国公路钢筋混凝土和预应力混凝土桥涵设计规范(JTG D62-2012)[6]中给出了预应力混凝土桥梁的各项预应力损失计算方法,结合相关设计资料,对该预应力混凝土桥梁跨中截面的各项预应力损失进行了计算。其中,预应力钢筋与管道壁之间的摩擦引起的预应力损失σl1,锚具变形、钢筋回缩和接缝压缩引起的预应力损失σl2,混凝土弹性压缩引起的预应力损失σl4,钢筋松弛引起的预应力损失σl5,混凝土收缩徐变引起的预应力损失σl6。按使用阶段计算有效预应力,该桥梁采用后张法施工,计算结果如下:
σl1=44.3 MPa,σl2=17.7 MPa
σl4=41.3 MPa,σl5=29.9 MPa
σl6=100.0 MPa,σcon=1 350 MPa, L=17.3%
4.3 基于美国桥梁规范的预应力损失分析(AASHTO 2012)规范[7]中规定后张法预应力构件的预应力损失由以下几项组成:摩擦引起的预应力损失ΔfpF,锚固装置引起的预应力损失ΔfpA,预应力加载时的弹性伸缩和外部荷载引起的预应力损失ΔfpES,混凝土的长期收缩徐变和钢筋的松弛引起的预应力损失ΔfpLT。经计算后各项预应力损失如下:
ΔfpF=96.4 MPa,ΔfpES=21.4 MPa, ΔfpLT=64.9 MPa
ΔfpA=0, σcon=1 350 MPa,L=13.5%
5 结论本文通过在实桥中埋设光纤光栅应变传感器和静力水准仪,结合几何学和力学的理论分析,建立了预应力简支桥梁预应力损失计算公式,计算了一座预应力简支箱梁桥成桥四年后桥梁的预应力损失,并与国内外相关规范[6-7]中的预应力损失计算结果进行了比较。主要结论有:
1)本文方法得到的预应力损失为14.6%,按我国公路桥规[6]计算的预应力损失为17.3%,按美国规范[7]计算的预应力损失为13.5%,本文方法的计算结果处于二者之间,更加接近(AASHTO 2012)规范[7]计算结果,我国(JTG D62-2012)规范[6]的计算结果略大,但三者计算结果基本接近,说明本文提出的方法具有一定的准确性和可靠性,能够应用于实际工程进行简支桥梁的预应力损失分析。
2)从公式可以看出,一旦桥梁结构确定,预应力损失只是跨中位移和应变比值的函数,相比规范中复杂的计算方法,该方法在计算预应力损失方面更加简便。同时,预应力损失计算是基于桥梁实测应变和位移,能更加真实反映桥梁实际预应力的变化。同时该方法还可以用于预应力损失的长期观测和桥梁的状态评估。
3)该公式的建立以简支结构力学分析为基础,与桥梁的截面形式、材料类型无关,所以该公式适用于所有类型的简支桥梁的预应力损失分析。
4)公式在建立过程中忽略了预应力简化后的轴力影响,同时混凝土材料的离散性对测量结果有一定影响,所以该预应力损失计算方法是一种近似方法,但从实际桥梁的预应力损失计算结果来看,这种影响很小,该方法的准确度能够达到要求。
| [1] |
贺志勇, 陈智凯, 易功超. 桥梁预应力损失和刚度变化预测方法研究[J].
中外公路, 2015, 35(3): 131–136.
HE Zhiyong, CHEN Zhikai, YI Gongchao. Study on predication method of bridge prestress loss and rigidity variation[J]. Journal of China & foreign highway, 2015, 35(3): 131–136. |
| [2] |
姚正中, 李银斌, 杨鸿波, 等. 四跨混凝土连续刚构桥预应力损失时效分析[J].
公路工程, 2014, 39(3): 134–139.
YAO Zhengzhong, LI Yinbin, YANG Hongbo, et al. Time-dependent analysis of prestress loss of four-spans prestressed concrete continuous frame bridge[J]. Highway engineering, 2014, 39(3): 134–139. |
| [3] | CARO L A, MARTI-VARGAS J R, SERNA P. Prestress losses evaluation in prestressed concrete prismatic specimens[J]. Engineering structures, 2013, 48: 704–715. DOI:10.1016/j.engstruct.2012.11.038 |
| [4] | BYMASTER J C, DANG N, FLOYD R W, et al. Prestress losses in pretensioned concrete beams cast with lightweight self-consolidating concrete[J]. Structures, 2015, 2: 50–57. DOI:10.1016/j.istruc.2015.01.003 |
| [5] | GILBERTSON C G, AHLBORN T M. A Probabilistic comparison of prestress loss methods in prestressed concrete beams[J]. PCI journal, 2004, 49(5): 52–69. DOI:10.15554/pcij |
| [6] |
JTG D62-2012, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京:人民交通出版社, 2012.
JTG D62-2012, Code for design of highway reinforced concrete and prestressed concrete bridges and culverts[S]. Beijing: China Communication Press, 2012. |
| [7] | AASHTO. AASHTO LRFD bridge design specifications[S]. 6th ed. (S.l.): AASHTO, 2012. |
| [8] | LUNDQVIST P, NILSSON L O. Evaluation of prestress losses in nuclear reactor containments[J]. Nuclear engineering and design, 2011, 241(1): 168–176. DOI:10.1016/j.nucengdes.2010.11.007 |
| [9] | ASAMOTO S, KATO K, MAKI T. Effect of creep induction at an early age on subsequent prestress loss and structural response of prestressed concrete beam[J]. Construction and building materials, 2014, 70: 158–164. DOI:10.1016/j.conbuildmat.2014.07.028 |
| [10] | HALVONIK J, DOLNAK J, BORZOVIC V. Long-term losses of prestress in precast members cast from HPC[J]. Procedia engineering, 2013, 65: 81–86. DOI:10.1016/j.proeng.2013.09.015 |
| [11] | OH B H, YANG I H. Realistic long-term prediction of prestress forces in psc box girder bridges[J]. Journal of structural engineering, 2001, 127(9): 1109–1116. DOI:10.1061/(ASCE)0733-9445(2001)127:9(1109) |
| [12] | KIM J T, PARK J H, HONK D S, et al. Vibration and impedance monitoring for prestress-loss prediction in PSC girder bridges[J]. Smart structures and systems, 2009, 5(1): 81–94. DOI:10.12989/sss.2009.5.1.081 |



