2. College of Mechanical Engineering, Chongqing University, Chongqing 400044, China
当前叶片专用翼型廓线的设计都是在单点攻角情况下,基于特定的几何轮廓,来研究其空气动力学特性,并进行参数的设计和优化。美国可再生能源实验室的Tangler等[1]基于Eppler理论及反设计方法设计出了35种用于各种工况条件下的NREL-S系列翼型,该系列翼型具有良好的升阻比特性。荷兰Delft大学的W.A.Timmer [2]基于混合设计方法设计出了相对厚度15%~40%的DU系列风力机专用翼型,该系列翼型考虑了翼型之间的几何兼容性和深失速特性,通过限制翼型上表面厚度以及在翼型尾部设计“S”型尾缘,提高了翼型的升力系数,与传统的航空翼型相比,翼型具有更加优良的气动特性。丹麦Risø国家实验室的FUGLSONG P[3]基于直接设计法耦合XFOIL软件对风力机翼型进行研发,已设计出了适用于不同运行工况和不同控制方式的风力机翼型。在国内,中国空气动力研究与发展中心的张维智等[4]在翼型上表面的恢复区内应用修正后的Stratford理想压力分布,采用Weber已知压力分布求解翼型外形的理论已设计出一套在低雷诺数时的新翼型,并对雷诺数为Re=5.6×105的情况进行了实验研究。西北工业大学的乔志德等[5]针对兆瓦级大型风力机,研究发展了以具有优良高雷诺数和高升力气动性能为特点的NPU-WA翼型系列,并进行了风洞实验对比研究,表明该翼型系列具有高的气动性能。重庆大学陈进等[6-7]基于保角变换理论及泛函分析法提出了通用翼型泛函集成表达理论,并结合多学科交叉优化设计思想,先后设计出了CQU-DTU、WT系列翼型并通过风洞实验验证了该翼型系列具有优越的气动性能。此外,国内外还有其他学者在风力机翼型设计方面做了很多创造性的研究工作[8-10],从不同角度对风力机叶片专用翼型进行了改进与优化设计,大都通过改变翼型的几何参数来提高翼型的气动性能,并取得了一定的效果。
然而,目前国内外风力机叶片翼型廓线设计理论研究,其出发点都是基于单点攻角(如设计攻角为6°)情况下,在研究其几何特性及空气动力特性的基础上进行改进和参数优化,以获得性能良好的叶片翼型。并没有考虑多点攻角情况下风力机翼型的设计与优化。对于单点攻角情况下设计出来的翼型往往在局部攻角范围内具有较好的气动性能,然而对于更广泛的攻角范围内其气动性能会不够理想。而实际风轮叶片要求在更广泛的攻角范围内变化时,叶片能够稳定运行。因此,这就引发我们考虑多点攻角情况下翼型的设计方法与优化,不能片面追求局部攻角范围内的高气动性能,而要寻求在更广泛的攻角范围内其气动性能整体提高。考虑多点攻角情况下翼型的设计与优化,其难点在于翼型气动力计算的收敛问题。关键问题在于翼型廓线数学模型表征方法及优化设计过程中,并没有考虑翼型廓线的曲率光滑连续性。而翼型廓线曲率光滑连续又与翼型表面压力分布密切相关,即翼型表面曲率光滑连续性好,则其表面压力分布局部波动小,气动力就容易收敛。因此,本文在建立翼型B样条函数表达式基础上,耦合翼型廓线表面曲率光滑连续性,实现多点设计攻角情况下的翼型型线控制与参数优化。
1 翼型B样条函数与表面曲率光滑连续性理论 1.1 翼型B样条函数理论对于风力机翼型廓线设计,以往的反设计方法是给定希望达到的压力分布以及初始的基本翼型,通过几何和流动控制方程,逐步逼近给定的气动特性,但是这种翼型设计方法计算量大,而且不能处理多学科优化设计问题。由于B样条曲线是依据有限个空间位置点坐标绘制出的一条光滑曲线,再通过将复杂廓线首尾点相连就可得到封闭的曲线。因此,本文基于B样条曲线的翼型廓线正设计方法,采用三次均匀B样条函数,该函数只需4个控制点即可表征一段光滑曲线,这样极大地减少了复杂曲线的控制变量,有利于风力机翼型廓线的参数化设计。
B样条函数的一般表达方式为
| ${{P}_{k,n}}\left( t \right)=\sum\limits_{k=0}^{9}{{{P}_{i+k}}{{G}_{i,n}}\left( t \right)},\ \ t\in \left[ 0,1 \right]$ | (1) |
式(1)为第k段n次B样条曲线段(k=0, 1, …, n),这些曲线段的全体称为n次B样条曲线,其顶点Pi(i=0, 1, …, n+m)所组成的多边形称为B样条曲线的特征多边形。其中,G(t)为基函数,表达式为
| $\begin{align} &{{G}_{i,n}}\left( t \right)=\frac{1}{n!}\sum\limits_{j=0}^{n-j}{{{\left( -1 \right)}^{j}}}C_{n+1}^{j}{{\left( t+n-i-j \right)}^{n}}, \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ t\in \left[ 0,1 \right]\ \ i=0,1,\ldots ,n \\ \end{align}$ | (2) |
由于基函数具有递推性、连续性及几何不变性等特点,使得能够较好的控制翼型廓线变化。采用三次B样条曲线,分别通过4个顶点来控制翼型的上、下翼面,而且上、下翼面首尾两个顶点重合。
对于三次B样条曲线,其基函数表达式为
| $\begin{align} &\left\{ \begin{array}{*{35}{l}} {{G}_{0,3}}\left( t \right)=\frac{1}{6}\left( -{{t}^{3}}+3{{t}^{2}}-3t+1 \right) \\ {{G}_{1,3}}\left( t \right)=\frac{1}{6}\left( 3{{t}^{2}}-3{{t}^{2}}+4 \right) \\ {{G}_{2,3}}\left( t \right)=\frac{1}{6}\left( -3{{t}^{3}}+3{{t}^{2}}+3t+1 \right) \\ {{G}_{3,3}}\left( t \right)=\frac{1}{6}{{t}^{3}} \\ \end{array} \right. \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ t\in \left[ 0,1 \right] \\ \end{align}$ | (3) |
因此,三次B样条函数写成矩阵的形式表示为
| $\begin{align} &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\mathit{\boldsymbol{P}}}_{0.3}}\left( t \right)= \\ &\frac{1}{6}\left[ 1\ \ t\ \ {{t}^{2}}\ \ {{t}^{3}} \right]\left[ \begin{matrix} 1&4&1&0 \\ -3&0&3&0 \\ 3&-6&3&0 \\ -1&3&-3&1 \\ \end{matrix} \right]\left[ \begin{matrix} {{P}_{0}} \\ {{P}_{1}} \\ {{P}_{2}} \\ {{P}_{3}} \\ \end{matrix} \right] \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ t\in \left[ 0,1 \right] \\ \end{align}$ | (4) |
式中:P0、P1、P2、P3为4个控制点,t为B样条曲线的横坐标。B样条曲线由两种表示复杂型线的方式,一种是曲线不经过给定的控制点,另外一种是曲线通过给定的控制点。为了便于翼型廓线的优化设计,本文采用第二种表达曲线的方式,即曲线通过给定的控制点,其中P0和P3为B样条曲线固定的首尾两点,P1和P2为未知控制点。
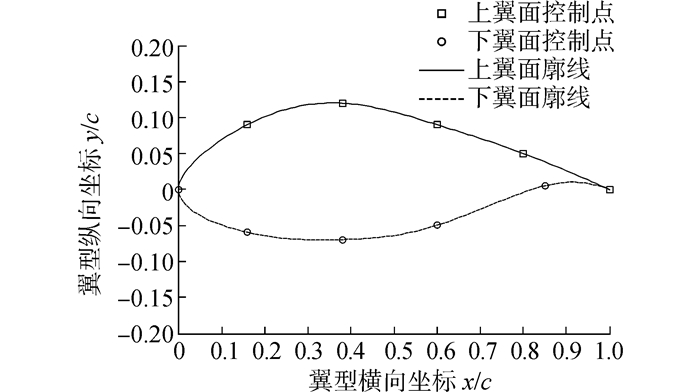
用式(4)分别表示翼型上、下翼面廓线坐标,即为翼型B样条函数设计方法理论。为了使翼型上、下翼面首尾两点相连且表现出光滑连续的特性,使上、下翼面B样条曲线控制点经过首尾两个给定的点,其中翼型上翼面尾缘处端点与翼型下翼面尾缘处端点同时经过翼型廓线坐标点(1, 0),翼型上翼面前缘处端点与翼型下翼面前缘处端点同时经过翼型廓线固定点(0, 0)。已知翼型上、下翼面首尾两个点,那么实际上翼型控制点只有四个,即上、下翼面各两个。图 1即为B样条曲线控制翼型廓线图,该方法只需控制四个参数点,就可变化出无穷形状的风力机翼型。
|
| 图1 B样条函数控制翼型廓线 Figure 1 Airfoil profiles used B-spline function |
文献[8]已对翼型曲率光滑连续性及如何影响压力分布进行了详尽的研究,然而,其研究在翼型优化设计过程中并未考虑翼型形函数的曲率光滑连续性。为了解决多点设计攻角情况下翼型气动力收敛问题,在翼型优化设计过程中,需考虑翼型表面的曲率光滑连续性。翼型型线曲率光滑连续性通常用曲率及曲率变化率来表示:
| $C=1/R=\frac{{{y}''}}{{{\left[ 1+{{{{y}'}}^{2}} \right]}^{3/2}}}$ | (5) |
| ${C}'=\frac{{y}'''\left[ 1+{y}' \right]-3{y}'{{{{y}''}}^{2}}}{{{\left[ 1+{{{{y}'}}^{2}} \right]}^{5/2}}}$ | (6) |
在设计雷诺数为Re=3.0×106,马赫数Ma=0.15的条件下,以光滑和粗糙条件下最大升阻比作为目标函数,不以单点攻角下的升阻比最大作为目标函数,而是以攻角变化范围在4°~9°下的升阻比加权最大作为目标函数:
| $f\left( x \right)\max \left( {{\mu }_{1}}{{C}_{Ld}}+{{\mu }_{2}}{{{{C}'}}_{Ld}} \right)$ | (7) |
式中:μ1、μ2为运行工况在光滑与粗糙条件下的权值系数,μ1,μ2∈[0 1],且μ1+μ2=1;
根据B样条函数表达复杂曲线的思想,选取翼型上、下翼面有限个控制点来控制翼型廓线变化,原则上控制点选得较多,则能更好的控制翼型几何曲线,选取翼型上、下翼4个控制点(翼型首尾两个固定控制点除外)共8个变量作为翼型优化设计变量:
| $X=\left( {{P}_{1,x}},{{P}_{1,y}},{{P}_{2,x}},{{P}_{2,y}},{{{{P}'}}_{1,x}},{{{{P}'}}_{1,y}},{{{{P}'}}_{2,x}},{{{{P}'}}_{2,y}} \right)$ | (8) |
为了使翼型廓线在可控制的范围内变化,将B样条曲线的控制点进行如下约束:
| ${{X}_{\min }}\le X\le {{X}_{\max }}$ | (9) |
设计变量约束范围如表 1所示。
| P1, x | P1, y | P2, x | P2, y | P′1, x | P′1, y | P′2, x | P′2, y | |
| 最大 值 |
0.9 | 0.1 | 0.5 | 0.2 | 0.5 | -0.1 | 1.0 | 0.1 |
| 最小 值 |
0.7 | 0.0 | 0.3 | 0.1 | 0.3 | -0.2 | 0.7 | -0.1 |
本研究分别选取最大相对厚度为15%、18%及21%的三种翼型进行优化设计,设定翼型最大厚度为
| $\frac{th}{c}=t\in \left[ 0.15,0.21 \right]$ | (10) |
除对最大相对厚度进行约束外,还需对翼型的最大厚度弦向位置进行约束:
| $0.24\le {{L}_{\max }}\le 0.35$ | (11) |
此外,在多点攻角情况下翼型优化设计过程中,最关键的问题是翼型气动力收敛问题。即在翼型优化过程中,在某一攻角情况下,设计翼型气动力收敛,然而在另一攻角情况下,设计翼型气动力可能不收敛,使优化程序无法继续进行。因此,考虑翼型连续攻角情况下优化时,有必要耦合翼型廓线表面曲率光滑连续性,实现连续攻角情况下的翼型型线控制与参数优化。建立翼型曲率及曲率变化率约束不等式:
| ${{C}_{\min }}\le {{C}_{i}}-{{C}_{i-1}}\le {{C}_{\max }}$ | (12) |
式中:Ci为优化翼型第i点坐标的曲率,Ci-1为优化翼型第i-1点坐标的曲率。
| ${{{C}'}_{\min }}\le {{{C}'}_{i}}-{{{C}'}_{i-1}}\le {{{C}'}_{\max }}$ | (13) |
式中:C′i为优化翼型第i点坐标的曲率变化率,C′i-1为优化翼型第i-1点坐标的曲率变化率。
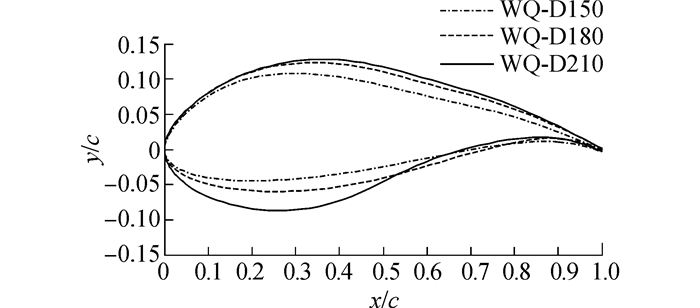
3 优化结果及对比分析采用多目标粒子群优化程序进行求解。相关算法参数为:学习因子均为0.5,变量维数为12,惯性权重为0.85,种群大小为30,最大迭代次数为400。将该算法与RFOIL软件耦合求解计算翼型气动性能,对风力机翼型进行型线优化设计。已知目标函数、设计变量及约束条件等参数,优化出了三种整体性能较好的风力机翼型(如图 2所示),分别命名为WQ-D150、WQ-D180和WQ-D210,其最大相对厚度分别为15%、18%和21%。
|
| 图2 WQ-D翼型系列 Figure 2 WQ-D airfoil series |
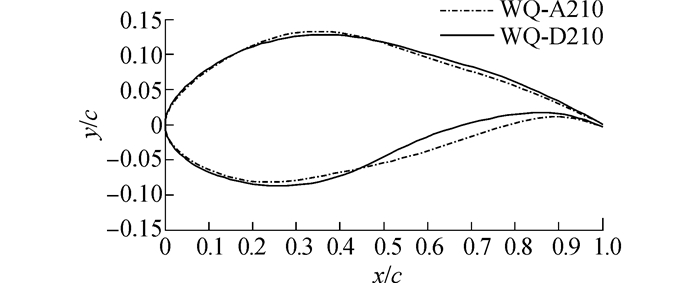
为了研究多点攻角情况下设计出来的新翼型与单点攻角情况下设计出来的翼型的几何特性及气动性能。将WQ-D210翼型与WQ-A210翼型(单点攻角情况下设计出来的)进行几何及气动特性对比。图 3为WQ-A210翼型与WQ-D210翼型几何轮廓线示意图,这两种翼型的最大相对厚度均为21%,最大的区别在翼型尾缘附近的厚度,WQ-D210翼型比WQ-A210翼型尾缘附近的厚度要薄。表面上看,这两种翼型曲线均光滑连续,然而实际并非如此。
|
| 图3 单点攻角及连续攻角优化翼型廓线 Figure 3 The optimal airfoil profiles of the one and multi-points angle of attack |
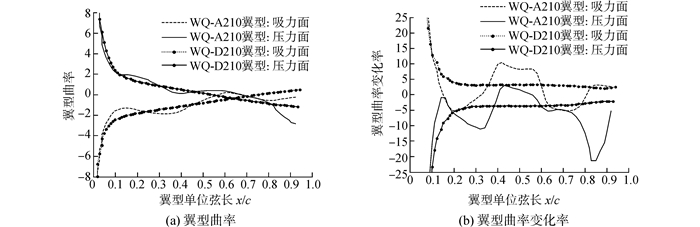
图 4为WQ-A210翼型与WQ-D210翼型曲率及曲率变化率。由图可知,WQ-D210翼型的曲率及曲率变化率均要优于WQ-A210翼型,尤其是曲率变化率。其主要原因在于多点设计攻角情况下翼型在优化过程中,耦合了翼型型线的曲率及曲率变化率,使得翼型表面曲率及曲率变化率在设定的范围光滑连续。而在翼型优化设计的过程当中,这种翼型光滑连续特性的控制能够解决多点攻角情况下的气动力收敛这一关键问题。
|
| 图4 WQ-A210与WQ-D210翼型曲率及曲率变化率对比 Figure 4 The comparison of curvature and curvature variation for profiles of WQ-A210 and WQ-D210 |
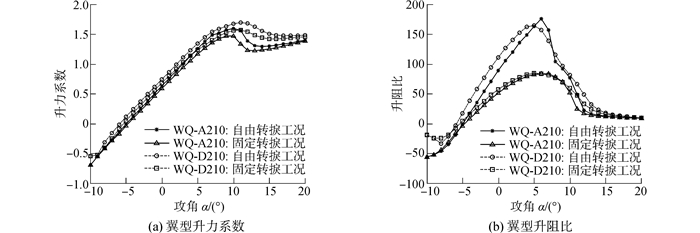
图 5为两种方法设计出来的翼型气动性能对比图(Re=3.0×106,马赫数Ma=0.15)。表 2列出了WQ-A210翼型、WQ-D210翼型关键气动参数。翼型的气动特性计算采用风力机气动性能计算软件RFOIL计算,文献[7, 9]已经验证该软件计算理论值的可靠性。结合图表可知:无论是光滑条件(自由转捩),还是粗糙条件(固定转捩),WQ-D210翼型的最大升力系数及一定攻角范围内的平均升力系数均要优于WQ-A210翼型;虽然在光滑条件下,WQ-D210翼型的最大升阻比(163.821)要低于WQ-A210翼型(176.112),降低了约6.98%;但是一定攻角范围内的平均升阻比要优于WQ-A210翼型,提高了约6.64%。主要原因在于WQ-A210翼型是依据单点攻角(通常攻角为6°)情况下设计出来了,以追求局部的最大升阻比特性;而WQ-D210翼型是依据多点攻角情况下设计出来的,以追求翼型整体的气动特性。
|
| 图5 WQ-A210翼型与WQ-D210翼型气动性能对比 Figure 5 Aerodynamic performances of the WQ-A210 and WQ-D210 |
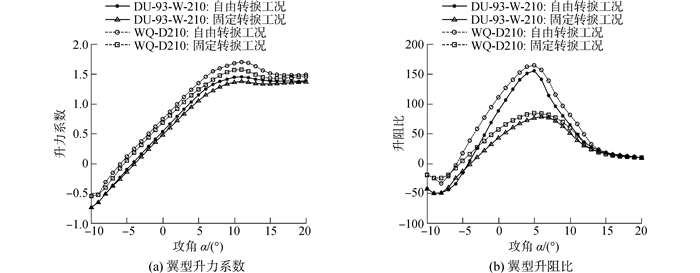
为了验证该方法设计出来的翼型具有高的气动性能,将WQ-D210翼型与国际知名的最大相对厚度相同的翼型DU93-W-210进行气动性能对比分析。图 6为两种翼型的气动性能对比图,表 2也列出了这两种翼型的关键气动参数。结合图表可知:无论是光滑条件,还是粗糙条件,相比DU93-W-210翼型,WQ-D210翼型的最大升力系数分别为1.685和1.586,分别提高了15.978%和15.598%;最大升阻比分别为163.821和83.351,分别提高了5.275%和7.604%;平均升阻比分别为120.762和69.951,提高了15.194%和12.252%。这种气动性能的全面提升将有助于叶片整体气动性能的提高。
|
| 图6 DU93-W-210翼型与WQ-D210翼型升力系数对比 Figure 6 Aerodynamic performances of the WQ-D210 and DU93-W-210 airfoil |
| 翼型名称 | 光滑条件 | 粗糙条件 | ||||||
| CL, max | CL, aver | L/D, max | L/D, aver | CL, max | CL, aver | L/D, max | L/D, aver | |
| DU93W210 | 1.453 (11°) |
1.231 (2°~12°) |
155.612 (5°) |
104.834 (2°~12°) |
1.372 (11°) |
1.145 (2°~12°) |
78.39 (6°) |
62.316 (2°~12°) |
| WQ-A210 | 1.601 (11°) |
1.344 (2°~12°) |
176.112 (6°) |
113.245 (2°~12°) |
1.471 (11°) |
1.232 (2°~12°) |
83.512 (7°) |
64.791 (2°~12°) |
| WQ-D210 | 1.685 (12°) |
1.461 (2°~12°) |
163.821 (5°) |
120.762 (2°~12°) |
1.586 (12°) |
1.342 (2°~12°) |
84.351 (5°) |
69.951 (2°~12°) |
| 注:括号内表示攻角位置或者范围,CL, max为最大升力系数,CL, aver为一定攻角范围内平均升力系数,L/D, max为最大升阻比,L/D, aver为一定攻角范围内平均升阻比。 | ||||||||
针对大部分单点攻角情况下设计出来翼型的缺点,即过于追求局部气动数据,而忽略翼型整体气动性能的提升。在翼型参数化设计过程中,考虑翼型表面曲率光滑连续性特性,本文提出多点攻角情况下风力机翼型设计的方法,以寻求在更广泛的攻角范围内,翼型整体气动性能的提高。并将多点攻角情况下设计出来的WQ-D翼型与单点攻角情况下设计出来的WQ-A翼型进行气动性能对比分析,分析结果表明:
1)虽然WQ-D翼型在光滑条件下最大升阻比不如WQ-A翼型,但是其整体气动性能要明显优于WQ-A翼型。
2)而实际风力机叶片需要在更广泛攻角范围内翼型的整体气动性能提升。因此,本方法设计出来的新翼型系列将有利于风轮叶片整体气动性能的提高。
| [1] | TANGLER J L, SOMERS D M. Status of the special-purpose airfoil families[C]//Proceedings of Windpower'87. San Francesco, USA: Solar Energy Research Inst, 1987: 229-335. |
| [2] | TIMMER W A, van ROOIJ R P J O M. Summary of the delft university wind turbine dedicated airfoils[J]. Journal of solar energy engineering, 2003, 125(4): 488–496. DOI:10.1115/1.1626129 |
| [3] | FUGLSANG P, BAK C. Development of the Risø wind turbine airfoils[J]. Wind energy, 2004, 7(2): 145–162. DOI:10.1002/(ISSN)1099-1824 |
| [4] |
张维智, 贺德馨, 张兆顺. 低雷诺数高升力翼型的设计和实验研究[J].
空气动力学学报, 1998, 16(3): 363–367.
ZHANG Weizhi, HE Dexin, ZHANG Zhaoshun. The design and experiment study for a high airfoil at low reynold numbers[J]. Acta aerodynamica sinica, 1998, 16(3): 363–367. |
| [5] |
乔志德, 宋文萍, 高永卫. NPU-WA系列风力机翼型设计与风洞实验[J].
空气动力学学报, 2012, 30(2): 260–265.
QIAO Zhide, SONG Wenping, GAO Yongwei. Design and experiment of the NPU-WA airfoil family for wind turbines[J]. Acta aerodynamica sinica, 2012, 30(2): 260–265. |
| [6] |
王旭东, 陈进, SHENWenzhong, 等. 风力机叶片翼型型线集成设计理论研究[J].
中国机械工程, 2009, 20(2): 211–213.
WANG Xudong, CHEN Jin, SHEN Wenzhong, et al. Integration study on airfoil profile for wind turbines[J]. China mechanical engineering, 2009, 20(2): 211–213. |
| [7] | 陈进, 汪泉. 风力机翼型及叶片优化设计理论[M]. 北京: 科学出版社, 2013 . |
| [8] | HAJEK J. Parameterization of airfoils and its application in aerodynamic optimization[C]//Proceedings of the 16th Annual Conference of Doctoral Students-WDS 2007, Charles University, Prague. Czech republic: Matfyzpress, 2007: 233-240. |
| [9] |
叶枝全, 包能胜, 霍副鹏, 等. 表明粗糙度对风力机翼型性能的影响[J].
太阳能学报, 2005, 26(4): 458–462.
YE Zhiquan, BAO Nengshen, HUO Fupeng, et al. Aerodynamic performance influence with goughness on wind turbine airfoil surface[J]. Acta enrglae solaris sinica, 2005, 26(4): 458–462. |
| [10] |
白井艳, 杨科, 李宏利, 等. 水平轴风力机专用翼型设计[J].
工程热物理学报, 2010, 31(4): 589–592.
BAI Jinyan, YANG Ke, LI Hongli, et al. Design of the horizontal axis wind turbine airfoils family[J]. Journal of engineering thermophysics, 2010, 31(4): 589–592. |
| [11] | CHEN Jin, WANG Quan, PANG Xiaoping, et al. Improvement of airfoil design using smooth curvature technique[J]. Renewable energy, 2013, 51: 426–435. DOI:10.1016/j.renene.2012.10.006 |
| [12] | FUGLSANG P, MADSEN H A. Optimization method for wind turbine rotors[J]. Journal of wind engineering and industrial aerodynamics, 1999, 80(1/2): 191–206. |



