2. School of Computer and Information Technology, Northeast Petroleum University, Daqing 163318, China
双足机器人的研究是近年来机器人领域的研究热点之一。Raibert及其同事成功研制了能够跑步的双足机器人Planar Biped[1], Fumiya Iida等[3]提出顺从腿模型来作为一种双足机器人跑步控制, Pratt等[2]设计的虚拟模型控制的策略用于将高层的任务级指令解析成底层的可执行控制命令, 各部件需要的力矩由对应的虚拟单元产生, 这一控制策略被运用到机器人Spring Turkey和Spring Flamingo上, 机器人的步态自然、稳定。为了提高双足机器人的技术, 日本索尼公司推出的QRIO机器人, 采用基于ZMP稳定性理论的控制算法实现了稳定的行走, 在此基础上增加了可即时控制机器人的跳跃方向以及在空中保持平衡状态姿势控制算法, 从而实现了跑步。日本本田公司研制的机器人ASIMO[4], 通过其自身建立的动力学模型, 在规划跑步运动轨迹的基础上, 分别采用相轨迹和关节轨迹跟踪控制的方法来实现跑步。
陈恳等[5-6]设计制造的THR-1机器人, 采用界面映射稳定性判据作为机器人稳定跑步的依据, 实现了初步的跑步运动。黄强等[8]规划仿人机器人跑步稳定性步态模型, 以ZMP为稳定性依据, 同时考虑到上身翻转问题, 通过满足质心角动量来研究跑步的稳定性步态模式。洪炳镕等[7]通过虚拟现实环境创建了虚拟人, 并对虚拟人跑步的基本运动模型和控制方法进行规划。雷旭升等[9]规划跑步运动各关节轨迹, 利用最小能量方程为优化工具, 采用遗传算法获得了跑步运动轨迹。
早在1975年, Albus[11]根据神经生理学小脑皮层结构特点, 提出了一种小脑模型关联控制器(cerebellar model articulation controller), 即CMAC神经网络。它类似于Perceptron网, 能学习任意多维非线性映射, 已广泛应用于函数逼近、模式识别和机器人控制等许多领域。由于这种网络具有在线学习自适应能力, 且算法简单, 学习速度快, 因此特别适合机器人的实时学习控制。从某种意义上说, CMAC神经网络与模糊逻辑不但能相互补充, 而且是相通的、可以有机的结合。将模糊理论引入CMAC, 对输入空间进行划分和激活联想强度进行了模糊处理, 并且在模糊化处理时采用了连续可微分的高斯基函数, 对输入划分方式以及输入状态激活联想强度的活性是可以在线调整的, 具有较强的自学习能力, 能够很好地应用于要求精度高且不确定性严重的场合[12-13]。由于双足机器人跑步模型的不确定性、非线性严重, 本文采用模糊CMAC神经网络对双足机器人进行跑步控制。
1 双足机器人跑步运动轨迹规划双足机器人的结构采用七连杆模型, 包括躯干、两条腿和两只脚, 如图 1所示。假定双足机器人的质量集中于其质心位置, 其运动局限于由铅垂轴和跑步方向的纵向轴所决定的二维平面内, 即髋关节、膝关节和踝关节只能在矢状面内旋转。
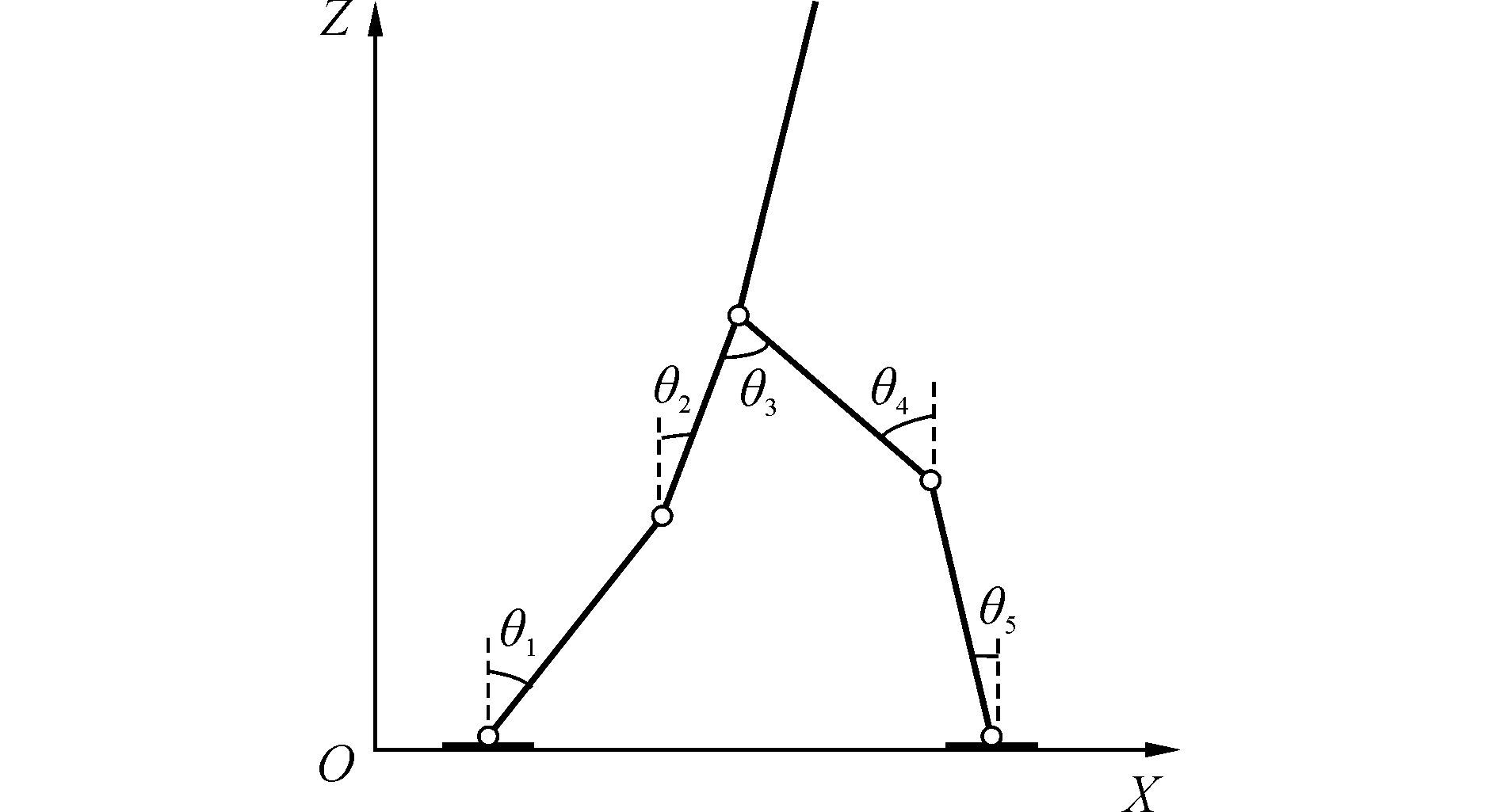
|
| 图1 双足机器人结构图 Figure 1 Structure of biped robot |
双足机器人跑步过程分为两个阶段:单腿支撑阶段和飞行阶段。在单腿支撑阶段, 双足机器人跑步满足ZMP准则;在飞行阶段, 双足机器人双脚离地, 脚部受到地面的作用力为零, 不满足ZMP准则。
1.1 单腿支撑阶段采用图 1模型, 建立双足机器人系统动能和势能, 通过拉格朗日方程求解, 得到双足机器人跑步过程中动力学模型表示为
| $A\left( \theta \right)\theta + B\left( {\theta ,\dot \theta } \right)\dot \theta + C\left( \theta \right) = \tau $ | (1) |
式中:θ和
双足机器人在飞行过程中, 双足均离开地面, 不会受到地面的作用力, 同时双腿向前有交叉动作, 为了不使双足机器人有翻转动作, 要求整个系统动能转化为势能, 可视双足机器人运动为抛物线运动, 在此过程中不能应用ZMP准则。双足机器人的质心分解为在水平方向上的匀速直线运行和竖直方向上的自由落体运动。其质心的水平速度为
| ${{\dot x}_{CoM}} = {{{x_{CoMi + 1}} - {x_{CoMi - 1}}} \over {2\Delta t}}$ | (2) |
式中:xCoMi-1和xCoMi+1分别为i-1和i+1时刻的质心在水平方向坐标。
1.3 质心轨迹规划双足机器人在满足动力学和运行学的条件下进行跑步运动, 主要是规划质心和双足的轨迹, 通过建立质心和単足作为支撑点时, 两者之间满足ZMP方程的条件下规划质心轨迹, 根据图 2模型, 小车在桌面上的运行轨迹看作是质心轨迹。运用五次多项式插值函数得到质心轨迹方程:
| $r\left( t \right) = {a_1}{t^5} + {a_2}{t^4} + {a_3}{t^3} + {a_4}{t^2} + {a_5}t + {a_6}$ | (3) |
式中:r(t)为质心轨迹函数, t时间变量, ai(i=1,2,…,6) 为五次多项式系数。
双足同时离地过程中, 质心轨迹规划为:在水平方向作匀速直线运行和在竖直方向上作自由落体运动, 水平方向质心轨迹:
| ${x_{CoM}} = {{\dot x}_{CoM}}t$ | (4) |
竖直方向质心轨迹:
| ${z_{CoM}} = {z_s} + {v_s}t - {1 \over 2}g{t^2}$ | (5) |
式中:zs为起跳时质心高度, vs起跳时质心速度。
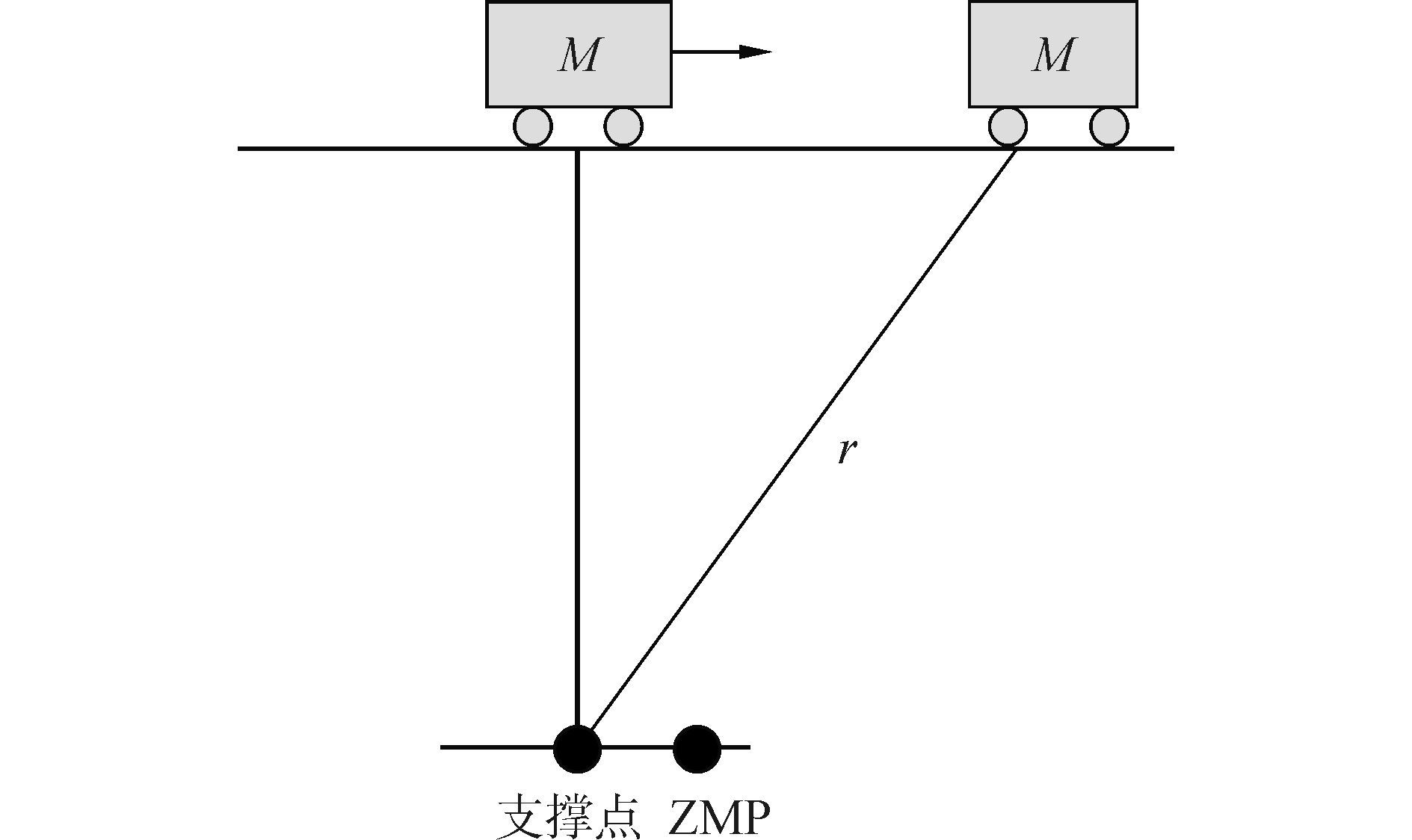
|
| 图2 小车-桌子模型 Figure 2 Cart-table model |
双足机器人在跑步时, 左足作为支撑点, 右足腾空, 接着双足同时腾空, 双足交替与地面接触, 双足运动轨迹相同, 时间上相差一个步长时间。由图 3可知, 步长时间t1+Ts+2Tf取决于起跳角度θs和落地角度θt, 两个角度过大将会增加步长时间, 同时会使支撑腿的膝关节在起跳和落地时力矩增大, 导致双足机器人起跳时动力不足, 或者落地时稳定性差。以左足为列, 在t4时刻足底中心点离地面的高度为H, 每时刻左足高度H不同, 通过三次差值函数得到左足运行轨迹:
| $H\left( t \right) = {b_1}{t^3} + {b_2}{t^2} + {b_3}t + {b_4}$ | (6) |
其中, t为时间变量, bi(i=1,2,3,4) 为三次多项式系数。
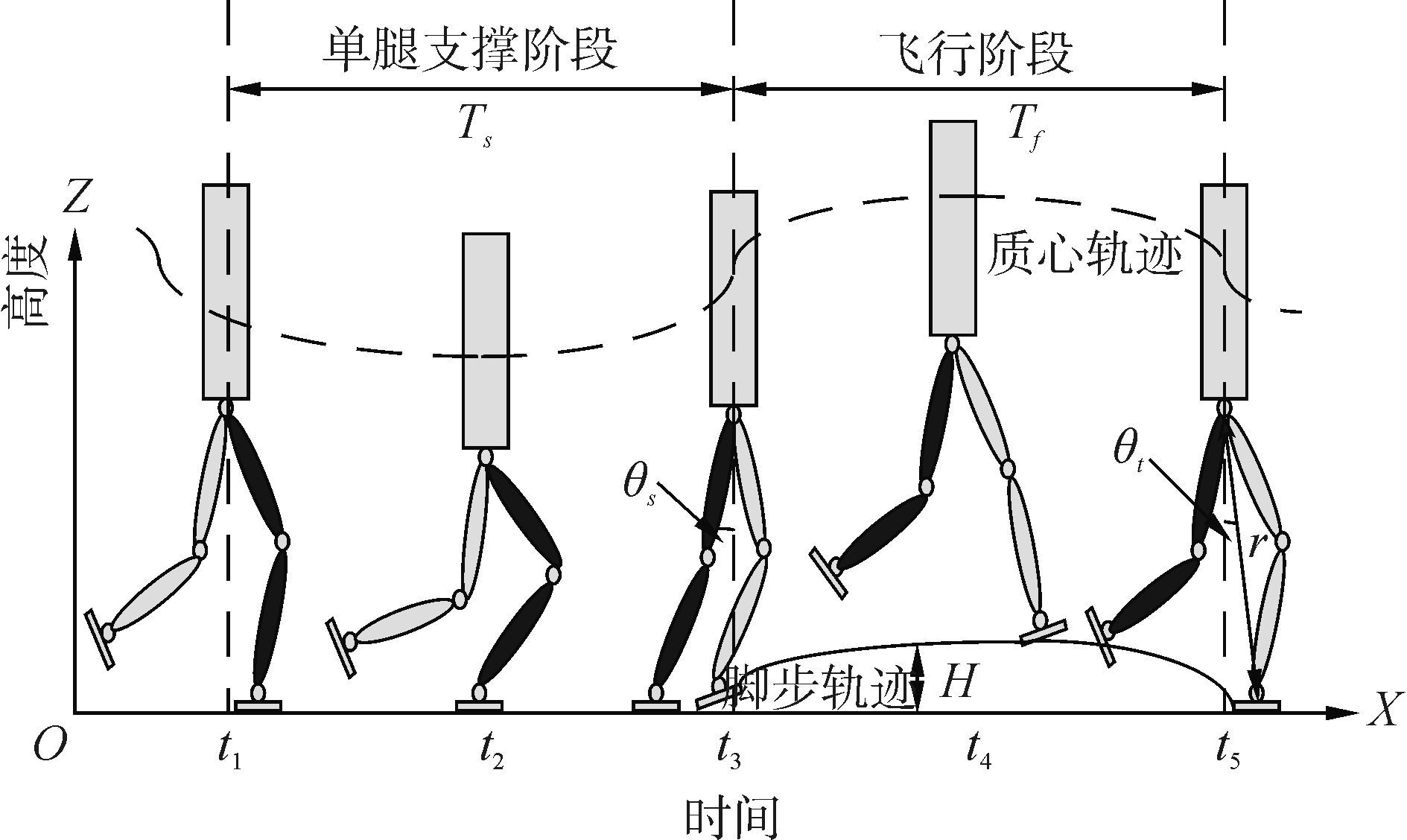
|
| 图3 双足机器人跑步过程 Figure 3 Biped robot running process |
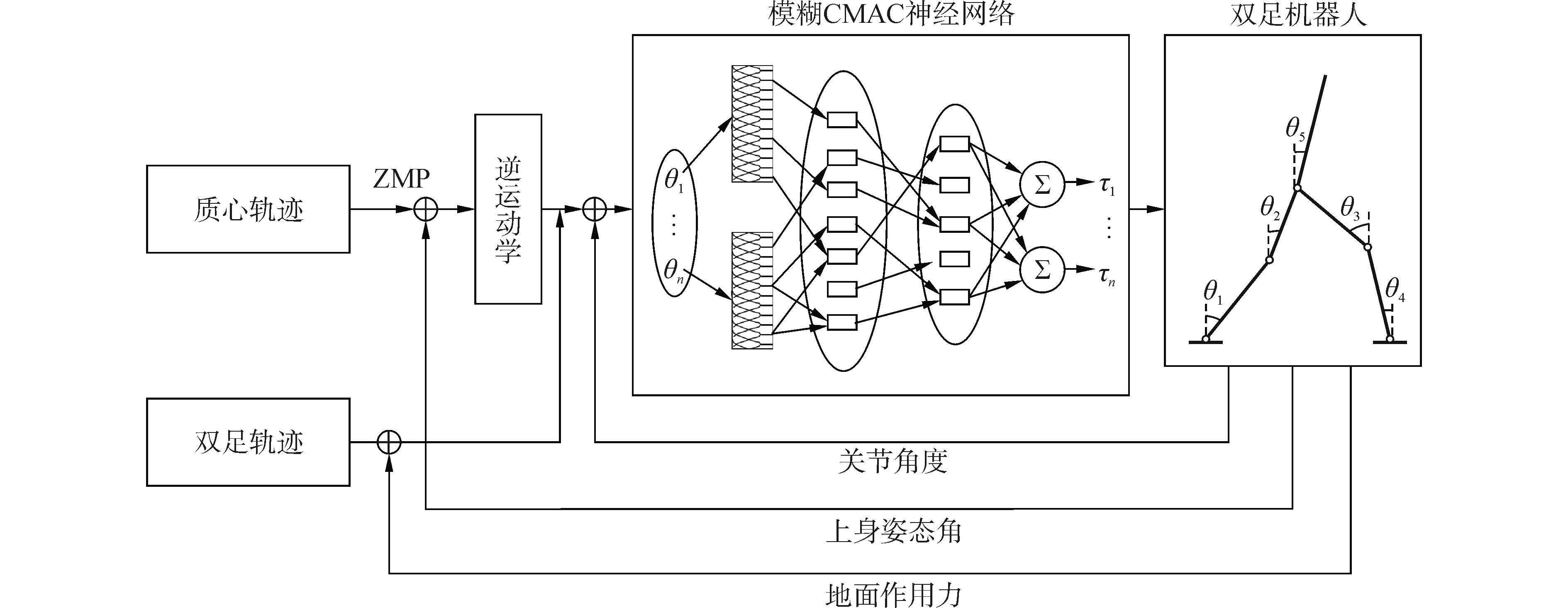
构建五层模糊CMAC神经网络模型, 如图 4所示, 即输入层、模糊化层、模糊相联层、模糊后相联层和输出层。模糊CMAC神经网络训练的权值包括联想强度、高斯隶属函数的中心值和宽度, 采用BP算法进行学习并对各权值修正。为了使双足机器人的运动轨迹达到预期设计的轨迹, 采用如图 5所示模糊CMAC神经网络的控制系统, 对图 1所示双足机器人进行跑步控制, Θ=(θ1,θ2,θ3,θ4,θ5)T为输入向量, T=(τ1,τ2,τ3,τ4,τ5)T为输出向量。通过式(1) 规划质心轨迹, 在系统的每个控制周期, 将离线预规划好的质心轨迹根据逆运动模块求出腿部各关节的角度, 加上双足轨迹函数以及双足机器人实际跑步时各关节反馈的角度值作为输入向量输入到模糊CMAC神经网络产生力矩控制仿人机器人步行, 系统开始运行时, 存储器中的权值为零, 在下一个控制周期, 根据系统的实际输出, 模糊CMAC网络通过学习进行权值调整, 调整后的权值存入存储器中, 经过几次训练后, 仿人机器人各关节的运动很快与要求的轨迹相一致。通过模糊CMAC神经网络学习得到满足双足机器人跑步各关节的力矩, 对双足机器人进行稳定跑步控制。
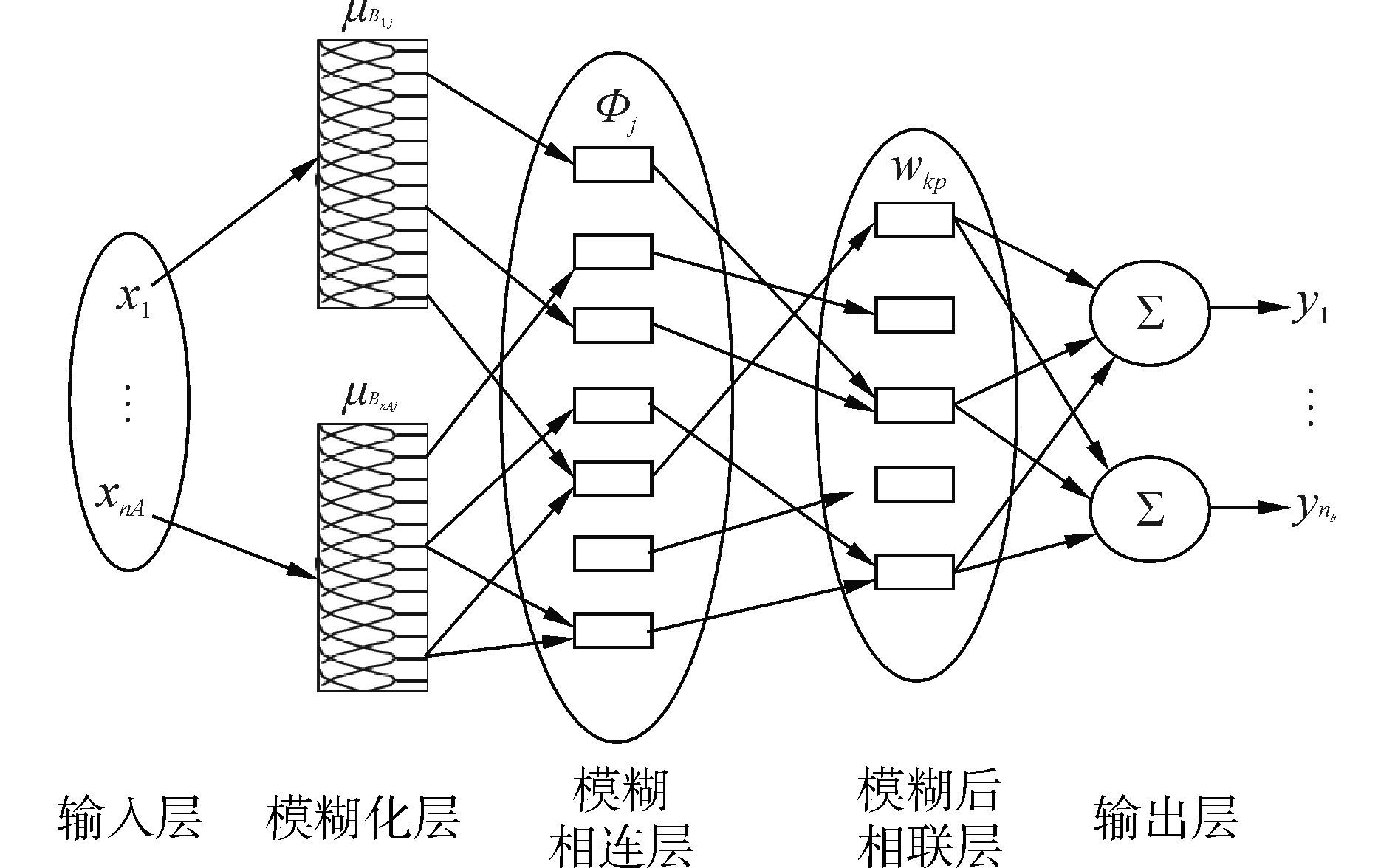
|
| 图4 模糊CMAC网络结构 Figure 4 Network structure of fuzzy CMAC |
|
| 图5 双足机器人模糊CMAC神经网络控制系统 Figure 5 Control system of fuzzy CMAC neural network for biped robot |
跑步运动步态生成算法描述:
1) 设置初始状态X0=(Θ0,
2) 设i=0。
3) 将状态Xi输入到模糊CMAC神经网络控制器中, 从网络输出中获得Ti。
4) 根据动力学方程式(1) , 用采样时间Δt进行离散化, 计算
5) 若i≤k,i=i+1, 转到3) 。
6) 在单足落地时, 判断脚是否接触地面, 若脚底受力fz>0, 转到3) 。
7) 在性能指标函数E最小的情况下, 网络的权值Wi定义目标函数为E=
8) 设Eprevious=Ecurrent, 计算Ecurrent=
9) 修正权值ωlk(i+1) =ωlk(i)+Δωlk(i), σlk(i+1) =σlk(i)+Δσlk(i), υlk(i+1) =υlk(i)+Δυlk(i) 转到2) 。
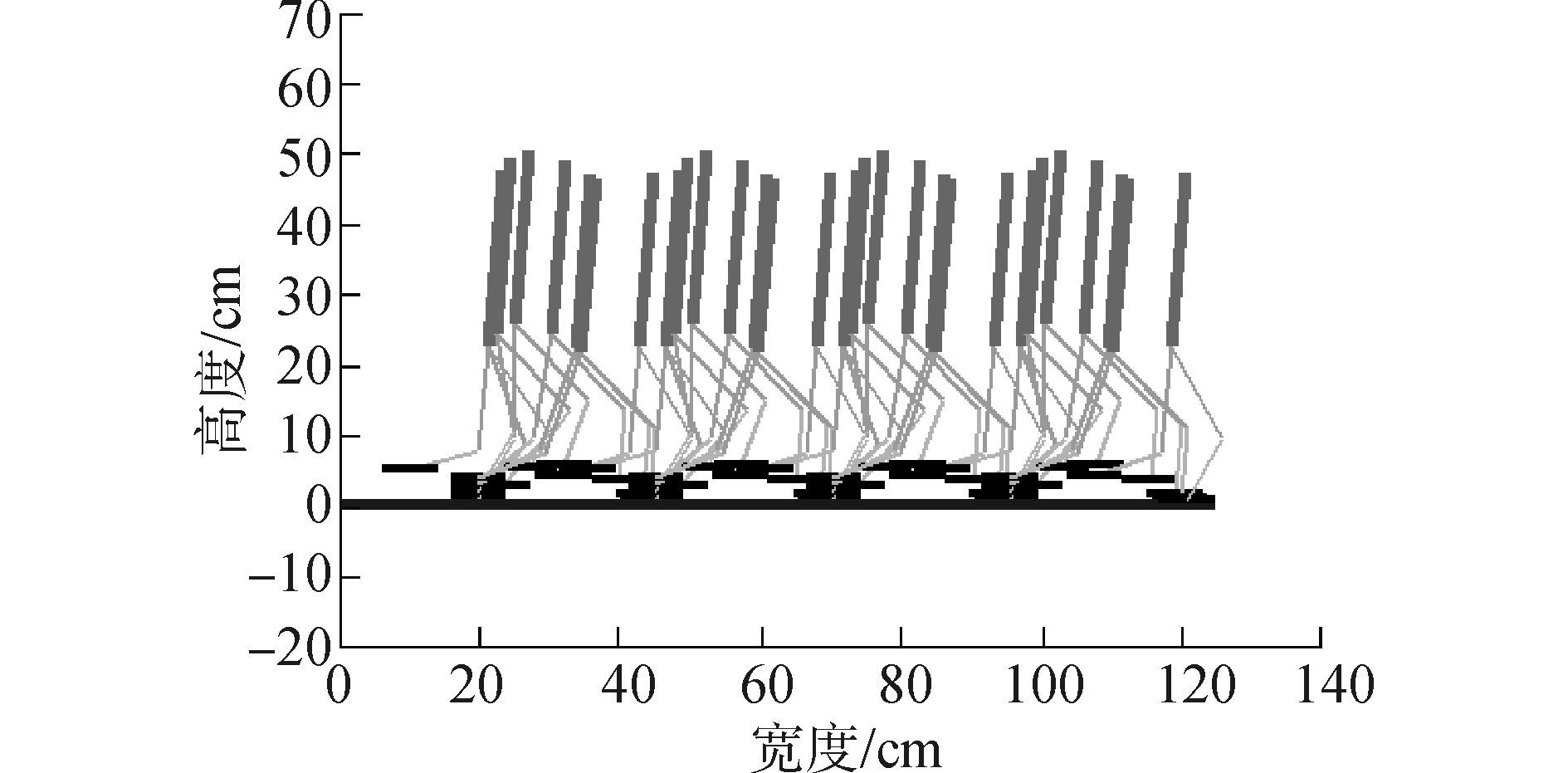
3 仿真实验为了验证方法的有效性, 双足机器人跑步过程的仿真采用Matlab仿真软件对图 1所示的双足机器人七连杆模型进行仿真, 在Matlab/Simulink环境里求解双足机器人的动力学方程, 积分算法采用4次龙格-库塔方法, 固定步长时间设为0.000 1 s。仿真用的双足机器人参数如表 1所示。双足机器人的初始位姿为双足并齐站立, 关节初始角度为
θa=(0,3.545 7,-2.192 6,2.281 9,-2.192 6,3.545 7,0) T
角速度为零, 质心的位置xCoM(0) =0.074 2 m, zCoM(0) =0.253 2 m。仿人机器人开始的状态为静止状态, 起跳时间为0.17 s, 质心的末速度为
| 名称 | 长度/m | 质量/kg | 转动惯量/(kg·m2) |
| 躯干 | 0.25 | 1.5 | 0.008 12 |
| 大腿 | 0.15 | 1.0 | 0.006 09 |
| 小腿 | 0.10 | 0.8 | 0.004 06 |
| 脚 | 0.14 | 0.1 | 0.005 68 |
|
| 图6 双足机器人跑步仿真图 Figure 6 Simulation of running for biped robot |
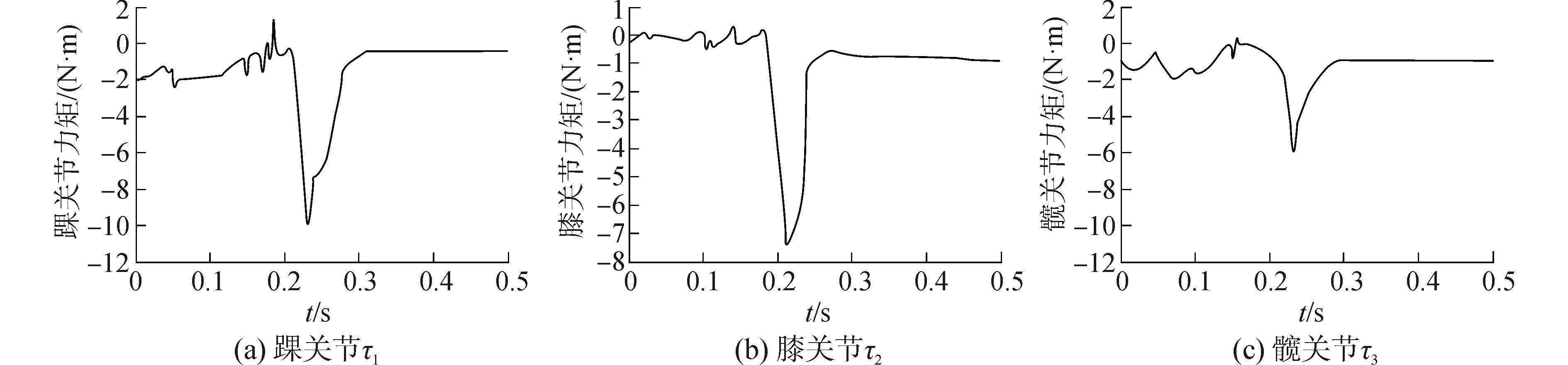
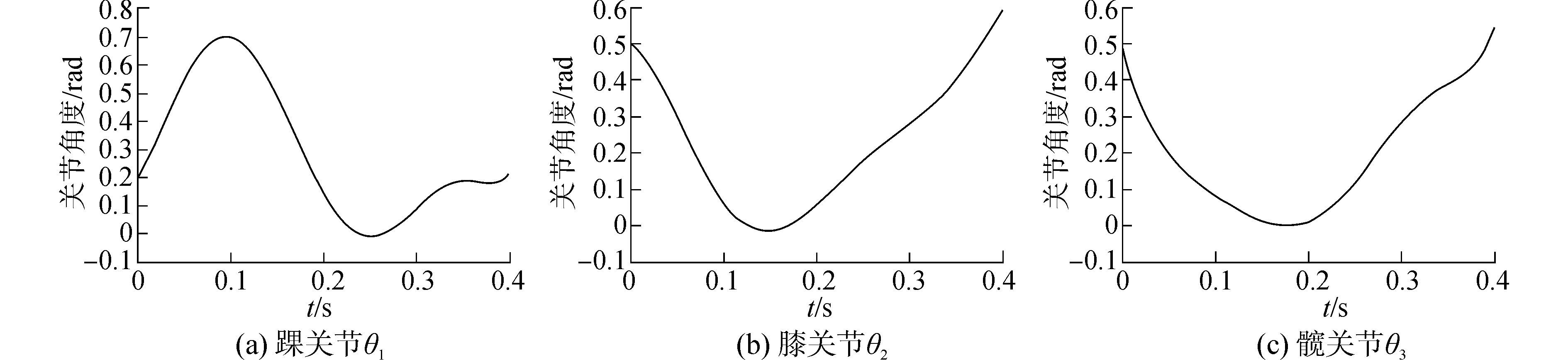
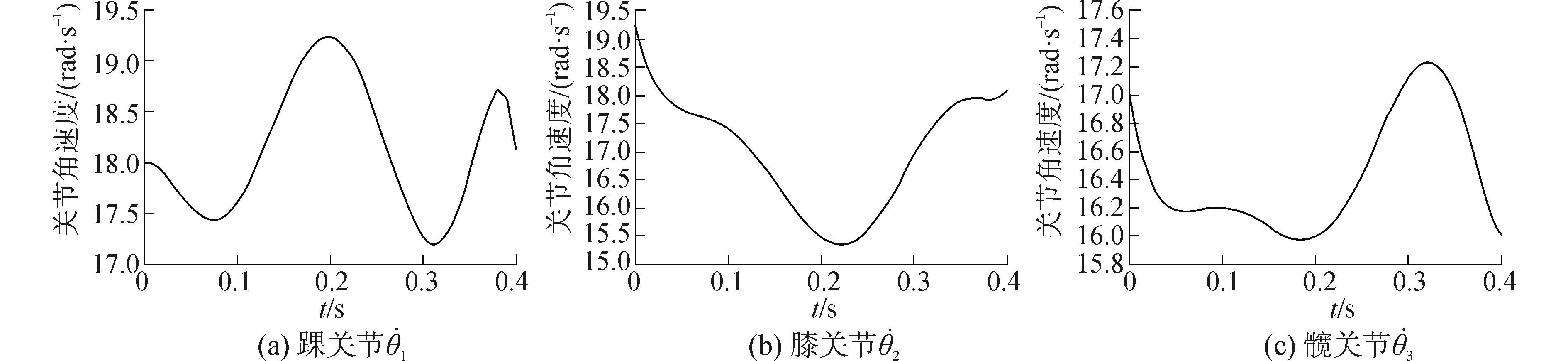
图 7为双足机器人跑步时右腿踝关节θ1、膝关节θ2和髋关节θ3的力矩随时间的变化曲线。图 8和图 9表示在0.5 s的时间内, 右腿各关节的角位置和角速度的曲线图。飞行时间为0.17~0.31 s, 碰撞发生在0.31~0.34 s, 在碰撞后, 速度变化迅速。平板脚落地后在0.01~0.03 s关节速度改变快。
|
| 图7 右腿各关节力矩 Figure 7 The joint torques on the right leg |
|
| 图8 右腿各关节角度 Figure 8 The joint angular positions on the right leg |
|
| 图9 右腿各关节角速度 Figure 9 The joint angular velocities on the right leg |
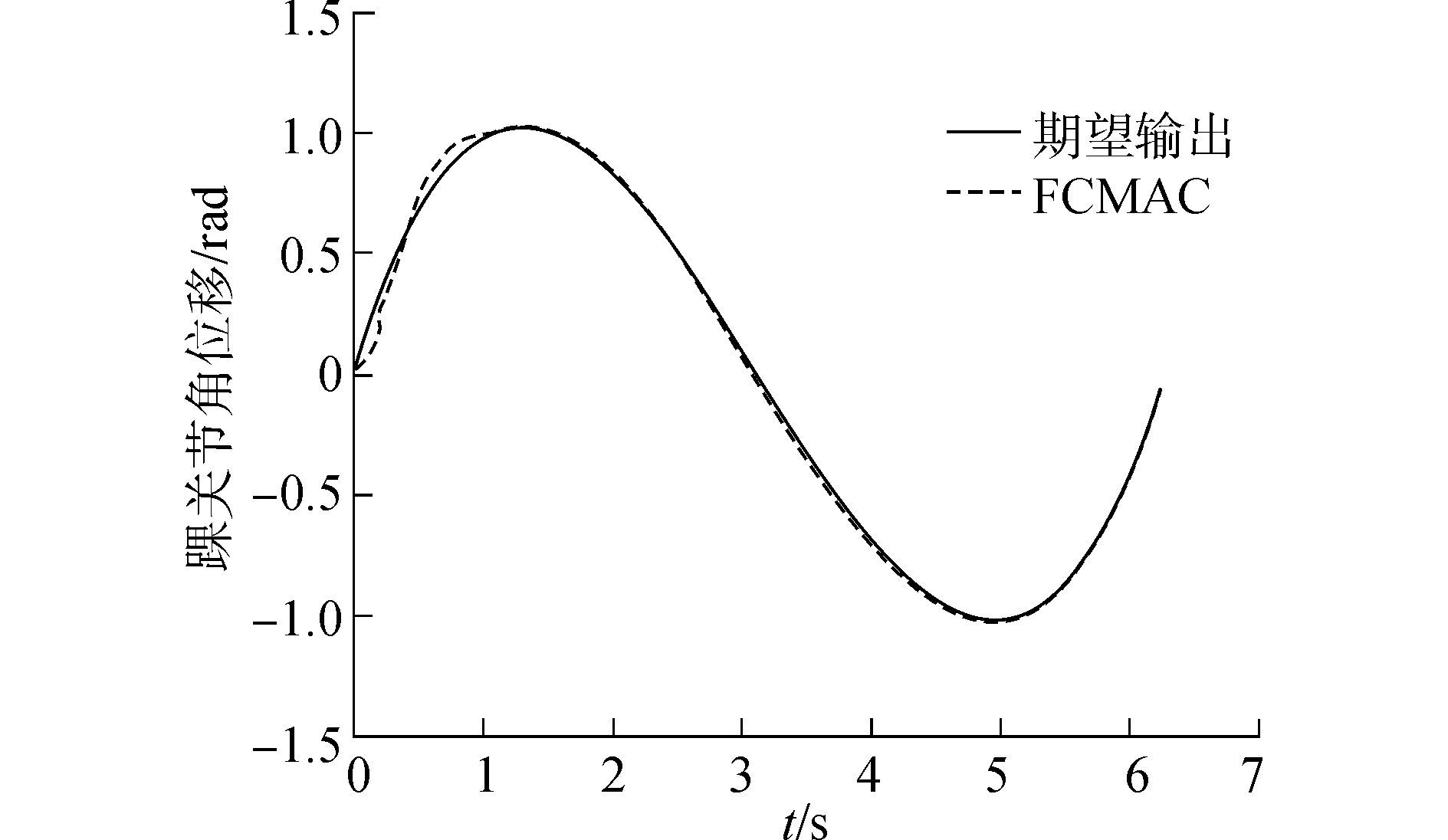
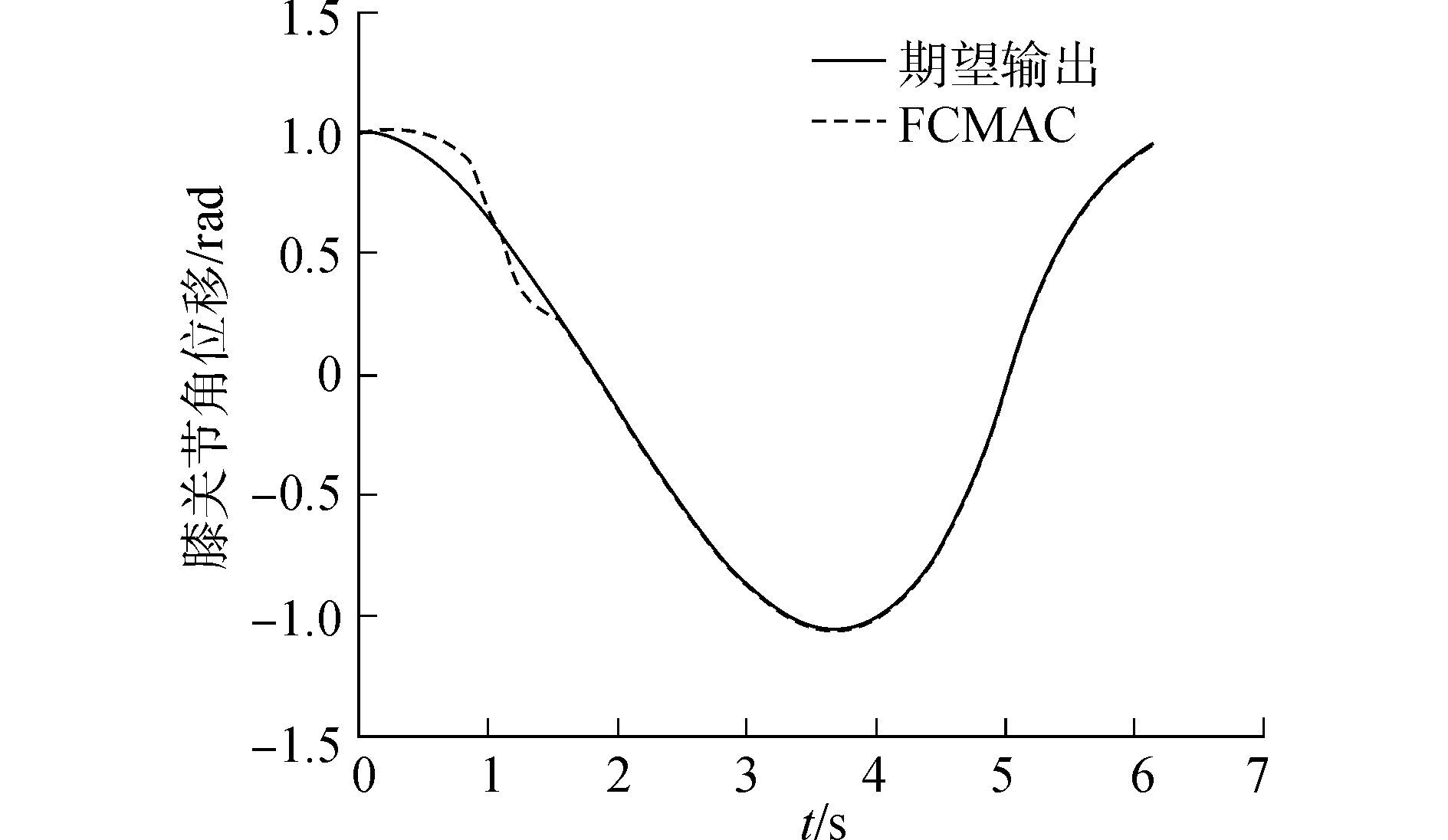
为验证模糊CMAC神经网络对仿人机器人各关节轨迹跟踪的有效性, 在Matlab环境中对图 1模型的踝关节和膝关节进行了仿真实验, 初始条件为
θ1(0) =0.5 rad, θ2(0) =1 rad
期望轨迹为
θ1d(t)=sin(πt), θ2d(t)=cos(πt)
高斯隶属函数的参数初值为kσi1(0) =-0.4, kσi2(0) =0.4, kυi1(0) =0.35, kυi2(0) =0.35(k=1,2;i=1,2) 其中, k=1, k=2分别表示踝关节和膝关节, 联想强度初值为[-1,1]的随机数。图 10、图 11分别为踝关节和膝关节的轨迹跟踪曲线, 可以看出经过学习后的模糊CMAC神经网络具有精确的跟踪特性和更强的鲁棒性。
|
| 图10 踝关节轨迹跟踪曲线 Figure 10 Trajectory tracking curves of ankle |
|
| 图11 膝关节轨迹跟踪曲线 Figure 11 Trajectory tracking curves of knee |
本文采用小车-桌子模型, 提出了一种基于模糊CMAC神经网络的双足机器人跑步轨迹规划的方法。
通过分析脚与地面的约束关系, 规划双足机器人质心和双脚的运动轨迹, 通过模糊CMAC神经网络控制实现跑步运动, 由以上内容可得到如下结论:
1) 考虑到脚与地面的碰撞力, 为减弱来自地面的反作用力, 采用收缩腿的长度, 上身控制采用踝关节力矩控制及目标ZMP控制。
2) 经过模糊CMAC神经网络的学习得到各关节的关节力矩, 使得关节角度连续变化, 并且角度变化平稳, 因此跑步过程比较平稳。
3) 改变起跳和落地的角度能够产生不同的跑步速度。在控制方面, 双脚离地高度不同的设置影响机器人的稳定性。
4) 质心高度不同的设置, 双脚受到地面的反作用力将有所变化。质心高度设置较高, 双脚落地时的地面反作用力较大, 对膝关节的冲击较大;质心高度设置得较低, 那么脚底受到地面反作用力较小, 而质心降低将增大膝关节的力矩。质心高度设置得太低反而不能实现跑步动作。
| [1] | RAIBERT M H. Legged robots that balance[M]. Cambridge: Massachusetts Institute of Technology, 1986. |
| [2] | PRATT J E. Exploiting inherent robustness and natural dynamics in the control of bipedal walking robots[D]. Cambridge, MA:Massachusetts Institute of Technology, 2000. |
| [3] | IIDA F, RUMMEL J, SEYFARTH A. Bipedal walking and running with compliant legs[C]//Proceedings of IEEE International Conference on Robotics and Automation. Roma, Italy:IEEE, 2007:3970-3975. |
| [4] | Honda Motor Co., Ltd. NewASIMO[EB/OL].[2015-06-21].http://world.honda.com/HDTV/ASIMO/New-ASIMO-run-6kmh-slomo/index.html. |
| [5] | FU Chenglong, CHEN Ken. Section-map stability criterion for biped robots Part I:theory[C]//Proceedings of International Conference on Mechatronics and Automation. Harbin:IEEE, 2007:1529-1534. |
| [6] | FU Chenglong, WANG Jianmei, HUANG Yuanlin, et al. Section-map stability criterion for biped robots part II:applications and experiments[C]//Proceedings of International Conference on Mechatronics and Automation. Harbin:IEEE, 2007:1535-1540. |
| [7] |
洪炳熔, 贺怀清. 虚拟人的步行和跑步运动控制方法的研究[J].
高技术通讯, 2001, 11(3): 91–95.
HONG Bingrong, HE Huaiqing. Research of walking and running locomotion control methods for virtual humans[J]. High technology letters, 2001, 11(3): 91–95. |
| [8] | LI Zhaohui, HUANG Qiang, LI Kejie, et al. Stability criterion and pattern planning for humanoid running[C]//Proceedings of IEEE International Conference on Robotics and Automation. New Orleans, LA, USA:IEEE, 2004:1059-1064. |
| [9] | LEI Xusheng, SU Jianbo. Running trajectory generation for humanoid robot[C]//Proceedings of International Conference on Machine Learning and Cybernetics. Shanghai:IEEE, 2004:1002-1007. |
| [10] |
梶田秀司. 仿人机器人[M]. 管贻生译. 北京:清华大学出版社, 2007.
KAJITA S. Humanoid robots[M]. GUAN Yisheng, trans. Beijing:Tsinghua University Press, 2007. |
| [11] | ALBUS J S. A new approach to manipulator control:the cerebellar model articulation controller (CMAC)[J]. Journal of dynamic systems, measurement, and control, 1975, 97(3): 220–227. DOI:10.1115/1.3426922 |
| [12] | CHIANG T S, CHIU C S. Adaptive Tanaka-Sugeno fuzzy cerebellar model articulation controller for output tracking control[C]//Proceedings of 2005 IEEE International Joint Conference on Neural Networks. Montreal:IEEE, 2005:2284-2289. |
| [13] | LIN Chengjian, CHEN H J, LEE C Y. A self-organizing recurrent fuzzy CMAC model for dynamic system identification[C]//Proceedings of 2004 IEEE International Conference on Fuzzy Systems. Budapest, Hungary:IEEE, 2004, 2:697-702. |



