2. School of Architecture and Construction, Huaqiao University, Xiamen 361021, China
近年来,随着钢骨超高强混凝土框架结构在高层及超高层建筑中的广泛应用[1-2],其抗震性能逐渐引起重视。由于超高强混凝土的脆性及截面破坏特征,混凝土一旦开裂,裂缝面光滑,骨料咬合作用削弱明显,对抗剪机制产生影响。而梁柱节点作为影响整体结构抗震性能的重要构件,其抗震性能与抗剪性能有必要在混凝土强度提高的前提下开展进一步研究。在国内外诸多规范的梁柱节点设计中,轴压比对节点抗震性能的影响规律一直存在争议[3-5]。例如JGJ(2001)与SNZ(1995)认为增大轴压比能提高构件承载力;而ACI(2002)则认为轴压比对构件承载力的影响可忽略。国内外大量试验表明[6-12],轴压比与体积配箍率是影响梁柱节点抗震性能的重要因素,闫长旺[4]开展钢骨超高强混凝土框架中节点抗震性能试验研究,研究表明:随着轴压比增大,中节点的极限荷载提高,而其延性及耗能能力降低。薛建阳[5]通过进行8个钢骨混凝土梁柱中节点低周往复试验,得出结论:轴压比是影响钢骨混凝土框架节点的重要参数,随着轴压比的增大,节点抗裂度与抗剪承载力提高,但并非无限制,当轴压比很大时,节点的破坏形态由剪切破坏转化为受压破坏。Lin等[6]通过对15个不同轴压比下的钢筋混凝土梁柱节点进行低周往复试验,研究了轴压比对构件承载力的影响,也得到了承载力随轴压比变化的相同规律。
由此可见,针对轴压比对钢骨超高强混凝土节点抗震性能的研究仍然有限且影响规律仍存在争议。另外,由于框架边节点传力机制与中节点有明显区别,且针对钢骨超高强混凝土框架边节点的抗震性能尚缺少足够的试验研究及理论分析。因此,本文在前人成果的基础上,研究了不同轴压比与体积配箍率下钢骨超高强混凝土框架边节点的破坏形态、延性、耗能能力、承载力及节点核心区箍筋应变规律,提出轴压比对节点抗剪承载力影响的分界点,建议在抗震设计中应予以考虑不同轴压比变化范围内钢骨超高强混凝土边节点抗震性能与抗剪性能的变化规律。
1 试验概况 1.1 试件设计框架结构在水平地震作用下,梁柱节点周边的弯矩情况如图 1所示。本次试验选取常规HSRUHSC框架结构中相邻梁柱反弯点之间的典型单元作为研究对象。

|
| 图1 节点组合体示意图 Figure 1 Reinforcement diagram of joint assembly |
轴压比选择0.25、0.38、0.45三个等级。
本次试验共设计6个试件,试件的截面尺寸完全相同,节点区箍筋采用HPB300级Φ6钢筋,其他区域箍筋采用HRB400级Φ6螺纹钢筋,钢骨采用普通热轧钢骨Q235。各试件试验参数如表 1。试件尺寸及配筋情况如图 2所示。
| 试件编号 | 试验轴压比 | 配箍率 | 箍筋直径与间距 |
| SRUHSC-25-0.8 | 0.25 | 0.8 | Φ6@100 |
| SRUHSC-38-0.8 | 0.38 | 0.8 | Φ6@100 |
| SRUHSC-45-0.8 | 0.45 | 0.8 | Φ6@100 |
| SRUHSC-25-1.2 | 0.25 | 1.2 | Φ6@65 |
| SRUHSC-38-1.2 | 0.38 | 1.2 | Φ6@65 |
| SRUHSC-45-1.2 | 0.45 | 1.2 | Φ6@65 |

|
| 图2 试件尺寸及配筋 Figure 2 Reinforcement details of specimens |
试件和混凝土试块采用同等条件养护,实测混凝土立方体抗压强度平均值为 105MPa,实测钢筋、钢骨力学性能见表 2。
| 钢筋类别 | 直径/mm | 屈服强度fy/MPa | 极限强度fu/MPa |
| Φ 6 | 6 | 342 | 450 |
| Φ14 | 14 | 358 | 469 |
| Φ20 | 20 | 420 | 571 |
| 钢骨 | h×b×tw×tf /mm | 屈服强度fy/MPa | 极限强度fu/MPa |
| I12 | 126×74×5×8.4 | 254 | 368 |
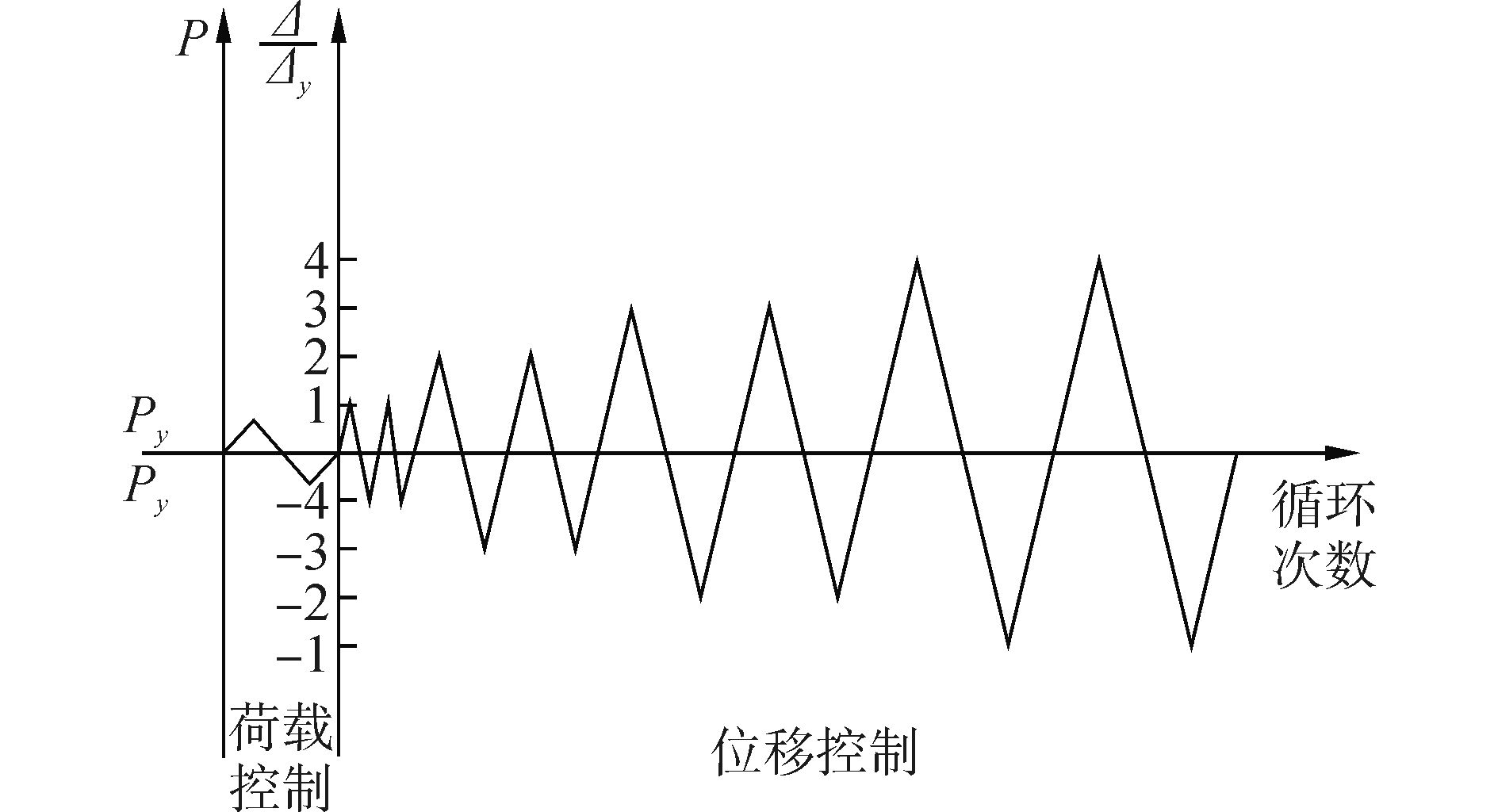
本次试验采用拟静力加载,如图 3所示。柱顶采用液压千斤顶施加轴向恒定荷载,梁端为自由端,采用30t千斤顶施加等量反对称低周往复荷载。加载制度采用力-位移混合控制,试件在达到屈服位移前采用荷载控制,达到屈服位移后采用位移控制,按照屈服位移的倍数分级加载,直至梁端荷载下降至极限荷载的85%或试件失去承载力为止。加载制度如图 4所示。

|
| 图3 加载装置 Figure 3 Experimental loading setup |
|
| 图4 试验加载制度 Figure 4 Loading program |
试验前,将所用位移计标定好,并在相应测点处贴好电阻应变计。试验过程中,采用imc64通道GRONOS PL-8数据采集设备采集梁端荷载传感器及位移计数据,进而研究不同轴压比下钢骨超高强混凝土框架边节点的滞回性能、延性及耗能能力;通过对节点核心区箍肢布置测点,获得不同轴压比及不同配箍率下水平箍肢的应变增长规律。
2 试验分析 2.1 破坏形态试件SRUHSC-25-0.8与SRUHSC-25-1.2轴压比为0.25,节点组合体发生典型的弯剪破坏,即梁首先受弯屈服,随着梁端位移加大,节点箍筋屈服,混凝土被压碎,节点核心区发生剪切破坏,构件失去承载力。加载过程中,在梁端荷载为30 kN时,距梁柱交界面15 cm处首先出现竖向受弯裂缝;梁端加载至75 kN,节点核心区出现斜向裂缝,裂缝宽度为0.08 mm;随着梁端荷载继续增加,梁端出现弯剪裂缝;加载至86 kN,梁受弯屈服;循环位移加载至22 mm,节点核心区裂缝加宽,裂缝宽度为0.2 mm;循环位移加载至33 mm,梁端受压区混凝土被逐渐压碎;循环加载至55 mm,节点核心区主裂缝迅速扩展,混凝土被压溃,箍筋被拉断,组合体失去承载力。
试件SRUHSC-38-0.8与SRUHSC-38-1.2轴压比为0.38,与SRUHSC-25-0.8相比,两者破坏过程均表现为首先在梁端出现受弯裂缝,继而产生节点核心区的剪切裂缝及梁端的弯剪裂缝。当加载至82 kN时,试件节点核心区出现斜向剪切裂缝,裂缝宽度为0.06 mm,说明轴压比增大提高了节点核心区的开裂荷载,抑制了节点核心区裂缝的出现及发展。文献[13]指出在剪压比一定的条件下,轴压比的增大能使梁筋屈服区向节点内渗透减慢,从而推迟节点斜裂缝的出现,对节点抗震有利,这与本文试验结果一致。
试件SRUHSC-45-0.8与SRUHSC-45-1.2轴压比为0.45,与试件SRUHSC-25-0.8及试件SRUHSC-38-0.8相比,试件SRUHSC-45-0.8与SRUHSC-45-1.2破坏过程明显缩短,且破坏前无先兆,表现出典型的脆性破坏特征。节点核心区裂缝形态以X型裂缝为主,伴随竖向裂缝,随着梁端位移加大,竖向裂缝也出现延伸,宽度增大。这是由于当轴压比进一步增大,斜压杆中的斜压力加大,使核心区混凝土斜向压溃,对节点的最终失效产生不利影响。加载结束时节点破坏形态如图 5所示。

|
| 图5 试件破坏形态 Figure 5 Failure patterns of specimens |
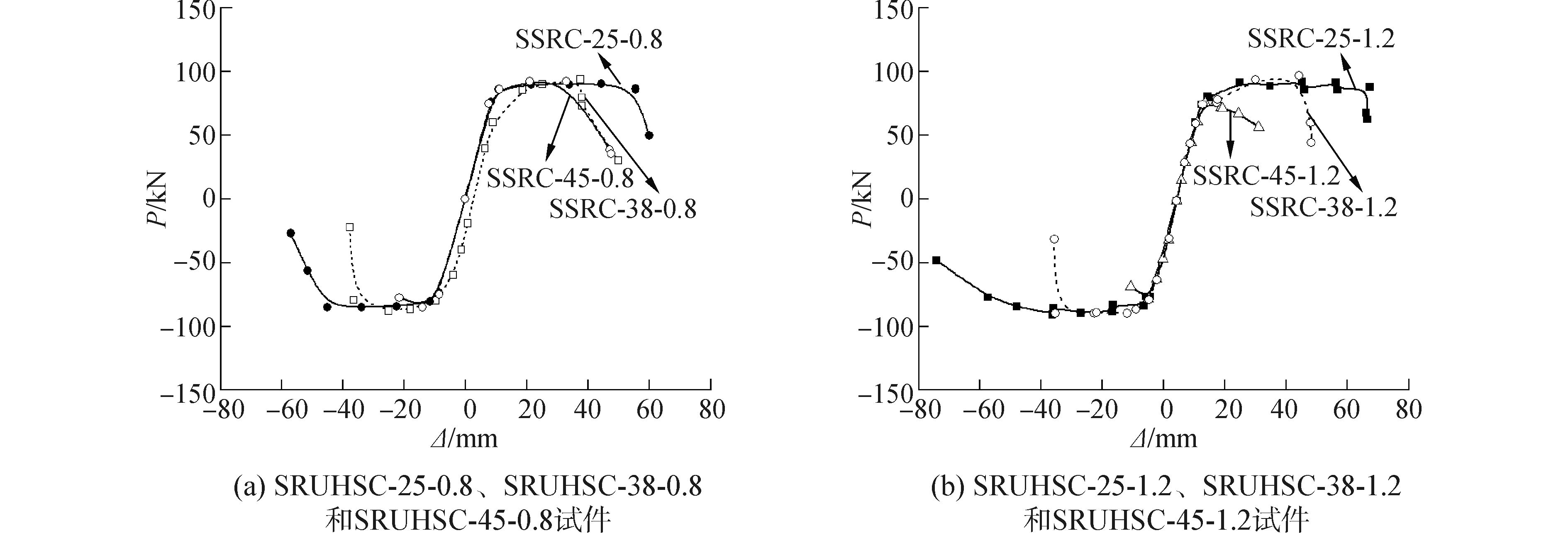
各试件的梁端荷载-位移曲线如图 6所示。从图 6中可以看出:

|
| 图6 试件的荷载-位移滞回曲线 Figure 6 Loading deflection hysteretic loops of specimens |
1) 弹性阶段时,混凝土尚未开裂,滞回曲线基本呈直线变化,卸载时无残余变形。屈服前,滞回曲线呈稳定的梭形,残余变形与刚度退化很小。随着荷载等级的加大,框架节点滞回曲线愈加饱满,没有明显捏缩现象,表明钢骨超高强混凝土边节点具有较好的耗能能力。
2) 配箍率相同的条件下,试件SRUHSC-45-0.8与SRUHSC-25-0.8相比较,循环次数明显减少,加载至弹塑性阶段后,随着位移循环次数的增加,荷载显著下降,耗能能力降低,表明轴压比越大,屈服后刚度退化快,荷载下降显著,延性及耗能能力越差;
3) 轴压比相同的情况下,配箍率较小的试件屈服后刚度退化较快,荷载显著下降,耗能能力降低,与配箍率较高的试件相比,其极限荷载明显较低,表明抗震延性及承载力随配箍率的降低而下降。
4) 试件SRUHSC-45-0.8,梁端屈服前,节点核心区发生剪切失效,该破坏形式达不到预期的抗震能力,延性差,这是因为:在高轴压比作用下,由节点区混凝土斜压杆机制及桁架机制共同传递的斜向压力过大,使得核心区混凝土在梁端及节点区域箍筋屈服前被斜向压碎,这种破坏纯属脆性破坏。
3 钢骨超高强混凝土边节点抗震性能 3.1 轴压比的影响 3.1.1 设计轴压比与试验轴压比的关系我国现行规范中设计轴压比与试验轴压比存在一定的换算关系:
| ${{n}_{t}}=\frac{{{N}_{k}}}{{{f}_{ck}}{{A}_{c}}+{{f}_{ak}}{{A}_{a}}}$ | (1) |
式中:nt为试验轴压比,Nk为试验轴压力标准值,fck为混凝土抗压强度标准值,Ac为柱截面面积,fak为钢骨抗压强度标准值,Aa为钢骨截面面积。
| ${{n}_{d}}=\frac{{{N}_{d}}}{{{f}_{c}}{{A}_{c}}+{{f}_{a}}{{A}_{a}}}$ | (2) |
式中:nd为设计轴压比,Nd为考虑地震作用组合的柱设计轴力,fc为混凝土抗压强度,fa为钢骨抗压强度设计值。
| ${{N}_{d}}={{\gamma }_{G}}{{N}_{GK}}+{{\gamma }_{E}}{{N}_{EK}}\approx 1.23{{N}_{k}}$ | (3) |
根据GB50010 (2010)[14],混凝土抗压强度标准值与设计值的转换关系为
| ${{f}_{c}}={{f}_{ck}}/{{\gamma }_{c}}={{f}_{ck}}/1.4$ | (4) |
| ${{f}_{a}}={{f}_{ak}}/{{\gamma }_{s}}$ | (5) |
式中:γc为混凝土材料分项系数,γs为钢骨材料分项系数。在本研究中,为实际应用方便,可偏于安全地取混凝土材料分项系数和钢材的材料分项系数相同,即γc=γs。
因此,可得设计轴压比与试验轴压比的关系如下:
| ${{n}_{d}}=\frac{{{N}_{d}}}{\frac{{{f}_{ck}}{{A}_{c}}}{{{\gamma }_{c}}}+\frac{{{f}_{ak}}{{A}_{a}}}{{{\gamma }_{s}}}}=\frac{1.23\times 1.4{{N}_{k}}}{{{f}_{ck}}{{A}_{c}}+{{f}_{ak}}{{A}_{a}}}=\frac{1.722{{N}_{k}}}{{{f}_{ck}}{{A}_{c}}+{{f}_{ak}}{{A}_{a}}}$ | (6) |
| ${{n}_{d}}=1.722{{n}_{t}}$ | (7) |
由此可知,本试验中所取试验轴压比相对应的设计轴压比分别为0.43、0.65、0.78,由于加载条件的限制,本试验未涉及更高轴压比的研究。
3.1.2 轴压比对延性的影响不同轴压比下试件梁端荷载-位移骨架曲线如图 7所示。从图中可以看出,轴压比是影响钢骨超高强混凝土边节点延性及承载力的主要因素之一,本文采用位移延性系数来表征构件延性大小。根据骨架曲线,采用能量法求屈服位移,极限位移为0.85峰值荷载对应的位移,极限位移与屈服位移之比即为位移延性系数[15]:
| ${{u}_{\Delta }}=\frac{{{\Delta }_{u}}}{{{\Delta }_{y}}}$ | (8) |
式中:uΔ为位移延性系数,Δu为极限位移,Δy为屈服位移。各试件位移延性系数如表 3所示。
| 试件 | Δu/mm | Δy /mm | μΔ |
| SRUHSC-25-0.8 | 55.5 | 10.98 | 5.05 |
| SRUHSC-38-0.8 | 42 | 12.5 | 3.36 |
| SRUHSC-45-0.8 | 20.00 | 9.24 | 2.06 |
| SRUHSC-25-1.2 | 64.00 | 10.61 | 5.70 |
| SRUHSC-38-1.2 | 42.00 | 10.85 | 3.87 |
| SRUHSC-45-1.2 | 35.00 | 11.6 | 3.01 |
从表 3中可以看出,轴压比从0.25提高至0.45,构件的位移延性系数显著下降,原因在于轴压比与混凝土的极限压应变有关,轴压比不同时,截面的应变分布明显不同,低轴压比时,截面的应变梯度较大,随着轴压比的增大,截面应变梯度减小,当轴压比很高时,截面应变分布类似于轴心受压构件[16]。从理论上分析可知:对轴压比较小的试件,当加载至极限荷载时,受压区高度较小,受拉箍筋及钢骨受拉翼缘屈服,表现为受拉破坏,受压区混凝土破坏较小,承载力衰减缓慢;对轴压比较大的试件,当加载至极限荷载时,受压区高度较大,表现为受压破坏特征,受压区混凝土破坏严重,承载力衰减快,延性较差。
从图 7中可以看出:轴压比从0.25提高至0.38,屈服荷载无显著变化,极限荷载略有提高,屈服段缩短,达到极限荷载后承载力及刚度退化加快;轴压比从0.38提高至0.45,极限荷载略有下降,承载力、刚度退化明显加快,对节点组合体抗震产生不利影响。
|
| 图7 不同轴压比下试件荷载-位移骨架曲线 Figure 7 Load-deflection skeleton curves of specimens under different axial compression ratios |
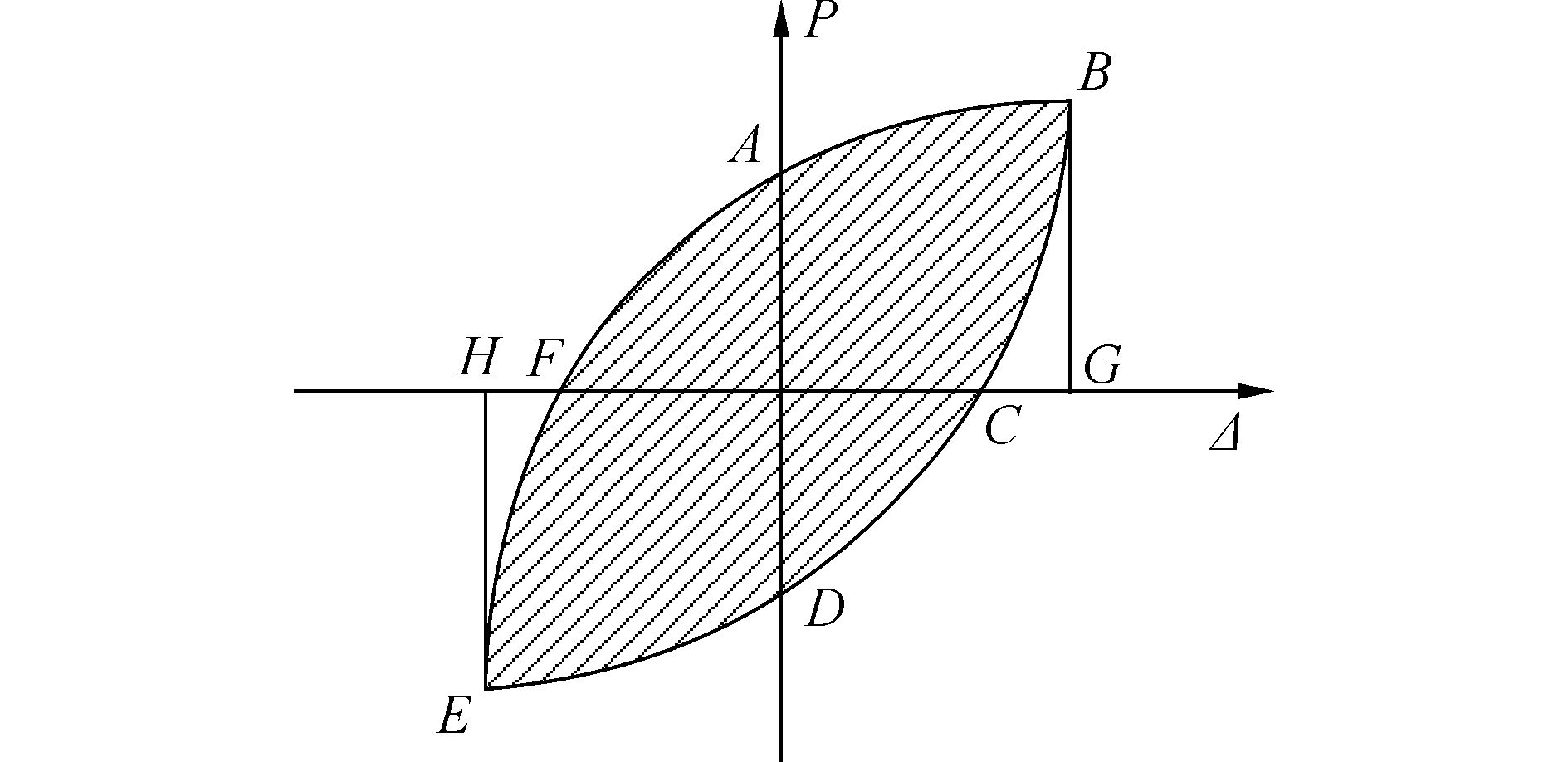
耗能能力是评价结构抗震性能的主要指标,本文采用等效黏滞阻尼系数he来表示(计算示意图如图 8所示)he越大,试件的耗能能力越强,其定义为[10]
|
| 图8 等效粘滞阻尼系数计算示意图 Figure 8 Schematic diagram of calculation of he |
| ${{h}_{e}}={{E}_{1}}/{{E}_{2}}$ | (9) |
式中:E1为对应于最大荷载时的滞回环面积,即结构储存能量的能力;E2为对应于最大荷载时的弹性变形能,按式(3)计算:
| ${{E}_{2}}=2\text{ }\!\!\pi\!\!\text{ (}{{P}_{\text{max}}}{{\Delta }_{\text{max}}}\text{+}{{P}_{\text{min}}}{{\Delta }_{\text{min}}})/2$ | (10) |
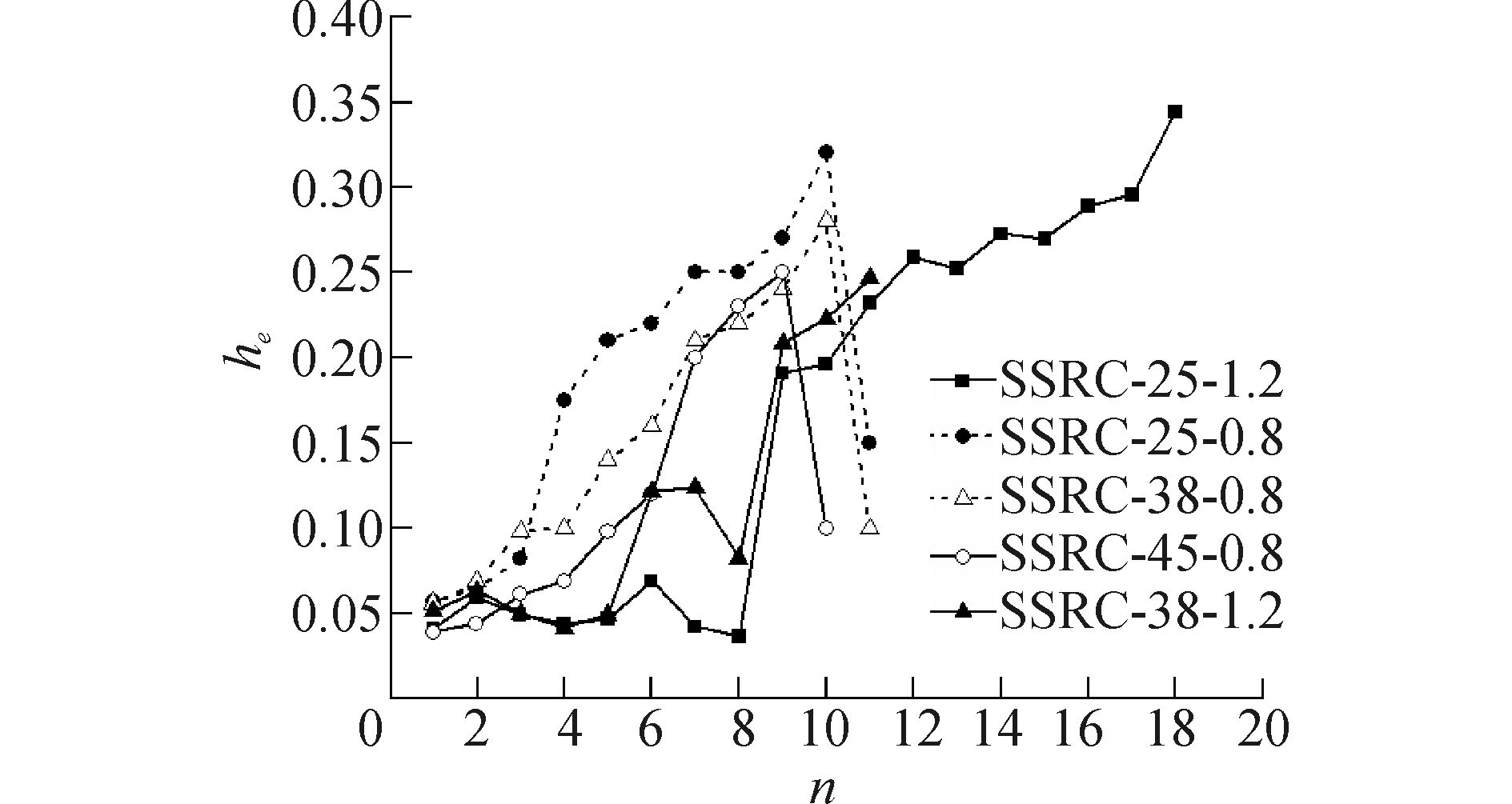
由此得出,各加载循环的等效黏滞阻尼系数,如图 9所示。
|
| 图9 不同轴压比下等效黏滞阻尼系数对比 Figure 9 Comparison of he under different axial compression ratios |
从图 9中可以看出:
1) 本试验中各试件在极限状态时的等效粘滞阻尼系数0.24≤he≤0.32,而钢骨高强混凝土柱-钢筋混凝土梁边节点he=0.182 [14],由此看出,本试验中的节点构件有更好的耗能能力;
2) 达到极限荷载前,等效粘滞阻尼系数与加载循环次数近似呈线性增长关系;
3) 梁屈服后,等效粘滞阻尼系数随位移等级的增大仍有一定的增长,但增长相对缓慢;
4) 随着轴压比的增大,等效阻尼粘滞系数减小,说明试件的耗能能力降低。
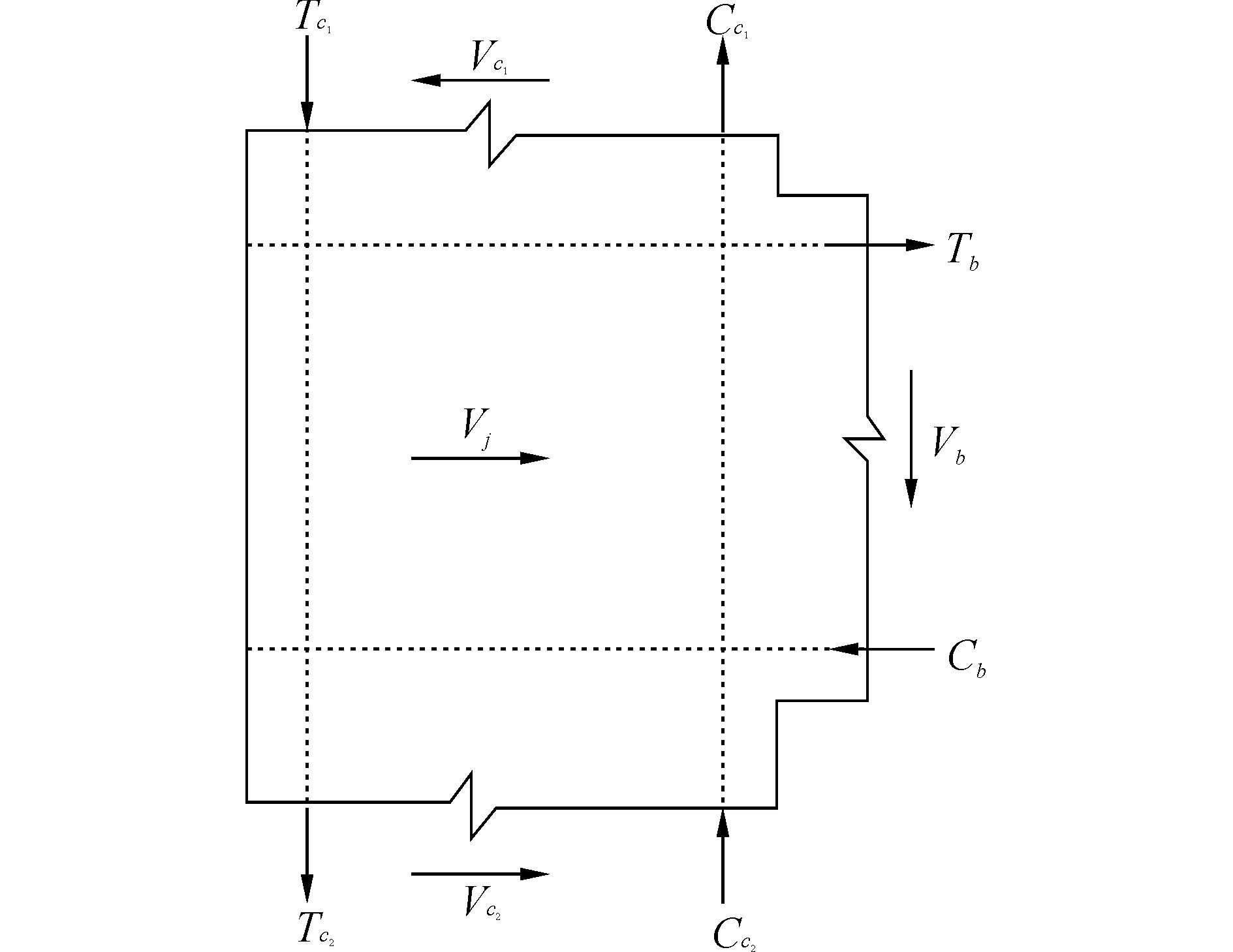
3.1.4 轴压比对承载力的影响钢骨超高强混凝土框架边节点在梁端施加低周往复荷载时,节点核心区极限状态受力情况如图 10所示。
|
| 图10 边节点受力图 Figure 10 External actions and internal shears at exterior joint |
由反弯点处弯矩为零可得
| ${{M}_{c1}}={{V}_{c}}{{h}_{1}}$ | (4) |
| ${{M}_{c2}}={{V}_{c}}{{h}_{2}}$ | (5) |
由节点处弯矩平衡可得
| ${{M}_{c1}}+{{M}_{c2}}={{M}_{b}}$ | (6) |
由式(4)~(6)可得
| ${{V}_{c}}=\frac{{{M}_{c1}}+{{M}_{c2}}}{{{h}_{1}}+{{h}_{2}}}=\frac{{{M}_{b}}}{H-{{h}_{b}}}$ | (7) |
由节点区平衡条件可得
| ${{T}_{b}}={{M}_{b}}/{{h}_{w}}$ | (8) |
| $Vj={{T}_{b}}-{{V}_{c}}=\frac{{{M}_{b}}}{{{h}_{w}}}-\frac{{{M}_{b}}}{H-{{h}_{b}}}=\frac{{{M}_{b}}}{{{h}_{w}}}(1-\frac{{{h}_{w}}}{H-{{h}_{b}}})$ | (9) |
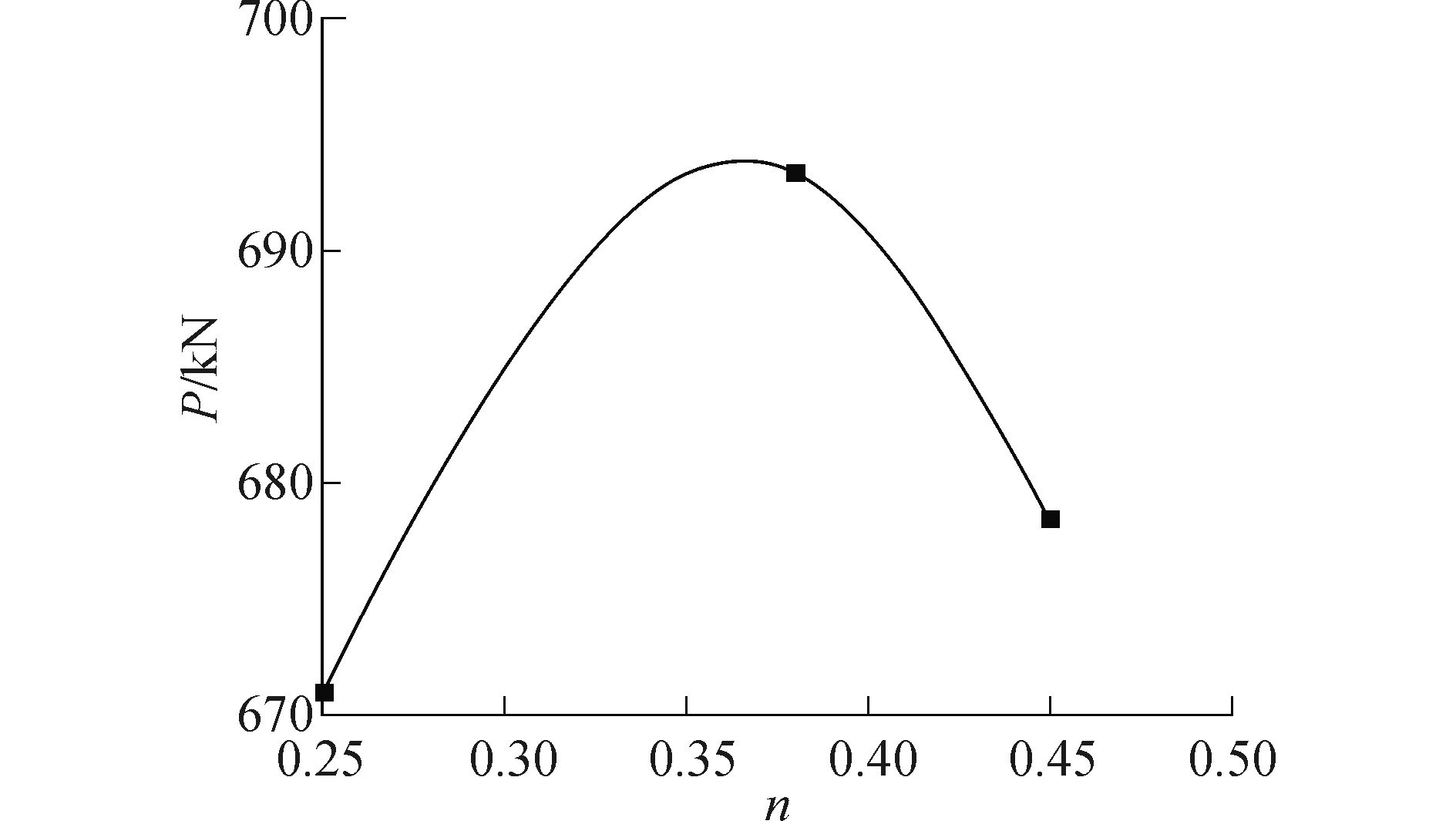
不同轴压比下节点核心区抗剪承载力如图 11所示。
|
| 图11 不同轴压比节点核心区抗剪承载力 Figure 11 Shear strength at joint core with various axial compression ratio |
从图 11中可以看出:
1) 轴压比对节点核心区的抗剪承载力影响以0.38为分界点,当轴压比从0.25增大至0.38,节点组合体的水平抗剪承载力略有增大,这是因为:一方面,轴压比的增大能延缓梁端塑性铰区梁纵筋向节点核心区的屈服渗透,从而适度改善梁筋贯穿段的黏结性能,减小混凝土与钢筋之间的黏结滑移[8]。
2) 轴压力可增强骨料间的咬合力,有效抑制节点核心区斜裂缝的开展,对节点组合体的抗震性能表现为有利的一面;而当轴压比继续增大至0.45,节点核心区的抗剪承载力反而下降,其原因为轴压比增大后,斜压杆与水平方向的交角增大,使得斜压杆所提供的水平分力减小,这对节点组合体的抗剪不利[9-10]。试件SRUHSC-45-0.8达到极限荷载后,承载力退化最快,其次是SRUHSC-38-0.8,说明高轴压比下,节点组合体破坏最为严重并呈现脆性破坏的特点。
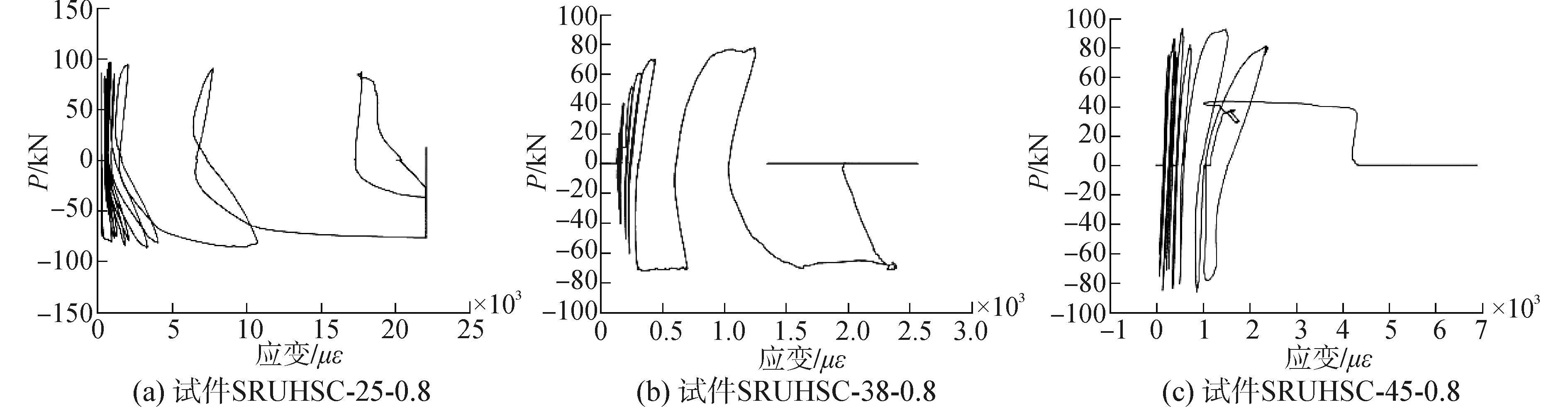
3.2 体积配箍率的影响各试件节点核心区箍筋应变与荷载曲线如图 12所示。
|
| 图12 不同轴压比下梁端荷载-箍筋应变 Figure 12 Load strain curves of stirrup under different axial compression ratios |
从图 12中可以看出:
1) 梁屈服前,节点区箍筋应变很小,仅为500 με左右,甚至更小,箍筋处于弹性阶段;梁屈服后,箍筋应变逐渐增大。研究表明随着组合体变形进一步增大,由于“贯穿段”的粘结退化,箍肢应力中桁架机构引起的部分将减小,而对核心区混凝土形成约束的部分将逐步扩大;当加载接近极限荷载时,箍筋应变迅速增大至屈服;箍筋一旦屈服,对节点核心区的混凝土约束作用也自行退化[7],此时斜压力较大,混凝土斜向压碎。
2) 当加载至极限荷载后,试件SRUHSC-25-0.8箍筋应变快速增长,甚至超过屈服应变,核心区开裂后其应变值比试件SRUHSC-38-0.8及SRUHSC-45-0.8大,表明在轴压比为0.25时,核心区箍筋约束作用更强。这是由于随着轴压比的增大导致斜压杆机制中斜压杆的宽度增大,从而增大了斜压杆机制所承担的剪力,而由桁架机构所占用的箍筋的抗拉能力减小[20-22],也就是说,当轴压比较小时,桁架机构中的箍筋能发挥更大的抗拉潜力。
从表 3中可看出,试件的位移延性系数随体积配箍率的提高而增大,当轴压比较低时,延性的增长幅度较高轴压比时更为显著。
4 结论本文考虑轴压比及体积配箍率的影响,研究了钢骨超高强混凝土框架节点的抗震性能,结论如下:
1) 轴压比水平的变化影响节点核心区的破坏形态。配箍率与含钢率相同的条件下,轴压比由0.25增大至0.38,节点核心区斜裂缝出现延缓,裂缝宽度减小,斜裂缝与水平轴的交角变大,对抗震表现有利的一面;而当轴压比由0.38继续增大至0.45,节点构件延性很差,表现出典型的脆性破坏,对抗震不利。
2) 在低周往复荷载作用下,轴压比水平的变化对节点组合体的骨架曲线屈服点影响不明显,而对极限荷载的影响以0.38为分界点,当轴压比由0.25增大至0.38时,极限荷载略有提高,而当轴压比继续增大至0.45,极限荷载反而下降。
3) 轴压比水平的变化对钢骨超高强混凝土边节点组合体的延性影响显著,随着轴压比增大,构件的延性明显降低,耗能能力大幅下降。
4) 轴压比较小的试件,节点核心区箍筋极限应变较大,箍筋能发挥更大的抗拉潜力,因此,当轴压比较低时,构件延性受节点核心区体积配箍率的影响更为显著。
5) 随着体积配箍率的增大,钢骨超高强混凝土边节点试件的延性提高,因此,在较高轴压力水平下,可通过提高节点核心区体积配箍率来满足实际工程抗震位移延性要求,但其提高幅度有限。
| [1] |
蒲心诚, 王志军, 王冲, 等. 超高强高性能混凝土的力学性能研究[J].
建筑结构学报, 2002, 23(6): 49–55.
PU Xincheng, WANG Zhijun, WANG Chong, et al. Mechanical properties of super high strength and high performance concrete[J]. Journal of building structures, 2002, 23(6): 49–55. |
| [2] |
孟刚, 贾金青, 王吉忠. 预应力超高强混凝土简支梁抗弯性能分析[J].
哈尔滨工程大学学报, 2013, 34(5): 575–580.
MENG Gang, JIA Jinqing, WANG Jizhong. Study on flexural behavior of prestressed ultra-high strength concrete beams[J]. Journal of Harbin Engineering University, 2013, 34(5): 575–580. |
| [3] | SHIN M, LAFAVE JM. Modeling of cyclic joint shear deformation contributions in RC beam-column connections to overall frame behavior[J]. Structural engineering and mechanics, 2004, 18(5): 645–69. DOI:10.12989/sem.2004.18.5.645 |
| [4] |
闫长旺. 钢骨超高强混凝土框架节点抗震性能研究[D]. 大连:大连理工大学, 2009.
YAN Changwang. Study on seismic performance of steel reinforced ultra high strength concrete frame connection[D]. Dalian:Dalian University of Technology, 2009. |
| [5] |
薛建阳, 赵鸿铁, 杨勇. 型钢混凝土节点抗震性能及构造方法[J].
世界地震工程, 2002, 18(2): 61–64.
XUE Jianyang, ZHAO Hongtie, YANG Yong. Seismic behavior and construction method of steel reinforced concrete joints[J]. World earthquake engineering, 2002, 18(2): 61–64. |
| [6] | LIN Chengming, RESTREPO J I. Seismic behaviour and design of reinforced concrete interior beam-column joints[J]. Bulletin of the New Zealand society for earthquake engineering, 2002, 35(2): 108–128. |
| [7] | AO M X, FAN J S, NIE J G. Seismic behavior of steel reinforced concrete column-steel truss beam hybrid joints[J]. Engineering structures, 2013, 56(3): 1557–1569. |
| [8] | TAO Z, HAN L H, ZHUANG J P. Axial loading behavior of CFRP strengthened concrete-filled steel tubular stub columns[J]. Advances in structural engineering, 2007, 10(1): 37–46. DOI:10.1260/136943307780150814 |
| [9] | ZHU W Q, JIA J Q, MENG G. Experimental studies on axial load performance of high strength concrete short columns[J]. ICE-Structures and Buildings, 2014, 167(9): 509–519. |
| [10] | WANG L C, FAN G X, QIN Q, SONG Y P. Experimental study on seismic behavior of reinforced concrete frame joints with consideration of strain rate effect[J]. Journal of building structures, 2014, 35(2): 38–45. |
| [11] |
郭子雄, 林煌, 刘阳. 不同配箍形式型钢混凝土柱抗震性能试验研究[J].
建筑结构学报, 2010, 31(4): 110–115.
GUO Zixiong, LIN Huang, LIU Yang. Experimental study on seismic behavior of SRC columns withdifferent stirrup configuration[J]. Journal of building structures, 2010, 31(4): 110–115. |
| [12] |
郭子雄, 黄群贤, 魏荣丰, 刘阳. 填充墙不规则布置对RC框架抗震性能影响试验研究[J].
土木工程学报, 2010, 11: 46–54.
GUO Zixiong, HUANG Qunxian, WEI Rongfeng, LIU Yang. Experimental study of the seismic behavior of irregularly brick infilled RC frames[J]. China civil egineering journal, 2010, 11: 46–54. |
| [13] | ZHANG Jiancheng, JIA Jinqing. Experimental study on seismic behavior of composite frame consisting of SRC beams and SRUHSC columns subjected to cyclic loading[J]. Construction and Building Materials, 2016, 125: 1055–1065. DOI:10.1016/j.conbuildmat.2016.08.157 |
| [14] |
傅剑平, 张川, 陈滔, 等. 钢筋混凝土抗震框架节点受力机理及轴压比影响的试验研究[J].
建筑结构, 2006, 27(3): 67–77.
FU Jianping, ZHANG Chuan, CHEN Tao, et al. Experimental investigation of shear mechanism and effect of axial-compression ratio on joints in earthquake-resistant reinforced concrete frames[J]. Journal of building structure, 2006, 27(3): 67–77. |
| [15] |
王立成, 范国玺, 秦全, 等. 考虑应变率效应的钢筋混凝土框架节点抗震性能试验研究[J].
建筑结构学报, 2014, 35(2): 38–45.
WANG Licheng, FAN Guoxi, QIN Quan, et al. Experimental study on seismic behavior of reinforced concrete frame joints with consideration of strain rate effect[J]. Journal of building structures, 2014, 35(2): 38–45. |
| [16] |
王连广, 贾连光, 张海霞. 钢骨高强混凝土边节点抗震性能试验研究[J].
工程力学, 2005, 22(1): 182–186.
WANG Lianguang, JIA Lianguang, ZHANG Haixia. Experimental study of aseismic behavior of steel-reinforced high strength concrete joints[J]. Engineering mechanics, 2005, 22(1): 182–186. |
| [17] |
刘伟, 贾金青, 李勇, 等. 型钢超高强混凝土边节点抗震性能研究[J].
武汉理工大学学报:交通科学与工程版, 2014, 38(6): 1333–1337.
LIU Wei, JIA Jinqing, LI Yong, et al. Study on seismic performance of exterior steel reinforced ultra high strength concrete frame connection[J]. Journal of Wuhan university of technology:transportation science & engineering, 2014, 38(6): 1333–1337. |
| [18] |
张蕾, 刘海峰, 郑鹏, 等. 钢筋混凝土板柱边节点抗震性能试验研究[J].
建筑结构, 2013, 43(5): 60–64.
ZHANG Lei, LIU Haifeng, ZHENG Peng, et al. Experimental study on seismic performance of RC column-slab edge connections[J]. Building structure, 2013, 43(5): 60–64. |
| [19] |
姚大立, 贾金青, 余芳. 预应力超高强混凝土梁剪切延性分析[J].
哈尔滨工程大学学报, 2013, 34(5): 593–598.
YAO Dali, JIA Jinqing, YU Fang. Analysis on shear ductility of prestressed ultra-high reinforced concrete beams[J]. Journal of Harbin engineering university, 2013, 34(5): 593–598. |
| [20] | GAN Dan, GUO Lanhui, LIU Jiepeng, et al. Seismic behavior and moment strength of tubed steel reinforced-concrete (SRC) beam-columns[J]. Journal of constructional steel research, 2011, 67(10): 1516–1524. DOI:10.1016/j.jcsr.2011.03.025 |
| [21] | LI Wei, LI Qingning, JIANG Weishan. Parameter study on composite frames consisting of steel beams and reinforced concrete columns[J]. Journal of constructional steel research, 2012, 77: 145–162. DOI:10.1016/j.jcsr.2012.04.007 |
| [22] |
薛建阳, 鲍雨泽, 任瑞, 等. 低周反复荷载下型钢再生混凝土框架中节点抗震性能试验研究[J].
土木工程学报, 2014, 47(10): 1–8.
XUE Jianyang, BAO Yuze, REN Rui, et al. Experimental study on seismic performance of steel reinforced recycled concrete inner-frame joints under low-cyclic reversed loading[J]. China civil engineering journal, 2014, 47(10): 1–8. |



