地震通常是以地震序列的形式发生的,可分为前震、主震和余震,主震发生后通常会伴随着较高震级的余震。余震的存在可能会使结构的地震需求超过主震时期,在最近发生的一系列地震中,很多结构在主震中只是发生了一定程度的破坏而并未倒塌,然而由于余震的发生导致了结构的进一步损坏而最终倒塌,如1995年日本的Kobe地震,一座9层钢筋混凝土建筑在主震中产生破坏后,在随后发生的余震中最终倒塌;2010年新西兰克赖斯特彻奇市发生的里氏7.2级地震后,大量建筑结构受到损伤并无法及时修复,在随后发生的6.3级余震下发生倒塌。然而对于余震的研究仍未得到工程抗震学界的足够重视,目前结构抗震设计所依据的抗震规范也并没有规定要考虑余震的影响,现今抗震学也依然认为桥梁工程所遭受的地震损伤主要由主震所产生的。目前已有学者对主震-余震序列波下结构的抗震性能进行了研究[2-7]。先驱学者Mahin[2]将1972年Managua地震后实测的主震-余震波序列作为输入,研究了单自由体系的响应在余震下的变化,发现结构的延性位移需求在余震后发生了明显的增加。Lee等[3-4]对主震-余震序列下多自由度体系的非线性响应进行了研究,发现将主震波放大或缩小来做为余震波会高估结构峰值位移。Hatzigeorgiou等[5]对4个规则与4个不规则框架在5条实测序列波与40条人工序列波下的响应进行了分析,发现在实测序列波下结构的位移延性需求明显增加。Ruiz- García等[6]研究了实测余震波对于钢结构建筑的影响,发现由于实测余震波的谱加速度峰值与结构的周期相差较大,因此地震需求并没有显著增加。Yue Li等[7]采用人工及实测序列波研究了框架结构在不同程度的主震损伤状态下的余震易损性,发现主震损伤越严重余震的易损性越大。然而之前的研究很少涉及桥梁结构领域,考虑实测主震-余震序列波对桥梁结构地震易损性的影响还有待进一步研究。
本文以一座三跨连续梁为例,利用OpenSees程序建立三维有限元模型,选取75个实测地震的主震-余震序列波,对有限元模型进行非线性时程动力分析,得到结构在主震-余震序列波下的地震响应,计算易损性时考虑支座位移和墩柱变形这两种构件的破坏形式,建立各构件在主震及主震-余震序列波下的概率地震需求模型(probabilistic seismic demand model,PSDM),并通过计算对选取各相关构件合适的损伤指标和极限状态,得到各构件的在主震波下及主震-余震序列波下的易损性曲线并对计算结果进行对比分析,最终得出余震对于桥梁结构易损性的影响。
1 地震易损性分析方法易损性曲线可以描述为在任意给定的地震强度(IM)下结构的需求(D)超出其能力(C)的条件概率[9]:
| ${{F}_{r}}=P[D\ge C|{{I}_{M}}\left] =P \right[D-C\ge 0|{{I}_{M}}]$ | (1) |
D为通过对有限元模型进行动力计算并对计算结果按照一定的方法进行分析得到的,C为通过对有限元模型中的构件进行极限状态(LS)分析得到的。
为了通过进行有限次动力计算而得到结构在任意给定地震强度(IM)下的需求(D),本文将采用“云图法”。“云图法”是通过一系列的动力时程分析,得到结构在不同IM下的响应,并根据结构响应与IM的指数回归关系得到结构响应的分布[10]。与同样作为计算概率性地震需求常用方法的IDA方法相比,“云图法”所得到的结构响应分布的方差为不随IM变化的常量,这样能够显著减少动力时程分析的计算量。此外,由于本文进行动力分析时所采用的地震波均为实测主震-余震序列波,地震强度(IM)均以实测为准而不做任何调幅,因而在此使用“云图法”较IDA方法更为合适。
| $ln{{S}_{d}}=lna+bln{{I}_{M}}$ | (2) |
式中:a和b是统计的回归系数。而对数标准差(βD|IM)可以表示为
| ${{\beta }_{D|{{I}_{M}}}}=\sqrt{\frac{\sum\limits_{i=1}^{n}{{}}{{\left[ ln{{d}_{i}}-(lna+bln{{I}_{M}}_{i}) \right]}^{2}}}{n-2}}$ | (3) |
式中:n为非线性时程分析的次数。因此,结合式(2)和式(3)可以得到概率地震需求模型(PSDM):
| $P[D\ge d|{{I}_{M}}]=1-\Phi \left( \frac{lnd-ln{{S}_{d}}}{{{\beta }_{D|{{I}_{M}}}}} \right)$ | (4) |
许多学者在研究的过程中假定,构件的能力极限状态(LS)服从对数正态分布[14]。因此,结合概率需求模型(PSDM)可以推出,易损性依然服从于对数正态分布,因此式(1)可以进一步表示为
| ${{F}_{r}}=P[D\ge C|{{I}_{M}}]=\Phi \frac{ln({{S}_{d}}/{{S}_{c}})}{\sqrt{{{\beta }^{2}}_{D|{{I}_{M}}}+\beta _{C}^{2}}}$ | (5) |
式中:Sc为结构能力的平均值。
2 地震动的选取 2.1 地震动强度指标地震动可以通过峰值加速度(PGA),峰值速度(PGV),周期对应的反应谱值Sa(T)等强度指标来描述[15]。Mackie等[16]建议,概率分析结果的线性一致性可以作为IM能否应用的判断标准。基于此标准,PGA和PGV都是IM的比较好的选择。Padgett等[17]对IM进行效率、可适用性以及危害可计算性的评价表明:PGA是比较合适的地震动强度指标。因此,本文选择PGA作为地震动强度指标。地震动只考虑纵向输入,研究在纵向地震作用下桥梁结构的响应。
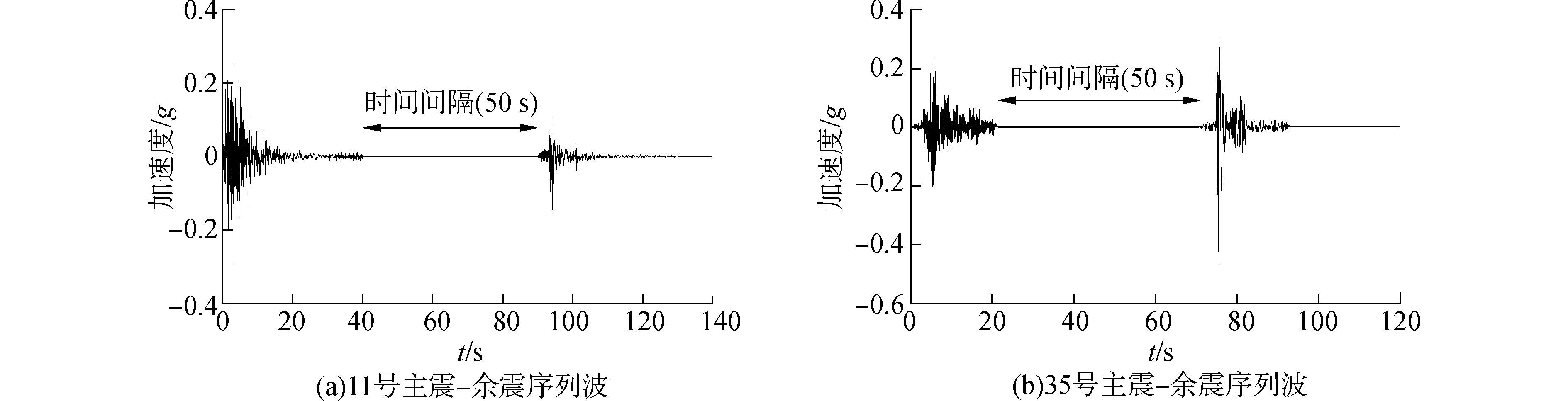
2.2 实测主震-余震序列波根据Negrete-Manriquez等[6]的研究,目前的人工生成的余震波与实际偏差较大,其精度尚无法满足要求,另外同一测站所测得的地震序列中余震中很少有包含了多余震的记录。因此,本文从PEER强震数据库[18]中选取75个实测地震序列,并且每个主震后只包含1条余震波。由于余震发生的时间一般距离主震结束的时间较短,主震所造成的结构损伤及破坏在余震到来之前很难及时修复,因而在做桥梁结构的余震抗震分析时不能认为桥梁结构是完整的,这是与主震下的桥梁抗震分析最大的区别。为了更好的考虑上述余震分析中结构所具有的损伤积累的特点,文中所选的大部分地震序列中余震都发生与主震结束后的一个月内,并将每个所选的地震序列都整理成一条主震-余震序列波,并在主震及余震之间添加50 s且地震加速度为0的间隔,以确保结构在余震发生前恢复静止状态。表 1给出了所选75个地震序列的主震波及余震波的具体信息。图 1给出了75个地震序列中所有主震波、余震波及主震-余震序列波在阻尼为5%时的伪加速度反应谱曲线及各自的平均谱加速度。从谱加速度的统计可以看出,主震的平均谱加速度要大于余震,而主震-余震序列波的平均谱加速度大于主震和余震。此外,文中所选的大部分地震序列中余震的震级以及PGA都小于主震,然而在少数地震序列中余震虽然震级小于主震,但是PGA会大于主震,如Janpan地震序列、Petrolia地震序列等。故图 2分别给出了主震PGA大于余震及主震PGA小于余震两种情况下具有代表性的主震-余震序列波的加速度时程曲线。
| 地震编号 | 地震名称 | 主震震级 | 余震震级 |
| 01-04 | Chi-Chi Taiwan | 7.62 | 6.20 |
| 05-06 | Coalinga | 6.36 | 5.09 |
| 07-12 | Chalfant Valley | 6.19 | 5.44 |
| 13-20 | Imperial Valley | 6.53 | 5.01 |
| 21-32 | Japan | 9.00 | 7.10 |
| 33-45 | Livermore | 5.80 | 5.42 |
| 46-51 | Mammoth Lakes | 6.06 | 5.94 |
| 52-63 | Northridge | 6.69 | 5.93 |
| 64-69 | Petrolia | 7.20 | 6.50 |
| 70-75 | Whittier Narrows | 5.99 | 5.27 |

|
| 图1 地震波反应谱 Figure 1 The response spectra of the ground motions |
|
| 图2 地震波时程 Figure 2 The time histories of the ground motions |
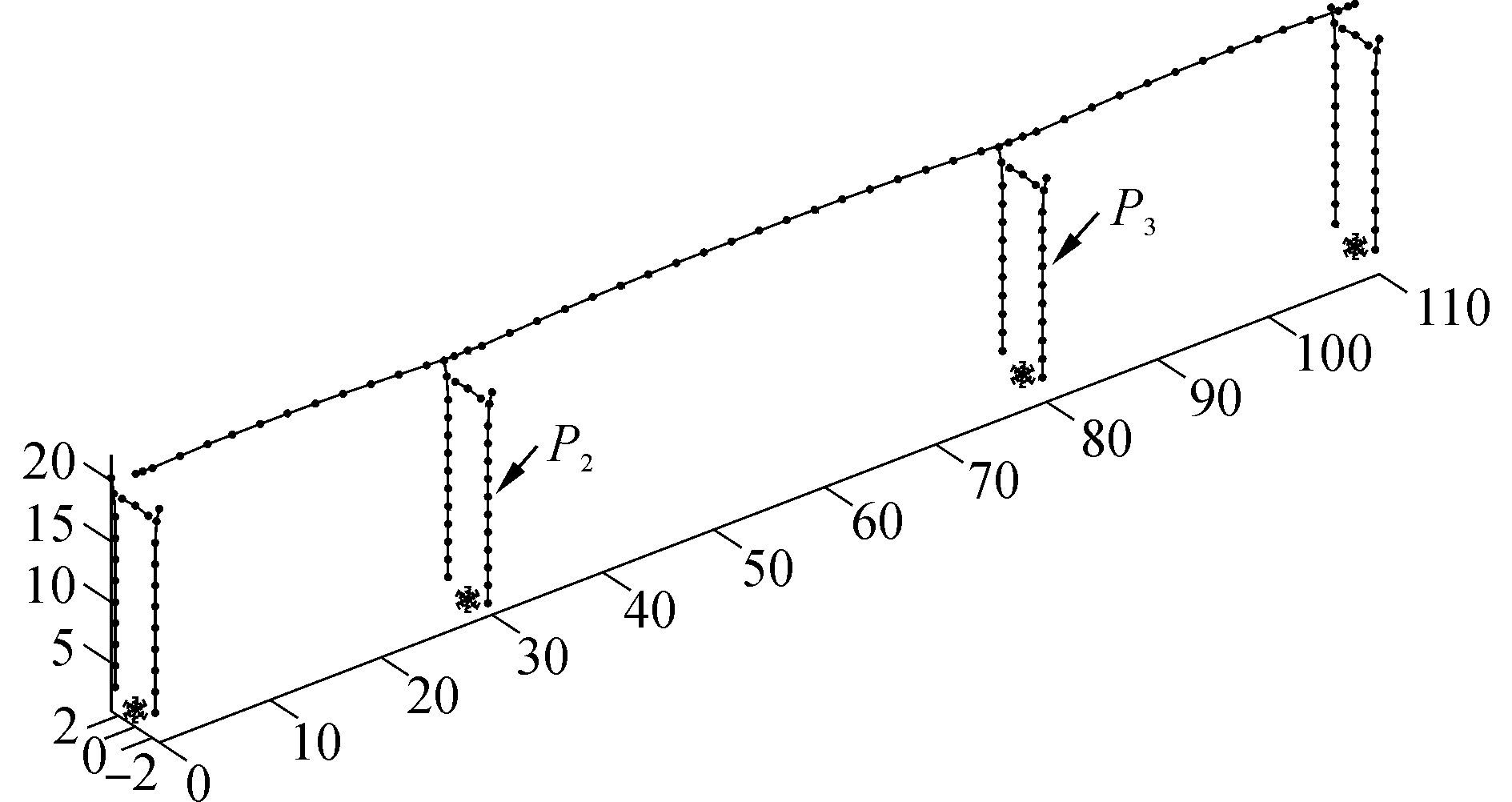
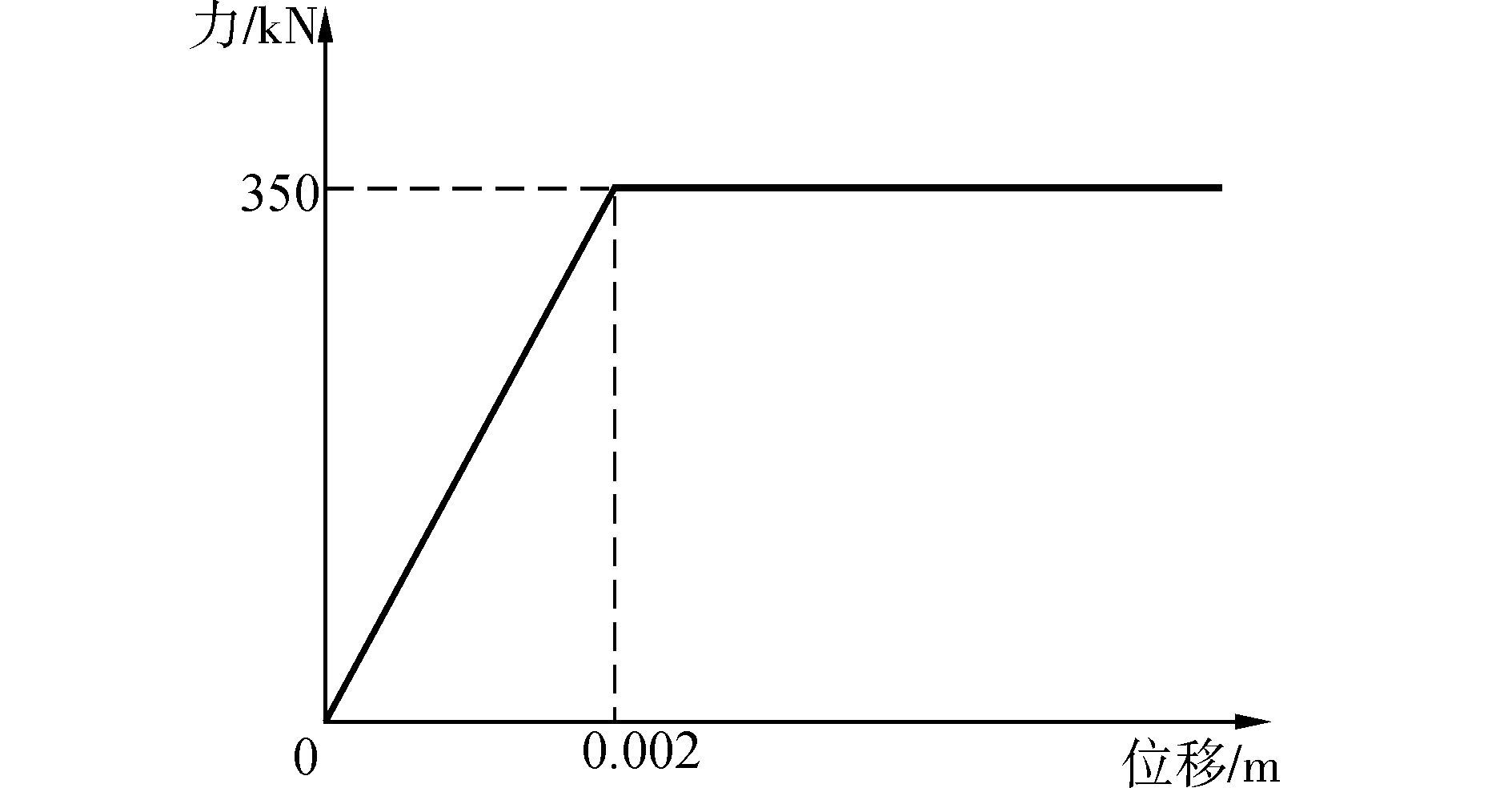
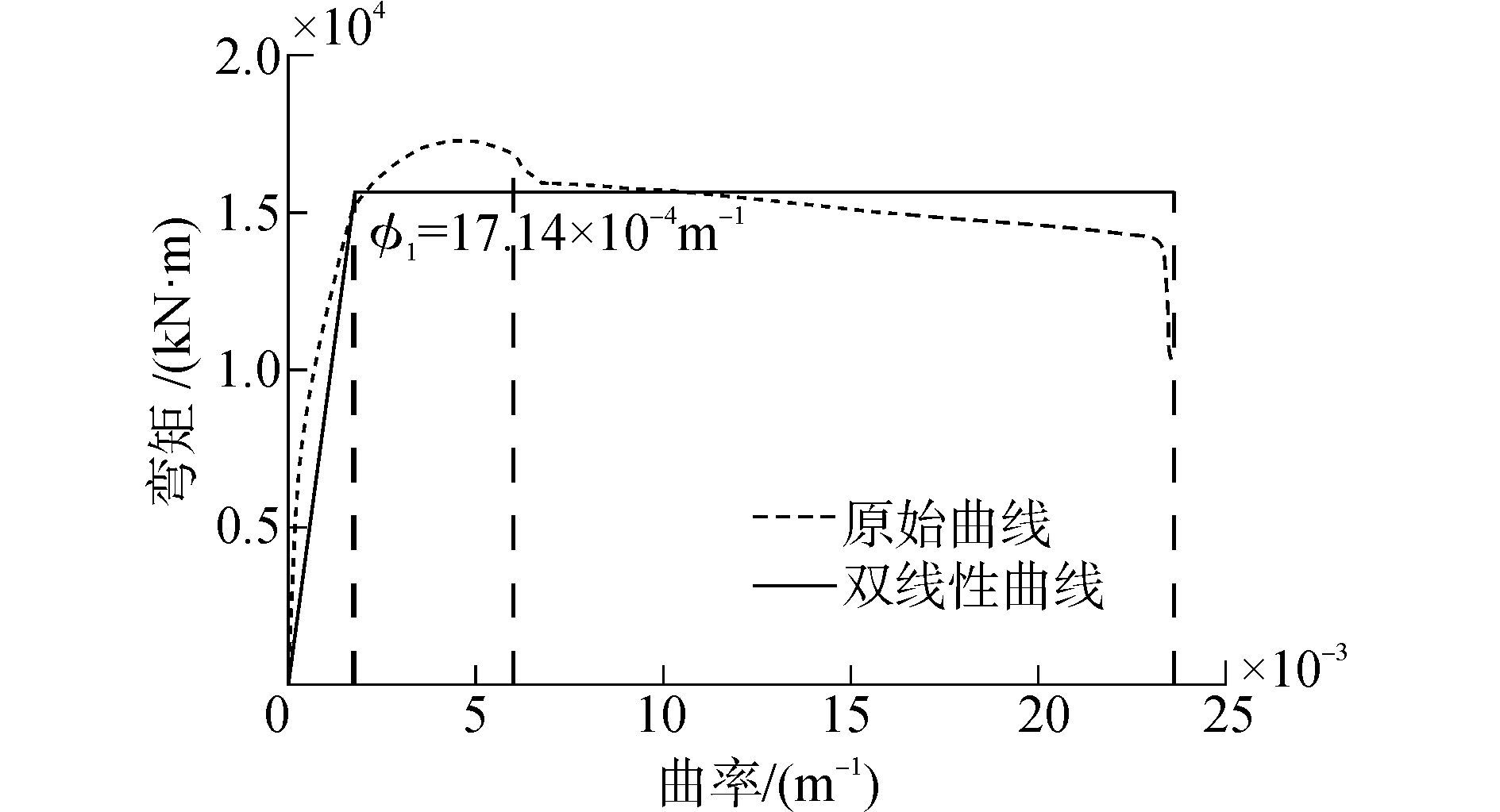
本文以一座钢筋混凝土连续梁桥中的主桥部分(见图 3)为例进行分析研究。跨径布置为30 m+50 m+35 m,主梁为等截面箱梁,材料采用C50混凝土;桥墩为双柱方形墩,墩宽1.6 m、墩高17 m,桥墩材料采用C40混凝土,纵向钢筋为二级钢筋,纵向配筋率为0.8%;承台材料为C40混凝土。墩顶与主梁通过球钢支座进行相连,P2支座为横向固定、纵向可滑动,P3墩为固定墩,支座其力学性能曲线见图 4。非线性有限元模型采用OpenSees程序[19]建立,认为上部结构在地震作用下基本保持弹性,因此使用线弹性梁柱单元模拟。墩柱及系梁在地震作用下有可能进入塑形,因此采用弹塑性纤维梁柱单元来模拟,钢筋采用双线性滞回模型,核心混凝土与保护层混凝土都采用了Kent-Scott-Park模型[20],且均不考虑混凝土的抗拉性能,为了更准确的计算有限元模型中桥墩的弯矩-曲率曲线,本文根据Nielson[21]、庞于涛等[22]的研究,采用OpenSees程序计算其弯矩-曲率曲线并进行双线性拟合,所得桥墩的弯矩-曲率曲线见图 5。模型中两边墩作为边界条件,非线性时程分析结果只考虑中间两个墩。本文考虑桩土相互作用,通过将承台与地面使用6弹簧进行连接的方式进行模拟。地震波输入方向为纵向输入。
|
| 图3 三跨连续梁桥的总体布置 Figure 3 The layout of the three-span continuous girder bridge |
|
| 图4 支座的力学曲线 Figure 4 The modeling of bearing |
|
| 图5 桥墩的弯矩曲率曲线 Figure 5 The moment-curvature curve of pier |
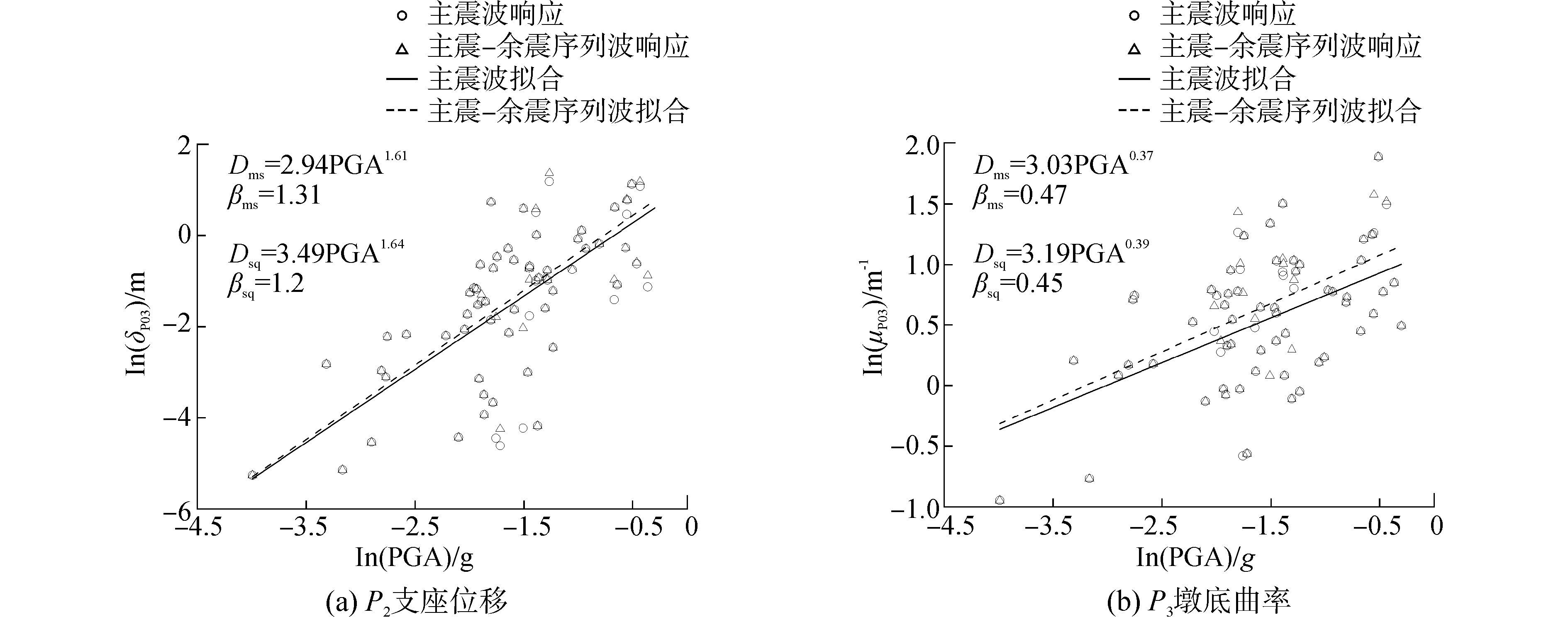
大量震害调查结果表明,落梁破坏、支座破坏和墩柱破坏都会导致结构系统失效,而落梁发生在支座破坏之后,故本文考虑支座和墩柱这两种构件破坏形式[23],使用章节3中选取的75条主震-余震序列波,利用Opensees程序对上述有限元模型进行了75次非线性时程分析,并记录了相关构件的地震响应时程,其中包括P2、P3墩上的支座位移以及墩底曲率。从时程结果中分别得到相关构件在主震及主震-余震序列波下的地震响应最大值,并分别得到75个各相关构件在主震下及在主震-余震序列波下的“响应-PGA ”样本对,使用“云图法”,得到地震响应云图后根据式(2)将所得的地震响应进行线性回归拟合,得到各构件在主震及主震-余震序列波下PGA取任意值时(0<PGA≤2)地震响应的均值和方差,即概率地震需求模型(PSDM)。图 6给出了支座位移及墩底曲率在主震及主震-余震序列波下的响应云图及线性回归数据,并进行对比分析。
|
| 图6 概率地震需求模型(PSDM) Figure 6 The probabilistic seismic demand model of bridge components |
从线性拟合的结果可以看出,结构在主震-余震序列波下的地震需求要大于只考虑主震波的情况,这说明受余震的影响,结构的地震概率需求变大。并且,考虑主震-余震序列波时线性拟合出的曲线斜率要大于主震波,这说明地震波PGA越大,两种情况下的概率需求相差越多,余震对结构的概率需求影响越大。
3.3 损伤指标及极限状态目前在易损性分析中所采用的破坏准则可以归纳为四类[8]:强度准则、变形准则、能量破坏以及变形和能量双重准则。本文使用变形作为支座和墩柱这两种构件破坏形式的破坏准则。Hwang H等[24]的研究表明,桥梁结构的破坏过程可用4种极限状态来描述,分别是:轻微损伤、中等损伤、严重损伤和完全损伤,即4个损伤阶段。为了确定支座位移的各极限状态值,根据球形钢支座设计规范得到支座允许设计位移量作为第1个极限状态值,其余各个极限状态系数与第1个极限状态之比分别取为[25-26]为2.0、4.0、8.0。墩底曲率各损伤阶段的确定方法同支座位移类似,通过截面弯矩-曲率分析得到单元截面首次屈服曲率,并将其作为第1个极限状态值,其余各个损伤等级曲率系数与第1个极限状态比值分别取为2.0、4.0、8.0。
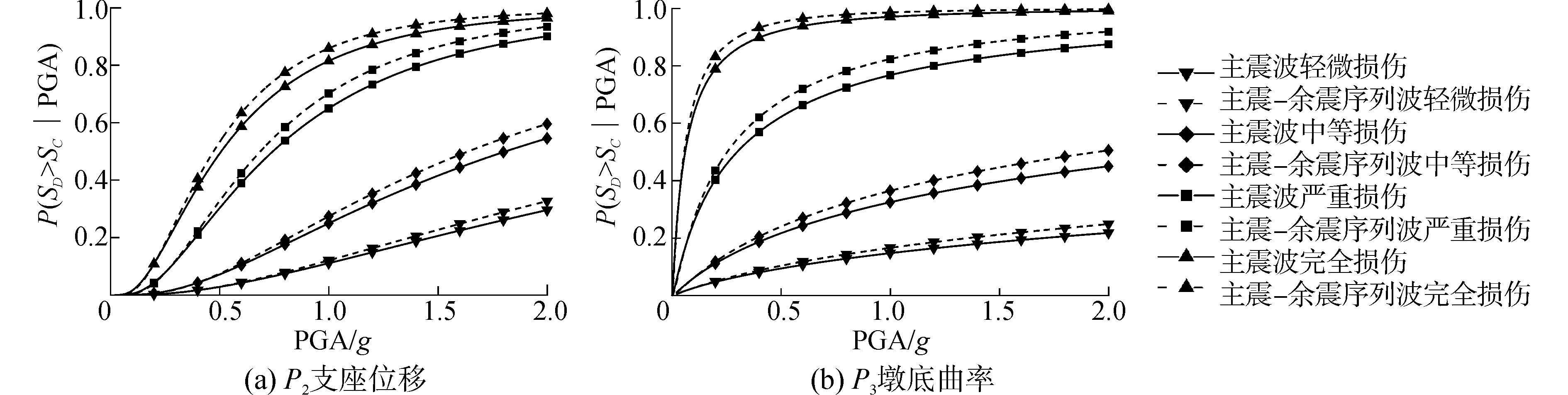
3.4 易损性曲线在得到各构件的概率地震需求模型(PSDM)及极限状态后,根据式(5)可以计算出构件各极限状态在给定PGA下的失效概率,得到易损性曲线。应当指出的是,3.2节中所得到的各相关构件在主震-余震序列波下的“响应-PGA”样本对中的PGA均为相应的主震波的PGA,因为本文的目的是研究余震对桥梁结构抗震性能的影响,而基于文中所述余震的特点可知余震的PGA与主震PGA的大小关系是不确定的,即无法根据主震来预测余震PGA的大小或者范围。因此,各样本对中的PGA取主震波PGA时,对余震的研究与实际更相符。图 7给出了各相关构件在不同极限状态下的易损性曲线,将各构件在主震波及主震-余震序列波下相应的地震易损性曲线放在同一张图中进行对比。可以看出,考虑余震后构件在各个极限状态下易损性均有较明显的提升,其中支座位移考虑余震后易损性与之前相比最大相差10.96%,而墩底曲率差值可达到13.98%。可见,考虑余震后结构遭受地震损伤的概率将明显增大,在对结构进行抗震性能分析时余震的影响不可忽视,仅考虑主震而不考虑余震的影响,往往会高估了结构的抗震能力。
|
| 图7 支座位移及墩底曲率的易损性曲线 Figure 7 Fragility curves of bridge bearing displacement and bottom pier curvature |
本文以一座三跨连续梁为例,选取75条主震-余震序列波对有限元模型进行非线性时程分析,得到结构在主震-余震序列波下的地震响应,计算易损性时考虑支座位移和墩柱变形这两种构件的破坏形式,建立各构件在主震及主震-余震序列波下的概率地震需求模型(PSDM),并通过计算对选取各相关构件合适的损伤指标和极限状态,得到各构件的在主震波下及主震-余震序列波下的易损性曲线并对计算结果进行对比分析,并最终得出以下结论:
1) 本文中选取的75条主震-余震序列波中,主震的平均谱加速度大于余震,而主震-余震序列波的平均谱加速度大于主震。
2) 余震会使各构件的地震概率需求变大,并且地震波的PGA越大,余震的影响越大。
3) 考虑余震后各构件在各极限状态下易损性均有较明显的提升,结构在考虑余震后更容易遭受地震破坏。在对结构进行抗震性能分析时,仅考虑主震而不考虑余震的影响,往往会高估结构的抗震能力。
4) 虽然余震震级一般比主震低,但余震可能会使得结构的损伤概率大于只考虑主震的情况,因此在进行结构抗震设计时,为了考虑余震的影响有必要在地震动输入时考虑主震-余震序列波。
| [1] |
蒋海昆, 郑建常, 吴琼, 等. 中国大陆中强以上地震余震分布尺度的统计特征[J].
地震学报, 2007, 29(2): 151–164.
Jiang Haikun, Zheng Jianchang, Wu Qiong, et al. Statostocal features of aftershock distribution size for moderate and large earth quakes in Chinese mainland[J]. Acta seismologica sinica, 2007, 29(2): 151–164. |
| [2] | MAHIN S A. Effects of duration and aftershocks on inelastic design earthquakes[C]//Proceedings of the 7th World Conference on Earthquake Engineering. Istanbul, 1980:677-680. |
| [3] | LEE K, FOUTCH D A. Performance evaluation of damaged steel frame buildings subjected to seismic loads[J]. Journal of structural engineering, 2004, 130(4): 588–599. DOI:10.1061/(ASCE)0733-9445(2004)130:4(588) |
| [4] | LI Quanwang, ELLINGWOOD B R. Performance evaluation and damage assessment of steel frame buildings under main shock-aftershock earthquake sequences[J]. Earthquake engineering & structural dynamics, 2007, 36(3): 405–427. |
| [5] | HATZIGEORGIOU G D, BESKOS D E. Inelastic displacement ratios for SDOF structures subjected to repeated earthquakes[J]. Engineering structures, 2009, 31(11): 2744–2755. DOI:10.1016/j.engstruct.2009.07.002 |
| [6] | RUIZ-GARCÍA J, NEGRETE-MANRIQUEZ J C. Evaluation of drift demands in existing steel frames under as-recorded far-field and near-fault mainshock-aftershock seismic sequences[J]. Engineering structures, 2011, 33(2): 621–634. DOI:10.1016/j.engstruct.2010.11.021 |
| [7] | LI Yue, SONG Ruiqiang, VAN DE LINDT J W. Collapse fragility of steel structures subjected to earthquake mainshock-aftershock sequences[J]. Journal of structural engineering, 2014, 140(12): . DOI:10.1061/(ASCE)ST.1943-541X.0001019,04014095 |
| [8] |
沈国煜, 袁万城, 庞于涛. 基于Nataf变换的桥梁结构地震易损性分析[J].
工程力学, 2014, 31(6): 93–100.
SHEN Guoyu, YUAN Wancheng, PANG Yutao. Bridge seismic fragility analysis based on Nataf transformation[J]. Engineering mechanics, 2014, 31(6): 93–100. |
| [9] | PADGETT J E, DESROCHES R. Methodology for the development of analytical fragility curves for retrofitted bridges[J]. Earthquake engineering & structural dynamics, 2008, 37(8): 1157–1174. |
| [10] |
吕大刚, 于晓辉, 潘峰, 等. 基于改进云图法的结构概率地震需求分析[J].
世界地震工程, 2010, 26(1): 7–15.
LYU Dagang, YU Xiaohui, PAN Feng, et al. Probabilistic seismic demand analysis of structures based on an improved cloud method[J]. World earthquake engineering, 2010, 26(1): 7–15. |
| [11] | CORNELL C A, JALAYER F, HAMBURGER R O, et al. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines[J]. Journal of structural engineering, 2002, 128(4): 526–533. DOI:10.1061/(ASCE)0733-9445(2002)128:4(526) |
| [12] | SHINOZUKA M, FENG M Q, LEE J, et al. Statistical analysis of fragility curves[J]. Journal of engineering mechanics, 2000, 126(12): 1224–1231. DOI:10.1061/(ASCE)0733-9399(2000)126:12(1224) |
| [13] | HWANG H, HUO J. Probabilistic seismic damage assessment of highway bridges[C]//6th US National Conference on Earthquake Engineering. Seattle, Washington:EERI, 1998. |
| [14] | MACKIE K R, STOJADINOVIĆ B. R-factor parameterized bridge damage fragility curves[J]. Journal of bridge engineering, 2007, 12(4): 500–510. DOI:10.1061/(ASCE)1084-0702(2007)12:4(500) |
| [15] | MACKIE K R, STOJADINOVIĆ B. Performance-based seismic bridge design for damage and loss limit states[J]. Earthquake engineering & structural dynamics, 2007, 36(13): 1953–1971. |
| [16] | MACKIE K R, STOJADINOVIĆ B. Fragility basis for California highway overpass bridge seismic decision making[R]. Berkeley:University of California, 2005. |
| [17] | PADGETT J E, NIELSON B G, DESROCHES R. Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios[J]. Earthquake engineering & structural dynamics, 2008, 37(5): 711–725. |
| [18] | ZHANG Sherong, WANG Gaohui, SA Wenqi. Damage evaluation of concrete gravity dams under mainshock-aftershock seismic sequences[J]. Soil dynamics and earthquake engineering, 2013, 50: 16–27. DOI:10.1016/j.soildyn.2013.02.021 |
| [19] | MAZZONI S, MCKENNA F, SCOTT M H, et al. OpenSees command language manual[R]. Pacific Earthquake Engineering Research (PEER) Center, 2006. |
| [20] | SCOTT B D, PARK R, PRIESTLEY M J N. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates[J]. ACI Journal Proceedings, 1982, 79(1): 13–27. |
| [21] | NIELSON B G. Analytical fragility curves for highway bridges in moderate seismic zones[D]. Georgia:School of Civil and Environmental Engineering, 2005. |
| [22] |
庞于涛, 袁万城, 党新志, 等. 考虑材料劣变过程的桥梁地震易损性分析[J].
同济大学学报:自然科学版, 2013, 41(3): 348–354.
PANG Yutao, YUAN Wancheng, DANG Xinzhi, et al. Stochastic fragility analysis of bridges with a consideration of material deterioration[J]. Journal of Tongji University:natural science, 2013, 41(3): 348–354. |
| [23] |
钟剑, 庞于涛, 曹飒飒, 等. 基于构件的RC连续梁桥地震体系易损性分析[J].
同济大学学报:自然科学版, 2015, 43(2): 193–198.
ZHONG Jian, PANG Yutao, CAO Sasa, et al. Seismic fragility methodology for RC continuous bridges based on components correlation[J]. Journal of Tongji University:natural science, 2015, 43(2): 193–198. |
| [24] | HWANG H, LIU Jingbo, CHIU Y H. Seismic fragility analysis of highway bridges[R]. Mid-America Earthquake Center CD Release 01-06, 2001. |
| [25] | YANG C S, DESROCHES R, PADGETT J E. Fragility curves for a typical California box girder bridge[C]//Proceedings of the 2009 ASCE Technical Council on Lifeline Earthquake Engineering Conference. San Francisco, CA, USA:ASCE, 2009. |
| [26] | CHOI E, DESROCHES R, NIELSON B. Seismic fragility of typical bridges in moderate seismic zones[J]. Engineering structures, 2004, 26(2): 187–199. DOI:10.1016/j.engstruct.2003.09.006 |



