能见度良好时,影响船舶领域的因素众多,确定船舶领域模型时很难将全部影响因素同时进行考虑。例如Goodwin[1]对水域类型和船舶密度对船舶领域的影响进行了统计,PIETRZYKOWSKI Z等和Hsu都对会遇局面对船舶领域的影响进行了研究[2-3],PIETRZYKOWSKI Z模型中同时对水域参数和船舶大小对船舶领域的影响进行了研究[4],Hansen等对水域类型和水域参数进行了研究[5],范贤华等所建模型中包含了船长、速度、潮流速度[6],王云英对限制性水域的领域进行了研究[7],王宁提出的四维船舶领域模型中船舶领域大小的确定包含影响因素船舶长度和速度[8-9]。王宁给出了船舶领域模型的四维解析框架,包含了船舶领域的全部影响因素,但模型较复杂[10]。基于神经网络[11-12]方法得到的船舶领域与其影响因素的关系,虽能同时考虑较多的影响因素,但这种方法是一种黑箱的方法。
众多影响船舶领域的因素给船舶领域的研究带来了困难,而不同因素对船舶领域影响的大小不同,目前缺乏对影响船舶领域的因素对船舶领域影响重要性的分析。确定不同影响因素的重要度,对其进行约简,可以简化建立船舶领域模型的难度与复杂性,且可以保证所建模型的合理性与精确性。
利用主成分回归分析与基于粗糙集的相关算法对影响船舶领域的因素的重要度进行分析,并对两种方法得到的结果进行对比确定了对船舶领域影响较重要的因素、重要度较小的因素和可删掉因素。
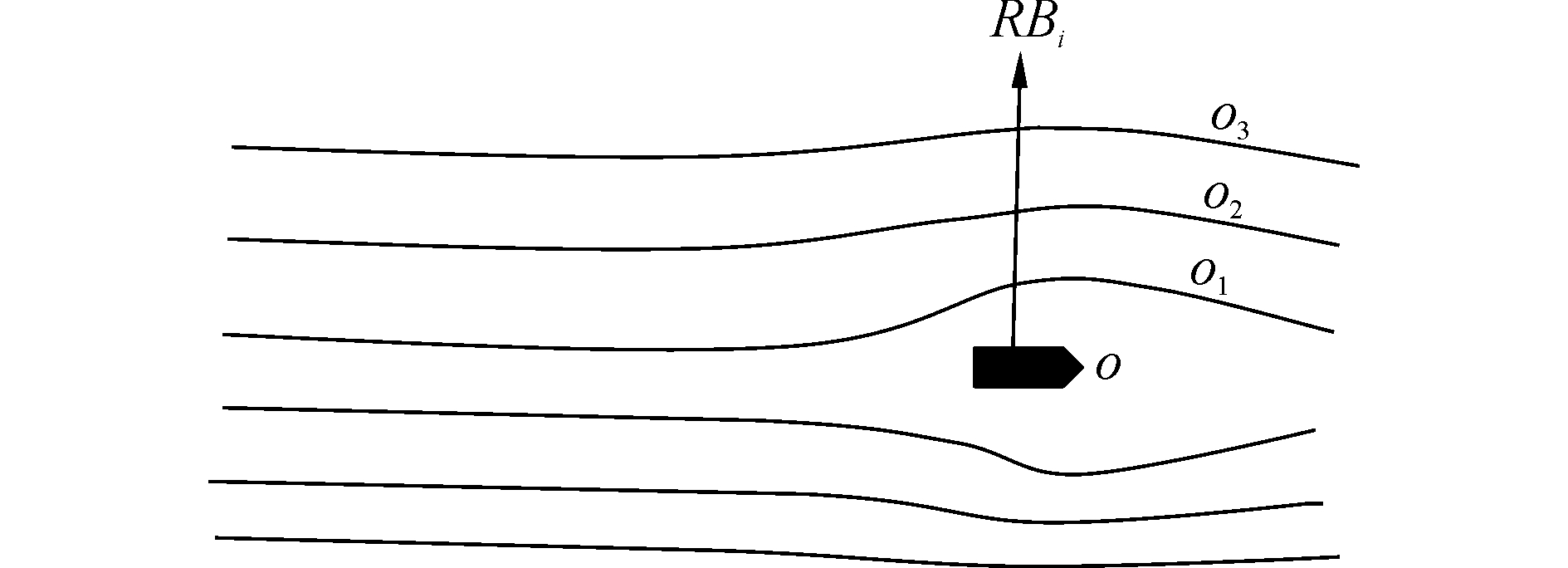
1 船舶领域与其影响因素 1.1 船舶领域 1.1.1 船舶领域样本的选取根据藤井和Goodwin对船舶领域的定义,船舶领域为驾驶员为保证航行安全想要保持的船舶之间的最小安全会遇距离,其一种具体体现即为采取避碰措施的船舶与中心船实际通过的最近会遇距离,设为d。其次,假设一密度均匀的船舶交通流在与某船舶会遇并采取避碰措施通过如图 1所示,船舶领域由船舶之间的最小安全会遇距离决定,且在中心船o周围同一方向RBi上,船o1的转向幅度必大于o2、o3,o1与中心船通过距离为d处船舶密度增大最多,即为船舶密度最大处,与藤井定义的领域边界吻合。所以以d作为对船舶领域影响因素进行分析的领域样本[2]。
|
| 图1 船舶避碰运动 Figure 1 Behavior of the ships collision avoidance |
船舶领域不同方位的边界到中心船的距离不同,样本数据中的船舶领域不能进行比较。所以将样本中,中心船周围不同方位上的领域大小转换为相同方位上的领域大小。设船舶领域模型中任意方位β上的领域边界到中心船的距离为dβ,尾部扇区长为l(中心船到尾部端点的距离),以中心船舶船首方向为0,船尾为180°,左右对称。参考Goodwin船舶领域模型[1],设船舶领域样本满足如下dβ与l的比例关系:
| $ l = \left\{ \begin{array}{l} \frac{9}{{14}}{d_\beta }, \;\;\;\;\;\;\;\;0^\circ \le \beta \le 112.5^\circ \\ {d_\beta }, \;\;\;\;\;\;\;\;\;\;\;\;112.5^\circ < \beta \le 180^\circ \end{array} \right. $ | (1) |
船舶领域影响因素主要可分为人、船、环境、管理四类。其中管理在所选水域范围内,存在的差异很小, 不予考虑。针对数据来源水域的特点,参考文献[2],对开阔水域能见度良好时,影响船舶领域的因素的选取如表 1。
| 影响因素 | 子影响因素 | 符号 |
| 船舶 | 船舶大小 | A1 |
| 船舶类型 | A2 | |
| 运动参数和交通状态 | 速度 | B1 |
| 密度 | B2 | |
| 会遇角度 | B3 | |
| 水文、气象 | 风 | C1 |
| 浪 | C2 | |
| 流 | C3 | |
| 能见度 | C4 | |
| 人为因素 | 驾驶员级别 | D1 |
根据渤海及黄海北部水域内的船舶自动识别系统AIS) 数据,通过计算,选择其中2 023起数据为样本,时间为2014年9月26日到2014年10月13日。气象数据来自于中央气象台的天气预报,水文数据来自于国家海洋环境预报中心的预报。A1、B1、C1、C2、C3、C4、l为常规度量方式,其他影响因素的度量方式如表 2,原始数据如表 3。
| 数据 | 度量方式 |
| A2/(1) | 随机对船舶类型取值为整数 |
| B2/(1) | 按照水域不同范围内的船舶密度大小将水域划分为4个区域,密度由小到大分别为1, 2, 3, 4 |
| B3/(°) | 中心船舶船首方向为0,船尾为180°,左右对称 |
| D1/(1) | 按照驾驶员级别三副、二副、大副分别为1, 2, 3 |
| 样本 | B1/ knot | B3/(1) | A1/m | D1/(1) | B2/(1) | C1/级 | C2/m | C3/kn | C4/km | A2/(1) | l/m |
| 1 | 0 | 90.994 0 | 31 | 2 | 4 | 5.6 | 1.5 | 0.2 | 20 | 2 | 677.024 1 |
| 2 | 2 | 49.758 7 | 100 | 1 | 3 | 4.5 | 1.2 | 0.1 | 20 | 4 | 1 919.022 4 |
| 3 | 0.1 | 15.826 4 | 47 | 1 | 2 | 6.7 | 1.8 | 0.4 | 15 | 1 | 945.713 4 |
| | | | | | | | | | | | |
| 2 023 | 18.8 | 163.999 0 | 15 | 1 | 1 | 7.8 | 3 | 0.4 | 15 | 3 | 2 237.151 9 |
首先对数据的相关性进行分析,根据数据特征选择较恰当的研究方法。利用SPSS软件进行kaiser meyer olkin (KMO) 测量和巴利特检验得到结果如表 4,其中近似卡方值显著性为0.000,KMO测量值为0.653,表明样本数据之间存在一定的相关性。对样本数据之间存在相关性的问题,可选择主成分回归分析法进行分析。而不同的方法有各自不同的优缺点,为了增加结果的可信度,选择基于粗糙集的算法对影响因素进行分析,并对两种方法得到的结果进行对比。由于基于粗糙集算法对数据没有较特殊的要求,所以两种算法均适用于研究需要。
| 统计量 | 数值 |
| KMO测量值 | 0.660 |
| Bartlett球体检验卡方估计值 | 9 647.089 |
| 自由度 | 45 |
| 显著性 | 0 |
主成分分析可以把相关性较强的自变量综合在同一主成分中,各主成分彼此独立,应用时选择其中包含了原数据大部分信息的主成分作为新的变量进行回归分析,然后把主成份回归方程转换为线性回归方程,得到因变量与原始自变量的回归系数。根据因变量与原始自变量的回归系数的大小可以找出影响因素中的重要因素。具体步骤为:
1) 数据标准化。
2) 计算影响因素数据的协方差矩阵∑。
3) 计算∑的征值λi(i=1, 2, …, p) 和特征向量aij(i, j=1, 2, …, p),并按λi(i=1, 2, …, p) 大小顺序排序,计算主成分贡献率及累计贡献率,选择前m个主成分的累计贡献率大于85%。
4) 对前m个主成分与船舶领域做回归分析。
5) 将主成分还原为原变量,得到原变量与船舶领域的回归方程。
使用SPSS统计软件IBM SPSS Statistics 22对影响船舶领域的因素观测数据进行主成分分析,得到主成分的特征根和方差百分比。从表 5的计算结果可以看到当提取前6个主成分时,主成分的累积方差贡献率达到了84.766%,可以近似满足对累积方差贡献率的要求,即包含了原数据的大部分信息,所以主成分的提取结果为前6个主成分。对前6个主成分做回归分析,主成分回归参数估计如表 5。
| 主成分 | 特征根 | 方差百分比/% | 累积/% |
| F1 | 3.159 | 31.589 | 31.589 |
| F2 | 1.463 | 14.628 | 46.217 |
| F3 | 1.061 | 10.614 | 56.831 |
| F4 | 0.982 | 9.819 | 66.650 |
| F5 | 0.945 | 9.454 | 76.104 |
| F6 | 0.866 | 8.662 | 84.766 |
| F7 | 0.698 | 6.975 | 91.741 |
| F8 | 0.597 | 5.969 | 97.710 |
| F9 | 0.198 | 1.977 | 99.687 |
| F10 | 0.031 | 0.313 | 100.000 |
表 6中只有第2、第3和第6主成分对应的P值小于0.05,其他主成分对应的P值都大于0.05,说明只有第2、第3和第6主成分是显著的。以第2、第3和第6主成分为自变量,以船舶领域为因变量做回归分析,得到如式(2) 所示的回归方程:
| 主成分 | 估计参数 | 标准误差 | t | 显著性 |
| 截距 | 2 415.085 | 27.615 | 87.454 | 0.000 |
| F1 | 31.899 | 27.622 | 1.155 | 0.248 |
| F2 | 213.648 | 27.622 | 7.735 | 0.000 |
| F3 | 74.654 | 27.622 | 2.703 | 0.007 |
| F4 | 40.766 | 27.622 | 1.476 | 0.140 |
| F5 | 6.571 | 27.622 | 0.238 | 0.812 |
| F6 | -314.419 | 27.622 | -11.383 | 0.000 |
| $ \mathop y\limits^ \gg = 213.648{F_2} + 74.654{F_3}-314.419{F_6} $ | (2) |
将主成分F2,F3与原始变量的关系式代入式(2),得到因变量与影响因素的关系:
| $ \begin{array}{l} \mathop y\limits^ \gg = \left( {107.393\;9, 187.590\;4, -69.848\;1, 160.802\;2, } \right.\\ \;\;\;\;\;\;-262.842\;4, 13.194\;2, 20.957\;9, 5.019\;3, \\ \left. {\;\;\;\;\;\;\;-19.128\;7, 50.265\;4} \right)\left( {{A_1}, } \right.{A_2}, {B_1}, {B_2}, \\ {\left. {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{B_3}, {C_1}, {C_2}, {C_3}, {C_4}, {D_1}} \right)^\prime } \end{array} $ | (3) |
式(3) 的回归系数中B3 (会遇角度) 的系数最大;其次A2 (船舶类型) 和B2 (密度) 的系数也很大,二者大小接近;A1 (船舶长度)、B1 (速度) 和D1 (驾驶员级别) 的系数也较大;C1 (风)、C2 (浪)、C3 (流) 和C4 (能见度) 的系数较小。
4 基于粗糙集的影响船舶领域的因素分析基于粗糙集理论的影响船舶领域的因素对船舶领域影响的重要度分析首先定义其对影响因素的依赖度,然后比较去掉某因素时,船舶领域对其他因素的依赖度与增加该因素时船舶领域对其他因素的依赖度的影响来判断某因素的重要性并进行属性约简。设影响因素集P,船舶领域Q,任一影响因素a,a的重要度及P的约简过程如下:
1) 计算ind(P-a) 与ind(Q)
2) 计算Q的P正域与Q的P-a正域
posP(Q)=posind(P)(ind(Q))
pos(P-{a})(Q)=posind(P-{a})(ind(Q))
3) 计算船舶领域依赖于影响因素的依赖度
γP(Q)=|posP(Q)|/|U|
γ(P-{a})(Q)=pos(P-a)(Q)|/|U|
4) 因素a重要度为
σPQ(a)=γP(Q)-γ(P-{a})(Q)
5) 因素约简若某影响因素子集P′的重要度σPQ(P′) 为0,则P-P′为P的Q约简。
数据的离散化划分如下:
1) 船舶长度:按照船舶长度等间隔划分,单位:m,1=[0,100),2=[100,200),3=[200,300),4=[300,400]。
2) 船舶类型:按照船舶类型的特殊性,1={其他船舶},2={港口作业船和特种船舶},3={货轮},4={油轮和化学品}。
3) 速度:按照船舶速度,以对地航速为5.5 kn等间隔划分,1=[0,5.5),2=[5.5,11),3=[11,16.5),4=[16.5,22]。
4) 密度:按照水域内不同区域密度的大小,密度相近的划分为一类,根据对数据的统计可将数据划分为:1={丹东、锦州、营口及天津与大连之间的密度较小水域},2={黄骅、东营、潍坊附近水域},3={大连、烟台、威海、龙口附近水域},4={天津港附近水域}。
5) 会遇角度:会遇角度以本船为对象,左右对称,船头方向为0°,船尾为180°。参考会遇局面划分,1=[0,5),2=[5,54),3=[54,112.5),4=[112.5,180]。
6) 风:按照风级数为1级等间隔划分,1=[4,5),2=[5,6),3=[6,7),4=[7,8]。
7) 浪:按照浪高为0.6 m等间隔划分,1=[1.2, 1.8),2=[1.8, 2.4),3=[2.4, 3.0),4=[3.0, 3.6]。
8) 流:按照平均流速为1 kn等间隔划分,1=[1,2),2=[2,3),3=[3,4),4=[4, 5]。
9) 能见度:按照能见度等级为2 km等间隔划分,1=[10, 12],2=[13,15],3=[16,18],4=[19,21]。
10) 驾驶员级别:按照驾驶员级别,1={三副},2={二副},3={大副}。
船舶领域大小的划分为:按照l的大小,m,等间隔划分。
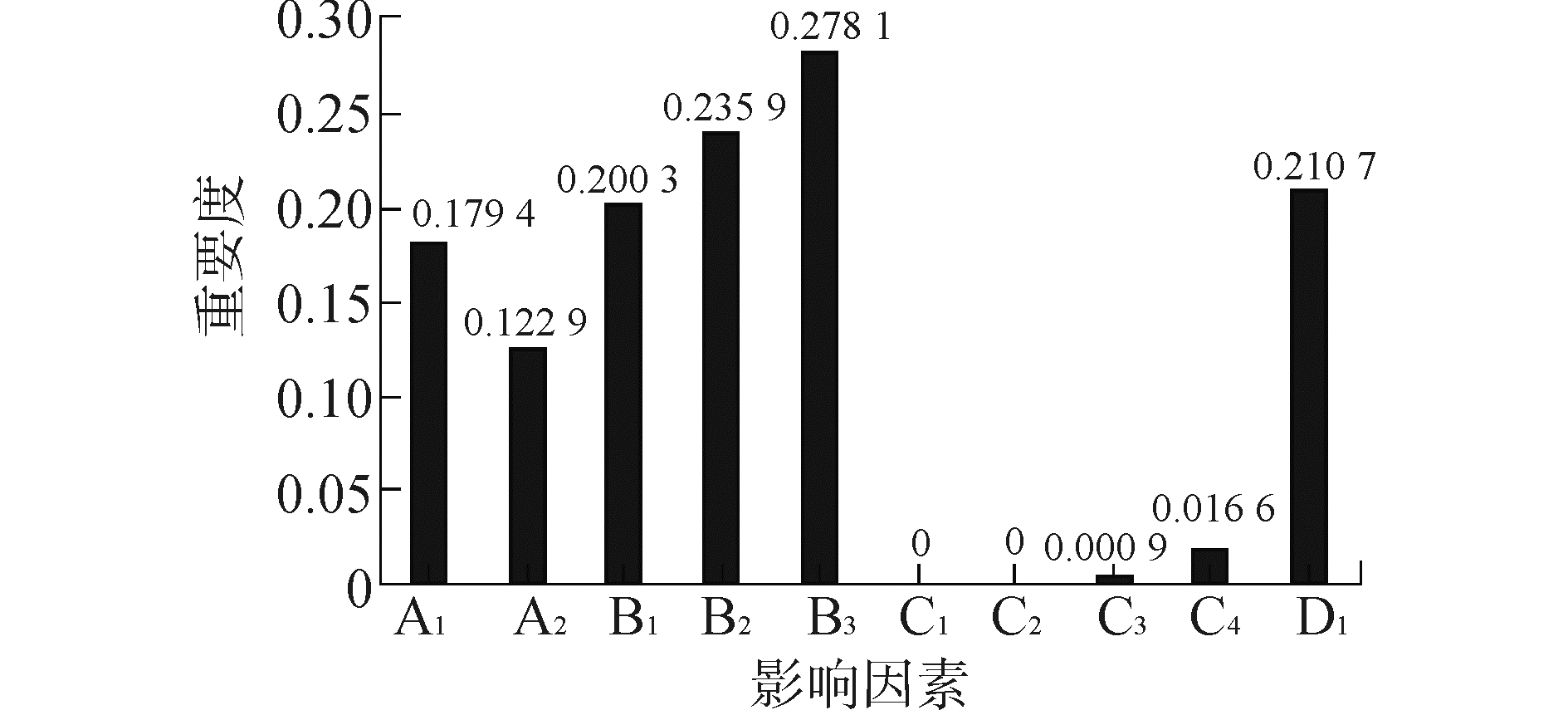
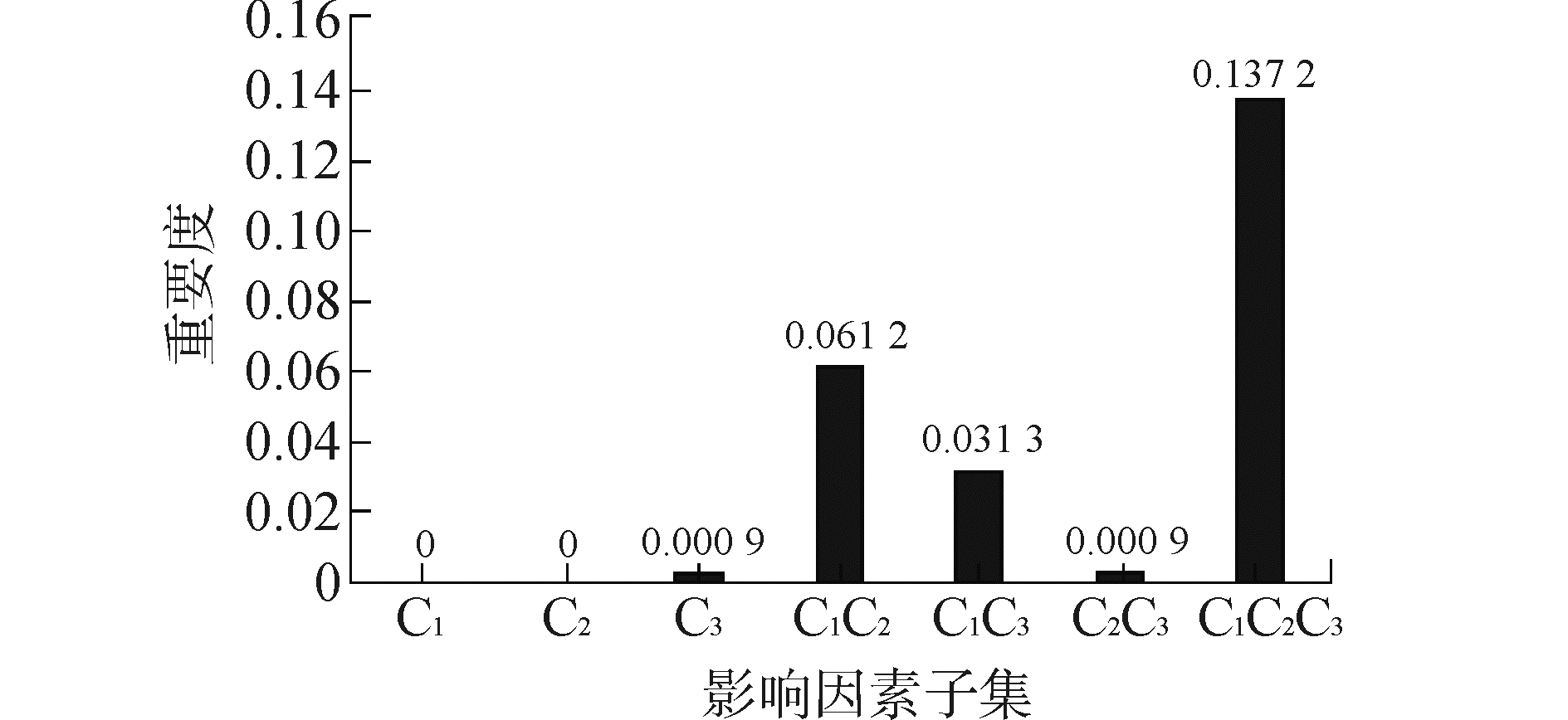
利用MATLAB编程计算,得到影响因素重要度结果如图 2。图中只有C1,C2,C3的属性重要度为0,根据属性重要度定义和属性约简定义可知,利用船舶领域影响因素重要度求相对约减,只需考虑重要度为0的因素,且不必要子集为重要度为0的最大子集。所以求影响船舶领域的因素的约减只需考虑C1,C2,C3。图 3为包含影响因素C1,C2,C3的可能不必要子集重要度计算结果, 其中属性重要度为0或近似为0且最大的子集分别为{C1}、{C2、C3}所以设影响船舶领域的因素约简集为R和S:
|
| 图2 影响船舶领域的因素重要度 Figure 2 The importance of the factors of ship domain |
|
| 图3 影响因素子集重要度 Figure 3 The importance of the factors subset |
R={会遇局面、船舶大小、速度、风、驾驶员级别、密度、船舶类型、能见度}
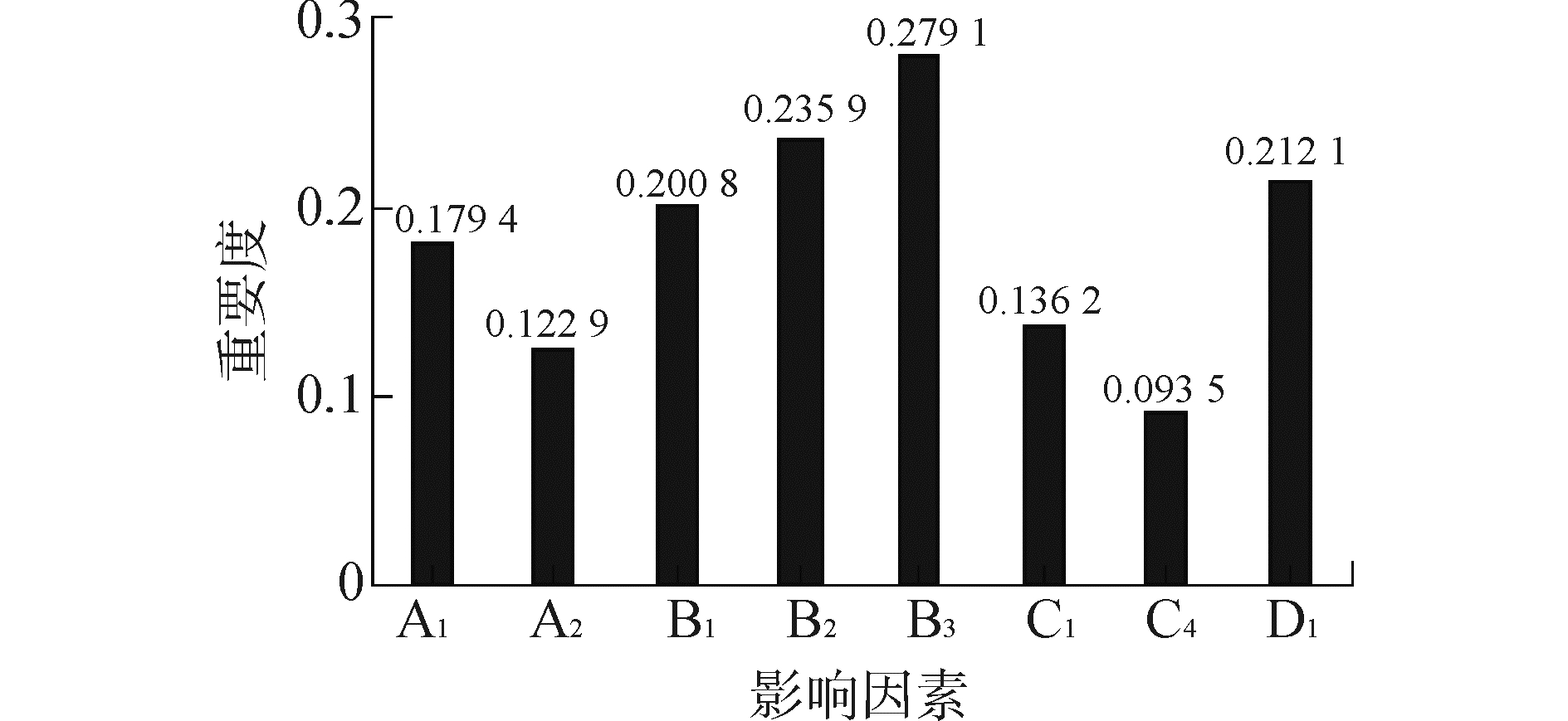
S={会遇局面、船舶大小、速度、浪、流、驾驶员级别、密度、船舶类型、能见度}约简集R、S的重要度如图 4、图 5。
|
| 图4 约简集R的影响因素重要度 Figure 4 The importance of the factors of reduction set R |
|
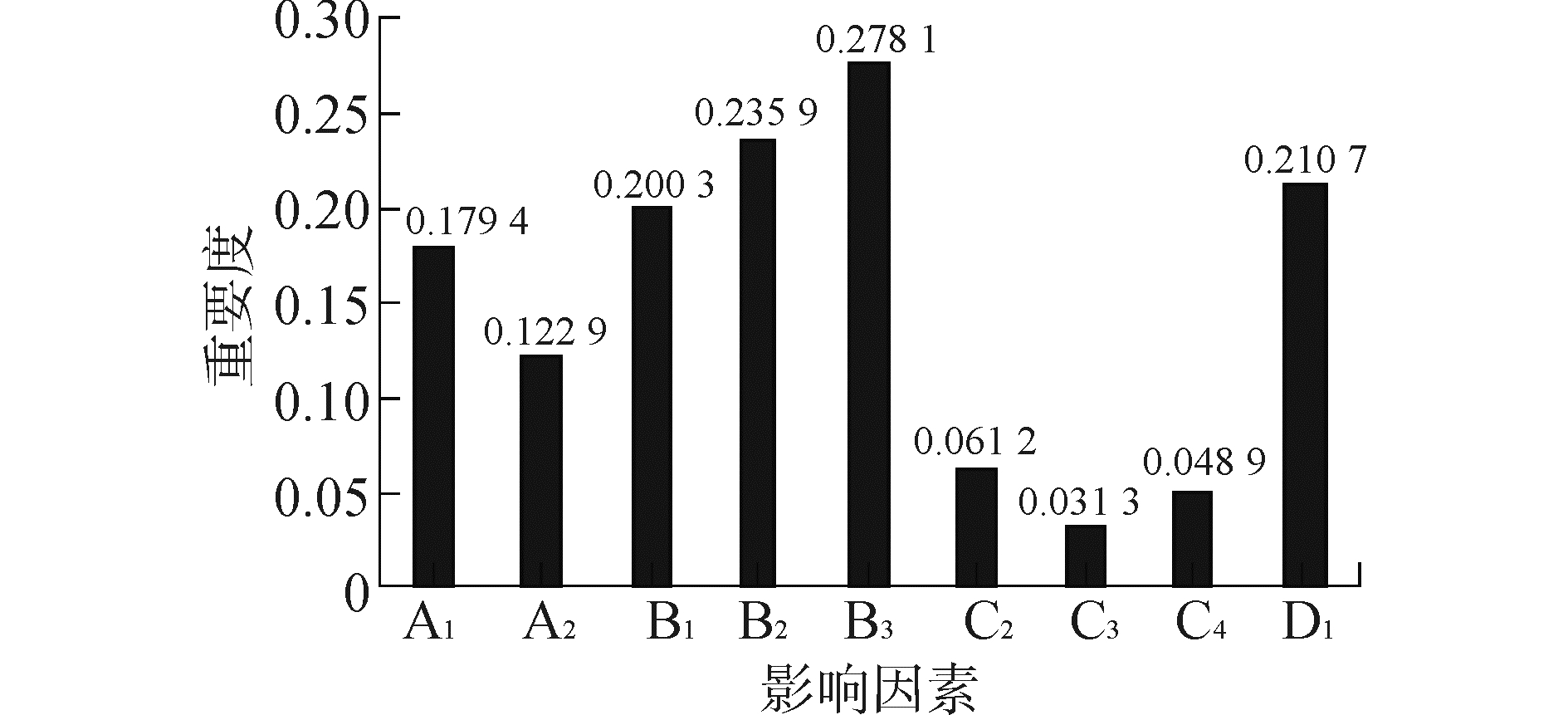
| 图5 约简集S的影响因素重要度 Figure 5 The importance of the factors of reduction set S |
图 2、4、5中同一影响因素重要度的差距很小,说明了约简掉的影响因素对其他影响因素的重要度影响很小,与属性约简的定义吻合。
根据粗糙集的计算结果,重要度最大的为B3(会遇角度),其次是B2(密度)、D1(驾驶员级别) 和B1(速度),A1(船舶长度) 和A2(船舶类型) 的重要度也较大,C4(能见度)、C1(风)、C2(浪) 和C3(流) 的重要度较小。
5 两种方法结果的比较基于粗糙集的影响因素重要度计算结果与主成分回归分析结果如表 7。
| 因素 | 重要度及排序(粗糙集) | 重要度及排序(主成分回归) |
| A1 | 0.149 ⑤ | 107.393 9 ④ |
| A2 | 0.104 ⑥ | 187.590 4 ② |
| B1 | 0.185 ④ | -69.848 1 ⑤ |
| B2 | 0.157 ② | 160.802 2 ③ |
| B3 | 0.239 ① | -262.842 4 ① |
| C1 | 0 ⑩ | 13.194 2 ⑨ |
| C2 | 0 ⑩ | 20.957 9 ⑦ |
| C3 | 0.001 ⑧ | 5.019 3 ⑩ |
| C4 | 0.015 ⑦ | -19.128 7 ⑧ |
| D1 | 0.165 ③ | 50.265 4 ⑥ |
两种方法比较得到的结论相同,影响船舶领域的因素中都较大的为B3(会遇角度)、B2(密度)、D1(驾驶员级别)、B1(速度)、A1(船舶长度) 和A2(船舶类型),较小的为C1(风)、C2(浪)、C3(流) 和C4(能见度)。且利用基于粗糙集的算法得到的结果中,风或浪、流被约简掉,基于主成分回归分析的算法中风或浪、流的重要度也非常小,两算法得到的结果也具有一致性。
6 结束语利用主成分分析理论对能见度良好时影响船舶领域的因素进行筛选的结果与利用粗糙集算法得到的结果大致相同,证明了两种算法分析的有效性,保证了结论的正确性。对影响船舶领域的因素进行筛选对降低研究船舶领域的复杂性具有重要意义,为研究船舶领域提供新的思路,利于对船舶领域的研究并简化其在实际中的应用。
| [1] | GOODWIN E M. A statistical study of ship domains[J]. The journal of navigation, 1975, 28(3): 328–344. DOI:10.1017/S0373463300041230 |
| [2] | PIETRZYKOWSKI Z, URIASZ J. The ship domain-a criterion of navigational safety assessment in an open sea area[J]. The journal of navigation, 2009, 62(1): 93–108. DOI:10.1017/S0373463308005018 |
| [3] | HSU H Z. Safety domain measurement for vessels in an overtaking situation[J]. International journal of e-navigation and maritime economy, 2014, 1: 29–38. DOI:10.1016/j.enavi.2014.12.004 |
| [4] | PIETRZYKOWSKI Z. Ship's fuzzy domain-a criterion for navigational safety in narrow fairways[J]. The journal of navigation, 2008, 61(3): 499–514. |
| [5] | HANSEN M G, JENSEN T K. Empirical ship domain based on AIS data[J]. The journal of navigation, 2013, 66(6): 931–940. DOI:10.1017/S0373463313000489 |
| [6] |
范贤华, 张庆年, 周锋, 等. 水流条件下内河船舶领域模型[J].
大连海事大学学报, 2013, 39(1): 46–48.
FAN Xianhua, ZHANG Qingnian, ZHOU Feng, et al. Model of ship domain in river water[J]. Journal of Dalian Maritime University, 2013, 39(1): 46–48. |
| [7] | WANG Yueying, CHIN H C. An empirically-calibrated ship domain as a safety criterion for navigation in confined waters[J]. The journal of navigation, 2016, 69(2): 257–276. DOI:10.1017/S0373463315000533 |
| [8] | WANG Ning. An intelligent spatial collision risk based on the quaternion ship domain[J]. The journal of navigation, 2010, 63(4): 733–749. DOI:10.1017/S0373463310000202 |
| [9] | WANG Ning, MENG Xianyao, XU Qingyang, et al. A unified analytical framework for ship domains[J]. The journal of navigation, 2009, 62(4): 643–655. DOI:10.1017/S0373463309990178 |
| [10] | WANG Ning. A novel analytical framework for dynamic quaternion ship domains[J]. The journal of navigation, 2013, 66(2): 265–281. DOI:10.1017/S0373463312000483 |
| [11] | WANG Ning, TAN Yue, LIU Shaoman. Ship domain identification using fast and accurate online self-organizing parsimonious fuzzy neural networks[C]//Proceedings of the 30th Chinese Control Conference. Yantai, China:IEEE, 2011:5271-5276. |
| [12] | ZHU Xiaolin, XU Hanzhen, LIN Junqing. Domain and its model based on neural networks[J]. The journal of navigation, 2001, 54(1): 97–103. DOI:10.1017/S0373463300001247 |



