与以TanDEM-X系统[1]为代表的分布式SAR卫星系统干涉基线周期性变化相比,Moccia[2]提出的绳系卫星SAR系统所提供的干涉基线在整个轨道周期内相对稳定,采用单基线即可实现对所有星下点纬度的覆盖。同时由于采用绳系形式,其在轨展开时间也由前者以天为量级大幅缩短到以小时为量级,大大提高了系统的在轨部署能力,为绳系卫星SAR系统的应急应用提供了可能。
在系绳SAR任务中,系统快速且稳定的成功展开是完成任务的前提。尽管针对空间绳系SAR具体任务的研究相对较少,但已有诸多学者针对普适性绳系卫星系统,尤其是是其展开控制律[3-6]开展了大量研究。Fujii等[7]使用共轭梯度法规划出绳系卫星系统展开和回收的最优轨迹,并基于Lyapunov函数提出一种反馈控制律来跟踪最优路径。Jin等[8]使用拟线性化和截断Chebyshev级数来规划3自由度绳系卫星展开最优路径。文浩等[9]基于二阶微分包含将绳系卫星系统非线性时间最优控制问题离散为大规模动态规划问题。Williams等[10-11]对比了在不同性能指标下绳系卫星系统展开最优路径。然而由于绳系系统建模时存在不确定性,以及初始状态偏差和外界扰动均会影响控制效率,因此需要对系统展开进行闭环控制。Williams等[12]将系统在最优轨迹附近线性化,并使用滚动时域法求解线性反馈增益,以使系统能够克服初始偏差和外界扰动跟踪最优轨迹,然而该方法计算量较大[13]。
本文针对主星与子星质量近似接近的绳系卫星系统,使用了系统三维动力学模型,然后将系统在Legendre-Gauss-Lobatto配点处离散,结合系统任务设计优化性能指标和约束,将系绳式InSAR系统的快速展开问题转换为非线性规划问题。在此基础上提出一种系绳张力自适应滑模控制器用来抵消模型误差及外扰扰动,并使用Lyapunov理论证明其稳定性。
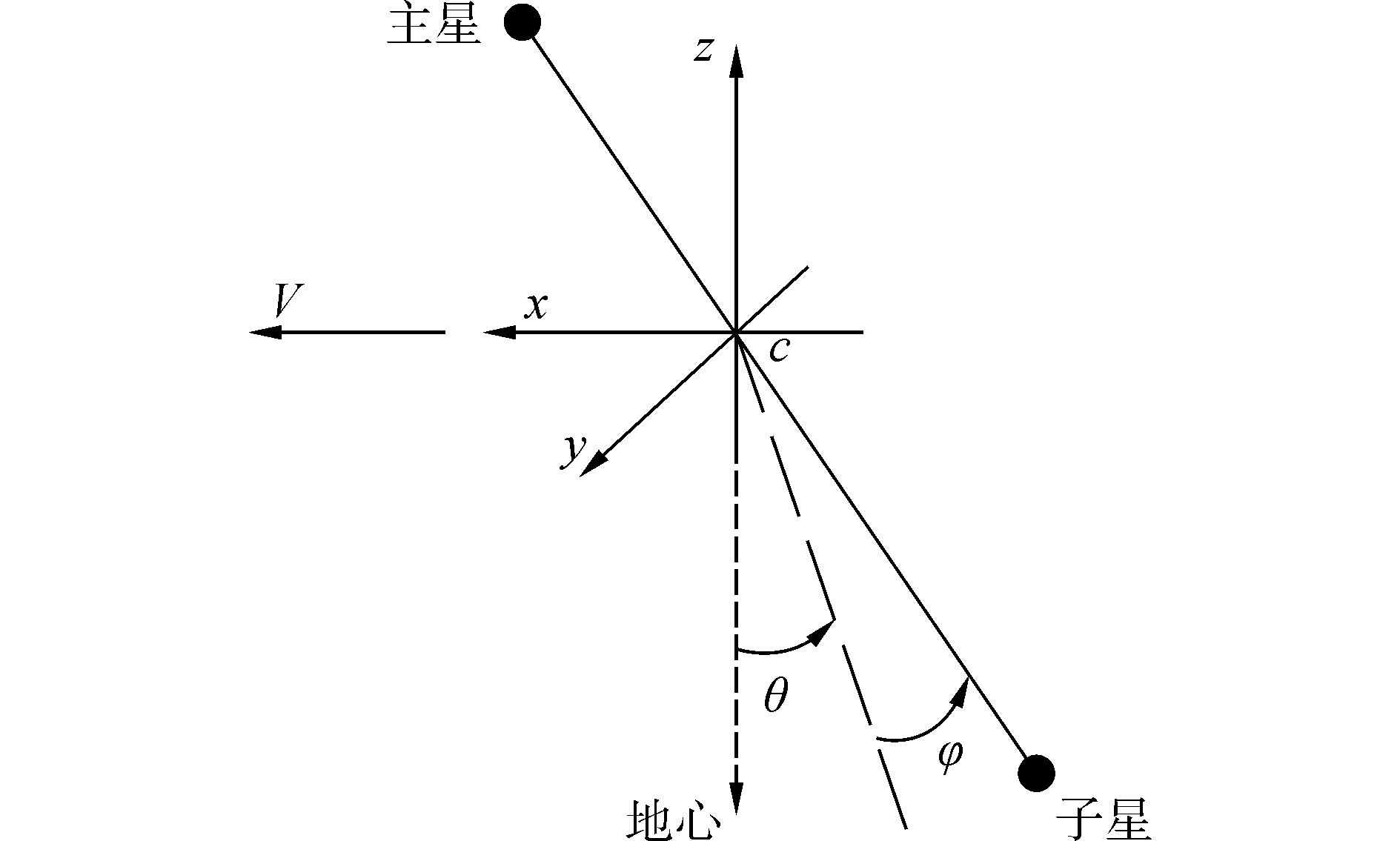
1 系绳式InSAR动力学模型通过系绳连接的绳系卫星系统 (见图 1) 在圆轨道或小偏心率椭圆轨道运行时会在重力梯度力矩作用下稳定在铅垂方向或其附近[14],利用该特性可以将绳系卫星系统作为InSAR系统的搭载平台来执行对地观测任务。系统的姿态可以用系绳长度和系绳相对于系统质心轨道坐标系的方位来描述。
|
| 图1 绳系卫星系统图 Figure 1 The tethered satellite system |
由于系绳质量远小于卫星质量,系统质心可近似认为在卫星质心连线上。另外本文中主星和子星面积比相差不大,故作用在系统上的大气阻力力矩较小,可作为扰动处理。同时为了简化系统动力学模型,在建模过程中做出如下假设:将卫星视为质点,认为卫星姿态可控,即不会因为卫星姿态失稳滚转而导致展开失败;系统质心轨道为Keplerian轨道;忽略系绳的扭转和弯曲,则在系统质心轨道坐标系中,其动力学方程可以通过Newton-Eular法推导表示为[12]:
| $\begin{align} & \theta \prime\prime =2\left( \theta \prime +1 \right)[\frac{\text{esin}v}{k}-\frac{{{m}_{m}}\left( {{m}_{p}}+{{m}_{t}}/2 \right)}{m{{m}^{*}}}\frac{\Lambda }{{}}+ \\ & \varphi \prime \text{tan}\varphi ]-\frac{3}{k}\text{sin}\theta \text{cos}\theta +\frac{{{Q}_{\theta }}}{{{m}^{*}}{{\Lambda }^{2}}{{L}^{2}}{{{\dot{v}}}^{2}}\text{co}{{\text{s}}^{2}}\varphi } \\ \end{align}$ | (1) |
| $\begin{align} & \varphi \prime\prime =\frac{\text{esin}v}{k}\varphi \prime -2\frac{{{m}_{m}}\left( {{m}_{p}}+{{m}_{t}}/2 \right)}{m{{m}^{*}}}\frac{\Lambda }{{}}\varphi \prime - \\ & [\left( \theta \prime +1 \right)2+\frac{3}{k}\text{co}{{\text{s}}^{2}}\theta ]\text{sin}\varphi \text{cos}\varphi +\frac{{{Q}_{\varphi }}}{{{m}^{*}}{{\Lambda }^{2}}{{L}^{2}}{{{\dot{v}}}^{2}}} \\ \end{align}$ | (2) |
| $\begin{align} & \mathit{\Lambda }\prime\prime =\frac{\text{esin}v}{k}\mathit{\Lambda }\prime -\frac{\left( 2{{m}_{m}}-m \right){{m}_{t}}/2}{{{m}_{m}}\left( {{m}_{p}}+{{m}_{t}} \right)}\frac{\mathit{\Lambda }{{\prime }^{2}}}{\mathit{\Lambda }}+ \\ & \frac{{{m}_{p}}+{{m}_{t}}/2}{{{m}_{p}}+{{m}_{t}}}\Lambda [\varphi {{\prime }^{2}}+\left( \theta \prime +1 \right)2\text{co}{{\text{s}}^{2}}\varphi + \\ & \frac{1}{k}(3\text{co}{{\text{s}}^{2}}\theta \text{co}{{\text{s}}^{2}}\varphi -1)]-\frac{T}{{{m}_{m}}{{{\dot{v}}}^{2}}L({{m}_{p}}+{{m}_{t}})/m} \\ \end{align}$ | (3) |
式中:θ、φ分别为系统的面内摆角和面外摆角;Λ=l/L为无量纲系绳长度;L为选定的系绳目标长度;mm=mm0-mt是主星质量,mm0为初始主星质量,mt=ρΛL已展开系绳质量;ρ是系绳线密度;mp为子星质量,m=mm+mt+mp系统总质量,m*=(mm+mt/2)(mp+mt/2)-mt/6;T为系绳张力;e为轨道偏心率,ν为轨道真近角,k=1+ecos ν;()′=d ()/dv。
| $\dot{\nu }=\left( 1+e\text{cos}{{\nu }^{2}} \right)\sqrt{\frac{\mu }{{{a}^{3}}{{\left( 1-{{e}^{2}} \right)}^{3}}}}$ | (4) |
式中:μ为地球引力常数,a为系统质心轨道半长轴。
2 绳系卫星系统展开最优轨迹规划近年来,由于高效的计算效率和对初值的不敏感,伪谱法逐渐成为最优控制问题求解方法的研究热点[15-18]。而Gauss伪谱法又在近似精度,估计精度及收敛速度上存在优势,因此选择Gauss伪谱法来规划系统展开的最优路径。
1.1 基于Gauss伪谱法的模型离散高斯伪谱法将系统的状态变量和控制变量均进行离散,并通过正交插值多项式对其进行近似。然后通过在配点处将系统状态变量导数与动力学方程进行比较,从而将动力学方程转化为约束。将时间区间[t0, tf]转换到[-1, 1],然后将系统状态变量和控制变量离散并通过Lagrange插值多项式近似,插值点为
| ${{\tau }_{0}},\ldots ,{{\tau }_{N-1}},{{\tau }_{i}}\in \left[ -1,1 \right],(i=0,\ldots ,N-1)$ |
其中LG点不包括初始点和终止点。
系统动力学微分方程写为
| $\mathit{\boldsymbol{\dot{x}}}=f\left( \mathit{\boldsymbol{x}} \right)$ | (5) |
式中:x=[θ φ Λ θ′ φ′ Λ′]T,为系统状态变量;f(x) 由动力学方程 (1)~(3) 可以得到。
使用高斯伪谱法可以将其在LG点处转换为动力学约束:
| $\begin{align} & \frac{{{t}_{f}}-{{t}_{0}}}{2}f\left( X\left( {{\tau }_{k}} \right),U\left( {{\tau }_{k}} \right),{{\tau }_{k}};{{t}_{0}},{{t}_{f}} \right)= \\ & \sum\limits_{i=0}^{N-2}{{{D}_{ki}}X\left( {{\tau }_{i}} \right),}\left( k=1,\ldots ,N-2 \right) \\ \end{align}$ | (6) |
式中:X(τ),U(τ) 为通过Lagrange插值得到的近似值,具体过程可以参考文献[16]。
1.2 面向任务的性能指标与约束以获取地面DEM数据为目标,工作时的系统基线在cxy平面内,结合绳系卫星系统的稳态构型是沿当地铅锤方向分布的,因此希望系统能够展开并稳定在铅锤方向附近。故系统展开终值应满足:
| ${{\mathit{\boldsymbol{x}}}_{tf}}=\left[ \begin{array}{*{35}{l}} 0 & 0 & 1 & 0 & 0 & 0 \\ \end{array} \right]$ | (7) |
以系绳式InSAR系统快速展开到终端位置为目标,同时使系统控制变量变化平滑,以避免展开过程中产生震荡。根据上述目标选择优化性能指标:
| $J={{t}_{f}}+\int \mathit{\Lambda }\prime\prime \text{d}t$ | (8) |
另外系统以系绳张力作为控制变量,因系绳只能产生拉力,故控制变量应始终大于零,又其存在最大值限制。因此控制变量应满足以下约束:
| ${{T}_{\text{min}}}\le T\le {{T}_{\text{max}}}$ | (9) |
最终,结合任务需求系绳式InSAR系统展开最优的性能指标和约束如下:
| $\left\{ \begin{array}{*{35}{l}} \rm{min }J={{t}_{f}}+\int \mathit{\Lambda }\prime\prime \rm{d}t \\ \rm{s}\rm{.t}.{{\mathit{\boldsymbol{x}}}_{tf}}=\left[ \begin{array}{*{35}{l}} 0 & 0 & 1 & 0 & 0 & 0 \\ \end{array} \right] \\ {{T}_{\rm{min}}}\le T\le {{T}_{\rm{max}}} \\ \end{array} \right.$ | (10) |
本节使用Gauss伪谱法将系统动力学方程离散为约束方程 (6),再选择合适的性能指标和终端及路径约束 (10),即将系统展开最优轨迹规划为题转化为非线性规划问题。而对于非线性规划问题已有多种成熟的优化算法工具包,本文使用序列二次规划法程序包SNOPT来获取系统展开的最优轨迹。
3 系绳张力自适应滑模控制器不考虑模型误差和外界扰动时,系统展开的偏差主要为插值近似偏差。然而在实际运行过程中,微小外界扰动和初始偏差总是不可避免的,采用开环控制将使系统展过程偏离最优轨迹,导致展开结束后系统存在较大的稳态误差,情况严重时甚至导致展开失败。因此,设计一种反馈控制器补偿系统误差和外界扰动对于系统展开是必要的。
大量关于绳系卫星系统的研究表明其面内运动与面外运动耦合较弱,通过改变系绳拉力无法有效控制系统的面外摆动[19]。在不考虑外界扰动时,如若系统初始面外摆角和面外摆动角速度为零时,则系统将会一直在轨道平面内运动。在规划系统展开最优路径时,设定初始面外摆角和面外摆动角速度均为零,那么得到的系统展开最优轨迹也将一直保持在轨道平面内,因此在设计系统展开反馈控制器时为了方便,仅考虑系统的面内运动,此时φ = φ′ =0。另外本文中系绳质量远小于卫星质量,在设计系统展开反馈控制器时可以忽略系绳质量,此时系统的动力学方程方程(1)~(3)可以简化为
| $\theta \prime\prime =2\left( \theta \prime +1 \right)\left[ e\text{sin}v/k-\mathit{\Lambda }\prime /\mathit{\Lambda } \right]-3\text{sin}\theta \text{cos}\theta /k$ | (11) |
| $\begin{align} & \mathit{\Lambda }\prime\prime =2e\text{sin}v\mathit{\Lambda }\prime /k+ \\ & \mathit{\Lambda }\left[ {{\left( \theta +1 \right)}^{2}} \right]+\left( 3\text{co}{{\text{s}}^{2}}\theta -1/k \right)-u \\ \end{align}$ | (12) |
式中:
从系统面内运动动力学方程可以发现系统的面内运动受Λ′/Λ控制,若系统能够跟踪展开绳长及其展开速度,则存在较小面内初始摆角偏差时,系统能够展开到目标位置附近。因此希望设计一种系绳张力控制器使系统能够跟踪其最优展开速度。
系统展开执行机构输出与控制指令之间存在误差,而且为了方便推导,对系统动力学方程 (1)~(3) 进行了简化,为了获取更加准确的结果,此处将上述简化和误差以系统模型误差的方式添加到系统动力学方程 (12) 中:
| $\begin{align} & \mathit{\Lambda }\prime\prime =\mathit{\Lambda }\left[ {{\left( \theta +1 \right)}^{2}}\left( 3\text{co}{{\text{s}}^{2}}\theta -1 \right)/k \right]+ \\ & 2e\text{sin}v\mathit{\Lambda }\prime /k-u+\Delta M+d \\ \end{align}$ | (13) |
式中:ΔM为系统建模时由于简化处理造成的误差,d为外界扰动。
实际上系统模型误差和外界扰动均有界,因此可以假设:
| $\Delta M+d\le b$ | (14) |
式中b为一未知非负常数。
系统绳长和展开速度的最优轨迹分别为Λd和Λ′d,则系绳展开长度和速度相对其参考轨迹的误差分别为
| ${{\mathit{\Lambda }}_{e}}=\mathit{\Lambda }-{{\mathit{\Lambda }}_{d}}\mathsf{ \Lambda }{{\prime }_{e}}=\mathit{\Lambda }\prime -\mathit{\Lambda }{{\prime }_{d}}$ | (15) |
定义滑模面:
| $s=\mathit{\Lambda }{{\prime }_{e}}+c{{\mathit{\Lambda }}_{e}}$ | (16) |
式中c为正值常数。其相对真近角的一阶微分可以表示为
| $\begin{align} & s\prime =\mathit{\Lambda }{{\prime\prime }_{e}}+c\mathit{\Lambda }{{\prime }_{e}}=2e\text{sin}v\mathit{\Lambda }\prime /k+\mathit{\Lambda }[{{\left( \theta \prime +1 \right)}^{2}}+ \\ & (3\text{co}{{\text{s}}^{2}}\theta -1)/k]-u+\Delta M+d+c\mathit{\Lambda }\prime -\mathit{\Lambda }{{\prime }_{d}}-\mathit{\Lambda }{{\prime\prime }_{d}} \\ \end{align}$ | (17) |
定理1:系统在系绳张力展开控制律:
| $\begin{align} & u=2e\text{sin}v/k+\mathit{\Lambda }\prime [{{\left( \theta +1 \right)}^{2}}\left( 3\text{co}{{\text{s}}^{2}}\theta -1 \right)/k]- \\ & \mathit{\Lambda }{{\prime\prime }_{d}}+c\left( \mathit{\Lambda }\prime -\mathit{\Lambda }{{\prime }_{d}} \right)+\hat{b}\text{sgn}\left( s \right)+\lambda s{{{\hat{b}}}^{\prime }}=\sigma \left| s \right| \\ \end{align}$ | (18) |
式中:λ、σ>0,控制下能够跟踪展开速度的最优轨迹。
证明:
设计Lyapunov函数:
| $V={{s}^{2}}/2+{{\left( b-\hat{b} \right)}^{2}}/(2\sigma )$ | (19) |
则其相对真近角的一阶微分为
| ${{V}^{\prime }}=s{{s}^{\prime }}+\left( b-\hat{b} \right)\left( -{{{\hat{b}}}^{\prime }} \right)/\sigma $ | (20) |
将式 (17) 代入式 (20) 得:
| $\begin{align} & {{V}^{\prime }}=s\left\{ 2e\text{sin}v\mathit{\Lambda }\prime /k-u+\Delta M+d \right.+ \\ & c\left( \mathit{\Lambda }\prime -\mathit{\Lambda }{{\prime }_{d}} \right)-\mathit{\Lambda }{{\prime\prime }_{d}}+\mathit{\Lambda }\left[ {{\left( {{\theta }^{\prime }}+1 \right)}^{2}} \right.+ \\ & \left. \left. \left( 3\text{co}{{\text{s}}^{2}}\theta -1 \right)/k \right] \right\}+\left( b-\hat{b} \right)\left( -{{{\hat{b}}}^{\prime }} \right)/\sigma \\ \end{align}$ | (21) |
将式 (18) 代入可得:
| $\begin{align} & {{V}^{\prime }}=s\left\{ \Delta M+d-\hat{b}\text{sgn}\left( s \right)-\lambda s \right\}-\left( b-\hat{b} \right)\left| s \right|= \\ & -\lambda {{s}^{2}}\left( \Delta M+d \right)s-\hat{b}\left| s \right|-\left( b-\hat{b} \right)\left| s \right| \\ & -\lambda {{s}^{2}}+bs-\hat{b}\left| s \right|-\left( b-\hat{b} \right)\left| s \right|\le -\lambda {{s}^{2}} \\ \end{align}$ | (22) |
因此
控制器 (18) 中由于sgn (s) 的存在不连续,滑模控制会产生抖动。为了减缓该现象,将控制律修改为
| $\begin{align} & u=2e\text{sin}v\mathit{\Lambda }\prime /k-\mathit{\Lambda }{{\prime\prime }_{d}}+c\left( \mathit{\Lambda }\prime -\mathit{\Lambda }{{\prime }_{d}} \right)+\hat{b}\text{sgn}\left( s \right)+ \\ & \lambda s+\mathit{\Lambda }\left[ {{\left( \theta +1 \right)}^{2}}\left( 3\text{co}{{\text{s}}^{2}}\theta -1 \right)/k \right] \\ \end{align}$ | (23) |
其中sat (s) 定义为
| $\text{sat}\left( s \right)=\left\{ \begin{array}{*{35}{l}} \text{sgn}\left( s \right) & \left| s \right|\ge \xi \\ s/\xi & \left| s \right|<\xi \\ \end{array} \right.$ | (24) |
式中ζ为滑模层厚度。
值得注意的是虽然控制器 (22) 中将切换函数sgn (s) 替换为饱和函数sat (s) 能够减弱抖动现象,但是无法消除抖动。控制器边界层±ζ厚度越小,系统稳态误差越小,但抖动增强,反之系统稳态误差变大,抖动减弱。
在控制器 (22) 作用下的闭环系统能够跟踪系统展开最优路径,其稳定性证明与控制器 (18) 类似,此处不再累述。相比于以前绳系系统展开控制中所用的反馈控制,控制器 (22) 能够克服系统建模中的未知有界误差和外界扰动,且相比于文献[12]中的控制方法,减少了控制过程中的计算量,以便于实现实时跟踪控制。
4 数值仿真分析根据任务需求选定系统参数:主星质量300 kg,子星质量200 kg,轨道半长轴6 645 km,轨道偏心率0.002 7,系绳长度1 km,系绳线密度0.000 185 kg/m,系绳弹性模量EA为6 000 N。假设初始时刻系统沿铅锤方向分离,展开机构开始工作时系绳长度为10 m,展开速度为2 m/s。则无量纲化后系统的初始状态为
| ${{\mathit{\boldsymbol{x}}}_{0}}=\left[ \begin{array}{*{35}{l}} 0 & 0 & 0.01 & 0 & 0 & 2/\left( L\dot{\nu } \right) \\ \end{array} \right]$ | (25) |
假设系统展开执行机构满足下面要求:
| $0\le T\le 5N$ |
由于闭环控制的目标是跟踪系统展开速度最优轨迹,为了给控制留有裕度,避免系绳回收,设定展开时最小速度为0.05 m/s。则系统的展开终端状态变为
| ${{\mathit{\boldsymbol{x}}}_{tf}}=\left[ \begin{array}{*{35}{l}} 0 & 0 & 1 & 0 & 0 & 0.05/\left( L\dot{\nu } \right) \\ \end{array} \right]$ |
影响系统展开的误差主要是系统初始状态偏差和外界摄动影响。其中外界摄动影响在低轨以大气阻力为主,结合文献[14]对系统受到的大气阻力进行估计,在250 km轨道高度处1 km长的系绳的大气阻力约为2 mN。假定系统使用推力器进行分离,推力器方向偏差最大为5%,且不考虑其对卫星姿态的影响,则系统的初始面内摆角最大约为3°。
为了验证所设计的控制器效果,分别对系统在开环控制和自适应滑模控制器作用下的展开过程进行仿真。系统所受外界摄动设为fd=2 m·N,模型误差设为ΔM=0.01sinν 1/rad2,其中对外界摄动力做无量纲化处理:
| $d={{f}_{d}}/\left[ {{m}_{m}}{{{\dot{v}}}^{2}}L\left( {{m}_{p}}+{{m}_{t}} \right)/m \right]$ |
闭环控制仿真参数选择为
| $\lambda =1,\sigma =0.01,c=1$ |
由于通过高斯伪谱法得到最优轨迹是离散的,仅离散点处能够得到确切的计算结果,但是实际使用时需要知道每一时刻的系统展开最优值,另外控制器 (18) 和 (22) 中还需要连续的Λ″d。在数值仿真验证中通过相邻离散点Λ′d的差分近似两离散点中间时刻的Λ″d,然后使用多项式拟合近似模拟所需参数的连续值。
仿真时系统的初始面内摆角偏差变化范围为±3°,每次变化0.5°。为了节省空间,仅以最大面内偏差Δ θ0=3°为例画图,其他情况则见表 2和表 3。
| 初始误差/(°) | 展开终值 | 稳态误差 | |||
| 真近角/
rad | 长度比 | 面内角/
(°) | 面内角/
(°) | 径向误差/m | |
| 3 | 2.845 0 | 1 | -0.233 2 | 1.91 | -12.5 |
| 2.5 | 2.887 0 | 1 | -0.008 3 | 1.05 | -7.7 |
| 2 | 2.905 4 | 1 | -0.001 7 | 0.67 | -7 |
| 1.5 | 2.959 0 | 1 | 0.109 8 | 0.12 | -2.5 |
| 1 | 3.004 7 | 0.995 3 | 0.156 3 | 0.44 | -6.1 |
| 0.5 | 3.004 7 | 0.986 2 | 0.209 6 | 0.55 | -14.4 |
| 0 | 3.004 7 | 0.979 5 | 0.260 6 | 0.74 | -21.9 |
| -0.5 | 3.004 7 | 0.968 5 | 0.367 1 | 1.10 | -34.4 |
| -1 | 3.004 7 | 0.957 9 | 0.478 6 | 1.03 | -47.4 |
| -1.5 | 3.004 7 | 0.947 7 | 0.596 8 | 1.35 | -56.8 |
| -2 | 3.004 7 | 0.936 8 | 0.718 4 | 1.68 | -65.6 |
| -2.5 | 3.004 7 | 0.925 7 | 0.813 5 | 1.91 | -76.6 |
| -3 | 3.004 7 | 0.913 2 | 0.982 5 | 2.04 | -86.8 |
| 初始误差/(°) | 展开终值 | 稳态误差 | |||
| 真近角/
rad | 长度比 | 面内角/
(°) | 面内角/
(°) | 径向误差/m | |
| 3 | 3.005 8 | 1 | -0.5676 | 1.04 | 0.4 |
| 2.5 | 3.005 5 | 1 | -0.432 2 | 0.84 | 0.5 |
| 2 | 3.005 7 | 1 | -0.322 5 | 0.68 | 0.8 |
| 1.5 | 3.005 0 | 1 | -0.197 9 | 0.51 | 0.4 |
| 1 | 3.005 4 | 1 | -0.075 5 | 0.35 | 0.4 |
| 0.5 | 3.005 5 | 1 | 0.048 2 | 0.20 | 0.4 |
| 0 | 3.006 5 | 1 | 0.170 4 | 0.21 | 0.4 |
| -0.5 | 3.005 8 | 1 | 0.289 5 | 0.32 | 0.4 |
| -1 | 3.005 1 | 1 | 0.406 1 | 0.46 | 0.5 |
| -1.5 | 3.006 0 | 1 | 0.524 2 | 0.59 | 0.4 |
| -2 | 3.005 1 | 1 | 0.636 7 | 0.72 | 0.4 |
| -2.5 | 3.005 2 | 1 | 0.751 9 | 0.85 | 0.4 |
| -3 | 3.004 9 | 1 | 0.863 9 | 0.98 | 0.4 |
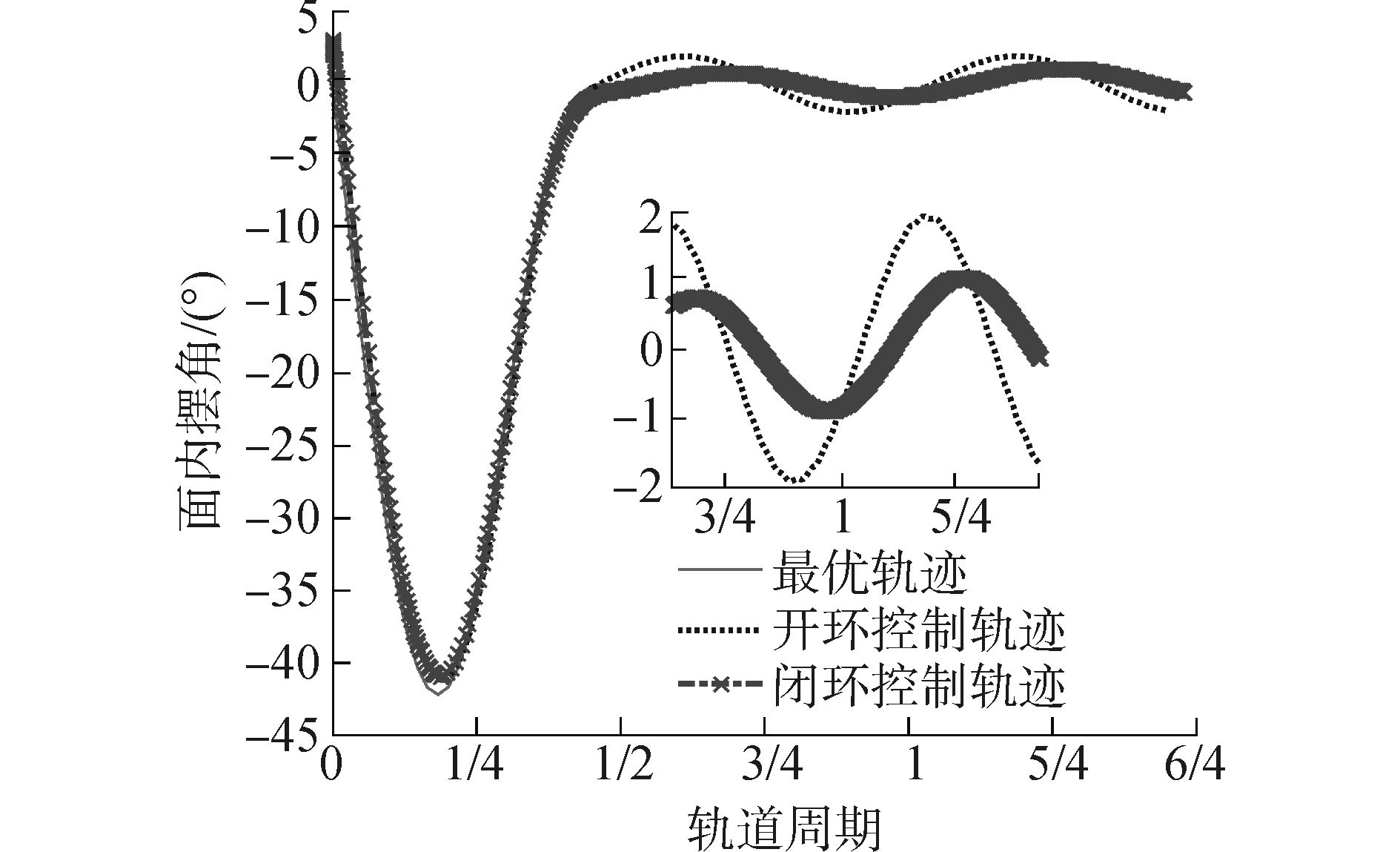
由仿真图 2~5可知,当系统面内摆角初始偏差为3度时,系统在开环控制下和闭环控制均能展开到目标长度,且系统面外运动不受面内运动影响。由图 2知在两种控制下系统的面内摆角均在最优轨迹附近,但是开环控制的稳态误差约为闭环控制的2倍。系统的面内角速度亦如此。由于假设系统的面外摆角不存在初始偏差,系统的面内摆角偏差不影响面外运动,这也验证了二者的耦合较弱。
|
| 图2 开环与闭环控制下系统面内摆角变化 Figure 2 The in-plane angle variations under two control laws and optimal trajectory |
|
| 图3 开环与闭环控制下系统面外摆角变化 Figure 3 The out-plane angle variations under two control laws and optimal trajectory |
|
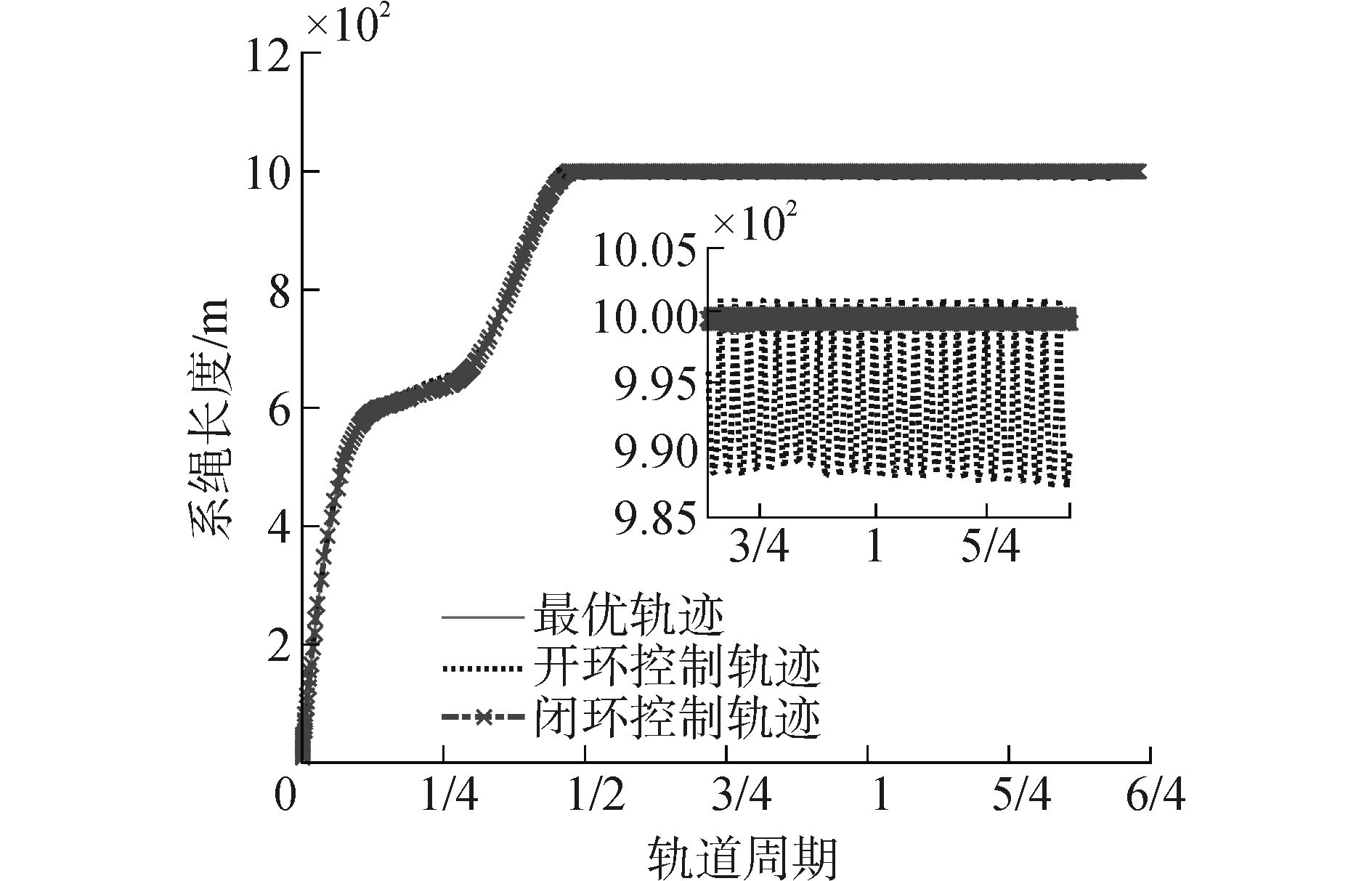
| 图4 开环与闭环控制下系绳径向变化速度 Figure 4 The tether length variations under two control laws and optimal trajectory |
|
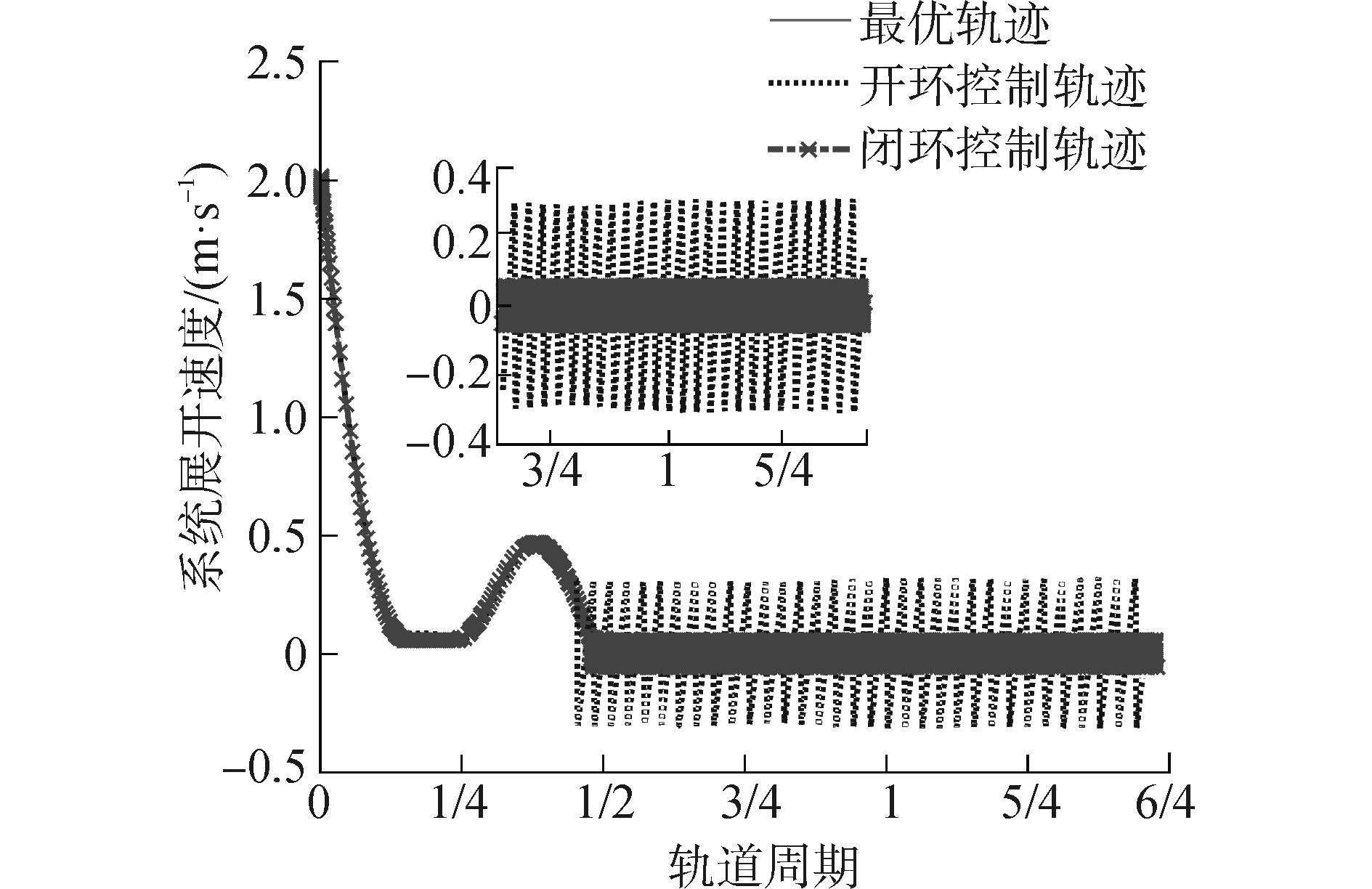
| 图5 开环与闭环控制下系绳径向变化速度 Figure 5 The deploy velocities under two control laws and optimal trajectory |
图 4和5为系统沿系绳径向的变化。图 4显示闭环控制能够有效减弱系统稳态阶段的径向震荡。可见两种控制均能在半个轨道周期内将系统展开,且开环控制更快一些。而闭环控制下,稳态阶段两颗卫星距离变化范围远小于开环控制,且相对速度亦比开环控制小几倍。
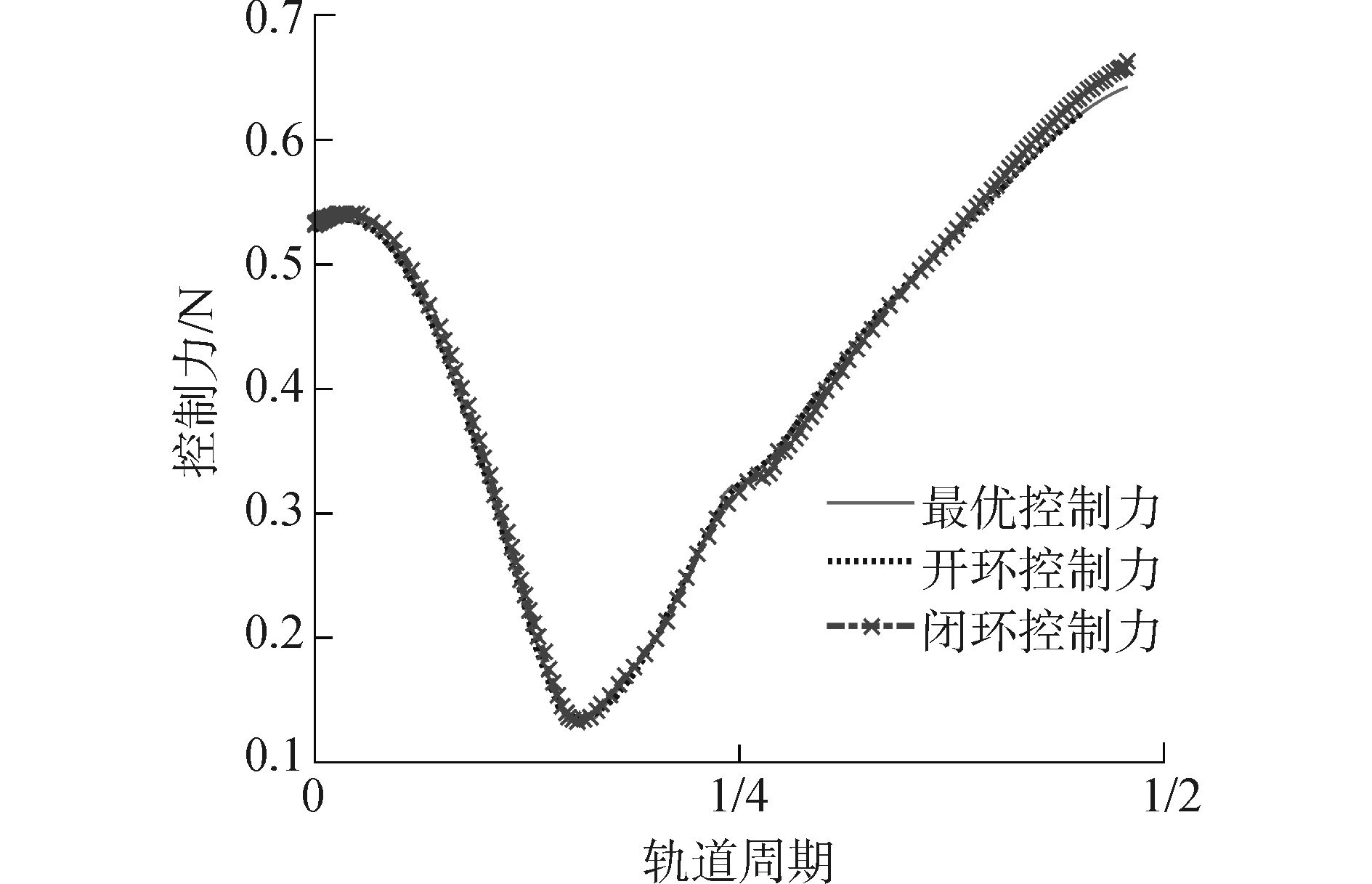
图 6所示,闭环控制时系统控制力相对开环控制力仅有微小增幅,而系统的稳态误差相对开环控制明显减小,因此该控制律是相当有效的。
|
| 图6 开环与闭环控制下系统控制力 Figure 6 The control forces under two control laws and optimal trajectory |
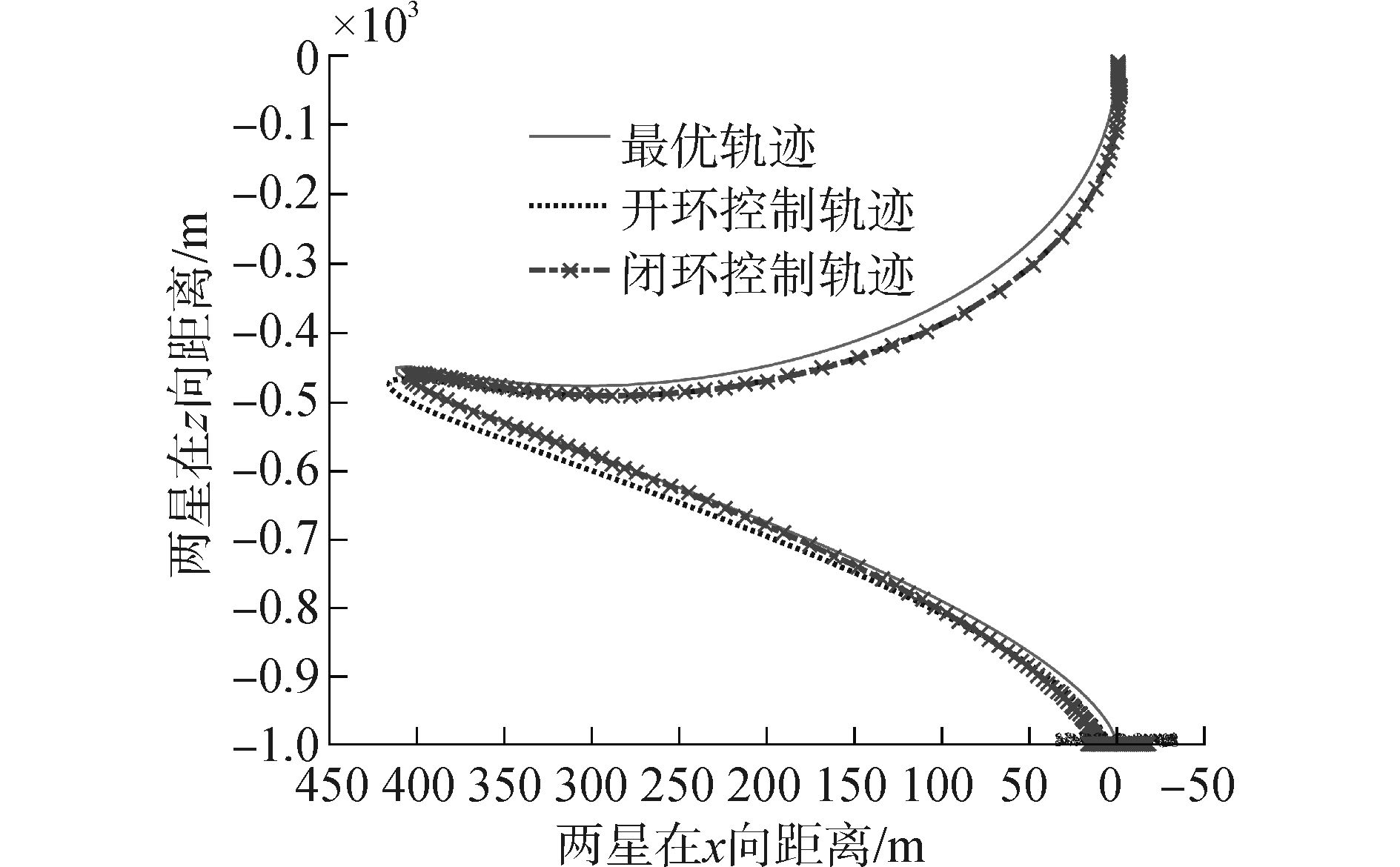
图 7为系统在两种控制下的面内运动轨迹及最优轨迹,表明闭环控制下系统稳态误差更小,这也与系统在闭环控制下有着更小的面内摆角误差和径向误差相对应。
|
| 图7 开环与闭环控制下系统面内运动轨迹 Figure 7 The in-plane trajectories under two control laws and optimal trajectory |
从系统面内运动轨迹来看系统展开结束后存在稳态误差,其原因一方面是由于展开跟踪控制器的抖动影响,导致系绳展开完成后速度不完全为零,如果选择较小的边界层厚度ζ,系绳展开结束速度会更小,但变化频率会更快;另一方面如文献[14]中指出当系统轨道为椭圆时,系统运行过程中系绳不会保持铅垂方向分布,即系绳的面内摆角不会一直保持为零,由系统动力学方程方程 (1)~(3) 可知系统面内运动存在强耦合,这也会导致系统展开后系绳长度和变化速度的震荡。不过,可以通过阻尼器来减弱系统运行过程中的纵向震荡。
为了验证该控制器的适用性,对不同面内摆角初始偏差下的系统分别进行开环控制和闭环控制,系统展开时间,展开长度和稳态阶段误差分别见表 2和表 3。
从表 2的结果可以知道,不同初始面内摆角偏差对开环控制影像很大。随着面内初始摆角偏差的减小,系统展开时间增加,当面内初始偏差减到1°时,系统在闭环控制下已无法在规定时间内完成展开,且系统展开长度会随着面内摆角初始偏差的反向增大而减小。当面内初始摆角偏差为1.5°时,系统的稳态误差最小,而理论上当面内初始摆角偏差为0时系统稳态误差最小,这是因为在开环控制下系统稳态误差除了受到面内初始摆角偏差的影响外,还受到外界扰动和建模误差的影响。当系统为开环控制时,有意使系统初始面内摆角偏差为正值有利于系统的展开,且若选择合适也可使系统展开到目标位置附近。
从表 3可以知道,系统在闭环控制下均能够展开到目标位置附近,不过展开时间稍有偏差。相比开环控制,系统的稳态误差明显减小,特别是系绳径向稳态误差,最大为0.8 m,绳长变化速率最大为0.08 m/s。系统面内摆角误差则随着初始误差的减小而减小,但由于外界扰动的存在,当面内摆角初始误差为零时其稳态误差并不为零。虽然系统在开环控制下也有几率展开的目标位置附近,但是亦有很大几率在规划时间内无法完成展开。因此相比于开环控制,所设计的系绳张力自适应滑模控制器能够保证系统在规划时间内展开到目标位置附近,快速完成系统配置。
4 结论本文面向系绳式InSAR系统任务要求,基于高斯伪谱法规划出系统快速展开的最优轨迹,并通过反馈控制使系统展开跟踪最优轨迹,结论如下:
1) 所设计的系绳张力自适应滑模控制器可以克服系统模型误差和外界扰动跟踪系统最优展开轨迹;
2) 在闭环控制下系统能够展开到目标位置附近,且系统面内摆角稳态误差随着系统面内摆角初始误差的减小而减小;
3) 与开环控制相比,闭环极大地提高了系统展开的成功率,有效地降低了系统的稳态误差,使系统能够完成快速配置。
| [1] | KRIEGER G, MOREIRA A, FIEDLER H, et al. TanDEM-X:a satellite formation for high-resolution SAR interferometry[J]. IEEE transactions on geoscience and remote sensing, 2007, 45(11): 3317–3341. DOI:10.1109/TGRS.2007.900693 |
| [2] | MOCCIA A, VETRELLA S. A tethered interferometric synthetic aperture radar (SAR) for a topographic mission[J]. IEEE transactions on geoscience and remote sensing, 1992, 30(1): 103–109. DOI:10.1109/36.124220 |
| [3] | CHEN Yi, HUANG Rui, HE Liping, et al. Dynamical modelling and control of space tethers:a review of space tether research[J]. Nonlinear dynamics, 2014, 77(4): 1077–1099. DOI:10.1007/s11071-014-1390-5 |
| [4] | KRUPA M, POTH W, SCHAGERL M, et al. Modelling, dynamics and control of tethered satellite systems[J]. Nonlinear dynamics, 2006, 43(1/2): 73–96. |
| [5] | SUN Guanghui, ZHU Z H. Fractional-order tension control law for deployment of space tether system[J]. Journal of guidance, control, and dynamics, 2014, 37(6): 2057–2062. DOI:10.2514/1.G000496 |
| [6] | MISRA A K. Dynamics and control of tethered satellite systems[J]. Acta astronautica, 2008, 63(11/12): 1169–1177. |
| [7] | FUJII H A, ANAZAWA S. Deployment/retrieval control of tethered subsatellite through an optimal path[J]. Journal of guidance, control, and dynamics, 1994, 17(6): 1292–1298. DOI:10.2514/3.21347 |
| [8] | JIN D P, HU H Y. Optimal control of a tethered subsatellite of three degrees of freedom[J]. Nonlinear dynamics, 2006, 46(1/2): 161–178. |
| [9] |
文浩, 金栋平, 胡海岩. 基于微分包含的绳系卫星时间最优释放控制[J].
力学学报, 2008, 40(1): 135–140.
WEN Hao, JIN Dongping, HU Haiyan. Time-optimal deployment of a tethered subsatellite based on differential inclusion[J]. Chinese journal of theoretical and applied mechanics, 2008, 40(1): 135–140. |
| [10] | WILLIAMS P. Optimal deployment/retrieval of tethered satellites[J]. Journal of spacecraft and rockets, 2008, 45(2): 324–343. DOI:10.2514/1.31804 |
| [11] | WILLIAMS P. Optimal deployment/retrieval of a tethered formation spinning in the orbital plane[J]. Journal of spacecraft and rockets, 2006, 43(3): 638–650. DOI:10.2514/1.17093 |
| [12] | WILLIAMS P, HYSLOP A, STELZER M, et al. YES2 optimal trajectories in presence of eccentricity and aerodynamic drag[J]. Acta astronautica, 2009, 64(7/8): 745–769. |
| [13] | PENG Haijun, GAO Qiang, WU Zhigang, et al. Efficient sparse approach for solving receding-horizon control problems[J]. Journal of guidance, control, and dynamics, 2013, 36(6): 1864–1872. DOI:10.2514/1.60090 |
| [14] | ALPATOV A P, BELETSKY V V, DRANOVSKII V I, et al. Dynamics of tethered space systems[M]. London: CRC Press, 2010: 20-50. |
| [15] |
雍恩米, 陈磊, 唐国金. 飞行器轨迹优化数值方法综述[J].
宇航学报, 2008, 29(2): 397–406.
YONG Enmi, CHEN Lei, TANG Guojin. A survey of numerical methods for trajectory optimization of spacecraft[J]. Journal of astronautics, 2008, 29(2): 397–406. |
| [16] |
黄诘, 张友安, 王丽英. 基于Radau伪谱法的非线性最优控制问题的收敛性[J].
控制理论与应用, 2014, 31(2): 263–267.
HUANG Jie, Zhang You'an, WANG Liying. Convergence of nonlinear optimal control problem using Radau pseudospectral method[J]. Control theory & applications, 2014, 31(2): 263–267. |
| [17] |
徐少兵, 李升波, 成波. 最优控制问题的Legendre伪谱法求解及其应用[J].
控制与决策, 2014, 29(12): 2113–2120.
XU Shaobing, LI Shengbo, CHENG Bo. Theory and application of Legendre pseudo-spectral method for solving optimal control problem[J]. Control and decision, 2014, 29(12): 2113–2120. |
| [18] |
闫循良, 廖守亿, 张金生, 等. 基于节点改善策略的伪谱轨迹优化[J].
宇航学报, 2013, 34(7): 891–900.
YAN Xunliang, LIAO Shouyi, ZHANG Jinsheng, et al. Trajectory optimization using pseudospectral method based on a grid node refinement strategy[J]. Journal of astronautics, 2013, 34(7): 891–900. |
| [19] | FEDI CASAS M. Dynamics and control of tethered satellite formations in low-earth orbits[D]. Barcelona:Universitat Politècnica de Catalunya, 2015:18-50. |



