2. 军事交通运输研究所, 天津 300161;
3. 天津市科委, 天津 300051;
4. 天津大学 水利工程仿真与安全国家重点实验室, 天津 300072
2. Military Transportation Institute, Tianjin 300161, China;
3. Tianjin Science and Technology Commission, Tianjin 300051, China;
4. State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China
随着海洋开采技术的发展,许多大的石油或天然气平台逐步出现,使得海上大型浮体结构的设计研究成为热点问题,其中浮体和浮体之间的连接技术又是一个关键性问题。在此方面,许多研究者研究了相连浮体的水作用响应[1-2]。Fang等[3]采用二维切片法计算了两平行布置的条状浮体间的水动力相互作用。Duncan等[4]采用Oortmerssen[5]的方法计算了两船体的运动响应,并在计算中考虑了锚泊缆和防碰垫的作用。Chen and Mahrenholtz用边界元的方法,讨论了两漂浮圆柱之间的连接刚度、间距及水深等参数的变化对圆柱运动响应的影响[6]。Newman[7]采用边界积分的方法,对两个相同的均质方箱在固接和铰接情况下的运动响应进行了数值计算。沈庆等[8]对于铰联结系泊多浮体系统,将其作为铰联结无根树系统,用多刚体力学方法进行了运动学分析。勾莹等[9]应用边界积分方程方法研究了波浪与2个相连三维浮体的相互作用问题,计算中考虑了浮体相互间的水动力干涉, 通过联立各浮体的运动方程以及运动连续条件求得浮体运动量。Hong等[10]通过数值计算研究系泊多浮体运动响应特性。Sun等[11]基于线性绕射理论,并采用拉格朗日乘子方法,探讨了两浮体在铰接、固接、弹性连接情况下的运动响应以及不同连接形式下连接点的受力情况。刘文玺等[12]在浮体和系泊系统的时域耦合分析中,将浮体的分析方法和系泊缆索的分析方法结合,建立了浮体和系泊系统非线性运动响应和缆索张力的耦合计算方法。许鑫等[13]对目前海洋工程中较为常见的多浮体系统进行了介绍,并就国内外在多浮体系统的水动力方面的研究进行了系统的阐述。
目前,浮体与浮体在水作用力下相互作用的研究已达到一定深度,但是关于浮体和固定物体连接作用的研究还不多见,尤其是船只与固定物体连接的动力学响应研究则更是鲜见报道。
1 船只补给悬链线系统理论分析船只补给悬链线系统是由船只、悬链线与固定物体组成。悬链线连接一般为索道连接,本文中悬链线统一称为索道。船只补给悬链线连接主要用于海上浮体与相对静止设施之间的物资和人员传送,它区别于浮体与浮体连接,表现为连接的功用不同,连接的方式不同,连接的距离也有差别。此外,船只补给悬链线系统的连接方式也不同于山地丛林的索道连接方式 [14],山地丛林索道主要是在固定的物体上展开。舰船补给索道连接[15]在舰船航行补给时,两船处于航行状态,保持适当的航速, 并利用操舵装置产生横向力, 抵消索道张力, 维持一定的船距。
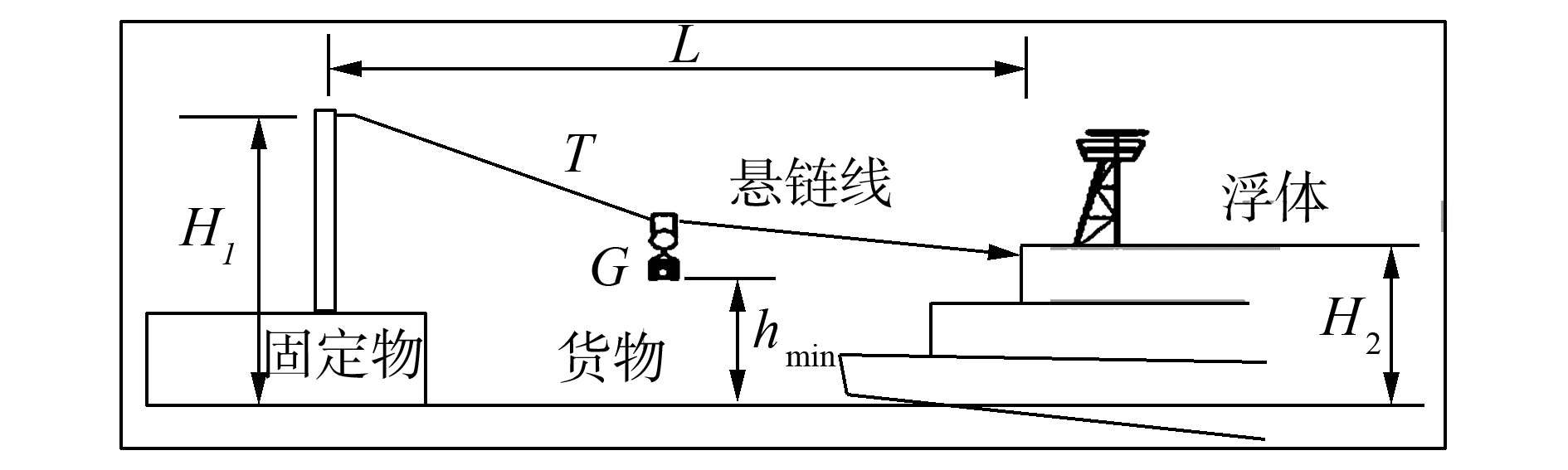
船只对固定目标补给时要求船只在锚泊状态下仅通过索道连接固定目标,索道只能依靠补偿装置自身来控制。具体连接工作方式是:带有补给品的船只当接近固定目标时,应在开阔的水域内锚泊确定其位置,如图 1中的浮体。而后人员在船只上抛送绳索一端到固定物目标上,将绳索与固定物的某处位置连接,然后绳索的另一端与船只连接,并通过恒张力补偿装置将绳索收紧,实现船只和固定物的索道连接。船只水线以上部分会受到风载作用,而船只水线以下部分会受到海流作用,船只受到的这两种作用载荷由船只抛锚的锚链力进行平衡,使船只在平衡位置附近漂浮运动。船只在水中漂浮运动时,索道会出现拉紧或松弛,系统中恒张力补偿装置自动收放索道使得索道处于张紧状态,从而保持恒定张力。这里恒张力补偿装置如何得到索道跨距以及补偿量等参数并严格控制索道张力,相关研究可见文献[16],本文只考虑船与固定物之间相对运动时(靠近或者离开) 缆的张力基本保持恒定,以确保物资能够在船只和固定物之间保持平稳运送的情况。
|
| 图1 船只和固定物的连接方式示意图 Figure 1 The connecting way of vessel and fixation object |
船只和固定物之间有一定的距离空间,二者通过悬链线相互作用。船只和固定物的距离变化与两个船只或浮体间的距离变化是不同的,两个船只间或浮体间的距离是通过航行或运动来保持。而固定物和船只的距离是通过船只抛锚固定的受力平衡方式保持。因此有必要研究船只锚泊情况下的波浪运动响应,为船只补给悬链线系统分析奠定基础。
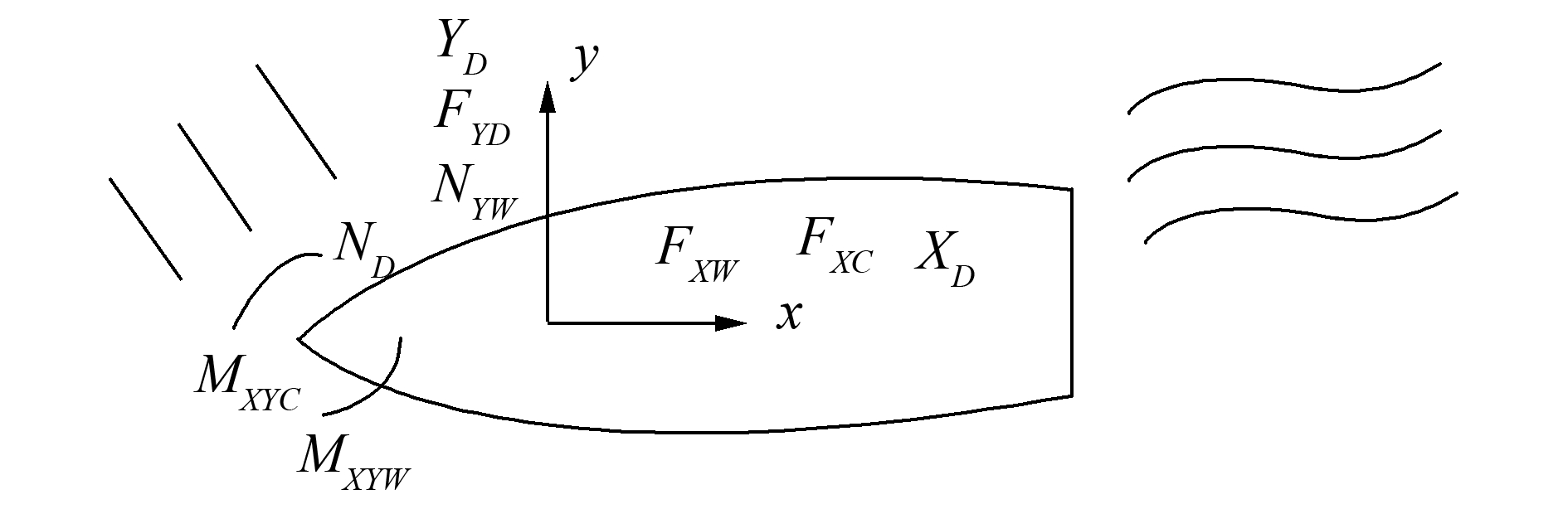
1.1 船只运动分析 1.1.1 船只运动平衡位置及稳定性分析船只在波浪中受到风、浪、流引起的力以及力矩的作用如图 2所示。
|
| 图2 船只受力分析示意图 Figure 2 The analysis of vessel forces |
作用在船只的纵向总载荷FXT、横向总载荷FYT及总摇艏力矩MXYT分别为
| $ \begin{array}{*{20}{c}} {{F_{XT}}={F_{XW}}+{F_{XC}}+{X_D}{F_{YT}}={F_{YW}}+{F_{YC}}+{Y_D}}\\ {{M_{XYT}}={M_{XYW}}+{M_{XYC}}+{N_D}, } \end{array} $ | (1) |
式中:FXW是纵向风力,FYW是横向风力,FXC是纵向流力,FYC是横向流力,XD是纵向二阶波浪漂移力,YD是横向二阶波浪漂移力,MXYC是流的摇艏力矩,MXYW是风的摇艏力矩,ND是漂移力的摇艏力矩。
对于单点系泊船只,平衡位置的计算方程为
| $ \sum \mathit{\boldsymbol{M}}={M_{XYW}}+{M_{XYC}}+{N_D}-{F_{YT}} \times {\rm{ARM}} $ | (2) |
式中:∑M为合力矩,ARM为船只中心和船艏系索点处的距离(一般取ARM=0.48LOA),LOA为总船长。
1.1.2 船只三维运动响应船只在水中的三维运动响应主要是受到不规则波的作用,这种不规则波可被分解成为多个规则子波进行处理,通过三维格林函数法计算规则波中船只的运动响应,然后进行叠加就可以得到船只总体三维运动响应。在不规则波的多规则波分解中,频率为n规则波能够被获得,命名为ωi,i=1, 2,…, n。
| $ {\boldsymbol{u}^k}={\left[{u_1^k\;\;u_2^k\;\;u_3^k\;\;u_4^k\;\;u_5^k\;\;u_6^k} \right]^{\rm{T}}}, k=1, 2 $ | (3) |
船只有6个自由度(u1k~u6k),分别是船只的纵荡、横荡、垂荡、横摇、纵摇、艏摇。运动方程如下:
| $ \sum\limits_{i=1}^n {\left[{-{\omega ^2}_i({\mathit{\boldsymbol{M}}_S}+\mathit{\boldsymbol{A}}{\rm{ }})+{\rm{i}}{\omega _i}({C_S}+{\rm{ }}\mathit{\boldsymbol{B}})+{\mathit{\boldsymbol{K}}_W}+{\mathit{\boldsymbol{K}}_L}} \right]{u_i}={F_e}} $ | (4) |
式中:MS为质量矩阵,A为附加质量矩阵,B为阻尼系数矩阵,KW为恢复力系数矩阵,Fe为激励力,CS为粘性阻尼,从试验或经验公式中获得,KL是缆索的刚度矩阵。通过三维格林函数计算船只在规则子波的运动,然后再进行叠加,进而得到船只在不规则波的运动响应。
1.1.3 船只与锚泊链耦合动力分析在对船只与锚泊链耦合动力分析中,船只的水动力学特性采用三维势流理论进行求解。船只的拖拽力采用莫里森公式进行计算分析,锚泊线的动力分析采用杆理论和有限元模型,在总体坐标系中建立控制方程进行计算,锚泊线和补给船舶之间的连接采用平动、转动弹簧以及阻尼器进行模拟,通过调整弹簧和阻尼器的控制参数可以模拟各种形式的连接,船只和锚泊线耦合系统的方程,如下所示
| $ \left[{\begin{array}{*{20}{c}} {{\boldsymbol{K}^L}}&{{K^C}}\\ {{\boldsymbol{K}^{CT}}}&{{\boldsymbol{K}^B}} \end{array}} \right]\left[\begin{array}{l} {\boldsymbol{U}^L}\\ {\boldsymbol{U}^B} \end{array} \right]=\left[\begin{array}{l} {\boldsymbol{F}^L}\\ {\boldsymbol{F}^B} \end{array} \right] $ | (5) |
式中: KL是锚泊线和弹簧(阻尼) 连接器的联合刚度矩阵,KB是刚度矩阵,KC和KCT分别是包含船只和锚泊线耦合项的耦合刚度矩阵及其转换矩阵,UL和UB分别是锚泊线和船只的位移列阵,FL和FB分别是作用在锚泊线和船只上的力列阵和力矩列阵。
1.2 悬链线(索道) 计算分析索道受力的计算理论主要有悬链线理论和抛物线理论,研究高架索道特性的方法主要有近似法和精确法;抛物线理论假定垂向载荷沿水平方向均匀分布,悬链线理论假定垂向载荷沿着索道长度弧度方向均匀分布。当索道只受到重力时,线的真实形状应该是悬链线[17-18]。根据文献[18]可得到索道悬链线的力学分析模型。
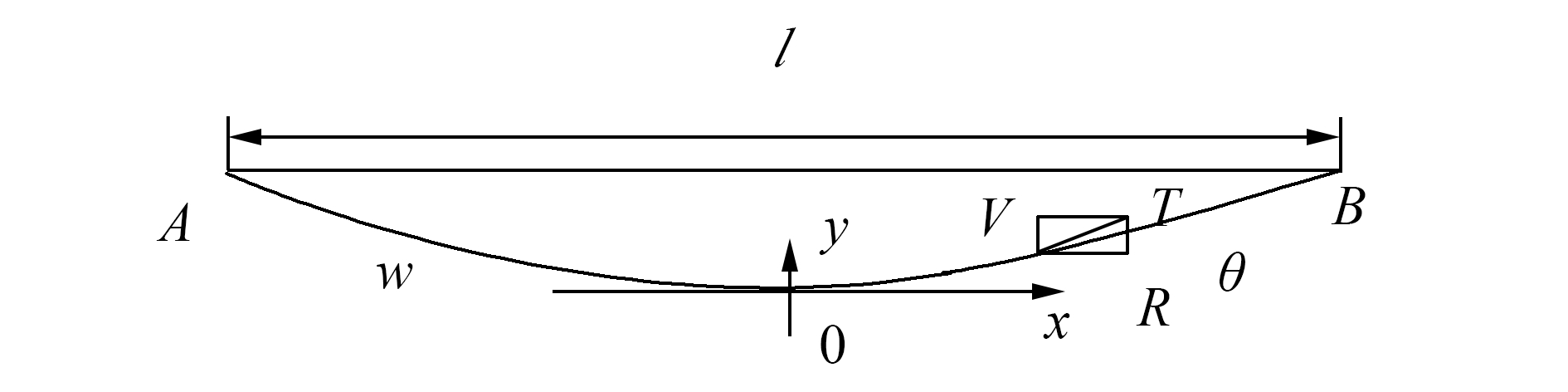
1.2.1 无载荷索道计算模型钢索在跨度内沿长度方向均匀分布,以钢索最低点为原点建立直角坐标系,见图 3。
|
| 图3 钢索曲线受力分析图 Figure 3 The analysis of ropeway forces |
悬链线的方程是一个双曲余弦函数,其方程形式为
| $ y=\frac{R}{w}{\rm{cosh}}\left({\frac{w}{R}x} \right)-\frac{R}{w} $ | (6) |
式中:R为无载荷索道钢索受到的水平分力,w是悬链线即钢索的单位长度重量,悬链线的斜率角θ。
| $ {\rm{tan}}\theta=\frac{{{\rm{d}}y}}{{{\rm{d}}x}}={\rm{sinh}}\left({\frac{w}{R}x} \right) $ | (7) |
钢索各点受到的拉力T为
| $ T=R\sqrt {1+{\rm{ta}}{{\rm{n}}^2}\theta }=R\sqrt {1+{\rm{s}}{{\rm{h}}^2}\left({\frac{w}{R}x} \right)}=R\cdot{\rm{ch}}\left({\frac{w}{R}x} \right) $ | (8) |
集中载荷是通过货物的重力引起的,货物重力Q作用在钢索时,其受力可表示为
| $ {T_a}=\frac{R}{{2{L_1}}}(k{l_0}+\frac{R}{w} \cdot {\rm{sh}}\frac{{wk{l_0}}}{R} \cdot {\rm{ch}}\frac{{wk{l_0}-2wk{x_{c1}}}}{R}) $ | (9) |
| $ \begin{array}{l} {T_b}=\frac{R}{{2{L_2}}}(\left({1-k} \right){l_0}+\frac{R}{w}\cdot{\rm{sh}}\frac{{w\left({1-k} \right){l_0}}}{R}\cdot\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ch}}\frac{{w\left({1-k} \right){l_0} - 2wk{x_{c2}}}}{R}) \end{array} $ | (10) |
式中:R为有荷载索道受到的水平拉力,Ta为有荷载索道AD段的平均拉力,Tb为有荷载索道DB段的平均拉力,k为AD的距离与DB距离的比值;l0为A、B支点的水平跨距,TB为有荷载索道AD段最低点的水平坐标,TL为有荷载索道DB段最低点的水平坐标,TR为有荷载索道AD段的悬链线长度,L2为有荷载索道DB段的悬链线长度。
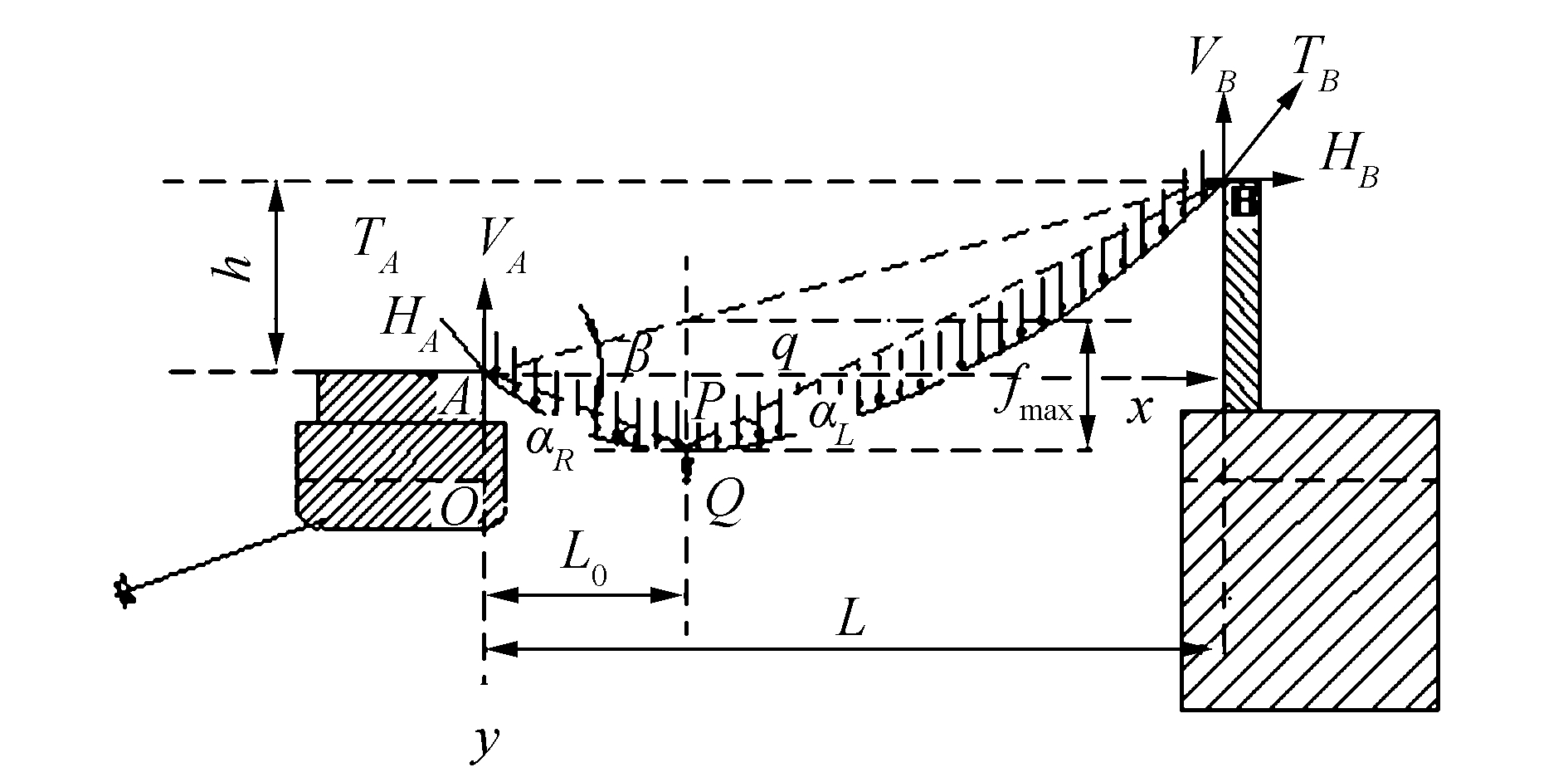
1.3 综合运动分析船只在波浪中的运动受到风、浪、流等影响较大,运动响应也与船只的类型有关,在低海况条件下,船只偏离平衡位置的距离通过索道的张紧装置得到补充,索道连接点的位置也变化较小,因此,低海况条件下,计算其综合运动时,可考虑索道长度的变化,忽略船只运动对索道的其他影响。连接索道受力分析模型如图 4所示,根据文献[19]可以得到货物的运动方程。
|
| 图4 船只补给悬链线系统的计算模型 Figure 4 The calculation model of vessel supply catenary system |
货物沿索道运动的轨迹为[19]
| $ y=\left({\frac{q}{{2H{\rm{cos}}\beta }}+\frac{Q}{{HL}}} \right)\left({L-x} \right)x-\frac{h}{L}x+{C_0} $ | (11) |
式中:q为钢索的单位长度质量,h为A、B两点的高度差,Q为货物(包括吊钩等) 重力,β为AB与水平方向的夹角,H为钢索的水平方向的分力,L为索道跨距,C0为常数。
货物运动方程为[19]
| $ \begin{array}{*{20}{c}} {m\ddot y+c\dot y=Q-H({\rm{tan}}\;{\alpha _L}+{\rm{tan}}{\alpha _R})}\\ {{\rm{tan}}\;{\alpha _L}=\frac{y}{{{L_0}}}{\rm{tan}}\;{\alpha _R}=\frac{{y+h}}{{L-{L_0}}}} \end{array} $ | (12) |
式中:m为货物(包括吊钩等) 质量;c为阻尼系数,c=2ζω0m;ζ为无量纲阻尼比;αL和αR为如图 4所示的PA、PB与水平方向的夹角,L0为A点和Q点的水平距离。
当x为L/2时,挠度最大,从式(11) 可得最大挠度fmax与水平力H的关系为
| $ {f_{{\rm{max}}}}=\frac{{q{L^2}}}{{8H{\rm{cos}}\;\beta }}+\frac{{QL}}{{4H}}-\frac{h}{2}+{C_0} $ | (13) |
由分析知:随着索道跨距的增加,最大挠度也随着增大,货物有可能落水;高度差h越大,最大挠度减小,最低点纵坐标值越小,即离水面越远;索道水平力与最大挠度成反比关系,索道张力越大,最大挠度越小,但是对索道的要求越高。因此,必须控制索道的跨距大小,保持两端一定的高度差,确保张力在安全范围内,这样才能安全运输物资。下面将对船只及悬链线系统的运动进行仿真分析。
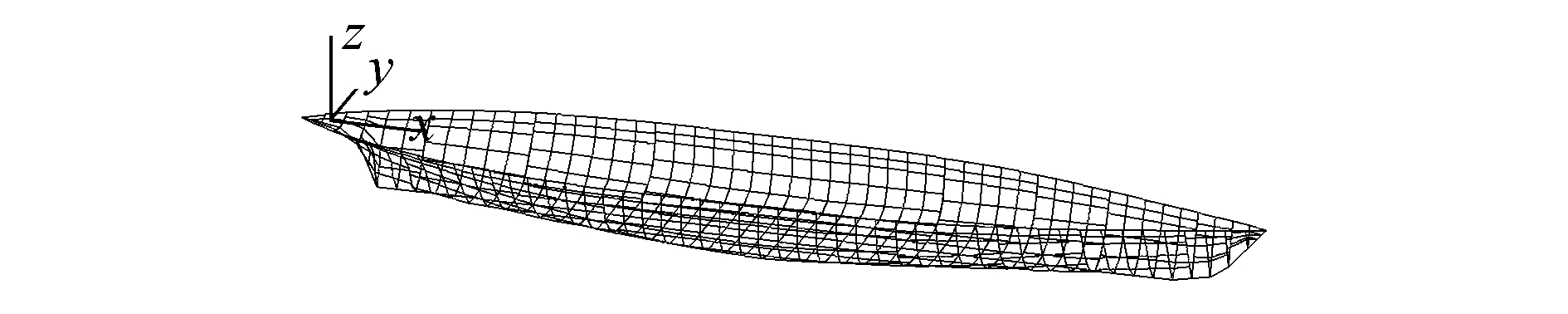
2 数值仿真模拟船只与固定物的连接,可以以运输船和海上石油平台为例。大型石油平台相对较大,可考虑为固定物。考虑到运输船和平台连接的安全性,连接设备在三级海况下展开,运输船的型深为4.7 m,非满载下,轻载状态时的高度为4.3 m,船舶吃水为1.955 m,悬挂点的高度为7.05 m,坐标系的原点建立在吃水线平面,船舶被分成20个部分,在每个部位均用面单元建立网格,运输船的模型见图 5。三级海况下的环境载荷见表 1,通过仿真模拟得到三级海况下运输船的运动位移、速度和加速度,结果见表 2~4。三级海况下的运输船耦合运动分析结果见图 6。
|
| 图5 运输船网格 Figure 5 The grid of carrier |
| 项目 | 数值 |
| 有义波高/m | 1.0 |
| 峰周期/s | 5.18 |
| 水平面以上10 m处的风速/(m·s-1) | 6.85 |
| 自由表面(0 m) 流速/(m·s-1) | 1.544 |
| 海底(-8 m) 流速/(m·s-1) | 0.515 |
| 纵荡/m | 横荡/m | 垂荡/m | 横摇/(°) | 纵摇/(°) | 艏摇/(°) | |
| 均方根 | 0.440 91 | 0.008 41 | 0.047 97 | 0.006 53 | 0.499 98 | 0.002 87 |
| 最大值 | 1.224 53 | 0.021 95 | 0.159 1 | 0.021 81 | 1.939 38 | 0.006 34 |
| 最小值 | -0.762 95 | -0.006 09 | -0.158 59 | -0.017 57 | -1.637 95 | -0.006 52 |
| 平均值 | 0.164 05 | 0.007 45 | -0.000 71 | 0.001 81 | 0.063 52 | -0.001 01 |
| 纵荡/ (m·s-1) | 横荡/ (m·s-1) | 垂荡/ (m·s-1) | 横摇/ ((°)·s-1) | 纵摇/ ((°)·s-1) | 艏摇/ ((°)·s-1) | |
| 均方根 | 0.089 06 | 0.000 52 | 0.062 32 | 0.004 99 | 0.666 31 | 0.000 2 |
| 最大值 | 0.292 22 | 0.001 62 | 0.191 19 | 0.015 39 | 2.512 31 | 0.000 51 |
| 最小值 | -0.394 23 | -0.001 55 | -0.210 57 | -0.015 08 | -2.830 21 | -0.000 6 |
| 平均值 | -0.002 03 | 0.000 01 | -0.000 38 | 0 | -0.000 73 | 0 |
| 纵荡/ (m·s-1) | 横荡/ (m·s-1) | 垂荡/ (m·s-1) | 横摇/ ((°)·s-1) | 纵摇/ ((°)·s-1) | 艏摇/ ((°)·s-1) | |
| 均方根 | 0.115 37 | 0.000 41 | 0.088 09 | 0.003 95 | 1.041 21 | 0.000 04 |
| 最大值 | 0.407 1 | 0.001 23 | 0.270 61 | 0.011 98 | 4.404 74 | 0.000 16 |
| 最小值 | -0.571 79 | -0.001 25 | -0.283 46 | -0.011 82 | -4.649 27 | -0.000 13 |
| 平均值 | -0.004 08 | 0 | -0.001 02 | 0 | -0.000 1 | 0 |
|
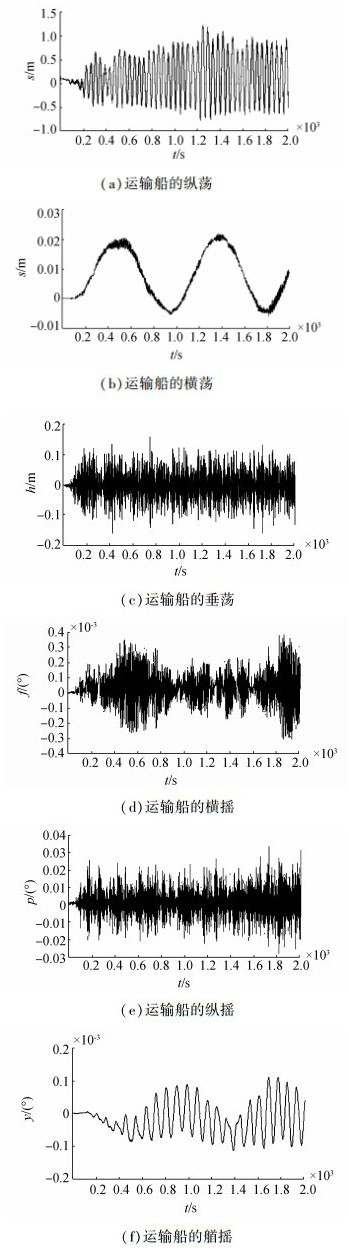
| 图6 三级海况下的运输船耦合运动分析结果 Figure 6 The analysis result of coupling motion at the level 3 sea states |
三级海况的环境载荷见表 1。
由分析可知,三级海况下,对船只和固定物连接影响较大的因素为纵荡和纵摇,纵荡的最大值可达到1.2 m,纵摇的速度达到2.5 m/s,纵摇加速度达到4.4 m/s2,这对索道连接是极其不利的。因此,在连接设备时应该使船只侧面对着固定物,连接点应该在船只的中心线上,降低纵荡和纵摇对索道的影响。垂荡会引起连接点位置的变化,在三级海况下垂荡的最大值为0.15 m,对连接点位置影响较小,可忽略其影响,在高海况条件下,应考虑该因素。
在考虑了锚泊系统耦合运动后,船只的运动较为复杂,在做周期运动的同时,也会随着锚链的影响做小范围运动,运动的幅度较小,对于索道的连接影响较小,但要注意锚的位置变化,高海况下,会发生走锚的现象,对于船只与固定物的连接较为不利。
连接绳索的跨距分别取40、60、80 m,三个索道的参数为:16、12、12 mm,绳索的长度为100、200、100 m。16 mm的索道单位质量为0.99 kg/m,其他类型的绳索单位质量为0.6 kg/m,货物的重量为50 kg,通过理论计算得到不同跨距下拉力及其挠度,见表 5。
| 索道 跨距 | 最小值状态 | 实际工作状态 | |||||
| 最小拉力 /N | 挠度 /m | 挠度 /m | 水平 拉力/N | 最大 拉力/N | 索道 长度/m | ||
| 80 | 1 725.5 | 24.4 | 7 | 2 488.8 | 2 840.8 | 81.6 | |
| 60 | 1 404.2 | 17.8 | 7 | 1 410.5 | 1826.0 | 62.13 | |
| 40 | 1 085.5 | 11.34 | 7 | 639.7 | 1 149.12 | 43.1 | |
从表 5来看,张力变化幅度随着挠度增大而减小。在相同的挠度时,张力随着距离的增大而减小。
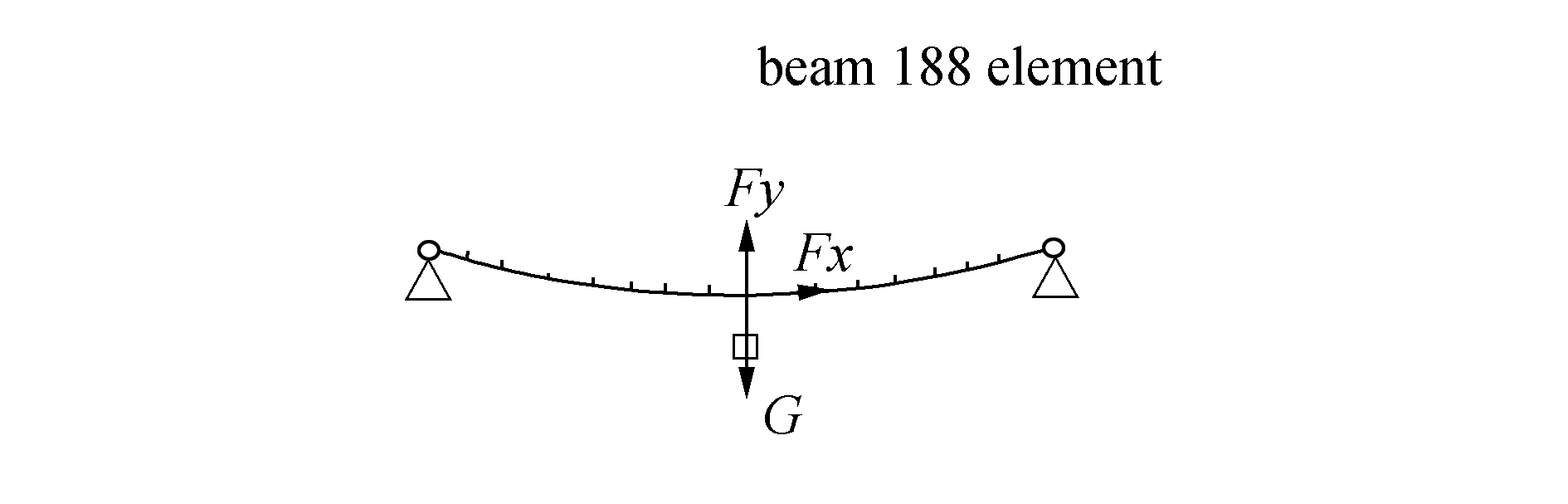
下面在ansys中模拟索道的连接,索道采用Beam 188单元建模,等效截面为9.5 mm,钢索密度为7.85 t/m3,重力加速度为9.8 m/s2,两端采用绞支,如图 7所示。仿真时接收索必须同放索保持相同速度,考虑到货物的重力为490 N,ANSYS仿真结果在表 6中,ANSYS仿真结果与悬链线计算的结果比较见表 7。
| 索道跨距/m | 索道重量/N | Fx/N | Fy/N |
| 80 | 1 778.7 | 2 515.4 | 889.34 |
| 60 | 1 354 | 1 425.9 | 676.9 |
| 40 | 939.3 | 646.68 | 469.65 |
| 索道 跨距 7/m | ANSYS结果 | 理论结果 | 差值 | |||||
| 拉力 /N | 索道 重量/N | 拉力 /N | 索道 重量/N | 拉力 /N | 索道 重量/N | |||
| 80 | 2 868.98 | 1 778.7 | 2 840.8 | 1 759.29 | 28.18 | 19.41 | ||
| 60 | 1 842.51 | 1 354 | 1 826 | 1 339.52 | 16.51 | 14.48 | ||
| 40 | 1 152.21 | 939.3 | 1 149.12 | 929.23 | 3.09 | 10.07 | ||
|
| 图7 索道模拟单元划分示意 Figure 7 The simulation of ropeway |
有限元仿真结果在表 6中,有限元仿真结果与悬链线计算的结果比较见表 7。
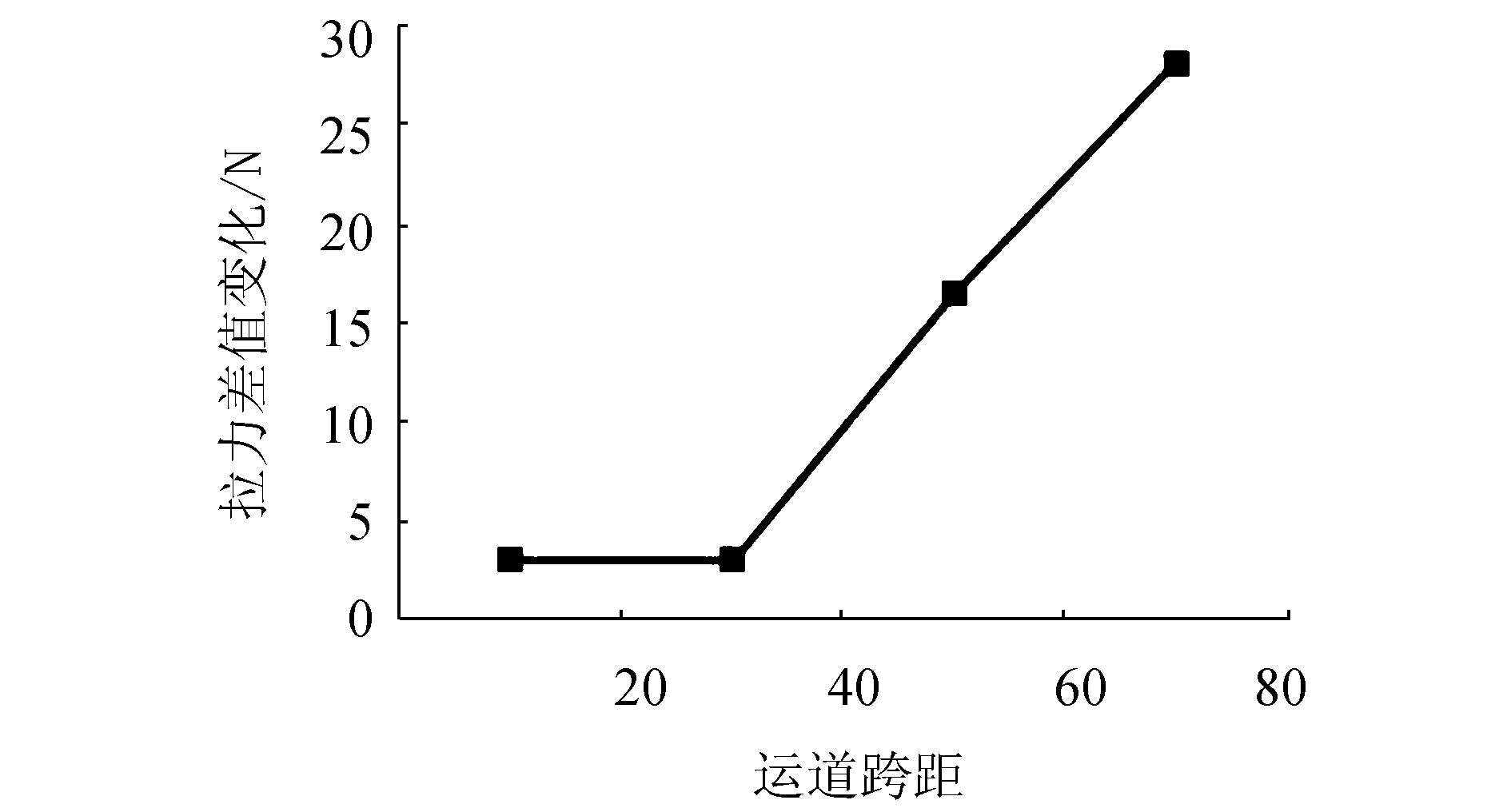
从表 7和图 8来看,仿真结果和理论结果整体吻合,随着跨距的增加,拉力差值在增大,在跨距为80 m时,拉力差值为28 N,与拉力的比值约为1%,理论分析值相对仿真结果值偏小,表明理论模型简化因素较多,随着跨距增加,索道跨距80 m之后,应以仿真分析模型为主。
|
| 图8 理论与仿真得到索道拉力差值随跨距变化 Figure 8 The ropeway tension difference between theoretical results and simulation results in different ropeway spans |
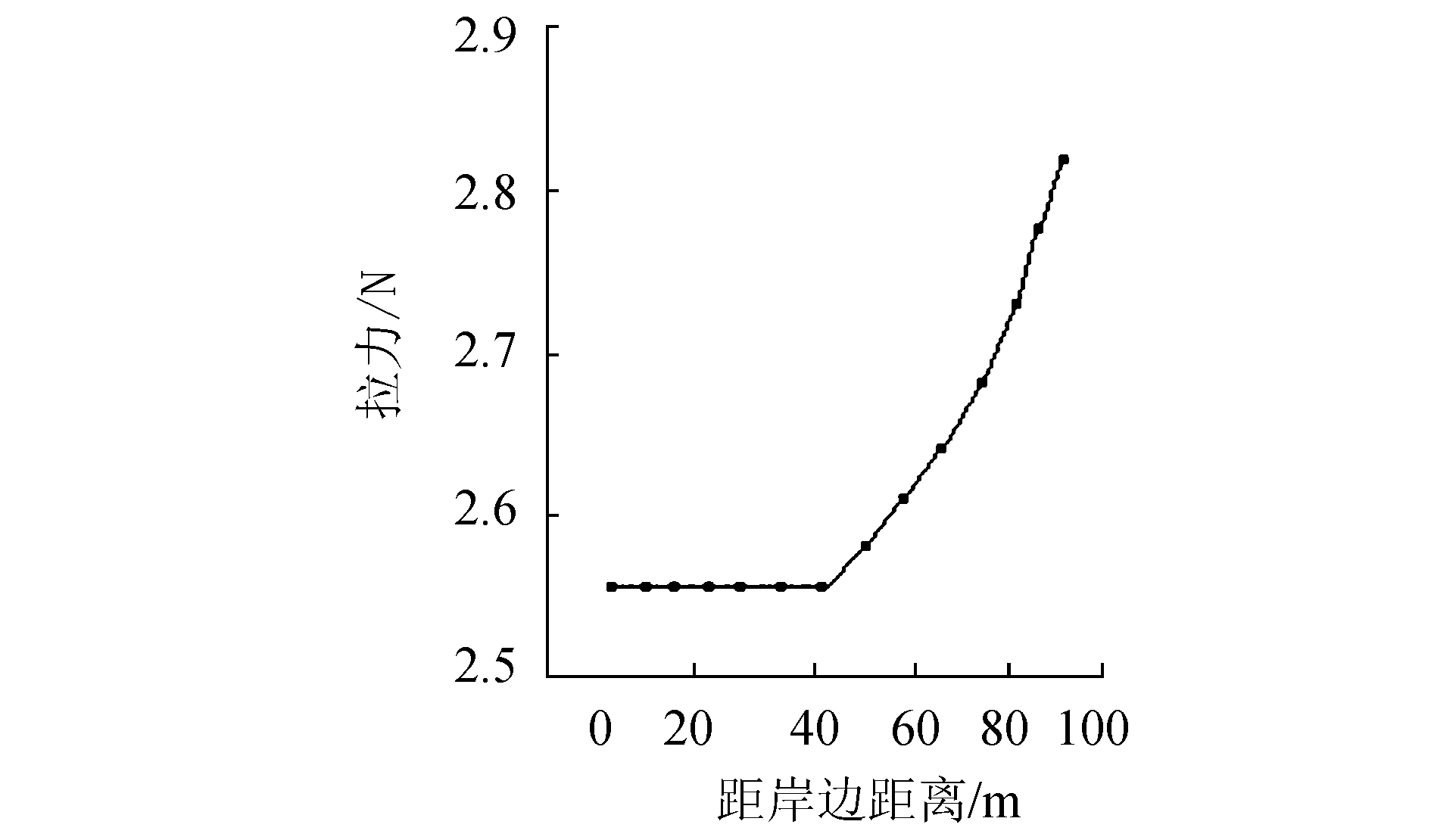
从图 9来看,在索道跨距80 m时,在船上牵引岸上的索具过程中,牵引拉力随距岸距离是变化的,牵引拉力在40 m的范围内变化不大,超越这一范围后,随着距离的增加呈线性增加,也会越来越费力。
|
| 图9 牵引拉力随离岸距离变化关系(索道跨距80 m) Figure 9 The ropeway tension in different ropeway spans. (The ropeway span is 80 m) |
本文主要分析了船只补给悬链线系统的运动特性,并考虑了船只与锚泊系统的耦合以及船只运动对索道的影响,通过理论分析和仿真模拟,得到了船只悬链线系统连接动力学响应,并对结果进行了分析,得到以下结论:
1) 通过对船只与悬链线运动分析,得到了系统连接的运动特性,为船只悬链线系统设计提供理论依据。
2) 三级海况下,对船只和固定物连接影响较大的因素为纵荡和纵摇,在连接设备时应将船只侧面对着固定物,连接点应在船只的中心线上,降低纵荡,纵摇对索道的影响。
3) 垂荡会引起连接点位置的变化,在三级海况下垂荡的最大值为0.15 m,对连接点位置影响较小,可忽略其影响,在高海况条件下,应考虑该因素。
4) 考虑了锚泊系统耦合运动后,船只的运动较为复杂,在做周期运动的同时,也会做小范围运动,对船只和固定物连接影响较小,但应注意防止走锚现象的发生。
5) 仿真结果和理论结果基本保持一致,随着跨距的增加,拉力差值在增大,跨距小于80 m时,拉力差值与拉力的比值为1%;理论分析值相对仿真结果值偏小,表明理论模型简化因素较多,随着跨距增加,索道跨距80 m之后,应以仿真分析模型为主。
6) 在索道跨距80 m时,在船上牵引岸上的索具过程中,牵引拉力随距岸距离是变化的,牵引拉力在40 m的范围内变化不大,超越这一范围后,随着距离的增加呈线性增加,也会越来越费力。
| [1] | CHEN S, MAHRENHOLTZ O. Interaction of water waves and floating twin cylinders in beam waves[J]. Applied ocean research, 1994, 14(6): 371–379. |
| [2] | MCTAGGART K, CUMMING D, HSIUNG C C, et al. Seakeeping of two ships in close proximity[J]. Ocean engineering, 2003, 30(8): 1051–1063. DOI:10.1016/S0029-8018(02)00084-7 |
| [3] | FANG M C, KIM C H. An analysis of water shipping between two floating platforms in the beam wave[C]//Proceedings of the Fifth International Symposium on Offshore Mechanics and Arctic Engineering. Tokyo, 1986, 1:499-505. |
| [4] | DUNCAN J H, BARR R A, LIU Y Z. Computations of the coupled response of two bodies in a seaway[C]//International Workshop on Ship and Platform Motions. Berkeley, CA, 1983. |
| [5] | VAN OORTMERSSEN G. Hydrodynamic interaction between two structures floating in waves[C]//Proceedings of 2nd International Conference on Behaviour of Off-shore Structures. London, 1979:339-356. |
| [6] | CHEN S, MAHRENHOLTZ O. Interaction of water waves and floating twin cylinders in beam waves[J]. Applied ocean research, 1992, 14(6): 371–379. DOI:10.1016/0141-1187(92)90041-H |
| [7] | NEWMAN J N. Wave effects on deformable bodies[J]. Applied ocean research, 1994, 16(1): 47–59. DOI:10.1016/0141-1187(94)90013-2 |
| [8] |
沈庆, 陈徐均. 系泊多浮体系统波浪运动响应的动力学分析[J].
解放军理工大学学报, 2002, 1(4): 31–36.
SHEN Qing, CHEN Xujun. Dynamic analysis of moored multi-body floating system's responses to regular waves[J]. Journal of PLA university of science and technology, 2002, 1(4): 31–36. |
| [9] |
勾莹, 滕斌, 宁德志. 波浪与两相连浮体的相互作用[J].
中国工程科学, 2004, 6(7): 75–80, 93.
GOU Ying, TENG Bin, NING Dezhi. Interaction effects between wave and two connected floating bodies[J]. Engineering science, 2004, 6(7): 75–80, 93. |
| [10] | HONG S Y, KIM J H, CHO S K, et al. Numerical and experimental study on hydrodynamic interaction of side-by-side moored multiple vessels[J]. Ocean engineering, 2005, 32(7): 783–801. DOI:10.1016/j.oceaneng.2004.10.003 |
| [11] | SUN L, TAYLOR R E, CHOO Y S. Responses of interconnected floating bodies[J]. The IES journal part a:civil & structural engineering, 2011, 4(3): 143–156. |
| [12] |
刘文玺, 周其斗, 张纬康, 等. 浮体与系泊系统的耦合动力分析[J].
船舶力学, 2014, 18(8): 940–957.
LIU Wenxi, ZHOU Qidou, ZHANG Weikang, et al. Dynamic analysis of the coupled floating body/mooring system[J]. Journal of ship mechanics, 2014, 18(8): 940–957. |
| [13] |
许鑫, 杨建民, 李欣, 等. 海洋工程中多浮体系统的水动力研究综述[J].
中国海洋平台, 2014, 29(4): 1–8, 13.
XU Xin, YANG Jianmin, LI Xin, et al. Review of the research on multi-body system hydrodynamics[J]. China offshore platform, 2014, 29(4): 1–8, 13. |
| [14] |
张立忠. 我国矿山载人索道现状及发展前景[J].
中国索道, 2002, 2(5): 1–4.
ZHANG Lizhong. Development and application of carrying people ropeway in the mine[J]. China ropeway, 2002, 2(5): 1–4. |
| [15] |
任爱娣, 张得伟, 何学军. 航行横向补给舰船运动对高架索张力影响[J].
舰船科学技术, 2014, 36(7): 94–96, 102.
REN Aidi, ZHANG Dewei, HE Xuejun. Influence of tension in highline cable of alongside replenishment by the motion of ships[J]. Ship science and technology, 2014, 36(7): 94–96, 102. |
| [16] |
余建星, 顾鹏. 海上干货补给技术[J].
海洋技术, 2005, 24(3): 105–110.
YU Jianxing, GU Peng. The technique of solid cargo supplying on the sea[J]. Ocean technology, 2005, 24(3): 105–110. |
| [17] |
郑丽凤, 周新年, 巫志龙. 悬索的理论计算与实测误差分析[J].
北华大学学报:自然科学版, 2010, 11(2): 162–168.
ZHENG Lifeng, ZHOU Xinnian, WU Zhilong. Error analysis among theoretical calculation and measure data of flexible cable[J]. Journal of Beihua university:natural science, 2010, 11(2): 162–168. |
| [18] |
周新年.
架空索道理论与实践[M]. 北京: 中国林业出版社, 1996: 140-200.
ZHOU Xinnian. Theory and practice of aerial ropeway[M]. Beijing: China Forestry Publishing House, 1996: 140-200. |
| [19] |
余建星, 顾鹏. 海上分离式轻型补给系统研究[J].
天津大学学报, 2006, 39(11): 1270–1271.
YU Jianxing, GU Peng. Offshore minitype detached replenishment system[J]. Journal of Tianjin university, 2006, 39(11): 1270–1271. |



