海事巡逻执法船属于政府公务船,是海事机构在水上执行监管业务的移动办公平台,也是海事执法的最重要基础装备。在我国,海事机构负责海上交通事故、船舶及相关水上设施污染事故的调查和处置等。对于海事机构管辖的一个水域,如何科学配备价值昂贵的巡逻船一直是一个难以解决的复杂优化问题[1]。这个问题一方面涉及到国家赋予海事机构的监管职责是否能够顺利实现,另一方面涉及国家投资的多少和投资的使用效率。
在船舶配置方面,以往针对商船船队做过较多的研究[2, 3, 4, 5]。但由于政府公务船舶的用途、功能与商用船舶截然不同,以往研发的商船队规划方法难以直接运用于政府公务船队的规划。而在海事船舶、公务船舶配置优化方面,能够查阅到的研究文献较少[6, 7, 8, 9]。近年,由于我国政府加大投资力度,海事船队的建设速度加快,海事船舶合理配置问题愈显突出,对于科学配置方法的需求更加迫切,国内也开始了对这一领域的研究和探索[10, 11, 12]。文献[13]中,主管机关根据理论分析和经验数据建立起一套海事船舶配备数量测算方法。这是一种半理论、半经验的方法,为便于求解,研究者对这一复杂问题做了简化计算处理,但在实际运用中有时仍然存在操作困难、计算结果受不确定性影响等问题。因此,本文在现有研究和实践经验基础上,基于监管任务需求的思路,提出了一种更加直接的海事船舶配备数量计算新方法。
1 问题描述与定义海事巡逻船配置问题通常从确定船型开始。由于不同海域的自然状况存在较大差异,以及海事业务对船舶性能的需求存在差异,在计算海事船舶配置数量之前,要先确定需要哪些类型的船舶。确定船型后,再根据各型船的单船监管能力决定各型船的配置数量。一艘海上巡逻船的监管能力是指基于该船本身的技术特征在巡逻执法中能够有效监管或威慑的水域面积。本文主要讨论船舶配置数量的确定。
海事船舶的配置要满足海事机构在管辖水域执行公务活动的要求。根据海事机构公务执法特点,在配置海事船舶时应该考虑的主要因素包括:1)辖区面积的大小及水域环境特征;2)辖区水域风险特征;3)辖区业务类型及业务量;4)船舶到达现场的时间要求等。
此外,在确定配船数量时,还要满足在给定水域上可以同时监视到的面积大小、对任一水域的巡逻频率或单位时间内巡逻监视次数等基本要求。对巡逻监视面积大小及巡逻频率的要求反映了对辖区安全监管的程度。
为了便于建立计算模型并说明其建模原理,文中采用如下定义和假设。
1)如果水域的风、浪、流等自然条件适合于船舶安全航行、作业,且水面上能见度极好,则称这种环境为海事巡逻船出航执行任务的理想环境,或简称理想环境。
2)在理想环境下,巡逻船上最高监视点能够监视的水面圆面积称之为巡逻船的单船监管面积或单船监视能力。
3)在理想环境下,当多艘巡逻船同时巡逻时,在各船监视圆面积中扣除因相邻船舶同时巡逻产生的重叠部分后的监管面积称之为巡逻船的有义监管面积或有义监视能力。当各巡逻船监管面积不发生重叠时,一艘巡逻船的有义监视能力就是其能够监视的水面圆面积,即单船监管面积。
4)在理想环境下,被监视水域的面积与辖区水域总面积之比称之为监视面积覆盖率。其中注意到,当两船或多船形成的监视面积重叠时,应扣除重叠部分的监视面积,即监视面积覆盖率是有义监管面积与辖区水域总面积之比。
假设辖区水域的面积为S,其边界上两个最远点的直线距离或最大长度为L,水面形状具有凸形图或近似凸形图特点。水域上只配置同型巡逻船,巡逻船监视圆的半径为d。
5)当S/L≤$\sqrt 2 $d时,称该辖区水域为狭长水域。
设某海事机构监管的水域为非狭长型水域,即有S/L>$\sqrt 2 $d。当派遣多艘巡逻船分布在水域上巡逻时,巡逻船以正方形网格方式分布或排列在水域上,即每个网格节点上配置一艘巡逻船,船与船之间的距离根据要求的水域面积监视能力确定。
基于上述假设和定义,认为辖区面积、特点、风险大小、巡航模式、任务需求等因素是影响船舶配备数量的主要因素。需要解决的问题表述为:在辖区水域处于理想环境下,计算满足辖区监管要求的船舶最少配备量。
2 船舶配置量测算模型为了确定一艘巡逻船的监管面积,将水面上的船舶简化成为一个以一定速度运行的监视点,该点的高度为执法人员站在船上最高执法位置时的视线位置或扫描雷达位置。巡逻船的监管能力取决于其船上最高监视位置的高度及监视海面面积的大小。考虑到地球表面存在曲度,监视点能够观测到的理论最远物标可以用下式计算[14]:
| $d = c\left( {\sqrt {{H_1}} + \sqrt {{H_2}} } \right)$ | (1) |
一艘巡逻船在海上某一点能够观测到的海面面积是以式(1)计算出的距离d为半径的圆形面积sj,称其为静态监管面积:
| ${s_j} = \pi {d^2}$ | (2) |
式中:d为地理视距或监视半径,n mile;H1为巡逻船上监视点高度,m;H2为海上物体或目标的高度,m;sj为单船静态监管面积,n mile2;c为常数2.09。
当某海事机构要求在任一时刻能够对监管水域施行监视全覆盖时,理论上该海事机构需要配备的船数为
| ${N_t} = \frac{S}{{{S_j}}} = \frac{S}{{\pi {d^2}}}$ | (3) |
式中:Nt为巡逻船的配置数量。
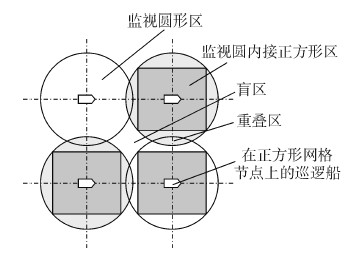
由式(3)计算出的是假设船舶静止分布在管辖水域范围内、监视面积与水域面积相等时的配船数理论值。事实上,按照此Nt值配船仅是监视面积与辖区面积在数量上的相等,而非监视面积恰好覆盖管辖水域。此时必然在S水域内存在监视面积重叠部分,也会存在监视盲区(见图 1)。因此,在确定监管水域总面积为S、单船监视能力为sj情况下需要配置的船舶数量时,还应考虑到船舶排列方式、水域边界形状等影响因素。
|
| 图 1 监管面积发生重叠 Fig. 1 Overlapping of surveillance area |
在监管水域的形状通常都不规则、每船的理论监视面积都是圆形的一般情况下,根据是否要求监视面积理论全覆盖、实际全覆盖或是满足规定的面积覆盖率来计算需要的船舶数量。设海事机构要求在监管水域上实现的监视面积覆盖率为β。
2.1 要求监管面积全覆盖(β=100%)情况β=100%时,单船的有义监视能力只能计及船舶监视圆面积sj中的圆内接正四边形面积,其值为2d2,见图 1。当S为矩形且其边长都为$\sqrt 2 $d的整数倍时,配船数理论上可由下式计算:
| ${N_{100}} = \frac{S}{{2{d^2}}}$ | (4) |
当S不为2d2的整数倍,且其边缘为不规则形状的一般情况时,先根据辖区水域形状截取与S等面积的矩形,并使此矩形与辖区水域重叠时,二者的重叠面积最大。在此矩形内按照正方形网格方式排列巡逻船,使其监管面积达到要求的覆盖率,然后根据监管面积外剩余未覆盖的辖区水域形状特点排布巡逻船,使其尽可能覆盖剩余的辖区水域面积。在这种情况下,使监管面积覆盖辖区水域需要的巡逻船数量不仅与辖区面积的大小有关,也与辖区水域边界形状有关。不妨将辖区水域边界形状不规则对船舶配置数量的影响看做是辖区面积发生增量变化。令Δ为与因辖区水域边界形状不规则而对船舶配置数量产生影响等同的辖区附加面积,则得出配船数近似计算公式如下
| ${N_P} = \frac{{S + \Delta }}{{2{d^2}}}$ | (5) |
式中:Δ为附加面积,是计算船舶配置数量时,辖区水域形状对辖区面积的影响函数。
为了确定Δ的取值范围,分析三种情况。1)当辖区水域的面积S为矩形,且其长、宽恰好是$\sqrt 2 $d的整数倍,此时Δ=0。2)当辖区水域形状接近并成为狭长水域形状时,有Δ < S。这表明若按照最多增加一倍狭长水域面积计算出的数量配船,一般会使巡逻船的监管面积完全覆盖辖区水域面积。3)更一般的情况,此时辖区水域形状远离狭长水域形状,并且一般有0 < Δ < S的关系。即:第1种情况,可以用式(4)直接计算辖区上需要配置的船舶数量,不需要对辖区增加附加面积;第2种情况辖区水域形状对附加面积影响最大,需要增加的附加面积也最大,在用式(5)计算巡逻船配置数量时,可以取Δ≈S;其他情况时,增加的附加面积一般在这两个数值之间。
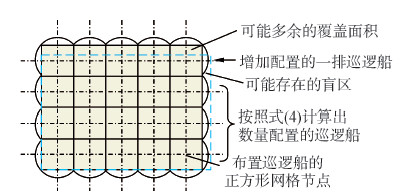
下面用辖区面积为正方形或接近正方形的典型情况进一步说明这种近似计算方法的原理。用式(4)计算出巡逻船配置数量后,沿辖区一侧按照覆盖面积最大化原则以正方形网格方式紧密排列巡逻船,如图 2所示。图 2中粗虚线表示辖区范围。如果Np艘巡逻船全部排列完毕后由于辖区形状特点还存在未覆盖的监管面积,则需要在辖区未被覆盖的一侧增加监视覆盖面积Δ,以便增加一排巡逻船,保证边缘部分的面积得到监视覆盖。因巡逻船监管面积圆内接四边形的边长为$\sqrt 2 $d,一侧边界需要增加监视的面积近似为矩形或带状,其长为$\sqrt S $,所以一排巡逻船增加的监管面积为Δ=d$\sqrt {2S} $。此时,式(5)变为
| ${N_P} = \frac{{S + d\sqrt {2S} }}{{2{d^2}}}$ | (6) |
|
| 图 2 监管水域全覆盖示意图 Fig. 2 Sketch map of water area fully covered by surveillance |
按照式(6)计算配船数,一方面计算出的配船数使其所有船的有义监视总面积有可能大于需要监视的水域面积,且极端情况下计算出的配船数最多可能超过满足全覆盖需要的$\sqrt S $/($\sqrt 2 $d)艘船舶;另一方面,因水域边界形状不规则及巡逻船监视面积为圆形而造成的盲区(若有)会远远小于已覆盖的监视面积。实际应用中,当S足够大且其形状趋近于正方形时,这两方面情况带来的计算误差都可以忽略。因此,式(6)为船舶全年运行,要求监视能力对辖区面积实际全覆盖时配船数的近似计算值。而式(3)为船舶全年运行,要求监视能力对辖区面积理论上全覆盖时配船数的近似计算值。显然,Nt < Np。
2.2 要求监管面积达到规定的覆盖率(β < 100%)情况当对水域的监管仅要求达到一定的监管面积覆盖率β(0≤β < 1)时,在给定海事辖区和单船监管能力的情况下,要求的监管面积覆盖率β越小,计算出的配船数也会越少,辖区配船数是要求的监管面积覆盖率的函数。
在多艘巡逻船按照正方形列阵同时巡逻、各船监管面积不发生重叠情况下,监管圆面积覆盖率达到最大值时,覆盖率的理论最大值为β=πd2/(4d2)=π/4。
参照式(3)、(6),当0≤β≤π/4时,有:
| ${N_\beta } = \beta \frac{{S + d\sqrt {2S} }}{{\pi {d^2}}}$ | (7) |
而当π/4 < β≤1时,在管辖水域上多艘巡逻船同时巡逻形成的监管面积之间会发生如图 1所示的重叠现象。在此种情况下,一般不能用式(7)计算配船数量Nβ,但可以设
| ${N_\beta } = R\left( \beta \right)\frac{{S + d\sqrt {2S} }}{{\pi {d^2}}}$ | (8) |
式中:R(β)为覆盖函数,并令覆盖函数R(β)=βπ/y(β),称y(β)为监视圆面积重叠函数。当两巡逻船接近、两船的监视圆面积互相重叠时,R(β)与因面积重叠而减少的监视面积有关。
作为近似计算,设y(β)为β的线性函数,并根据式(6)、(7),当β=π/4时,y(β)=π,当β=1时,y(β)=2,推导出:
| $y\left( \beta \right) = 4\left( {\pi - 2} \right)\left( {\beta - 1} \right)/\left( {\pi - 4} \right) + 2$ |
因此有
| $R\left( \beta \right) = \beta \pi \left( {\pi - 4} \right)/\left( {4\pi \beta - 2\pi - 8\beta } \right)$ |
整合式(7)、(8)可知覆盖函数:
| $R\left( \beta \right) = \left\{ \begin{array}{l} \frac{{\beta \pi \left( {\pi - 4} \right)}}{{4\pi \beta - 2\pi - 8\beta }},\;\;\;\pi 4 < \beta \le 1\\ \beta ,\;\;\;\;\;0 \le \beta \le \pi /4 \end{array} \right.$ | (9) |
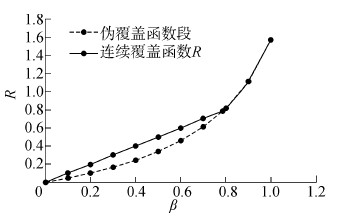
覆盖函数只与β有关,其关系曲线如图 3所示。从而,式(8)、(9)是在辖区水域上巡逻船静态分布时测算海事巡逻船配置量的基本公式。
|
| 图 3 覆盖函数曲线 Fig. 3 Curves of covering function |
在大、中型巡逻船上携带飞行器或直升机的情况下,其水上巡逻执法的监视能力显著提高,主要体现在监视范围明显扩大、执法力量到达现场的速度明显加快。这种情况下,可以将监视点的高度H1提升为飞行器常用的巡航高度,并由此计算出监视半径d和巡逻船的监视圆面积sj,再代入式(8)求得船舶配置数量。
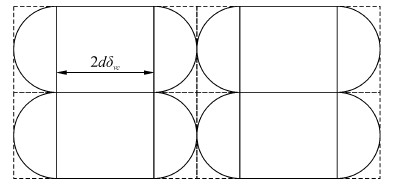
2.4 对辖区水面有巡视频率要求的情况船舶(监视点)在水面上具有移动能力,可以按照一定的航速动态巡航,遇到紧急情况时还可以提高航速全速航行。设船舶以巡航速度vc沿某一方向直线航行,δ时间内监视点因航行增加的监视覆盖面积为2dδvc,见图 4,巡视的面积为
| ${s_d}\left( \delta \right) = \pi {d^2} + 2d\delta {v_c}$ | (10) |
式中:sd(δ)为δ时间内巡视一次的动态监管面积。
|
| 图 4 巡逻船航行δ时间形成的监管面积 Fig. 4 Surveillance area shaped by patrol boats in δ time |
可知,在多船联合巡逻、各船以一定间距同向航行情况下,如果要求水域上任何部分都必须得到监视(24 h监视能力),则采用式(8)测算船舶配备数量;如果要求在δ时间段内辖区水面至少得到一次巡视,则式(8)分母应修正为式(10)决定的sd(δ)。
这里需要指出,在这种情况下,覆盖函数R(β)的关于β的取值区间实际上发生了微量变化,覆盖函数R(β)的表达式也变得更加复杂。但考虑到其仅在β的[(πd+2δvc)/(4d+2δvc),1]区间发生变化,且变化量不大(偏于保守),仍然采用式(9)近似计算覆盖函数R(β)。因此由式(8)、(9)得到近似计算公式:
| ${N_\beta } = R\left( \beta \right)\frac{{S + d\sqrt {2S} }}{{\pi {d^2} + 2d\delta {v_c}}}$ | (11) |
| $R\left( \beta \right) = \left\{ \begin{array}{l} \frac{{\beta \pi \left( {4 - \pi } \right)}}{{4\pi \beta - 2\pi - 8\beta }},\;\;\frac{{\pi d + 2\delta {v_c}}}{{4d + 2\delta {v_c}}}\; < \beta \le 1\\ \beta ,\;\;\;\;\;0 \le \beta \le \frac{{\pi d + 2\delta {v_c}}}{{4d + 2\delta {v_c}}} \end{array} \right.$ | (12) |
在确定一个海事辖区上需要配置船舶数量的实践中:1)根据海事辖区水域面积及其形状特点计算出的船舶配置的基本数量。2)考虑不同辖区水域的风险大小、分布形式、巡航模式或习惯等因素对巡逻船数量做出专项增量计算。3)根据海事辖区的特殊情况和难以量化计算的其他因素对辖区船舶配置量做出微量调整。海事辖区的特殊情况和难以量化的其他因素包括但不限于需要特殊监管的重要航道、桥梁、施工作业现场、危险品运输通道、临时任务、基层海事单位设置特点等。将上述分项计算结果汇总,得到船舶配置数量的理论值。4)考虑到船舶不可能全年每天都出航执勤,除特别恶劣海况不能出航外,船舶每年还需要有一定的维护修理、业务训练等不能出航执行任务的时间。船舶出航执勤率是指船舶适航且可用于执行巡逻、护航、现场监管等海事监管任务的时间与船舶总时间之比。根据船舶出航执勤率确定满足各项要求的船舶配置数量。
此外,需说明两点:1)当监管水域上配置不同类型的巡逻船时,可以先根据水域环境特征将整个辖区划分成适用不同船型的水域,然后对每一水域计算其需要的船舶配置数量;也可以按照类似的原理和方法直接推导船舶配置数量的近似计算方法。2)当考虑辖区水域不总能达到理想环境的一般情况时,可以根据辖区海域常见的能见度或规定的能见度修正距离参数d,然后将经过修正的d值代入相应公式计算巡逻船配置数量。
3 计算案例设在海事机构G管辖的近海水域内适用于J型巡逻船的水域面积1×104 n mile2。J型巡逻船的相关技术参数如表 1。其中J型船是近海航区巡逻船,可携带中型直升机。假设海上物标高度H2= 0。
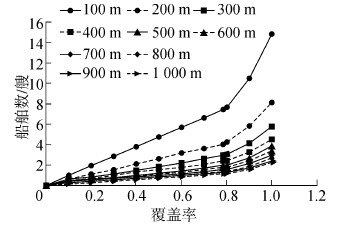
将表 1中的数据代入式(3)、(8),并基于对辖区水域不同的监视覆盖率要求计算出各种情况下的配船数如表 2所示。配船数不仅与要求的监管面积覆盖率有关,也与船上监视点高度或船载飞行器巡航高度有关。图 5中描绘了辖区配船数量与要求的监管面积覆盖率β和监视点高度H1的关系曲线。在[100,1 000]区间每隔100 m计算出的每条曲线对应一个监视点高度H1。
| 船型 | J型船 |
| 船长/m | 60 |
| 船宽/m | 9.2 |
| 巡航速度/kn | 16.5 |
| 最大航速/kn | 22 |
| 监视点高度/m | 6.2 |
| 飞行器巡航高度/m | 500 |
| 飞行器速度/kn | 60 |
| 船上监视半径dc/n mile | 5.20 |
| 船上监视圆盘面积sjc/n mile2 | 85.08 |
| 船上监视圆内接正方形面积sjnc/n mile2 | 54.16 |
| 飞行器监视半径df/n mile | 46.73 |
| 飞行器监视圆盘面积sjf/n mile2 | 6 861.41 |
| 飞行器监视圆内接正方形面积sjnf/n mile2 | 4 368.10 |
|
| 图 5 β和H1对配船数量的影响 Fig. 5 The influence of β and H1to the number of allocating ships |
表 2和图 5中的计算结果表明,在单船监管能力一定的情况下,随着监管面积覆盖率β的提高,在给定辖区面积上需要配备的船数增加。当β在[π/4,1]区间时,随着β的提高,需要配备的船数快速增加。此外,随着监视距离的增加或监视手段的改善(对应更先进的监测技术),在给定辖区面积上根据规定监视覆盖率计算出的配船数减少。从而在给定辖区配船数与要求的监管强度和船舶技术先进程度之间建立起直接的函数关系。案例计算结果也证明,海事巡逻船携带飞行器巡逻,能够大幅度提高其监管面积,在同样监管强度要求的条件下,有助于大幅度减少辖区水域上需要配备的巡逻船数量。
| 监视点位置 | 监视面积覆盖率 | 配船数 |
| 只考虑船舶本身的监视范围 | 理论全覆盖 | 118 |
| 只考虑船舶本身的监视范围 | 实际全覆盖 | 198 |
| 只考虑船舶本身的监视范围 | β=π/4 | 99 |
| 只考虑船舶本身的监视范围 | β=50% | 63 |
| 考虑船载飞行器,且其监视点高度为500 m的情况 | 实际全覆盖 | 4 |
| 考虑船载飞行器,且其监视点高度为500 m的情况 | β=π/4 | 2 |
| 考虑船载飞行器,且其监视点高度为500 m的情况 | β=50% | 1 |
| 注:表中第2行是按照式(3)计算出的达到理论全覆盖需要的配船数;其他由式(8)计算需要的配船数。 | ||
基于对我国海事履职要求、船舶性能与任务匹配及相关影响因素的分析,提出了一套新的海事巡逻船配置量测算方法。该方法的主要特点为:
1)在测算船舶监视能力的基础上,引入水域监视覆盖率和覆盖函数,并基于水域监视覆盖函数测算船舶配置数量。水域监视覆盖率需求直观反映了配置的船舶能够达到的监管水平。覆盖函数的引入,增加了对于不同水域可以施行不同监管强度的灵活性,即β取不同值。这种灵活性更易于满足国家对不同水域提出不同管控目标的实际需要。
2)为了计及海事辖区形状不规则对配船数量的影响,引入辖区水域形状对监管面积的影响函数,其值完全由辖区边界形状确定。对于一个给定辖区,在理论分析的基础上通过长期实践验证,可以确定面积影响函数的合理值。
3)建立了根据水域自然特征、风险统计数据、巡逻执法模式计算和非量化因素调整,定量计算与定性分析相结合,以定量计算为主的分步计算、累加式海事船舶配置数量测算程序。
4)在确定单船监管能力时,考虑了不同船载监测装备或设施(如飞行器)可能带来的效果。建立了定量分析监测点高度对巡逻船监管面积大小影响程度的关系式,为海事船型论证和船舶配置优化奠定了基础。
采用本文中提出的海事船舶配置计算方法,能够充分考虑现代执法装备(如电子监视装置、飞行器等)的运用效果,能够合理确定船舶需求数量,有助于科学规划海事船队规模,使国家投资建造的海事船舶充分发挥作用。今后研究的方向是改进覆盖函数和面积影响函数的计算精度,探索建立各种复杂情况下覆盖函数和面积影响函数的理论表达式。就船舶配置数量计算方法而论,案例分析结果已经验证了其实用性。适当调整计算公式中的有关参数,该方法的原理和程序也适用于内河水域海事船舶、海警船舶以及类似公务船舶配置数量的测算。
| [1] |
何忠龙, 李云芝. 海域管护舰艇需求的数学模型[J]. 装备指挥技术学院学报, 2007, 18(4): 6-9. HE Zhonglong, LI Yunzhi. The mathematical model of naval vessel requirement[J]. Journal of the academy of equipment command & technology, 2007, 18(4): 6-9. |
| [2] | EVERETT J L, HAX A C, LEWINSON V A, et al. Optimization of a fleet of large tankers and bulkers: A liner programming approach[J]. Marine technology, 1972, 9(4): 430-438. |
| [3] | XIE Xinlian, JI Zhuoshang, YANG Yu. Nonlinear programming for fleet planning[J]. International shipbuilding progress, 1993, 40(421): 93-103. |
| [4] | XIE Xinlian, XU Dongling, YANG Jianbo, et al. Ship selection using a multiple-criteria synthesis approach[J]. Journal of marine science and technology, 2008, 13(1): 50-62. |
| [5] |
谢新连, 桑惠云, 杨秋平, 等. 中国进口原油运输船队规划案例研究[J]. 系统工程理论与实践, 2013, 33(6): 1543-1548. XIE Xinlian, SANG Huiyun, YANG Qiuping, et al. Case study on fleet planning for carriers of China importing crude oil[J]. Systems engineering-theory & practice, 2013, 33(6): 1543-1548. |
| [6] | BHARGAVA H K. Fleet mix planning in the U.S. Coast Guard: issues and challenges for DSS[R]. Recent Developments in Decision Support Systems, NATO ASI Series Volume 101, 1993: 575-598. |
| [7] | DARBY-DOWMAN K, FINK R K, MITRA G, et al. An intelligent system for US Coast Guard cutter scheduling[J]. European journal of operational research, 1995, 87(3): 574-585. |
| [8] | United States General Accounting Office. Coast guard: deepwater program acquisition schedule update needed[R]. Washington, D.C.: GAO, 2004. |
| [9] | JOHN P H. Preliminary observations on deepwater program assets and management challenges[R/OL].[2007-02-15]. Washington, D.C.: United States Government Accountability Office. http://www.gao.gov/cgi-bin/getrpt?GAO-07-446T. |
| [10] |
杨立波. 海上交通巡逻和救助船舶配置规模研究[J]. 船舶工程, 2013, 35(2): 19-22. YANG Libo. Study of maritime traffic patrol and rescue ships configuration amount[J]. Ship engineering, 2013, 35(2): 19-22. |
| [11] |
黄鹏飞, 周建文, 李子富. 基于AHP的海事巡逻船配置[J]. 大连海事大学学报, 2010, 36(4): 14-16. HUANG Pengfei, ZHOU Jianwen, LI Zifu. Allocation study of marine patrol craft resources based on AHP[J]. Journal of Dalian maritime university, 2010, 36(4): 14-16. |
| [12] |
赵福波, 谢新连, 高成男, 等. 沿海巡逻执法船配置研究现状[J]. 大连海事大学学报, 2014, 40(4): 42-48. ZHAO Fubo, XIE Xinlian, GAO Chengnan, et al. Research status of coastal patrol and law-enforcement vessel configuration[J]. Journal of Dalian maritime university, 2014, 40(4): 42-48. |
| [13] | 交通部. 《海事船舶配备管理规定(试行)》(交规划发[2007] 3号)[R]. 北京: 交通部, 2007. |
| [14] |
谢新连. 船舶运输管理与经营[M]. 大连: 大连海事大学出版社, 2009: 72. XIE Xinlian. Shipping management and orperations[M]. Dalian: Dalian Maritime University Press, 2009: 72. |



