2. Science and Technology Research Institute, Harbin Engineering University, Harbin 150001, China;
3. China National Aeronautical Radio Electronics Research Institute, Shanghai 200241, China
舰载机纵向偏差对着舰效果影响很大,位置过高会导致落点靠前而无法顺利挂索,位置过低可能发生撞舰的严重事故。特别是舰载机在时刻运动的航母上完成着舰任务更加困难,需要根据航母的运动状态实时调整位置和姿态。因此在纵向上,自动着舰系统有重要的实际意义,可降低着舰风险,提高着舰成功率。
文献[1-2]以大量的试验数据为依托,在静平衡点的基础上建立着舰风险模型并设计自动着舰系统,但并未考虑理想下滑道的时变特点;文献[3]采用甲板预报的方式实现甲板运动补偿的目的,但只是在相位上超前,并未结合甲板运动特性;近几年,学者们对智能控制理论尤为青睐,常采用智能控制来设计舰载机着舰引导律,如文献[4]和文献[5]分别采用指令滤波积分反步控制方法和模糊PID控制方法,设计舰载机自动着舰纵向控制系统,但这两个文献中舰载机动力学模型仍为线性形式,同时甲板运动补偿的实时性也未解决。文献[6]利用一种新颖的预测控制方法来处理轨迹跟踪问题,本文对此有所借鉴。
本文将通过动平衡点线性化的方式建立舰载机着舰数学模型,然后构建着舰风险模型,并与传统MPC相结合,形成时变风险权值的MPC算法。
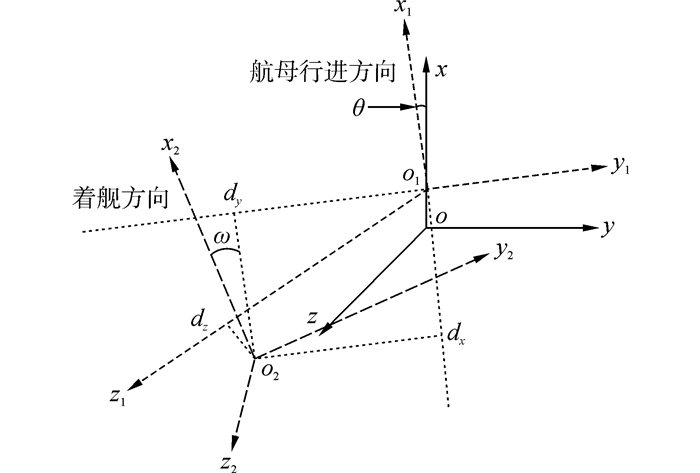
1 舰载机纵向动力学模型本文涉及的相关坐标系定义如图 1所示[7-8]。图 1中:oxyz为大地坐标系,原点o为航母初始位置,x方向指向北方,y方向指向东方,z方向垂直于海平面向下;o1x1y1z1为航母本体系,原点o1为航母摇摆中心,x1方向为航母行进方向,y1方向指向航母右舷,z1方向垂直向下;o2x2y2z2为着舰坐标系,原点为舰载机的理想着舰点(甲板面第2、3道阻拦索中间位置),x2方向为垂直于阻拦索向前,y2方向平行于阻拦索向右,z2方向垂直与甲板面向下。在上图中,ω为斜角甲板与航母行进方向夹角,dx、dy和dz分别为理想着舰点在航母本体系中的坐标值。
|
| 图1 相关坐标系示意图 Figure 1 Related coordinate system |
| $ \left\{ {\begin{array}{*{20}{l}} {\dot V =-\frac{D}{m} + g\left( {\cos \theta \sin \alpha-\sin \theta \cos \alpha } \right) + \frac{T}{m}\cos \alpha }\\ {\dot \alpha =-\frac{L}{{mV}} + q + \frac{g}{V}\left( {\cos \theta cos\alpha + sing\alpha sin\theta } \right) - }\\ {\;\;\;\;\;\;\;\;\frac{{T\sin \alpha }}{{mV}}}\\ {\dot q = M/{I_{yy}}}\\ {\dot \theta = q}\\ {{{\dot P}_z} = - V\sin \left( {\alpha - \theta } \right)} \end{array}} \right. $ | (1) |
式中:V、α、q、θ和pz分别表示进舰速度、迎角、俯仰角速度、俯仰角和纵向位置;D、L、T和M分别表示气动阻力、气动升力、发动机推力和俯仰力矩。
设xd={Vd(t), αd(t), qd(t), θd(t), Pzd(t)}为舰载机实时着舰平衡态,则状态偏差ex可用下式表示:
| $ {\mathit{\boldsymbol{e}}_x} = \mathit{\boldsymbol{x}}- {\mathit{\boldsymbol{x}}_d} = \left[{\begin{array}{*{20}{c}} {{e_V}}\\ {{e_\alpha }}\\ {{e_q}}\\ {{e_\theta }}\\ {{e_{{P_z}}}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {V-{V_d}\left( t \right)}\\ {\alpha-{\alpha _d}\left( t \right)}\\ {q-{q_d}\left( t \right)}\\ {\theta - {\theta _d}\left( t \right)}\\ {{P_z} - {P_{zd}}\left( t \right)} \end{array}} \right] $ | (2) |
为便于后文预测控制中对偏差的抑制[11-12],此处将式(2)代入式(1),可得到基于状态偏差的舰载机纵向动力学模型。
在航母行进过程中,设舰载机在着舰坐标系下的坐标为Pa2(t)=(xa2(t), ya2(t), za2(t)),下滑道入口处的进舰距离为Pdist,航母航速为Vc,理想下滑角为γ,仿真步长为Δt,则Pa2(t)可由下式表示:
| $ \left\{ {\begin{array}{*{20}{l}} {{x_{{a_2}}}\left( t \right) = {P_{{\rm{dist}}}}-k\left( {{V_d}\left( t \right)\cos \gamma-{V_c}\cos \omega } \right)\Delta t}\\ {{y_{a2}} = 0}\\ {{z_{a2}}\left( t \right) = {x_{a2}}\left( t \right)\tan \gamma } \end{array}} \right. $ | (3) |
由着舰坐标系至航母本体系,再至大地坐标系变换后,舰载机理想下滑位置在大地坐标系下的坐标Pa(t)=(xa(t), ya(t), za(t))可由下式计算:
| $ {\mathit{\boldsymbol{P}}_a}\left( t \right) = {\mathit{\boldsymbol{L}}_y}\left( {\theta \left( t \right)} \right)\left( {{\mathit{\boldsymbol{L}}_z}\left( \omega \right){\mathit{\boldsymbol{P}}_{a2}}\left( t \right) + {\mathit{\boldsymbol{T}}_1}} \right) + {\mathit{\boldsymbol{T}}_2}\left( t \right) $ | (4) |
其中
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{L}}_z}\left( \omega \right) = \left[{\begin{array}{*{20}{l}} {\cos \omega }&{\sin \omega }&0\\ {-\sin \omega }&{\cos \omega }&0\\ 0&0&1 \end{array}} \right]}\\ {{\mathit{\boldsymbol{L}}_y} = \left( {\theta \left( t \right)} \right) = \left[{\begin{array}{*{20}{l}} {\cos \left( {\theta \left( t \right)} \right)}&0&{-\sin \left( {\theta \left( t \right)} \right)}\\ 0 &1&0\\ {\sin \left( {\theta \left( t \right)} \right)}&0&{\cos \left( {\theta \left( t \right)} \right)} \end{array}} \right]}\\ {{\mathit{\boldsymbol{T}}_1} = {\rm{diag}}\left( {{d_x}, {d_y}, {d_z}} \right)}\\ {{\mathit{\boldsymbol{T}}_2}\left( t \right) = {\rm{diag}}\left( {{p_x}\left( t \right), 0, {p_z}\left( t \right)} \right)} \end{array} $ |
式中:θ(t)为航母纵摇角,px(t)和pz(t)分别为航母在大地坐标系中x方向和z方向坐标值。
在实际着舰过程中,舰载机进场动力补偿系统可使飞机保持恒定的进舰速度和迎角[13],因此期望的进舰速度Vd(t)和期望的迎角αd(t)分别为恒定值Vd0和αd0,则舰载机着舰期望平衡态如下
| $ \left\{ {\begin{array}{*{20}{l}} {{V_d}\left( t \right) = {V_{d0}}}\\ {{\alpha _d}\left( t \right) = {\alpha _{d0}}}\\ {{P_z}_d\left( t \right) = {z_a}\left( t \right)}\\ {{\theta _d}\left( t \right) = {\alpha _d}\left( t \right)-\arctan \left( {\frac{{{z_a}\left( t \right)}}{{{x_a}\left( t \right)}}} \right)}\\ {{q_d}\left( t \right) = \frac{{{\theta _d}\left( t \right)-\theta \left( {t-1} \right)}}{{\Delta t}}} \end{array}} \right. $ | (5) |
同理,将控制量也以偏差形式表示,即eu={eδstab, eT},eδstab为升降舵舵角的偏差量,eT为油门开度的偏差量,则非线性模型经离散线性化为
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\dot e}}}_x}\left( {k + 1} \right) = \mathit{\boldsymbol{A}}\left( k \right){e_x}\left( k \right) + \mathit{\boldsymbol{B}}\left( k \right){\mathit{\boldsymbol{e}}_u}\left( k \right)}\\ {{\mathit{\boldsymbol{e}}_y}\left( {k + 1} \right) = \mathit{\boldsymbol{C}}\left( k \right){\mathit{\boldsymbol{e}}_x}\left( k \right) + \mathit{\boldsymbol{D}}\left( k \right){\mathit{\boldsymbol{e}}_u}\left( k \right)} \end{array}} \right. $ | (6) |
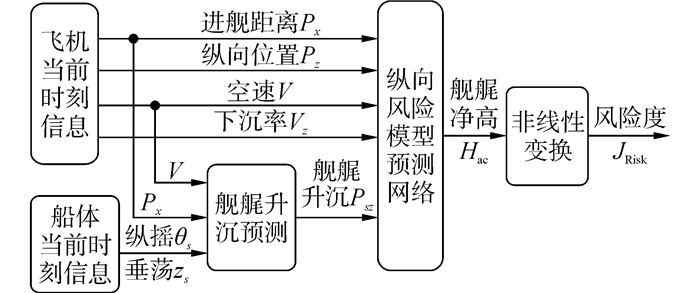
舰载机纵向风险主要来自机体或尾钩撞击航母舰艉,是否会撞击舰艉取决于飞机与舰艉的纵向位置。舰艉净高是指舰载机进舰末段到达舰艉处,与舰艉的垂向距离[8],因此可用舰艉净高来定性衡量纵向风险的大小,本文用Hac表示舰艉净高。通过建立舰载机飞行状态和航母运动状态与舰艉净高的关系,可建立与纵向风险的关系,纵向风险建模原理如图 2所示。
|
| 图2 纵向风险建模原理图 Figure 2 Principle of modeling longitudinal risk |
舰艉净高的极限值需要通过舰载机执行复飞指令来获得,即在相同的初始状态下,舰载机执行复飞操控时的舰艉净高是最大的。因此根据舰载机当前的进舰距离px,纵向位置pz,进舰速度V,下沉率Vz和舰载机到达舰艉时的舰艉升沉Psz,即刻执行复飞指令,可获得此次着舰试验的舰艉净高值。当以上变量遍历所有可能取值时,可获得着舰所有情况的舰艉净高,并将舰艉净高按满足实际情况的非线性形式映射到0~1的量化数值,本文将此值作为纵向风险值,纵向风险JRisk可用下式表示:
| $ {J_{{\rm{Risk}}}} = f\left( {{P_x}, {P_z}, V, {V_z}, {P_{sz}}} \right) $ | (7) |
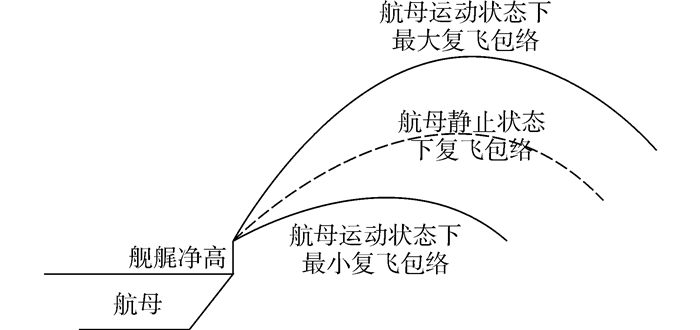
式中:f(*)为着舰风险非线性表达式。本文采用如下复飞准则[14]:1)飞行员响应复飞指令延迟时间为0.7 s;2)复飞操控动作为最大推力控制,并维持一定迎角。当不考虑甲板运动时,假设要求舰载机执行复飞指令,舰艉净高为某一特定值,则其复飞包络如图 3虚线所示;当考虑航母的纵向运动时,舰载机复飞包络如图 3两条实线所示。
|
| 图3 舰载机复飞包络示意图 Figure 3 Carrier-base aircraft waveoff envelope |
在海况为4级、航母航速为24 kn情况下,航母垂荡zs和纵摇θs可由下式表示:
| $ \left\{ {\begin{array}{*{20}{l}} {{z_s} = 1.22\sin \left( {0.6t} \right) + 0.305\sin \left( {0.2t} \right)}\\ {{\theta _s} = 0.5\sin \left( {0.6t} \right) + 0.3\sin \left( {0.63t} \right) + 0.25} \end{array}} \right. $ | (8) |
因此垂荡最大值为zsmax=1.38 m,垂荡最小值为zsmin=-1.38 m,纵摇最大值为θsmax=1.1°,纵摇最小值为θsmin=-0.6°。航母纵摇中心与舰艉的水平距离Ls=116 m,通过几何运算,航母舰艉升沉最大值Hsmax和最小值Hsmin分别3.5 m和-2.5 m。
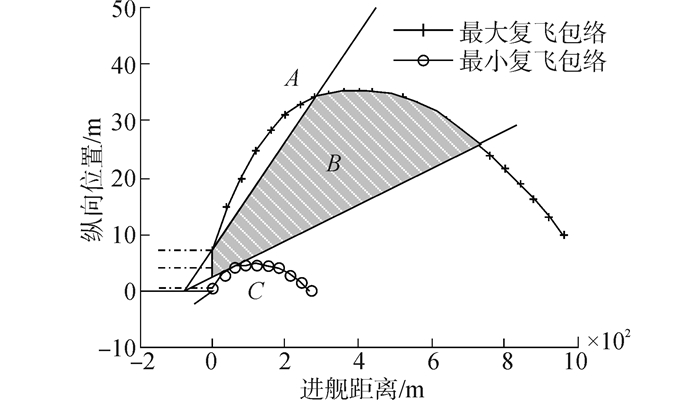
为计算复飞包络范围,本文假设舰载机最小进舰速度V=55 m/s,最大下沉率Vz=8 m/s,舰艉升沉最大值Hsmax=3.5 m,此时可获得最小复飞包络;舰载机最大进舰速度V=85 m/s,最小下沉率为Vz=0 m/s,舰艉升沉最小高度Hsmin=-2.5 m,此时可获得最大复飞包络。考虑菲涅尔灯光影响,理想着舰点距离舰艉78 m,理想下滑道与水平面夹角为3.5°,菲涅尔灯每层光束纵向张角为0.34°,则菲涅尔灯光最上层和最下层与水平面分别成4.2°和2.8°,可获得舰载机需要复飞的区域如下图B区域,本文纵向风险建模区域为B区域。
图 4将着舰过程的纵向平面分为三个区域:A、B和C,在A区域执行复飞,舰载机无撞舰风险,在C区域执行复飞,舰载机始终会撞击舰艉,故本文设定在A区域和C区域的纵向风险值JRisk(px, pz)如下
|
| 图4 舰载机纵向风险建模区 Figure 4 Carrier-base aircraft longitudinal risk modeling area |
| $ {J_{{\rm{Risk}}}} = \left( {{P_x}, {P_z}} \right) = \left\{ {\begin{array}{*{20}{l}} {0.1\;\;\;\left( {{P_x}, {P_z}} \right) \in A}\\ {0.9\;\;\;\left( {{P_x}, {P_z}} \right) \in C} \end{array}} \right. $ | (9) |
在纵向风险建模区中,以不同px、pz、V、Vz和Psz,按照复飞准则,执行复飞操控指令,重复仿真可获得一系列舰艉净高值。本文在图 4中B区域平均选取px和pz共105个位置,其他变量如下:
1)V/(m·s-1):55、60、65、70、75、80、85;
2)Vz/(m·s-1):0、4、8;
3)Psz/m:-2.5、-1、0、1、2、3.5。
因此可获得13 230组数据,部分样本数据如表 1。
| 序号 | px | pz | V | Vz | Psz | Hac |
| 1 | 50 | 11.77 | 55 | 0 | 0.0 | 6.681 |
| 2 | 50 | 6.77 | 55 | 0 | 0.0 | 1.854 |
| 3 | 50 | 4.08 | 55 | 0 | 0.0 | 0.0 |
| 4 | 100 | 16.29 | 55 | 0 | 0.0 | 9.618 |
| 13 229 | 200 | 15.34 | 70 | 4 | -1.0 | 7.235 |
| 13 230 | 250 | 19.87 | 70 | 4 | -1.0 | 11.79 |
为便于将舰艉净高归一化处理,当Hac>10 m时,舰载机不会有撞舰风险,本文将该情况下所有JRisk定为10 m;当Hac < 0 m时,一定会发生撞舰事故,本文将该情况下所有JRisk定为0 m。
本文制定着舰风险归一化映射函数原则如下:
1)与式(9)并集可覆盖所有风险取值,故将纵向风险建模区内的舰艉净高映射在0.1~0.9范围内;
2)映射函数与舰艉净高满足反比例关系;
3)舰艉净高在3 m处附近的风险变化明显。
本文采用如下Sigmoid型函数作为映射函数:
| $ {J_{{\rm{Risk}}}} = \left( {{P_x}, {P_z}} \right) = \frac{4}{{5 + 2{{\rm{e}}^{\left( {2{H_{ac}}-5} \right)}}}} + 0.1\;\;\;\left( {{P_x}, {P_z}} \right) \in B $ | (10) |
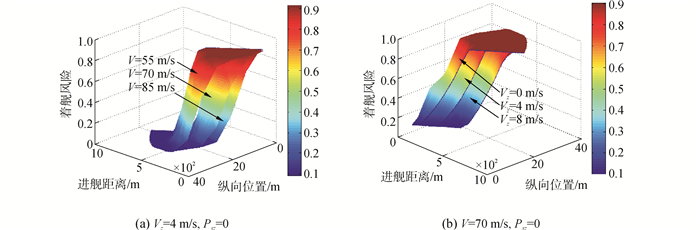
式(9)和式(10)共同构成了舰载机纵向着舰风险模型,根据表 1中全部的样本数据,利用BP神经网络训练,并根据式(10)将着舰风险归一化。BP神经网络输入层节点为5个,输出层节点为1个,隐层节点为7个,隐层选用双曲正切S型激活函数,训练次数为500次,训练后的误差为0.000 227。由于输入量的组合情况较多,为此本文选择有代表性的纵向风险三维图如图 5所示。
|
| 图5 纵向风险三维效果图 Figure 5 3-dimension figure of longitudinal risk |
从图 5中可以看出高风险区和低风险区比较集中,某些高维区域是高风险区,应重点关注,某些高维区域为低风险区,可适当弱化考虑,因此可建立纵向风险与风险影响因素的数值关系, 又由于风险影响因素可与式(6)中着舰状态偏差建立关系,则纵向风险权值矩阵QRisk可由下式表示:
| $ {\mathit{\boldsymbol{Q}}_{{\rm{Risk}}}} = {\rm{diag}}\left( {{Q_{{e_V}}}, {Q_{{e_\alpha }}}, {Q_{{e_q}}}, {Q_{{e_\theta }}}, {Q_{{e_{{P_z}}}}}} \right) $ | (11) |
矩阵QRisk将纵向着舰风险与舰载机状态偏差建立了关系,本文将使其影响MPC中状态权值来实现时变权值控制的目的。为增加滚动优化求解速度,本文建立QRisk关于进舰距离dap的系数矩阵K(dap)如下
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{K}}\left( {{d_{ap}}} \right) = }\\ {{\rm{diag}}\left( {{k_V}\left( {{d_{ap}}} \right), {k_\alpha }\left( {{d_{ap}}} \right), {k_q}\left( {{d_{ap}}} \right), {k_\theta }\left( {{d_{ap}}} \right), {k_{{P_z}}}\left( {{d_{ap}}} \right)} \right)} \end{array} $ | (12) |
式中:kV(dap)、kα(dap)、kq(dap)、kθ(dap)和kpz(dap)分别表示QeV、Qeα、Qeq、Qeθ和Qepz关于进舰距离dap的权值。K(dap)作为变参数主要有两个作用:1)当舰载机距舰较远时,通过增大QeV、Qeα和Qepz的权值来快速消除下滑偏差,同时放宽对俯仰角的控制约束;2)当舰载机距舰较近时,通过增大Qeq和Qeθ的权值以增加对俯仰角和跟踪甲板运动的控制。式(12)中各元素的变化曲线仍采用Sigmoid函数形式,前文中已将纵向风险归一化处理,并结合系数矩阵的物理意义,本文将kV(dap)、kα(dap)和kpz(dap)的取值范围设定为[0,3],将kq(dap)和kθ(dap)的取值范围设定为[1,2]。预测控制性能指标中的状态项权值矩阵Q(k):
| $ \mathit{\boldsymbol{Q}}\left( k \right) = \mathit{\boldsymbol{K}}\left( {{d_{ap}}} \right){\mathit{\boldsymbol{Q}}_{{\rm{Risk}}}} $ | (13) |
Q(k)的物理意义为:在性能指标滚动优化过程中,对各状态偏差的消除力度,其中权值越大,对相应状态偏差消除力度也越大,反之越小。同理,控制权值矩阵R(k)如下
| $ \mathit{\boldsymbol{R}}\left( k \right) = {\rm{diag}}\left( {{R_{{\rm{stab}}}}\left( {{d_{ap}}} \right), {R_{{\rm{thrust}}}}\left( {{d_{ap}}} \right)} \right) $ | (14) |
式中:Rstab(dap)和Rthrust(dap)分别表示升降舵和油门关于进舰距离的权值,权值的选取原理与Q(k)相同,因此Q(k)和R(k)都是单调递减的权值矩阵。
3 预测控制算法实现由于实际着舰中很多着舰状态不能直接获得,为此本文设计如下状态观测器来预估当前状态:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\bar e}}\left( {k + 1} \right) = \mathit{\boldsymbol{A}}\left( k \right)\mathit{\boldsymbol{\bar e}}\left( k \right) + \mathit{\boldsymbol{B}}\left( k \right){\mathit{\boldsymbol{e}}_u}\left( k \right) + }\\ {{\mathit{\boldsymbol{P}}_L}\left( {{\mathit{\boldsymbol{e}}_y}\left( k \right)-\mathit{\boldsymbol{C}}\left( k \right)\mathit{\boldsymbol{\bar e}}\left( k \right)} \right)} \end{array} $ | (15) |
式中:
| $ {\mathit{\boldsymbol{e}}_m}\left( {k + 1} \right) = \left( {\mathit{\boldsymbol{A}}\left( k \right)-{\mathit{\boldsymbol{P}}_L}\mathit{\boldsymbol{C}}\left( k \right)} \right){\mathit{\boldsymbol{e}}_m}\left( k \right) $ | (16) |
定理1 满足下面LMI的状态观测器是稳定的,并且可保证状态观测值收敛到实际状态值[7]:
| $ \left[{\begin{array}{*{20}{c}} {\lambda {\mathit{\boldsymbol{P}}_m}-{\mathit{\boldsymbol{P}}_L}}&*\\ {{\mathit{\boldsymbol{P}}_m}\mathit{\boldsymbol{A}}\left( k \right)-{\mathit{\boldsymbol{Y}}_\mathit{\boldsymbol{e}}}\mathit{\boldsymbol{C}}\left( k \right)}&{{\mathit{\boldsymbol{P}}_m}} \end{array}} \right] > 0 $ | (17) |
式中:Pm为正定对称阵,Ye=PePL,λ为延迟率。“*”表示矩阵中关于主对角线对称位置元素的转置,该表示方式在后文LMIs中均适用。
后文使用状态观测值
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\bar e}}\left( {k + 1 + i\left| k \right.} \right) = }\\ {\mathit{\boldsymbol{A}}\left( k \right)\mathit{\boldsymbol{\bar e}}\left( {k + i\left| k \right.} \right) + \mathit{\boldsymbol{B}}\left( k \right){\mathit{\boldsymbol{e}}_u}\left( {k + i\left| k \right.} \right)} \end{array} $ | (18) |
MPC的最优化问题的指标函数J0∞(k)如下[15]
| $ \begin{array}{*{20}{c}} {J_0^\infty \left( k \right) = \sum\limits_{i = 0}^\infty {{{\left\{ {\mathit{\boldsymbol{\hat e}}} \right.}_x}{{\left( {k + i|k} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( k \right){{\mathit{\boldsymbol{\hat e}}}_x}\left( {k + i|k} \right)} + }\\ {\left. {{\mathit{\boldsymbol{e}}_u}{{\left( {k + i|k} \right)}^{\rm{T}}}\mathit{\boldsymbol{R}}\left( k \right){\mathit{\boldsymbol{e}}_u}\left( {k + i|k} \right)} \right\}} \end{array} $ | (19) |
为增加算法可解性并提高算法计算速度,现将最优化指标函数J0∞(k)分为J01(k)和J1∞(k)两部分:
| $ \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{c}} {J_0^1\left( k \right) = \mathit{\boldsymbol{\bar e}}{{\left( {k|k} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( k \right)\mathit{\boldsymbol{\bar e}}\left( {k|k} \right) + }\\ {{\mathit{\boldsymbol{e}}_u}{{\left( {k|k} \right)}^{\rm{T}}}\mathit{\boldsymbol{R}}\left( k \right){\mathit{\boldsymbol{e}}_u}\left( {k|k} \right)} \end{array}}\\ {\begin{array}{*{20}{c}} {J_0^\infty \left( k \right) = \sum\limits_{i = 0}^\infty {{{\left\{ {\mathit{\boldsymbol{\bar e}}} \right.}_x}{{\left( {k + i|k} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( k \right){{\mathit{\boldsymbol{\bar e}}}_x}\left( {k + i|k} \right)} + }\\ {\left. {{\mathit{\boldsymbol{e}}_u}{{\left( {k + i|k} \right)}^{\rm{T}}}\mathit{\boldsymbol{R}}\left( k \right){\mathit{\boldsymbol{e}}_u}\left( {k + i|k} \right)} \right\}} \end{array}} \end{array}} \right. $ | (20) |
式中:Q(k)和R(k)由式(13)和(14)计算。
预测控制系统输入采用如下状态反馈形式:
| $ {\mathit{\boldsymbol{e}}_u}\left( {k + i|k} \right) = \mathit{\boldsymbol{G}}\left( k \right){{\mathit{\boldsymbol{\bar e}}}_x}\left( {k + i|k} \right), i \ge 1 $ | (21) |
取二次型函数L(
| $ \begin{array}{*{20}{c}} {L\left( {\mathit{\boldsymbol{\bar e}}\left( {k + i|k} \right)} \right) = \mathit{\boldsymbol{\bar e}}{{\left( {k + i|k} \right)}^{\rm{T}}}\mathit{\boldsymbol{H}}\left( k \right)\mathit{\boldsymbol{\bar e}}\left( {k + i|k} \right), }\\ {i \ge 1} \end{array} $ | (22) |
式中:H(k)为正定对称阵,并假设L(0)=0,
此处令L(
| $ \begin{array}{*{20}{c}} {L\left( {\mathit{\boldsymbol{\bar e}}\left( {k + 1 + i|k} \right)} \right)- L\left( {\mathit{\boldsymbol{\bar e}}\left( {k + i|k} \right)} \right) \le }\\ {- \left[{\mathit{\boldsymbol{\bar e}}{{\left( {k + i|k} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( k \right)\mathit{\boldsymbol{\bar e}}\left( {k + i|k} \right) + } \right.}\\ {\left. {{\mathit{\boldsymbol{e}}_u}{{\left( {k + i|k} \right)}^{\rm{T}}}\mathit{\boldsymbol{R}}\left( k \right){\mathit{\boldsymbol{e}}_u}\left( {k + i|k} \right)} \right], i \ge 1} \end{array} $ | (23) |
将式(23)左右两边同时从i=1加至i=∞得:
| $ J_1^\infty \left( k \right) \le L\left( {\mathit{\boldsymbol{\bar e}}\left( {k + i|k} \right)} \right) $ | (24) |
此处令ζ(k)为J0∞(k)的上界,则有下式成立:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\bar e}}{{\left( {k|k} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( k \right)\mathit{\boldsymbol{\bar e}}\left( {k|k} \right) + {\mathit{\boldsymbol{e}}_u}{{\left( {k|k} \right)}^{\rm{T}}}\mathit{\boldsymbol{R}}\left( k \right){\mathit{\boldsymbol{e}}_u}\left( {k|k} \right) + }\\ {\mathit{\boldsymbol{\bar e}}{{\left( {k + 1|k} \right)}^{\rm{T}}}\mathit{\boldsymbol{H}}\left( k \right)\mathit{\boldsymbol{\bar e}}\left( {k + 1|k} \right) < \zeta \left( k \right)} \end{array} $ | (25) |
因此,本文设计控制算法满足如下
| $ \mathop {\min }\limits_{{\mathit{\boldsymbol{e}}_u}\left( {k|k} \right),\mathit{\boldsymbol{S}}\left( k \right),\mathit{\boldsymbol{Y}}\left( k \right)} \zeta \left( k \right) $ | (26) |
定理2 对于满足输入输出约束条件的系统(6),通过求解下面LMIs可获得满足式(26)的最优解,并且该系统为渐近稳定的闭环系统:
| $ \left[{\begin{array}{*{20}{c}} 1&*&*&*\\ {\mathit{\boldsymbol{W}}\left( k \right)}&{\mathit{\boldsymbol{S}}\left( k \right)}&*&*\\ {\mathit{\boldsymbol{Q}}{{\left( k \right)}^{0.5}}{{\mathit{\boldsymbol{\hat e}}}_x}\left( {k|k} \right)}&0&{\zeta \left( k \right)\mathit{\boldsymbol{I}}}&*\\ {\mathit{\boldsymbol{R}}{{\left( k \right)}^{0.5}}{\mathit{\boldsymbol{e}}_u}\left( {k|k} \right)}&0&0&{\zeta \left( k \right)\mathit{\boldsymbol{I}}} \end{array}} \right] > 0 $ | (27) |
| $ \left[{\begin{array}{*{20}{c}} {\mathit{\boldsymbol{S}}\left( k \right)}&*&*&*\\ {\mathit{\boldsymbol{A}}\left( k \right)\mathit{\boldsymbol{S}}\left( k \right) + \mathit{\boldsymbol{B}}\left( k \right)\mathit{\boldsymbol{Y}}\left( k \right)}&{\mathit{\boldsymbol{S}}\left( k \right)}&*&*\\ {{\mathit{\boldsymbol{Q}}^{0.5}}\mathit{\boldsymbol{S}}\left( k \right)}&0&{\zeta \left( k \right)\mathit{\boldsymbol{I}}}&*\\ {{\mathit{\boldsymbol{R}}^{0.5}}\mathit{\boldsymbol{Y}}\left( k \right)}&0&0&{\zeta \left( k \right)\mathit{\boldsymbol{I}}} \end{array}} \right] > 0 $ | (28) |
| $ \left[{\begin{array}{*{20}{c}} {\mathit{\boldsymbol{U}}\left( k \right)}&*\\ {{\mathit{\boldsymbol{Y}}^{\rm{T}}}\left( k \right)}&{\mathit{\boldsymbol{S}}\left( k \right)} \end{array}} \right] > 0 $ | (29) |
| $ \left[{\begin{array}{*{20}{c}} {\mathit{\boldsymbol{S}}\left( k \right)}&*\\ {\mathit{\boldsymbol{C}}\left( k \right)\left( {\mathit{\boldsymbol{A}}\left( k \right)\mathit{\boldsymbol{S}}\left( k \right) + \mathit{\boldsymbol{B}}\left( k \right)\mathit{\boldsymbol{Y}}\left( k \right)} \right)}&{\mathit{\boldsymbol{E}}{{\left( k \right)}^2}\mathit{\boldsymbol{I}}} \end{array}} \right] > 0 $ | (30) |
式中:Y(k)=G(k)S(k),H(k)=ζ(k)S(k)-1,W(k)=A(k)
证明将式(15)代入式(25)得:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\tilde e}}{{\left( {k|k} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( k \right)\mathit{\boldsymbol{\tilde e}}\left( {k|k} \right) + {\mathit{\boldsymbol{e}}_u}{{\left( {k|k} \right)}^{\rm{T}}}\mathit{\boldsymbol{R}}\left( k \right){\mathit{\boldsymbol{e}}_u}\left( {k|k} \right) + }\\ {\mathit{\boldsymbol{W}}{{\left( k \right)}^{\rm{T}}}\mathit{\boldsymbol{H}}\left( k \right)\mathit{\boldsymbol{W}}\left( k \right) < \zeta \left( k \right)} \end{array} $ | (31) |
在式(31)中,令H(k)=ζ(k)S(k)-1,根据Schur补引理,式(31)可转化为式(27)。
将式(18)、(21)代入式(23)可得:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{H}}\left( k \right)- \mathit{\boldsymbol{Q}}\left( k \right)- \mathit{\boldsymbol{G}}{{\left( k \right)}^{\rm{T}}}\mathit{\boldsymbol{R}}\left( k \right)\mathit{\boldsymbol{G}}\left( k \right)- }\\ {{{\left[{\mathit{\boldsymbol{A}}\left( k \right) + \mathit{\boldsymbol{B}}\left( k \right)\mathit{\boldsymbol{G}}\left( k \right)} \right]}^{\rm{T}}}\mathit{\boldsymbol{H}}\left( k \right)\left[{\mathit{\boldsymbol{A}}\left( k \right) + \mathit{\boldsymbol{B}}\left( k \right)\mathit{\boldsymbol{G}}\left( k \right)} \right] > 0} \end{array} $ | (32) |
由于H(k)=ζ(k)S(k)-1, 式(32)左右两边同乘S(k), 应用Schur补引理可化为式(28)。式(29)和(30)的推导参见文献[15]。
4 仿真验证分析满足LMIs的式(17)、(27)~(30)是针对动平衡点线性化后得出的控制算法,本节将该算法应用于舰载机着舰非线性模型,并在半实物仿真平台上完成验证工作,半实物仿真平台如图 6所示。

|
| 图6 舰载机着舰仿真平台 Figure 6 Carrier-base aircraft landing simulation platform |
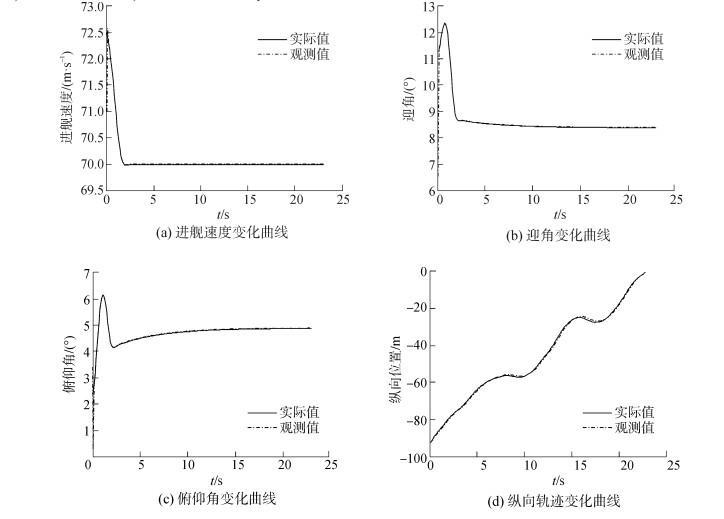
仿真初始工况设置如下:速度偏差2.5 m/s,迎角偏差3.1°,俯仰角偏差2.5°,观测器速度偏差1.0 m/s,观测器迎角偏差-2.0°,初始俯仰角偏差-2.0°,纵向偏差10 m,航母航速24 kn。按照上述工况完成仿真任务,结果如图 7所示。
|
| 图7 半物理平台仿真曲线 Figure 7 Simulation curves on semi-physical platform |
从图 7(a)和图 7(b)可以看出,舰载机可快速消除速度和迎角偏差,并维持70 m/s的进舰速度和8.4°的迎角,本算法实现效果与舰载机进场动力补偿作用保持一致。由于舰载机初始仿真工况中存在俯仰角偏差和纵向偏差,舰载机需要调整俯仰角来改变飞行姿态。又由于飞机通过调整俯仰角来跟踪目标轨迹,正如图 7(c)所示,俯仰角不断被调整并最终达到稳态。经过图 7(a)、(b)、(c)实际值与观测值的对比可以看出,状态观测器能够以较高精度预估当前状态值。图 7(d)中虚线为甲板运动下的目标轨迹,实线为本文MPC算法控制下的实际轨迹,从图中可以看出,实际轨迹可在幅值和相位上跟踪目标轨迹,实现甲板运动补偿目的。
5 结论通过舰载机着舰纵向时变权值鲁棒预测控制的理论描述与半物理仿真可得以下结论:
1)基于动平衡点线性化的方法可实现舰载机跟踪航母运动状态下的理想滑道,完成甲板运动补偿的任务;
2)利用舰载机复飞时的舰艉净高可建立高维纵向着舰风险模型,并可量化为一维风险值;
3)高维纵向着舰风险模型可为MPC性能指标提供时变的权值矩阵,可有针对性地消除响应状态偏差,最终实现舰载机安全有效的着舰任务。
另外,本文未考虑舰艉流对舰载机着舰风险的影响,这将是下一阶段的研究内容。
| [1] | TIAN Jin, DAI Ying. Research on the relationship between mishap risk and time margin for control: a case study for carrier landing of aircraft[J]. Cognition, technology & work, 2014, 16(2): 259–270. DOI:10.1007/s10111-013-0262-y |
| [2] |
夏桂华, 董然, 孟雪, 等. 舰载机着舰的动力学建模[J].
哈尔滨工程大学学报, 2014, 35(4): 445–456.
XIA Guihua, DONG Ran, MENG Xue, et al. Research on the dynamic modeling for the landing of a carrier-based aircraft[J]. Journal of Harbin engineering university, 2014, 35(4): 445–456. |
| [3] |
王敏, 张晶, 申功璋. 基于甲板运动预报的自动着舰系统综合设计[J].
系统仿真学报, 2010, 22(S1): 119–122.
WANG Min, ZHANG Jing, SHEN Gongzhang. Design of automatic carrier landing system based on deck motion prediction[J]. Journal of system simulation, 2010, 22(S1): 119–122. |
| [4] |
黄得刚, 章卫国, 邵山, 等. 舰载机自动着舰纵向控制系统设计[J].
控制理论与应用, 2014, 31(12): 1731–1739.
HUANG Degang, ZHANG Weiguo, SHAO Shan, et al. Design of automatic control system for longitudinal landing on carrier[J]. Control theory & applications, 2014, 31(12): 1731–1739. |
| [5] |
朱齐丹, 邱兵, 林圣琳, 等. 舰载机全自动着舰纵向控制系统设计[J].
计算机仿真, 2014, 31(11): 69–73.
ZHU Qidan, QIU Bing, LIN Shenglin, et al. Design of longitudinal control in automatic carrier landing system[J]. Computer simulation, 2014, 31(11): 69–73. |
| [6] |
裴辛哲, 刘志远, 裴润.基于MPC的轮式移动机器人鲁棒轨迹跟踪控制[C]//第二十二届中国控制会议论文集--预测控制和滚动时域估计, 2005: 791-795.
PEI Xinzhe, LIU Zhiyuan, PEI Run. Robust Trajectory tracking control of wheeled mobile robot based on MPC[C]//Model Predictive Control and Receding Horizon Control-the Twenty-second Chinese Control Conference, 2005: 791-795. |
| [7] |
朱齐丹, 王立鹏, 张智, 等. 舰载机着舰侧回路时变风险权值矩阵线性变参数预测控制[J].
控制理论与应用, 2015, 32(1): 101–109.
ZHU Qidan, WANG Lipeng, ZHANG Zhi, et al. Aircraft lateral linear parameter varying model predictive control with time varying weight[J]. Control theory & applications, 2015, 32(1): 101–109. |
| [8] | EASTBURG S R. Natops landing signal officer manual, Navair 00-80T-104[R]. Washington, DC: American Navy Naval Air Systems, 2001. |
| [9] | CHAKRABORTY A, SEILER P, BALAS G J. Applications of linear and nonlinear robustness analysis techniques to the F/A-18 flight control laws[C]//AIAA Guidance, Navigation, and Control Conference. Chicago, Illinois: AIAA, 2009: 10-13. |
| [10] | CHAKRABORTY A, SEILER P, BALAS G J. Susceptibility of F/A-18 flight controllers to the falling-leaf mode: linear analysis[J]. Journal of guidance, control, and dynamics, 2011, 34(1): 57–72. DOI:10.2514/1.50674 |
| [11] | PEI Xinzhe, LIU Zhiyuan, PEI Run. Robust trajectory tracking controller design for mobile robots with bounded input[J]. Acta automatica sinica, 2003, 29(6): 876–882. |
| [12] | GREGOR K, IGOR S. Tracking-error model-based predictive control for mobile robots in real time[J]. Robotics and autonomous systems, 2007, 55(6): 460–469. DOI:10.1016/j.robot.2007.01.002 |
| [13] |
朱齐丹, 王立鹏, 张智. 基于实际行为策略的飞行员着舰模型[J].
华中科技大学学报:自然科学版, 2015, 43(7): 98–103.
ZHU Qidan, WANG Lipeng, ZHANG Zhi. Pilot landing model based on actual behavioral strategies[J]. Journal of huazhong university of science and technology: natural science edition, 2015, 43(7): 98–103. |
| [14] |
杨京.舰载飞机着舰导引特殊技术研究[D].南京:南京航空航天大学, 2000: 53-58.
YANG Jing. Research on landing and guiding special technique of carrier-based aircraft[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2000: 53-58. |
| [15] | LU Yaohui, ARKUN Y. Quasi-Min-Max MPC algorithms for LPV systems[J]. Automatica, 2000, 36(4): 527–540. DOI:10.1016/S0005-1098(99)00176-4 |



