2. College of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;
3. School of Resources and Safety Engineering, Central South University, Changsha 410083, China
随着我国地下隧道空间的高速发展,全断面隧道掘进机(TBM)以其掘进高效率、高可靠性等诸多优点而被广泛应用于地下隧道开挖。TBM滚刀作为隧道开挖的主要工具,其工作特性直接关乎整个TBM的工作效果,为此国内外对于TBM滚刀破岩做了大量研究。Rostamin等[1-2]采用线性试验台对TBM滚刀破岩开展了大量的实验研究,并以此得到了CSM模型,该模型被广泛应用于工程实际。Bruland[3]根据现场掘进参数提出了NTNU模型,在欧洲等国被广泛应用。在数值模拟方面,Gong等[4]利用UDEC建立了双滚刀侵入破岩模型,对裂纹扩展进行了详细的探讨并基于切入率指标得到了最优刀间距。谭青等[5]采用PFC从细观角度对双滚刀侵入破岩过程进行分析,得到了不同切深下的最优刀间距,并利用回转试验台进行验证。霍军周等[6-7]采用有限元对不同模式下的滚刀破岩进行研究,确定了最优刀间距和最优顺次切削角度。
上述成果对于研究TBM滚刀破岩具有很好的参考价值,但上述研究成果很少考虑真实地层存在的实际因素,如高围压、高地热、强渗流水压以及岩层内部节理等。工程数据、室内试验结果[8-9]无不表明TBM滚刀破岩效果与围压、渗流以及节理等具有密切的关联。其中节理岩体是TBM开挖普遍接触的地层[10],当TBM遭遇节理岩层时,其滚刀破岩特性显然不同于常规均一地层下的破岩特性,节理的存在使得裂纹的扩展、岩石破碎模式、破碎载荷等均会发生改变[11-14],研究节理条件下的滚刀破岩更加贴合工程实际。
本文采用颗粒离散元技术建立不同节理岩体下两种滚刀的侵入破岩模型,尝试从细观角度研究节理岩体下两种滚刀的破岩机制。
1 节理岩体下单、双刃滚刀破岩模型 1.1 模型建立通过对真实掘进过程中TBM滚刀破岩进行简化,建立如图 1所示的TBM单、双刃滚刀侵入节理岩体的破岩模型。

|
| 图1 TBM滚刀破岩模型 Figure 1 Numerical model of breaking rock by TBM cutters |
其中节理岩体尺寸为300 mm×160 mm,节理倾角α为y轴与节理面之间的夹角,两节理面之间的法相距离定义为节理间距s,节理岩体左右两侧以及下侧被限定住自由度,不能发生位移。TBM滚刀的刀刃宽设定为10 mm,刀刃角设定为20°,对于双刃滚刀需要额外定义一个刀间距,定义为l,无论是单刃还是双刃滚刀,在模拟过程中都假定为刚性体即不考虑TBM滚刀的变形特点,由刚性墙代替。考虑TBM掘进过程中可能存在的节理倾向以及间距情况,设定节理间距为40、60、80 mm三种情况,节理倾角设定为0°、15°、30°、45°、60°、75°、90°七种情况。
1.2 岩体及节理的宏细观参数确定颗粒离散元在模拟真实对应的岩体时,首先要对颗粒离散元中的细观参数与真实的岩体宏观参数进行匹配,Moon等[15]通过研究发现,通过单轴压缩和巴西劈裂就能很好的在离散元软件中进行数值匹配,本课题组基于此法对不同岩体进行了大量的匹配工作,确定了水泥砂浆、花岗岩等在颗粒离散元中的细观参数[16-17]。本文中模拟的岩体对象选用常见的花岗岩,其对应的宏细观参数见表 1和表 2。
| 密度/(kg·m-3) | 弹性模量/GPa | 抗压强度/MPa | 抗拉强度/MPa | 泊松比 | 内聚力/MPa | 内摩擦角/(°) |
| 2 700 | 40 | 100 | 15 | 0.18 | 25 | 40 |
| 颗粒密度/(kg·m-3) | 法向强度/MPa | 切向强度/MPa | 法向刚度/(N·m-1) | 切向刚度/(N·m-1) | 摩擦系数 |
| 3 375 | 87.5 | 87.5 | 12×1010 | 4.8×1010 | 0.1 |
颗粒离散元中岩体内部节理通过输入相应的位置参数确定节理倾角和节理间距,最后将该处的颗粒重新赋予新的细观参数得到相应的节理。节理的细观参数需要通过剪切实验进行标定得到,标定过程见文献[16],节理的细观参数为:粘结强度50 kPa,摩擦系数0.15,宏观参数为:内聚力8.45 MPa,内摩擦角50°。利用颗粒离散元建立上述单、双刃滚刀侵入节理岩体模型,岩体的产生通过赋予表 2中的细观参数得到,同时在对应的岩体中产生相应的节理,开展不同节理特征下的单、双刃滚刀侵入破岩研究。
2 破岩数值计算结果及分析 2.1 单、双刃滚刀侵入节理岩体的动态过程分析图 2为两种滚刀侵入节理间距为40 mm,节理倾角为45°下的破岩过程图。单刃滚刀侵入时,裂纹首先在刀刃下方萌生,并且初步形成主裂纹,该阶段是微裂纹起裂阶段,如图 2(a)左图所示。随着侵深逐渐增加,主裂纹扩展到节理面后开始沿着节理面扩展延伸,此时节理面对于裂纹的扩展具有引导作用,如图 2(b)、(c)左图所示。当刀刃继续下压时,侧向裂纹迅速扩展并穿过节理面达到自由面形成破碎块,如图 2(d)左图所示。双刃滚刀侵入节理岩体时,其侵入前期与单刃侵入前期下的裂纹生成和扩展情况类似,即先在刀刃下方形成微裂纹,随后主裂纹扩展至节理面并沿节理面扩展。但在侵入后期,随着双刀刃继续侵入,双刀刃之间的侧向裂纹迅速扩展并最终交汇,使得双刃之间的岩体被剥落形成破碎块。即双刃侵入过程中的裂纹扩展不同于单刃,双刃滚刀侵入破岩存在协同作用,有利于双刃之间的侧向裂纹交汇以及破碎块的形成。

|
| 图2 两种滚刀侵入过程图 Figure 2 The diagram of intrusion process by two kinds of cutters |
对单、双刃滚刀侵入破岩过程中的所受垂直力和裂纹数目情况进行实时采集得到图 3,观察可知,裂纹数目随侵深增加持续增加,无论是单刃还是双刃滚刀,当侵深在1 mm附近以前时裂纹生成最为迅速,随着侵深增加,裂纹数目的增加呈现两个阶段:急剧增加阶段和稳定增加阶段,这两个阶段与前面分析裂纹的形成分为起裂和扩展两个阶段具有一定的对应性。如图 3中,在0~1 mm时裂纹急剧增加阶段,在1~3.7 mm时稳定增加阶段,在3.7~4.2 mm后又短暂急剧增加,后续循环往复。值得注意的是裂纹的稳定增加的持续时间大于裂纹的急剧增加的持续时间,另外裂纹急剧增加所对应的力普遍处于峰值附近,即裂纹的急剧增加需要更大的力。双刃滚刀相对于单刃滚刀,其对应的裂纹数目始终要多,这主要是因为双刃滚刀与岩体接触面积大,破坏区域相对也大导致裂纹数目相对较多。

|
| 图3 两种滚刀侵入过程受力和裂纹情况 Figure 3 The condition of force and crack by two kinds of cutters |
对比两种滚刀的受力情况可知,双刃滚刀受力明显大于单刃滚刀受力,且当侵入行程在1 mm以前,单、双刃滚刀之间的受力差异较大,在后续侵入过程中,两者的受力差异缩小。这主要是因为在1 mm以前为裂纹萌生阶段,在该阶段刀刃与岩体接触面积越大则需要更大的力,而当侵入行程大于1 mm以后,主要以裂纹的扩展为主,另外由于前期刀刃下方的岩体已经压碎,后续持续侵入存在短暂悬空以及二次破碎现象,因此在侵入行程大于1 mm后,双刀刃受力虽然大于单刀刃受力,但其差异会减小。
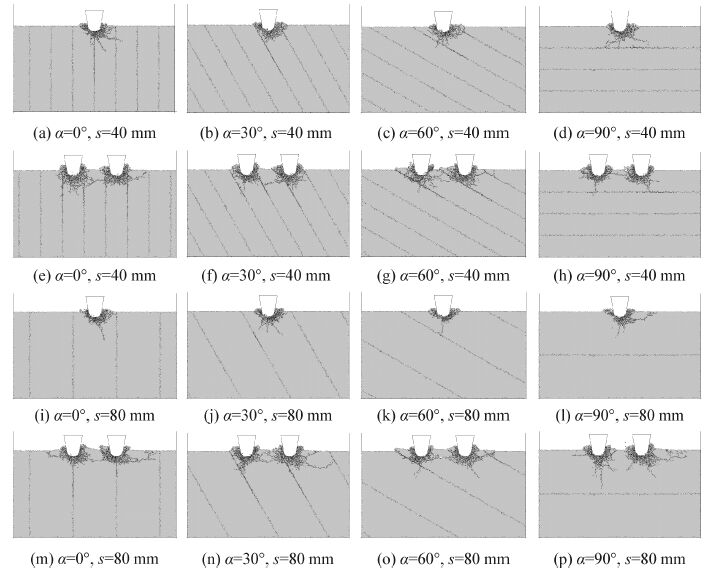
2.2 节理特征对单、双刃滚刀裂纹扩展效应分析统计不同节理特征下的破岩状态图得到图 4,图 4中对应的滚刀侵深为10 mm,双刃滚刀的刀刃间距为80 mm(限于篇幅原因,只列出四种节理倾角和两种节理间距的破岩效果图)。观察可知,节理对单、双刃滚刀的侵入破岩过程中裂纹的扩展主要存在两方面的影响:引导效应、阻隔效应。值得注意的是当节理间距大到一定程度后,如本文中节理间距为80 mm时,节理对单刃滚刀侵入过程中裂纹扩展影响不大,即引导和阻隔效应不明显,如图 4(i)、(j)、(k)、(l)。
|
| 图4 裂纹扩展状态图 Figure 4 State diagram of crack propagation |
当节理倾角较小时(0~30°),无论是单刃还是双刃滚刀作用,当主裂纹到达节理面后,裂纹几乎是沿着节理方向向岩体内部扩展,此时的节理具有引导效应,如图 4(a)、(b) 、(e) 、(f)所示,但双刃相对于单刃滚刀而言,双刃更有利于裂纹沿节理岩体内部扩展,影响范围更大且当刀刃间距合适时能促进刀刃之间的侧向裂纹扩展,进而剥落双刃之间的岩体,但两刀刃以外的侧向裂纹一般不能穿越邻近节理,如图 4(f)、(n)(刀刃与节理面距离过小时除外,如图 4(e)。另外,对比图 4(i)、(j)和4(m)、 (n)可知,即使在节理间距较大的情况下,双刃滚刀作用下的裂纹扩展依然会受到节理的影响,即节理倾角较小时对裂纹扩展所表现的引导效应。
当节理倾角较大(60°~90°)时且节理间距较小时如本文中的40 mm,由于节理的作用,无论是单刃还是双刃作用,下方的裂纹均被节理阻断,不能向岩体内部继续扩展,表现出阻隔效应,这主要是因为节理面强度远比岩体其他部位的强度低,当节理面阻断裂纹扩展后,节理不会沿强度高的岩体内部扩展,如图 4(c)、(d)、(h)等。值得注意的是当节理间距大到一定程度后如80 mm,节理倾角在90°附近时,节理间距对单、双刃滚刀作用下的裂纹阻隔效应不明显,如图 4(l)、(p)。这说明节理对滚刀侵入破岩是否有阻隔效应,不仅要求节理倾角较大还要求节理间距够小。
当节理倾角适中(30°~60°)时,节理对裂纹扩展是起阻隔还是引导效应关键在于刀刃与节理面的相对位置,当刀刃与节理面相邻时表现为引导效应,当刀刃与节理面相距较远时表现为阻隔效应。
采用中南大学拉压试验机,利用刀头对岩板进行加压试验,观察节理对单刃滚刀作用下裂纹扩展规律。图 5为不同节理倾角下对应的破岩状态图,左图为侵入后的实物图,右图通过对实物图中的裂纹扩展情况进行素描得到,其中节理由水泥砂浆对所切割的空隙进行填充得到。

|
| 图5 单刃在不同节理倾角下破岩状态图 Figure 5 Formation of rock chips under jointed rock |
由图 5可知,节理倾角在0°和30°时,节理对滚刀下的裂纹扩展具有很好的引导作用,诱导裂纹扩展到岩体内部深处,如5(a)、(b)所示。节理倾角在60°和90°时,滚刀下的主裂纹沿垂直方向扩展,直到节理面后沿垂直方向扩展受到阻碍,具有明显的阻隔效应,试验观测到的单刃滚刀作用下节理的引导和阻隔效应与数值模拟结果具有很好的一致性。
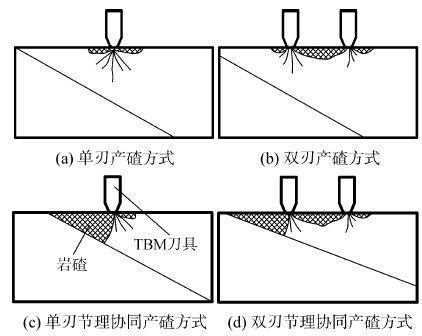
2.3 节理特征对单、双刃滚刀作用下岩碴形成分析结合上述分析可知,当节理间距大到一定程度且节理倾角合适,节理面对两种滚刀破岩影响不大,滚刀作用下产生岩碴方式如图 6(a)、(b)所示,此时对应的岩碴呈细粒状或扁平状,整体尺寸较小,这种岩碴产生的破岩方式为常规破岩,另外双刃相对于单刃滚刀而言,由于双刃的协同作用能产生更为扁长的岩碴。当滚刀不断侵入时,滚刀与节理面不断接近,此时节理面能协同滚刀破岩,产生岩碴的方式如图 6(c)、(d)所示,此时的岩碴由刀刃下的主裂纹和节理面的破坏共同产生,对应的主岩碴呈块状,整体尺寸较大,这种岩碴产生的破岩方式为节理协同破岩,显然由于节理的协同作用,岩碴的块度大大增加,破岩效率相对要高。另外当节理间距较小时(如上述40 mm),无论是单刃还是双刃滚刀破岩始终呈现出节理协同破岩方式。
|
| 图6 节理条件下的岩碴产生方式 Figure 6 Formation of rock chips under jointed rock |
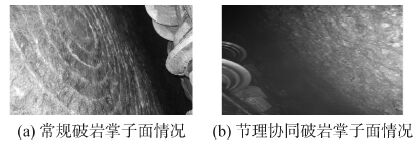
工程中当节理面间距较大时,由于TBM是连续掘进,因此两种破岩方式会交替出现,岩碴也呈现细小和大块交替出现的情况。如图 7所示为某一掘进工程中不同阶段下破岩的真实排碴情况,该掘进地段富含节理,图 7(b)为节理协同破岩时产生的岩碴。另外当TBM滚刀常规破岩时,掌子面往往相对平整且能观察到明显的滚刀滚过的凹槽(同心圆),如图 8(a)所示,而当处于节理面协同破岩时,掌子面一般凹凸不平,无法观测到刀刃滚过的凹槽,无同心圆现象,如图 8(b)所示。

|
| 图7 常规与节理协同方式对应的排碴 Figure 7 Rock chips under two kinds of modes of breaking rock |
|
| 图8 两种破岩方式对应的掌子面 Figure 8 Tunnel face under two kinds of modes of breaking rock |
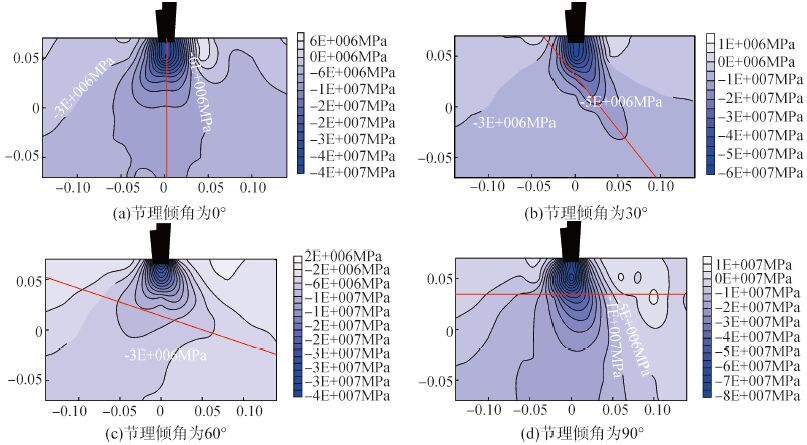
在滚刀作用下,岩体内部的应力分布规律关乎岩体的破坏形式以及裂纹的扩展规律,图 9和图 10分别为节理间距为40 mm下不同节理倾角所对应的单刃和双刃滚刀作用下的应力云图。
|
| 图9 不同节理倾向单刃滚刀作用下的垂向应力云图 Figure 9 Vertical stress contour map in different joint orientation by single-point cutter |
|
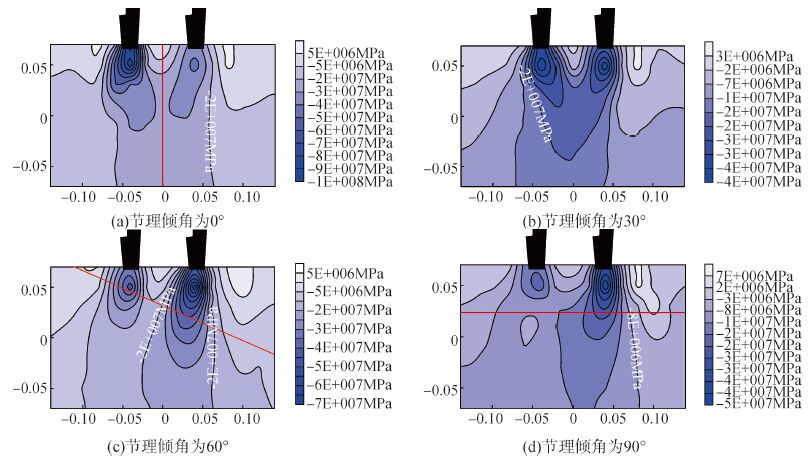
| 图10 不同节理倾向的垂向应力云图 Figure 10 Vertical stress contour map in different joint orientation by double-point cutter |
由图 9可知,当单刃作用节理岩体,刀刃下方为负应力区,即刀刃下方的接触岩体主要以压失效为主,刀刃两侧为正应力区即以拉应力失效为主。当节理存在一定的倾向时,应力椭圆分布不再对称而呈偏转趋势。如图 9(b),此时节理倾角为30°,岩体内部的应力椭圆偏转方向几乎和节理方向一致,当节理倾角增加到60°时,应力椭圆向左偏转,与节理的方向几乎垂直,如图 9(c)所示。当节理倾角不存在倾向时,即节理倾角为0°和90°时,对应的应力椭圆基本上对称,如图 9(a)、(d)所示。由此可知,当岩体内部存在倾向节理时,单刃作用下岩体内部应力椭圆会发生一定偏转,不再呈对称分布。
观察图 10,双刃滚刀侵入节理岩体后,双刃下方均会产生相应的应力椭圆,但由于节理的存在,左右的应力圆分布存在一定的区别,另外双刃之间的应力分布为正应力区,这说明双刃之间的碎块由拉应力产生。总体来说,当节理倾角存在倾向时对双刃滚刀作用下的应力分布的影响不同于单刃滚刀,双刃滚刀下的应力椭圆随节理倾角的改变没有明显的偏转趋势。
Goodman[18]在考虑岩体内部只有一组等间距节理下,将滚刀侵入简化为集中力q加载,得到岩体内部垂向应力分量[18]:
| ${\sigma _z} = \frac{{qh}}{{\pi r}}\left[ {\frac{{cos\alpha cos\gamma + gsin\alpha sin\gamma }}{{(co{s^2}\gamma - gsi{n^2}\gamma ) + {h^2}si{n^2}\gamma co{s^2}\gamma }}} \right]co{s^2}\left( {\alpha + \gamma } \right)$ |
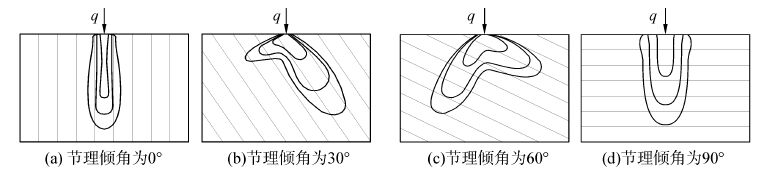
式中取节理倾角α为0°、30°、60°、90°,通过计算可得到不同节理倾角下垂直力的分布规律示意图,如图 11所示。由图可知,当节理倾角存在一定倾向时,应力分布呈现一定的偏转,而当节理对称分布即没有倾向时,应力分布对称。对比图 9和图 11可知,两者在不同节理倾角下所对应的应力偏转方向几乎一致,理论上得到的应力分布规律整体上和离散元数值模拟结果具有很好的一致性。
|
| 图11 不同节理倾角下岩体内部应力分布理论解 Figure 11 Theory resolution of vertical stress contour map in different joint orientation |
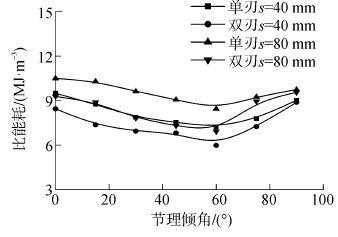
表征破岩效果的好坏通常由破岩效率来说明,而破岩效率与破岩比能耗密切相关,比能耗是指单位体积下的岩石发生破碎时所需要的能量,其值越大说明破岩效率越低。图 12为单刃和双刃滚刀侵入不同节理岩体下对应的破岩比能耗关系图(此时对应的双刃滚刀之间的刀间距为80 mm),由图可知,无论是单刃还是双刃滚刀,其对应的比能耗随节理倾角增加,比能耗先减小后增加且在60°时取得最小值,这说明存在一个节理倾角使得破岩能耗最低。另外,对于同一种滚刀,随节理间距增加破岩比能耗相应增加。当节理间距和节理倾角相同时,双刃滚刀对应的比能耗均小于单刃滚刀对应的比能耗,这说明在侵入节理岩体时,双刃滚刀破岩效果要优于单刃滚刀。导致这种现象的主要原因可能是因为双刃滚刀之间由于刀间距合适两刃所体现的协同效应,能剥落双刀刃之间的岩体,增加破碎体积,进而提高破岩效率。
|
| 图12 两种滚刀破岩比能耗关系图 Figure 12 Relationship of specific energy between two kinds of cutters |
通过2.5节分析可知,当双刃刀间距合适时,双刃滚刀侵入岩体的破岩效率高于单刃滚刀的破岩效率。对于刀刃之间的间距取值一直是双刃滚刀设计的关键问题,课题组通过实验和数值模拟研究得到了无节理岩体条件下的双刃最优刀间距,然而考虑节理条件下的最优刀间距鲜见报道。由2.2节分析可知,当节理间距过大时,节理间距对裂纹的扩展不大,此时滚刀最优刀间距与无节理岩体下的最优刀间距相近。文中选择节理间距为40 mm,切深为10 mm,研究不同节理倾角下破岩效率随刀间距的变化规律。
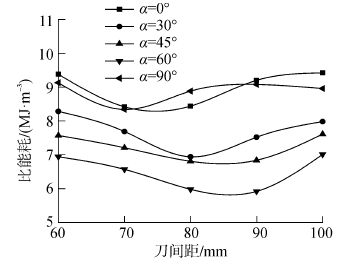
由图 13可知,当刀间距相同时,节理倾角在60°时比能耗最低。当节理倾角相同时,随刀间距增加,破岩比能耗先减小后增加,存在一个最优刀间距使得破岩效率最高。值得注意的是随着节理倾角的依次增加,最优刀间距先增加后减小,如节理倾角在0°时,最优刀间距在75 mm左右,节理倾角在60°时,最优刀间距在85 mm左右,节理倾角在90°时,最优刀间距在70 mm左右。
|
| 图13 不同节理倾角下比能耗和刀间距的关系 Figure 13 Relationship between specific energy and cutter spacing under different jointed rock |
本文通过颗粒离散元对节理岩体下的单刃和双刃滚刀侵入破岩进行分析,得到了以下结论:
1) 两种滚刀在侵入节理岩体时,裂纹的形成分为起裂、扩展过程。两种滚刀在受力、裂纹的扩展和数目上存在差异,双刃滚刀存在协同作用;
2) 依据节理特征的不同,节理对两种滚刀作用下的裂纹扩展具有引导和阻隔两种效应,与试验观测结果一致;
3) 双刃滚刀作用下产生的岩碴相对单刃下的岩碴较为扁长。根据节理特征的不同,两种滚刀作用下产生的岩碴方式主要有常规破岩和节理面协同破岩两种形式;
4) 单刃作用下的应力分布受节理的影响呈现一定的偏转且与理论解析一致,双刃作用下应力分布受节理的影响不大;
5) 两种滚刀在节理倾角为60°时破岩比能耗取得最小值,破岩效率随节理间距增加而增加,双刃滚刀相比单刃滚刀其侵入节理岩体破岩效率要高;
6) 存在最优刀间距使破岩效率最高且最优刀间距随节理倾角增加先增大后减小。
| [1] | ROSTAMI J. Development of a force estimation model for rock fragmentation with disc cutters through theoretical modeling and physical measurement of crushed zone pressure[D].: Colorado School of Mines, 1997. |
| [2] | ROSTAMI J. Hard rock TBM cutterhead modeling for design and performance prediction[J]. Geomechanik und tunnelbau, 2008, 1(1): 18–28. DOI:10.1002/(ISSN)1865-7389 |
| [3] | BRULAND A. Hard rock tunnel boring[D]. Trondheim: Norwegian University of Science and Technology, 1998. |
| [4] | GONG Q M, ZHAO J, HEFNY A M. Numerical simulation of rock fragmentation process induced by two TBM cutters and cutter spacing optimization[J]. Tunnelling and underground space technology, 2006, 21(3/4): 263. |
| [5] |
谭青, 易念恩, 夏毅敏, 等. TBM滚刀破岩动态特性与最优刀间距研究[J].
岩石力学与工程学报, 2012, 31(12): 2453–2464.
TAN Qing, YI Nian'en, XIA Yimin, et al. Research on rock dynamic fragmentation characteristics by TBM cutters and cutter spacing optimization[J]. Chinese journal of rock mechanics and engineering, 2012, 31(12): 2453–2464. |
| [6] |
霍军周, 杨静, 孙伟, 等. 不同模式下TBM刀群三维回转切削仿真与优化设计[J].
哈尔滨工程大学学报, 2014(11): 1403–1408.
HUO Junzhou, YANG Jing, SUN Wei, et al. Simulation and optimization design of three-dimensional rotating cutting action of TBM cutter group with different modes[J]. Journal of Harbin Engineering University, 2014(11): 1403–1408. |
| [7] |
霍军周, 孙伟, 郭莉, 等. 多滚刀顺次作用下岩石破碎模拟及刀间距分析[J].
哈尔滨工程大学学报, 2012, 33(1): 96–99.
HUO Junzhou, SUN Wei, GUO Li, et al. Numerical simulation of the rock fracture process induced by multi-disc-cutters and cutter spacing design[J]. Journal of Harbin Engineering University, 2012, 33(1): 96–99. |
| [8] | FARROKH E, ROSTAMI J. Effect of adverse geological condition on TBM operation in Ghomroud tunnel conveyance project[J]. Tunnelling and underground space technology, 2009, 24(4): 436–446. DOI:10.1016/j.tust.2008.12.006 |
| [9] | INNAURATO N, OGGERI C, ORESTE P P, et al. Experimental and numerical studies on rock breaking with TBM tools under high stress confinement[J]. Rock mechanics and rock engineering, 2007, 40(5): 429–451. DOI:10.1007/s00603-006-0109-4 |
| [10] | BARTON N R. TBM tunnelling in jointed and faulted rock[M]. Rotterdam: CRC Press, 2000 . |
| [11] | BEJARI H, HAMIDI J K. Simultaneous effects of joint spacing and orientation on TBM cutting efficiency in jointed rock masses[J]. Rock mechanics & rock engineering, 2013, 46(4): 897–907. |
| [12] | BEJARI H, REZA K, ATAEI M, et al. Simultaneous effects of joint spacing and joint orientation on the penetration rate of a single disc cutter[J]. Mining science and technology (China), 2011, 21(4): 507–512. DOI:10.1016/j.mstc.2011.06.008 |
| [13] | GONG Qiuming, ZHAO Jian, JIAO Yuyong. Numerical modeling of the effects of joint orientation on rock fragmentation by TBM cutters[J]. Tunnelling and underground space technology, 2005, 20(2): 183–191. DOI:10.1016/j.tust.2004.08.006 |
| [14] | GONG Qiuming, JIAO Yuyong, ZHAO Jian. Numerical modelling of the effects of joint spacing on rock fragmentation by TBM cutters[J]. Tunnelling and underground space technology, 2006, 21(1): 46–55. DOI:10.1016/j.tust.2005.06.004 |
| [15] | MOON T, OH J. A study of optimal rock-cutting conditions for hard rock TBM using the discrete element method[J]. Rock mechanics and rock engineering, 2012, 45(5): 837–849. |
| [16] |
谭青, 张旭辉, 夏毅敏, 等. 不同围压与节理特征下盘形滚刀破岩数值研究[J].
煤炭学报, 2014, 39(7): 1220–1228.
TAN Qing, ZHANG Xuhui, XIA Yimin, et al. Numerical study on breaking rock by disc cutter at different confining pressure and joint characteristics case[J]. Journal of china coal society, 2014, 39(7): 1220–1228. |
| [17] |
徐孜军, 谭青, 夏毅敏, 等. 盾构切刀顺次破岩机制的数值模拟研究[J].
岩土力学, 2013, 34(12): 3625–3632.
XU Zijun, TAN Qing, XIA Yimin, et al. Research on numerical simulation of sequential fragmentation mechanism of shield machine cutters[J]. Rock and soil mechanics, 2013, 34(12): 3625–3632. |
| [18] | GOODMAN R E. Introduction to rock mechanics[M]. New York: John Willey and Sons Inc, 1989: 352 -361. |



