近年来研究海洋消波结构物的学者越来越多,而且在港湾工程中也可以看到许多消波结构物的实际案例,此种消波结构物最大的特色是具有孔隙的结构,能允许波浪通过结构物,进而消减波浪透过的能量,降低波浪作用力,来达到保护海岸设施的目的。最早采用开孔板式消波结构物可追溯至加拿大学者Jarlan[1],因此又称为Jarlan-type防波堤,港湾工程中防波堤及码头等水下工程的建造多会使用到沉箱工法,所谓沉箱可分为开口和压气沉箱,从沉箱形状又可分为圆形沉箱、方形沉箱,或因为工程需要而设计特殊形状的异形沉箱。台湾各港口的建造除高雄港第二港口(1967-1975年)防波堤曾使用不透水圆形沉箱外,大多使用方形沉箱[2]。日本鸟取县境港市则使用外壁透空内柱不透水的二重圆筒沉箱式防波堤作为外海防波堤之一部分。
有关外壁透空双重圆筒此方面研究有:滕斌等[3]利用特征函数展开法和流体通过多孔隙壁内速度与两壁间压力差成正比的关系,并针对单一双筒柱建立了线性解析解。孙路[4]从理论分析和试验研究两方面着手,通过物理模型试验,只要反射率(KR)及透过率(KT)由试验求得,即可求得孔隙影响参数。Tao等[5]利用比例边界有限元法(scaled boundary finite-element method, SBFEM)解析短峰波通过单一不透水圆柱的波浪相对溯上、惯性力系数(CM)、抗力系数(CD)及总力,并说明利用此方法只需对求解领域边界进行有限元离散。其后,Song等[6]同样用SBFEM计算短峰波通过单一透水同心圆柱。由于从过去研究结果得知采用直立式双层开孔结构要比单层开孔结构对波浪的吸收效果更好[7-8]都有相同研究结果,因此,刘俊等[9]同样利用SBFEM计算三维短峰波(含平面波、驻波)对最外层为双层开孔外筒,而中心为一不透水圆筒新型结构其水动力特性的研究。发现采用双层开孔结构对降低内筒波浪作用力会比仅为单层开孔效果来的更好。Liu等[10]也是以SBFEM计算带双层开孔外筒的圆筒结构,数值计算结果显示当绕射参数ka=0.8及6.4时,分别发现在外筒及中筒无因次波力值很小几乎为零,而此时内筒波力会达到最大值。
其后研究者也发现除了双层开孔圆筒外,岳与翁[11]利用复合边界元素法(composite boundary element method, CBEM)解析规则波通过单根透水cosine-type型同心圆柱结构物的无因次波力及绕射现象,发现结构物外壁采用透水型式可以大幅降低结构物四周的水面波动。岳景云等[12]利用复合边界元素法(CBEM)研究波浪入射沉箱外壁全透水,或仅向浪侧一边透水双方形沉箱的无因次波力及绕射现象,数值计算结果显示全透水外方柱无因次波力会随着透水参数增加而降低,内方柱波力则随透水参数增加而增加。
本研究最主要目的为针对单一座传统外壁透空双筒柱沉箱进行加以改良,外部结构物仍为圆形薄板结构并为全透水形式,而内部结构物则改为全透水圆筒或方筒加以组合成所谓“外圆内圆或外圆内方双层沉箱”。
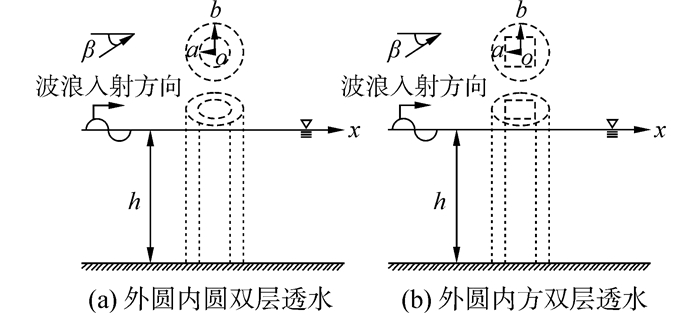
1 理论分析与数值方法将单座内、外壁皆透空的双层透水沉箱设置于等水深h海域中,双层透水沉箱为刚性结构,且内、外壁透空部分在水深方向均匀分布,其中,内筒半径及半边长以a表示;而外圆筒半径以b表示,取坐标原点o位于内部结构柱中心点与静水面交界处,且z轴垂直向上,其定义图如图 1所示,波浪入射角度与x轴夹角为β。
|
| 图1 内、外壁透空双层透水沉箱示意图 Figure 1 Definition sketch of dual porous cylinders |
假设海底底床不透水,波浪为线性规则波,流域内为不可压缩、无黏滞性、无旋性流体,故存在速度势,当外海领域内有一振幅ζ0、周频率为σ(σ=2π/T,T为入射波周期)的入射波浪,则各领域流体运动速度势可表示如下
| $ \mathit{\Phi} \left( {x,y,z,t} \right) = \frac{{g{\zeta _0}}}{\sigma }\varphi \left( {x,y,z} \right){{\rm{e}}^{ - i\sigma t}} $ | (1) |
其中,φ(x, y, z)为势函数满足Laplace方程式:
| $ \frac{{{\partial ^2}\varphi }}{{\partial {x^2}}} + \frac{{{\partial ^2}\varphi }}{{\partial {y^2}}} + \frac{{{\partial ^2}\varphi }}{{\partial {z^2}}} = 0 $ | (2) |
计算领域边界条件以下4个。
1) 线性化后自由水面的边界条件:
| $ \bar \varphi = \frac{{\partial \varphi }}{{\partial z}} = \frac{{{\sigma ^2}}}{g}\varphi ,z = 0 $ | (3) |
2) 假设海底底床为固定且不透水,故法线方向流速为0:
| $ \bar \varphi = \frac{{\partial \varphi }}{{\partial z}} = 0,z = - h $ | (4) |
3) 透水结构物的边界条件
若忽略内、外薄壁厚度,在薄壁处需满足透水结构物的边界条件可以下式表示:
| $ \frac{{\partial {\varphi _ + }}}{{\partial n}} = \frac{{\partial {\varphi _ - }}}{{\partial n}} = - ik{G_1}\left( {{\varphi _ + } - {\varphi _ - }} \right),r = a $ | (5) |
| $ \frac{{\partial {\varphi _ + }}}{{\partial n}} = \frac{{\partial {\varphi _ - }}}{{\partial n}} = - ik{G_2}\left( {{\varphi _ + } - {\varphi _ - }} \right),r = b $ | (6) |
式中:φ+、φ-分别表示透水薄板位于半径a及b处外侧与内侧的势函数,G1、G2为透水内、外结构物的复数透水影响参数,其定义与Yu[13]的复数透水影响参数相同。G值与流体黏滞性、结构物厚度及均匀透空薄板孔隙率有关,由试验决定。
4) 无穷远处边界的绕射波势函数φs须满足Sommerfeld辐射边界条件:
| $ \mathop {\lim }\limits_{kr \to \infty } \sqrt {kr} \left( {\frac{{\partial {\varphi _s}}}{{\partial r}} - ik{\varphi _s}} \right) \to 0 $ | (7) |
因水深h为一定值,故可将领域内的势函数分离为水深z方向的已知函数,与平面(x, y)方向的未知函数,即:
| $ \varphi \left( {x,y,z} \right) = \left[ {{\varphi _i}\left( {x,y} \right) + {\varphi _s}\left( {x,y} \right)} \right]\frac{{\cosh \left( {k + \left( {h + z} \right)} \right)}}{{\cosh \left( {kh} \right)}} $ | (8) |
式中:φi(x, y)为入射波势函数,φs(x, y)为绕射波势函数,k为周波数,且满足色散关系式:
| $ {\sigma ^2} = gk\tanh \left( {kh} \right) $ | (9) |
假设入射波方向与x轴夹角为β, 则其水面波形可以表示为
| $ \begin{array}{l} {\zeta _i}\left( {x,y;t} \right) = {\zeta _0}\cos \left[ {k\left( {x\cos \beta + y\sin \beta } \right) - \sigma t} \right],\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 < \beta < \pi \end{array} $ | (10) |
则入射波的势函数φi(x, y)可表示为
| $ {\varphi _i}\left( {x,y} \right) = - i\exp \left[ {ik\left( {x\cos \beta + y\sin \beta } \right)} \right] $ | (11) |
将式(8)代入式(2),可得绕射波势函数φs(x, y)应满足Helmholtz方程式:
| $ \frac{{{\partial ^2}{\varphi _s}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{\varphi _s}}}{{\partial {y^2}}} + {k^2}{\varphi _s} = 0 $ | (12) |
本文使用的数值方法为复合边界元素法(composite BEM),配合Helmholtz方程式的基本解G(Q, P)=i/4H0(1)(kr),r为P、Q两点间的距离,H0(1)(kr)为第一类零阶Hankel函数。
若将领域内点P移至边界上特定点Q,并假定边界线是平滑的,其绕射波势函数可以下列边界积分方程式表示:
| $ \frac{1}{2}{\varphi _s}\left( p \right) = \int {_\mathit{\Gamma} } \left( {{\varphi _s}\left( Q \right)\frac{\partial }{{\partial {n_Q}}}G\left( {Q,P} \right) - \frac{{\partial {\varphi _s}}}{{\partial {n_Q}}}G\left( {Q,P} \right)} \right){\rm{d}}s $ | (13) |
nQ表示边界在线Q点法向量,Γ为边界线当内、外结构视为薄板时,厚度趋近于零,需将式(13)改写为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}{\varphi _s}\left( P \right) = \\ \int {_\mathit{\Gamma} } \left( {{\varphi _s}\left( Q \right)\frac{{\partial G\left( {Q,P} \right)}}{{\partial {n_Q}}} - G\left( {Q,P} \right)\frac{{\partial {\varphi _s}\left( Q \right)}}{{\partial {n_Q}}}} \right){\rm{d}}s,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;P \in {\mathit{\Gamma} ^R} \end{array} $ | (14) |
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}{\varphi _s}\left( {{P^ \pm }} \right) = \\ \int {_\mathit{\Gamma} } \left( {{\varphi _s}\left( Q \right)\frac{{\partial G\left( {Q,{P^ \pm }} \right)}}{{\partial {n_Q}}} - G\left( {Q,{P^ \pm }} \right)\frac{{\partial {\varphi _s}\left( Q \right)}}{{\partial {n_Q}}}} \right){\rm{d}}s,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{P^ \pm } \in {\mathit{\Gamma} ^ \pm } \end{array} $ | (15) |
式中:ΓR表示非退化的规则边界,Γ+及Γ-表示退化边界的两侧,整个积分边界为Γ=ΓR+Γ++Γ-而点P∈ΓR、P+∈Γ+及P-∈Γ-。其次,再将式(14)、(15)作法向偏微分,能够求出另一超奇异法向偏微分边界积分方程,可以用下式表示:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}\frac{{{\varphi _s}\left( P \right)}}{{\partial {n_P}}} = \\ \int {_\mathit{\Gamma} } \left( {{\varphi _s}\left( Q \right)\frac{{{\partial ^2}G\left( {Q,P} \right)}}{{\partial {n_P}\partial {n_Q}}} - \frac{{\partial {\varphi _s}\left( Q \right)}}{{\partial {n_Q}}}\frac{{\partial G\left( {Q,P} \right)}}{{\partial {n_P}}}} \right){\rm{d}}s,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;P \in {\mathit{\Gamma} ^R} \end{array} $ | (16) |
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}\frac{{{\varphi _s}\left( {{P^ \pm }} \right)}}{{\partial {n_{P \pm }}}} = \\ \int {_\mathit{\Gamma} } \left( {{\varphi _s}\left( Q \right)\frac{{{\partial ^2}G\left( {Q,{P^ \pm }} \right)}}{{\partial {n_{P \pm }}\partial {n_Q}}} - \frac{{\partial {\varphi _s}\left( Q \right)}}{{\partial {n_Q}}}\frac{{\partial G\left( {Q,{P^ \pm }} \right)}}{{\partial {n_{P \pm }}}}} \right){\rm{d}}s,\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{P^ \pm } \in {\mathit{\Gamma} ^ \pm } \end{array} $ | (17) |
此数值方法特性是将式(14)~(17)作线性组合,称之为复合边界积分方程式:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{{\bar U}_{ij\;\;{\mathit{\Gamma} ^R}{\mathit{\Gamma} ^R}}}}&{{{\bar U}_{ij\;\;{\mathit{\Gamma} ^R}{\mathit{\Gamma} ^ + }}}}&{{{\bar U}_{ij\;\;{\mathit{\Gamma} ^R}{\mathit{\Gamma} ^ - }}}}\\ {{{\bar U}_{ij\;\;{\mathit{\Gamma} ^ + }{\mathit{\Gamma} ^R}}}}&{{{\bar U}_{ij\;\;{\mathit{\Gamma} ^ + }{\mathit{\Gamma} ^ + }}}}&{{{\bar U}_{ij\;\;{\mathit{\Gamma} ^ + }{\mathit{\Gamma} ^ - }}}}\\ {{{\overline {{L_{ij\;}}} }_{{\mathit{\Gamma} ^ - }{\mathit{\Gamma} ^R}}}}&{{{\overline {{L_{ij\;}}} }_{{\mathit{\Gamma} ^ - }{\mathit{\Gamma} ^ + }}}}&{{{\overline {{L_{ij\;}}} }_{{\mathit{\Gamma} ^ - }{\mathit{\Gamma} ^ - }}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\varphi _{s{\mathit{\Gamma} ^R}}}}\\ {{\varphi _{s{\mathit{\Gamma} ^ + }}}}\\ {{\varphi _{s{\mathit{\Gamma} ^ - }}}} \end{array}} \right] = \\ \left[ {\begin{array}{*{20}{c}} {{{\bar U}_{ij\;\;{\mathit{\Gamma} ^R}{\mathit{\Gamma} ^R}}}}&{{{\bar U}_{ij\;\;{\mathit{\Gamma} ^R}{\mathit{\Gamma} ^ + }}}}&{{{\bar U}_{ij\;\;{\mathit{\Gamma} ^R}{\mathit{\Gamma} ^ - }}}}\\ {{{\bar U}_{ij\;\;{\mathit{\Gamma} ^ + }{\mathit{\Gamma} ^R}}}}&{{{\bar U}_{ij\;\;{\mathit{\Gamma} ^ + }{\mathit{\Gamma} ^ + }}}}&{{{\bar U}_{ij\;\;{\mathit{\Gamma} ^ + }{\mathit{\Gamma} ^ - }}}}\\ {{{\overline {{L_{ij\;}}} }_{{\mathit{\Gamma} ^ - }{\mathit{\Gamma} ^R}}}}&{{{\overline {{L_{ij\;}}} }_{{\mathit{\Gamma} ^ - }{\mathit{\Gamma} ^ + }}}}&{{{\overline {{L_{ij\;}}} }_{{\mathit{\Gamma} ^ - }{\mathit{\Gamma} ^ - }}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\frac{{\partial {\varphi _s}}}{{\partial n{\;_{{\mathit{\Gamma} ^R}}}}}}\\ {\frac{{\partial {\varphi _s}}}{{\partial n{\;_{{\mathit{\Gamma} ^ + }}}}}}\\ {\frac{{\partial {\varphi _s}}}{{\partial n{\;_{{\mathit{\Gamma} ^ - }}}}}} \end{array}} \right] \end{array} $ | (18) |
再将内、外薄板结构物的边界条件及自由水面、海底边界条件代入式(18),重新整理,即可得如下的系数向量:
| $ {\boldsymbol{A}^*}{\boldsymbol{\varphi} _s} = {\boldsymbol{B}^*} $ | (19) |
内、外壁透空双层透水沉箱四周及结构物表面上任一点的波高与入射波高比值即绕射系数Kd,可以由下式计算:
| $ \boldsymbol{{K_d}} = \left| {\left( {{\varphi _i} + {\varphi _s}} \right)} \right| $ | (20) |
经由线性化的伯努利方程求得动压后,对水深积分可分别求得作用在内、外结构物上的波力,用下式表示:
| $ F = \int_0^{2\pi } {\int_{ - h}^0 {P\;{\rm{d}}z{\rm{d}}\theta } } $ | (21) |
利用此式可分别计算波浪作用在内、外壁透空的两侧表面上力计算而得到透水内筒波浪力(|FI|)及透水外筒波浪力(|FO|)及波浪总力(|FT|)。
2 数值模式验证为了验证本文采用CBEM数值模式的正确性以及可行性,因此分别与Tao等[14-15]利用SBFEM数值计算结果作比较及验证,其结果如图 2、3所示。

|
| 图2 内筒及外筒的相对爬升(G1=0,G2=1.0) Figure 2 Wave relative run-up on the inner and outer cylinder (G1=0, G2=1.0) |
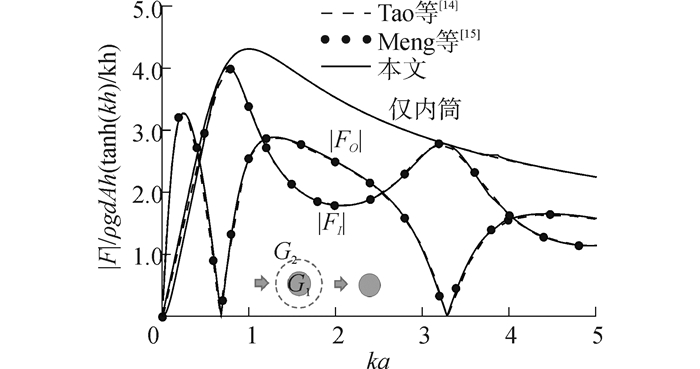
|
| 图3 内筒及外筒的无因次波力(G1==0,G2==1.0) Figure 3 Non-dimensional wave forces experienced by inner and outer cylinder (G1==0, G2==1.0) |
图 2为波浪通过透水同心圆柱其内筒、外筒无因次爬升值(|η|/H),其计算条件为:外筒相对水深b/h=2/3,内筒相对水深a/h=2/15,a/b=0.2,内筒不透水G1=0,外筒透水参数G2=1.0,kh=1.2;由图中发现爬升值不但变化趋势一致而且几乎互相重迭非常吻合。
图 3则为波浪通过透水同心圆柱无因次波力的比较,其计算条件为b/h=2.0,a/b=0.5,G1=0,G2=1.0;图中,本文计算结果分别与Tao等[14-15]内筒(|FI|)及外筒(|FO|)无因次波力作比较,均得到良好结果。
3 数值计算结果与讨论本节分别讨论当波浪入射外圆内圆及外圆内方双层透水同心结构物的相对爬升及无因次波力,而波力无因次化与文献[15]中表示相同,除上ρgdAh(tanh (kh)/kh),其中ρ:流体密度,g:重力加速度,d:特征长度(本文取内筒半径a),A:振幅,h:水深,计算条件为:b/h=2.0、a/b=0.5,G1=G2=1.0、2.0。
3.1 外圆内圆双层透水同心结构物图 4分别为波浪作用于内、外筒的波力及总力,由图 4(a)显示内筒无因次波力值会随G1、G2值增加而降低;而且在ka=1.85时都会有波力接近于零出现,而且ka在3.0~4.0,内筒波力变化不大几乎为一定值。图 4(b)外筒波力会随ka增加而呈现波动状的变化;波力峰值会逐渐降低;同样波力会随G1、G2值增加而降低,但外筒较不易出现波力为零现象。图 4(c)为波浪作用于外圆内圆双层沉箱无因次总力与ka的关系,由于内、外筒波力同时考虑时,总力变化较为单调,不太容易出现峰、谷值变化,会随着ka的逐渐增加而快速上升到总力最大值,其后则随着ka增加,总力慢慢降低再渐渐上升。由图中显示当G1=G2=1.0时,ka=0.46有最大无因次总力值达到4.131;而当G1、G2值增加为2.0时,最大无因次总力下降为3.218,发生位置ka往较小值左侧偏移,出现在ka=0.41。

|
| 图4 外圆内圆的无因次波力(b/h=2.0,a/b=0.5) Figure 4 Non-dimensional wave forces experienced by inner circular and outer cylinder (b/h=2.0, a/b=0.5) |
图 5为外圆内圆与外圆内方相对爬升的比较结果。由图显示当内部结构物形状由圆形改变为方形,对于外筒内、外圈爬升值在向浪侧(θ/π=1.0)变化较大;而且外圆内方爬升值大于外圆内圆;但是在背浪侧爬升值变化(θ/π=0)则不明显。另外,在内筒内、外圈爬升值除了在方筒角隅处(大约在θ/π=0.25、0.75附近)有明显增大现象,另外,大约在θ/π=0.61(θ=110°)附近爬升值会降低,在向浪侧、背浪侧其爬升值差异不大。

|
| 图5 外圆内圆柱及外圆内方柱相对爬升的比较(a/h=1.0,b/h=2.0,a/b=0.5,kh=1.2) Figure 5 Comparison of wave relative run-up on the dual porous cylinder (b/h=2.0, a/b=0.5, kh=1.2) |
图 6为外圆内圆与外圆内方无因次波力的比较。图中整体显示透水参数增加确实可降低内、外筒的波力;由图 6(a)亦显示内方筒波力明显较内圆筒波力来得大;而图 6(b)则显示仅小幅度改变内部结构物形状,对于外圆筒波力变化影响并不明显。图 6(c)为外圆内圆及外圆内方无因次总力的比较,由图中可发现无因次总力大约以ka=3.5为一分界,ka < 3.5时外圆内方总力大于外圆内圆,而ka > 3.5右侧则是外圆内方总力小于外圆内圆。

|
| 图6 外圆内圆及外圆内方无因次波力的比较(b/h=2.0,a/b=0.5) Figure 6 Comparison of non-dimension wave forces experienced by the dual porous cylinder (b/h=2.0, a/b=0.5) |
本文除了将外圆内圆与外圆内方无因次波力作比较外;并将传统外圆内圆(不透水)双重圆筒亦一并加以讨论并比较,分别以型态a、型态b、型态c表示,计算条件为G1=G2=1.0及G1=0、G2=1.0,其结果如图 7所示。由图 7(a)显示,当内筒为不透水时(型态c,G1=0),波力明显大于采用透水结构物,而且一般采用方形结构(型态b)大约在ka=1.6~4.4其波力明显较圆形结构(型态a)来得大;但是对于外筒结构物(图 7(b))三者波力变化趋势相似,除了波力峰、谷值发生位置ka值会有所改变外,当内筒采用不透水形式,对外筒波力较容易出现波力为零现象。图 7(c)为三者无因次总力与ka的关系图,由图中显示若内筒为不透水,因此大约在ka > 1.0之后,型态c总力远大于内筒为透水总力型态a及型态b。

|
| 图7 三种不同型态结构物无因次波力的比较(b/h=2.0,a/b=0.5,G1=G2=1.0) Figure 7 Comparison of non-dimension wave forces experienced by three geometrical cross section (b/h=2.0, a/b=0.5, G1=G2=1.0) |
本文将传统单座仅有外壁透空双筒柱沉箱改变成内、外壁皆透空双层透水沉箱,并利用复合边界元素法(CBEM)数值计算, 可得到以下结论:
1) 当波浪作用于传统外壁透空同心圆柱时,当不透水内筒波力达到峰值附近时,此时透水外筒波力会降到谷值;但是此种现象在外圆内圆或外圆内方双层透水沉箱中较不易发生。
2) 透水参数G1、G2值增加确实可降低内、外筒的波力;而且内方筒波力明显较内圆筒波力来得大;而透水参数增加对于外圆筒波力变化影响不明显。
3) 当内筒采用不透水型式,外筒波力较容易出现波力为零现象;而当内筒改为透水型式,此时外筒较不易出现波力为零现象。
4) 双层透水沉箱除了能降低波浪作用例外,也具备消除堤头导浪、降低船迹波、减少二次反射、提高港内静稳、避免港池共振、增加生物多样性及内、外海水循环达到净化港内水质等多功能的目标,在未来海洋港湾工程有极大的发展潜力。
| [1] | JARLAN G E. A perforated vertical wall breakwater[J]. Dock and harbour authority, 1961, 41(486): 394–398. |
| [2] |
林启正.沉箱拖放之时机与技术[R].基隆:基隆港务局, 1975.
LIN Chicheng. The technical and occasion of floating caisson[R]. Keelung: Keelung Harbor Bureau, 1975. |
| [3] |
滕斌, 李玉成, 孙路. 波浪与外壁透空双筒柱的相互作用[J].
中国工程科学, 2001, 3(10): 41–47.
TENG Bin, LI Yucheng, SUN Lu. Wave interaction with a partial porous double-wall cylinder[J]. Engineering science, 2001, 3(10): 41–47. |
| [4] |
孙路.波浪对外壁开孔双圆筒结构的作用[D].大连:大连理工大学, 2005.
SUN Lu. Wave interaction with combined cylinders structure with perforated outer wall[D]. Dalian: Dalian University of Technology, 2005. |
| [5] | TAO Longbin, SONG Hao, CHAKRABARTI S. Scaled boundary FEM solution of short-crested wave diffraction by a vertical cylinder[J]. Computer methods in applied mechanics and engineering, 2007, 197(1/2/3/4): 232–242. |
| [6] | SONG Hao, TAO Longbin. Short-crested wave interaction with a concentric porous cylindrical structure[J]. Applied ocean research, 2007, 29(4): 199–209. DOI:10.1016/j.apor.2008.01.001 |
| [7] |
李玉成, 刘洪杰, 滕斌. 双层局部开孔板沉箱对波浪反射的理论研究[J].
海洋工程, 2005, 23(1): 18–32.
LI Yucheng, LIU Hongjie, TENG Bin. Theoretical analysis of the wave reflection by caissons with double-layered perforated wall[J]. The ocean engineering, 2005, 23(1): 18–32. |
| [8] |
汪宏, 沈丽玉, 王勇. 双层开孔直立式板结构的消波性能试验[J].
水运工程, 2011(2): 21–25.
WANG Hong, SHEN Liyu, WANG Yong. Test on wave-dissipating performance of double-layer-hole vertical plate structure[J]. Port & waterway engineering, 2011(2): 21–25. |
| [9] |
刘俊, 林皋, 李建波. 带双层开孔外筒的圆筒结构的水动力特性研究[J].
物理学报, 2012, 61(12): 120202.
LIU Jun, LIN Gao, LI Jianbo. A study of the hydrodynamic behavior of cylindrical structure with double porous outer shelters[J]. Acta physica sinica, 2012, 61(12): 120202. |
| [10] | LIU Jun, LIN Gao, LI Jianbo. Short-crested waves interaction with a concentric cylindrical structure with double-layered perforated walls[J]. Ocean engineering, 2012, 40: 76–90. DOI:10.1016/j.oceaneng.2011.12.011 |
| [11] |
岳景云, 翁文凯. 波浪通过透水cosine-type同心圆柱结构物绕射之研究[J].
海洋工程, 2014, 32(6): 1–8.
YUEH Chingyun, WENG Wenkai. Wave diffraction by a porous cosine-type cylinder with a solid interior cylinder[J]. The ocean engineering, 2014, 32(6): 1–8. |
| [12] |
岳景云, 何翊钧, 庄世璇, 等. 波浪与外壁透空双方形沉箱的相互作用[J].
海洋工程, 2015, 33(3): 10–18.
YUEH Chingyun, HO Yichun, CHUANG Shihhsuan, et al. Wave action on dual-square caisson with perforated outer wall[J]. The ocean engineering, 2015, 33(3): 10–18. |
| [13] | YU Xiping. Diffraction of water waves by porous breakwaters[J]. Journal of waterway, port, coastal, and ocean engineering, 1995, 121(6): 275–282. DOI:10.1061/(ASCE)0733-950X(1995)121:6(275) |
| [14] | TAO Longbin, SONG Hao, CHAKRABARTI S. Scaled boundary FEM model for interaction of short-crested waves with a concentric porous cylindrical structure[J]. Journal of waterway, port, coastal, and ocean engineering, 2009, 135(5): 200–212. DOI:10.1061/(ASCE)0733-950X(2009)135:5(200) |
| [15] | MENG Xiannan, ZOU Zaojian. Wave interaction with a uniform porous cylinder of arbitrary shape[J]. Ocean engineering, 2012, 44: 90–99. DOI:10.1016/j.oceaneng.2012.01.025 |



