2. College of Shipbuilding Engineering,Harbin Engineering University, Harbin 150001, China
在实际水平轴潮流电站中,为了充分利用表面较高的流速,水平轴潮流能水轮机一般由漂浮式载体或固定式载体支撑其远离海底而靠近自由面,水轮机叶轮面临水中空化、自由面以及重力水波引起的速度梯度等不同程度的影响,这种影响一方面导致叶轮功率特性变差,另一方面则可能导致干扰载荷累积、使水轮机或支撑结构疲劳甚至断裂破坏,酿成重大事故。
水平轴潮流能叶轮[1-5]近水面运行时,叶轮的运动会造成自由面的变形,自由面的变形反过来会影响叶轮的性能。叶轮和自由面相互影响的过程会涉及到旋涡、湍流与自由面的非定常、非线性相互作用,使水平轴潮流能叶轮周围流场变得非常复杂。因此,准确预报水平轴叶轮在自由面条件下的水动力性能显得尤为重要。
Bahaj等[6-9]在不同翼型、桨距角以及两种不同叶尖浸没水深条件下,采用模型试验方法,研究了水轮机性能、叶片空化以及双转子干扰问题,得出了水轮机在不同叶尖浸没水深时的功率及载荷规律。Coiro等[10]在拖曳水池中对S805翼型水翼进行了测试。水轮机直径0.8 m,水轮机浸没水深在自由面下1.3 m。拖车速度范围1.3~3.5 m/s,桨距角范围-4~4°,试验过程中没有研究空化问题。Maganga等[11]针对来流湍流度8%~25%,偏航角-10~20°,自由面以下深度0.94D、1.37D和2.04D(D为叶轮直径)等条件下在一个封闭的循环水槽中对3叶片水轮机进行实验研究。实验揭示了来流有较高湍流度时,效率与推力系数下降约9%,在较大偏航角时,水轮机性能明显下降,并给出了不同叶尖浸没水深下的效率和推力系数。国内针对不同叶尖浸没水深下水平轴潮流能叶轮水动力性能鲜有研究。
从以上研究可以看出,针对自由面条件下水平轴水轮水动力问题的研究主要采用模型试验的方法,该方法主要不足之处在于:模型试验一般测试的是水轮机旋转过程中的平均效率及载荷,无法体现自由面对水轮机瞬时性能的影响;模型试验无法给出复杂的流场细节。因此,本文基于ANSYS CFX方法,研究叶尖浸没水深对水平轴叶轮水动力性能及载荷的影响规律,为潮流电站设计提供设计依据,以及为工程应用提供参考和借鉴。
1 CFD数值模拟 1.1 计算模型建立叶轮计算模型采用哈尔滨工程大学深海中心可再生能源的实验模型。该实验模型的叶轮直径D为0.7 m,叶片数为2。叶片采用变弦长及变桨距角形式,除叶片根部外,展向各位置处的截面翼型均为S809。叶轮模型如图 1所示。计算模型建好之后,为了提交计算精度,需建立一个足够大的计算域来模拟流场,计算域的出口与入口都是正方形,边长是10倍叶轮直径;入口到叶轮旋转平面的距离是5倍叶轮直径;出口到叶轮旋转平面的距离为15倍叶轮直径。
1.2 网格划分网格划分是CFD模拟过程中较为关键的环节,也是比较耗时的环节,网格质量的好坏直接影响数值模拟精度和计算效率。本文采用结构化网格和非结构化网格相结合的网格形式对流场进行离散,旋转域由于叶片外形复杂,采用非结构化网格形式,静止域采用结构化网格形式。文献[12]对网格数量及收敛性进行了研究,结果表明:当网格数量达到231万,模型表面网格第一层高度0.000 5 m时,继续加密网格,计算结果已基本上没有变化,因此该文计算中采用此网格数类型。如图 1所示。
1.3 边界条件设置模拟自由面的难点是需要模拟两相流,即水和空气,水汽交界面采用体积分数法(VOF)处理。在CFD数值模拟中,多相流模拟的稳定性及收敛性是比较差的,对网格要求比较高。具体设置如下:设置大气压为参考压力,给定重力加速度的方向;将入口边界设置为速度入口条件,给定均匀来流速度 、湍流参数及水和空气的体积分数,体积分数根据叶尖浸没水深H(叶尖浸没水深是指叶尖距水面最短距离)得到;出口边界设置为开放的压力边界,给定相对压力及水和空气的体积分数,相对压力设为水的静压,水和空气的体积分数与入口一致;流体计算域的左右两侧和底面设置为自由滑动壁面;流体计算域的顶部设置为开放的压力边界,相对压力设为0,水的体积分数为0,空气的体积分数为1;叶片及轮毂表面设置为不可滑移壁面;给定旋转域旋转角速度;静止域和旋转域之间通过交界面连接。计算中湍流模型采用SST模型,求解器为瞬态求解器,时间步长为叶轮旋转2°所用的时间。
多相流模拟时经常会出现发散的现象,特别在刚开始计算的时候。因为在刚开始计算时,由于流体及物体的突然运动,导致相与相之间的交界面变化显著,很容易导致计算发散。为了避免出现类似错误,先计算得到叶轮不旋转时稳定的自由表面条件,让自由面适应网格模型,以此为初始条件,计算叶轮旋转时的水动力性能。

|
| 图1 模型及网格示意图 Figure 1 Schematic and mesh model |
采用上述网格模型及边界条件设置对哈尔滨工程大学深海中心可再生能源所试验状态(流速U=1.5 m/s,H=0.79D)进行模拟,得到叶轮在自由面条件下的能量利用率及轴向载荷系数。水轮机的能量利用率CP是表示叶轮吸收潮流动能能力的参数,叶轮轴向载荷系数CZ是叶轮沿旋转轴方向载荷的无量纲化,叶尖速比是叶尖旋转线速度与来流速度的比值,表达式为
| ${{C}_{P}}=\frac{P}{\frac{1}{2}\rho {{U}^{3}}\pi {{R}^{2}}}$ | (1) |
| ${{C}_{Z}}=\frac{{{F}_{Z}}}{\frac{1}{2}\rho {{U}^{2}}\pi {{R}^{2}}}$ | (2) |
| $\lambda =\frac{\omega R}{U}=\frac{\pi nR}{30U}$ | (3) |
式中:P为叶轮功率,W;ρ为流体密度,kg/m3;U为流体流速,m/s;FZ为叶轮旋转轴方向载荷,N;ω为叶轮旋转角速度,rad/s;R为叶轮半径,m;n为叶轮转速,r/min。
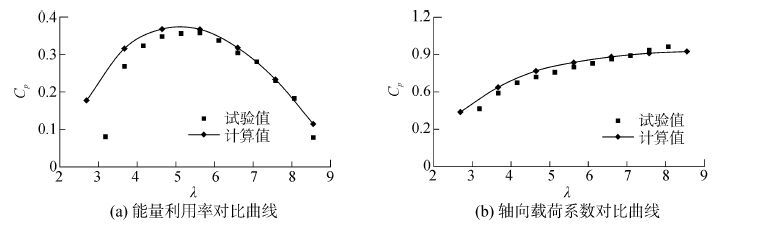
计算结果的平均值与试验值对比如图 2所示,图中实验值是在哈尔滨工程大学船舶拖曳水池中进行测试的,平均值是指叶轮旋转一圈时计算结果的算术平均。从图 2中可以看出:在高速比时计算值与试验值吻合比较好,基本一致,但在低速比时计算值高于实验值,速比越低,差异越明显。这是因为能量利用率最大值所对应的速比为最优速比,而在叶片设计时,最优速比一般与翼型的最优攻角对应。当速比大于最优速比时,叶轮旋转时叶片各截面翼型的实际攻角小于翼型的最优攻角,流动不发生分离,计算值与试验值吻合比较好;但当速比小于最优速比时,叶片各截面翼型的实际攻角大于翼型的最优攻角,流动产生分离,甚至出现失速现象,计算值与试验值存在一定偏差。整体上来说,计算值与试验值吻合较好,验证了该数值方法研究水平轴叶轮在自由面条件下的水动力的可行性与准确性。
|
| 图2 计算值与试验值对比 Figure 2 Comparison between calculated and experimental values |
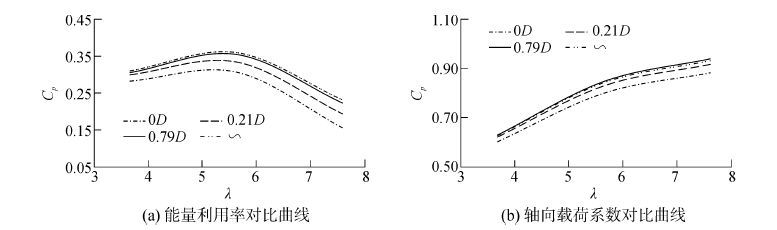
在上述数值计算的基础上,分别对另外两个不同叶尖浸没水深(H=0,H=0.21D)和无自由面进行模拟,分别计算三种不同转速(150、230、310 r/min)下的能量利用率及轴向载荷系数。不同转速下计算结果的平均值如图 3所示,图例中∽表示无自由面,流速1.5 m/s。从图 3可以看出:随着叶尖浸没水深的增加,能量利用率和轴向载荷系数逐渐增加,且转速越大,增加越明显;叶尖浸没水深为0.79D时的计算结果与无自由面时的计算结果非常接近,说明叶尖浸没水深达到0.79D时,自由面对叶轮的水动力已几乎无影响。这是因为叶轮旋转使自由面产生兴波,且叶尖浸没水深越小,兴波越明显,从而使叶轮水动力性能及载荷随叶尖浸没水深的减小而减小。
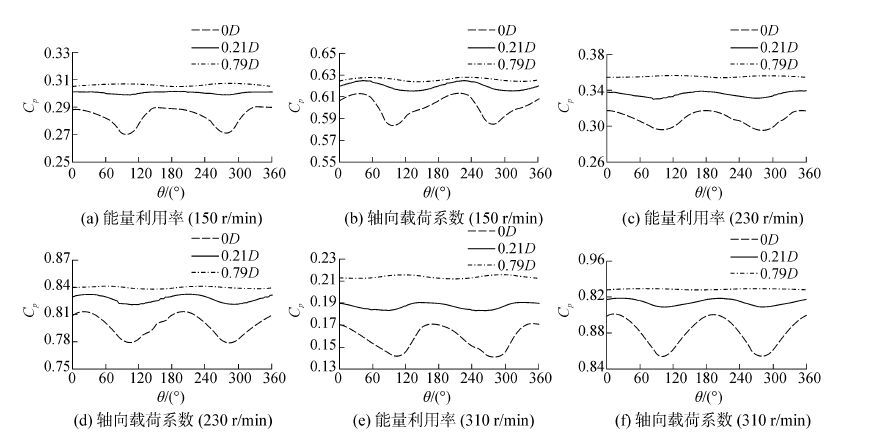
不同叶尖浸没水深下轴向载荷系数及能量利用率瞬时值随叶片方位角的变化规律如图 4所示,方位角为0°时,叶片轴线与水平面平行。从图 4中可以得知:自由面使叶轮轴向载荷系数及能量利用率的瞬时值产生波动,波动幅值随叶尖浸没水深的增加而减小;当叶尖浸没水深达到0.79D时,叶轮轴向载荷系数及能量利用率的瞬时值的波动已经很小了,说明自由面对叶轮的水动力已几乎没影响。这是因为叶尖浸没水深越小,叶轮旋转过程中水面兴波越大,能量耗散越多,从而导致叶轮水动力性能及载荷降低。载荷的波动影响叶轮结构的疲劳寿命,能量利用率的波动不利于电能的稳定输出,在结构和电控系统设计中需要特别考虑。
|
| 图3 不同叶尖浸没水深下的平均计算值 Figure 3 The average calculated values of different tip-immersion |
|
| 图4 不同叶尖浸没水深的瞬时计算值 Figure 4 The instantaneous calculated values of different tip-immersion |
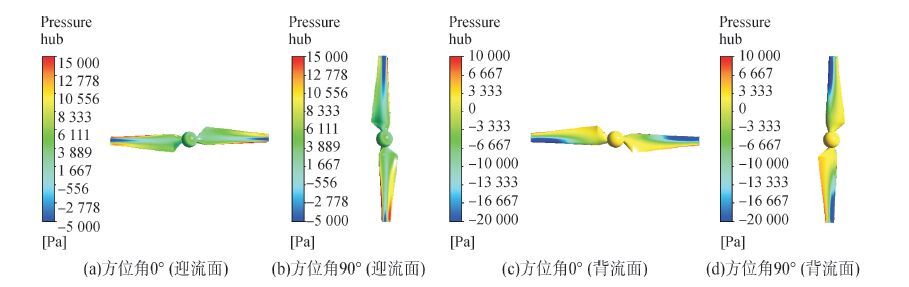
图 5给出了计算模型在转速为230 r/min,叶尖浸没水深为0时,叶片在不同方位角下表面压力分布。从图 5中可以看出:叶片迎流面的压力明显高于背流面的压力,从而形成来流方向的压力差,即轴向载荷;当叶片轴线与水平面平行时,两个叶片的压力分布相同;但当叶片轴线与水平面垂直时,两个叶片的压力分布明显不同,即靠近自由液面的叶片的表面压力比较低。由于叶片在不同位置时表面压力不同,从而导致叶片载荷在旋转过程中发生波动。
图 6给出了计算模型在转速230 r/min时,不同叶尖浸没水深下自由面示意图,由图 6可以看出:当叶尖浸没水深为0时,自由液面出现非常明显的兴波,在向下游传播过程中,兴波逐渐减小并向两侧扩散;随着叶尖浸没水深的增加,自由液面兴波逐渐减小,能量耗散降低,从而导致水轮机轴向载荷及能量利用率增加。
|
| 图5 叶片表面压力分布 Figure 5 Pressure distribution of blade |

|
| 图6 自由面示意图 Figure 6 The diagram of free surface |
采用ANSYS CFX对三维水平轴叶轮在自由面条件下的水动力特性进行了计算分析,研究结果表明:
1) 自由面使叶轮轴向载荷系数及能量利用率的瞬时值产生波动,波动幅值随叶尖浸没水深的增加而减小,载荷的波动影响叶轮结构的疲劳寿命,能量利用率的波动不利于电能的稳定输出,在结构和电控系统设计中需要特别考虑;
2) 轴向载荷系数及能量利用率的平均值随叶尖浸没水深的增加而增加,并逐渐接近于无自由面时的计算结果;
3) 当叶尖浸没水深为0.79D时,轴向载荷系数及能量利用率已基本不随叶片方位角的变化而改变,即自由面已几乎无影响。
| [1] |
沈云, 李龙, 朱多彪. 水平轴潮流水轮机转轮尾流特性数值分析[J].
水电能源科学, 2013, 31(10): 149–151.
SHEN Yun, LI Long, ZHU Duobiao. Numerical analysis of wake performance of horizontal-axis tidal current turbine[J]. Water resources and power, 2013, 31(10): 149–151. |
| [2] | MILNE I A, DAY A H, SHARMA R N, et al. Blade loading on tidal turbines for uniform unsteady flow[J]. Renewable energy, 2015, 77: 338–350. DOI:10.1016/j.renene.2014.12.028 |
| [3] | MILNE I A, DAY A H, SHARMA R N, et al. Blade loads on tidal turbines in planar oscillatory flow[J]. Ocean engineering, 2013, 60: 163–174. DOI:10.1016/j.oceaneng.2012.12.027 |
| [4] | BAHAJ A S, MOLLAND A F, CHAPLIN J R, et al. Power and thrust measurements of marine current turbines under various hydrodynamic flow conditions in a cavitation tunnel and a towing tank[J]. Renewable energy, 2007, 32(3): 407–426. DOI:10.1016/j.renene.2006.01.012 |
| [5] | LEE J H, PARK S, KIM D H, et al. Computational methods for performance analysis of horizontal axis tidal stream turbines[J]. Applied energy, 2012, 98: 512–523. DOI:10.1016/j.apenergy.2012.04.018 |
| [6] | BAHAJ A S, BATTEN W M J, MCCANN G. Experimental verifications of numerical predictions for the hydrodynamic performance of horizontal axis marine current turbines[J]. Renewable energy, 2007, 32(15): 2479–2490. DOI:10.1016/j.renene.2007.10.001 |
| [7] | BATTEN W M J, BAHAJ A S, MOLLAND A F, et al. Experimentally validated numerical method for the hydrodynamic design of horizontal axis tidal turbines[J]. Ocean engineering, 2007, 34(7): 1013–1020. DOI:10.1016/j.oceaneng.2006.04.008 |
| [8] | BATTEN W M J, BAHAJ A S, MOLLAND A F, et al. The prediction of the hydrodynamic performance of marine current turbines[J]. Renewable energy, 2008, 33(5): 1085–1096. DOI:10.1016/j.renene.2007.05.043 |
| [9] | BATTEN W M J, BAHAJ A S, MOLLAND A F, et al. Hydrodynamics of marine current turbines[J]. Renewable energy, 2006, 31(2): 249–256. DOI:10.1016/j.renene.2005.08.020 |
| [10] | COIRO D P, MAISTO U, SCHERILLO F, et al. Horizontal axis tidal current turbine: numerical and experimental investigations[C]//Offshore Wind and Other Marine Renewable Energies in Mediterranean and European Seas. Rome, Italy: European Seminar, 2006. |
| [11] | MAGANGA F, GERMAIN G, KING J, et al. Experimental characterisation of flow effects on marine current turbine behaviour and on its wake properties[J]. IET renewable power generation, 2010, 4(6): 498–509. DOI:10.1049/iet-rpg.2009.0205 |
| [12] |
王树齐, 肖钢, 张亮, 等. 潮流能水平轴水轮机支撑立柱干扰研究[J].
华中科技大学学报: 自然科学版, 2014, 42(4): 81–85.
WANG Shuqi, XIAO Gang, ZHANG Liang, et al. Supporting column influence analysis of Horizontal axis tidal current turbine[J]. Journal of huazhong university of science and technology: natural science edition, 2014, 42(4): 81–85. |



