无线传感器网络(wireless sensor network,WSN)中的分布式检测(distributed detection,DD)问题[1-3],近年来成为研究热点。其由大量低功耗的传感器节点和一个融合中心(fusion center,FC)组成,通过协同工作的方式来检测一个未知信号的存在性。由于传输网络中存在能量和带宽的约束,每个传感器节点在发送数据时需要将本地原始观测信息进行量化或者压缩,降低数据的传输量。DD主要针对两类不同的信源,一种是随机参数,另一种是确定性未知参数。迄今国内外一些研究者对确定性未知参数的检测取得了许多研究成果:文献[4-5]表明对于二元假设检验问题,无论是贝叶斯准则还是纽曼皮尔逊准则(Neyman-Pearson criterion,NPC),传感器本地最优判决准则都是似然比检验(likelihood ratio test,LRT)。然而在实际情况中,待检测信号的统计信息往往未知,在传感器节点处无法计算LRT。通过在FC处使用广义似然比检验(generalized likelihood ratio test,GLRT),可以很好地解决这个问题。文献[6]提出了基于1-bit量化的GLRT检测方法,在保证一定检测性能的前提下,降低了所需传输的信息量。文献[7]提出了运算效率更高的基于1-bit量化的Rao检测方法。但原始信息损失过多,性能上与未量化的检测方案相比损失较大。为了解决这个问题,文献[8]研究了基于局部软决策GLRT融合准则下的目标检测与定位。与直观的计数融合准则相比,文中提出的系统性能较高,但并未考虑量化阈值的选取对检测性能的影响。文献[9]在每个传感器节点引入多比特量化器,有效地提高了系统性能,但文中假设传感器节点对观测信息做均匀量化处理,并不是最优的量化方案。文献[10]研究了分布式量化卡尔曼滤波问题,提出了一种动态量化器设计方法,但并未考虑量化阈值的选取与优化。
针对上述方法存在的问题,本文在文献[8]和[9]中多比特量化器结构的基础上,将文献[6]中渐进检测性能的思想引入量化阈值优化的过程中,提出一种基于局部量化观测的分布式Rao检测方法,对局部量化阈值进行了优化,并得到检测器的解析表达式。
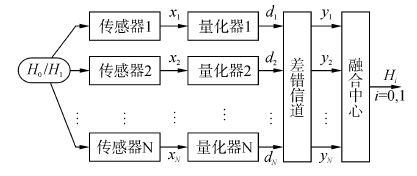
1 分布式检测模型图 1为WSN中基于局部软决策分布式检测框图。考虑WSN采用并行结构,由N个传感器节点组成,传感器节点分别独立地感知环境中感兴趣的特征参数。由于网络中存在带宽以及功率受限的问题,传感器节点需要将感知到的原始观测信息进行量化处理。最后将这些量化后的比特信息传送至FC,FC基于接收到的量化观测数据根据某种融合准则对目标的状态做出实时检测,则检测问题可以描述为
| $\left\{ \begin{array}{l} {H_0}:{x_n} = {\omega _n}\\ {H_1}:{x_n} = \theta + {\omega _n} \end{array} \right.,n \in r$ | (1) |
式中:$n \in r \buildrel \Delta \over = \left\{ {1,2, \ldots ,N} \right\}$,xn表示第n个传感器节点的原始观测值,ωn为观测噪声。假设各个传感器节点之间的噪声相互独立。
|
| 图1 基于局部量化观测的分布式检测框图 Figure 1 DD diagram based on local quantized measurements |
考虑到实际WSN中存在发射功率和传输带宽的限制,每个传感器节点需将观测到的原始信息通过一个量化深度为q的标量量化器对其进行量化。假设第n个传感器节点处的q比特量化器表示为Qn,q(q∈Z+),将观测空间R划分为2q个互不重叠的量化区间。定义τn,k(k=0,1,…,2q)为量化阈值,满足如下关系,τn,0 <τn,1<… <τn,2q,且τn,0=-∞,τn,2q=+∞。第n个传感器节点处的q比特量化器输出数据dn可表示为
| ${d_n} = {Q_{n,q}}\left( {{x_n}} \right) = {b_{n,i}},{x_n} \in \left[ {{\tau _{n,i - 1}},{\tau _{n,i}}),i = 1,2, \cdots ,{2^q}} \right]$ | (2) |
式中:bn,i为第i个量化电平被编码的q比特二进制码字,${b_{n,i}} = {\left[ {{b_{n,i,q}},{b_{n,i,q - 1}}, \cdots {b_{n,i,1}}} \right]^{\rm{T}}}{b_{n,i,q}} \in \left\{ {0,1} \right\}$。
在第n个传感器节点处,原始观测信息xn落入量化器Qn,q中第j个量化区间τn,j-1,τn,j内的概率表示为
| $\begin{array}{l} P_{{\omega _n}}^{n,j}\left( \theta \right) = P\left( {{d_n} = {b_{n,i}};\theta } \right) = P\left( {{\tau _{n,j - 1}} \le {x_n} < {\tau _{n,j}};\theta } \right) = \\ {F_{{\omega _n}}}\left( {{\tau _{n,j - 1}} - \theta } \right) - {F_{{\omega _n}}}\left( {{\tau _{n,j}} - \theta } \right) \end{array}$ | (3) |
式中:Fωn(·)表示噪声ωn的互补累积分布函数(complementary cumulative distribution function,CCDF)。量化后的q比特信息{dn}n=1N通过差错信道后进入FC。
|
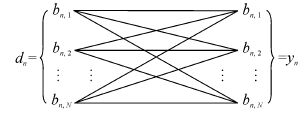
| 图2 差错信道 Figure 2 Distortion channel |
文献[8-9]对基于多比特量化的检测问题进行了研究,但仅考虑了信息发送到FC不发生差错的情况,本文将考虑差错信道对量化阈值和检测性能的影响。假设传感器各节点之间相互独立,且每个信道模型可构造为一个基于二元对称信道(binary symmetric channel,BSC)的多元差错信道,其中每一比特的错误转移概率记为${\tilde P}$,1-${\tilde P}$为正确接收0或1的概率。q比特多元差错信道如图 2所示。由于差错信道的影响,FC接收到第n个传感器节点发送的信息yn可能是二进制码字集中的任意一个。当第n个传感器节点向FC传输q比特信息bn,j,FC通过差错信道接收到bn,i的条件概率为
| $\begin{array}{l} P\left( {{y_n} = {b_{n,i}}|{d_n} = {b_{n,j}}} \right) = {{\tilde P}^{{D_{n,i,j}}}}{\left( {1 - \tilde P} \right)^{\left( {q - {D_{n,i,j}}} \right)}} = \\ \Phi \left( {q,\tilde P,{D_{n,i,j}}} \right) \end{array}$ | (4) |
式中:Dn,i,j为q比特信息bn,j和bn,i之间的汉明距离,表示传输码字bn,j与接收码字bn,i之间总的错误接收比特数,通过计算可表示为
| ${D_{n,i,j}} \buildrel \Delta \over = D\left( {{b_{n,i}},{b_{n,j}}} \right) = q - \sum\limits_{k = 0}^{q - 1} {I\left( {{b_{n,i,q - k}},{b_{n,j,q - k}}} \right)} $ | (5) |
式中:I(·)为指示函数,当A≠B时,I(A,B)=0,否则,I(A,B)=1。在备选假设H1下,通过差错信道后到达FC处的接收信息yn的概率分布列(probability mass function,PMF)为
| $\begin{array}{l} \sum\limits_{i = 1}^{2q} {\sum\limits_{j = 1}^{2q} {P\left( {{y_n} = {b_{n,i}}|{d_n} = {b_{n,j}}} \right)} } P\left( {{d_n} = {b_{n,j}}} \right) = \\ {\prod\limits_{i = 1}^{2q} {\left\{ {\sum\limits_{j = 1}^{2q} {\Phi \left( {q,\tilde P,{D_{n,i,j}}} \right)} P_{{\omega _n}}^{n,j}\left( \theta \right)} \right\}} ^{{I^{\left( {{y_n},{b_{n,i}}} \right)}}}} \end{array}$ | (6) |
式中:Pωnn,j(θ)已在式(3)中定义。
2 融合准则传感器节点向FC发送量化信息,FC根据接收到的信息通过一定的融合准则,对待检测信号的存在性做出全局判决。本节将讨论融合准则的选取。
当虚警概率(probability of false alarm,PFA)恒定时,要使得检测概率(probability of detection,PD)最大,需采用NPC准则。广义似然比检验(general likelihood ratio,GLRT)[11]具有结构简单,不需要待检测信号的先验知识,性能良好等优点,在实际中得到了广泛的应用。在大数据记录(N→∞)的情况下,GLRT的渐进概率密度函数(probability density function,PDF)与Rao检验的相同。然而GLRT需要分别计算H0和H1条件下未知参数的MLE,计算量较大,会增加检测器结构的复杂度。而且在非高斯问题中未知参数的MLE很难获得。Rao检验只需要计算在H0条件下θ的MLE,运算量较低,结构简洁,因此在FC处,本文选择Rao检验作为融合准则。在满足如下条件时,基于q比特量化观测的Rao检验判决为H1 :
| ${\left\{ {{T_R}\left( Y \right) \buildrel \Delta \over = \frac{{{{\left( {\partial \ln \left[ {P\left( {Y;\theta } \right)/\partial \theta {|_{\theta = {\theta _0}}}} \right]} \right)}^2}}}{{{\rm{FI}}\left( {{\theta _0}} \right)}}} \right\}^{{H_1}}} > \gamma $ | (7) |
式中:TR(Y)表示Rao检测统计量,γ为Rao检测器阈值,FIθ为费舍尔信息(fisher information,FI),即$J\left( \theta \right) \buildrel \Delta \over = - E\left\{ {{\partial ^2}\ln P\left( {Y;\theta } \right)/\partial {\theta ^2}} \right\}$。为了求得TR(Y)的解析表达式,将ln[P(Y;θ)]展开为
| $\begin{array}{l} \ln \left[ {P\left( {Y;\theta } \right)} \right] = \sum\limits_{n = 1}^N {\ln } \left[ {P\left( {{y_n};\theta } \right)} \right] = \\ \sum\limits_{n = 1}^N {\sum\limits_{i = 1}^{2q} {\left\{ {I\left( {{y_n},{b_{n,i}}} \right)\ln \left[ {\sum\limits_{j = 1}^{2q} {\Phi \left( {q,\tilde P,{D_{n,i,j}}} \right)P_{{\omega _n}}^{n,j}} } \right]} \right\}} } \end{array}$ | (8) |
对式(8)求关于θ的二阶导数,再取负期望,可求得FI为
| $\psi \left( \theta \right) = \sum\limits_{n = 1}^N {\sum\limits_{i = 1}^{2q} {\frac{{{{\left\{ {\sum\limits_{j = 1}^{2q} {\Phi \left( {q,\tilde P,{D_{n,i,j}}} \right)P_{{\omega _n}}^{n,j}\left( \theta \right)} } \right\}}^2}}}{{\sum {_{j = 1}^{2q}\Phi \left( {q,\tilde P,{D_{n,i,j}}} \right)P_{{\omega _n}}^{n,j}\left( \theta \right)} }}} } $ | (9) |
式中:pωn(·)为观测噪声ωn的PDF,可表示为
| $P_{{\omega _n}}^{n,j}\left( \theta \right) = {P_{{\omega _n}}}\left( {{\tau _{n,j - 1}} - \theta } \right) - {p_{{\omega _n}}}\left( {{\tau _{n,j}} - \theta } \right)$ | (10) |
对式(8)求关于θ的一阶导数,将结果与式(9)一并代入式(7),可计算得到Rao检验的解析表达式为
| ${T_R}\left( Y \right) = {\left\{ {\sum\limits_{n = 1}^N {\sum\limits_{j = 1}^{2q} {I\left( {{y_n},{b_{n,i}}} \right)} } \frac{{\sum\limits_{j = 1}^{2q} {\Phi \left( {q,\tilde P,{D_{n,i,j}}} \right)P_{{\omega _n}}^{n,j}\left( {\theta = 0} \right)} }}{{\sum\limits_{j = 1}^{2q} {\Phi \left( {q,\tilde P,{D_{n,i,j}}} \right)P_{{\omega _n}}^{n,j}\left( {\theta = 0} \right)} }}} \right\}^2} \times {\left[ {\psi \left( {\theta = 0} \right)} \right]^{ - 1}}$ | (11) |
从式(11)可以看出,TR(Y)是量化阈值τn=[τn,1,…,τn,2q-1]T的函数。通过优化得到最优量化阈值τn*,可以使Rao检验的性能达到渐进最优。
3 量化阈值的优化与分析本文选取大样本条件下检测器的渐进性能[11]作为量化阈值的优化准则。根据等效大数据记录检验理论可知,在小信噪比下(微弱信号下),Rao检测方法的理论检测性能与GLRT的渐进性能一致,其检测统计量TR(Y)渐进地服从如下分布:
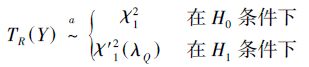
|
(12) |
式中:“a”表示渐进PDF,χ12表示1个自由度的chi平方PDF,${x'}$12(λQ )表示1个自由度的非中心chi平方PDF,非中心参数λQ为
| ${\lambda _Q} = {\left( {{\theta _1} - {\theta _0}} \right)^2}\psi \left( \theta \right){|_{\theta = {\theta _0}}}$ | (13) |
式中:θ0=0和θ1=θ分别表示在H0和H1条件下的待检测参数的真实值。根据式(12)可知,在给定的虚警概率PFA下,λQ越大,渐进检测性能越好。因此,为了得到使检测概率最大的最优量化阈值,可通过求解如下优化问题:
| ${\tau ^*} = \arg \mathop {\max }\limits_\tau {\lambda _Q}$ | (14) |
式中: τ为量化阈值构成的矩阵,即τ=[τ1,τ2,…,τN]。根据1.2小节的假设,即各传感器节点之间相互独立,可知各传感器节点使用相同的量化器Qn,q对原始观测信号进行量化。通过式(9)可知FI具有可加性,又因为λQ是关于FI的函数,上述优化问题式(14)可简化为
| $\begin{array}{l} \arg \mathop {\max }\limits_{{\tau _n}} \sum\limits_{i = 1}^{2q} {\frac{{{{\left\{ {\sum {_{j = 1}^{2q}{{\tilde P}^{_{n,i,j}}}{{\left( {1 - \tilde P} \right)}^{\left( {q - {D_{n,i,j}}} \right)}}\rho _{{\omega _n}}^{n,j}\left( 0 \right)} } \right\}}^2}}}{{\sum {_{j = 1}^{2q}{{\tilde P}^{_{n,i,j}}}{{\left( {1 - \tilde P} \right)}^{\left( {q - {D_{n,i,j}}} \right)}}\rho _{{\omega _n}}^{n,j}\left( 0 \right)} }}} \\ {\rm{s}}.{\rm{t}}. {\tau _n} = {\left[ {{\tau _{n,0}},{\tau _{n,1}}, \cdots ,{\tau _{n,2q}}} \right]^{\rm{T}}}\\ - \infty < {\tau _{n,1}} < {\tau _{n,2}} \cdots < {\tau _{n,2q}} < + \infty \end{array}$ | (15) |
假设式(1)中的观测噪声ωn的PDF服从具有一般形式的广义高斯分布:
| ${p_{{\omega _n}}}\left( x \right) = \frac{\beta }{{2\alpha \Gamma \left( {1/\beta } \right)}}{\rm{eap}}\left\{ { - {{\left| {\frac{{x - \mu }}{\alpha }} \right|}^\beta }} \right\}$ | (16) |
式中:μ、α、β分别为GGD的均值,形状参数和尺度参数,Γ(·)为Gamma函数。当β→1时,GGD的PDF为拉普拉斯型;当β=2时,为高斯型;当β→∞时,PDF趋近于均匀分布。
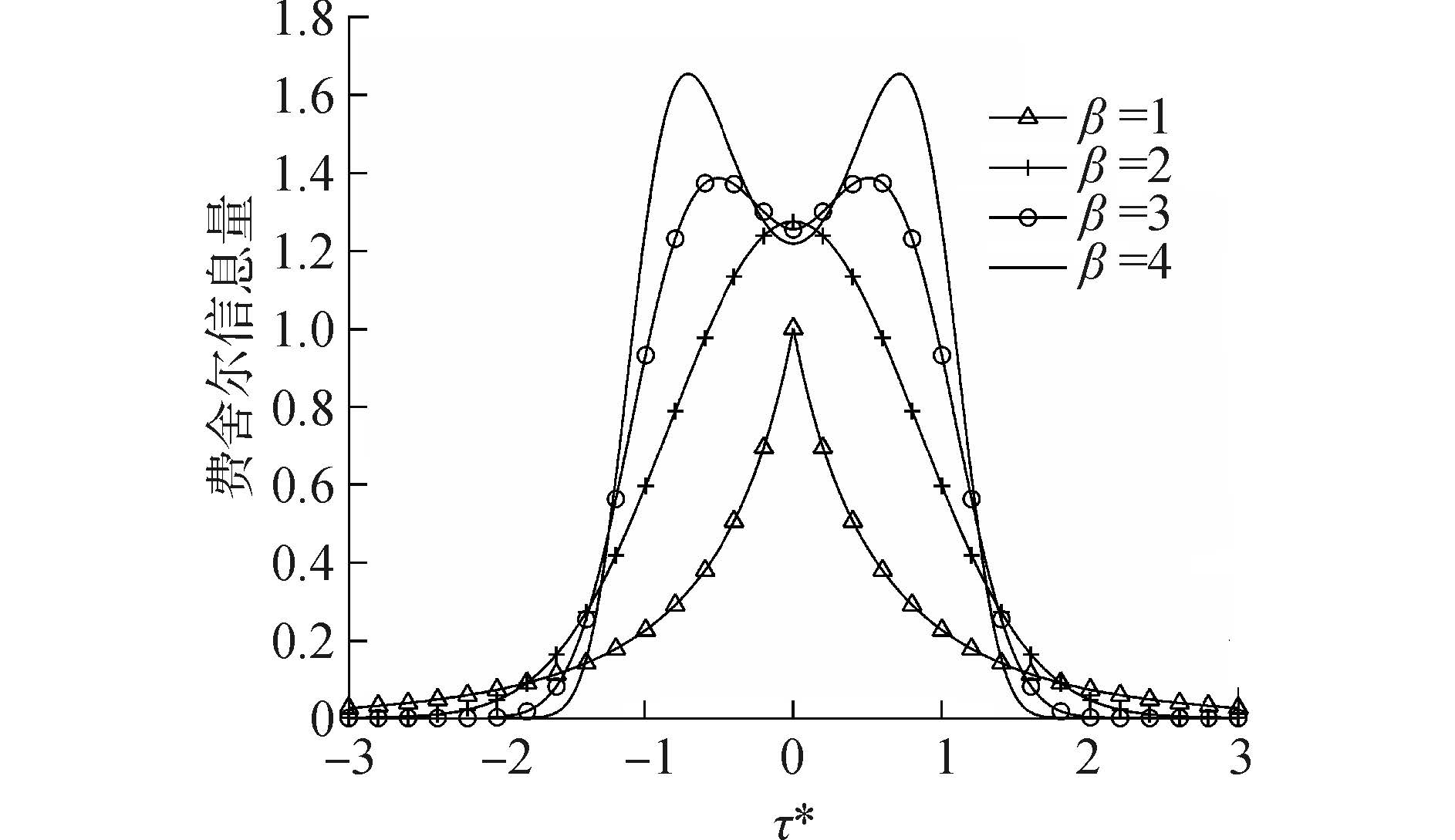
量化阈值τ的优化过程实质就是求解式(15),其中1-bit量化的情况显然是最直观且容易求得的。将q=1,$\tilde P = 0$,$\alpha = \sqrt 2 $,σ2=1和β=1,2,3,4分别代入式(16),得到FI与β的关系如图 3所示。根据第3章的讨论可知,最优量化阈值τ*是使FI最大的一组值。
|
| 图3 β对1-bit最优量化阈值的影响 Figure 3 The effect on the 1-bit optimum quantization threshold |
从图 3中可以看出,FI取得最大值的位置会受到尺度参数β的影响。当β=1和2时,FI具有单峰且中心对称性,性质类似高斯噪声;当β=3和4时,FI呈现双峰特性,取得最大值的位置由中心向两侧偏移。因此本文考虑具有代表性的β=2(高斯)和β=4(非高斯)两种情况来讨论。将q∈{1,2,3},${\tilde P}$∈{0,0.2},β∈{2,4}分别代入式(15),通过求解得到最优量化阈值。值得注意的是当q=1时,式(15)是一个较为容易求解的一维优化问题。在高斯噪声背景下,理想信道和差错信道下的1-bit最优量化阈值均为0;在GGD噪声下,理想信道和差错信道下的最优量化阈值分别为-0.713 8和-0.336 9。而当q≥2时,式(15)是一个非线性、非凸函数优化问题。传统的优化方法(梯度搜索法等)由于自身算法的特点可能会在不解析点停止搜索或者在搜索过程中容易陷入局部最优解而无法取得全局最优解。本文运用粒子群优化算法(particle swarm optimization algorithm,PSOA)对式(15)进行求解。PSOA具有全局优化能力和隐含并行性两大优点,使其适合于大规模复杂优化问题的求解。具体算法这里就不再赘述。通过求解后,得到3-bit最优量化阈值如表 1所示。
| 量化 阈值 | GGD | Gauss | ||||
| $\left( {\tilde P = 0} \right)$ | $\left( {\tilde P = 0.2} \right)$ | $\left( {\tilde P = 0} \right)$ | $\left( {\tilde P = 0.2} \right)$ | |||
| τ0* | -∞ | -∞ | -∞ | -∞ | ||
| τ1* | -1.200 6 | -0.631 8 | -1.747 9 | -4.999 9 | ||
| τ2* | -0.987 9 | -0.630 5 | -1.050 0 | -4.999 1 | ||
| τ3* | -0.777 6 | -0.630 1 | -0.500 5 | -0.315 2 | ||
| τ4* | -0.503 1 | -0.630 0 | 0 | 0 | ||
| τ5* | 0.586 2 | -0.452 3 | 0.500 5 | 0.315 2 | ||
| τ6* | 0.880 2 | 0.504 3 | 1.050 0 | 4.999 1 | ||
| τ7* | 1.133 5 | 0.504 4 | 1.747 9 | 4.999 9 | ||
| τ8* | +∞ | +∞ | +∞ | +∞ | ||
从表 1可以看出,在高斯噪声和GGD噪声背景下的量化方法都是非线性量化方法。在高斯噪声背景下的最优量化阈值呈现中心对称的结构特点,而在GGD噪声背景下并无明显规律。
4.2 检测性能分析根据式(12)所示的Rao检测器的渐进统计性能,虚警概率为
| ${P_{FA}} = {Q_{x_1^2}}\left( {2\ln \eta } \right)$ | (17) |
式中:Qχ12(·)表示自由度为1的卡方分布的右尾概率。相应地,检测概率为
| ${P_d} = {Q_{x'\mathop 2\limits_1 }}_{\left( {{\lambda _q}} \right)}\left( {2\ln \eta } \right)$ | (18) |
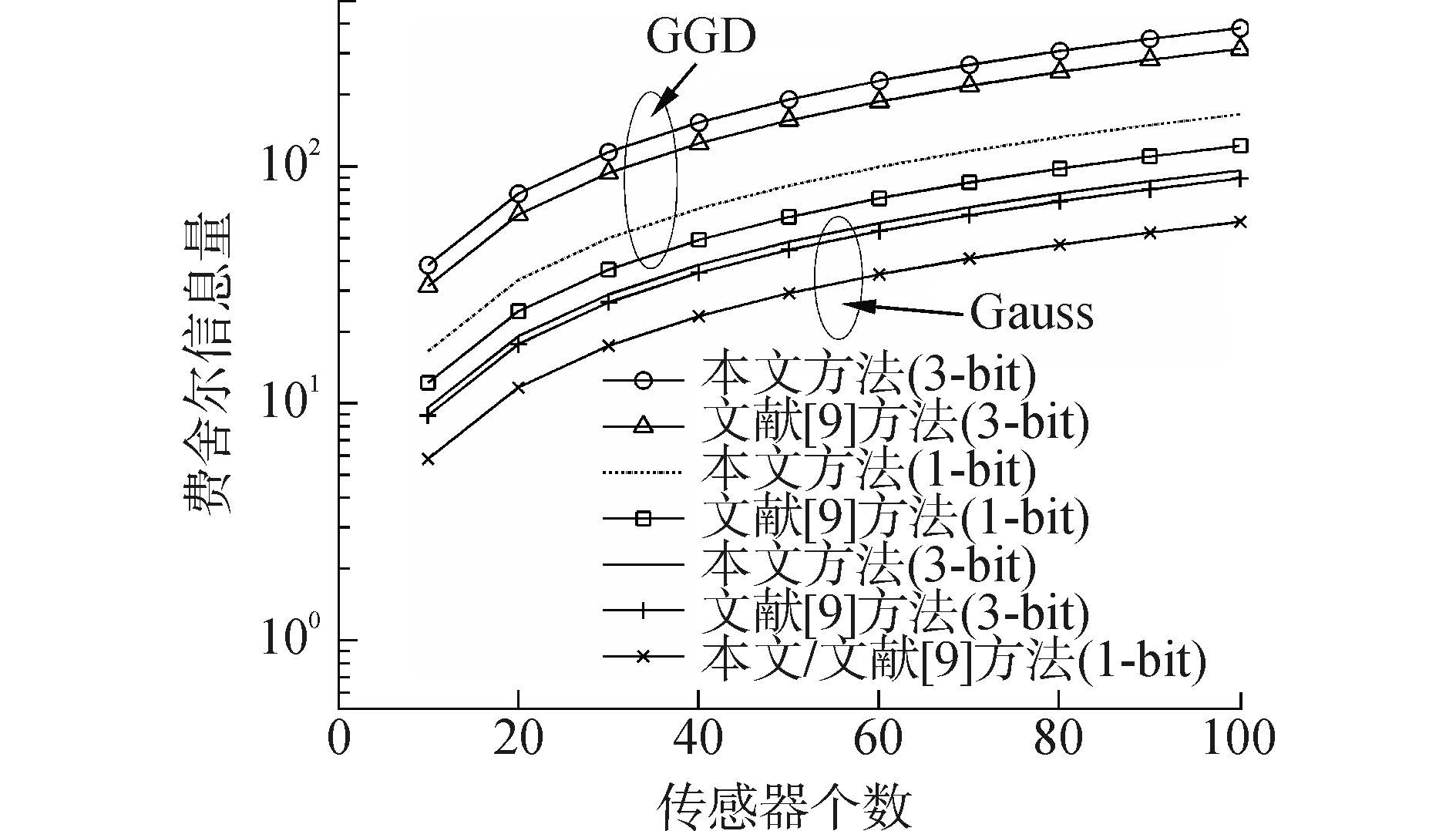
式中:${Q_{x'\mathop 2\limits_1 }}_{\left( {{\lambda _q}} \right)}$(·)表示自由度为1、非中心化参数为λq的非中心化卡方分布的右尾概率。图 4所示的是在高斯噪声和非高斯噪声背景下,本文方法与文献[9]方法的FI对比曲线。由式(12)可知,FI越大,检测性能越好。文献[12]证明了量化会带来FI的损失,而增加量化深度q可以相应地提高FI。从图中可以看出,当传感器个数N增大或量化深度q增大时,本文方法和文献[9]方法的FI随之增大。无论在高斯噪声还是在GGD噪声背景下,本文方法的FI在不同的量化深度q下均大于文献[9]方法,说明了本文方法性能优于文献[9]方法。当量化深度q=3时,在两种噪声下相应的FI相较于q=1的FI有显著提高,说明本文方法中基于局部多比特量化方案(q≥2)可有效地解决1-bit方案造成损失信息过多的问题。
|
| 图4 不同噪声下的费舍尔信息对比 Figure 4 The fisher information comparison for different noises versus the number of sensors |
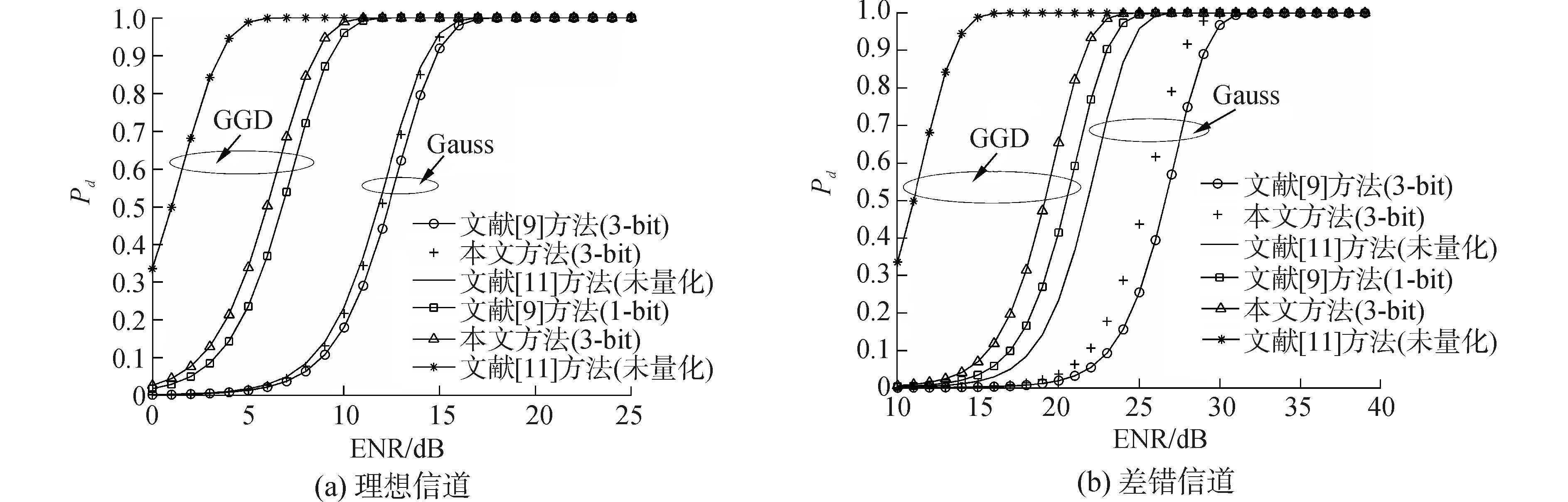
图 5给出了本文方法与文献[9]方法和文献[11]方法在不同噪声和信道下的检测性能对比曲线。横坐标采用信号能量噪声比(signal energy-to-ratio,ENR),其定义为ENR=10lg(Nθ2/σ2)。根据之前的讨论,由于量化会导致检测性能降低,而文献[11]方法中各传感器节点不对观测信息量化,因此没有性能损失,本文将其作为检测性能的上限进行对比。从图 5(a)和(b)中可以看出,当给定的传感器个数为N=100,FC的虚警概率为PFA=10-4时,本文方法的检测性能均优于文献[9]方法的检测性能。在图 5(a)中,当量化深度q=3时,在高斯噪声情况下本文方法的检测性能接近文献[11]未量化方法的性能,说明q=3时,本文方法性能已接近上限;在GGD噪声情况下,本文方法的性能与文献[11]方法性能相比仍有可提升的空间,说明需进一步增加量化深度q来接近检测性能的上限。从图 5(b)可知,由于引入差错信道,各个方案的性能严重恶化。本文方法的检测性能优于文献[9]方法,当检测概率Pd达到0.8时,本文方法的性能相较于文献[9]方法的检测性能提升了1.3 dB。
|
| 图5 不同噪声和信道下的检测性能对比 Figure 5 The detection performance comparison for different noises versus signal energy-to-noise ratio |
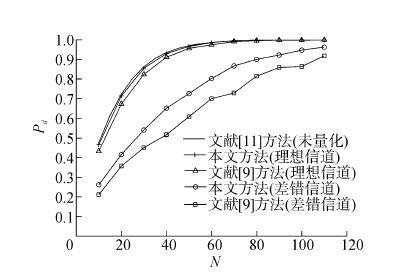
从图 4和图 5可以看出,在量化观测的前提下,最差性能发生在高斯噪声情况下,这与文献[11]对基于未量化观测方案的分析结果一致。这是由于GGD噪声的PDF具有强拖尾现象,在零值附近显得较窄,很容易检测到信号引起的均值微小偏移,因此在GGD噪声环境中Rao检测器与针对高斯噪声设计的检测器相比,性能有很大的改善。由于高斯噪声下性能最差,下面给出高斯噪声下的检测性能分析,仿真结果如图 6所示(虚警概率为0.1,105蒙特卡洛实验)。从图 6中可以看出,当量化深度q=3时,随着传感器个数的增加,检测性能提高。当传感器节点个数达到30时,在理想信道下,本文方法的检测概率Pd约为0.86,文献[9]方法的Pd约为0.82。而在差错信道下,两种方案性能大大降低,本文方法性能仍优于文献[9]方法。在理想信道下,本文方法在量化深度为3时接近检测性能上界。
|
| 图6 高斯噪声下的3-bit量化方案检测性能对比 Figure 6 The detection performance comparison of the 3-bit schemes for Gaussian noise versus the number of sensors |
针对无线传感器网络中功率和带宽受限所带来的检测问题,对1-bit量化研究一般化,提出了基于局部量化观测的分布式Rao检测方法,优化了最优局部量化阈值,并给出Rao检测器、虚警概率和检测概率的闭合表达式。仿真结果表明:
1 ) 在高斯噪声和GGD噪声下,随着传感器个数和量化深度的增大,本文方法的检测性能有明显的提高;
2 ) 在高斯噪声下,当量化深度为3时,检测性能接近上限。本文方法在GGD噪声下性能的提升将作为进一步的研究内容。
| [1] | BLUM R S, KASSAM S A, POOR H V. Distributed detection with multiple sensor. Part 2:-advanced topics[J]. Proceedings of the IEEE, 1997, 85(1): 64–79. DOI:10.1109/5.554209 |
| [2] |
沈晓静. 多传感器分布式检测和估计融合[J].
中国科学: 数学, 2014, 44(2): 105–116.
SHEN Xiaojing. Multi-sensor distributed detection and estimation fusion[J]. Scientia sinica mathematica, 2014, 44(2): 105–116. DOI:10.1360/012013-152 |
| [3] |
赵文辉, 姜宇, 刘大昕. 高精度无线传感器网络节点定位算法[J].
哈尔滨工程大学学报, 2009, 30(4): 466–471.
ZHAO Wenhui, JIANG Yu, LIU Daxin. A high precision positioning algorithm for wireless sensor network nodes[J]. Journal of Harbin Engineering University, 2009, 30(4): 466–471. |
| [4] | REIBMAN A R, NOLTE L W. Optimal detection and performance of distributed sensor systems[J]. IEEE transactions on aerospace and electronic systems, 1987, AES-23(1): 24–30. DOI:10.1109/TAES.1987.313355 |
| [5] | HOBALLAH I Y, VARSHNEY P K. Distributed Bayesian signal detection[J]. IEEE transactions on information theory, 1989, 35(5): 995–1000. DOI:10.1109/18.42208 |
| [6] | FANG Jun, LIU Yumeng, LI Hongbin, et al. One-bit quantizer design for multisensor GLRT fusion[J]. IEEE signal processing letters, 2013, 20(3): 257–260. DOI:10.1109/LSP.2013.2243144 |
| [7] | CIUONZO D, PAPA G, ROMANO G, ROSSI P S, WILLETT P. One-bit decentralized detection with a Rao test for multisensor fusion[J]. IEEE signal processing letters, 2013, 20(9): 861–864. DOI:10.1109/LSP.2013.2271847 |
| [8] | NIU Ruxin, VARSHNEY P K. Joint detection and localization in sensor networks based on local decisions[C]//2006 Fortieth Asilomar Conference on Signals, Systems, and Computers. Pacific Grove, CA, USA, 2006: 525-529. |
| [9] | AZIZ A M. A simple and efficient suboptimal multilevel quantization approach in geographically distributed sensor systems[J]. Signal Processing, 2008, 88(7): 1698–1714. DOI:10.1016/j.sigpro.2008.01.006 |
| [10] |
陈军勇, 邬依林, 祁恬. 无线传感器网络分布式量化卡尔曼滤波[J].
控制理论与应用, 2011, 28(12): 1729–1739.
CHEN Junyong, WU Yilin, QI Tian. Distributed quantized kalman filtering for wireless sensor networks[J]. Control theory & applications, 2011, 28(12): 1729–1739. |
| [11] | KAY S M. Fundamentals of statistical signal processing, Volume Ⅱ: Detection theory. Upper Saddle River, NJ: Prentice Hall[M]. , 1998 . |
| [12] | FARIAS R C, BROSSIER J M. Scalar quantization for estimation: from an asymptotic design to a practical solution[J]. IEEE transactions on signal processing, 2014, 62(11): 2860–2870. DOI:10.1109/TSP.2014.2318140 |



