2. Research Laboratory for Turbine, China Gas Turbine Establishment, Aviation Industry Corporation of China, Chengdu 610500, China
空心涡轮叶片是现代航空发动机的关键部件之一, 其设计结构和制造质量直接影响着发动机整体性能。在涡轮叶片的制造过程中, 为提高叶片的质量和精度, 实际生产中全部采用熔模精密铸造方式成形。通过相关某型号叶片调研发现, 在后续的热处理工艺中叶片榫头进气窗口区域出现严重的再结晶的现象。由于单晶叶片不含或含少量的晶界强化元素, 再结晶成为叶片的薄弱环节, 这对叶片高温力学性能和使用寿命产生极大的影响[1]。因此对再结晶消除的方式的研究具有重要的意义。
分析表明叶片的再结晶与铸造过程中该区域热残余应力过大, 形成局部的应力集中相关[2]。目前国内外的研究消除再结晶的手段主要集中在工艺手段:回复处理和表面处理两大类[3]。回复处理通过热处理的方法释放大部分应变储能的方式实现抑制或消除再结晶[4]。表面处理是直接去除表面变形层、渗碳和表面涂层等方式消除再结晶影响[5]。但这两种方式都是只能针对变形量小于5%的合金, 即残余应力较小的合金。由于热残余应力与再结晶有着密切的关系, 因此本研究在材料及工艺方案确定的前提下, 从铸造中产生变形的源头出发, 通过对叶片榫头进气窗细节结构的优化, 控制热残余应力水平的方式来实现榫头进气窗口的再结晶[6]的抑制或消除。
1 结构优化建模涡轮叶片局部细节形状、尺寸是影响整个叶片极限状态下性能的直接因素, 因此合理的叶片细节结构是获得高性能的必要条件之一。在进气窗口设计时, 为了保证其最小壁厚和冷却设计要求, 榫头进气孔几何形状一般采用矩形或平行四边形;同时, 考虑到便于陶芯模具的工艺操作, 实现叶片内腔结构一体化成形, 榫头进气孔结构首选平行四边形状。常见的叶片内腔结构的设计是按照壁面厚度分布函数计算叶栅平面的内腔通道整体外形, 再根据肋的位置参数计算各内腔通道的外形数据文件, 建立内腔通道外形[7-8]。带肋的叶身内腔通道, 其几何参数包括进/出口面积、当量直径、安装角度、周长、肋高、肋间距、光滑边长度、进/出口半径位置、叶片转速等[9]。结合设计中的强度要求, 冷气通流面积以及通过实验得到的DD6合金发生再结晶时的临界条件, 设定如下约束条件:
1) 最大残余应力约束条件。为了使单晶涡轮叶片榫头进气窗口区域铸造残余应力不超过DD6单晶材料的再结晶临界应力σc, 以避免发生再结晶。
2) 最大通流面积约束条件。根据设计要求, 每件叶片榫头进气窗口最小面积A应该不小A0, 以免造成冷却能力下降、冷效不足。
3) 强度极限尺寸条件。在叶片内、外形状确定的条件下, 决定叶片榫头结构强度的几何参数主要有, 如图 1榫头宽度H和榫头进气孔间加强筋宽度L4;考虑到叶片除了受极限应力外, 还受疲劳应力的作用。为了保证叶片满足抗疲劳设计要求, 取榫头进气孔壁厚最小值不小于H-H1, 即H-H1是定值, 也是强度要求的尺寸最小值。
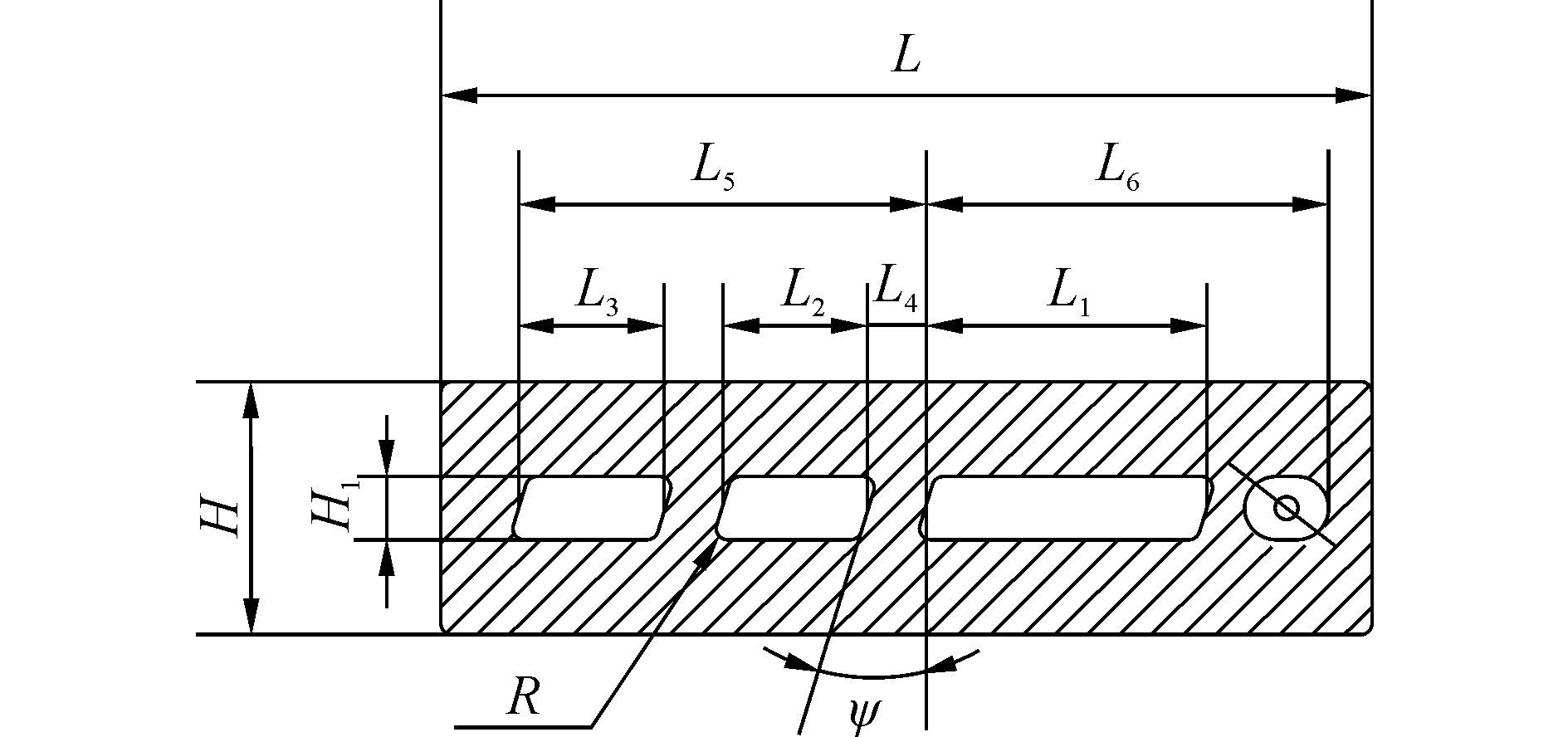
|
| 图1 榫头进气窗口截面 Figure 1 Cross section of tenon intake window |
优化目标为铸造残余应力, 优化变量为结构布局参数与尺寸参数, 优化的数学模型为目标函数:
| ${\rm{min }}{\sigma _{r{\rm{max}}}}\left( {R,T} \right)$ | (1) |
约束条件:
| $\left\{ \matrix{ k = {{{\sigma _{r{\rm{max}}}}} \over {{\sigma _c}}} \le 1 \hfill \cr 0.97 \le {{{A_0}} \over A} \le 1 \hfill \cr {\sigma _{r{\rm{max}}}} = \varphi \left( {{R_i},{T_i}} \right) \hfill \cr {\sigma _c} = f\left( T \right),{\rm{ }}{T_L} \le T \le {T_U} \hfill \cr A = {L_i}\cdot{H_1} - {R^2}\cdot4 - \pi ,{\rm{ }}i = 1,2, \ldots ,S \hfill \cr {A_0} = {L_i}\cdot{H_1},{\rm{ }}\psi = 17^\circ ,{\rm{ }}i = 1,2, \ldots ,S \hfill \cr} \right.$ | (2) |
式中: k为应力集中系数,Ai为进气孔通流面积,σrmax为最大残余应力,Ri为设计变量,φ(R,T)为目标函数,σc=f(T)为约束函数。
2 优化方案设计由于叶片平行四边形榫头进气通道形成小角度窄宽度形状, 且壁厚较大, 其在制备过程中, 极易产生较大的铸造热应力, 同时形成的残余应变能难以弹性变形方式释放, 进而引起局部残余应力过大。为了避免或减缓这种因结构不连续性导致的应力集中问题, 常见的做法是将尖角进行倒圆处理, 增加结构连续性, 以降低应力集中。实际上, 在单晶气冷叶片的榫头结构优化设计中, 进气窗口形状、尺寸设计受到强度和冷却设计的限制, 其进气孔圆角的曲率半径R是决定应力集中系数α的主要因子。因此, 通过修改榫头进气窗口的形状来改善性能是很难做到的, 但可采用优化进气窗口转角处形状与尺寸的分布来达到控制局部应力的目标。故本文通过优化进气窗口转角半径R的大小, 使圆角处的最大残余应力低于DD6单晶合金再结晶临界应力值, 实现抑制再结晶现象的发生的目的。
榫头进气窗口结构优化设计变量主要为各窗口转角R的曲率半径, 根据铸造手册中的内圆角的设计准则[10], 可铸造最小半径为0.5 mm, 最大为1.5 mm。建立相关的优化方案如表 1。
| 方案 | 设计参数/mm | 约束条件 |
| Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ | R=0.5 R=0.8 R=1.0 R=1.2 R=1.4 | H,H1 L1,L2 L3,L4 φ为定值 |
在选定优化策略前提下, 建立合理的结构优化模型, 结合有限元仿真技术, 对影响进气窗口区域铸造残余应力的细节结构特征参数进行优化, 以获得最优的结构应力水平与分布。该方法的优点是直接从经验尺寸赋初始值, 再进行迭代优化设计, 通过仿真方法预测区域应力场, 然后与实验获得的DD6单晶再结晶临界应力模型作比值, 从而得到优化后的进气窗口尺寸控制模型。具体流程如图 2。
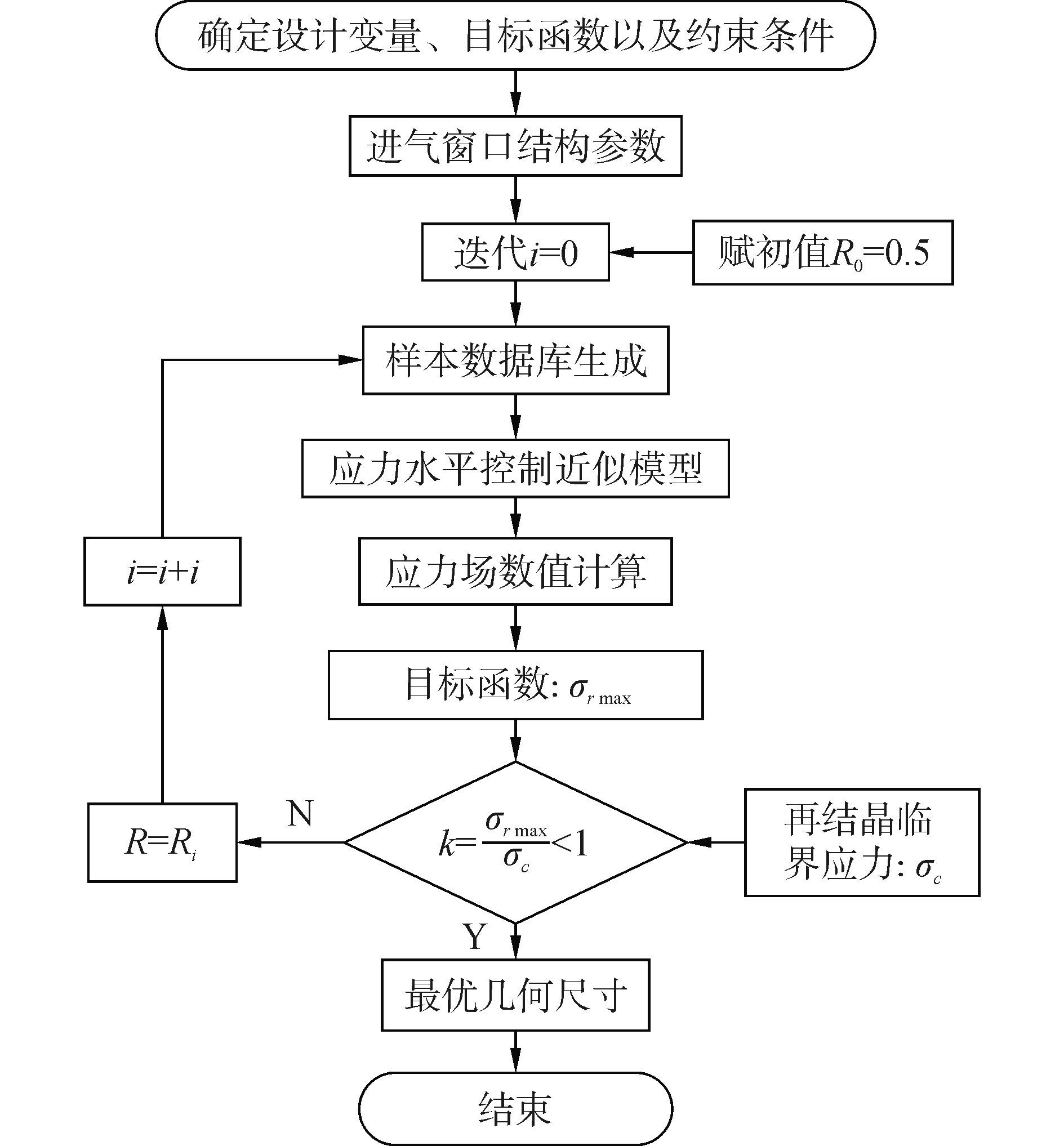
|
| 图2 优化流程 Figure 2 Optimization flow |
利用尺寸优化与计算仿真相结合的优化方法, 对设计变量进行同步优化处理, 并给出了各自参数优化结果。通过上面所述的优化过程, 得到了如图 3所示优化后的榫头进气窗口。从图中可以看出, 优化后进气窗口的位置与优化前相同, 而进气窗口的形状和尺寸较初始通孔有细微变化, 可明显提高榫头结构的完整性。
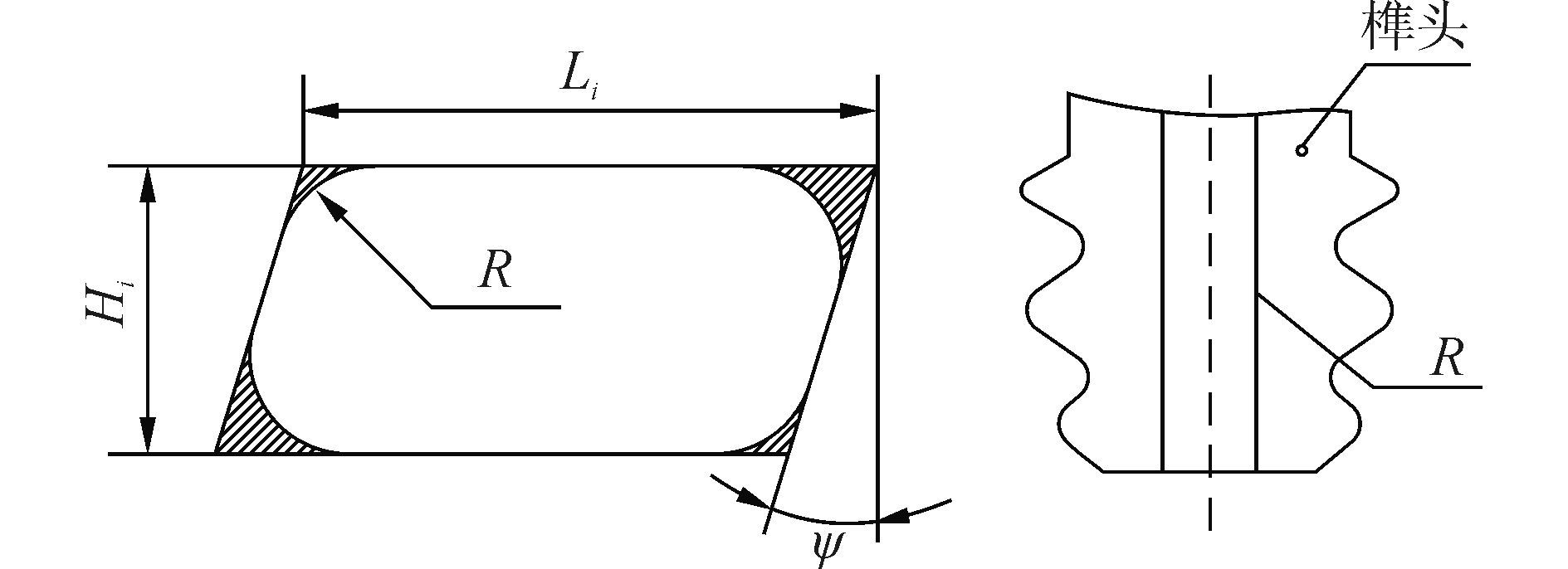
|
| 图3 优化后进气窗口结构示意图 Figure 3 Structure diagram of optimized intake window |
根据仿真方案提供的方法依次建立仿真的参数化模型[11-17], 通过ProCAST软件进行仿真, 具体参数设定依据相关参考文献[18-20]。提取仿真结果如表 2所示。
| H1截面 | 温度/℃ | ||||
| 优化参数 | 1 000 | 1 100 | 1 200 | 1 300 | |
| 残余热应力 | R0.5 R0.8 R1.0 R1.2 R1.4 | 370 363 328 266 495 | 224 215 202 163 345 | 196 198 176 107 208 | 117 103 86 48 188 |
通过二元多次线性回归[21]的方式建立曲面拟合函数:
| ${\sigma _{r{\rm{max}}}} = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^m {{a_{ij}}{x^{i - 1}}{y^{j - 1}}} } $ | (3) |
在进行一元函数拟合时候, 根据数学原理, 拟合多项式的指数m越高, 所给数据点逼近的精度也越高, 但为保证拟合函数不失真, 其次数m通常小于数据规模M。同理在拟合曲面的时候为保证曲面的拟合精度, 需要对多项式的m与n值进行确定。为保证拟合函数的精度, 将数据分为两部分, 一部分为样本数据R0.8~R1.4, 一部分为测试数据R0.5。根据表 2中的样本数据MXN的规模, 初步确定m-1<M, n-1<N。
设定x为温度, y为半径, 在Matlab中实现曲面函数的拟合, 函数中不同x、y指数对应的确定系数的值如图 4所示。
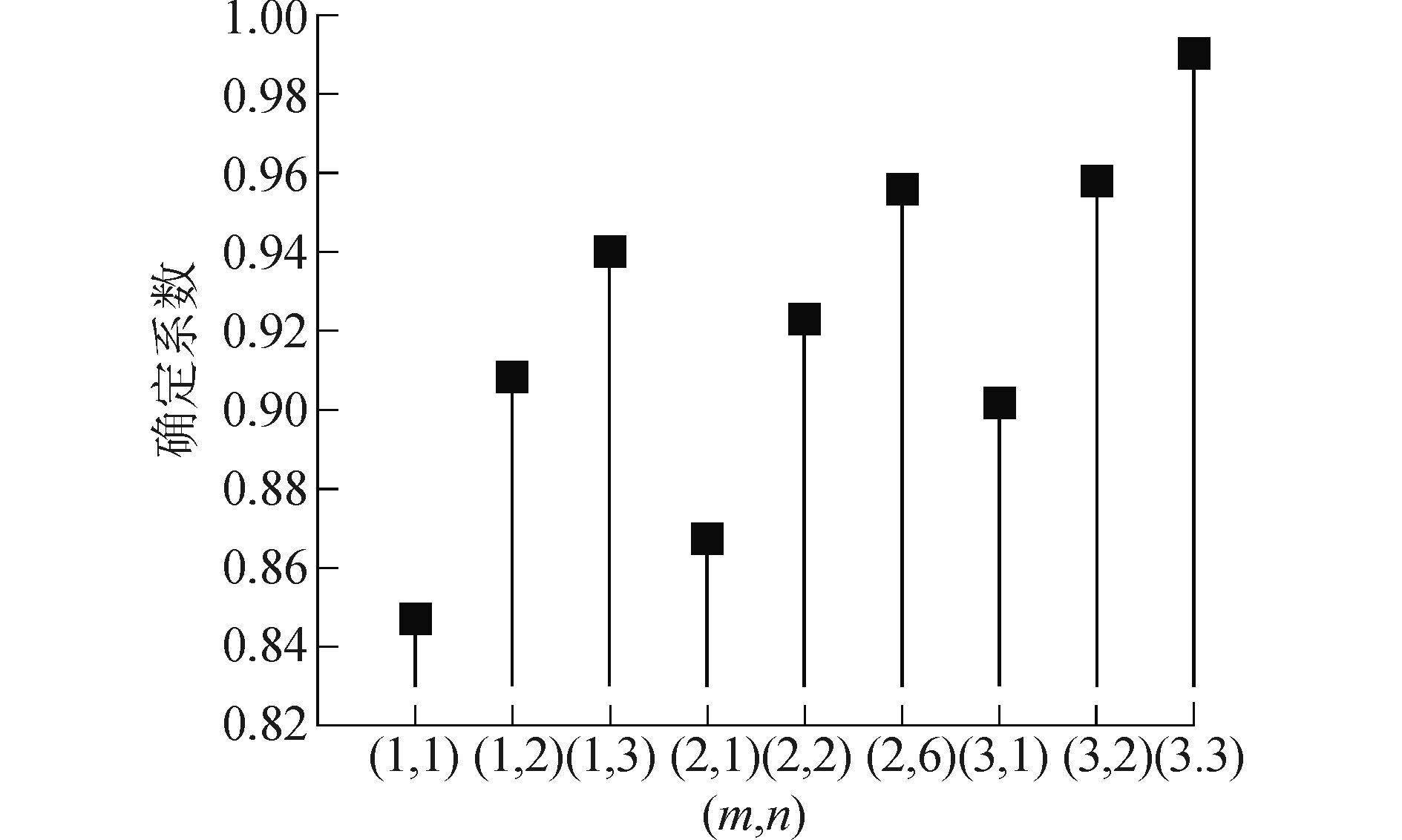
|
| 图4 拟合函数的确定系数与指数的关系 Figure 4 Fitting function′s R-square and index′s relationship |
一般情况下确定系数越接近于1, 函数的拟合程度越好。从图 4可以看出半径的最高指数对确定系数的影响比温度的高, 且在二者的次数为(3,3) 的时候达到最大。因此得到截面最大残余应力与温度以及半径的函数关系式:
| $\eqalign{ & {\sigma _{r{\rm{max}}}} = A\left( 1 \right){\rm{ }} + A\left( 2 \right){\rm{ }}x + A\left( 3 \right){\rm{ }}y + A\left( 4 \right){\rm{ }}{x^2} + \cr & A\left( 5 \right){\rm{ }}xy + A\left( 6 \right){\rm{ }}{y^2} + A\left( 7 \right){\rm{ }}{x^3} + A\left( 8 \right){\rm{ }}{x^2}y + \cr & A\left( 9 \right){\rm{ }}x{y^2} + A\left( {10} \right){\rm{ }}{y^3} \cr} $ | (4) |
式中:x指温度, ℃;y表示半径, mm;σrmax表示最大的应力, MPa;A(i), i=1,2,…,10为常数。具体的曲面拟合图 5。
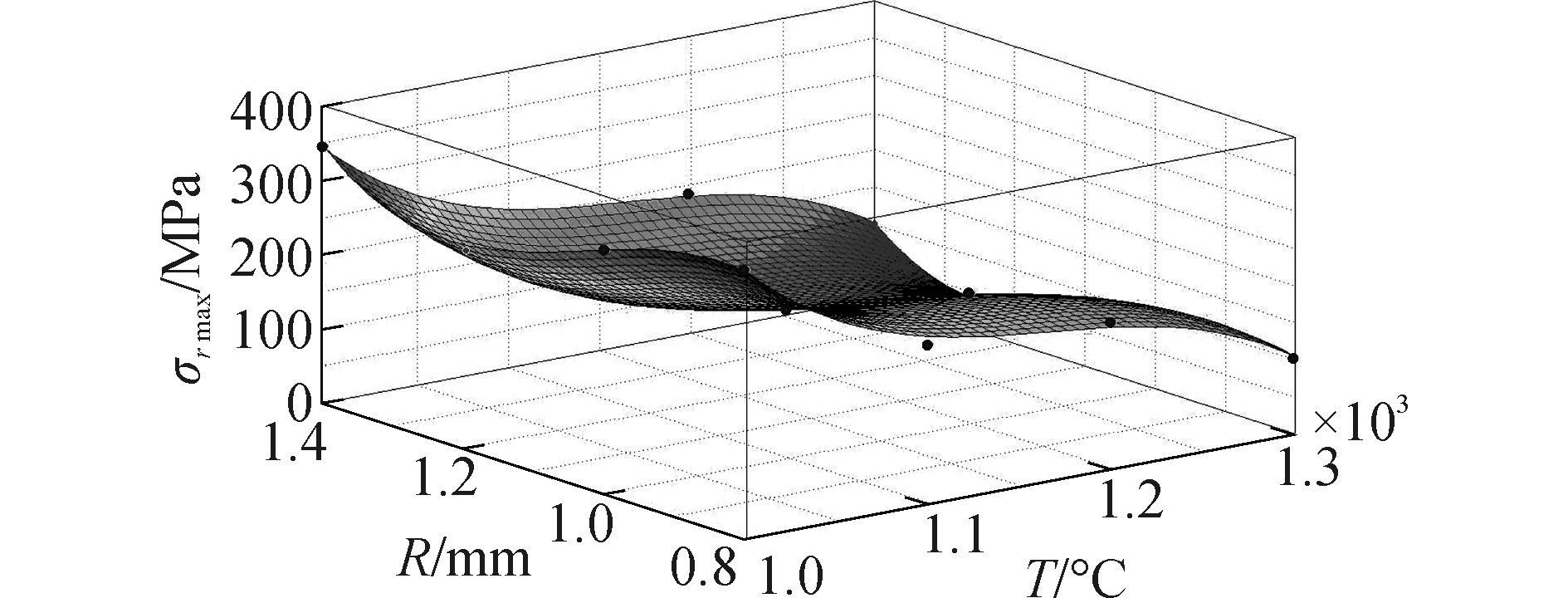
|
| 图5 曲面拟合图 Figure 5 Surface fitting diagram |
将R0.5的测试数值与拟合函数建立的预测数据对比, 如图 6所示, 从图中可以看出在1 200℃时两者的误差达到最大, 但没有改变残余应力随温度变化的趋势, 且曲线呈现明显的凹陷, 到最后预测模型数据与仿真建模数据近似重合, 这说明该模型虽然存在一定误差, 但对于目标函数的最优解没有影响。
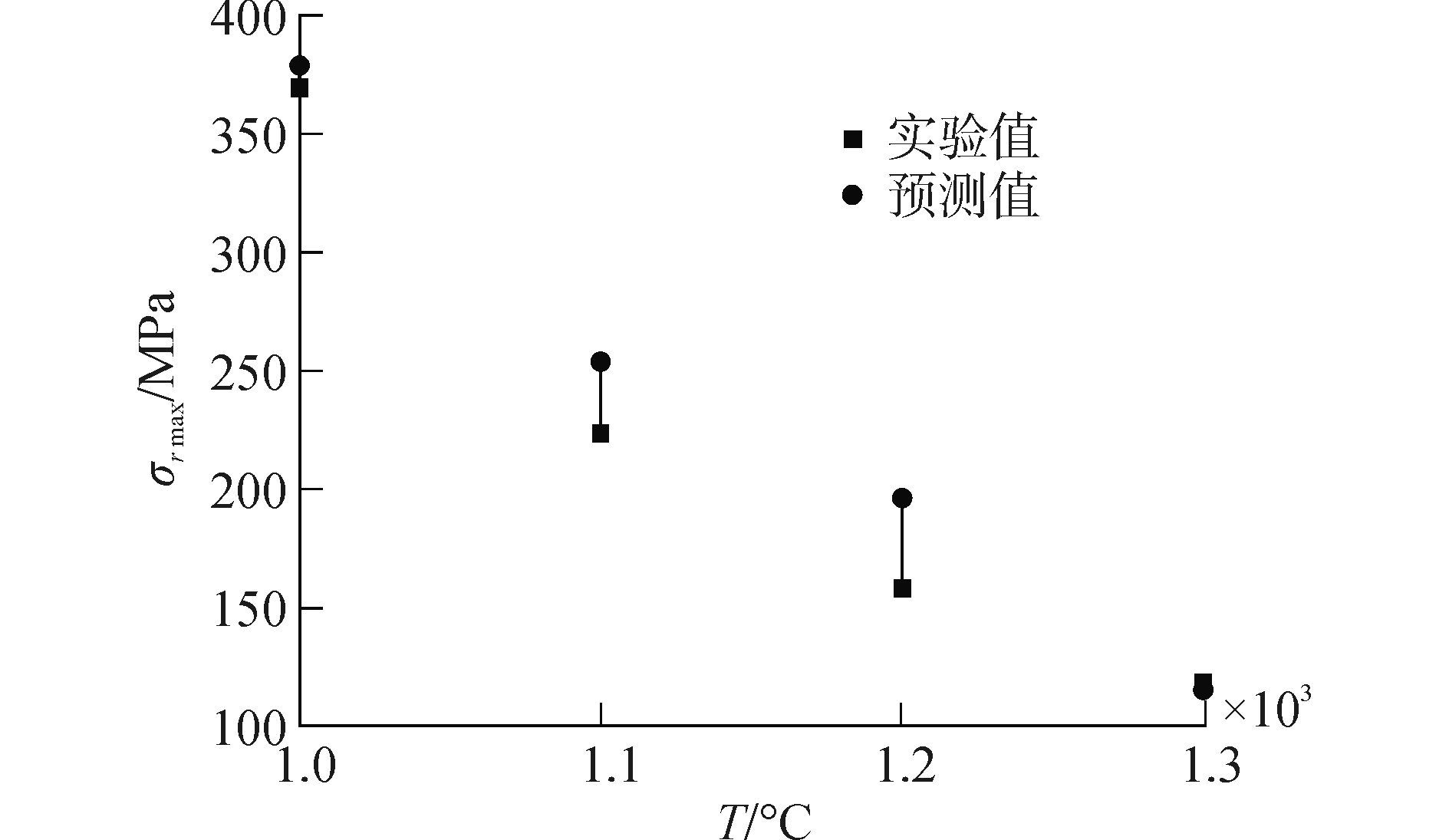
|
| 图6 函数拟合误差分析图 Figure 6 Fitting function error analysis diagram |
令函数中的温度T为常数, 通过Matlab对函数进行多约束单变量的优化求解, 得到表 3。根据优化参数R对榫头进气窗口最大铸造热应力的影响规律, 以及与DD6单晶高温合金再结晶临界应力[22]的对比, 如图 7所示。从图中可以看出优化参数R1.2与R1.23的最大应力值均在临界应力值下方, 但优化结果R1.23的数值波动较大。榫头进气窗口区域面积的约束(R大于等于1.15 mm), 故最终优化结果R=1.2 mm。
| 温度/℃ | 1 000 | 1 050 | 1 100 | 1 150 | 1 200 | 1 250 | 1 300 |
| R/mm | 1.226 5 | 1.227 2 | 1.227 9 | 1.228 6 | 1.229 4 | 1.230 2 | 1.231 |
| σrmax/MPa | 272.136 4 | 187.561 2 | 146.632 8 | 130.382 1 | 119.840 2 | 96.0381 | 40.006 8 |
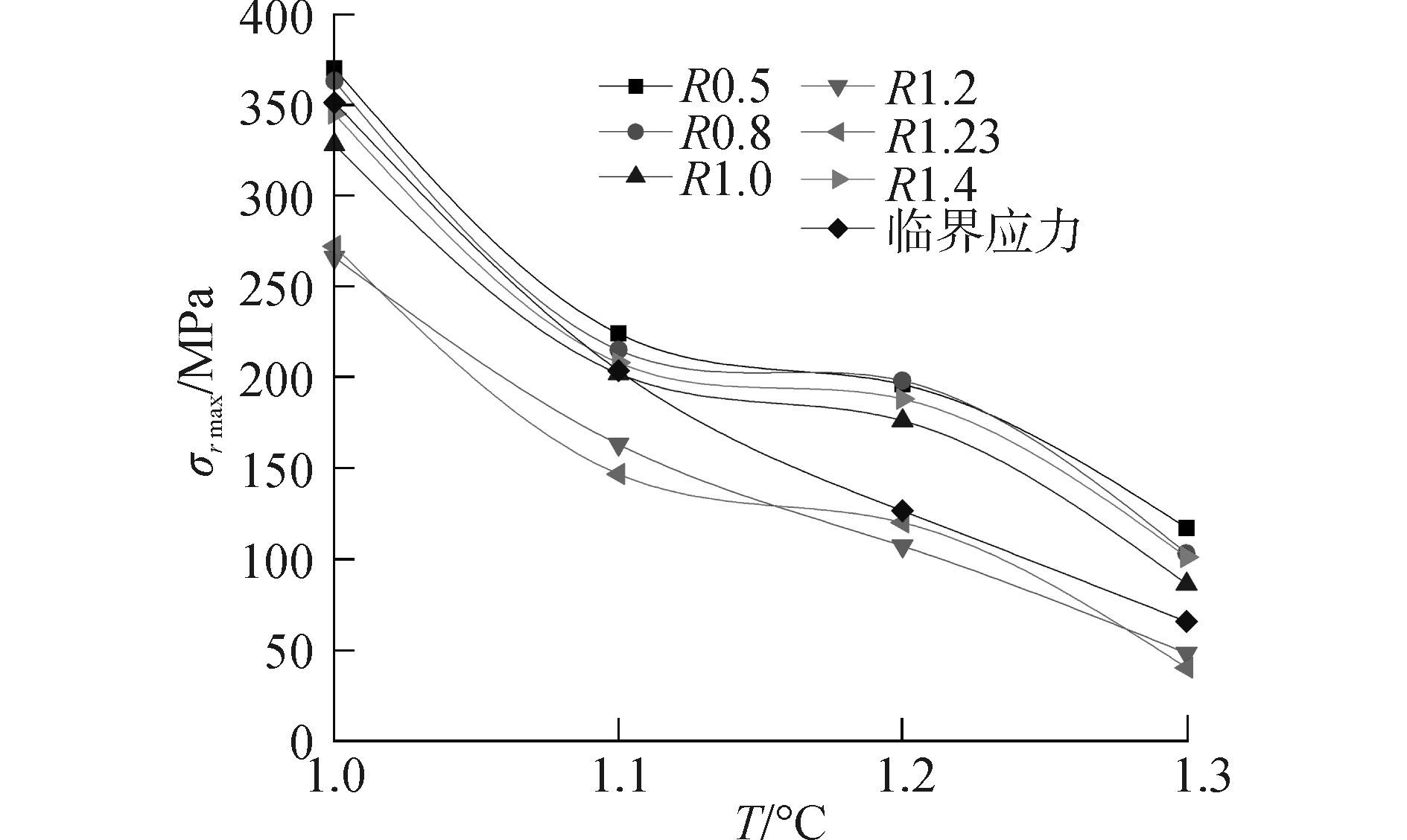
|
| 图7 优化参数R对铸造热应力的影响 Figure 7 Optimization parameters R influence on the casting thermal stress |
截取仿真中同一温度时刻的优化前R0.5的榫头进气窗口截面与优化后的R1.2的进气窗截面应力云图, 如图 8所示。对比发现。应力集中区域的应力水平下降明显, 应力集中区域的最大值优化后结果与优化前下降了28.1%。由此说明通过圆角半径的优化实现了对残余应力的调控。
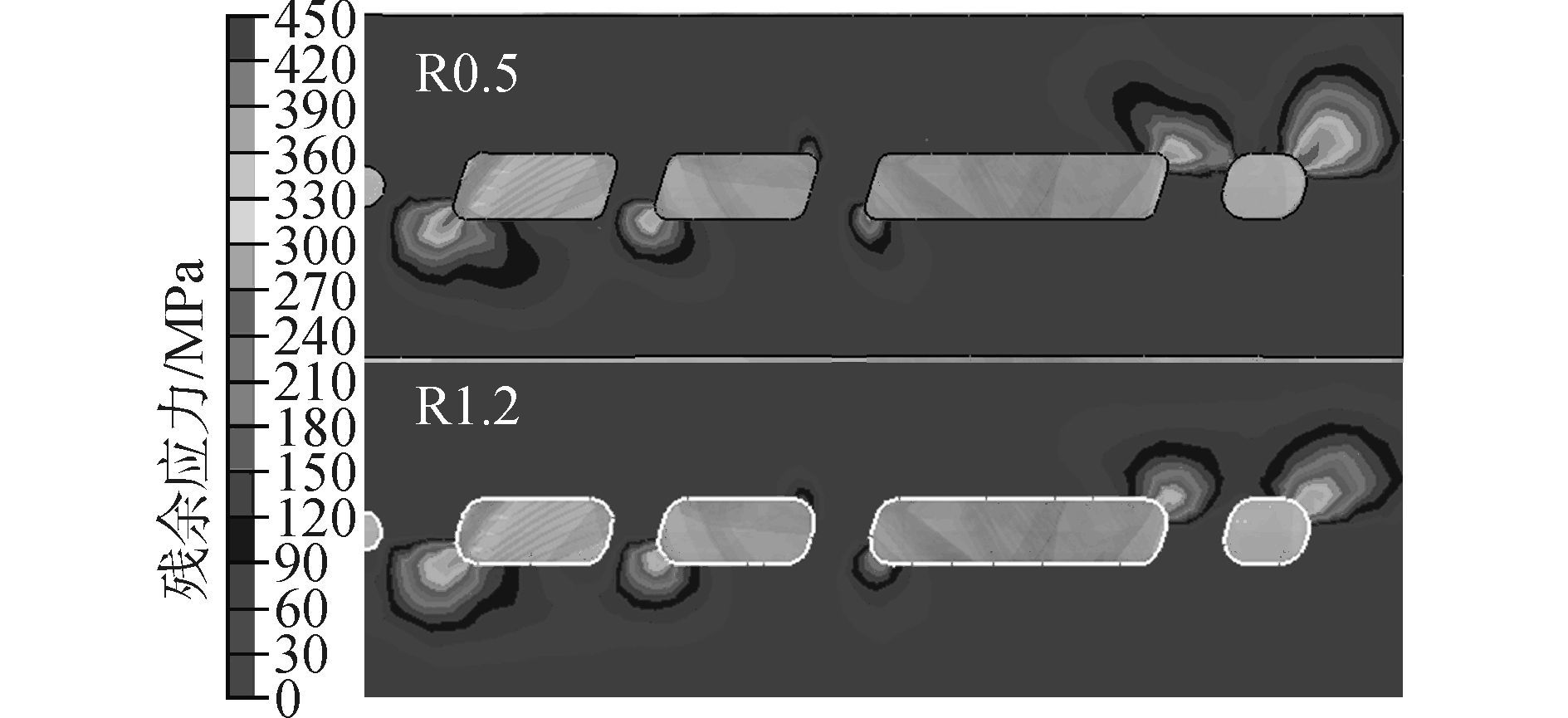
|
| 图8 R0.5/R1.2残余应力云图 Figure 8 R0.5/R1.2 Residual stress cloud chart |
根据优化结果对设计变量值进行优化, 在简化模型中将叶片榫头进气窗口转角、材料分别设置为1.2 mm和DD6。然后依据实际工艺浇注出叶片铸件, 待定向凝固冷却切去浇注系统, 去除陶芯后, 再在室温下通过Proto公司生产的X衍射设备进行应力测量。依据仿真结果选定图 9(a)、(b)截面Point1、Point2、Point3、Point4四个点作为测量点。测量结果如表 4。

|
| 图9 测量点规划 Figure 9 Measurement points planning |
| 点号 | Point1 | Point2 | Point3 | Point4 | |
| 优化前 | σtest/MPa | 898.763 | 716.657 | 508.579 | -489.982 |
| σsimulate/MPa | 375 | 335 | 266 | -278 | |
| 优化后 | σtest/MPa | 649.06 | 511.571 | 477.675 | -331.877 |
| σsimulate/MPa | 266 | 185 | 112 | -137 | |
根据测量结果可以发现, 仿真数据的变化趋势与测量结果变化趋势一致, 这表明基于ProCAST的定向凝固的应力场数值模拟与生产实际中应力分布情况类似。对比优化前后的结果, 测量结果与仿真结果均显示, 通过修改局部细节结构的方式, 可以有效降低榫头区域的应力集中水平, 根据测量结果得到其应力水平下降27.78%。随后对叶片进行热处理, 通过水浸法观察发现, R1.2的榫头区域再结晶现象得到消除。由此可知通过调整结构可以实现对残余应力水平的调整, 并实现对由于局部应力集中引起的再结晶的控制。
4 结论1) 为降低榫头残余应力水平, 在对榫头设计结构分析的基础上, 提出优化圆角半径的方法, 在强度、冷通流面积、临界再结晶应力优化约束基础上, 通过仿真迭代的优化流程得到优化的最优解R为1.2 mm。
2) 经仿真验证优化后的榫头进气窗口的应力集中区域残余应力下降达到28.1%。通过实验验证优化后的榫头进气窗结构, 再结晶现象得到消除。基于此, 说明控制残余应力的方法可以有效降低再结晶的现象的发生。
| [1] |
陈荣章. 单晶高温合金发展现状[J].
材料工程, 1995(8): 3–12.
CHEN Rongzhang. Development status of single crystal superalloys[J]. Journal of materials engineering, 1995(8): 3–12. |
| [2] |
熊继春, 李嘉荣, 赵金乾, 等. 单晶高温合金DD6再结晶晶界析出相特征及其形成机制[J].
金属学报, 2009, 45(10): 1232–1236.
XIONG Jichun, LI Jiarong, ZHAO Jinqian, et al. Characteristic and formation mechanism of precipitates at recrystallization grain boundaries of single crystal superalloy DD6[J]. Acta metallurgica sinica, 2009, 45(10): 1232–1236. |
| [3] |
孟杰, 金涛. 镍基单晶高温合金的再结晶[J].
材料工程, 2011(6): 92–98.
MENG Jie, JIN Tao. Recrystallization of single crystal nickel-based superalloys[J]. Journal of materials engineering, 2011(6): 92–98. |
| [4] | OKAZAKI M, OHTERA I, HARADA Y. Damage repair in CMSX-4 alloy without fatigue life reduction penalty[J]. Metallurgical and materials transactions a, 2004, 35(2): 535–542. DOI:10.1007/s11661-004-0364-5 |
| [5] |
张兵, 曹雪刚, 刘昌奎. 单晶高温合金再结晶的抑制方法研究进展[J].
失效分析与预防, 2013, 8(3): 191–196.
ZHANG Bing, CAO Xuegang, LIU Changkui. Review on inhibition methods of recrystallization of single crystal superalloys[J]. Failure analysis and prevention, 2013, 8(3): 191–196. |
| [6] | BVRGEL R, PORTELLA P D, PREUHS J. Recrystallization in single crystals of nickel base superalloys[C]//Superalloys 2000. Warrendale:The Minerals, Metals & Materials Society, 2000:229-238. |
| [7] |
岳珠峰, 李立州, 虞跨海, 等.
航空发动机涡轮叶片多学科设计优化[M]. 北京: 科学出版社, 2007.
YUE Zhufeng, LI Lizhou, YU Kuahai, et al. MDO technology applied to the aeroengine turbine blade design[M]. Beijing: Science Press, 2007. |
| [8] |
赵海. 涡轮榫头/榫槽结构设计方法研究[D]. 南京:南京航空航天大学, 2005.
ZHAO Hai. Research on design method of turbine tenon/mortise[D]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2005. |
| [9] |
曹志廷, 郭文, 潘炳华, 等. 涡轮叶片冷却设计优化方法研究[J].
燃气涡轮试验与研究, 2012, 25(4): 30–36.
CAO Zhiting, GUO Wen, PAN Binghua, et al. Optimization of turbine blade cooling design with iSIGHT[J]. Gas turbine experiment and research, 2012, 25(4): 30–36. |
| [10] |
姜不居.
熔模铸造手册[M]. 北京: 机械工业出版社, 2000.
JIANG Buju. Handbook of investment casting[M]. Beijing: China Machine Press, 2000. |
| [11] |
董一巍. 净成形空心涡轮叶片精铸模具型腔优化设计方法研究[D]. 西安:西北工业大学, 2012.
DONG Yiwei. Optimization design method of investment casting die profile for net-shaped hollow turbine blade[D]. Xi'an:Northwestern Polytechnical University, 2012. |
| [12] | WANG P, XIAO N, LI D, et al. Numerical simulation of deformation during hot procedure for large hydraulic turbine runner blade[J]. Materials science forum, 2010(654-656): 1565–1569. |
| [13] | CUI K, WANG W, JIANG R, et al. Reverse adjustment algorithm of ceramic core locators in hollow turbine blade investment casting die[J]. Acta aeronautica et astronautica sinica, 2011, 32(10): 1934–1929. |
| [14] | DONG Y W, KUN B U, DOU Y Q, et al. Determination of wax pattern die profile for investment casting of turbine blades[J]. Transactions of nonferrous metals society of China, 2011, 21(2): 378–387. DOI:10.1016/S1003-6326(11)60725-5 |
| [15] | DONG Y W, ZHANG D H, BU K, et al. An optimum-curved die-profile for investment casting of turbo blades[J]. Advanced materials research, 2011, 314-316: 630–633. DOI:10.4028/www.scientific.net/AMR.314-316 |
| [16] | REED R. The superalloys[M]. Cambridge: Cambridge University Press, 2006. |
| [17] |
卜昆, 李永毅, 董一巍, 王红霞, 田琨. 精铸涡轮叶片非线性收缩率计算方法的研究[J].
西北工业大学学报, 2009, 27(2): 214–218.
Bu Kun, Li Yongyi, Dong Yiwei, Wang Hongxia, Tian Kun. Exploring calculation method of nonlinear shrinkage rate for investment casting turbine blade[J]. Journal of Northwestern Polytechnical University, 2009, 27(2): 214–218. |
| [18] |
袁帅. 基于实验的单晶叶片精铸成形仿真边界条件求解研究[D]. 西安:西北工业大学, 2012.
YUAN Shuai. The calculation of simulative boundary condition during the investment casting of single crystal blade based on the experiment[D]. Xi'an:Northwestern Polytechnical University, 2012. |
| [19] | DONG Yiwei, BU Kun, DOU Yangqing, et al. Determination of interfacial heat-transfer coefficient during investment-casting process of single-crystal blades[J]. Journal of materials processing technology, 2011, 211(12): 2123–2131. DOI:10.1016/j.jmatprotec.2011.07.012 |
| [20] |
卜昆, 傅将威, 董一巍, 等. 基于仿真的单晶涡轮叶片精铸工艺参数优化[J].
特种铸造及有色合金, 2013, 33(4): 353–357.
BU Kun, FU Jiangwei, DONG Yiwei, et al. Parameters optimization of investment casting single crystal turbine blade based on numerical simulation[J]. Special casting & nonferrous alloys, 2013, 33(4): 353–357. |
| [21] |
李云雁, 胡传荣.
实验设计与数据处理[M]. 2版. 北京: 化学工业出版社, 2008.
LI Yunyan, HU Chuanrong. Experiment design and data processing[M]. 2nd ed. Beijing: Chemical Industry Press, 2008. |
| [22] |
马健, 李世峰, 何爱杰, 等. DD6单晶涡轮叶片缘板裂纹与再结晶研究[J].
航空动力学报, 2012, 27(5): 1068–1073.
MA Jian, LI Shifeng, HE Aijie, et al. Platform crack and recrystallization of DD6 single crystal turbine blade[J]. Journal of aerospace power, 2012, 27(5): 1068–1073. |



