2. 大连理工大学 海岸和近海工程国家重点实验室,辽宁 大连 116024;
3. 天津大学 水利工程仿真与安全国家重点实验室,天津 300072
2. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian, Liaoning 116024, China;
3. State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China
海底管道在海洋油气开发中的结构安全问题不容忽视。随着水深增加,静水压力也不断升高,当管道存在初始缺陷时,容易发生局部屈曲压溃进而发生屈曲传播,从而造成大范围的管道结构破坏,为减小事故损失,通常在管道上安装止屈器(如扣入式止屈器等)以阻止大范围的屈曲传播。
国内外学者对海底管道屈曲传播和止屈问题开展了大量研究工作。在管道屈曲传播研究方面,Dyau和Kyriakides[1]采用三维圆柱壳模型,对管道屈曲传播的发生和发展过程进行了模拟,不同径厚比管道的屈曲传播压力计算值与试验值吻合较好;Kyriakides和Netto[2]运用ABAQUS有限元软件对管道的准静态和动态屈曲传播进行了数值模拟研究;Xue[3]运用ABAQUS有限元软件分析了非均匀和受腐蚀海底管道在外压作用下的局部屈曲和屈曲传播特性。在止屈器研究方面,大多数学者采用有限元数值模拟以及试验手段来对带止屈器管道的屈曲行为进行研究。Kyriakides[4]运用缩尺比试验方法研究了扣入式止屈器的止屈效率上下限问题;Lee和Kyriakides[5, 7]运用ABAQUS有限元软件对扣入式止屈器的止屈效率问题进行了模拟分析;Kyriakides和Lee[6-7]运用ABAQUS有限元软件对围腔内受限管道的屈曲传播进行了准静态模拟,并与试验结果进行了对比。可以看出,国内外学者对管道屈曲传播和止屈问题的理论研究工作并不多见,且国内研究与国外研究还存在较大差距。
安装扣入式止屈器管道屈曲分析的主要难点在于其同时涉及了三种非线性问题,即:管道大变形的几何非线性、管壁应变较大区域的材料塑性行为非线性以及管壁与扣入式止屈器之间的接触非线性。在加载过程中,三种非线性共同影响管道的变形行为,从而增加了问题分析和求解的复杂性。本文对安装扣入式止屈器管道的屈曲传播问题进行理论研究,理论结果与ABAQUS有限元软件的数值模拟结果进行了对比;之后基于Maxwell能量平衡法,求出了扣入式止屈器穿越压力的理论下限,并与全比例管道止屈试验结果进行了对比分析。
1 管道屈曲传播力学模型 1.1 管道模型为了采用二维环模型来作为管道的力学模型,在三维管道的基础上作出以下基本假定来进行模型简化[8-9]:
1) 管壁环向应变沿管壁厚度方向满足直法线假定条件;
2) 管壁的径向应变忽略不计;
3) 忽略扣入式止屈器与管道之间以及管道自身内壁之间的相对切向运动摩擦;
4) 管道变形过程中,材料保持各向同性;
5) 仅考虑管道初始椭圆度几何缺陷;
6) 加载过程为准静态过程。
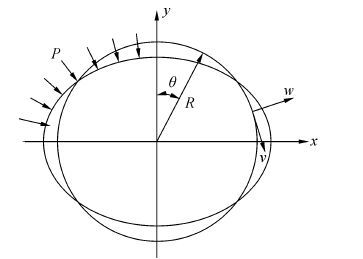
具有初始椭圆度几何缺陷的二维管道环模型如图 1所示。
|
| 图1 管道二维环模型坐标系 Figure 1 Coordinates of the 2D ring model |
以管道中心为原点建立整体坐标系,et、exp t分别为水平轴和竖直轴,用以描述管道的实际空间形状;在管壁中性层上任意点处建立局部坐标系,v、w分别表示管壁单元的环向和径向位移,用以分析管道应变。R是未发生变形管道的中性层半径,中性层上任一点的位置可以用R和θ来表示;P表示管壁的内外压差。两个坐标系的关系表示为
| $x=Rsin\theta +\omega sin\theta -\nu cos\theta $ | (1) |
| $y=Rcos\theta +\omega cos\theta +\nu sin\theta $ | (2) |
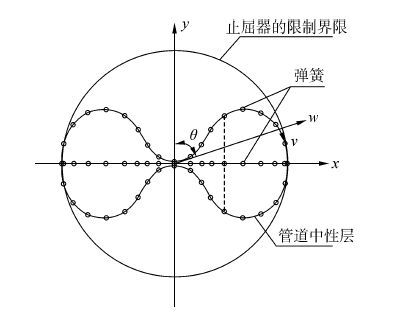
假定扣入式止屈器为完全刚性,其截面形状不发生变化。运用非线性离散弹簧模型来模拟管道自身内壁之间以及管道外壁与扣入式止屈器内壁之间的接触边界,在管道内外壁发生接触的位置建立一系列离散的非线性弹簧模型,如图 2所示。弹簧接触力与接触距离之间呈非线性关系。
|
| 图2 管壁上的接触弹簧模型 Figure 2 Spring models on pipeline′s inner and outer walls |
对于管道内壁的弹簧模型,设定与离散弹簧对应的距离量为l,用以表征接触面之间的接触情况。计算加载过程中各内弹簧所对应的距离量l,中性层与相邻界面距离为g0(等于壁厚t的一半)。当l首次达到g0时,认为该点开始发生接触,而其余lg0处的未接触弹簧则暂时不予考虑。对于发生接触的内弹簧模型:当lg0时,弹簧力为正,阻止管壁发生穿透;当lg0时,弹簧力为负,阻止已接触管壁发生分离[10]。内弹簧的弹簧力F与接触距离l之间的关系式为
| $F={{F}_{0}}{{\left( 1-\frac{l}{{{g}_{0}}} \right)}^{\beta }}$ | (3) |
式中:F0为内弹簧刚度系数,β为内弹簧反作用力的增长率。
对于管道外壁的弹簧模型,取管道中性层离散点的径向位移全量w^为离散弹簧所对应的距离量。当管道外壁与扣入式止屈器内壁恰好接触时w^=0;当两者交错时w^≥0;外弹簧启动施加弹簧力,外弹簧力大小Fa是关于接触点处外围圆环法线方向上位移ga的函数,即:
| ${{F}_{a}}={{F}_{a0}}\times {{g}_{a}}^{{{\beta }_{a}}}$ | (4) |
式中:Fa0为外弹簧刚度系数,βa为外弹簧反作用力的增长率;ga=x2+y2-R,x、y为接触点的坐标。
1.3 基本方程求解此二维环模型的屈曲问题需要建立三类基本方程,即几何方程、本构方程和平衡方程,从而分别建立位移与应变、应力与应变、位移与外力之间的关系。
1.3.1 几何方程利用Sanders[11]圆柱壳非线性大变形理论和基尔霍夫-勒夫假定,环模型环向方向的总应变为
| ${{\varepsilon }_{\theta }}={{E}_{\theta }}+z/\left( 1+z \right)\cdot {{K}_{\theta }}$ | (5) |
式中:Eθ为环向薄膜应变,Kθ为环向弯曲应变,z为沿中性层法线方向坐标。考虑管道横截面大变形中的高阶项,环向的薄膜应变与弯曲应变分别为
| ${{E}_{\theta }}=\frac{1}{R}\cdot \left( \frac{\partial v}{\partial \theta }+w \right)+\frac{1}{2{{R}^{2}}}{{\left( \frac{\partial v}{\partial \theta }+w \right)}^{2}}+\frac{1}{2{{R}^{2}}}{{\left( \frac{\partial w}{\partial \theta }-v \right)}^{2}}$ | (6) |
| $\begin{align} & {{K}_{\theta }}=\frac{1}{{{R}^{3}}}\cdot \frac{1}{{{\left( 2{{E}_{\theta }}+1 \right)}^{1/2}}}\cdot \left( \frac{{{\partial }^{2}}v}{\partial {{\theta }^{2}}}+2\cdot \frac{\partial w}{\partial \theta }-v \right)\cdot \left( \frac{\partial w}{\partial \theta }-v \right)-\frac{1}{{{R}^{2}}}\cdot {{\frac{1}{2{{E}_{\theta }}+1}}^{1/2}}\cdot \\ & \left( \frac{{{\partial }^{2}}w}{\partial {{\theta }^{2}}}-2\cdot \frac{\partial v}{\partial \theta }-w-R \right)\cdot \left( 1+\frac{1}{R}\cdot \frac{\partial v}{\partial \theta }+\frac{1}{R}\cdot w \right)-\frac{1}{R} \\ \end{align}$ | (7) |
考虑管道屈曲过程中的大变形,管道会进入弹塑性变形阶段,采用J2塑性流动理论来建立二维管道的环向和轴向应力-应变关系[12],即
| $\left[ {{{\dot{\varepsilon }}}_{\theta }} \right]=\left[ -\frac{\nu }{E}+\frac{\alpha }{h}\sigma {{\prime }_{\theta }}\sigma {{\prime }_{x}}\frac{1}{E}+\frac{\alpha }{h}\sigma {{\prime }_{\theta }}\sigma {{\prime }_{\theta }} \right]{{\dot{\sigma }}_{\theta }}$ | (8) |
式中:
| $\frac{1}{h}=\frac{9}{4}\frac{1}{{{\left( {{\sigma }^{*}}_{eq} \right)}^{2}}}\left( \frac{1}{{{E}_{t}}}-\frac{1}{E} \right)\alpha =\left\{ \begin{matrix} 1{{\sigma }_{eq}}={{\sigma }^{*}}_{eq} \\ 0{{\sigma }_{eq}}<{{\sigma }^{*}}_{eq} \\ \end{matrix} \right.$ |
其中,σeq为某点处的Mises等效应力;σeq*为该点处Mises等效应力的历史最大值;E是材料弹性模量,Et是材料的切向弹性模量,是关于σeq的函数;σx是轴向应力,σθ是环向应力。
1.3.3 能量平衡方程考虑管道大变形的特点,对外压进行逐步加载。利用虚功原理建立每个载荷步下的平衡方程,即外力功增量对位移函数的变分δW·等于内能增量对位移函数的变分δU·,即
| $\delta \dot{W}=\delta \dot{U}$ | (9) |
准静态加载过程中的外力功增量为[9]
| $\delta \dot{W}=-P\cdot \delta \left( \Delta S \right)=-PR{{\int }^{2\pi }}_{0}[\delta w\cdot +\frac{1}{2R}(2w\delta \dot{w}+2v\delta \dot{v}+w\delta \dot{v}\prime +v\prime \delta \dot{w}-v\delta \dot{w}\prime -w\prime \delta \dot{v})]d\theta $ | (10) |
总的应变能增量由管道结构应变能增量U·p、管道内弹簧应变能增量U·s和管道外弹簧应变能增量U·as三部分组成,即
| $\dot{U}={{\dot{U}}_{p}}+{{\dot{U}}_{s}}+{{\dot{U}}_{as}}$ | (11) |
管道环模型的应变能增量为
| $\delta {{\dot{U}}_{p}}={{\int }^{\pi /2}}_{0}{{\int }^{t/2}}_{-t/2}[{{\sigma }_{\theta }}+{{\dot{\sigma }}_{\theta }}\delta {{\dot{\varepsilon }}_{\theta }}+{{\sigma }_{x}}+{{\dot{\sigma }}_{x}}\delta \varepsilon {{\cdot }_{x}}]\left( R+z \right)dzd\theta $ | (12) |
式中:σ·θ为环向应力增量,ε·θ为环向应变增量;σ·x为轴向应力增量,ε·x为轴向应变增量。
内弹簧应变能增量的变分为所有已发生接触内弹簧应变能之和的变分:
| $\delta U{{\cdot }_{s}}=\sum\limits_{i=1}^{I}{\left( {{F}_{i}}+{{{\dot{F}}}_{i}} \right)}i\delta {{\dot{l}}_{i}}~$ | (13) |
式中:I为被激活的内弹簧总数,l·i为第i个内弹簧的接触距离增量。
外弹簧应变能增量的变分为所有已发生接触外弹簧应变能之和的变分:
| $\delta U{{\cdot }_{as}}=\sum\limits_{i=1}^{{{I}_{a}}}{\left( {{F}_{ai}}+{{{\dot{F}}}_{ai}} \right)}\times \delta {{\dot{g}}_{ai}}$ | (14) |
式中:Ia为被激活的外弹簧总数,$\dot{g}$ai为第i个外弹簧接触点处外围圆环法线方向上的位移增量。
2 理论结果与有限元数值模拟 2.1 理论结果以管材API 5L X65为例,弹性模量为E=2.06×105 MPa,屈服极限为σ0=448 MPa,分别计算了具有初始椭圆度的325 mm×10 mm、406 mm×10 mm两种径厚比管道的屈曲变形过程。
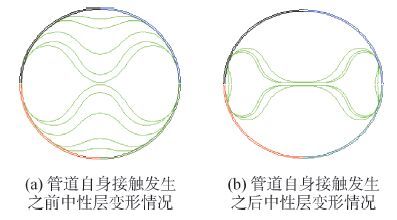
管道自身接触发生之前以及管道自身接触发生之后的管道中性层变形情况如图 3所示。
|
| 图3 管道中性层变形情况 Figure 3 Deformation of neutral layer |
从图 3中可以看出,在管道自身接触发生之前,管道截面按预想的变形方式在扣入式止屈器内产生“狗骨式”变形;当管道截面变形至自身上下内壁发生接触后,管道水平轴上的离散弹簧模型开始启用。
2.2 有限元模拟对比采用与上述理论计算相同的模型参数,运用ABAQUS软件进行有限元数值模拟,如图 4所示。
|
| 图4 管道和止屈器的有限元模型 Figure 4 Finite element model of the pipeline and arrestor |
管道外部运用二维壳模型建立四分之一圆环来模拟扣入式止屈器,止屈器材料定义为弹性模量很大的刚性体;管道和止屈器网格划分均采用非协调应力单元(CPS4I);模型采用流体加载,并在管道外部采用二维线模型建立与管道同心四分之一圆作为流体加载的外壳;模型运用二维刚性面在管道水平轴上建立长度小于管道内径的刚性面,用以模拟管道自身内壁的接触平面。
理论计算和有限元模拟的管道外压变化曲线对比如图 5所示。
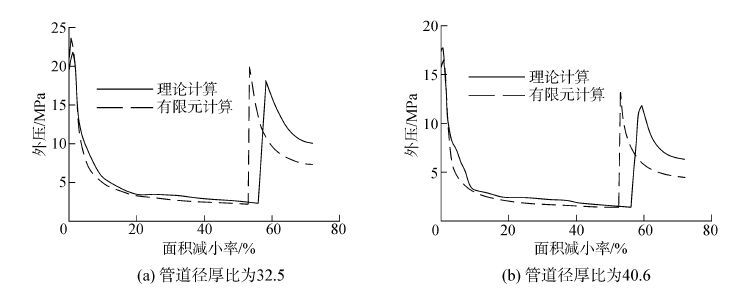
|
| 图5 理论计算和有限元模拟的管道外压变化曲线 Figure 5 External pressure curves of the theoretical calculation and finite element simulation |
对于325 mm×10 mm、406 mm×10 mm两种径厚比的管道,理论计算和有限元模拟所得的外压变化曲线在管道内壁发生接触后的上升段有较大差别,这可能是由于有限元单元的定义、划分以及有限元模拟和理论计算接触边界的模型不同所致,但外压的整体变化趋势比较吻合,因此可以说明该理论计算方法是正确的。
3 扣入式止屈器的穿越压力 3.1 穿越压力的理论计算根据围腔内受限管道的屈曲传播分析研究[6],其外压-时间的准静态变化曲线如图 6所示。
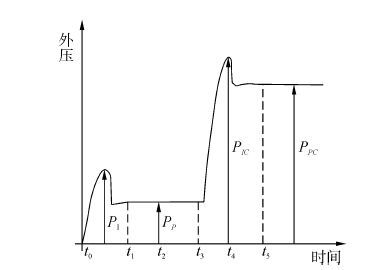
|
| 图6 部分围腔内受限管道的外压-时间准静态变化曲线 Figure 6 External pressure-time history of a quasi-static test on a partially confined pipeline |
图 6中PI表示管道的屈曲压溃压力,PP表示管道的屈曲传播压力,PIC可以认为是围腔内受限管道的屈曲压溃压力,PPC表示围腔内受限管道的屈曲传播压力,也可以看成管道屈曲“穿越”长围腔的最小压力。如果将长围腔缩短至扣入式止屈器的长度,则PPC便是该扣入式止屈器的穿越压力下限,而PIC则是穿越压力上限。
图 7为管道外压随其截面变形的曲线(P-δυ),认为管道在外压PPC作用下进行准静态屈曲传播,单位长度管道发生屈曲传播的外力功为
PPC(δυC-δυA)
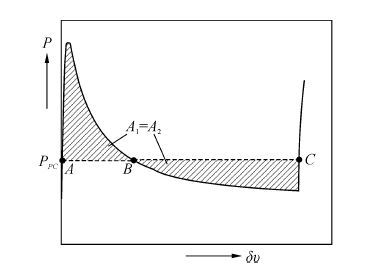
|
| 图7 P-δυ变化曲线和Maxwell作图法 Figure 7 Curve of P-δυ and Maxwell′s construction |
式中:A是管道未发生变形时的初始状态,C是管道发生屈曲传播后的最终状态。
假定材料行为与路径无关,此时管道应变能变化便只与管道截面的初始状态A和最终状态C有关,而应变能变化量应等于外力功,即
| $\int_{\partial vA}^{\partial vc}{{{{\hat{p}}}_{\left( \partial v \right)}}}d\partial v={{p}_{pc}}\left( \partial {{v}_{c}}-\partial {{v}_{A}} \right)$ | (15) |
对于弹性变形,材料行为与路径无关,式(15)严格满足;但对于塑性变形,材料行为与路径相关,式(15)并不严格满足,尽管如此,这里仍用该方法来进行近似求解。
基于本文带扣入式止屈器二维管道理论模型所求出的外压-截面积变化曲线,可以运用Maxwell作图法[6-7]来确定扣入式止屈器的穿越压力下限PPC。为满足式(15),可以将PPC的水平线画在P-δυ图中,保证面积A1等于面积A2即可。
3.2 扣入式止屈器的止屈试验为了验证理论分析和有限元模拟结果的可靠性,笔者在天津大学深海压力舱试验室[13-14]进行了安装扣入式止屈器管道的屈曲试验。
扣入式止屈器有多种形式,考虑到制作及试验安装的便捷性,试验中采用螺栓夹紧型止屈器,如图 8所示。
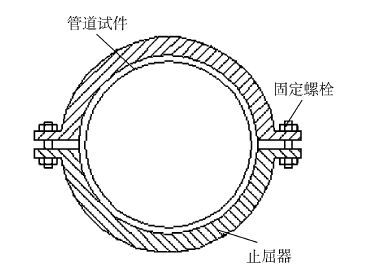
|
| 图8 螺栓夹紧型止屈器剖面 Figure 8 Cross section of clamped arrestors |
1) 制作螺栓夹紧型止屈器,并将其安装在管件中心位置,之后在管件两端安装固定密封法兰,并在管件上每隔一定间距沿环向粘贴深海应变片,然后将管件放入压力舱内部并固定。
2) 压力舱密封后,将舱体内部完全注满水,然后通过加压系统进行加压,采集记录水压数据(如图 9所示)及变形数据。
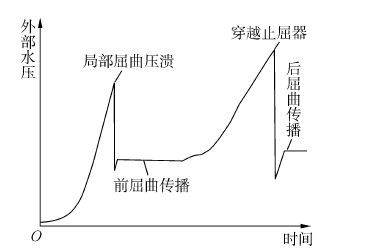
|
| 图9 扣入式止屈器试验中的水压变化曲线 Figure 9 Variation of water pressure in the slip-on arrestor′s experiment |
3) 当舱体内部水压达到一定值时,由于管件左端存在初始椭圆度缺陷,因此管件左端首先发生局部屈曲,此为试验第1)阶段:局部屈曲压溃阶段。
4) 由于压力舱内部密封,管件发生局部屈曲后体积骤然减小,舱内水容积增大,导致水压瞬间大幅下降,然后继续加压,当水压上升到某一值时,便会发生屈曲传播,此时舱内水压基本维持在一个稳定值,此为试验第2)阶段:止屈器前屈曲传播阶段。
5) 屈曲传播遇到止屈器后便被抑制,当舱内水压继续上升至一定水压值后,屈曲传播便会穿越止屈器继续传播,此时所对应的水压值即为该止屈器的穿越压力,此为试验第3)阶段:屈曲传播穿越止屈器阶段。该阶段中管道外壁与扣入式止屈器内壁间的接触如图 10所示。

|
| 图10 管道外壁与扣入式止屈器内壁间的接触 Figure 10 Contact between pipeline′s outer wall and slip-on arrestor′s inner wall |
6)在屈曲传播穿越止屈器后,水压会有小幅下降而后上升至稳定值,此为试验第4)阶段:止屈器后屈曲传播阶段。
3.3 理论结果与试验结果对比分析试验测出的扣入式止屈器穿越压力值和3.1节中的穿越压力理论值对比如表 1所示。可以看出,对于同一径厚比的管道来说,扣入式止屈器的厚度比长度对穿越压力的影响更为显著,止屈器越厚,穿越压力越大;另外从文献[6]可知,当扣入式止屈器较长时,管道会在PPC外压下在止屈器内部发生屈曲传播而穿越止屈器。
由于本文理论采用的是带扣入式止屈器的二维管道模型,因此,止屈器长度可以看作无限长,所求出的理论值只是穿越压力的下限值PPC。
| 径厚比D/t | 止屈器尺寸/mm×mm | 穿越压力/MPa | |
| 试验值 | 理论值 | ||
| 160×10 | 3.441 | 3.189 | |
| 32.5 | 160×20 | 6.237 | 6.021 |
| 320×10 | 4.348 | 4.155 | |
| 200×10 | 2.052 | 1.820 | |
| 40.6 | 200×20 | 3.820 | 3.608 |
| 400×10 | 2.587 | 2.354 | |
1) 通过理论计算和有限元数值模拟对比,说明本文的二维管道环模型和接触弹簧模型可用于研究带扣入式止屈器海底管道在外部静水压力作用下的截面变形及外压变化情况。
2) 由于假定扣入式止屈器为完全刚性,因此,所求出的穿越压力理论值更适用于厚度较大的止屈器;接下来应进一步研究止屈器厚度对止屈效果的影响机制。
3) 运用Maxwell能量平衡法求得的穿越压力下限值,由于未考虑材料塑性行为的路径相关性,所求出的穿越压力理论值略小于试验值。
| [1] | DYAU J Y, KYRIAKIDES S. On the propagation pressure of long cylindrical shells under external pressure[J]. International journal of mechanical sciences, 1993, 35(8): 675–713. DOI:10.1016/0020-7403(93)90018-P |
| [2] | KYRIAKIDES S, NETTO T A. On the dynamics of propagating buckles in pipelines[J]. International journal of solids and structures, 2000, 37(46/47): 6843–6867. |
| [3] | XUE Jianghong. A non-linear finite-element analysis of buckle propagation in subsea corroded pipelines[J]. Finite elements in analysis and design, 2006, 42(14/15): 1211–1219. |
| [4] | KYRIAKIDES S. Efficiency limits for slip-on type buckle arrestors for offshore pipelines[J]. Journal of engineering mechanics, 2002, 128(1): 102–111. DOI:10.1061/(ASCE)0733-9399(2002)128:1(102) |
| [5] | LEE L H, KYRIAKIDES S. On the arresting efficiency of slip-on buckle arrestors for offshore pipelines[J]. International journal of mechanical sciences, 2004, 46(7): 1035–1055. DOI:10.1016/j.ijmecsci.2004.07.009 |
| [6] | KYRIAKIDES S, LEE L H. Buckle propagation in confined steel tubes[J]. International journal of mechanical sciences, 2005, 47(4/5): 603–620. |
| [7] | LEE L H. On the design of slip-on buckle arrestors for offshore pipelines[D]. Austin: The University of Texas at Austin, 2007. https://repositories.lib.utexas.edu/handle/2152/3734?show=full |
| [8] |
余建星, 李智博, 杜尊峰, 等. 深海管道非线性屈曲理论计算方法[J].
海洋工程, 2013, 31(1): 54–60.
YU Jianxing, LI Zhibo, DU Zunfeng, et al. Theoretical calculation method of the nolinear buckling of deepsea pipes[J]. The ocean engineering, 2013, 31(1): 54–60. |
| [9] |
杨源. 海底管道屈曲破坏与止屈器研究[D]. 天津: 天津大学, 2013.
YANG Yuan. The research of submarine pipeline buckling failure and buckle arrestor[D]. Tianjin: Tianjin University, 2013. |
| [10] | DYAU J Y. Localization and propagation of instabilities in long cylindrical shells under external pressure[D]. Austin: The University of Texas at Austin, 1993. |
| [11] | SANDERS J L JR. Nonlinear theories for thin shells[J]. Quarterly of applied mathematics, 1963, 21(1): 21–36. |
| [12] |
黄克智, 黄永刚.
固体本构关系[M]. 北京: 清华大学出版社, 1999 .
HUANG Kezhi, HUANG Yonggang. Constitutive relationship of solid[M]. Beijing: Tsinghua University Press, 1999 . |
| [13] |
卞雪航, 吴海欣, 余杨, 等. 深水海底管道屈曲传播试验设计[J].
海洋技术, 2011, 30(4): 93–95.
BIAN Xuehang, WU Haixin, YU Yang, et al. Scheme design for deep water pipeline buckling propagation experiment[J]. Ocean technology, 2011, 30(4): 93–95. |
| [14] |
余建星, 卞雪航, 余杨, 等. 深水海底管道全尺寸压溃试验及数值模拟[J].
天津大学学报, 2012, 45(2): 154–159.
YU Jianxing, BIAN Xuehang, YU Yang, et al. Full-scale collapse test and numerical simulation of deepwater pipeline[J]. Journal of Tianjin University, 2012, 45(2): 154–159. |



