在船舶设计中,船体在波浪中的运动和水动力性能预报一直是一个关键问题,而船舶辐射摇荡和波浪绕射问题是预报船舶在波浪中运动性能的基础。目前关于船舶辐射摇荡的研究大多基于模型试验和势流理论。其中,传统物理试验方法成本高、存在尺度效应、易受设备技术条件限制,难以精确预报实尺度船舶周围的复杂流场。势流理论凭借计算量小、效率高的优点,得以长足的发展,已日趋成熟。Xu和Duan[1]采用时域边界积分方程方法模拟了三维波浪辐射问题。Bai和Teng[2]应用时域二阶方法分别对固定和浮动圆柱的非线性波相互作用进行了数值模拟,研究其辐射和绕射精度。He和Kashiwagi[3]基于时域高阶边界元法对潜椭球和Wigley船的辐射问题进行了研究,计算了附加质量和辐射阻尼系数。但是势流理论假设流体不可压缩、无粘性和无旋,难以考虑非线性影响及对强非线性运动进行预报。
实际上,船体周围粘性流场非常复杂,且流体与船体之间的强非线性作用影响也不容忽略,因此基于粘性流理论的数值模拟已成为近年来水动力学研究的热点。随着计算科学技术的迅猛发展,运算量大的问题得以缓解,计算流体力学(CFD)方法取得了长足进步。吴乘胜等[4]基于N-S (Navier-Stokes)方程,对航行船舶的强制垂荡和强制纵摇进行了数值模拟,计算的附加质量和辐射阻尼,与DUT (delft university of technology) 实验数据进行了比较。朱仁传等[5]基于CFD理论对船体二维横剖面绕流进行了数值模拟,计算了不同振荡模态下浮体的附加质量和辐射阻尼。方昭昭等[6]基于CFD方法对航行船舶的摇荡辐射运动进行了数值模拟,并给出了一种求解航行船舶辐射运动的水动力系数的方法。胡俊明[7]基于Fluent软件实现了二维、三维物体辐射问题的数值模拟,提出了计算附加质量和辐射阻尼系数的方法,并探讨了参数设置、网格划分、振荡频率和控制域变化对数值结果的影响。
FINE/Marine是NUMECA公司针对解决复杂自由液面的难题,开发的求解非结构自由液面粘性流场的新型CFD软件,可以处理破碎波和复杂自由液面问题。近年来被广泛用于航行器、螺旋桨等各行业,但是其在船舶水动力性能分析上的应用研究却鲜有报道。本文基于FINE/Marine首先建立了船舶水动力分析模型;然后,对该数值模型的可靠性和精确性进行了系统、全面验证和研究;航行船舶的辐射问题是预报船舶耐波性能的基础,最后利用该建立的数值模型对Wigley船的摇荡辐射运动进行了数值模拟;将计算所得的强制垂荡和纵摇的附加质量和辐射阻尼系数,与实验数据和势流理论结果进行比对,来验证基于FINE/Marine船舶水动力性能分析方法在船舶非定常辐射问题上的适用性和精确性。
1 数学模型及数值方法本文数值模型基于粘性流理论,以质量和动量守恒方程为控制方程:
| $\frac{\partial }{\partial t}{{\int }_{V}}\rho dV+{{\int }_{S}}\rho (U-{{U}_{d}})\cdot ndS=0$ | (1) |
| $\begin{align} & \frac{\partial }{\partial t}{{\int }_{V}}\rho {{U}_{i}}dV+{{\int }_{S}}\rho {{U}_{i}}(U-{{U}_{d}})\cdot ndS= \\ & {{\int }_{S}}({{\tau }_{ij}}{{I}_{j}}-p{{I}_{i}})\cdot ndS+{{\int }_{V}}\rho {{g}_{i}}dV \\ \end{align}$ | (2) |
式中:t为时间,ρ为密度,V为控制体,S为控制面,Ud为S上n方向的速度,U和p分别为速度和压力,Ui为在xi坐标轴方向上的平均速度分量,τij和gi分别为粘性应力张量和重力矢量,Ii和Ij分别为方向向量。
采用k-ω (SST-Menter) 湍流模型,其湍动能k和比耗散率ω输运方程为[8]
| $\begin{align} & \frac{\partial \rho K}{\partial \tau }+\frac{\partial }{\partial {{x}_{j}}}\left[ \rho {{U}_{j}}K-\left( \mu +{{\sigma }_{k}}{{\mu }_{t}} \right)\frac{\partial K}{\partial {{x}_{j}}} \right]= \\ & {{\tau }_{ij}}{{S}_{ij}}-{{\beta }^{*}}\rho \omega K \\ \end{align}$ | (3) |
| $\begin{align} & \frac{\partial \rho \omega }{\partial \tau }+\frac{\partial }{\partial {{x}_{j}}}\left[ \rho {{U}_{j}}\omega -\left( \mu +{{\sigma }_{\omega }}{{\mu }_{t}} \right)\frac{\partial \omega }{\partial {{x}_{j}}} \right]= \\ & {{P}_{\omega }}-\beta \rho {{\omega }^{2}}+2\left( 1-{{F}_{1}} \right)\frac{\rho {{\sigma }_{\omega 2}}}{\omega }\frac{\partial K}{\partial {{x}_{j}}}\frac{\partial \omega }{\partial {{x}_{j}}} \\ \end{align}$ | (4) |
式中: τ为分子内应力,μ为分子粘性系数,μt为湍动粘度,Sij为平均变形速度张量,δij为克罗尼克尔二阶张量,F1为混合函数。模化常数分别为
σk = 1,β*= 0.09,γ= 0.44,
Pω≡2γSij-ωSnnδij/3Sij≈γρΩ2
求解器基于非结构化动网格技术,通过直接求解三维粘性不可压多相流体的雷诺平均方程来模拟固-液-气多相流复杂流场变化。微分方程的离散采用具有2阶时间和空间精度的隐式有限体积法;动量方程的离散采用GDS (Gamma differencing scheme) 格式;自由液面捕捉采用BRICS (blended reconstruction interface capturing scheme) 可压缩型离散格式,实现减小自由液面附近流体体积分数的数值扩散。
采用自由液面捕捉法来重构自由液面。对气体 (空气) 和液体 (水) 两种流体,通过引入一个构成函数ci (i流体的体积占网格单元体积的份额),按单一流体进行统一处理。两种流体的性能和空间的变化也易从密度和粘性系数等物理量及构成函数ci来确定。如:构成函数ci在空气中为0,在水中为1。通过求解以下运动方程可确定构成函数ci:
| $\frac{\partial }{\partial t}{{\int }_{V}}{{c}_{i}}dV+{{\int }_{S}}{{c}_{i}}(U-{{U}_{d}})\cdot ndS=0$ | (5) |
与自由液面跟踪法相比,自由液面捕捉法具有更好的灵活性和适应性,可较好地处理波浪破碎、水花飞溅等复杂的自由液面大变形问题。
2 数据分析方法波浪中航行船舶的自由运动主要可看作:定常问题、辐射问题和绕射问题的叠加。精确分析辐射和绕射问题是准确计算船舶自由运动的基础。辐射问题是分析船舶在静水中受迫动摇的水动力系数,包括附加质量和辐射阻尼系数。本文拟采用与日本大阪大学试验船模相一致的2.0 m Wigley船,研究其在傅汝德数Fn = 0.2航速下以不同摇荡频率进行的强制垂荡和纵摇运动,将计算所得的附加质量和辐射阻尼系数与大阪大学的实验数据进行对比[9-11]。
2.1 Wigley船模型Wigley船模型可以用以下数学公式表示:
| $\begin{align} & \frac{2y\left( x,z \right)}{B}=\left[ 1-{{\left( \frac{z}{d} \right)}^{2}} \right]\left[ 1-{{\left( \frac{2x}{L} \right)}^{2}} \right]\cdot \\ & \left[ 1+0.2{{\left( \frac{2x}{L} \right)}^{2}} \right]+{{\left( \frac{z}{d} \right)}^{2}}\left[ 1-{{\left( \frac{z}{d} \right)}^{8}} \right]{{\left[ 1-{{\left( \frac{2x}{L} \right)}^{2}} \right]}^{4}} \\ \end{align}$ | (6) |
式中:L、B、d分别对应船模的船长、船宽和标准吃水。本文计算中船长L = 2.0 m,船宽B = 0.3 m,吃水d = 0.125 m。
2.2 辐射运动实验日本大阪大学的强制动摇实验主要摇荡参数如表 1中所示,垂荡的幅值固定为0.01 m,无因次化波数KL 变化范围为4.0 ~ 30,纵摇的幅值固定为1.36°。
以强制垂荡为例,船体以傅汝德数Fn=U/$\sqrt{gL}$= 0.20的航速航行。强制垂荡运动可表示为
| $t=Re\left[ {{\xi }_{3}}{{e}^{i\omega t}} \right]$ | (7) |
式中:ω= 2π / T,T为垂荡周期。基于线性理论假设,测量的力可以表示为
| ${{f}_{1}}=\left[ -{{\omega }^{2}}{{A}_{13}}+i\omega {{B}_{13}} \right]{{\xi }_{3}}$ | (8) |
| ${{f}_{3}}=\left[ -{{\omega }^{2}}\left( \rho \nabla +{{A}_{33}} \right)+i\omega {{B}_{33}}+{{C}_{33}} \right]{{\xi }_{3}}$ | (9) |
| ${{f}_{5}}=\left[ -{{\omega }^{2}}{{A}_{53}}+i\omega {{B}_{53}}+{{C}_{53}} \right]{{\xi }_{3}}$ | (10) |
式中:ρ为流体密度,∇为排水体积,Aij、Bij、Cij分别为附加质量、辐射阻尼和恢复力系数。截取稳定后数个周期的实测数据进行傅里叶变换分析,忽略高阶小量 (如:ω的2阶及3阶量),由式(8) ~ (10) 可得以下无因次化的附加质量和辐射阻尼系数:
| $\frac{{{A}_{13}}}{\rho \nabla }=\frac{-Re\left( {{f}_{1}}/{{\xi }_{3}} \right)}{{{\omega }^{2}}\rho \nabla }$ | (11) |
| $\frac{{{B}_{13}}}{\rho \nabla \omega }=\frac{-Im\left( {{f}_{1}}/{{\xi }_{3}} \right)}{{{\omega }^{2}}\rho \nabla }$ | (12) |
| $\frac{{{A}_{33}}}{\rho \nabla }=\frac{-Re\left( {{f}_{3}}/{{\xi }_{3}} \right)-{{\omega }^{2}}\rho \nabla +{{C}_{33}}}{{{\omega }^{2}}\rho \nabla }$ | (13) |
| $\frac{{{B}_{33}}}{\rho \nabla \omega }=\frac{-Im\left( {{f}_{3}}/{{\xi }_{3}} \right)}{{{\omega }^{2}}\rho \nabla }$ | (14) |
| $\frac{{{A}_{53}}}{\rho \nabla L}=\frac{-Re\left( {{f}_{5}}/{{\xi }_{3}} \right)+{{C}_{53}}}{{{\omega }^{2}}\rho \nabla L}$ | (15) |
| $\frac{{{B}_{53}}}{\rho \nabla \omega L}=\frac{-Im\left( {{f}_{5}}/{{\xi }_{3}} \right)}{{{\omega }^{2}}\rho \nabla L}$ | (16) |
同理可得,强制纵摇的水动力系数。
| 强制垂荡 | 强制纵摇 | |
| 船长/m | L = 2.000 | |
| 船宽/m | B =0.300 | |
| 吃水/m | d =0.125 | |
| 排水体积/m3 | ∇= 0.043 | |
| 强制动摇幅值 | ξ3 = 0.01 m | ξ5 = 1.36 ° |
| 无因次化波数 | 4.0≤KL ≤ 30 | 4.0≤KL ≤ 30 |
基于FINE/Marine的船舶水动力分析模型可以准确地预报标准Wigley船的静水航行兴波阻力问题[12]。本文将该数值模型拓展到船舶非定常辐射问题。通过模拟Wigley船的受迫摇荡运动,计算其水动力系数;与实验测量值进行对比,验证该数值模拟方法在求解非定常辐射问题上的水动力精度。
计算域的建立与定常兴波问题[12]类似,利用对称性,只采用半个船体和计算域,有效地减少了网格进而节约了计算时间。方形计算域的大小设置成沿x轴方向:-3.5 L~ 2L,沿y方向:0 ~ 2L,沿z方向:-1 L~ 0.5L (L为船长)。为了保证数值模拟的稳定性,船从静止状态按1/2正弦曲线变化逐渐加速到设定航速U。基于FINE/Marine构建的三维方形计算域如图 1所示。
|
| 图1 数值计算域示意图 Figure 1 The rectangular computational domain |
在对Wigley船的辐射运动问题展开全面研究之前,对数值模型的收敛性进行了系统的研究。与定常兴波问题[12]类似,收敛性研究主要对数值模拟影响较大的关键参数进行展开,包括计算域大小、网格数量和时间步。船体的强制动摇运动可以表示为
| ${{\xi }_{j}}={{A}_{j}}cos({{\omega }_{e}}t)\text{ }\left( j=1,2,\ldots ,6 \right)$ | (17) |
式中:j代表运动模态,如:j = 3表示垂荡运动,j = 5表示纵摇运动;A代表摇荡幅值;ωe代表遭遇频率。将纵荡力Fx和垂荡力Fz以ρ∇Aωe进行无因次化,其中ρ为流体密度,∇为排水体积;时间的无因次化因子为Te= 2π / ωe (Te为摇荡周期)。以Wigley船的航速Fn= 0.3,KL = 30的强制垂荡运动进行收敛性研究。
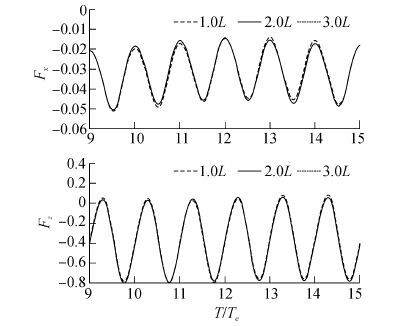
1) 计算域大小对收敛性的影响:将计算域宽度分别取为1.0L、2.0L、3.0L。从图 2可以发现,计算域过小时,计算结果与较宽的计算域存在一定差异;原因为计算域边界的消波不彻底,有波浪被反射回到计算域。因此综合考虑计算的精度和效率,宽度选取2.0L。
|
| 图2 计算域宽度对数值模型的收敛性的影响 Figure 2 Sensitivity of hydrodynamic forces to domain width for the Wigley model at Fn = 0.3 |
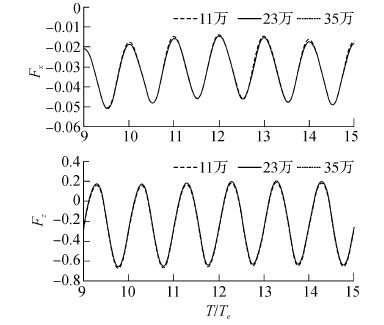
2) 网格数量对收敛性的影响:如图 3所示,网格数量分别约为11万、23万和35万。网格越密计算会越精确但是计算时间会越长;网格数量23万的计算结果,要比网格数量11万的结果更加接近35万网格的结果;考虑计算精度及经济性,以下的数值模拟采用约23万的网格。
|
| 图3 网格数量对数值模型的收敛性的影响 Figure 3 Sensitivity of hydrodynamic forces to grid number for the Wigley model at Fn= 0.3 |
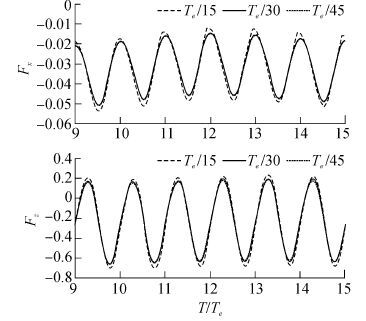
3) 时间步长对收敛性的影响:如图 4所示,当时间步长△t分别取为Te / 15,Te / 30和Te / 45,计算结果并没有较大差异,Te / 30更接近于Te / 45,综合考虑计算时间和精度,后续计算时间步长采用Te / 30。
3.2 附加质量和辐射阻尼系数基于前述的收敛性研究,数值模拟采用2倍船长的计算域宽度,23万左右网格,Te/ 30的时间步长。数值方法一共模拟了15个动摇周期Te,选用最后6个稳定的周期来计算水动力系数 (附加质量和辐射阻尼系数)。
|
| 图4 时间步长对数值模型的收敛性的影响 Figure 4 Sensitivity of hydrodynamic forces to time step for the Wigley model at Fn= 0.3 |
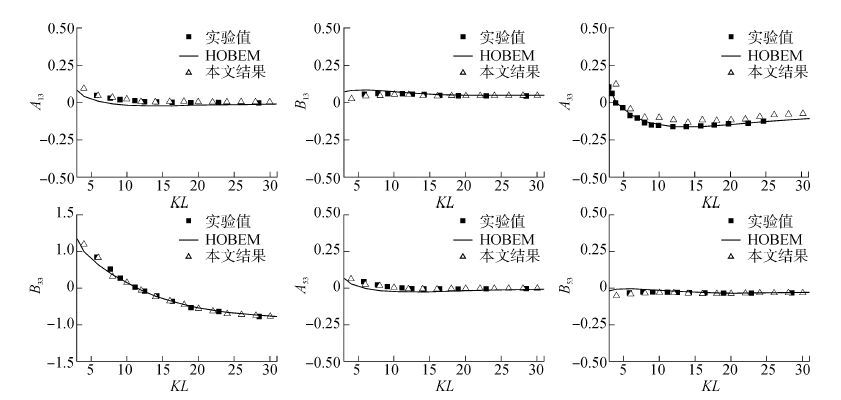
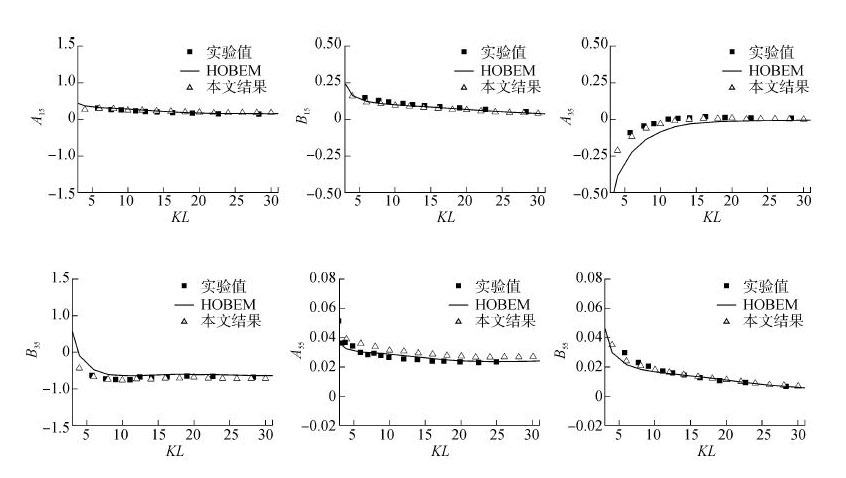
将数值模拟结果与大阪大学拖曳实验测量值和基于三维时域势流理论的高阶边界元方法 (higher-order boundary element method,HOBEM)[11]进行对比。强制垂荡结果如图 5所示,强制纵摇结果如图 6所示。
|
| 图5 强制垂荡运动的附加质量和辐射阻尼系数 Figure 5 Added mass and damping coefficients in forced heave oscillation for the Wigley model advancing at Fn = 0.2 |
|
| 图6 强制纵摇运动的附加质量和辐射阻尼系数 Figure 6 Added mass and damping coefficients in forced pitch oscillation for the Wigley model advancing at Fn = 0.2 |
从图中可以发现:1)本文所采用的数值方法与高阶边界元法结果、实验结果均吻合良好,变化趋势一致,幅值相近;2)强制垂荡和强制纵摇运动下计算值与实验测量值非常吻合,尤其在低频部分 (KL < 10),本文的数值方法比高阶边界元法更接近实验值,因为CFD方法考虑粘性和非线性影响,故更接近实际情况;3)对于A33和A55,本文数值模拟方法结果与实验值的差异要略大于高阶边界元法,但整体变化趋势与实验值一致;两者差异很小且近似稳定于固定微小值。
从以上结果分析可得:基于FINE/Marine建立的数值模拟方法满足精度要求,且能够准确地模拟附加质量和辐射阻尼系数。因为该方法基于CFD粘流理论,已计入粘性和非线性的影响,更接近实际,更能真实地反映和模拟流场。
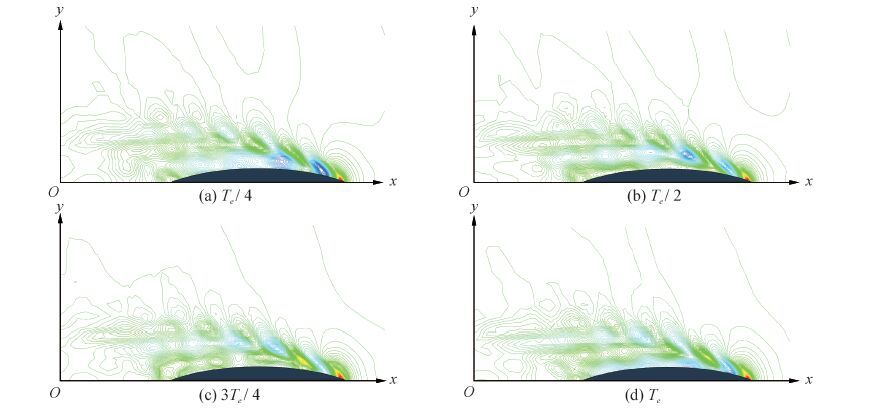
3.3 非定常波形图 7给出了Wigley船以Fn = 0.2和KL = 30做强制垂荡运动的非定常波形图。图 7中,x轴正方向为Wigley船航行方向,y轴为船宽方向;分别为一个运动周期内的4个相位(Te / 4,Te / 2,3Te / 4, Te)。
从图 7中可以看出:计算是稳定的、周期性变化的。没有发现从计算域的边界上反射波浪回来,而影响数值模拟的结果。比较图 7中(a)与(c)可得:两者的等高线正负值正好相反,因为它们的相位正好相差180°;该现象在图 7中(b)与(d)中也能看出。同时对于强制纵摇运动也有类似结论,限于篇幅不再展示。
|
| 图7 强制垂荡运动的非定常波形 Figure 7 The heave radiation wave patterns generated by the Wigley model (Fn= 0.2,KL = 30) |
本文基于CFD商业软件FINE/Marine建立了数值波浪水池,对Wigley船的垂荡和纵摇辐射问题进行了数值模拟,计算了其附加质量和辐射阻尼系数。由以上研究内容可得到如下结论:
1) 该数值模型对计算域大小、网格数量和时间步长是收敛的;
2) 利用FINE/Marine对Wigley船在航速Fn = 0.2下强制垂荡和纵摇进行了数值模拟,附加质量和辐射阻尼系数的计算结果与实验结果和时域势流理论计算结果均吻合良好,验证了该数值模拟方法的辐射问题的水动力精度。
基于FINE/Marine的船舶水动力分析模型可以准确预报船舶的耐波性和运动特性,预报精度可满足工程要求,且无尺度效应、费用低廉,考虑粘性及非线性影响,更接近实际流场,具有较为广阔的应用前景。
| [1] | XU Gang, DUAN Wenyang. Time-domain simulation for water wave radiation by floating structures (Part A)[J]. Journal of marine science and application, 2008, 7(4): 226–235. DOI:10.1007/s11804-008-8033-5 |
| [2] | BAI Wei, TENG Bin. Simulation of second-order wave interaction with fixed and floating structures in time domain[J]. Ocean engineering, 2013, 74: 168–177. DOI:10.1016/j.oceaneng.2013.07.014 |
| [3] | HE Guanghua, KASHIWAGI M. Radiation-problem solutions using a time-domain iterative HOBEM[J]. International journal of offshore and polar engineering, 2014, 24(2): 81–89. |
| [4] |
吴乘胜, 朱德祥, 顾民. 基于N-S方程的航行船舶辐射问题数值模拟[J].
船舶力学, 2008, 12(4): 560–567.
WU Chengsheng, ZHU Dexiang, GU Min. Simulation of radiation problem moving with forward speed by solving N-S equations[J]. Journal of ship mechanics, 2008, 12(4): 560–567. |
| [5] |
朱仁传, 郭海强, 缪国平, 等. 一种基于CFD理论船舶附加质量与阻尼的计算方法[J].
上海交通大学学报, 2009, 43(2): 198–203.
ZHU Renchuan, GUO Haiqiang, MIAO Guoping, et al. A computational method for evaluation of added mass and damping of ship based on CFD theory[J]. Journal of Shanghai jiaotong university, 2009, 43(2): 198–203. |
| [6] |
方昭昭, 朱仁传, 缪国平. 数值波浪水池中航行船舶辐射问题的数值模拟[J].
水动力学研究与进展, 2011, 26(1): 65–72.
FANG Zhaozhao, ZHU Renchuan, MIAO Guoping. Numerical simulation on radiation problems of moving vessels in numerical wave tank[J]. Chinese journal of hydrodynamics, 2011, 26(1): 65–72. |
| [7] |
胡俊明. 基于Fluent的波浪辐射与绕射问题数值模拟研究[D]. 哈尔滨: 哈尔滨工程大学, 2011: 45-64.
HU Junming. Numerical simulation of wave radiation and diffraction problems based on Fluent[D]. Harbin: Harbin Engineering University, 2011: 45-64. http://epub.cnki.net/kns/detail/detail.aspx?QueryID=10&CurRec=1&recid=&FileName=1012264975.nh&DbName=CMFD2012&DbCode=CMFD&pr= |
| [8] |
刘山. 基于CFD技术数值模拟平面运动机构试验[D]. 武汉: 武汉理工大学, 2012: 6-20.
LIU Shan. Numerical simulation of planar motion mechanism test based on CFD technology[D]. Wuhan: Wuhan University of Technology, 2012: 6-20. http://cdmd.cnki.com.cn/article/cdmd-10497-1012405842.htm |
| [9] | KASHIWAGI M, KAWASOE K, INADA M. A study on ship motion and added resistance in waves[J]. Journal of the Kansai society of naval architects, Japan, 2000(234): 85–94. |
| [10] | WAKABAYASHI T. Hydrodynamic study on added resistance by means of wave pattern analysis[D]. Suita, Osaka, Japan: Osaka University, 2012. http://cn.bing.com/academic/profile?id=2507428688&encoded=0&v=paper_preview&mkt=zh-cn |
| [11] | HE Guanghua, KASHIWAGI M. A time-domain higher-order boundary element method for 3D forward-speed radiation and diffraction problems[J]. Journal of marine science and technology, 2014, 19(2): 228–244. DOI:10.1007/s00773-013-0242-1 |
| [12] |
陈丽敏, 何广华, 王大政, 等. 基于FINE/Marine的Wigley船的兴波阻力分析[C]// 2015年船舶水动力学学术会议论文集. 哈尔滨: 中国造船工程学会, 2015: 207-213.
CHEN Limin, HE Guanghua, WANG Dazheng, et al. Study on the wave-making resistance of Wigley hull based on FINE/Marine[C]//Proceedings of the Symposium on Ship Hydrodynamics. Harbin: The Chinese Society of Naval Architecture and Marine Engineers, 2015: 207-213. |



