2. College of Information Science and Technology, Dalian Maritime University, Dalian 116026, China
风翼助航船舶依靠风翼的空气动力特性[1],对船舶产生辅助力,风翼对船舶的辅助力可以分解为船舶航行方向的助推力和垂直于船舶航行方向的横向力,风翼受力的变化直接影响船舶运动姿态,因此风翼受力大小与方向是风翼助航船舶运动控制的两项重要参数,获得准确的风翼受力是提高船舶操纵与推进性能、减小船舶摇荡性能的关键。通过安装风翼桅杆上的风速风向传感器对视风的测量[2],结合风翼的空气动力特性,可以从理论上计算得到风翼受力[3]。但由于海面上风况的纵向梯度变化[4],以及采用多个风翼会导致风翼之间气流的相互扰动,风翼迎风面接受来风并不均匀,而将风速风向传感器布满整个帆面也是不现实的,因此不能测量风翼迎风面的全局风况,从而计算得出的风翼受力与实际风翼受力存在一定的误差[5]。
目前,关于风翼受力的研究,国内外学者更多集中于对风翼空气动力特性的研究,以及为提高推进性能对其进行改造。胡以怀等[6]通过理论计算与风洞实验得到了翼型帆以及椭圆形翼帆的空气动力特性,并证明了翼型帆相对于普通风帆具有较高的升阻比;林煜翔[7]对襟翼帆进行了设计,通过CFD理论计算与仿真验证,证明给风翼加装襟翼,会提高风翼的推力系数;Yoo Jaehoon等[8] 采用CFD软件对三维翼型帆受力进行了计算,结果证明两个翼型帆组合产生的升力比两个单独翼型帆产生的升力之和大;Amin Hamid等[9]对刚性风帆的速度预测进行了理论研究;Foresta Maurizio[10] 和Grassi C[11]等对串联对称翼特性进行研究。上述文献均是在理想均匀风况下进行的理论研究。针对非理想风况,A Rossetti等[5] 提出了采用聚合压力无线传感系统的设计,通过在风翼面上采用网络结构布置压力传感器,并通过压力监测系统获得风翼面的压力分布,但并没有给出风翼受力的测量结果。目前,关于风翼受力的测量,多集中在理论研究,且基于理想风况。本文则采用弯曲应变技术,脱离风况变化的影响,对风翼受力的测量方法进行了理论分析与试验研究。
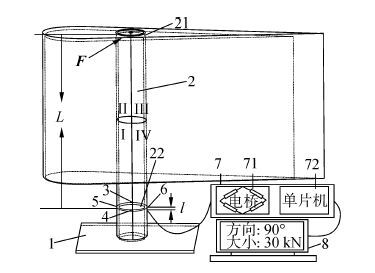
1 风翼受力测量系统结构图1为风翼受力测量结构图,结合该结构图,针对船舶上安装的风翼系统,给出如下规定与假设:1)规定风翼桅杆采用材质均匀的实心或空心弹性圆柱体;2)规定风翼体与桅杆连接采用单截面连接方式,即风翼与桅杆所有连接固定点在桅杆的同一截面上,图中示例为风翼顶端固定在桅杆的顶端截面,且该截面为二者固定的唯一截面;3)规定风翼的重心线与风翼桅杆轴线重合,即在没有风力的情况下,不会因为风翼的重力而使风翼桅杆产生弯曲应变;4)假设风翼受力的作用方向为指向桅杆轴心的方向,力的作用点在桅杆受力截面所在的桅杆外围表面。
|
| 图1 风翼受力测量结构图 Fig.1 The structure diagram of wing thrust 注:1.桅杆支座(船舶甲板);2.风翼桅杆;3、4、5、6.电阻应变片; 7.检测模块;8.显示单元;21.桅杆受力截面;22.应变片所在截面;71.检测电路;72.处理器(单片机) |
以材质均匀的空心圆柱形桅杆为例,设定风翼与桅杆的连接点仅为桅杆顶端所在截面的外围表面一周。在桅杆受力点与桅杆支座之间的外周围同一高度,均匀设置四个相同的电阻应变片,即每两个相邻电阻应变片相隔90°。电阻应变片的测量电路采用的是带有非线性补偿功能的半桥差动电路,即相对的两个电阻应变片为一组,每组电阻应变片分别与两个相等电阻构成半桥差动电路(检测电路)。当风翼受力,风翼作用力会转移到桅杆受力面,使桅杆产生弯曲应变,4个电阻应变片分别会有拉伸和压缩的组合作用,4个电阻应变片的阻值会发生变化,电阻应变片阻值变化会带动半桥差动电路产生差动电压。根据差动电压与应变片电阻之间的关系、应变片电阻与桅杆弯曲应变之间关系、桅杆弯曲应变与桅杆弯矩之间关系、桅杆弯矩与桅杆受力之间关系,最终得到风翼作用力的大小。通过控制器对数据的检测、判断与计算,得到风翼受力的大小与方向,并通过显示屏显示出来,便于观察。
风翼受力测量系统主要包括传感器、检测电路、微处理器和显示四部分。其中,传感器采用电阻应变片系统,检测电路采用半桥差动电路。
如图1所示,桅杆受力截面与电阻应变片所在截面距离为L,应变片的高度为l。为分析方便,设定以电阻应变片4为基准,按照顺时针方向将圆柱桅杆划分4个扇形区域。其中应变片4与5之间的扇形区域为Ⅰ区,应变片5与3之间的扇形区域为Ⅱ区,应变片3与6之间的扇形区域为Ⅲ区,应变片6与4之间的扇形区域为Ⅳ区。
2 测量原理与方法 2.1 基于弯曲应变测量原理由于电阻应变片具有体积小、动态响应快、测量精度高和使用方便等优点,广泛应用于应变测量、力测量、扭矩测量、位移测量、加速度测量[12]等。因此本文采用的应变测量元件为电阻应变片。
图1中的电阻应变片3、4、5、6对应的电阻值分别为Rf、Rb、Rl、Rr,设定4个电阻应变片的初始阻值为
Rf0=Rb0=Rl0=Rr0=R0
(1)
若风翼受合推力的作用点在Ⅰ区,会导致空心圆柱桅杆的弯曲应变,使得电阻应变片4(Rb)与电阻应变片5(Rl)受拉,电阻应变片3(Rf)与电阻应变片6(Rr)受压,且相对的两个电阻应变片各自对应的阻值变化大小相等、符号相反,即对应的阻值变化情况如下:
R=R0+ΔR
(2)
设定电阻应变片3(Rf)与4(Rb)的线应变大小均为ε1,电阻应变片5(Rl)与6(Rr)的线应变大小均为ε2,4个电阻应变片的灵敏系数均为K,则
ΔRb/Rb0=-ΔRf/Rf0=Kε1
(3)
ΔRl/Rl0=-ΔRr/Rr0=Kε2
(4)
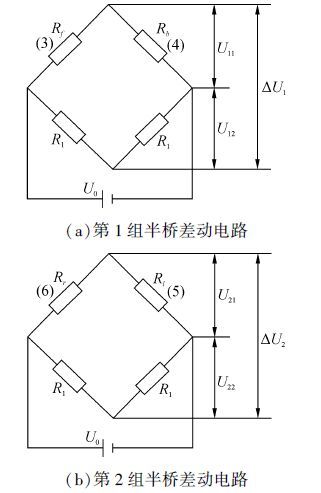
设置电阻应变片3(Rf)与电阻应变片4(Rb)一组、电阻应变片5(Rl)与电阻应变片6(Rr)一组,每组电阻应变片分别与两个相等的固定电阻R1构成半桥差动电路,如图2所示[13]。
|
| 图2 由电阻应变片构成的半桥差动电路 Fig.2 Half bridge differential circuit by resistance strain gauge |
半桥差动电路的给定电压为U0,输出差动电压分别为ΔU1和ΔU2,则
$$\eqalign{
& \Delta {U_1} = \left( {{{{R_b}} \over {{R_f} + {R_b}}} - {{{R_1}} \over {2{R_1}}}} \right) = \cr
& \left( {{{{R_0} + \Delta {R_b}} \over {2{R_0}}} - {{{R_1}} \over {2{R_1}}}} \right){U_0} = {{{U_0}} \over 2}{{\Delta {R_b}} \over {{R_0}}} = {{{U_0}} \over 2}K{\varepsilon _1} \cr} $$
(5)
$$\eqalign{
& \Delta {U_2} = \left( {{{{R_l}} \over {{R_l} + {R_r}}} - {{{R_1}} \over {2{R_1}}}} \right) = \cr
& \left( {{{{R_0} + \Delta {R_l}} \over {2{R_0}}} - {{{R_1}} \over {2{R_1}}}} \right){U_0} = {{{U_0}} \over 2}{{\Delta {R_l}} \over {{R_0}}} = {{{U_0}} \over 2}K{\varepsilon _1} \cr} $$
(6)
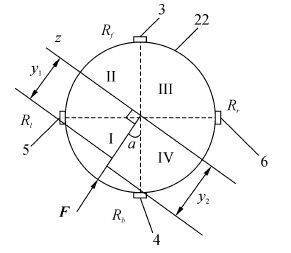
图3所示为电阻应变片所在风翼桅杆截面俯视图,图中表示出受力点在Ⅰ区,且受力方向与应变片4的夹角为α时,该截面弯曲应变的受力分析。
如图3所示。风翼受推力作用点在桅杆Ⅰ区,桅杆产生弯曲应变后,形成的中性层曲率半径为ρ,电阻应变片所在截面的中性轴为z轴(该轴与受力方向垂直且通过桅杆轴心)。则距中性轴为y处的电阻应变片所在位置的线应变ε为
ε=y/ρ
(7)
如图3所示,电阻应变片3和电阻应变片4(其线应变为ε1)距中性轴z的距离均为y1,电阻应变片5和电阻应变片6(其线应变为ε2)距中性轴z的距离均为y2,因此ε1 = y1 / ρ;ε2 = y2 / ρ。
|
| 图3 电阻应变片所在桅杆截面俯视图 Fig.3 The top view of resistance strain gauge's location section |
设桅杆的弹性模量为E,电阻应变片所在截面应力为σ ,电阻应变片所在截面弯矩为[14]
$$M = \int {_Ay\sigma dA} = \int {_AyE{y \over \rho }dA = } {E \over \rho }\int {_A} {y^2}dA = {E \over \rho }{I_2}$$
(8)
$${1 \over \rho } = {M \over {E{I_2}}}$$
(9)
Iz=πD4-d4/64
(10)
由式(7)、(9)和(10)可得风翼桅杆应变片处的线应变
ε=64My/[EπD4-d4]
(11)
又如图3的受力分析可得,y1=(D/2)cos α,y2=(D/2)sin α,结合式(11)可得
$$\eqalign{
& {\varepsilon _1} = {{64M} \over {E\pi \left( {{D^4} - {d^4}} \right)}} \cdot {y_1} = {{64M} \over {E\pi \left( {{D^4} - {d^4}} \right)}} \cdot \cr
& {D \over 2}\cos \alpha = {{32M \cdot D} \over {E\pi \left( {{D^4} - {d^4}} \right)}}\cos \alpha \cr} $$
(12)
$$\eqalign{
& {\varepsilon _2} = {{64M} \over {E\pi \left( {{D^4} - {d^4}} \right)}} \cdot {y_2} = {{64M} \over {E\pi \left( {{D^4} - {d^4}} \right)}} \cdot \cr
& {D \over 2}\sin \alpha = {{32M \cdot D} \over {E\pi \left( {{D^4} - {d^4}} \right)}}\sin \alpha \cr} $$
(13)
根据式(5)、(6)、(12)和(13),得到风翼受力角度值与应变电路参数变化关系如表1所示。
电阻应变片所在截面弯矩亦为风翼受力在该处产生的力矩,因此
$$\eqalign{
& M = FL = F{1 \over l}\int_{h - {1 \over 2}}^{h + {1 \over 2}} {(H - x)} dx = \cr
& F\left( {H - h} \right) = FL \cr} $$
(14)
根据式(14)、(12)、(5)及表1,得到风翼受力大小与应变电路参数变化关系如表2所示。
| 序号 | 力作用区域 | 电阻大小变化 | 半桥输出电压变化 | 风翼受力方向角 |
| 1 | Ⅰ区 | Rb >Rf且Rl >Rr | ΔU1>0且ΔU2>0 | α = arctan | ΔU2 / ΔU1 | |
| 2 | Ⅱ区 | Rb <Rf且Rl >Rr | ΔU1 <0且ΔU2>0 | α= 180°- arctan | ΔU2 / ΔU1 | |
| 3 | Ⅲ区 | Rb <Rf且Rl < Rr | ΔU1<0且ΔU2 <0 | α=180°+ arctan | ΔU2 / ΔU1 | |
| 4 | Ⅳ区 | Rb <Rf且Rl <Rr | ΔU1>0且ΔU2 <0 | α= 360°-arctan | ΔU2 / ΔU1 | |
| 5 | Ⅳ、Ⅰ区交界点 | Rb >Rf且Rl =Rr | ΔU1>0且ΔU2=0 | 0° |
| 6 | Ⅱ、Ⅲ区交界点 | Rb <Rf且Rl =Rr | ΔU1 <0且ΔU2=0 | 180° |
| 7 | Ⅰ、Ⅱ区交界点 | Rb =Rf且Rl >Rr | ΔU1=0且ΔU2>0 | 90° |
| 8 | Ⅲ、Ⅳ区交界点 | Rb =Rf且Rl <Rr | ΔU1=0且ΔU2 <0 | 270° |
| 序号 | 力作用区域 | 半桥输出电压变化 | 角度计算公式 | 风翼受力大小 |
| 1 | Ⅰ区 | ΔU1>0且ΔU2>0 | α = arctan | ΔU2 / ΔU1 | | $$F = {{E\pi \left( {{D^4} - {d^4}} \right)\Delta {U_1}} \over {16KDL{U_0}\cos \alpha }}$$ |
| 2 | Ⅱ区 | ΔU1 <0且ΔU2>0 | α = 180°- arctan | ΔU2 / ΔU1 | | |
| 3 | Ⅲ区 | ΔU1 <0且ΔU2 <0 | α = 180°+ arctan | ΔU2 / ΔU1 | | |
| 4 | Ⅳ区 | ΔU1>0且ΔU2 <0 | α = 360°-arctan | ΔU2 / ΔU1 | | |
| 5 | Ⅳ、Ⅰ区中间点 | ΔU1>0且ΔU2=0 | 0° | $$F = {{E\pi \left( {{D^4} - {d^4}} \right)\Delta {U_1}} \over {16KDL{U_0}}}$$ |
| 6 | Ⅱ、Ⅲ区中间点 | ΔU1 <0且ΔU2=0 | 180° | |
| 7 | Ⅰ、Ⅱ区中间点 | ΔU1=0且ΔU2>0 | 90° | $$F = {{E\pi \left( {{D^4} - {d^4}} \right)\Delta {U_2}} \over {16KDL{U_0}}}$$ |
| 8 | Ⅲ、Ⅳ区中间点 | ΔU1=0且ΔU2 <0 | 270° |
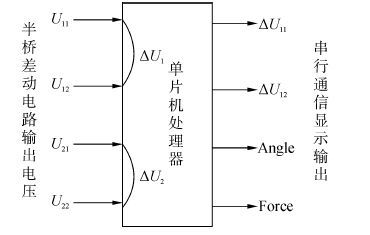
检测装置的控制器核心选择带有A/D转换功能的单片机,A/D通道用于半桥差动电路输出电压的采集。根据风翼测量原理得到相关公式,单片机对半桥差动检测电路的输出电压进行采集、判断、处理,得到应变片传感器检测得到的风翼受力大小与方向角,最终将得出的风翼受力的大小与方向输出给显示装置,以便于观察。其中单片机处理器的功能框图如图4所示。
|
| 图4 单片机处理器功能框图 Fig.4 The functional block diagram of microcontrollers |
模拟桅杆选用弹性模量较小的PPR空心管,外径为51 mm,内径为37.5 mm,弹性模量为850 MPa。
图5为实际搭建的风翼受力测量实验台。其中,图5(a)为模拟桅杆应变片传感器安装与受力截面角度标定。在模拟桅杆的同一截面圆周,每隔90°粘贴电阻应变片,分别为Rb、Rl、Rf和Rr。实验中设定受力截面距应变片距离为1 m,以应变片Rb对应受力点位置为0°,逆时针方向增大,环绕桅杆受力截面一周标注角度刻度0° ~ 360°。

|
| 图5 风翼受力测量实验台 Fig.5 Experimental table of wing thrust measurement |
图5(b)为模拟桅杆检测装置,包括电源、单片机处理器、以及由应变片与电阻组成的半桥差动电路。将电阻应变片接入到半桥差动电路中,单片机检测半桥差动电路输出电压值,并通过单片机与PC机的通讯,经由PC机显示屏显示桅杆受力情况。
半桥差动电路采用带有温度自补偿功能的应变片BE120-5AA(11),使用温度范围-30 ℃~ +80 ℃,应变极限为2%,灵敏度系数为2.11±1%。经测量,4个应变片的初始阻值均为119.1 Ω,电桥固定电阻阻值为499 Ω,电压源电压为4.96 V。控制系统核心控制器采用的是stm32单片机,通过ADC端口对半桥电路的输出电压值进行检测,并经由单片机相应程序运算处理,最终得到桅杆受力方向与大小值。通过单片机与PC机通讯,采用SSCON串口调试软件将检测结果显示出来,如图6所示。输出数据分别为两个半桥差动电路输出电压(mV)、桅杆受力方向(°)和桅杆受力大小(N)。

|
| 图6 桅杆受力检测显示窗口 Fig.6 Display window of the mast thrust measurement |
根据设计要求,桅杆受力点距离应变片截面为1 m,采用弹簧测力计在受力截面对桅杆施加水平力。通过弹簧测力计的显示值与对应的桅杆受力截面上标注的受力角度,可以直接读出桅杆受力大小与方向。与此同时,通过单片机处理得到的应变片传感器测量结果,显示并存储在PC机的串口调试窗口上。对应每一个力,应变片传感器检测系统读取10组数据,对该10组数据求取平均值,作为最终检测结果。实验测量中,对风翼受力的多方向,多个力值进行测试。表3列出了具有代表性的六个方向的力,以及每一个方向上的三个大小不同的受力值,共列出18组实验数据对比结果。
| 实验 组号 | 实测值 | 控制器检测值 | 误差绝对值 | |||||
| 角度/(°) | 力/N | 角度/(°) | 力/N | 角度/(°) | 力/N | |||
| 48.34 | 0.18 | 46.82 | 0.18 | 1.52 | ||||
| 1 | 0 | 77.20 | 0.34 | 77.12 | 0.34 | 0.08 | ||
| 86.69 | 0.07 | 86.21 | 0.07 | 0.48 | ||||
| 13.48 | 60.15 | 12.84 | 0.15 | 0.64 | ||||
| 2 | 60 | 26.88 | 59.97 | 27.03 | 0.03 | 0.15 | ||
| 60.42 | 60.21 | 60.97 | 0.21 | 0.55 | ||||
| 58.52 | 120.87 | 57.18 | 0.87 | 1.34 | ||||
| 3 | 120 | 77.12 | 120.56 | 77.25 | 0.56 | 0.13 | ||
| 95.87 | 120.08 | 96.58 | 0.08 | 0.71 | ||||
| 10.88 | 199.87 | 11.72 | 0.13 | 0.84 | ||||
| 4 | 200 | 40.27 | 199.73 | 39.87 | 0.27 | 0.40 | ||
| 80.23 | 200.12 | 80.59 | 0.12 | 0.36 | ||||
| 35.88 | 269.77 | 34.76 | 0.23 | 1.12 | ||||
| 5 | 270 | 48.94 | 270.31 | 49.23 | 0.31 | 0.29 | ||
| 60.31 | 270.59 | 59.68 | 0.59 | 0.63 | ||||
| 43.93 | 350.62 | 44.67 | 0.62 | 0.26 | ||||
| 6 | 350 | 60.09 | 350.51 | 58.32 | 0.51 | 1.77 | ||
| 75.94 | 350.26 | 76.57 | 0.26 | 0.63 | ||||
如表3所示,列出了对模拟桅杆分别进行的0°、60°、120°、200°、270°和350°六个具有代表性角度施加力的实验数据,其中每个角度对应的三个拉力取值随机。通过检测值与实测值的受力方向与大小对比,得到角度检测误差值与拉力误差值如表中所示。通过大量的实验得到:角度误差值均在1°范围内,受力大小误差值在2 N范围内。随着拉力的增大,检测得到的拉力误差率减小。
通过实验数据表明,采用弯曲应变测量方法获得风翼系统的风翼助推力的大小与方向的测量值与实际值是相符的,因此采用该方法对理想圆柱风翼桅杆的受力测量是可行的。
4 结论风翼助航船舶的风翼作用力直接影响船舶操纵性、快速性和耐波性,本文针对目前尚未出现能够直接获得风翼受力的测量方法,提出了采用弯曲应变原理测量基于圆柱形桅杆的风翼受力大小与方向,并进行了实验研究。主要结论如下:
1)通过理论分析,对于理想条件下的圆柱形风翼桅杆,采用弯曲应变测量原理,以4个完全相同的电阻应变片作为桅杆弯曲应变检测的传感器元件,能够获得风翼桅杆受力大小与方向。
2)风翼桅杆受力检测传感器电路,采用由两个相对电阻应变片与两个相同的固定电阻构成的半桥差动电路,可以消除由于温度变化引起的虚应变,做到了检测系统的非线性补偿功能,测量结果稳定可靠。
3)采用搭建的风翼受力测量实验台进行实验测试,将实验测量结果与理论计算结果进行对比,得到风翼受力大小误差值小于2 N,受力方向误差值小于1°,实验测试结果与理论分析结果相吻合,且随着风翼受力值的增大,风翼受力大小测量的误差率减小。
4)采用弯曲应变方法测量圆柱形桅杆的受力大小与方向,能够准确地将船舶辅助动力——风翼的受力情况实时反馈给船舶操控人员,以便操控人员能够根据风翼受力反馈值,及时调整船舶操纵状态,既提高了风翼助航船舶的操纵与推进性能,同时也提高了船舶的安全性能。
本文对风翼受力测量方法进行了探索性研究。对研究对象——风翼系统进行了理想化假设,测量方法并不适用于所有结构的风翼系统。在后续工作中,基于该测量原理,针对船舶实际采用的不同形状的桅杆、不同形式的风翼,同时考虑传感器的测量范围、精度等条件的局限性,将对风翼受力测量方法进行进一步研究。
| [1] | 胡文蓉, 祖洪彪, 丁祖荣, 等. 风帆在梯度风中空气动力性能的数值研究[J]. 上海交通大学学报, 2008, 42(11): 1900-1903. HU Wenrong, ZU Hongbiao, DING Zurong, et al. Computational study of the aerodynamics of sails in a twisted wind[J]. Journal of Shanghai Jiao Tong University, 2008, 42(11): 1900-1903. |
| [2] | 王国峰, 赵永生, 范云生. 风速风向测量误差补偿算法的研究[J]. 仪器仪表学报, 2013, 34(4): 786-790. WANG Guofeng, ZHAO Yongsheng, FAN Yunsheng. Research on error compensation algorithm for wind speed and direction measurement[J]. Chinese journal of scientific instrument, 2013, 34(4): 786-790. |
| [3] | FUJIWARA T, HEARN G E, KITAMURA F, et al. Steady sailing performance of a hybrid-sail assisted bulk carrier[J]. Journal of marine science and technology, 2005, 10(3): 131-146. |
| [4] | 陈登俊. 航海气象学与海洋学[M]. 北京: 人民交通出版社, 2009. |
| [5] | ROSSETTI A, CODELUPPI R, GOLFARELLI A, et al. Design and characterization of polymeric pressure sensors for wireless wind sail monitoring[J]. Sensors and actuators A: Physical, 2011, 167(2): 162-170. |
| [6] | HU Yihuai, LI Songyue, ZENG Xiangming. Research on the aerodynamic characteristics of ellipse wing sail[J]. Advanced materials research, 2012, 347-353: 2249-2254. |
| [7] | 林煜翔. 风力助航船舶襟翼帆的设计研究[D]. 大连: 大连海事大学, 2013. LIN Yuxiang. Design and research of flap wing sail for wind-assisted vessel[D]. Dalian: Dalian Maritime University, 2013. |
| [8] | YOO J, KIM J, PARK I R, et al. CFD calculations on the sail-like three dimensional airfoils[C]//Proceedings of High Performance Yacht Design Conference. New Zealand, 2006. |
| [9] | AMINI H, RAD M. A fundamental theory of sailing and its application to the design and velocity prediction of a rigid airfoil sail craft[J]. Journal of Harbin engineering university, 2006, 27(2): 133-141. |
| [10] | FORESTA M, GRASSI C, KATZ J, et al. Lift and drag measurements of tandem, symmetric, airfoils[C]//Proceedings of the 31st AIAA Applied Aerodynamics Conference. San Diego, USA, 2013. |
| [11] | GRASSI C, FORESTA M, LOMBARDI G. Study of rigid sail aerodynamics[J]. Transactions of the royal institution of naval architects Part B: International journal of small craft technology, 2013, 155(1): 13-24. |
| [12] | MONTERO W, FARAG R, DÍAZ V, et al. Uncertainties associated with strain-measuring systems using resistance strain gauges[J]. Journal of strain analysis for engineering design, 2011, 46(1): 1-13. |
| [13] | AJOVALASIT A. The measurement of large strains using electrical resistance strain gages[J]. Experimental techniques, 2012, 36(3): 77-82. |
| [14] | 刘颖. 工程力学[M]. 北京: 化学工业出版社, 2010. |



