2. School of Computer Science and Technology, Anhui University, Hefei 230601,China
随着互联网搜索引擎日趋多元化,用户已经习惯于在互联网上借助各类搜索引擎搜索各种信息,包括文本、图像和视频等。现有主流的互联网搜索引擎,如Google、Bing、百度等,进行图像相关搜索时,主要利用图像周遭的文本信息实现图像的搜索和排序,缺乏考虑图像间内在的联系和图像自身的内容,导致基于文本的图像搜索结果不尽如人意[1]。 如何将符合用户所需的图像排在搜索结果中靠前的位置,提高图像相关搜索结果的质量,已经得到了众多研究者的关注。
图像重排序是在基于初始搜索结果的前提下,挖掘图像间内在的联系和图像自身的内容,对初始排序结果重新进行排序,将符合用户所需的图像排在靠前的位置[2-5]。目前,图像重排序方法大体可以分为四类:基于线性组合的重排序[6-7]、基于聚类的重排序[8-9]、基于分类的重排序[10-11]和基于图的重排序[12-14]。基于线性组合的重排序方法首先通过若干种重排序方法得到多组排序结果,进而利用权值向量将多组排序结果进行线性组合。基于聚类的重排序方法将视觉上相似的图像聚集到一起,从而进行重排序。基于分类的重排序方法将重排序问题转变为二分类问题,对返回图像只做相关或不相关的辨别。基于图的重排序方法构建一个图,顶点表示图像,边表示图像对之间的相似度,将图的相关理论应用于重排序的优化过程。文献[12]提出了一种基于图的多模态重排序算法,该算法自适应地将多模态集成到一个基于图的重排序框架中。
现有基于图的重排序方法采用伪相关方法设置初始排序得分,即默认检索结果越靠前的图像得分越高。但事实并非如此。由于初始结果是基于文本检索所得,没有考虑到图像自身视觉信息以及图像间内在联系,往往存在靠前的图像不符合用户检索需求,而靠后的图像更符合用户检索需求。因此,本文提出了一种基于图的多模态随机游走重排序算法(multimodal graph-based reranking through random walk,MGRRW),MGRRW算法将多模态融合应用到随机游走算法中,以期避免单一模态抽取图像内容信息的片面性,从而获得更为丰富的图像内容信息,并利用多模态随机游走算法初始化图像序列得分列表初值,然后采用多模态重排序方法最优化目标函数,对相关参数和得分列表进行迭代更新。
1 基于图的多模态重排序和随机游走模型 1.1 基于图的重排序假设将重排序返回的图像序列的得分列表expt看做一个随机变量,重排序是在给定图像样本集合χ和初始图像序列的得分列表$\bar{r}$的情况下,得到具有最大后验概率的最优排序得分列表r*,重排序函数f(χ,r)可以描述为[16]
| ${{r}^{*}}=f\left( \chi ,\bar{r} \right)=arg\underset{r}{\mathop{max}}\,p\left( r|\chi ,\bar{r} \right)$ | (1) |
式中:p(r|χ,r)为后验概率。根据贝叶斯公式,后验概率与条件先验概率p(r|χ)和似然p(r|r)的乘积成正比,即
| $p\left( r|\chi ,\bar{r} \right)\propto p\left( r|\chi \right)\times p\left( \bar{r}|r \right)$ | (2) |
由此可得,贝叶斯重排序的过程可以表示为
| ${{r}^{*}}=f\left( \chi ,\bar{r} \right)=arg\underset{r}{\mathop{maxp}}\,\left( r|\chi \right)\times p\left( \bar{r}|r \right)$ | (3) |
大多数重排序基于以下两点假设[12]:
1) 重排序后的排序列表和初始列表差距不应过大,即基于文本信息本身的排序能够提供基本合理的排序列表。
2) 视觉一致性假设,即视觉相似的图像排序得分应该靠近。
根据假设1),似然p(r|r)可以定义为
| $p\left( \bar{r}|r \right)=(1/{{Z}_{1}})exp\left( -\lambda L\left( r,\bar{r} \right) \right)$ | (4) |
式中:Z1=∑rexp(-λL(r,r)),L(r,r)为惩罚项,用来度量两个得分列表的不一致性。λ为惩罚因子。
根据假设2),先验条件概率p(r|χ)可以定义为
| $p\left( r|\chi \right)=(1/{{Z}_{2}})exp\left( -R\left( r,\chi \right) \right)$ | (5) |
式中:Z2=∑rexp(-R(r,χ)),R(r,χ)为正则项,用来描述相似图像排序得分的一致性。
将式(4)、(5)代入式(3)可得到
| $r*=\arg \underset{r}{\mathop{\max }}\,\left( 1/Z \right)\exp \left( -\left( R\left( r,x \right)+\lambda L\left( r,\bar{r} \right) \right) \right)$ | (6) |
式中:Z=Z1Z2为归一化参数。
令
| $Q(r,\bar{r})=R\left( r,\chi \right)+\lambda L\left( r,\bar{r} \right)$ | (7) |
最大化式(6)等价于最小化式(7)。 Q(r,r)即为图像搜索结果重排序的目标函数。
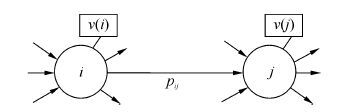
1.2 随机游走模型随机游走是指随机选取节点并移动的过程,即确定一个图模型和一个节点i,并以一定概率pij移至邻接节点j,而后以节点j为新起点并重复上述的操作。随机游走过程节点间连结示例如图 1所示。 v(i)和v(j)为节点i和j的初始得分。
|
| 图1 随机游走过程节点间示意图 Figure 1 Example of a graph for random walk |
文献[15]将重排序问题转化为随机游走过程,将每幅图像看作一个节点,用图像间的相似度W来表示节点间的权重,根据图像节点的关系构造一个加权无向图。每次游走后得出一个概率分布,如第m-1次游走后的概率分布X(m-1),该概率分布刻画了第m-1次游走后每一节点被访问到的概率。某一节点被访问到的概率越大,说明该图像的排序应该越靠前。使用X(m-1)作为下次随机游走模型的输入,反复迭代这一过程,最终所得概率分布会趋于收敛。第m次随机游走后概率分布计算:
| ${{X}^{(m)}}=\beta P{{X}^{(m-1)}}+\left( 1-\beta \right)V$ | (8) |
式中:X为返回图对应的稳态概率向量,β∈[0,1]为权衡因子,P为状态转移矩阵,可通过相似度矩阵W按列归一化获得。V为返回图像的初始排序得分列表,经过式(8)的不断迭代,X将达到稳定状态,最终根据稳态概率向量X的降序对返回图像进行重排序。
1.3 多模态及相关参数优化多模态是指多种模态特征。单一模态特征往往不能较好的表达图像的语义信息,基于多模态的图像重排序可以获得更为丰富的图像语义信息。图像的多模态包括颜色、纹理以及边缘分布等不同模态。
多模态的融合分为早融合和迟融合。为了避免早融合导致“维度灾难”,本文采用后融合,先对各模态特征加以处理,然后对处理结果加权融合。
根据图像模态特征分布情况,本文采用了文献[12]中的图像相似度计算方法及参数优化方法。在图像相似性度量中采用了马氏距离:
| ${{W}_{k,ij}}=exp(-{{({{x}_{k,i}}-{{x}_{k,j}})}^{T}}{{M}_{k}}({{x}_{k,i}}-{{x}_{k,j}}))$ | (9) |
式中:Wk,ij为第k个模态下第i幅与第j幅图像间的相似度。 xk,i与xk,j为第k个模态下第i幅与第j幅图像的特征。Mk矩阵为第k个模态对应的对称半正定矩阵。将Mk矩阵分解:
| ${{M}_{k}}={{A}_{k}}^{T}{{A}_{k}}$ | (10) |
将式(10)代入式(9),得到
| ${{W}_{k,ij}}=exp(-\|{{A}_{k}}({{x}_{k,i}}-{{x}_{k,j}}){{\|}^{2}})~$ | (11) |
利用拉普拉斯正则化[17-18],式(7)中R(r,χ)和L(r,r)可定义为
| $R\left( r,\chi ,\alpha ,{{A}_{1}},{{A}_{2}},\ldots ,{{A}_{k}} \right)=\sum\limits_{k=1}^{K}{\sum\limits_{i,j}{{{\alpha }_{k}}}}{{W}_{k,ij}}{{({{r}_{i}}{{d}_{ii}}-{{r}_{j}}{{d}_{jj}})}^{2}}+\zeta \|\alpha {{\|}^{2}}$ | (12) |
| $L\left( r,\bar{r} \right)=\|r-\bar{r}{{\|}^{2}}$ | (13) |
式中:α=[α1,α2,…,αK
| $minimizeQ(r,\chi ,\alpha ,{{A}_{1}},{{A}_{2}},\ldots ,{{A}_{k}})=\sum\limits_{k=1}^{K}{\sum\limits_{i,j}{{{\alpha }_{k}}}}{{W}_{k,ij}}{{(\frac{{{r}_{i}}}{{{d}_{ii}}}-\frac{{{r}_{j}}}{{{d}_{jj}}})}^{2}}+\zeta \|\alpha {{\|}^{2}}+\lambda \|r-\bar{r}{{\|}^{2}}~$ | (14) |
采用交替优化的思想,迭代更新r,Ak(k=1,2,…,K),和1/Zn。
首先固定Ak(k=1,2,…,K),和1/Zn,可导出公式:
| $r={{(I+\frac{1}{\lambda }\sum\limits_{k=1}^{K}{{{\alpha }_{k}}}{{\bar{L}}_{k}})}^{-1}}\bar{r}$ | (15) |
式中:L=I-D-1/2WD-1/2;D=diag(d)为以d=[d1 d2 … dN]T为对角线元素的矩阵,di=∑jWij;I为单位矩阵;λ为惩罚因子。
然后固定r和1/Zn。使用梯度下降法对式(14)中的模态Ak进行更新:
| ${{A}_{k}}^{\left( t+1 \right)}={{A}_{k}}^{\left( t \right)}-{{\eta }_{t}}\frac{\partial Q}{\partial Ak}{{|}_{Ak=Ak\left( t \right)}}$ | (16) |
式中:模态的当前迭代次数为t,步长参数为ηt。若目标函数Q(Ak(t+1))小于Q(Ak(t)),则ηt+1=2ηt;若Ak(t+1)等于Ak(t),则ηt+1=ηt/2。循环至指定步长后输出rk(m)。
最后,固定r,Ak,利用坐标下降法更新αk。式(14)可转换为
| $min\alpha {{\alpha }_{k}}{{g}_{k}}+\|\alpha {{\|}^{2}}$ | (17) |
| ${{g}_{k}}=\sum\limits_{i,j}{{{W}_{k,ij}}}(\frac{{{r}_{i}}}{{{d}_{ii}}}-\frac{{{r}_{j}}}{{{d}_{jj}}})$ | (18) |
即从K个权值中随机抽取αi和αj进行更新,固定其余的K-2个权值。可以看出,由于$\sum\limits_{k=1}^{K}{{{a}_{k}}}$,因此αi+αj的值总是保持不变。 按照式(19)的规则迭代,直到式(17)趋于收敛。
| $\left\{ \begin{matrix} {{\alpha }^{*}}_{i}=0,{{\alpha }^{*}}_{j}={{\alpha }_{i}}+{{\alpha }_{j}},if~2\zeta \left( {{g}_{i}}+{{g}_{j}} \right)+\left( {{\alpha }_{j}}-{{\alpha }_{i}} \right)\le 0 \\ {{\alpha }^{*}}_{i}={{\alpha }_{i}}+{{\alpha }_{j}},{{\alpha }^{*}}_{j}=0,if~2\zeta ({{g}_{i}}+{{g}_{j}})+({{\alpha }_{i}}-{{\alpha }_{j}})\le 0 \\ {{\alpha }^{*}}_{i}=\frac{2\zeta ({{g}_{i}}+{{g}_{j}})+({{\alpha }_{j}}-{{\alpha }_{i}})}{4\zeta },{{\alpha }^{*}}_{j}={{\alpha }_{i}}+{{\alpha }_{j}}-{{\alpha }^{*}}_{i},otherwise \\ \end{matrix} \right.$ | (19) |
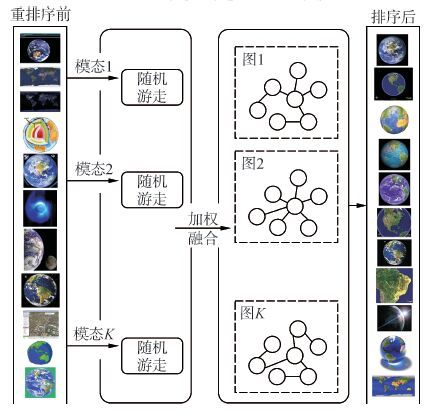
本文提出一种基于图的多模态随机游走重排序算法(multimodal graph-based re-ranking through random walk,MGRRW),该算法的一般过程如图 2所示。
|
| 图2 基于图的多模态随机游走重排序的一般过程 Figure 2 The general process of multimodal graph-based reranking through random walk |
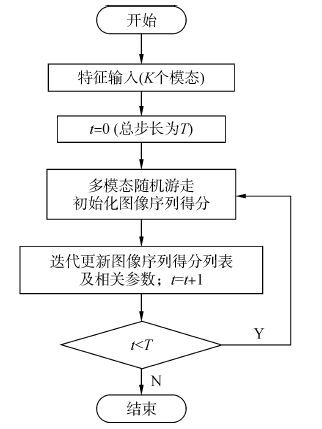
MGRRW算法首先对检索返回的图像集提取K种模态特征,生成K个特征矩阵。然后将多模态融合应用于随机游走模型中,即分别对每个模态特征,利用随机游走算法进行处理,并将处理后的结果进行加权融合,作为多模态重排序中图像序列得分列表初值,最后采用基于图的多模态重排序算法,对初始的K种模态进行更新,迭代指定步长后结束。图 3为MGRRW算法的总体流程框架。
|
| 图3 算法总体流程框架 Figure 3 The frame of general algorithm procedure |
具体算法描述如算法1。
算法1: 基于图的多模态随机游走重排序算法
输入:检索返回的初始图像序列
输出:重排序后返回的图像序列
1) 初始化
①将步数t设置为0;
②A1(t),A2(t),…,Ak(t)设置为I/σ1,I/σ2,…,I/σk,其中σk为第k个模态的欧氏距离中值;
③构建相似度矩阵W1(t),W2(t),…Wk(t),其中Wk,ij=exp(-‖Ak(Xk,i-Xk,j)‖2);
④依次计算D1(t),D2(t),…,Dk(t)和$\tilde{L}$1(t),$\tilde{L}$2(t),…,$\tilde{L}$k(t);
其中D=diag(d)是以d=[d1 d2 … dN]T为对角线元素的矩阵; di=∑jWij;$\tilde{L}$=I-D-1/2WD-1/2;I是单位矩阵。
2) 多模态随机游走初始化图像序列得分列表
①由W1(t),W2(t),…Wk(t)通过列归一化得出P1(t),P2(t),…,Pk(t)。
②对每一个模态依次执行以下循环,分别计算出K个得分列表r1,r2,…,rK:
rk(m)=μPk(t)rk(m-1)+(1-μ)V,
式中:μ为权衡因子,μ∈[0,1];m表示迭代的层级,Pk表示第k个模态下的状态转移矩阵。rk表示第k个模态下图像对应的概率分布;阻尼向量V表示图像的初始得分;为了突出视觉一致性假设,V的成员取值逐次递减,将上式不断迭代,最终达到稳定状态。
③加权融合,将所有模态的rk(k=1,2,…,K)进行加权融合得到$\bar{r}$:$\bar{r}$=β1r1+β2r2+…+βkrk。
其中β1,β2,…,βk∈[0,1],为各模态得分列表的权值,根据各模态特征维数占模态特征维数总和的百分比设置,且β1+β2+…+βk=1;
3) 迭代更新得分列表及相关参数
①根据式(15),计算r(t);
②根据式(16),更新A1(t+1),A2(t+1),…,Ak(t+1);
③根据式(19),更新a1(t+1),a2(t+1),…,ak(t+1);
④根据A1(t+1),A2(t+1),…,Ak(t+1),依次计算出D1(t+1),D2(t+1),…,Dk(t+1)和$\tilde{L}$1(t+1),$\tilde{L}$2(t+1),…,$\tilde{L}$k(t+1);
⑤ if t <T
{t=t+1,跳到②;}
else
输出图像序列得分,按照得分从高到低,给出重排序后的图像序列。
3 实验结果与分析 3.1 数据集与评价指标本文使用了MSRA-MM1.0版本数据集[19]。该数据集包括68类,每类约有1 000幅图像,共有65 443幅。所有图像都是微软在线收集,每幅图像有一个关联标准,分别是非常关联,关联和不关联。对应三个关联值分别是2、1、0。图 4为该数据集中的部分示例。

|
| 图4 数据库示例 Figure 4 Examples in image base |
该数据集中图像包括7种模态特征,具体包括:1) 225维分块颜色矩;2)256维RGB颜色直方图;3) 144维颜色相关图;4)75维边缘分布直方图;5)64维HSV颜色直方图;6)128维小波纹理图;7)7维人脸特征图。本文使用了前六种模态特征。
实验使用归一化有损积累增益[20](normalized discounted cumulative gain,NDCG)作为衡量排序效果的评价指标。计算公式为
| $NDCG@n=\frac{1}{{{Z}_{n}}}\sum\limits_{j=1}^{n}{\frac{{{2}^{m(j)}}-1}{log\left( j+1 \right)}}$ | (20) |
| ${{Z}_{n}}=\sum\limits_{j=1}^{n}{\frac{{{2}^{l(j)}}-1}{log\left( j+1 \right)}}$ | (21) |
式中:n表示检索返回的图像个数,1/Zn是归一化参数,使得最优的NDCG@n=1。NDCG@n∈[0,1],其值越接近1表明排序效果越好。m(j)是重排序算法迭代后的第j幅图像对应的关联程度。l(j)是第j幅图像在最优排序中对应的关联程度。
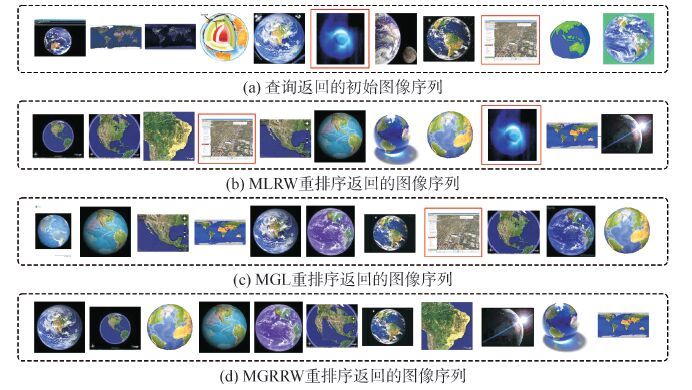
3.2 三种重排序算法在不同类别中的性能比较为了检验本文所提出的基于图的多模态随机游走重排序算法(MGRRW)的排序效果,实验将MGRRW与多模态随机游走算法(multimodal learning through random walk,MLRW)和基于图的多模态重排序算法(multimodal graph-based learning,MGL)[12]进行了对比实验。返回图像的数量设置为100。从表 1可以看出,本文所提出的MGRRW比MLRW和MGL的平均NDCG@100值有了明显提高,表明本文所提出的算法比其他两个算法排序效果更好。图 5为在查询条件为“Earth”下,初始的查询返回结果和3种重排序算法重排序后返回的结果示例。方框内的图像是与查询不相关的图像,可以看出本文所提算法可以较好剔除不相关的图像。
|
| 图5 查询初值和三种重排序返回图像序列示例 Figure 5 The three reranking methods for an example Earth |
| 类别 | 初始值 | MLRW | MGL | MGRRW |
| Earth | 0.865 | 0.859 | 0.897 | 0.925 |
| People | 0.906 | 0.915 | 0.919 | 0.938 |
| Panda | 0.840 | 0.854 | 0.855 | 0.861 |
| Tiger | 0.904 | 0.911 | 0.891 | 0.932 |
| Cat | 0.859 | 0.858 | 0.890 | 0.920 |
| Hawaii | 0.825 | 0.818 | 0.879 | 0.894 |
| Lion | 0.954 | 0.944 | 0.961 | 0.968 |
| Fruit | 0.901 | 0.905 | 0.889 | 0.927 |
| Wolves | 0.856 | 0.860 | 0.904 | 0.924 |
| Cake | 0.960 | 0.968 | 0.952 | 0.980 |
本实验检验检索返回图像的个数对三种重排序算法效果的影响。实验设置了4个检索返回图像的数量,即n分别取值为10、20、50和100。实验对所有查询类别求其平均NDCG@n值。实验结果如表 2所示。实验结果显示:
1)本文所提出的算法MGRRW在不同的返回图像数量的情况下,排序结果均优于其他两种算法MLRW和MGL。
2)随着返回图像的个数逐渐增多,返回图像集的平均NDCG@n值随之略有减小。由此说明,当返回结果逐渐增多的情况下,检索结果的准确度也会随之降低。
| 重排序算法 | 10 | 20 | 50 | 100 |
| 初始值 | 0.885 | 0.864 | 0.860 | 0.853 |
| MLRW | 0.892 | 0.888 | 0.876 | 0.872 |
| MGL | 0.895 | 0.885 | 0.874 | 0.870 |
| MGRRW | 0.909 | 0.901 | 0.893 | 0.890 |
本实验检验单一模态对图像重排序的影响,对六种模态分别进行重排序实验。表 3 中“75D-EDH”、“225D-CM”、“64D-HSV”、“114D-CORR”、“128D-Wave”、“226D-RGB”等代表使用相应单一模态的基于图的随机游走重排序算法。返回图像的数量设置为100,表格左边第二列为检索返回的图像序列的初始平均NDCG@100。可以看出:相对于初始查询返回的图像序列,单一模态在大部分情况下,能提高重排序算法的排序效果。最右一列加黑部分为本文所提出的MGRRW算法的平均NDCG@100,对比可见MGRRW算法的排序效果更好,由此可看出多模态融合的重排序算法较单一模态的重排序算法的排序效果更加显著,对所有类别的排序结果均有提高,这表明多模态融合的算法可以更好的抽取图像丰富的内容信息,避免单模态算法可能抽取片面的内容信息而造成排序效果下降的可能,因而适应面也更广。
| 类别 | 初始值 | 75D-EDH | 225D-CM | 64D-HSV | 144D-CORR | 128D-Wave | 256D-RGB | MGRRW |
| Earth | 0.865 | 0.892 | 0.877 | 0.935 | 0.885 | 0.870 | 0.873 | 0.925 |
| People | 0.906 | 0.903 | 0.913 | 0.922 | 0.895 | 0.925 | 0.920 | 0.938 |
| Panda | 0.840 | 0.857 | 0.851 | 0.843 | 0.870 | 0.810 | 0.846 | 0.861 |
| Tiger | 0.904 | 0.930 | 0.913 | 0.928 | 0.907 | 0.912 | 0.929 | 0.932 |
| Cat | 0.859 | 0.870 | 0.843 | 0.860 | 0.913 | 0.832 | 0.896 | 0.920 |
| Hawaii | 0.825 | 0.874 | 0.835 | 0.881 | 0.846 | 0.899 | 0.849 | 0.894 |
| Lion | 0.954 | 0.872 | 0.893 | 0.935 | 0.883 | 0.906 | 0.966 | 0.968 |
| Fruit | 0.901 | 0.936 | 0.919 | 0.823 | 0.904 | 0.914 | 0.896 | 0.927 |
| Wolves | 0.856 | 0.894 | 0.894 | 0.925 | 0.896 | 0.882 | 0.848 | 0.924 |
| Cake | 0.960 | 0.870 | 0.854 | 0.971 | 0.876 | 0.875 | 0.916 | 0.980 |
本文提出了一种基于图的多模态随机游走重排序算法。实验结果表明将多模态融合应用到随机游走算法中,并利用多模态随机游走算法初始化图像序列得分列表初值,能够有效的提高图像重排序的效果。
重排序仍然是信息检索领域中一项富有挑战性的研究课题。由于每位用户所关注的内容和个人的喜好不同,所期望的检索效果也不同。未来的研究将考虑如何将个性化信息融合到图像结果重排序中,以期更加符合用户个性化的检索需求。
| [1] | CAI Junjie, ZHA Zhengjun, WANG Meng, et al. An attribute-assisted reranking model for web image search[J]. IEEE transactions on image processing, 2015, 24(1): 261–272. DOI:10.1109/TIP.2014.2372616 |
| [2] | HOU Hongmei, XU Xinshun, WANG Gang, et al. Joint-Rerank: a novel method for image search reranking[J]. Multimedia tools and applications, 2015, 74(4): 1423–1442. DOI:10.1007/s11042-014-1962-x |
| [3] | YANG Linjun, HANJALIC A. Prototype-based image search reranking[J]. IEEE transactions on multimedia, 2012, 14(3): 871–882. DOI:10.1109/TMM.2012.2187778 |
| [4] | LIU Yuan, MEI Tao, WANG Meng, et al. Typicality-based visual search reranking[J]. IEEE transactions on circuits and systems for video technology, 2010, 20(5): 749–755. DOI:10.1109/TCSVT.2010.2045801 |
| [5] | JI Zhong, PANG Yanwei, HE Yuqing, et al. Semi-supervised LPP algorithms for learning-to-rank-based visual search reranking[J]. Information sciences, 2015, 302: 83–93. DOI:10.1016/j.ins.2014.10.037 |
| [6] | LI Xirong, WANG Dong, LI Jianmin, et al. Video search in concept subspace: a text-like paradigm[C]//Proceedings of the 6th ACM International Conference on Image and Video Retrieval. Amsterdam, Netherlands: ACM, 2007: 603-610. |
| [7] | NATSEV A, HAUBOLD A, TEŠIĈ J, et al. Semantic concept-based query expansion and re-ranking for multimedia retrieval[C]//Proceedings of the 15th ACM International Conference on Multimedia. Augsburg, Bavaria, Germany: ACM, 2007: 991-1000. |
| [8] | BERG T L, FORSYTH D A. Animals on the web[C]//Proceedings of 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. New York: IEEE, 2006, 2: 1463-1470. |
| [9] | HSU W H, KENNEDY L S, CHANG S F. Video search reranking via information bottleneck principle[C]//Proceedings of the 14th ACM International Conference on Multimedia. Santa Barbara, USA: ACM, 2006: 35-44. |
| [10] | YAN Rong, HAUPTMANN A G. Co-retrieval: a boosted reranking approach for video retrieval[M]//ENSER P, KOMPATSIARIS Y, O'CONNOR N E, et al. Image and Video Retrieval. Berlin Heidelberg: Springer, 2004: 60-69. |
| [11] | FERGUS R, PERONA P, ZISSERMAN A. A visual category filter for google images[M]//PAJDLA T, MATAS J. Computer Vision-ECCV 2004. Berlin Heidelberg: Springer, 2004: 242-256. |
| [12] | WANG Meng, LI Hao, TAO Dacheng, et al. Multimodal graph-based reranking for web image search[J]. IEEE transactions on image processing, 2012, 21(11): 4649–4661. DOI:10.1109/TIP.2012.2207397 |
| [13] | DENG Cheng, JI Rongrong, TAO Dacheng, et al. Weakly supervised multi-graph learning for robust image reranking[J]. IEEE transactions on multimedia, 2014, 16(3): 785–795. DOI:10.1109/TMM.2014.2298841 |
| [14] | YANG Xiaopeng, ZHANG Yongdong, YAO Ting, et al. Click-boosting multi-modality graph-based reranking for image search[J]. Multimedia systems, 2015, 21(2): 217–227. DOI:10.1007/s00530-014-0379-8 |
| [15] | HSU W H, KENNEDY L S, CHANG S F. Video search reranking through random walk over document-level context graph[C]//Proceedings of the 15th ACM International Conference on Multimedia. Augsburg, Bavaria, Germany: ACM, 2007: 971-980. |
| [16] | TIAN Xinmei, YANG Linjun, WANG Jingdong, et al. Bayesian video search reranking[C]//Proceedings of the 16th ACM International Conference on Multimedia. Vancouver, Canada: ACM, 2008: 131-140. |
| [17] | ZHOU Dengyong, BOUSQUET O, LAL T N, et al. Learning with local and global consistency[C]//Advances in Neural Information Processing Systems 16. Cambridge, MA: MIT Press, 2004: 321-328. |
| [18] | ZHU XIAOJIN, GHAHRAMANI Z, LAFFERTY J. Semi-supervised learning using gaussian fields and harmonic functions[C]//Proceedings of the Twentieth International Conference on Machine Learning. Washington, DC, USA: ICML, 2003: 912-919. |
| [19] | WANG M, YANG L, HUA X S. MSRA-MM: bridging research and industrial societies for multimedia information retrieval[R]. Microsoft Research Asia. Technology Report, 2009. |
| [20] | JĂRVELIN K, KEKĂLĂINEN J. Cumulated gain-based evaluation of IR techniques[J]. ACM transactions on information systems (TOIS), 2002, 20(4): 422–446. DOI:10.1145/582415.582418 |



