反共振指的是弹性系统在某些特定频率的激励作用下,多自由度系统某些部位出现谐和反应等于零的情形,也就是指在某些频率上系统某些部位的动柔度(导纳)为零[1]。反共振现象得到了许多学者的关注和研究,并得以应用到各种减振设备的设计中。动力反共振隔振器(dynamic anti-resonant vibration isolator)是典型的利用反共振原理的隔振器,最早由W.G.Flannelly[2]于1964年作为一项发明专利提出,他利用杠杆机构并联在弹簧质量块隔振系统中,实现反共振。随后,有关动力反共振隔振器的研究也逐渐增多。Suzuki[3]分析了动力反共振结构在强迫振动下力的幅值和相位的关系,并对动力反共振的结构进行了优化和改进。Jones,Robert等[4]通过理论分析与实验证明了动力反共振隔振器在抑制直升机螺旋桨振动上有十分良好的效果,实现了动力反共振隔振器在实际中的应用。在国内,顾仲权、李五洲、刘劲涛等[5-7]考虑了阻尼在动力反共振结构中的影响,使用Lagrange方程推导了一阶动力反共振结构的力和位移传递比,从理论上分析了动力反共振隔振器相对于一般弹簧阻尼隔振器的优势,并证明反共振频率的大小仅与动力反共振结构参数有关。周为民[8-9]在动力反共振隔振器上增加了主动装置,将被动隔振器改进为主动隔振器,使得反共振频率可以根据激振频率作出变化,保证隔振器的隔振效率,这一研究引入了主动控制,扩大了这类隔振器的使用范围,并进一步拓宽了动力反共振隔振器的研究思路。
实际上,反共振结构不仅仅局限于杠杆结构,惯容器(inerter)是Smith[10]于2001年提出的一种全新的机械结构,能够在隔振器中作为反共振元件,它同弹簧和阻尼器一样是具有两个独立自由端点的元件,其所受的力是与两端的加速度成正比,所产生的惯性力可以抵消一定的弹性力而减少振动传递。从惯容器概念的提出至今,有关惯容器的研究逐渐增多,而且在工业领域上也有了应用,比如汽车、列车的悬架系统等。常用的惯容器形式包括齿轮齿条式,滚珠丝杆式,液压式等,这类惯容器也得到了许多学者的研究[11-12]。Wang等[13]将惯容器作为一种类质量元件,利用理论分析和数值仿真分析了由于惯容器内部摩擦,安装间隙等原因产生的非线性对系统隔振性能的影响。Papageorgiou等[14]则从实验上验证了惯容器非线性对于振动系统的影响,其结果与相关的理论分析一致,说明考虑非线性因素可以提升理论分析的准确性,让理论结果与实验结果更加接近。
目前,关于一般被动隔振器的特性研究比较多见[15],与惯容器有关的实用隔振设备性能研究也有[16],但是有关惯容器结合反共振的新型隔振器理论研究仍然很少。因此,本文在前人的研究基础上,将惯容器作为一种新型反共振结构,探究含有惯容器的动力反共振隔振器的动力学特性,研究惯容器在低频线谱隔振中的作用机理,分析惯容器及其他各元件的参数对于隔振器低频线谱隔振能力影响,以期为隔振器的低频线谱隔振提供新的借鉴和参考。
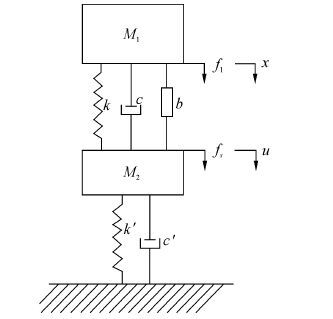
1 含惯容器隔振器的数学模型本文使用一个两自由度的振动系统作为动力反共振隔振器的数学模型,其结构形式如图 1所示。为了更好的模拟隔振器的工作环境,一个自由度系统表示隔振器,而另一个用来代表具有非零刚度的弹性基础。在第一个自由度上,M1表示被隔振设备的质量,k为隔振器的刚度,c为阻尼,b表示惯容器的惯容量,其单位和质量单元的单位一致;在第二个自由度上,M2表示基座的参振质量,c′、k′则用来表示基座的阻尼以及刚度。x、u分别为激励点处和基座处的位移,f为激励力的幅值。该振动系统的动力学方程为(1)所示。在简谐激励力下,经过推导可以得到方程(2)。
| $\left\{ \begin{matrix} {{M}_{1}}\ddot{x}+b\left( \ddot{x}-\ddot{u} \right)+c\left( x\cdot -u\cdot \right)+k\left( x-u \right)={{f}_{1}} \\ {{M}_{2}}\ddot{u}+k\left( u-x \right)+b\left( \ddot{u}-\ddot{x} \right)+c\left( \dot{u}-\dot{x} \right)+{{k}^{\prime }}u+{{c}^{\prime }}u=0 \\ {{M}_{2}}\ddot{u}+k\prime u+{{c}^{\prime }}\dot{u}={{f}_{s}} \\ \end{matrix} \right.$ | (1) |
| $\left[ \begin{matrix} -{{\omega }^{2}}{{M}_{1}}-{{\omega }^{2}}b+jc\omega +k & {{\omega }^{2}}b-jc\omega -k \\ {{\omega }^{2}}b-jc\omega -k & -{{\omega }^{2}}{{M}_{2}}-{{\omega }^{2}}b+j\omega \left( c+c\prime \right)+\left( k+k\prime \right) \\ \end{matrix} \right]\left[ \begin{matrix} x \\ u \\ \end{matrix} \right]=\left[ \begin{matrix} f \\ 0 \\ \end{matrix} \right]$ | (2) |
式(2)为动力反共振隔振器的动力学方程组,通过求解此方程组可解得x和u,从而得到考虑基础非刚性条件下隔振器的基本动力学特性以及隔振性能。但是在实际分析中,为了着重研究某些参数的作用,常常在不影响结果准确性的前提下对式(2)进行适当简化,以便研究。
|
| 图1 隔振器的数学模型示意图 Figure 1 The mathematical model of isolator |
|
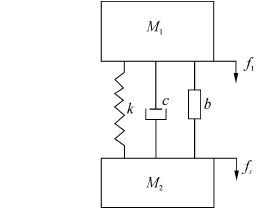
| 图2 隔振器的简化模型 Figure 2 The simplified model of vibration isolator |
从式(2)可以得到结构的位移和力的传递特性,由于位移的传递特性受基座刚度的影响,而力的传递特性只和隔振器的属性有关,因此本文在分析中以力传递特性的研究为主,以力传递率评价隔振器的隔振效果。在隔振器的实际工作中,隔振器基础并非是绝对刚性的,基座处也会存在振动的响应,但是基础的质量相对设备质量而言通常较大,基础刚度相对隔振器而言也较大,即 M1$\ll $M2,k$\ll $k′。因此在分析过程中,通常可以借此对方程进行适当简化而不影响结果的精确性,其简化模型如图 2所示。f1为激励力,fs为基座处的受力。分析中取G(1)为弹簧的弹性力,H(1)为阻尼器的阻尼力,I(1)为惯容器的惯性力,表达式如式(3)所示。因此,简谐激励下该结构模型的动力学方程组为
| $\left\{ \begin{matrix} G\left( 1 \right)=k\left( x-u \right) \\ H\left( 1 \right)=c\left( \dot{x}-\dot{u} \right) \\ I\left( 1 \right)=b\left( \ddot{x}-\ddot{u} \right) \\ \end{matrix} \right.$ | (3) |
| $\left\{ \begin{matrix} {{M}_{1}}\ddot{x}+I\left( 1 \right)+G(1)+H\left( 1 \right)={{f}_{1}} \\ I\left( 1 \right)+G(1)+H\left( 1 \right)={{M}_{2}}\ddot{u} \\ {{f}_{s}}+I\left( 1 \right)+G(1)+H\left( 1 \right)=0 \\ \end{matrix} \right.$ | (4) |
对式(4)进行合并化简可以得到:
| $\frac{{{M}_{1}}{{M}_{2}}\left( \ddot{x}-\ddot{u} \right)}{{{M}_{1}}+{{M}_{2}}}+G\left( 1 \right)+H\left( 1 \right)+I\left( 1 \right)=\frac{{{M}_{2}}{{f}_{1}}}{{{M}_{1}}+{{M}_{2}}}$ | (5) |
在简谐激励下,通过式(5)可以得到位移的中间关系式为
| $x-u=\frac{{{M}_{2}}}{{{M}_{1}}+{{M}_{2}}}{{f}_{1}}-(\frac{{{M}_{1}}{{M}_{2}}}{{{M}_{1}}+{{M}_{2}}}+b){{\omega }^{2}}+jc\omega +k$ | (6) |
将式(6)代入式(4)中,可以得到基座处的受力为
| ${{f}_{s}}=\frac{(-b{{\omega }^{2}}+jc\omega +k)\frac{{{M}_{2}}}{{{M}_{1}}+{{M}_{2}}}{{f}_{1}}}{-(\frac{{{M}_{1}}{{M}_{2}}}{{{M}_{1}}+{{M}_{2}}}+b){{\omega }^{2}}+jc\omega +k}$ | (7) |
根据式(7)可以得到该隔振器的力传递率为
| ${{T}_{f}}=\frac{{{M}_{2}}}{{{M}_{1}}+{{M}_{2}}}\left| \frac{-b{{\omega }^{2}}+jc\omega +k}{-(\frac{{{M}_{1}}{{M}_{2}}}{{{M}_{1}}+{{M}_{2}}}+b){{\omega }^{2}}+jc\omega +k} \right|$ | (8) |
进一步,考虑到M1$\ll $M2,力传递率可简化为
| ${{T}_{f}}=\frac{{{f}_{s}}}{{{f}_{1}}}=\left| \frac{-b{{\omega }^{2}}+jc\omega +k}{-({{M}_{1}}+b){{\omega }^{2}}+jc\omega +k} \right|$ | (9) |
考虑到M1$\ll $M2,经过合理的简化,求解式(4)可以得到含惯容器的动力反共振隔振器的力传递率的表达式(9)。对结构参数赋值后,求解式(9)就可以对隔振器的隔振效果进行分析。
3 含惯容器的隔振器隔振特性计算根据以上分析,对隔振器的各个元件进行赋值,讨论隔振器的隔振特性,选取的隔振器参数如表 1所示。
| 参数类型 | 参数值 |
| M1/kg | 100 |
| M2/kg | 1 000 |
| K/(kN·m-1) | 40 |
| K′/(kN·m-1) | 4 000 |
| b/kg | 10 |
| ζ | 0.1 |
将这些参数分别代入式(9)中,设定激励力的频率范围为0~50 Hz,得到隔振器的力传递率曲线,如图 3所示。力传递率的表达式为TF=20log(1/Tf)=Lf1-Lfs,其中Tf即为式(9)的计算结果,Lf1=20logf1为激励力的力级,Lfs=20logfs为传递到基座处的力级,TF即表示激振力与传递到基座上力的力级之差,该值越大则表示基座受力相对激励力越小,隔振器的隔振效果越好,且该值大于0才表明系统有隔振效果。

|
| 图3 两种隔振器的力传递率随频率变化曲线 Figure 3 Force transmissibility with inerter and no inerter |
根据方程(9)可以求得固有圆频率为ωnf=kM+b,而没有惯容器的普通弹簧质量系统的固有圆频率为ωn=KM,因此,并联惯容器可以使隔振器的固有频率有所降低,其效果相当于增加了隔振设备的质量,而对于隔振器而言,较低的固有频率可以将隔振频带向低频移动,从而获得更好的低频隔振性能。由图 3可见,惯容器隔振器的隔振效果并不是随着激振频率增加而增加,当激振频率处于反共振频率附近时,含有惯容器的隔振器比无惯容器的隔振器具有更好的隔振效果,尤其当激振频率等于反共振频率时,隔振器在该激振频率下隔振效果最好。机电设备工作时往往产生的振动是纯频振动,而且工作环境稳定,激振频率十分集中,调整含惯容器的反共振隔振器的惯容值,使反共振频率接近设备的振动频率,隔振器就能够发挥更好的隔振效果。
另外,从图 3也可以看到,随着激振频率的增加,基于惯容器的动力反共振隔振器的力传递率会趋于平稳,这说明在高频段,惯容器的隔振效果和传统隔振器相比并没有优势,因此,在实际应用中,可针对被隔振设备的振动频段对惯容器进行优化。
4 系统动力学参数对于隔振器的影响由于隔振器的刚度,阻尼器的阻尼值以及惯容器的惯容值对隔振器的动力学性能具有显著影响。为了更好的分析基于惯容器的动力反共振隔振器的隔振性能,以下分别讨论弹簧刚度,阻尼和惯容值等参数的变化对隔振器性能的影响。
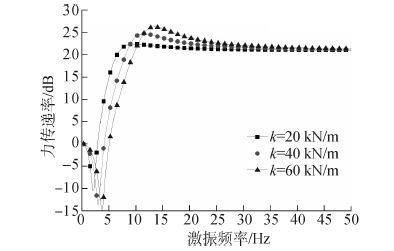
4.1 弹簧刚度对隔振器隔振效果的影响此算例中保持其他参数不变,仅仅改变弹簧的刚度,分析中分别取弹簧刚度为20、40、60 kN/m。弹簧的刚度不同时,隔振器的力传递率会出现较大的差异,如图 4所示。
|
| 图4 不同刚度下隔振器的力传递率 Figure 4 Force transmissibility in different spring stiffness |
降低弹簧刚度可以减小隔振器的固有频率,这与普通的隔振器是一致的,同时动力反共振隔振器的反共振频率也会降低。但是弹簧刚度对于反共振频率处力传递率的值影响不大,而且随着激振频率的增加,不同弹簧刚度下隔振效果的差异逐渐减小,高频段趋于一致。另一方面值得注意是弹簧刚度降低后,系统的稳定性也会受到一定影响。
4.2 阻尼对隔振器隔振效果的影响在小阻尼隔振系统中,阻尼的主要作用是衰减沿结构传递的振动能量,减小共振频率附近的振动响应,以及降低结构自由振动。分析中改变隔振器中阻尼器的阻尼值,分别取隔振器的阻尼比为0.1、0.15、0.2,其他参数保持不变,力传递率变化曲线如图 5所示。

|
| 图5 不同阻尼下隔振器的力传递率 Figure 5 Force transmissibility in different damp |
从图 5中可见,结构振动在共振频率处最明显,因此,阻尼越大,共振频率处的力传递率会变大。同样,较大的阻尼抑制了惯容器的反共振,因此在反共振频率处,力传递率也会降低。较大的阻尼会抑制共振频率处的振动传递,也会降低反共振频率处的隔振效果,同时对高频的隔振效果也有一定影响。
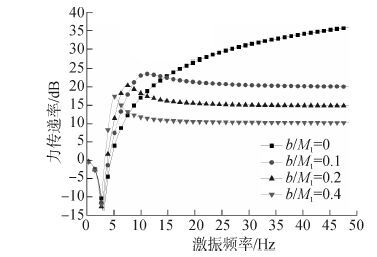
4.3 惯容器对隔振器隔振效果的影响惯容器是该动力反共振隔振器的核心部件,它的惯容值大小直接影响隔振器的动力学特性,算例中分别取惯容值与隔振质量的比值b/M1为0、0.1、0.2、0.4,取零时表明隔振器中无惯容,其他参数不变,图 6给出不同惯容器惯容值下的力传递率曲线。
|
| 图6 不同惯容下隔振器的力传递率 Figure 6 Force transmissibility in different inerter |
根据图 6中的结果,并结合式(9)可以发现当惯容器的惯容值变大时,隔振器的共振频率f会减小。隔振器的隔振频段下限一般是2f,随着惯容值的增大,隔振器的有效隔振频段会向低频移动,使得隔振器的隔振频段更宽。另一方面,惯容值越大,反共振频率也会减小,但是反共振频率处的隔振效果会减弱,也会使高频隔振的效果降低。在保证隔振频带带宽足够的前提下,可以适当降低惯容值,保证反共振频率处良好的隔振效果。
5 结论本文设计了一种基于惯容器的动力反共振隔振器,将惯容器与弹簧、阻尼单元并联实现动力反共振隔振,分析了该动力反共振隔振器的基本动力学特性和隔振性能,讨论了隔振器中各参数对隔振器隔振效果的影响。基于本文的研究,可以得到以下结论:
1) 在隔振系统中加入惯容器可以降低隔振系统的固有频率,从而获得更好的低频隔振性能;同时产生一个反共振频率,在此频率附近含有惯容器的隔振器比无惯容器的隔振系统具有更好的隔振效果。
2) 基于惯容器的动力反共振隔振系统在高频段相对一般的隔振器优势不明显,该隔振器主要用于低频的线谱振动,当激励源频率接近反共振频率时具有最好的隔振效果。
3) 隔振器中的弹簧刚度会改变共振频率和反共振频率,刚度越大,隔振器的共振频率和反共振频率越大。在高频处,弹簧刚度的改变对隔振器的隔振效果没有很大的影响。
4) 阻尼在隔振器中起到抑制共振的作用,较大的阻尼不仅会抑制共振频率处的共振,也会降低反共振频率处的隔振性能。在其他激振频率下,阻尼效果不明显。
5) 惯容器的惯容大小直接影响动力反共振隔振器的隔振效果。惯容器惯容值越大,共振频率越小,隔振频带越宽,但是较大的惯容会降低隔振器反共振频率处以及高频的隔振效果。在保证有效隔振频段带宽的前提下,可以适当降低惯容值以获得更好的纯频隔振效果。
在接下来的研究中,隔振器中的非线性因素的影响以及实验工作也会进行。本文的研究工作对设备低频线谱隔振设计和分析提供了新的思路和方法,具有一定的借鉴意义。
| [1] |
方同. 多自由度系统中的反共振[J].
力学学报, 1979(4): 360–366.
FANG Tong. Antiresonances in multi-degree-of-freedom systems[J]. Chinese journal of theoretical and applied mechanics, 1979(4): 360–366. |
| [2] | FLANNELLY W G. Dynamic antiresonant vibration isolator: America, 3322379[P]. 1964. |
| [3] | SUZUKI H. Dynamic antiresonant vibration isolator[J]. Bulletin of the college of engineering, Hosei university, 1983, 19: 55–61. |
| [4] | JONES R, MCGARVEY J. Helicopter rotor isolation evaluation utilizing the dynamic antiresonant vibration isolator: SAE Technical Paper 760894[R].: SAE, 1976. http://cn.bing.com/academic/profile?id=2035783226&encoded=0&v=paper_preview&mkt=zh-cn |
| [5] |
顾仲权. 动力反共振隔振[J].
噪声与振动控制, 1989(6): 36–40.
GU Zhongquan. Dynamic anti-resonance isolation[J]. Noise and vibration control, 1989(6): 36–40. |
| [6] |
李五洲. 反共振隔振装置隔振原理分析[J].
直升机技术, 2004(1): 6–8.
LI Wuzou. The Isolation principle analysis on anti-resonance isolator[J]. Helicopter technique, 2004(1): 6–8. |
| [7] |
刘劲涛, 李小号, 高洪波, 等. 单质体反共振隔振振动机械的理论及应用[J].
东北大学学报: 自然科学版, 2011, 32(5): 724–727.
LIU Jintao, LI Xiaohao, GAO Hongbo, et al. Theory and application of single-mass anti-resonance vibration isolation vibration machinery[J]. Journal of Northeastern University: Natural Science, 2011, 32(5): 724–727. |
| [8] |
周为民, 顾仲权. 主动反共振隔振装置的研究(一)理论分析与优化设计[J].
南京航空航天大学学报, 1989, 21(3): 1–8.
ZHOU Weimin, GU Zhongquan. Research on active dynamic antiresonant vibration isolator-part 1 theoretical analysis and optimization design[J]. Journal of Nanjing aeronautical institute, 1989, 21(3): 1–8. |
| [9] |
周为民, 顾仲权. 主动反共振隔振装置的研究(二)试验研究[J].
南京航空航天大学学报, 1989, 21(4): 1–6.
ZHOU Weimin, GU Zhongquan. Research on active dynamic antiresonant vibration isolator-part 2 experimental study[J]. Journal of Nanjing aeronautical institute, 1989, 21(4): 1–6. |
| [10] | SMITH M C. Synthesis of mechanical networks: the inerter[J]. IEEE transactions on automatic control, 2002, 47(10): 1648–1662. DOI:10.1109/TAC.2002.803532 |
| [11] |
陈龙, 沈钰杰, 杨晓峰, 等. 基于惯容器-弹簧结构体系的车辆悬架结构设计与试验[J].
振动与冲击, 2014, 33(22): 83–87.
CHEN Long, SHEN Yujie, YANG Xiaofeng, et al. Design and experiment of vehicle suspension based on inerter-spring structure[J]. Journal of vibration and shock, 2014, 33(22): 83–87. |
| [12] |
杜甫, 毛明, 陈轶杰, 等. 基于动力学模型与参数优化的ISD悬架结构设计及性能分析[J].
振动与冲击, 2014, 33(6): 59–65.
DU Fu, MAO Ming, CHEN Yijie, et al. Structure design and performance analysis of inerter-spring-damper suspension structure based on dynamic model and parameter optimization[J]. Journal of vibration and shock, 2014, 33(6): 59–65. |
| [13] | WANG Fucheng, SU Weijun. Impact of inerter nonlinearities on vehicle suspension control[J]. Vehicle system dynamics, 2008, 46(7): 575–595. DOI:10.1080/00423110701519031 |
| [14] | PAPAGEORGIOU C, HOUGHTON N E, SMITH M C. Experimental testing and analysis of inerter devices[J]. Journal of dynamic systems, measurement, and control, 2009, 131(1): 011001. DOI:10.1115/1.3023120 |
| [15] |
闫振华, 王国强, 苏丽达, 等. 非线性被动隔振器刚度特性研究[J].
振动与冲击, 2013, 32(19): 139–143.
YAN Zhenhua, WANG Guoqiang, SU Lida, et al. Stiffness characteristics of a non-linear passive vibration isolator[J]. Journal of vibration and shock, 2013, 32(19): 139–143. |
| [16] |
陈龙, 杨晓峰, 汪若尘, 等. 基于二元件ISD结构隔振机理的车辆被动悬架设计与性能研究[J].
振动与冲击, 2013, 32(6): 90–95.
CHEN Long, SHEN Xiaofeng, WANG Ruochen, et al. Design and performance study of vehicle passive suspension based on two-element inerter-spring-damper structure vibration isolation mechanism[J]. Journal of vbiration and shock, 2013, 32(6): 90–95. |



